A Laser Damage Threshold for Microscope Glass Slides
Abstract
:1. Introduction
2. Materials and Methods
2.1. Microscope Glass Slides
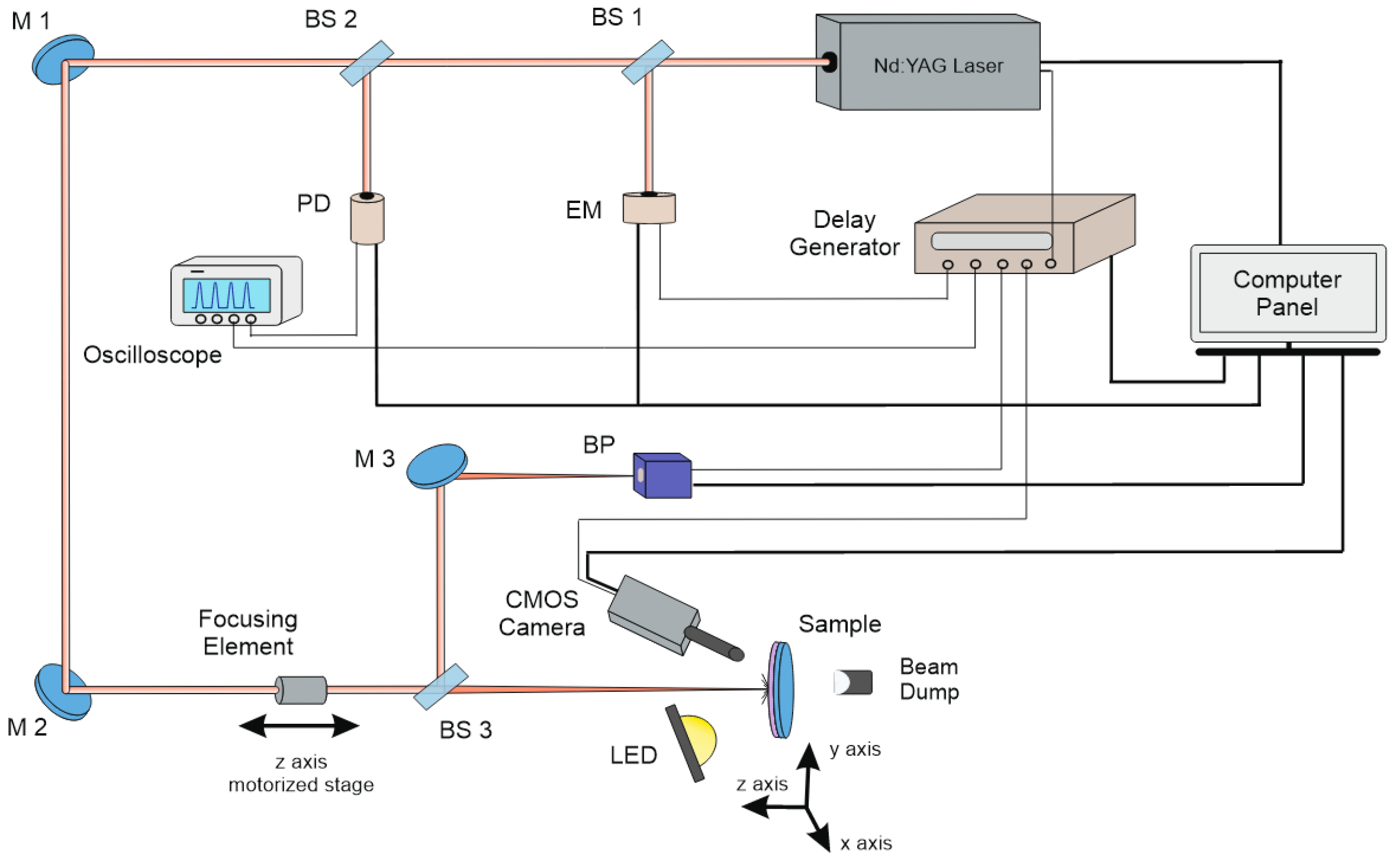
2.2. The LIDT Measurement System
2.2.1. Beam Diagnostics
2.2.2. Real-Time Damage Detection
2.3. The S-on-1 Test Method Summary
2.4. Cleaning
3. Results
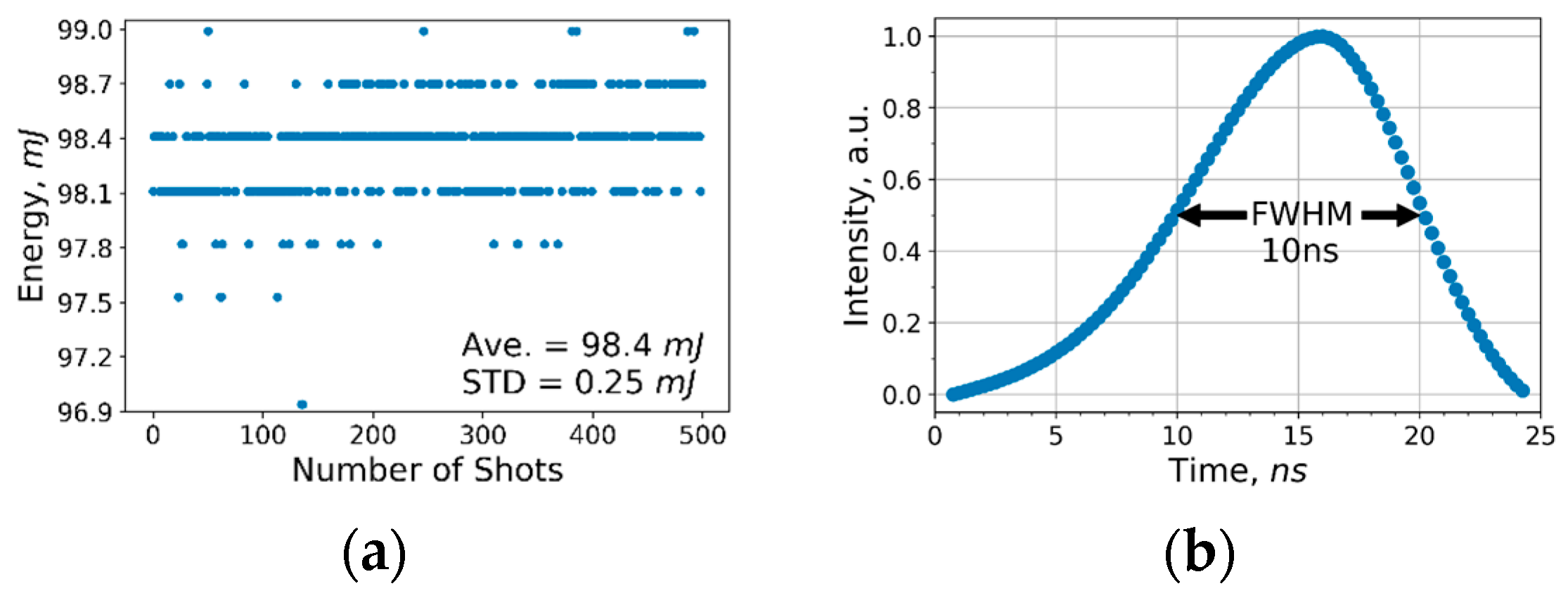
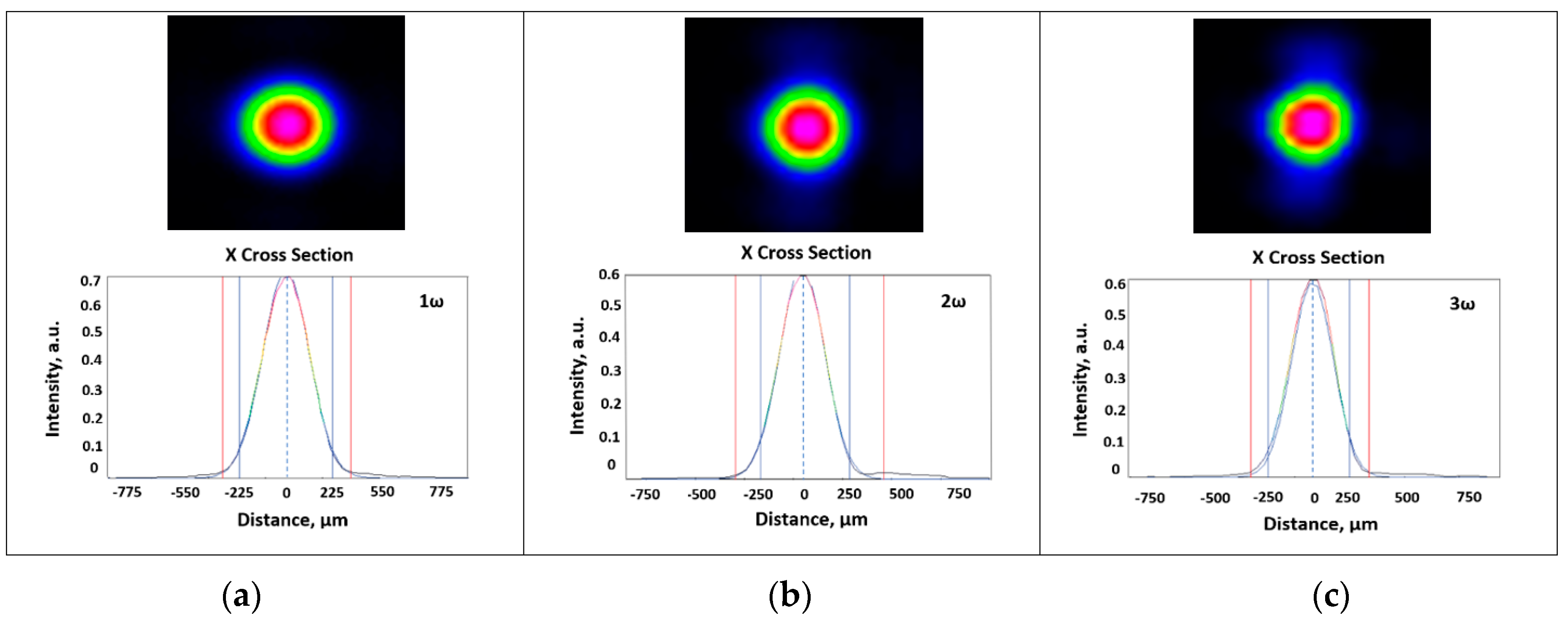
3.1. The Test System Characterization
3.1.1. Stability of Energy and Temporal Profile of Typical Pulses
3.1.2. Spatial Beam Profile
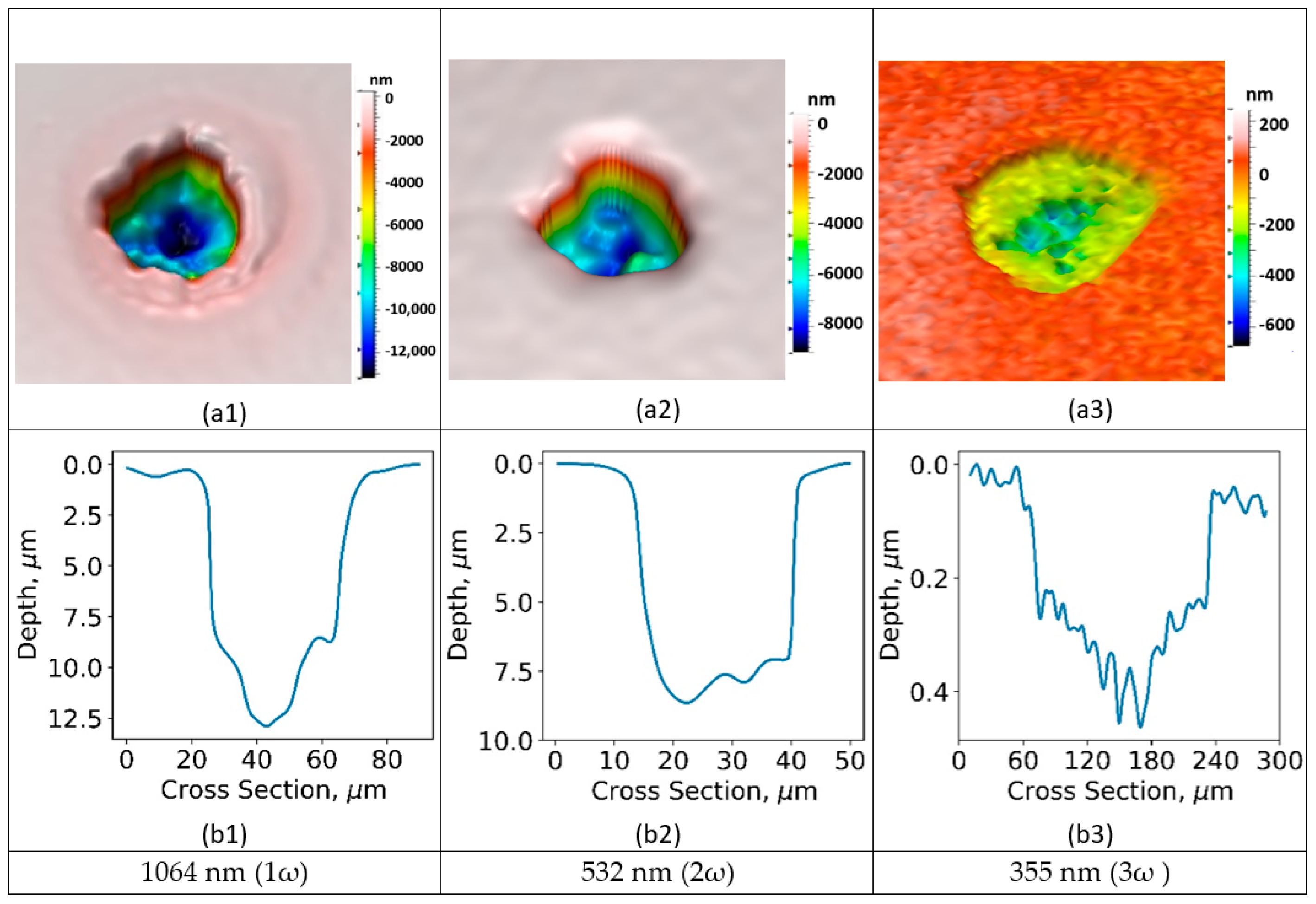
3.2. The LIDT Test Results
3.2.1. Damage Morphology
3.2.2. Characteristic Damage Curves
3.2.3. Measurement Uncertainty
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wan, Z.; Nguyen, N.; Gao, Y.; Li, Q. Laser-induced graphene for biosensors. Sustain. Mater. Technol. 2020, 25, e00205. [Google Scholar] [CrossRef]
- Mukundan, H.; Anderson, A.S.; Grace, W.K.; Grace, K.M.; Hartman, N.; Martinez, J.S.; Swanson, B.I. Waveguide-Based Biosensors for Pathogen Detection. Sensors 2009, 9, 5783–5809. [Google Scholar] [CrossRef]
- Ming, Y.; Hao, S.; Wang, F.; Lewis-Israeli, Y.R.; Volmert, B.D.; Xu, Z.; Goestenkors, A.; Aguirre, A.; Zhou, C. Longitudinal morphological and functional characterization of human heart organoids using optical coherence tomography. Biosens Bioelectron. 2022, 207, 114136. [Google Scholar] [CrossRef] [PubMed]
- Kwaśny, M.; Bombalska, A. Applications of Laser-Induced Fluorescence in Medicine. Sensors 2022, 22, 2956. [Google Scholar] [CrossRef]
- Papp, Z.F.; Demel, U.; Tilz, G.P. Laser scanning confocal fluorescence microscopy: An overview. Int. Immunopharmacol. 2003, 3, 1715–1729. [Google Scholar] [CrossRef]
- Wood, R.M. Damage Theory. In Laser-Induced Damage of Optical Materials, 1st ed.; Brown, R.G.W., Pike, E.R., Eds.; Institute of Physics Publishing: Bristol, UK; Philadelphia, PA, USA, 2003; pp. 54–99. [Google Scholar]
- ISO (International Organization for Standardization). Lasers and Laser-Related Equipment—Test Methods for Laser-Radiation-Induced Damage Threshold—Part 1: Definitions and General Principles; ISO 21254-1; ISO: Geneva, Switzerland, 2011. [Google Scholar]
- ISO (International Organization for Standardization). Lasers and Laser-Related Equipment—Test Methods for Laser-Radiation-Induced Damage Threshold—Part 2: Threshold Determination; 21254-2; ISO: Geneva, Switzerland, 2011. [Google Scholar]
- ISO (International Organization for Standardization). Lasers and Laser-Related Equipment—Test Methods for Laser-Radiation-Induced Damage Threshold—Part 3: Assurance of Laser Power (Energy) Handling Capabilities; 21254-3; ISO: Geneva, Switzerland, 2011. [Google Scholar]
- ISO (International Organization for Standardization). Lasers and Laser-Related Equipment—Test Methods for Laser-Radiation-Induced Damage Threshold—Part 4: Inspection, Detection and Measurement; 21254-4; ISO: Geneva, Switzerland, 2011. [Google Scholar]
- Stratan, A.; Zorila, A.; Rusen, L.; Simion, S.; Blanaru, C.; Fenic, C.; Neagu, L.; Nemes, G. Automated test station for laser-induced damage threshold measurements according to ISO 21254-1,2,3,4 standards. In Laser-Induced Damage in Optical Materials: 2012; SPIE: Bellingham, WA, USA, 2012; Volume 85301, pp. 85301Y-1–85301Y-9. [Google Scholar] [CrossRef]
- Melninkaitis, A.; Miksys, D.; Balciunas, T.; Balachninaite, O.; Rakickas, T.; Grigonis, R.; Sirutkaitis, V. Automated test station for laser-induced damage threshold measurements according to ISO 11254-2 standard. In Laser Beam Control and Applications; SPIE: Bellingham, WA, USA, 2006; Volume 6101, pp. 61011J-1–61011J-10. [Google Scholar] [CrossRef]
- Ma, B.; Zhang, Y.; Ma, H.; Liu, H.; Ji, Y. Automated laser damage threshold test systems of different test modes for optical elements. In Laser-Induced Damage in Optical Materials: 2012; SPIE: Bellingham, WA, USA, 2012; Volume 8530, pp. 85301P-1–85301P-8. [Google Scholar] [CrossRef]
- Allenspacher, P.; Riede, W.; Wernham, D.; Capanni, A.; Era, F. Vacuum laser damage test bench. In Laser-Induced Damage in Optical Materials: 2005; SPIE: Bellingham, WA, USA, 2005; Volume 5991, pp. 599128-1–599128-9. [Google Scholar] [CrossRef]
- Riede, W.; Allenspacher, P.; Schrröder, H.; Wernham, D.; Lien, Y. Laser-induced hydrocarbon contamination in vacuum. In Laser-Induced Damage in Optical Materials: 2005; SPIE: Bellingham, WA, USA, 2005; Volume 5991, pp. 59910H-1–59910H-13. [Google Scholar] [CrossRef]
- Zhu, C.; Liang, L.; Yuan, H.; Zhou, L.; Li, Y.; Wang, W. Investigation of stress wave and damage morphology growth generated by laser-induced damage on rear surface of fused silica. Opt. Express 2020, 28, 3942–3951. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Xiang, X.; Yuan, X.; Zheng, W.; He, S.; Lv, H.; Yan, Z.; Wang, H.; Liao, W.; Miao, X.; et al. Bulk damage and stress behavior of fused silica irradiated by nanosecond laser. Opt. Eng. 2014, 53, 047103. [Google Scholar] [CrossRef]
- Ma, B.; Ma, H.; Jiao, H.; Cheng, X.; Wang, Z. Damage growth characteristics of different initial damage sites of fused silica under 355nm small laser beam irradiation. Opt. Laser Technol. 2014, 57, 136–144. [Google Scholar] [CrossRef]
- Dahmani, F.; Lambropoulos, J.C.; Schmid, A.W.; Papernov, S.; Burns, S.J. Crack arrest and stress dependence of laser-induced surface damage in fused-silica and borosilicate glass. Appl. Opt. 1999, 38, 6892–6903. [Google Scholar] [CrossRef]
- Shi, Z.; Sun, L.; Shao, T.; Liu, H.; Huang, J.; Ye, X.; Wang, F.; Yang, L.; Zheng, W. Statistically Correlating Laser-Induced Damage Performance with Photothermal Absorption for Fused Silica Optics in a High-Power Laser System. Photonics 2022, 9, 137. [Google Scholar] [CrossRef]
- Jee, Y.; Becker, M.F.; Walser, R.M. Laser-induced damage on single-crystal metal surfaces. J. Opt. Soc. Am. B Opt. Phys. 1988, 5, 648–659. [Google Scholar] [CrossRef]
- Ma, B.; Wang, K.; Han, J.; Zhang, Z.; Cheng, X. Difference in laser-induced damage behavior between back and front surfaces. Laser Phys. 2020, 30, 036003. [Google Scholar] [CrossRef]
- Scheer, U. Historical roots of centrosome research: Discovery of Boveri’s microscope slides in Würzburg. Phil. Trans. R. Soc. B 2014, 369, 20130469. [Google Scholar] [CrossRef]
- Wilson, C.R.; Hutchens, T.C.; Busse, L.E.; Frantz, H.A.; Shaw, L.B.; Sanghera, J.S.; Aggarwal, I.D. Antireflective structured surfaces on soda-lime windows for high power laser applications. In Advanced Optics for Imaging Applications: UV through LWIR V; SPIE: Bellingham, WA, USA, 2020; Volume 11403, pp. 114030H-1–114030H-5. [Google Scholar] [CrossRef]
- Melninkaitis, A.; Rakickas, T.; Miksys, D.; Grigonis, R.; Sirutkaitis, V.; Skrebutenas, A.; Buzelis, R.D.; Abromavicius, G.; Juskenas, R.; Selskis, A. Effect of deposition method and substrate surface quality on laser-induced damage threshold for repetitive 13-ns and 130-fs pulses. In Laser-Induced Damage in Optical Materials: 2004; SPIE: Bellingham, WA, USA, 2004; Volume 5647, pp. 43–52. [Google Scholar] [CrossRef]
- Bingelyte, V.; Sirutkaitis, V.; Eckardt, R.C. S-on-1-induced damage thresholds of high-reflection metallic coatings at 1064 nm. In Laser-Induced Damage in Optical Materials: 2002, Proceedings of the 7th International Workshop on Laser Beam and Optics Characterization, San Diego, CA, USA, 22–23 August 2003; SPIE: Bellingham, WA, USA, 2002; Volume 4932, pp. 513–519. [Google Scholar] [CrossRef]
- Jensen, L.; Mrohs, M.; Gyamfi, M.; Mädebach, H.; Ristau, D. Higher certainty of the laser-induced damage threshold test with a redistributing data treatment. Rev. Sci. Instrum. 2015, 86, 103106. [Google Scholar] [CrossRef]
- Liu, J.M. Simple technique for measurements of pulsed Gaussian-beam spot sizes. Opt. Lett. 1982, 7, 196–198. [Google Scholar] [CrossRef]
- Rastogi, V.; Chaurasia, S.; Munda, D.S. Laser induced damage studies in borosilicate glass using nanosecond and sub nanosecond pulses. J. Non Cryst. Solids 2017, 463, 138–147. [Google Scholar] [CrossRef]
- Stuart, B.C.; Feit, M.D.; Rubenchik, A.M.; Shore, B.W.; Perry, M.D. Laser-Induced Damage in Dielectrics with Nanosecond to Subpicosecond Pulses. Phys. Rev. Lett. 1995, 74, 2248–2251. [Google Scholar] [CrossRef]
- Stuart, B.C.; Feit, M.D.; Herman, S.; Rubenchik, A.M.; Shore, B.W.; Perry, M.D. Nanosecond-to-femtosecond laser-induced breakdown in dielectrics. Phys. Rev. B 1996, 53, 1749–1761. [Google Scholar] [CrossRef]
- Vogel, A.; Busch, S.; Jungnickel, K.; Birngruber, R. Mechanisms of intraocular photodisruption with picosecond and nanosecond laser pulses. Lasers Surg. Med. 1994, 15, 32–43. [Google Scholar] [CrossRef]
- Chen, X.Q.; Zu, X.-T.; Zheng, W.-G.; Jiang, X.D.; Lü, H.B.; Ren, H.; Zhang, Y.Z.; Liu, C.M. Experimental research of laser-induced damage mechanism of the sol-gel SiO2 and IBSD SiO2 thin films. Acta Phys. Sin. 2006, 55, 1201–1206. [Google Scholar] [CrossRef]
- Kuzuu, N.; Yoshida, K.; Yoshida, H.; Kamimura, T.; Kamisugi, N. Laser-induced bulk damage in various types of vitreous silica at 1064, 532, 355, and 266 nm: Evidence of different dam-age mechanisms between 266-nm and longer wavelengths. Appl. Opt. 1999, 38, 2510–2515. [Google Scholar] [CrossRef]
- Ma, B.; Ma, H.; Jiao, H.; Cheng, X.; Wang, Z. Laser-damage growth characteristics of fused silica under 1064- and 532-nm laser irradiation. Opt. Eng. 2013, 52, 116106. [Google Scholar] [CrossRef]
- Zhang, L.; Ma, B.; Wang, K.; Jiao, X.; Cheng, X.; Wang, Z. Morphology and growth properties of nano- and submicrometer-scale initial damage sites under 355 nm wavelength pulsed laser irradiation. Appl. Opt. 2018, 57, 3166–3171. [Google Scholar] [CrossRef]
- Norton, M.A.; Adams, J.J.; Carr, C.W.; Donohue, E.E.; Feit, D.M.; Hackel, R.P.; Hollingsworth, W.G.; Jarboe, A.J.; Matthews, M.J.; Rubenchik, A.M.; et al. Growth of laser damage in fused silica: Diameter to depth ratio. In Laser-Induced Damage in Optical Materials: 2007; SPIE: Bellingham, WA, USA, 2007; Volume 6720, pp. 67200H-1–67200H-10. [Google Scholar] [CrossRef]
- Zhang, F.; Miao, X.; Wang, B.; Liu, X.; Xu, M.; Liu, H.; Lü, T.; Qiu, R.; Guo, D.; Zhou, Q. Nanosecond laser-induced multi-focusing damage in the bulk of fused silica. Opt. Commun. 2023, 533, 129305. [Google Scholar] [CrossRef]



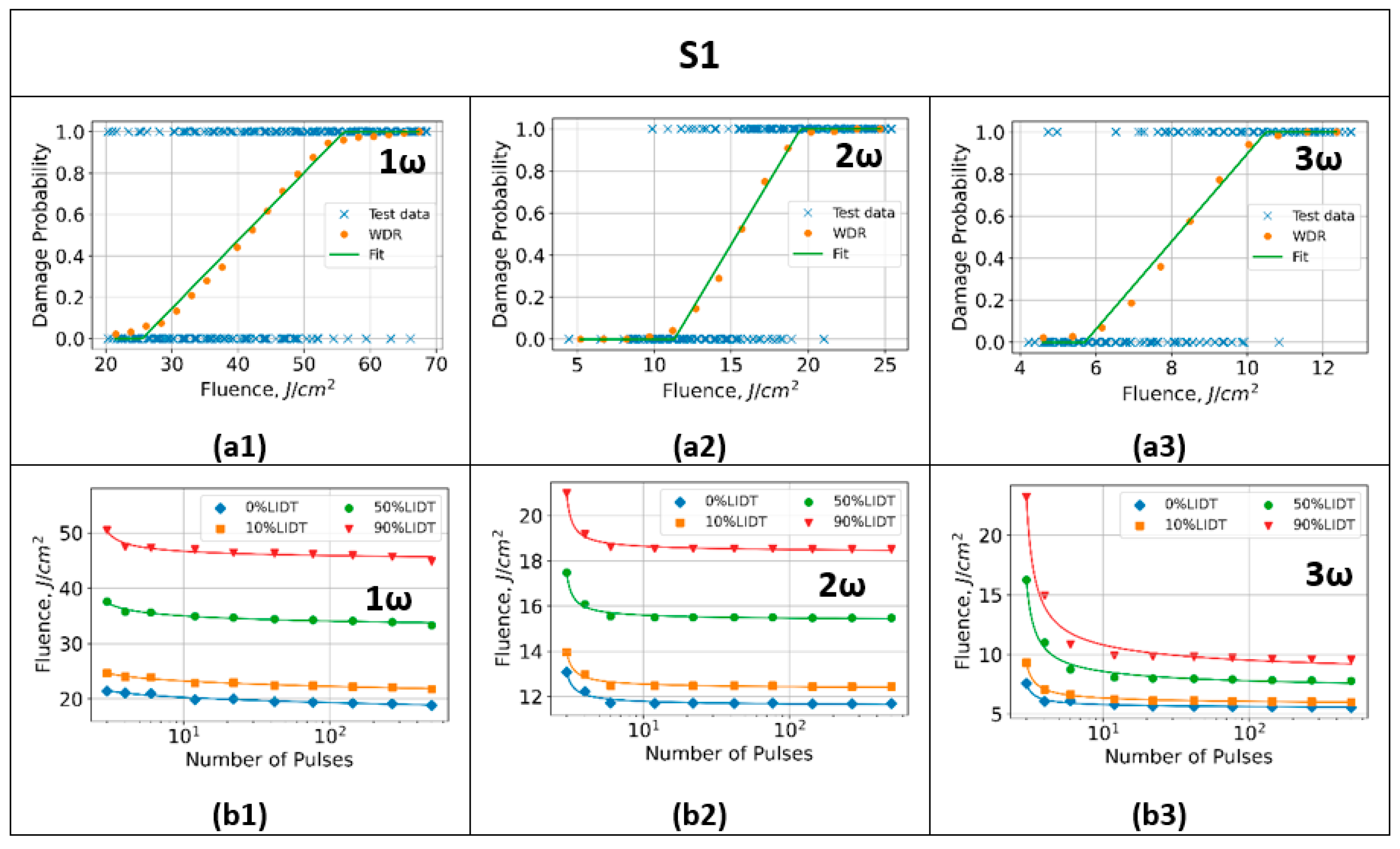
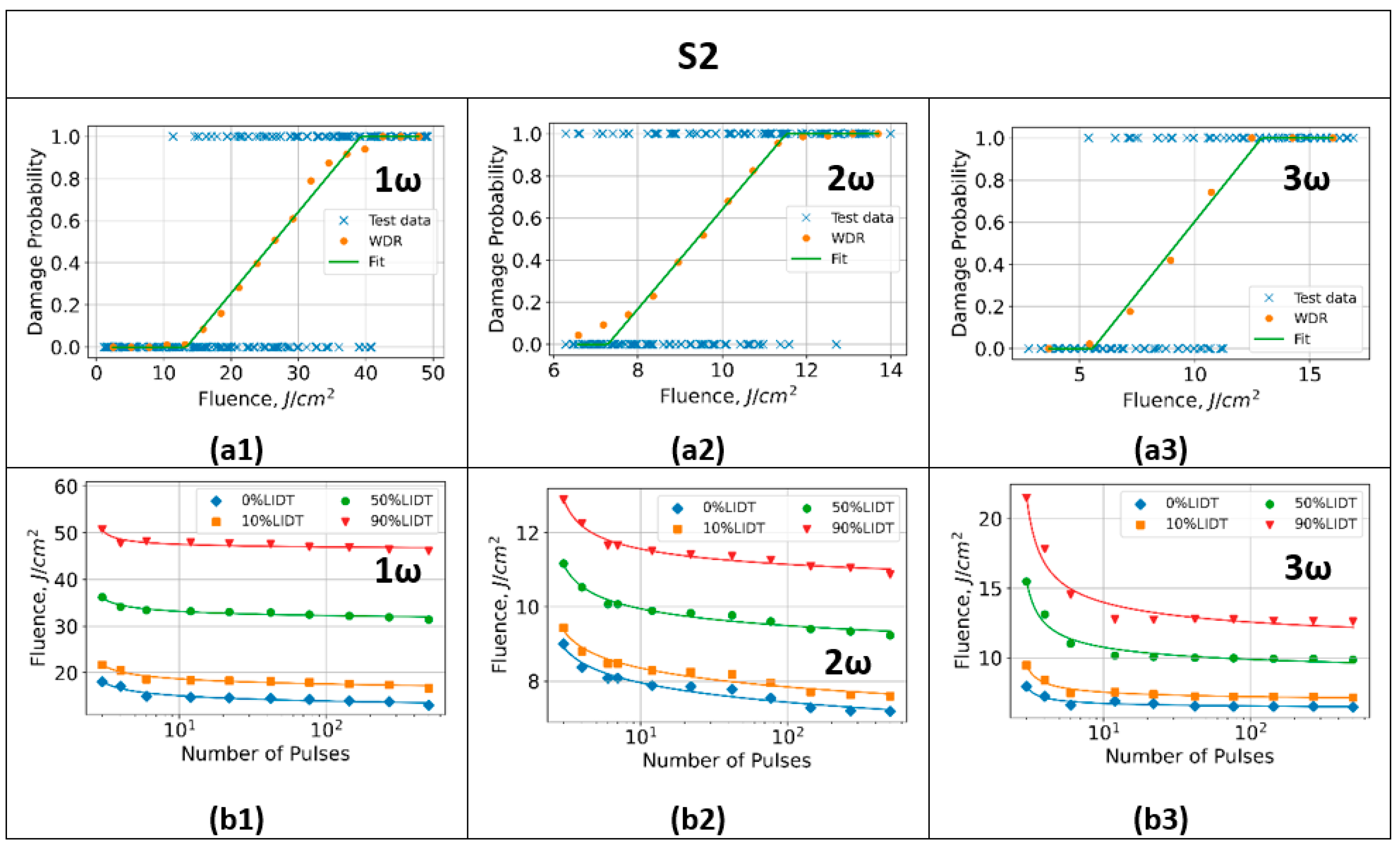
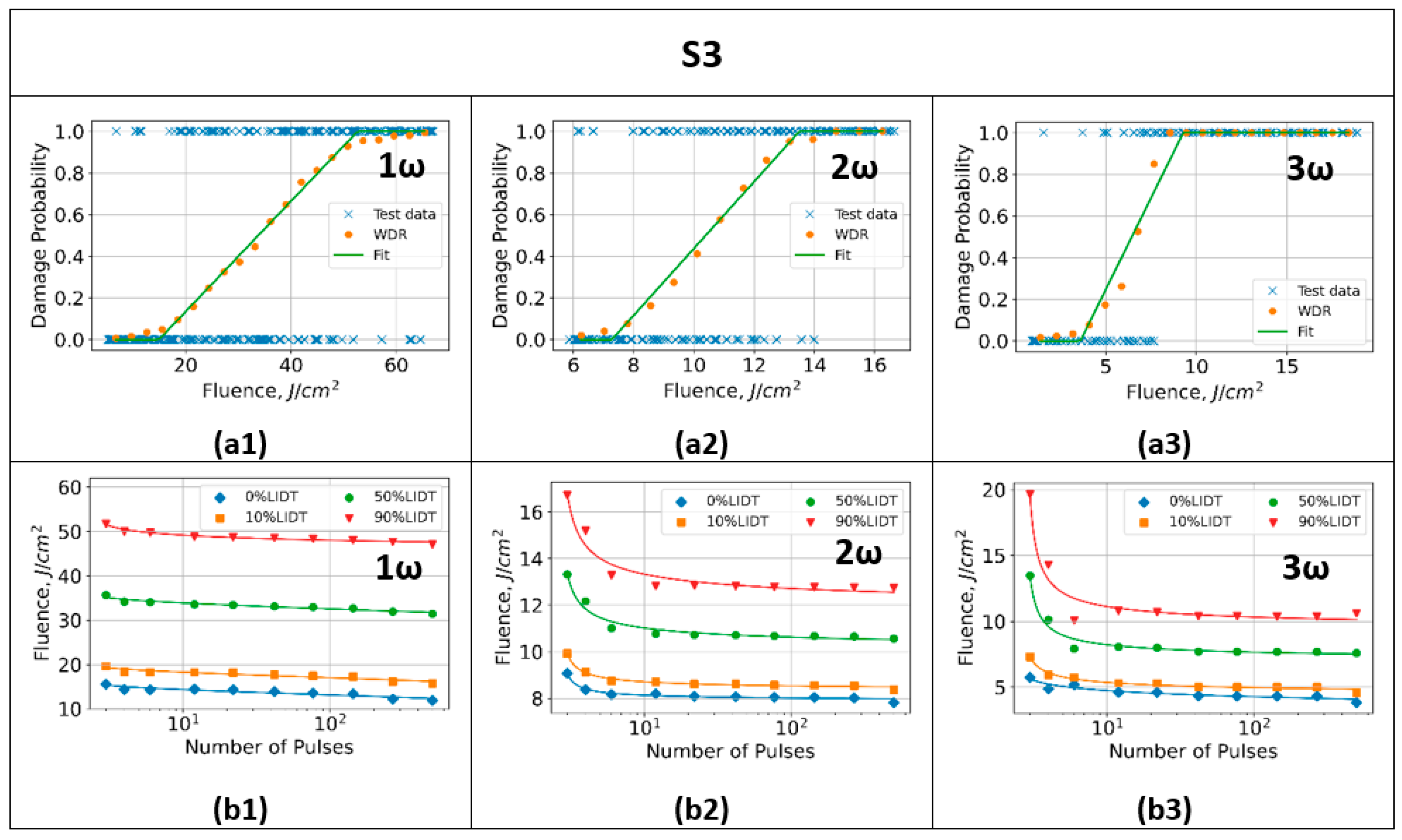
| Wavelength (nm) | Output Energy (mJ) | Energy Stability (StdDev, %) | Spot Size (μm) | Spot Area (10−4 cm2) | Maximum Fluence (J/cm)2 | |
|---|---|---|---|---|---|---|
| 1064 | 150 | <0.5 | 1.6 | 453 | 8.1 | 3820 |
| 532 | 60 | <1.5 | 1.7 | 502 | 9.9 | 1528 |
| 355 | 37 | <2.0 | 2.2 | 503 | 9.9 | 236 |
| S1 LIDT (J/cm)2 | S2 LIDT (J/cm)2 | S3 LIDT (J/cm)2 | |
|---|---|---|---|
| 1064 nm | 19.3 ± 0.9 | 14.0 ± 0.9 | 13.4 ± 2.2 |
| 532 nm | 11.7 ± 0.5 | 7.5 ± 0.9 | 8.0 ± 1.3 |
| 355 nm | 8.6 ± 0.8 | 6.5 ± 0.7 | 4.5 ± 2.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tüzün, P.; Kadı, Ö.F.; Yıldız, F.; Hamid, R.; Nasibov, H. A Laser Damage Threshold for Microscope Glass Slides. Photonics 2023, 10, 967. https://doi.org/10.3390/photonics10090967
Tüzün P, Kadı ÖF, Yıldız F, Hamid R, Nasibov H. A Laser Damage Threshold for Microscope Glass Slides. Photonics. 2023; 10(9):967. https://doi.org/10.3390/photonics10090967
Chicago/Turabian StyleTüzün, Pervin, Ömer Faruk Kadı, Fikret Yıldız, Ramiz Hamid, and Humbat Nasibov. 2023. "A Laser Damage Threshold for Microscope Glass Slides" Photonics 10, no. 9: 967. https://doi.org/10.3390/photonics10090967
APA StyleTüzün, P., Kadı, Ö. F., Yıldız, F., Hamid, R., & Nasibov, H. (2023). A Laser Damage Threshold for Microscope Glass Slides. Photonics, 10(9), 967. https://doi.org/10.3390/photonics10090967





