Synthetic Mueller Imaging Polarimetry

Abstract

The transformation of the state of polarization of a light beam via its linear interaction with a material medium can be modeled through the Stokes–Mueller formalism. The Mueller matrix associated with a given interaction depends on many aspects of the measurement configuration. In particular, different Mueller matrices can be measured for a fixed material sample depending on the spectral profile of the light probe. For a given light probe and a given sample with inhomogeneous spatial behavior, the polarimetric descriptors of the point-to-point Mueller matrices can be mapped, leading to respective polarimetric images. The procedure can be repeated sequentially using light probes with different central frequencies. In addition, the point-to-point Mueller matrices, consecutively measured, can be combined synthetically through convex sums leading to respective new Mueller matrices, in general with increased polarimetric randomness, thus exhibiting specific values for the associated polarimetric descriptors, including the indices of polarimetric purity, and generating new polarimetric images which are different from those obtained from the original Mueller matrices. In this work, the fundamentals for such synthetic generation of additional polarimetric images are described, providing a new tool that enhances the exploitation of Mueller polarimetry.

1. Introduction

Nowadays, Mueller imaging polarimetry constitutes a mature set of technologies and procedures with an enormous variety of applications that, among many others, cover areas like analysis of biological tissues [1,2] and remote sensing [3,4,5].

Once the point-to-point Mueller matrices of a given sample have been measured, the mathematical treatment of the information obtained is crucial for its exploitation. In fact, the methods used for the serial or parallel decompositions of the measured Mueller matrices as well as for the identification of significant physical descriptors related to the enpolarizing, retarding and depolarizing properties of the sample stand out in polarimetry.

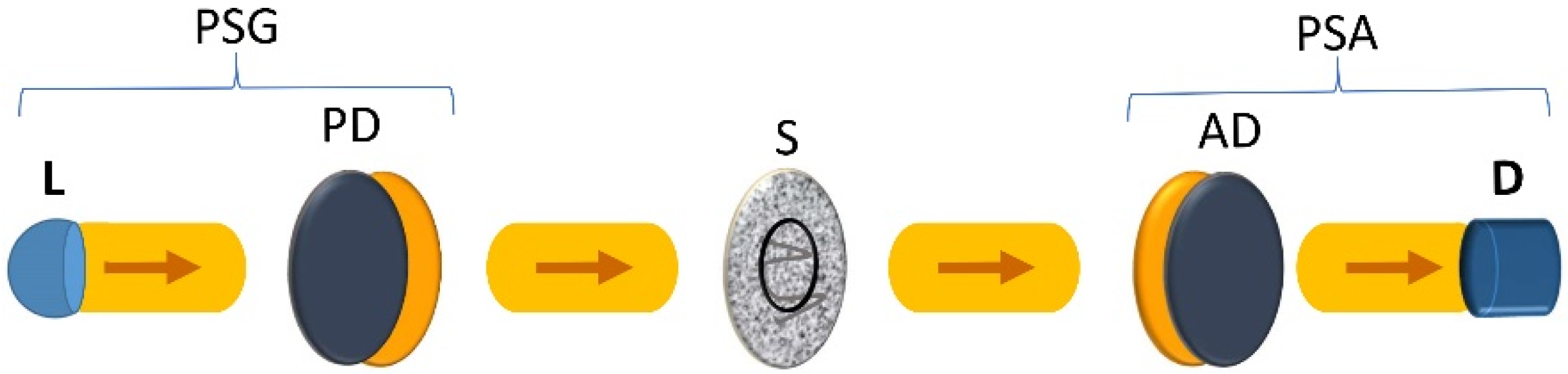
Mueller polarimeters are composed of (see Figure 1) [6,7,8,9,10,11,12,13,14,15,16]

• A collimated light source with a fixed spectral profile.
• A polarization state generator (PSG) that modulates the state of a polarization incident on the material sample.
• A setup for the appropriate placement and relative orientation of the material sample on which the light probe beam impinges.
• A polarization state analyzer (PSA) that modulates the state of polarization of the light probe after its interaction with the sample.
• A detection, record and processing device that allows the measurement of the intensity of the light probe after passing through the PSG, the sample and the PSA.

Specific Mueller polarimeters are designed for their operation on samples with a homogeneous behavior over the cross-section covered by the light probe, in which case a single Mueller matrix is obtained for each measurement, while the so-called imaging Mueller polarimeters are designed for the measurement of the point-to-point Mueller matrices covering a certain area of the sample with heterogeneous spatial behavior.

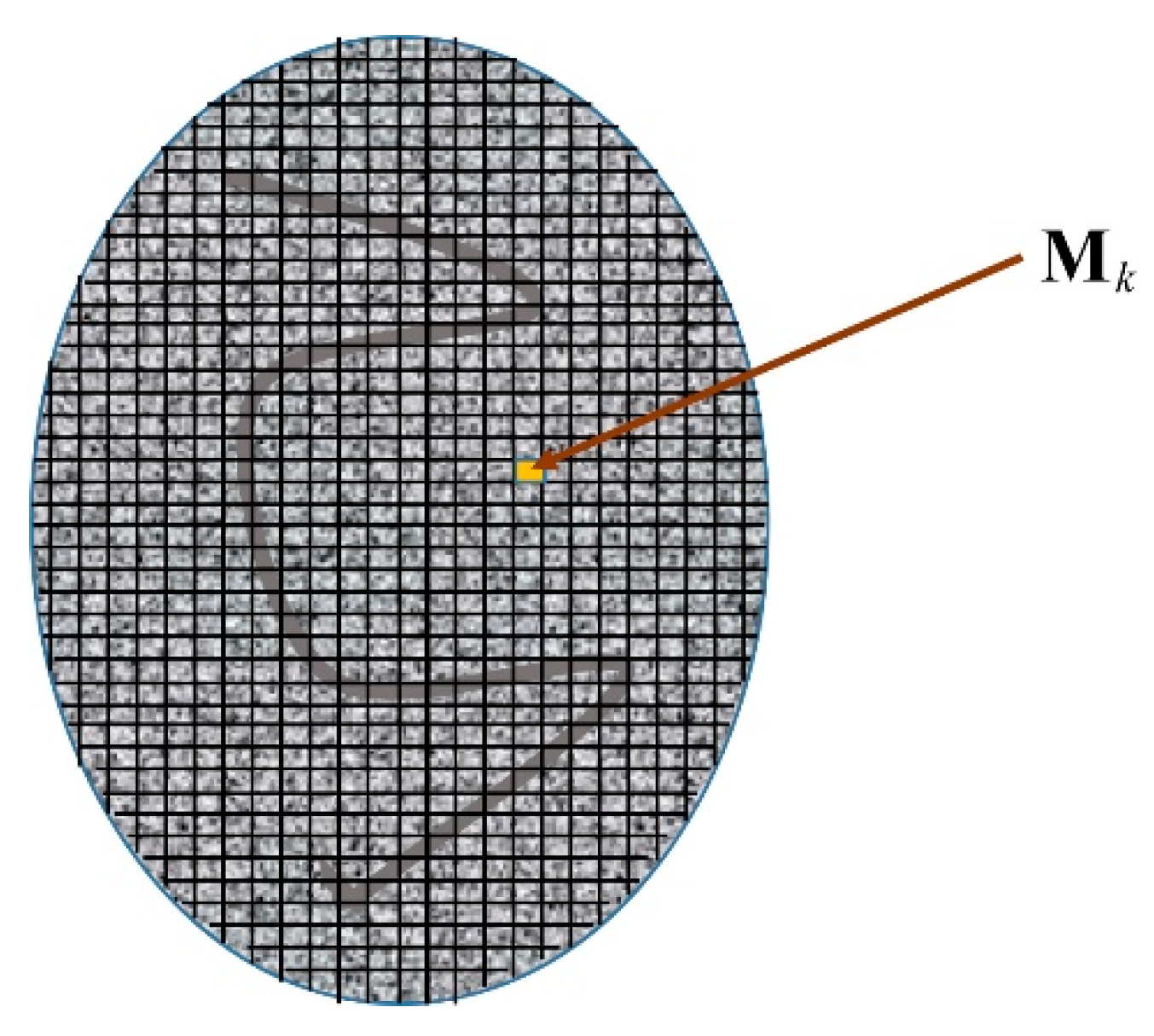
Thus, in Mueller imaging polarimetry, the sample can be considered pixelated, in such a manner that a different Mueller matrix is measured for each pixel (Figure 2). Note that we are using the term pixels to refer to small areas of the sample, which in general have a common shape and size, so that a number of pixels cover the entire cross-section of the sample under measurement. Therefore, each pixel is characterized by a specific and fixed Mueller matrix, which is in general different from those of other pixels. Since, in general, a given Mueller matrix can be parameterized in terms of up to sixteen independent parameters, up to sixteen independent images can be obtained for each complete polarimetric measurement. Nevertheless, when appropriate, additional images can be generated from specific polarimetric descriptors.

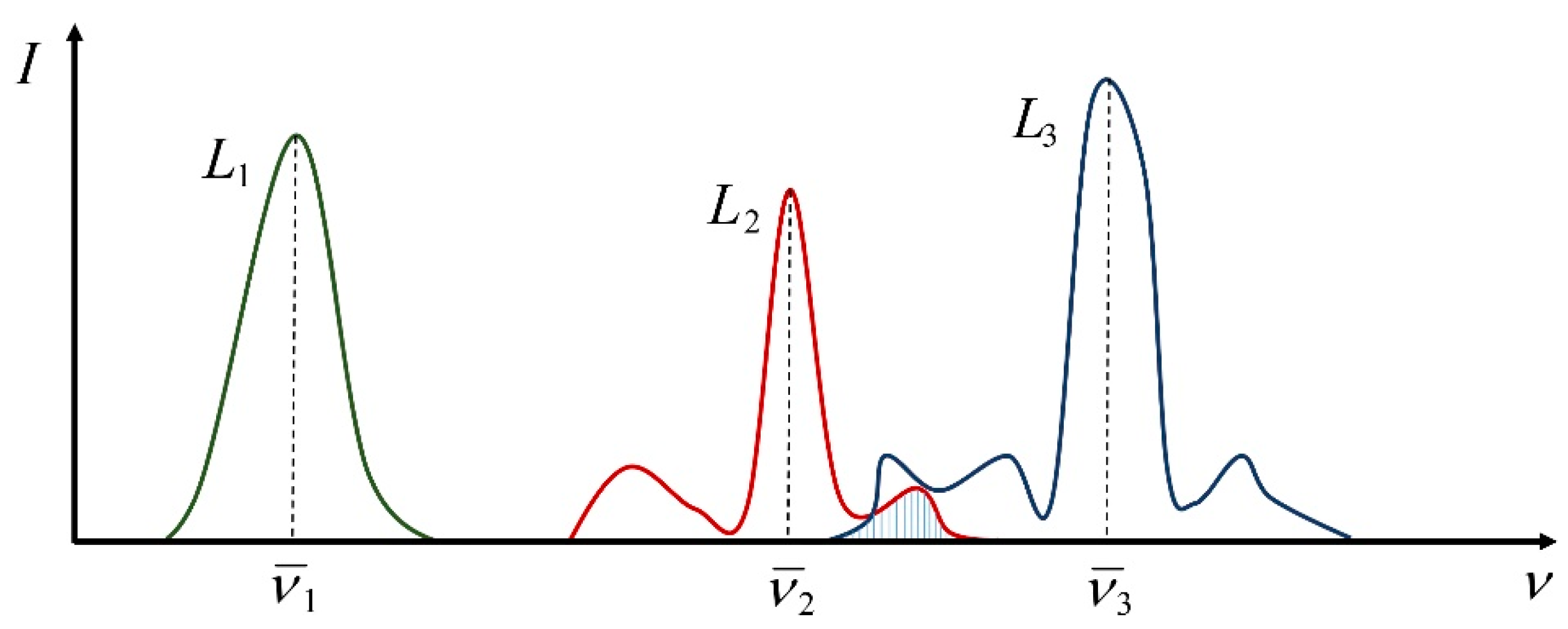
Let us now consider a sequence of n independent measurements over a given fixed material sample, which are performed with different light probes with respective spectral profiles (Figure 3), in such a manner that each independent measurement produces a specific set of m point-to point Mueller matrices, which are denoted as $M_{kl}$ $(k=1,\dots ,m$, $l=1,\dots ,n)$ where indices k and l refer, respectively to the k pixel and the l measurement.

Depending on the central frequency, shape and width of the spectral profile used in a given measurement l, the Mueller matrix of the k pixel adopts a specific form $M_{kl}$, which can be either nondepolarizing (or pure, in the sense that it preserves the degree of polarization of incident totally polarized light), or depolarizing. In general, samples exhibiting inhomogeneous behavior over the cross-section covered by the light probe are considered and consequently, the separate representations of the sixteen elements $m_{kl,ij}$ $(i,j=0,1,2,3)$, where k maps the entire set of m pixels of the sample under measurement, lead to specific images.

It is well known that the elements $m_{kl,ij}$ of $M_{kl}$ do not provide direct and independent information about the polarimetric properties of the sample for the spectral profile of the light probe used in the corresponding measurement, but are related to the enpolarizing (diattenuating and polarizing), retarding and depolarizing properties in an intricate manner. This is the reason why alternative sets of polarimetric descriptors (other than $m_{kl,ij}$) are frequently used to generate more significant polarimetric images that describe, in a more or less decoupled manner, the spatial variation of specific properties. A possible parameterization of $M_{kl}$ in terms of sixteen independent parameters directly related to specific polarimetric features is based on the so-called arrow decomposition of Mueller matrices [17,18,19,20].

The main argument which will be dealt with in this work relies on the fact that, beyond the polarimetric images obtained for each measurement l, the information already obtained through a set of n independent measurements of $M_{kl}$ can be used to generate new sets of synthetic images that enhance the contrast or visualization of certain properties or structures of the sample. In particular, for instance, let us build the Mueller matrix

$$\begin{array}{c}{M}_k=c_1{M}_{k1}+c_2{M}_{k2}+\dots +c_n{M}_{kn},\\ \left[c_1+c_2+\dots +c_n=1,c_i>0,i=1,\dots n\right],\end{array}$$

(1)

which is directly synthesized from the independent n measurements but whose associated enpolarizing, retarding and depolarizing properties are different from those of each $M_{kl}$. In fact, $M_k$ carries information about the variation of the polarimetric behavior of the sample as the spectral profile of the probing light is modified. In other words, the set of measured $M_{kl}$ contains implicit information on certain properties of the sample that can only be represented in the form of polarimetric images obtained from synthetic parallel combinations performed as indicated in Equation (1).

It should be emphasized that the abovementioned Mueller imaging measurements are performed through conventional methods and that the aim of this work is to describe the general theoretical framework used for the synthesis, through a very simple averaging procedure which does not add computational complexity, of significant polarimetric images based on the parallel composition of the Mueller matrices obtained through a set of n (with $n\ge 2$) independent conventional measurements of a given material sample. To achieve this, this communication is organized as follows. The main necessary concepts and notations are summarized in Section 2. Section 3 is devoted to the general formulation of the synthetic Mueller imaging polarimetry approach, whose nature and scope is discussed in Section 4. The main conclusions are summarized in Section 5.

Note that although the term “light” is used in this communication, it should be understood in the wide sense of referring generally to arbitrary frequencies within different areas of the electromagnetic spectrum and not exclusively within the optical range. This is the case, for example, for synthetic aperture radar polarimetry (SAR polarimetry) for which the electromagnetic probe belongs to the microwave range.

2. Theoretical Background

The transformation of polarized light by the action of a linear medium (under fixed interaction conditions) can always be represented mathematically as $s^{\prime }=Ms$, where s and $s^{\prime }$ are the Stokes vectors that represent the polarization states of the incident and emerging light beams, and M is the Mueller matrix that performs the linear transformation, which can be expressed in the partitioned form [21,22,23]

$$\begin{array}{c}M=m_{00}\widehat{M}, \hat{\mathbf{M}}\equiv \left(\begin{array}{cc}1& D^{\mathrm{T}}\\ P& m\end{array}\right),\\ m\equiv \frac{1}{m_{00}}\left(\begin{array}{ccc}{m}_{11}& m_{12}& m_{13}\\ m_{21}& m_{22}& m_{23}\\ m_{31}& m_{32}& m_{33}\end{array}\right),\\ D\equiv \frac{{\left(m_{01},m_{02},m_{03}\right)}^{\mathrm{T}}}{m_{00}},P\equiv \frac{{\left(m_{10},m_{20},m_{30}\right)}^{\mathrm{T}}}{m_{00}},\end{array}$$

(2)

where $m_{ij}$ $(i,j=0,1,2,3)$ denote the elements of M; superscript T indicates transpose; $m_{00}$ represents the mean intensity coefficient (MIC), i.e., the ratio between the intensity of the emerging light and the intensity of incident unpolarized light; D and P are the diattenuation and polarizance vectors, with absolute values D (diattenuation) and P (polarizance), and m is the normalized 3 × 3 submatrix associated with M.

A proper measure of the ability of M to preserve the degree of polarization of totally polarized incident light is given by the degree of polarimetric purity of M (also called depolarization index) [24], $P_{\Delta }$, which can be expressed as

$$P_{\Delta }=\sqrt{\frac{D^2+P^2+3P_S^2}{3}}=\sqrt{\frac{2P_P^2}{3}+P_S^2}\left[P_P\equiv \sqrt{\frac{D^2+P^2}{2}}\right],$$

(3)

where $P_S$ is the polarimetric dimension index (also called the degree of spherical purity), defined as

$$P_S\equiv \frac{{‖m‖}_2}{\sqrt{3}}\left[{‖m‖}_2\equiv \frac{1}{m_{00}}\sqrt{{\displaystyle \sum _{k,l=1}^3{m}_{kl}^2}}\right],$$

(4)

${‖m‖}_2$ being the Frobenius norm of m, and $P_P$ is the so-called degree of polarizance, or enpolarizance, giving an overall measure of the power of M to increase the degree of polarization of the interacting light in either forward or reverse interactions [17,18,19].

Maximum degree of polarimetric purity, $P_{\Delta }=1$, is exhibited uniquely by nondepolarizing (or pure) media (i.e., media that do not decrease the degree of polarization of totally polarized incident light), while $P_{\Delta }=0$ corresponds to perfect depolarizers, with an associated Mueller matrix $M_{\Delta 0}=m_{00}\mathrm{diag}(1,0,0,0)$. Maximum $P_S$, $P_S=1$, implies $P_{\Delta }=1$ with $P_P=0$ (nondepolarizing and nonenpolarizing media), which corresponds uniquely to retarders; minimal $P_S$, $P_S=0$, corresponds to media exhibiting $m=0$. Maximal enpolarizance,$P_P=1$, implies $P_{\Delta }=1$ and corresponds to perfect polarizers, while the minimal, $P_P=0$, is exhibited by nonenpolarizing interactions (either nondepolarizing or depolarizing) [18,19].

In general, two kinds of decompositions of a Mueller matrix can be considered, namely serial decompositions (through product of Mueller matrices) and parallel decompositions (through weighted sums of Mueller matrices) [25,26].

Parallel decompositions consist of representing a Mueller matrix as a weighted sum of Mueller matrices. The physical meaning of parallel decompositions is that the incoming electromagnetic wave splits into a set of pencils that interact, without overlapping, with a number of material components that are spatially distributed in the illuminated area, and the emerging pencils are incoherently recombined into the emerging beam.

Thus, the notion of parallel composition of Mueller matrices underlies the very concept of the Mueller matrix and obeys the rule that the coefficients of the Mueller components in the sum should be positive and sum to one (convex sum) [25,26]. This property is directly linked to the so-called covariance criterion, namely, given a Mueller matrix M, its associated Hermitian coherency matrix $C(M)$ is positive semidefinite [27], which is equivalent to the fact that any Mueller matrix can be expressed as a sum of nondepolarizing Mueller matrices [28]. The explicit expression of $C(M)$, in terms of the elements $m_{ij}$ of M, is given by [26,27]

$$C\left(M\right)=\frac{1}{4}\left(\begin{array}{cccc}\begin{array}{c}{m}_{00}+m_{11}\\ +m_{22}+m_{33}\end{array}& \begin{array}{c}{m}_{01}+m_{10}\\ -i\left(m_{23}-m_{32}\right)\end{array}& \begin{array}{c}{m}_{02}+m_{20}\\ +i\left(m_{13}-m_{31}\right)\end{array}& \begin{array}{c}{m}_{03}+m_{30}\\ -i\left(m_{12}-m_{21}\right)\end{array}\\ \begin{array}{c}{m}_{01}+m_{10}\\ +i\left(m_{23}-m_{32}\right)\end{array}& \begin{array}{c}{m}_{00}+m_{11}\\ -m_{22}-m_{33}\end{array}& \begin{array}{c}{m}_{12}+m_{21}\\ +i\left(m_{03}-m_{30}\right)\end{array}& \begin{array}{c}{m}_{13}+m_{31}\\ -i\left(m_{02}-m_{20}\right)\end{array}\\ \begin{array}{c}{m}_{02}+m_{20}\\ -i\left(m_{13}-m_{31}\right)\end{array}& \begin{array}{c}{m}_{12}+m_{21}\\ -i\left(m_{03}-m_{30}\right)\end{array}& \begin{array}{c}{m}_{00}-m_{11}\\ +m_{22}-m_{33}\end{array}& \begin{array}{c}{m}_{23}+m_{32}\\ +i\left(m_{01}-m_{10}\right)\end{array}\\ \begin{array}{c}{m}_{03}+m_{30}\\ +i\left(m_{12}-m_{21}\right)\end{array}& \begin{array}{c}{m}_{13}+m_{31}\\ +i\left(m_{02}-m_{20}\right)\end{array}& \begin{array}{c}{m}_{23}+m_{32}\\ -i\left(m_{01}-m_{10}\right)\end{array}& \begin{array}{c}{m}_{00}-m_{11}\\ -m_{22}+m_{33}\end{array}\end{array}\right).$$

(5)

The general formulation for the synthesis of a Mueller matrix associated with a linear polarimetric interaction from the properties of the parallel components of the medium on which the considered light beam interacts has been dealt with in [26,29,30,31,32,33,34].

Since C is a positive semi-definite Hermitian matrix, it can always be diagonalized through a unitary transformation of the form

$$C=U\mathrm{diag}\left({\lambda }_0,{\lambda }_1,{\lambda }_2,{\lambda }_3\right)U^{†}.$$

(6)

where ${\lambda }_i$ are the four ordered $(0\le {\lambda }_3\le {\lambda }_2\le {\lambda }_1\le {\lambda }_0)$ nonnegative eigenvalues of C. The columns $u_i$ $\left(i=0,1,2,3\right)$ of the $4\times 4$ unitary matrix U are the orthonormal eigenvectors of C.

Nondepolarizing Mueller matrices have the genuine property that they exhibit a single nonzero eigenvalue (i.e., ${\lambda }_0\ne 0$, ${\lambda }_1={\lambda }_2={\lambda }_3=0$) and hereafter, wherever appropriate, we will use the subscript J to refer to Mueller and coherency matrices associated with nondepolarizing media, which will be generically denoted as $M_J$ and $C_J$. The coherency matrix $C_J$ associated with a nondepolarizing Mueller matrix $M_J$ can always be expressed as $C_J=m_{00}(c\otimes c^{†})$, where $c$ (called the coherency vector of $M_J$) is a unit vector with four complex components [34].

Complete quantitative information on the structure of polarimetric purity-randomness exhibited by the interaction represented by M is provided by the set of three indices of polarimetric purity (IPP) defined as follows from the normalized eigenvalues of C [35]

$$\begin{array}{c}{P}_1\equiv {\widehat{\lambda }}_0-{\widehat{\lambda }}_1,P_2\equiv {\widehat{\lambda }}_0+{\widehat{\lambda }}_1-2{\widehat{\lambda }}_2,P_3\equiv {\widehat{\lambda }}_0+{\widehat{\lambda }}_1+{\widehat{\lambda }}_2-3{\widehat{\lambda }}_3,\\ \left[{\widehat{\lambda }}_i\equiv {\lambda }_i/m_{00}\left(i=0,1,2,3\right),0\le P_1\le P_2\le P_3\le 1\right].\end{array}.$$

(7)

Given a Mueller matrix M, it can always be submitted to the so-called arbitrary decomposition [25,36]

$$\begin{array}{c}M={\displaystyle \sum _{i=0}^{r-1}{k}_i M_{Ji}},\\ M_{Ji}=m_{00i}{\widehat{M}}_{Ji},{\widehat{M}}_{Ji}\equiv \left(\begin{array}{cc}1& D_i^T\\ P_i& m_i\end{array}\right)\equiv M_J \left(c_i\right),\\ m_{00i}\left(1+D_i\right)\le 1,k_i=\frac{m_{00}}{m_{00i}}\frac{1}{c_i^{†} C^{-} c_i},\left[{\displaystyle \sum _{i=0}^{r-1}{k}_i}=1\right],\end{array}$$

(8)

where $r=\mathrm{rank}C$, with $1\le r\le 4$, which coincides with the number of independent nondepolarizing parallel components of M; $C^{-}$ is the pseudoinverse of $\widehat{C}$, defined as $C^{-}=U{\Lambda }^{-} U^{†}$, with ${\Lambda }^{-}$ being the diagonal matrix whose r first diagonal elements are $1/{\lambda }_{ 0},1/{\lambda }_{ 1},\dots ,1/{\lambda }_{r-1}$ and whose last $4-r$ elements are zero [36].

Consider now the following modified singular value decomposition of the submatrix m of M,

$$\begin{array}{c}m=m_{RO}{m}_A{m}_{RI},\\ \left[\begin{array}{c}{m}_{Ri}^{-1}=m_{Ri}^{\mathrm{T}},\det m_{Ri}=+1\left(i=I,O\right),\\ m_A\equiv \mathrm{diag}\left(a_1,a_2,\epsilon a_3\right),a_1\ge a_2\ge a_3\ge 0,\epsilon \equiv \det m/\left|\det m\right|,\end{array}\right]\end{array}$$

(9)

where the nonnegative parameters $(a_1,a_2,a_3)$ are the singular values of m (taken in decreasing order), and $m_{Ri}$ are proper orthogonal $3\times 3$ matrices, and consequently the associated $4\times 4$ matrices of the form

$$M_{Ri}=\left(\begin{array}{cc}1& 0^{\mathrm{T}}\\ 0& m_{Ri}\end{array}\right)\left(i=I,O\right)$$

(10)

are orthogonal Mueller matrices (representing respective transparent retarders). The arrow form $M_A (M)$ of M is then defined as [17]

$$\begin{array}{c}{M}_A\left(M\right)\equiv M_{RO}^{\mathrm{T}} M{M}_{RI}^{\mathrm{T}}=m_{00}\left(\begin{array}{cc}1& D_A^{\mathrm{T}}\\ P_A& m_A\end{array}\right)\\ \left[\begin{array}{c}{m}_A\equiv m_{RO}^{\mathrm{T}} m{m}_{RI}^{\mathrm{T}}=\mathrm{diag}\left(a_1,a_2,\epsilon a_3\right)\\ a_1\ge a_2\ge a_3\ge 0,\epsilon \equiv \det m/\left|\det m\right|\\ D_A=m_{RI} D,P_A=m_{RO}^T P\end{array}\right]\end{array}$$

(11)

and contains up to ten nonzero elements. The corresponding arrow decomposition of M is defined as

$$M=M_{RO}{M}_A M_{RI}.$$

(12)

Note that the diattenuation and polarizance vectors, D and P, of M are recovered from those of $M_A$ through the respective transformations $D=m_{RI}^{\mathrm{T}}{D}_A$ and $P=m{ }_{RO} P_A$, which preserve the absolute values of the transformed vectors.

The arrow decomposition allows for the parameterization of M in terms of the following significant sixteen parameters [20,37]:

• The three angular parameters $({\phi }_I,{\chi }_I,{\Delta }_I)$ determining the entrance retarder, where ${\phi }_I$ and ${\chi }_I$ are the azimuth and ellipticity of the fast eigenstate and ${\Delta }_I$ is the retardance;
• The three angular parameters $({\phi }_O,{\chi }_O,{\Delta }_O)$ determining the exit retarder;
• The three parameters $({\phi }_D,{\chi }_D,D)$ determining the diattenuation vector D of M, where ${\phi }_D$ and ${\chi }_D$ are the azimuth and ellipticity of the eigenstate with smaller attenuation; or, alternatively, the three parameters $({\phi }_{DA},{\chi }_{DA},D)$ determining the diattenuation vector $D_A=m_{RI}D$ of $M_A$;
• The three parameters $({\phi }_P,{\chi }_P,P)$ determining the polarizance vector P of M or, alternatively, the three parameters $({\phi }_{PA},{\chi }_{PA},P)$ determining the polarizance vector $P_A=m_{RO}^{T}D$ of $M_A$;
• The three indices of polarimetric purity $P_1,P_2,P_3$ of M (which coincide with those of $M_A$);
• The MIC $m_{00}$ of M (which coincides with that of $M_A$).

Consequently, independent mappings of the above sixteen descriptors provide respective polarimetric images that reflect the variations and associated contrast of each parameter. Obviously, many other parameterizations of M are also possible, but we emphasize the fact that those listed above provide separate information on the enpolarizing (D and P vectors), retarding ($M_{RI}$ and $M_{RO}$ matrices), depolarizing $(P_1,P_2,P_3)$ and MIC $(m_{00})$ properties for each spectral profile of the light probe used in the imaging polarimeter.

Furthermore, despite the implicit redundancy of the information held by other descriptors, it can be useful to generate additional images associated with parameters like, for instance, $P_{\Delta },P_S$ and $P_P$.

The parallel composition of Mueller matrices that only differ in their MICs does not produce changes in the fifteen remaining parameters described above. Thus, hereafter, the fifteen parameters ${\phi }_I,{\chi }_I,{\Delta }_I,$${\phi }_O,{\chi }_O,{\Delta }_O,$${\phi }_D,{\chi }_D,D,$${\phi }_P,{\chi }_P,P,$$P_1,P_2,P_3$ will be referred to as the polarimetric descriptors of the Mueller matrix to which they correspond.

In the case of nondepolarizing Mueller matrices, the arrow decomposition adopts the symmetric form [26,38,39]

$$M_J=M_{RO} M_{DL0} M_{RI}$$

(13)

where the central matrix has the general form

$$M_{DL0}=m_{00}\left(\begin{array}{cccc}1& D& 0& 0\\ D& 1& 0& 0\\ 0& 0& \sqrt{1-D^2}& 0\\ 0& 0& 0& \sqrt{1-D^2}\end{array}\right),$$

(14)

so that it represents a horizontal-aligned linear diattenuator, while the set of entrance and exit retarders depends on five parameters through the expressions [26]

$$M_{RI}=M_{RL0} \left(\Delta /2\right)M_{RL1} \left({\phi }_1,{\Delta }_1\right),M_{RO}= M_{RL2}\left({\phi }_2,{\Delta }_2\right) M_{RL0} \left(\Delta /2\right),$$

(15)

where $M_{RL1} ({\phi }_1,{\Delta }_1)$, $M_{RL2}({\phi }_2,{\Delta }_2)$ and $M_{RL0} (\Delta /2)$ represent respective linear retarders with retardances ${\Delta }_1$, ${\Delta }_2$ and $\Delta /2$, and whose fast axes are oriented at angles ${\phi }_1$, ${\phi }_2$ and zero. Recall that diattenuation and polarizance necessarily coincide for nondepolarizing Mueller matrices $(P=D)$.

3. Synthetic Mueller Imaging Polarimetry

For the sake of clarity, let us first consider a fixed material sample submitted to two independent point-to-point Mueller measurements which only differ in the spectral profile of the light probe, with respective central frequencies denoted as ${\nu }_1$. and ${\nu }_2$. It is also assumed that the shift ${\nu }_2-{\nu }_1$ is big enough for the sample to have different polarimetric behavior, that is to say, some or all of the set of fifteen polarimetric descriptors described in the last paragraph of Section 2 take different values for both light probes. No particular assumptions are made about the shapes and bandwidths of the spectral profiles, although the implications of their possible partial overlap will be discussed in Section 4.

Let $M_{kl}$ $(k=1,\dots ,m$, $l=1,2)$ be the point-to-point Mueller matrices obtained from each independent measurement $(l=1,2$ corresponding, respectively, to the light probes with central frequencies ${\nu }_1$. and ${\nu }_2)$, where we are using the notation introduced in Section 1.

For a given pixel k, one can always build the synthetic Mueller matrix

$$M_k=\frac{1}{2}{M}_{k1}+\frac{1}{2}{M}_{k2}.$$

(16)

As long as a certain property of the sample behaves differently in both measurements, a respective new polarimetric image associated with $M_k$ arises. Note that other pairs of coefficients $c_1,c_2$ (with $c_1+c_2=1$) different from $c_1=c_2=1/2$ can be used, but there is no apparent advantage in straying from the simpler option.

To emphasize the power of this simple procedure, let us consider the special (but common) case in which both $M_{k1}$ and $M_{k2}$ are nondepolarizing. Then, provided ${\widehat{M}}_{k1}\ne {\widehat{M}}_{k2}$ (that is, proportional Mueller matrices are excluded because of their equivalent polarimetric behavior, which only differ in their respective MICs), $M_k$ is depolarizing, so that its polarimetric descriptors differ from those of both $M_{k1}$ and $M_{k2}$. In particular, the inequality $P_1<1$ is necessarily satisfied (recall that nondepolarizing Mueller matrices always satisfy $P_1=P_2=P_3=P_{\Delta }=1$) and, consequently, the mapping of $P_1$ associated with each pixel k provides a new and peculiar polarimetric image whose nature is substantially different from the images obtained for $M_{k1}$ and $M_{k2}$. In fact, it can be said that certain images obtained from the synthetic $M_k$ provide information about the differences in the polarimetric behavior of the sample for both spectral profiles considered.

Obviously, when either $M_{k1}$ or $M_{k2}$ is depolarizing, the polarimetric descriptors of $M_k$ are also genuinely different from those of the sole $M_{k1}$ or $M_{k2}$.

The power of the synthetic procedure for the generation of images that hold information about the changes in the polarimetric behavior for different spectral profiles of the light probe can be enhanced by using more than two light probes (i.e., $n>2$). In general, new point-to-point Mueller matrices can be synthesized through the simple procedure indicated in Equation (1). The larger n and the larger ${\nu }_2-{\nu }_1$ are (within the range considered: optical, microwave…), the greater polarimetric randomness is generated in $M_k$, in such a manner that the point-to-point values of the three IPP of $M_k$ decrease correspondingly and move away from unity. In general, up to three new respective images for the three IPP are generated, while the images obtained for the remaining twelve polarimetric descriptors adopt specific new features, which can reflect different aspects of the variation of the polarimetric behavior of the sample as different spectral profiles of the light probe are used.

Thus, the above procedure for obtaining synthetic Mueller matrices $M_k$ for the respective pixels of the sample as well as the associated synthetic polarimetric images determined by a set of polarimetric descriptors (for instance those derived from the arrow decomposition of each $M_k$), can be straightforwardly generalized for n independent measurements performed with respective light probes (see Figure 4).

4. Discussion

Given a point-to-point Mueller matrix measurement on a given material sample with spatially heterogeneous polarimetric behavior (under fixed interaction conditions; i.e., relative orientation of the sample with respect to the direction of the collimated light probe, transmission, reflection or scattering operation mode, angle of observation, etc.), infinite polarimetric images can be generated through the spatial dependence of parameters defined as functions of the sixteen elements of the measured Mueller matrices. Nevertheless, once the spectral profile of the light probe of the imaging polarimeter is fixed, the images obtained for a set of sixteen well-suited parameters representing independent and significant properties, like, for instance, the one derived from the arrow decomposition of the point-to-point Mueller matrix, constitute a reasonable and sufficient framework for inspecting the polarimetric image features of the sample.

Obviously, for each different spectral profile of the light probe used, a new set of images is generated, extending the power to analyze the sample. The changes from one set of images to another one depend on the specific behavior of the sample for each spectral profile, in such a way that both the central frequency and the bandwidth and shape of the profile influence the measurement. In particular, as the bandwidth increases, the more polarimetric randomness is introduced by the interaction with the sample and, consequently, the lower the corresponding indices of polarimetric purity. It can be said that, as the bandwidth is reduced, the more deterministic the polarimetric behavior of the sample is and vice versa, and that, as the bandwidth is increased, the composition of the polarimetric behaviors of the sample for the different frequencies involved increases the depolarization of the emerging light probe before reaching the polarization state analyzer of the polarimeter.

In addition to the specific images obtained for different spectral profiles of the light probe of the polarimeter, which provide specific information for each corresponding kind of interaction, new sets of images can be generated by the synthetic parallel composition of the point-to-point Mueller matrices obtained in each independent experiment. These new Mueller matrices encompass, in a peculiar manner, information on the differences in the behavior of the sample as the type of the light probe changes.

When two independent measurements are taken using spectral profiles whose frequencies do not overlap, the synthesized Mueller matrices coincide (at least from a theoretical point of view) with those obtained through a simple measurement in which both light probes are used simultaneously (provided the relative weights of the Mueller matrices in the convex sum coincide with the relative weights of the intensities used). Nevertheless, when the spectral profiles overlap to some extent, the synthetic matrices differ from those potentially generated experimentally through a simultaneous combination of both light probes. This in no way detracts from interest of the general synthesis of point-to-point Mueller matrices through parallel composition of the ones obtained from independent measurements. In fact, the synthesis leads to a new arrangement of the polarimetric information already obtained in each measurement, which allows us to obtain new images that are well defined from an algebraic point of view.

It should be emphasized that the potential improvements in the contrast of images strongly depend on the nature of the material sample and are not necessarily realized for each independent parameter, but can be made evident for some descriptors, which are different for each case. Some preliminary analyses of certain samples of biological tissues allow us to say that the new approach enhances the visualization of certain structures. Specific and comprehensive analyses for particular kinds of material samples (thin films, LCD devices, scattering by particles, biological tissues, samples inspected by SAR polarimetry…) require further studies that have a strongly contextual nature and could be the subject of future works that fall outside the scope of this communication, whose main objective is to present the theoretical approach to synthetic imaging Mueller polarimetry.

In general, all the polarimetric descriptors of the synthetic point-to-point Mueller matrix $M_k$ are different from those of the n measured Mueller matrices $(M_{k1},\dots M_{kn})$ used as its parallel components of $M_k$ $[M_k=(1/n)(M_{k1}+M_{k2}+\dots +M_{kn})]$, while the integer number r of IPP with values below their maximum (with $P_1\le P_2\le P_3\le 1)$ increases as the number of measurements involved increases (recall that $r=\mathrm{rank}C(M_k)$). This property is evident when the measured Mueller matrices are nondepolarizing, thus satisfying $1=r=P_{\Delta }(M_{kl})=P_1(M_{kl})=P_2(M_{kl})=P_3(M_{kl})$ $(l=1,\dots ,n)$, while the synthetic $M_k$ is necessarily depolarizing, with $2\le r(M_k)\le 4$. The specific value of r exhibited by $M_k$ depends strongly on the nature and differences among its components $M_{kl}$ $(l=1,\dots ,n)$.

5. Conclusions

The sets of point-to-point Mueller matrices associated with a given material sample and obtained via a number n of independent Mueller imaging measurements provide information that, beyond that held by the measured Mueller matrices themselves, can be rearranged into a set of synthetic point-to-point Mueller matrices whose polarimetric descriptors (enpolarizing, retarding and depolarizing parameters) depend on the changes in the polarimetric behavior of the sample when the spectral profile of the light probe of the polarimeter changes.

The procedure used to generate the point-to-point synthetic Mueller matrices is as simple as calculating the respective mean Mueller matrices, which exhibit polarimetric descriptors that, in general, are different from those of the measured Mueller matrices. This allows us to generate new polarimetric images of the sample that can enhance the visualization of certain structural properties of the sample.