Hybrid Constellation Shaping 64QAM Based on Hexagonal Lattice of Constellation Subset
Abstract
:1. Introduction
2. Theory and Principle
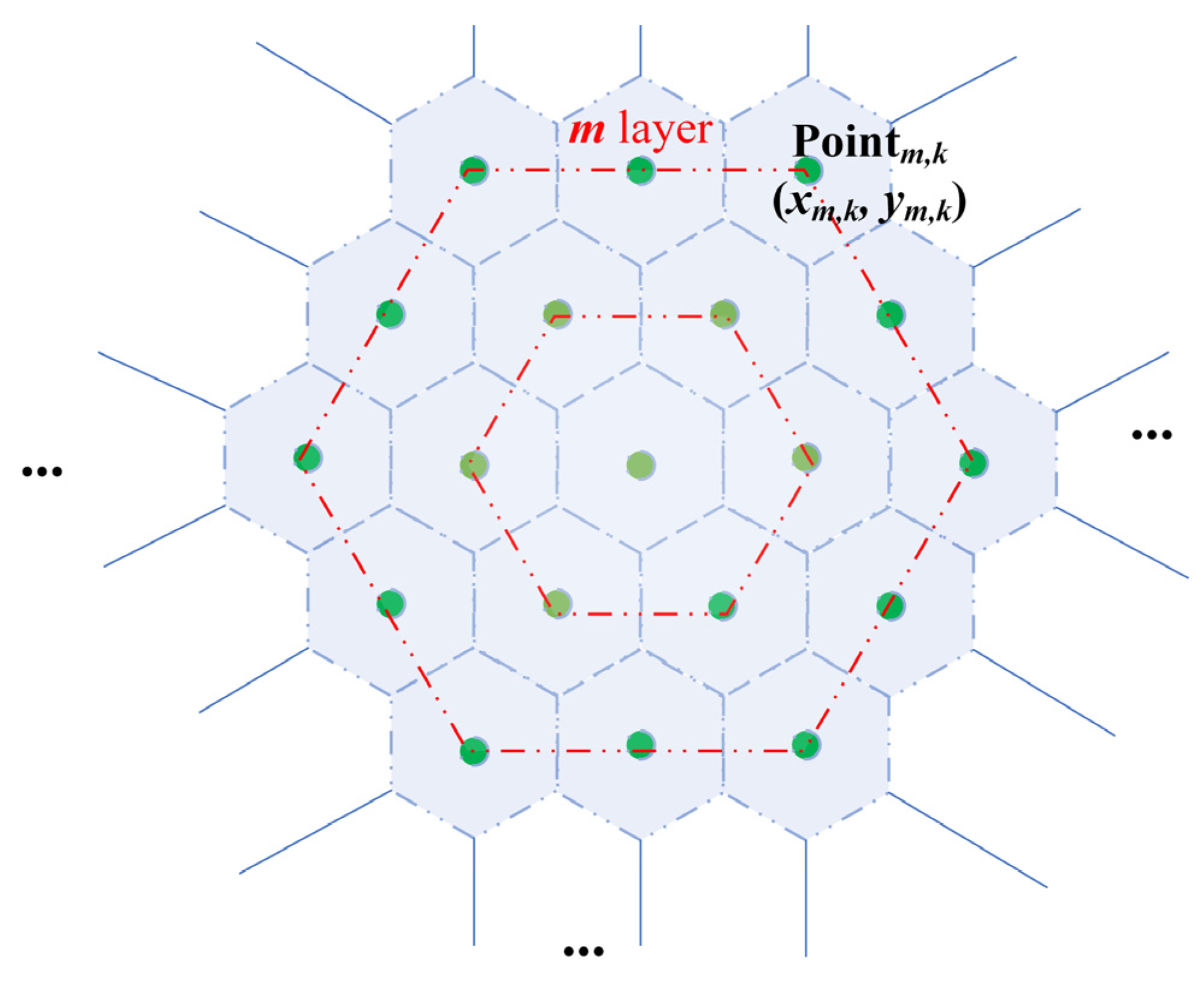
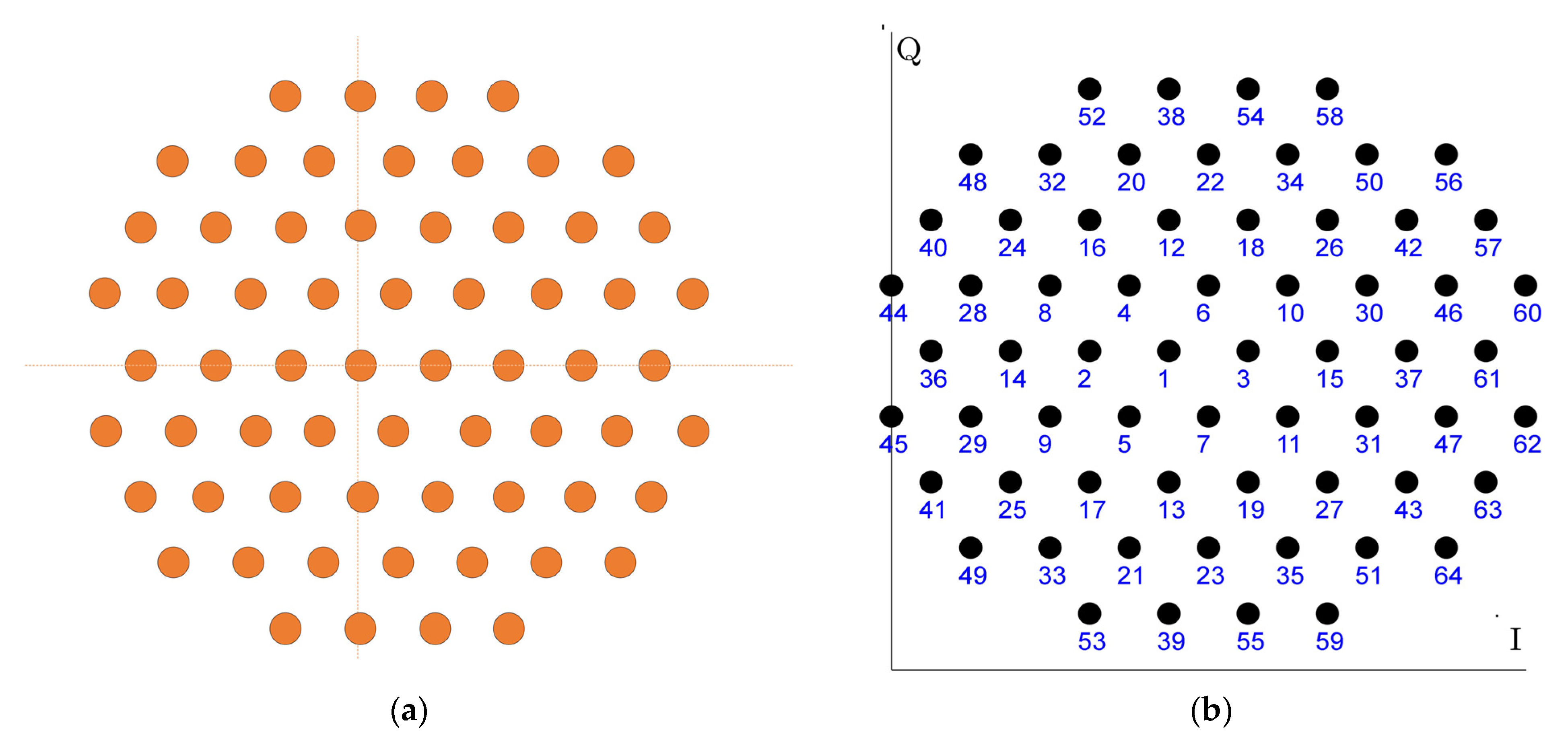
2.1. The Initial Quantitative Characterization of the 64QAM Constellation
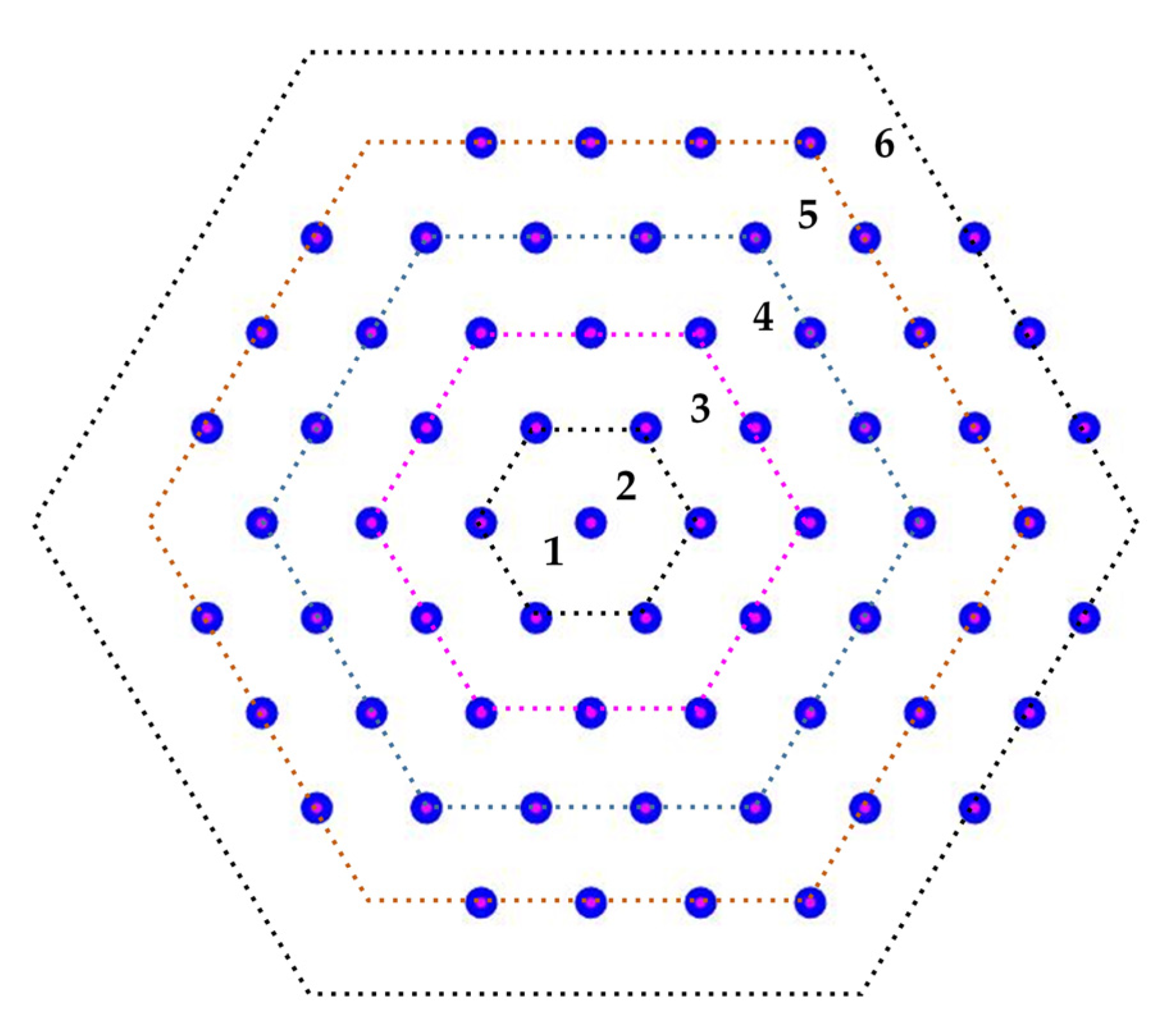
2.2. Generation of the GS-64QAM Signal
2.3. Generation of the HS-64QAM Signal
3. Experimental Setup and Results
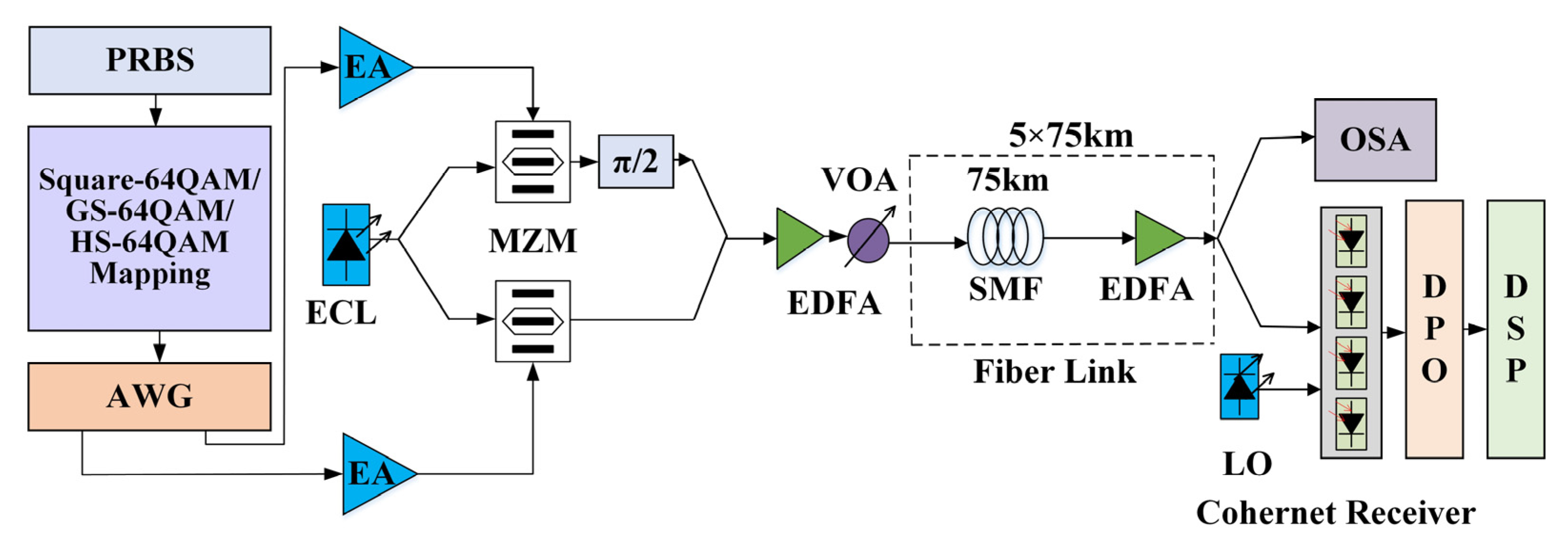
3.1. Experimental Setup
3.2. Results and Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gong, Y.; Yao, H.; Wang, J.; Li, M.; Guo, S. Edge Intelligence-driven Joint Offloading and Resource Allocation for Future 6G Industrial Internet of Things. IEEE Trans. Netw. Sci. Eng. 2022. [Google Scholar] [CrossRef]
- Wang, F.; Yao, H.; Zhang, Q.; Wang, J.; Gao, R.; Guo, D.; Guizani, M. Dynamic Distributed Multi-Path Aided Load Balancing for Optical Data Center Networks. IEEE Trans. Netw. Serv. Manag. 2022, 19, 991–1005. [Google Scholar] [CrossRef]
- Mai, T.; Yao, H.; Zhang, N.; Xu, L.; Guizani, M.; Guo, S. Cloud Mining Pool Aided Blockchain-Enabled Internet of Things: An Evolutionary Game Approach. IEEE Trans. Cloud Comput. 2023, 11, 692–703. [Google Scholar] [CrossRef]
- Wang, F.; Gao, R.; Zhou, S.; Li, Z.; Cui, Y.; Chang, H.; Wang, F.; Guo, D.; Yu, C.; Liu, X.; et al. Probabilistic Neural Network Equalizer for Nonlinear Mitigation in OAM Mode Division Multiplexed Optical Fiber Communication. Opt. Express 2022, 30, 47957–47969. [Google Scholar] [CrossRef] [PubMed]
- Chai, F.; Zhang, Q.; Yao, H.; Xin, X.; Gao, R.; Guizani, M. Joint Multi-task Offloading and Resource Allocation for Mobile Edge Computing Systems in Satellite IoT. IEEE Trans. Veh. Technol. 2023, 72, 7783–7795. [Google Scholar] [CrossRef]
- Yu, C.; Sheng, X.; Gao, R.; Wang, F.; Li, Z.; Chang, H.; Huang, L.; Zhang, Q.; Xin, X.; Huang, X.; et al. Experimental Demonstration of Twin-Single-Sideband Signal Detection System Based on a Single Photodetector and Without Optical Bandpass Filter. Opt. Express 2022, 30, 37341–37349. [Google Scholar] [CrossRef]
- Yankov, M.P.; Zibar, D.; Larsen, K.J.; Christensen, L.P.B.; Forchhammer, S. Constellation Shaping for Fiber-Optic Channels with QAM and High Spectral Efficiency. IEEE Photon. Technol. Lett. 2014, 26, 2407–2410. [Google Scholar] [CrossRef]
- Singya, P.K.; Shaik, P.; Kumar, N.; Bhatia, V.; Alouini, M.-S. A Survey on Higher-Order QAM Constellations: Technical Challenges, Recent Advances, and Future Trends. IEEE Open J. Commun. Soc. 2021, 2, 617–655. [Google Scholar] [CrossRef]
- Zhang, Q.; Shu, C. Viterbi and Viterbi Algorithm based Phase Recovery for Probabilistically Shaped Signals. J. Light. Technol. 2021, 39, 1364–1370. [Google Scholar] [CrossRef]
- López-Salcedo, J.A.; Del Peral-Rosado, J.A.; Seco-Granados, G. Survey on Robust Carrier Tracking Techniques. IEEE Commun. Surv. Tutor. 2014, 16, 670–688. [Google Scholar] [CrossRef]
- Sasai, T.; Matsushita, A.; Nakamura, M.; Okamoto, S.; Hamaoka, F.; Kisaka, Y. Laser Phase Noise Tolerance of Uniform and Probabilistically Shaped QAM Signals for High Spectral Efficiency Systems. J. Light. Technol. 2020, 38, 439–446. [Google Scholar] [CrossRef]
- Sillekens, E.; Liga, G.; Lavery, D.; Bayvel, P.; Killey, R.I. High-Cardinality Geometrical Constellation Shaping for the Nonlinear Fibre Channel. J. Light. Technol. 2022, 40, 6374–6387. [Google Scholar] [CrossRef]
- Galdino, L.; Edwards, A.; Yi, W.; Sillekens, E.; Wakayama, Y.; Gerard, T.; Pelouch, W.S.; Barnes, S.; Tsuritani, T.; Killey, R.I.; et al. Optical Fibre Capacity Optimisation via Continuous Bandwidth Amplification and Geometric Shaping. IEEE Photon. Technol. Lett. 2020, 32, 1021–1024. [Google Scholar] [CrossRef]
- Ding, J.; Zhang, J.; Wei, Y.; Zhao, F.; Li, C.; Yu, J. Comparison of Geometrically Shaped 32-QAM and Probabilistically Shaped 32-QAM in a Bandwidth-Limited IM-DD System. J. Light. Technol. 2020, 38, 4352–4358. [Google Scholar] [CrossRef]
- Hu, F.; Zou, P.; Li, G.; Yu, W.; Chi, N. Enhanced Performance of CAP-Modulated Visible Light Communication System Utilizing Geometric Shaping and Rotation Coding. IEEE Photonics J. 2019, 11, 1–2. [Google Scholar] [CrossRef]
- Mirani, A.; Agrell, E.; Karlsson, M. Low-Complexity Geometric Shaping. J. Light. Technol. 2021, 39, 363–371. [Google Scholar] [CrossRef]
- Skvortcov, P.; Phillips, I.; Forysiak, W.; Koike-Akino, T.; Kojima, K.; Parsons, K.; Millar, D.S. Nonlinearity Tolerant LUT-Based Probabilistic Shaping for Extended-Reach Single-Span Links. IEEE Photon. Technol. Lett. 2020, 32, 967–970. [Google Scholar] [CrossRef]
- Tong, T.; Chen, X.; Chen, Y.; Sun, Q.; Chen, Z.; Liu, D.; Tang, M. Performance-Enhanced DMT System with Joint Precoding and Probabilistic Constellation Shaping. IEEE Photonics J. 2021, 13, 1–12. [Google Scholar] [CrossRef]
- Cho, J.; Winzer, P.J. Probabilistic Constellation Shaping for Optical Fiber Communications. J. Light. Technol. 2019, 37, 1590–1607. [Google Scholar] [CrossRef]
- Cai, J.-X.; Batshon, H.G.; Mazurczyk, M.V.; Paskov, M.; Davidson, C.R.; Hu, Y.; Sinkin, O.V.; Bolshtyansky, M.; Foursa, D.G.; Pilipetskii, A.N. Performance Comparison of Probabilistically Shaped QAM Formats and Hybrid Shaped APSK Formats with Coded Modulation. J. Light. Technol. 2020, 38, 3280–3288. [Google Scholar] [CrossRef]
- Wu, X.; Liu, B.; Zhang, L.; Mao, Y.; Xu, X.; Ren, J.; Zhang, Y.; Jiang, L.; Xin, X. Probabilistic Shaping Design Based on Reduced-Exponentiation Subset Indexing and Honeycomb-Structured Constellation Optimization for 5G Fronthaul Network. IEEE Access 2019, 7, 141395–141403. [Google Scholar] [CrossRef]
- Rode, A.; Geiger, B.; Chimmalgi, S.; Schmalen, L. End-to-end Optimization of Constellation Shaping for Wiener Phase Noise Channels with a Differentiable Blind Phase Search. J. Light. Technol. 2023, 41, 3849–3859. [Google Scholar] [CrossRef]
- Zhang, S.; Yaman, F. Constellation Design with Geometric and Probabilistic Shaping. Opt. Commun. 2018, 15, 7–12. [Google Scholar] [CrossRef]
- Ding, J.; Sang, B.; Wang, Y.; Kong, M.; Wang, F.; Zhu, B.; Zhao, L.; Zhou, W.; Yu, J. High Spectral Efficiency WDM Transmission Based on Hybrid Probabilistically and Geometrically Shaped 256QAM. J. Light. Technol. 2021, 39, 5494–5501. [Google Scholar] [CrossRef]

| Point Index | QG-Bit | Normalized Coordinates | Point Index | QG-Bit | Normalized Coordinates | Point Index | QG-Bit | Normalized Coordinates |
|---|---|---|---|---|---|---|---|---|
| 1 | 000000 | 0 + 0i | 23 | 010110 | 0.1770 + 0.9197i | 45 | 101100 | −1.2390 + 0.3066i |
| 2 | 000001 | −0.3540 + 0i | 24 | 010111 | −0.7080 − 0.6131i | 46 | 101101 | 1.2390 − 0.3066i |
| 3 | 000010 | 0.3540 + 0i | 25 | 011000 | −0.7080 + 0.6131i | 47 | 101110 | 1.2390 + 0.3066i |
| 4 | 000011 | −0.1770 − 0.3066i | 26 | 011001 | 0.7080 − 0.6131i | 48 | 101111 | −0.8850 − 0.9197i |
| 5 | 000100 | −0.1770 + 0.3066i | 27 | 011010 | 0.7080 + 0.6131i | 49 | 110000 | −0.8850 + 0.9197i |
| 6 | 000101 | 0.1770 − 0.3066i | 28 | 011011 | −0.8850 − 0.3066i | 50 | 110001 | 0.8850 − 0.9197i |
| 7 | 000110 | 0.1770 + 0.3066i | 29 | 011100 | −0.8850 + 0.3066i | 51 | 110010 | 0.8850 + 0.9197i |
| 8 | 000111 | −0.5310 − 0.3066i | 30 | 011101 | 0.8850 − 0.3066i | 52 | 110011 | −0.3540 − 1.2263i |
| 9 | 001000 | −0.5310 + 0.3066i | 31 | 011110 | 0.8850 + 0.3066i | 53 | 110100 | −0.3540 + 1.2263i |
| 10 | 001001 | 0.5310 − 0.3066i | 32 | 011111 | −0.5310 − 0.9197i | 54 | 110101 | 0.3540 − 1.2263i |
| 11 | 001010 | 0.5310 + 0.3066i | 33 | 100000 | −0.5310 + 0.9197i | 55 | 110110 | 0.3540 + 1.2263i |
| 12 | 001011 | 0 − 0.6131i | 34 | 100001 | 0.5310 − 0.9197i | 56 | 110111 | 1.2390 − 0.9197i |
| 13 | 001100 | 0 + 0.6131i | 35 | 100010 | 0.5310 + 0.9197i | 57 | 111000 | 1.4160 − 0.6131i |
| 14 | 001101 | −0.7080 + 0i | 36 | 100011 | −1.0620 + 0i | 58 | 111001 | 0.7080 − 1.2263i |
| 15 | 001110 | 0.7080 + 0i | 37 | 100100 | 1.0620 + 0i | 59 | 111010 | 0.7080 + 1.2263i |
| 16 | 001111 | −0.3540 − 0.6131i | 38 | 100101 | 0 − 1.2263i | 60 | 111011 | 1.5930 − 0.3066i |
| 17 | 010000 | −0.3540 + 0.6131i | 39 | 100110 | 0 + 1.2263i | 61 | 111100 | 1.4160 + 0i |
| 18 | 010001 | 0.3540 − 0.6131i | 40 | 100111 | −1.0620 − 0.6131i | 62 | 111101 | 1.5930 + 0.3066i |
| 19 | 010010 | 0.3540 + 0.6131i | 41 | 101000 | −1.0620 + 0.6131i | 63 | 111110 | 1.4160 + 0.6131i |
| 20 | 010011 | −0.1770 − 0.9197i | 42 | 101001 | 1.0620 − 0.6131i | 64 | 111111 | 1.2390 + 0.9197i |
| 21 | 010100 | −0.1770 + 0.9197i | 43 | 101010 | 1.0620 + 0.6131i | |||
| 22 | 010101 | 0.1770 − 0.9197i | 44 | 101011 | −1.2390 − 0.3066i |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhang, Q.; Xin, X.; Wang, Y.; Tian, F.; Tian, Q.; Yang, L.; Zhao, Y. Hybrid Constellation Shaping 64QAM Based on Hexagonal Lattice of Constellation Subset. Photonics 2023, 10, 1008. https://doi.org/10.3390/photonics10091008
Liu X, Zhang Q, Xin X, Wang Y, Tian F, Tian Q, Yang L, Zhao Y. Hybrid Constellation Shaping 64QAM Based on Hexagonal Lattice of Constellation Subset. Photonics. 2023; 10(9):1008. https://doi.org/10.3390/photonics10091008
Chicago/Turabian StyleLiu, Xiangyu, Qi Zhang, Xiangjun Xin, Yongjun Wang, Feng Tian, Qinghua Tian, Leijing Yang, and Yi Zhao. 2023. "Hybrid Constellation Shaping 64QAM Based on Hexagonal Lattice of Constellation Subset" Photonics 10, no. 9: 1008. https://doi.org/10.3390/photonics10091008
APA StyleLiu, X., Zhang, Q., Xin, X., Wang, Y., Tian, F., Tian, Q., Yang, L., & Zhao, Y. (2023). Hybrid Constellation Shaping 64QAM Based on Hexagonal Lattice of Constellation Subset. Photonics, 10(9), 1008. https://doi.org/10.3390/photonics10091008








