Abstract
Station arrangement optimization of photoelectric theodolites in shooting ranges presents a non-convex and non-linear problem, and the method required to seek the global optimal solution remains an open question. This paper proposes an efficient traversal algorithm that could solve this problem by utilizing discretization of regions with a finite length of mesh, in which both the terrain of the station arrangement region and the observation airspace region are discretized through triangulation. To enhance the computational efficiency of the traversal algorithm, two strategies are employed to speed up the calculation: reducing the dimension of the observation airspace and using the Euclidean distance matrix to compute the intersection angle. After the global optimal solution with discrete finite precision was obtained through the traversal algorithm, it was then used as the initial points for local mesh refinement and to implement gradient-based optimization in order to further improve the precision of the solution. The proposed approach is demonstrated to be practical through application to numerical examples used for the optimization of station arrangements that involve two to four stations.
1. Introduction
Optical measurement and radar measurement systems are key components in shooting ranges; each system has its own advantages. Optical measurement devices can achieve passive measurement by receiving image information from the measured target, and they have the characteristics of good concealment, presenting projected two-dimensional images of the targets, and high positioning accuracy, etc. [1]. Photoelectric theodolite is the optical measurement device most widely used to measure the external ballistic parameters of the flying targets in shooting ranges, as its dynamic angular measurement accuracy can reach arc-second level [2]. Where the dynamic angular measurement accuracy is concerned, station arrangement optimization is one of the most critical methods used to improve the measurement accuracy of the target. This process involves optimizing the location of the photoelectric theodolite stations based on the ballistic range of the test target, target characteristics, equipment performance, terrain, etc. [3].
The station arrangement optimization problem for bearing measurement and distance measurement devices (or time-of-arrival measurement devices) is still challenging due to its non-convexity and non-linearity. Currently, there is still no widely recognized optimization algorithm that can efficiently and stably achieve the global optimal solution, while local optimization is usually infeasible. To address this issue, researchers have proposed theoretical analysis [4,5,6,7,8,9], as well as various optimization algorithms, including the genetic algorithm [10,11,12,13,14,15], simulated annealing algorithm [16,17], and particle swarm optimization algorithm [18,19], to optimize the station arrangement. The studies discussed in [4,8,9] investigated the optimization of distance-measuring devices, using the Cramer–Rao bound and the geometric dilution of precision (GDOP) as objective functions. The papers [5,6,7] optimized the station arrangement of bearing-only positioning devices using GDOP and the minimum circular probable error as objectives. However, studies based on theoretical analysis and mathematical calculation lack a comprehensive consideration of practical constraints, such as the position changes in the test targets, observation conditions, geographical environment, etc. As a result, these methods have poor practical applicability. The studies discussed in [10,11,17] used the genetic algorithm to optimize node arrangement in WSNs (Wireless Sensor Networks) based on the distance range of the sensors, though paper [17] combined this approach with the simulated annealing algorithm. The papers in [12,14,15] established different mathematical models for optimal arrangement of radar netting, among which distance is one of the main factors. They adopted the genetic algorithm to solve the problems. Similarly, the studies discussed in [18,19] also implemented radar placement, though they used the particle swarm optimization algorithm. The station arrangement optimization problem of photoelectric theodolite was solved by introducing niche technology into genetic algorithms in [13]. Ref. [16] coped with the sensor placement problem for target location under constraints of cost limitation and distance range coverage using the simulated annealing algorithm. But, in general, when solving non-linear station arrangement optimization problems using heuristic optimization algorithms, the stability is insufficient, and these algorithms usually fail to find all of the global optimal solutions.
In order to address the above challenges, this paper proposes an efficient traversal algorithm to seek a global optimal solution to the station arrangement optimization problem stably that ensures discrete finite precision. We adopt the method of reducing the discrete dimension of the observation airspace and calculating the intersection angle using the Euclidean distance matrix to improve the efficiency of the traversal algorithm. Next, the precision of station arrangement is further enhanced using local grid refinement and the local optimization method with the gradient information. Computational examples demonstrate the effectiveness of the proposed method.
The structure of this paper is organized as follows: Section 2 presents the basis of tracking the test target using the method of intersection measurement and by establishing a mathematical optimization model to solve the station arrangement problem; Section 3 discretizes the station arrangement region and observation airspace and provides a solution to the problem of terrain obstruction during measurement; Section 4 focuses on accelerating the computation of the traversal algorithm and enhancing the precision of the station arrangement; the applicability of the proposed method is demonstrated through an example and the case of relay station arrangement in Section 5; and, finally, Section 6 concludes the paper.
2. Optimization Model of Station Arrangement
2.1. Principle of Intersection Measurement
The photoelectric theodolite was classified as a type of angular optical measurement device. Once the directional calibration was completed, a single photoelectric theodolite only measured the elevation angle and the azimuth angle between its location and the flying target. Taking measurements using the photoelectric theodolite also required consideration of factors such as the curvature of the earth, measurement errors, station elevation, etc. Processing methods used for these factors can be found in [20,21,22,23,24] and will not be reiterated in this study. As depicted in Figure 1, given the distance between two stations, elevation angle and azimuth angle , as well as the direction angle and observation distance , could be derived by solving the measurement triangle. Subsequently, the position of the test target was determined based on the stations’ locations.
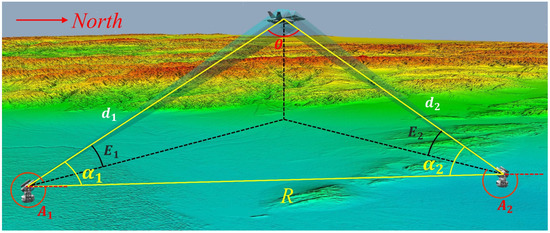
Figure 1.
Method of intersection measurement.
2.2. Objective Function
Intersection angle (shown in Figure 1) was the main factor that affected measurement precision when measuring with two photoelectric theodolites. According to references [25,26], the estimated standard deviation of the test target position coordinate could be calculated as follows:
where refers to the estimation error of the direction vector perpendicular to the measurement baseline on the horizontal plane, is the estimation error of the target height, and is the estimation error of the direction of the measurement baseline. The highest measurement precision was achieved when the intersection angle was 90°, as demonstrated in Figure 2. To ensure high measurement precision, the main objective of station arrangement optimization was .
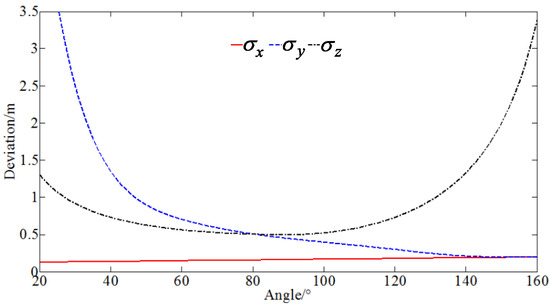
Figure 2.
Relationship between the intersection angle and the estimated standard deviation.
2.3. Constraint Conditions
The constraints of the station arrangement optimization problem of photoelectric theodolites were determined based on the performance parameters of the photoelectric theodolites, observation conditions, and terrain conditions of the stations. These constraints include the observation distance, elevation angle, solar exclusive angle, distance between two stations, intersection angle, and the obstruction caused by the terrain during the measuring process. The elevation angle referred to the angle between the measurement baseline and the horizontal plane on which the station was located. The solar exclusive angle, which was the angle between the sun, photoelectric theodolite, and target, also needs to be considered to prevent interference caused by sunlight. The relationship between the measurement precision and the intersection angle, as previously discussed in Section 2.2, was generally required to be 60–120°. The distance between two stations could not be too short, as shortness could result in a small intersection angle. Additionally, factors such as observation horizon, traffic, communication, and living conditions were also considered, as the stations should not be placed on unoccupied peaks or mountainsides.
For the station arrangement optimization problem of photoelectric theodolites, the station arrangement region was specified based on a range of longitudes and latitudes, and the terrain was composed of multiple continuous and non-convex triangular facets. The measurement station could measure multiple maneuvering test targets, and its observation range encompassed several target trajectories. Therefore, the observation airspace was a three-dimensional domain. To facilitate calculation, a unified coordinate system was established in the station arrangement optimization model, which converted latitude and longitude information into coordinate information. After the optimization was completed, the station coordinates were converted back to latitude and longitude.
As shown in Figure 3, we selected a zero-meter elevation point as the coordinate origin and establish a Cartesian coordinate system, with the coordinate of the target point in the airspace being , the coordinate of the point in the station arrangement region being , and the sunlight direction being the constant vector .
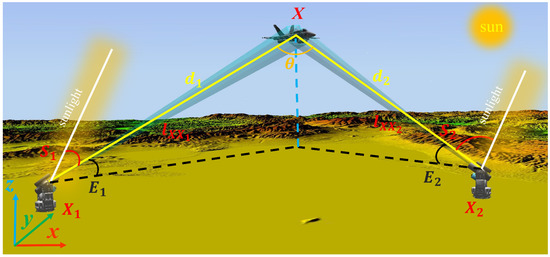
Figure 3.
Constraint conditions of intersection measurement.
We assumed that the performance parameters of the two photoelectric theodolite stations were identical. According to the objective function and constraint conditions outlined above, a mathematical model for station arrangement optimization could be written as follows:
where
here, represents the observation distance and elevation angle between the photoelectric theodolite station and the target, respectively; represents the solar exclusive angle; represents the intersection angle between the two stations and the target; represents the mean value of the station arrangement region; and represents the gradient value of the station situation. These measures represent the criteria used to judge whether a station is located on a mountain. represents the line segment between the station and the target. and are two constants, which are the height and gradient of the mountain peaks determined by the terrain.
As derived from Equation (2), the station arrangement optimization problem constituted a non-linear programming problem with a non-convex objective function and constraint conditions, and using a local search algorithm to solve the problem was usually not a good choice. Even if the station arrangement region and observation airspace were divided into multiple convex polyhedrons, the non-convexity of the optimization problem remained unchanged. Moreover, the station arrangement region and observation airspace could also be artificially specified as discrete points, which were hard to divide into convex sets. To ensure that the station arrangement optimization problem stably converges to create a global optimal solution, it is currently true that the use of the traversal algorithm is the most viable strategy.
3. Discretization of Optimization Model
The purpose of using the traversal algorithm was to discretize the station arrangement region and the observation airspace into grid nodes. Since the terrain does not have locally severe oscillations and the observation airspace is a continuous three-dimensional region, while both the objective and constraint functions are continuous, the grid density is sufficient to ensure continuity within the unit. Therefore, during computation, discrete nodes could be used to replace the terrain of the station arrangement region and the observation airspace.
3.1. Discretize Optimization Model
In order to obtain accurate information regarding the elevation and terrain features of the station arrangement region and enhance the practicality and accuracy of the optimization results, this paper utilized detailed digital elevation model (DEM)-based terrain information about the region. DEM is a discrete mathematical expression of the Earth’s surface terrain that records elevation values on a regular grid [27]; it can be expressed as follows:
where represents the coordinate of somewhere, and is the corresponding elevation. The DEM plays a crucial role in conducting mapping and environmental spatial analysis in fields such as landslide, route optimization, and terrain analysis [28]. The relevant DEM data were extracted based on the latitude and longitude range of the station arrangement region, and the terrain could be obtained through interpolation. Due to the large amount of data in the commonly used 90-m DEM resolution, it was difficult to traverse so many discrete points. Therefore, the terrain of the station arrangement region needed to be reconstructed, with sparser discrete points used in flat areas and denser points used in complex areas. Using a regular rectangular grid to represent complex terrain could lead to a loss of terrain accuracy within the units; thus, a triangular mesh was more suitable for describing the scale of variation in the terrain. As shown in Figure 4, through triangulation, the station terrain was represented by multiple triangular planes, and discrete triangular nodes with elevation information were obtained.
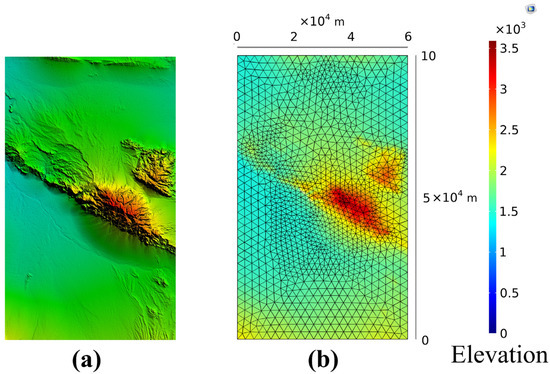
Figure 4.
DEM of the station arrangement region (a) and its discrete grid (b).
Observation airspace was a three-dimensional domain, which was represented as a three-dimensional entity in the geometric model. When discretizing 3D geometric entities, tetrahedron or hexahedron subdivision was typically employed. The station arrangement region that consisted of triangular surfaces after discretization is recorded as , and the number of terrain grid nodes is recorded as . Observation airspace is after discretization, and the number of its grid node was ; thus, the original optimization problem is expressed as follows:
where is the average elevation of the station’s adjacency points.
3.2. Solution to Terrain Obstruction
Current research typically places no spatial restrictions on the station arrangement region, meaning that the devices can be located at any position along a two-dimensional plane. However, this method is only applicable to flat terrain characterized by small altitude changes in the station arrangement region, as in reality, measurement stations are affected by complex terrain when they are located on the ground. In particular, when measuring low-altitude flying targets, there is a significant deviation between the computation results and the actual measurement results due to elevation differences between the measurement stations. Moreover, the observation of the station may also be obstructed by terrain, resulting in unobservable areas being present when taking measurements using photoelectric theodolites (as shown in Figure 5, where the observation airspace is denoted as ).
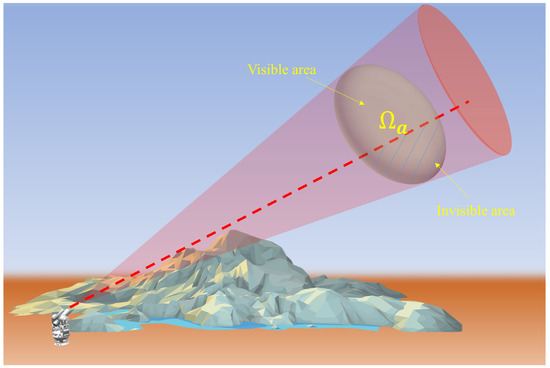
Figure 5.
Measurement range of photoelectric theodolite obstructed by the terrain.
Therefore, the geographical environment in which the photoelectric theodolite station is located should be taken into consideration. During the process of measuring, the measurement baseline should not be obstructed by mountains or other obstacles; otherwise, the target may disappear from sight. After the station arrangement region and airspace was discretized into grid nodes, the problem of whether the optical line of the photoelectric theodolite is obstructed by mountains was equivalent to the positional relationship between the line segments that extended from the station to points in the observation airspace and the faces of triangular meshes. If the line segment intersected with the faces, we considered that the optical line of the photoelectric theodolite would be blocked when taking measurements.
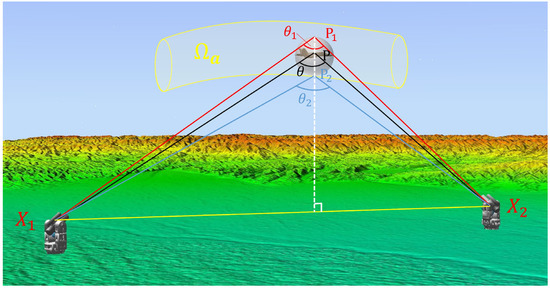
As shown in Figure 6, a triangular terrain grid is the triangle , the station is the ray source , and the direction of station to observation airspace is ; thus, any point within triangle satisfies
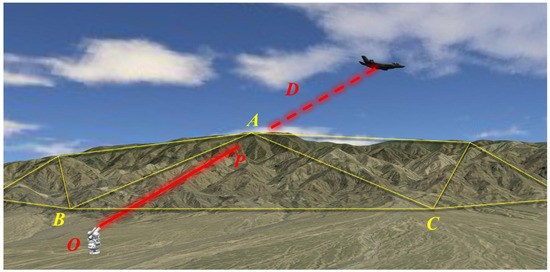
Figure 6.
Angle obstructed by mountain peak during measuring.
When the ray intersects the triangle , it satisfies
where are parameters, meaning that they do not have actual meaning. Equation (10) can be expressed using the vector form as follows:
From Cramer’s rule, we know that
If , the line intersects with the triangle ; if is an infeasible station site, the optical line will be obstructed by the mountain during measuring.
4. The Fast Traversal Algorithm
Though the computational efficiency of the traversal algorithm is often criticized, it remains a trustworthy method that can be used to solve the station arrangement optimization problem. It has the advantage of obtaining accurate elevation information related to the discrete traversal points and the stable convergence to the optimal solution without relying on the objective function and constraints. With advancements in computer capacity for processing large matrices, the station arrangement optimization problem could be efficiently using solved the traversal algorithm. When using the algorithm to solve this problem, it was necessary to calculate the numerical solution of each node, determine whether it is a feasible point that satisfies all constraints, and compute the optimal solution based on the objective function value among the feasible points.
The optimization model for station arrangement was characterized by the constraint of the intersection angle requiring a significant number of traversals, which were typically several orders of magnitude greater than other constraints. This high technical constraint was required because it simultaneously affects the configurations of two stations. Assuming that the number of discrete nodes for the station arrangement region and observation airspace are denoted as and , respectively, once the intersection angle is calculated using the traversal algorithm, it would require a maximum of loop computation. Instead of using a brute-force method, two strategies were employed in this paper to enhance the algorithm’s running efficiency in terms of solving the station arrangement optimization problem. The first strategy was to reduce the discrete dimension of the observation airspace to decrease the number , while the second strategy was to employ the Euclidean distance matrix to reduce the number of loop computations.
4.1. Acceleration Strategy
4.1.1. Reducing the Discrete Dimension of the Airspace
The number of discrete points was a pivotal factor that affected the accuracy and efficiency of the traversal algorithm. As the number increased, the solution became increasingly precise, though it gained computational complexity. In this section, based on the method of reducing the discrete dimension of the observation airspace, fewer discrete points were needed without affecting the precision.
To demonstrate the feasibility of reducing the discrete dimension of the observation airspace to solve the station arrangement optimization problem of photoelectric theodolites, we introduced the following Corollaries.
Corollary 1.
If the boundary of the observation airspace is feasible, the entire observation airspace is also feasible.
Proof.
Taking the intersection angle constraint as an example, as shown in Figure 7, represents a point interior of the observation airspace, and represent the two photoelectric theodolites. There is a ball contained in the observation airspace with a center and radius ; thus, the line through point that is perpendicular to the straight line must intersect with ball at two points and . are located on the same plane, where and . Therefore, for any point in the interior of the observation airspace, its intersection angle is neither the maximum value nor the minimum value. Thus, if the boundary satisfies the constraint , the entire observation airspace also satisfies the constraint of intersection angle. The proofs for the remaining constraints are similar. □

Figure 7.
Maximum and minimum values of constraints are likely found on the boundary of the observation airspace.
Corollary 2.
The optimal point will be achieved on the boundary of the observation airspace.
Proof.
As both the maximum intersection angle and the minimum intersection angle are located on the boundary of the observation airspace, the objective function was also achieved on the boundary. Therefore, for any three-dimensional observation airspace, we offered the following proposition. □
Proposition 1.
When discretizing the observation airspace, only its boundary needs to be discretized to solve the station arrangement optimization problem.
Since the observation airspace is a three-dimensional solid region, the number of boundary nodes is significantly lower than the number of interior nodes after discretization. The use of a surface grid for the boundary of the observation airspace could greatly reduce the number of discrete points while maintaining precision.
4.1.2. Solving Intersection Angle with Euclidean Distance Matrix
The efficiency of loop computation is relatively lower than that of matrix calculation. In order to reduce the number of computational loops and improve the efficiency of numerical calculations, the intersection angle was computed using the angle information included in the Euclidean distance matrix (EDM). The EDM describes the square distance between every two points in the Euclidean space, and it is widely used in geodesy, economics, biochemistry, engineering, and other fields [29,30]. Given the following points in a list
The EDM is defined as , where
Since stations will not be set in the same place, any three points not located on the same line in Euclidean space will be able to form a triangle; thus, every three elements in the EDM satisfy
Therefore
If , we set a certain point in the airspace as the first point in , and the rest of the points represent all of the discrete points in the station arrangement region; therefore, the rest of the points represent all of the discrete nodes in the station arrangement region. We then set the point in the observation airspace as subscript , and the intersection angle between any two points in the station arrangement region and a certain point in the airspace can be expressed as . Using the Equation (13), we find that
If we combine Equations (14) and (16), we have
Therefore
where refers to a diagonal matrix with principal diagonal ; thus, it is easy to compute .
We determine the computational efficiency of this method by running Equation (19) in MATLAB; the CPU is AMD Ryzen R9 5900X. Our results show that the method can handle points within 2.5 s via the sparse matrix algorithm.
4.2. Improve Precision of Station Arrangement via Local Optimization
4.2.1. Local Grid Refinement
After utilizing the traversal algorithm to find the optimal solution for the station arrangement optimization problem with finite discrete precision, the solution was used as the starting point for further refinement. Through grid subdivision, the precision of the station arrangement could be further improved based on the continuity of the station arrangement region. As shown in Figure 8, when refining the local mesh, the terrain area to be refined was selected based on the locations of the initial points found within the feasible range of the station arrangement region, and a more detailed terrain grid was constructed.
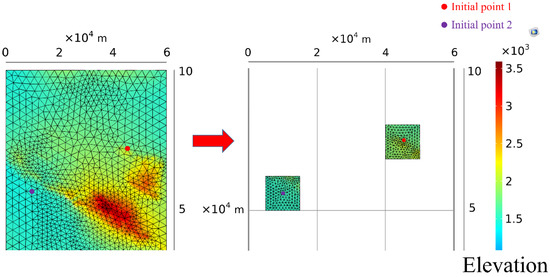
Figure 8.
Refinement of local grid.
4.2.2. Solving by Fitting Continuous Terrain
By traversing the local grid, we could obtain a new optimal solution. The new optimal solution was then used as the initial points, and the feasible polygonal areas adjacent to the initial points were selected as the design domain for the station arrangement optimization problem. We then further subdivided the grid to obtain more accurate elevation values, which required DEM data with higher resolution. However, in the design domain, fitting the terrain function as a quadric surface already met the precision requirement for elevation. Since the points in the design domain already satisfied all constraints, the optimization problem could be formulated as follows:
where denotes the station arrangement region approximated as a quadratic surface, which is still a non-differentiable and non-convex optimization problem. We could solve this problem via the interior point method. Generally, non-linear optimization methods failed to find a global optimal solution [31], while using traversal algorithm, as previously stated, we obtained a fine domain and initialization for non-linear solvers. When this optimization problem converged to find a local optimal solution, we designated it as the global optimal solution to the station arrangement optimization problem.
5. Numerical Examples
5.1. Arrangement Optimization of Two Stations
We chose a zero-meter elevation at a specific location as the coordinate origin and a 60 km × 100 km area as the station arrangement region. The SRTMDEMUTM 90-m DEM data were adopted. Without losing generality, we selected a 1/4 annular non-convex domain as the observation airspace to simulate the active flight section, with the y-axis positive direction being set in a northerly direction. The parameters of the constraint conditions were as follows: the maximum measurement distance of the photoelectric theodolite was 70 km, while the minimum observation distance was ignored. The measurement moment was 16:00, and the minimum solar exclusive angle was 35°. The minimum distance between the two stations was 40 km. The ranges of the elevation angle and intersection angle were 5–65° and 60–120°, respectively. According to the algorithm described in this paper, we discretized 1673 nodes in the station arrangement region, along with 3209 triangular units, to denote the terrain. The maximum distance between adjacent discrete nodes was about 2.5 km. Using the method outlined in Section 4.1.2, the number of discrete nodes on the boundary of the observation airspace was 326, while the discrete nodes on the whole observation airspace was 773. The grid data are shown in Figure 9.
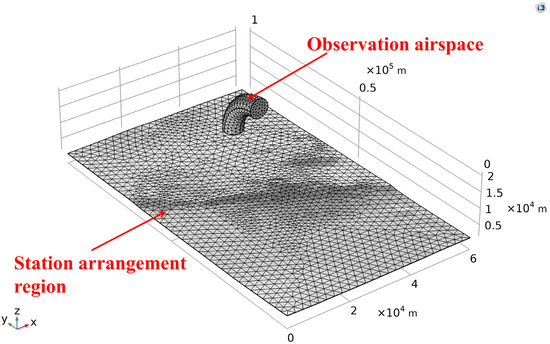
Figure 9.
Discretization of station arrangement region and observation airspace.
In accordance with the objective function and constraint conditions, initial points with discrete finite precision were obtained by traversing discrete nodes, utilizing the methods outlined in Section 4.1. Additionally, by assessing whether the values at each node satisfy the constraint conditions, we directly obtained multiple feasible locations of the two stations, which satisfied the constraints known as feasible point pairs. Next, feasible points and feasible regions for each station were determined according to the feasible point pairs. As the intersection angle was the main factor that affected measurement precision, we show different feasible regions under different intersection angle ranges in Figure 10. Subsequently, as depicted in Figure 11, we chose rectangle regions based on the optimal points achieved by traversing coarse girds. Next, the girds within the rectangle regions were locally refined. By traversing these local refined nodes, we could determine the new optimal solutions. Ultimately, as shown in Figure 12, we selected the nodes adjacent to the optimal solutions solved via the method outlined above, and we fitted continuous terrain while creating the rectangle design domains based on these points. Therefore, the optimal stations were attained through gradient-based optimization via the method outlined in Section 4.2.2. Using optimal station locations and values of objective function determined through traversing coarse grids, local refinement and local optimization could be found, as shown in in Table 1.
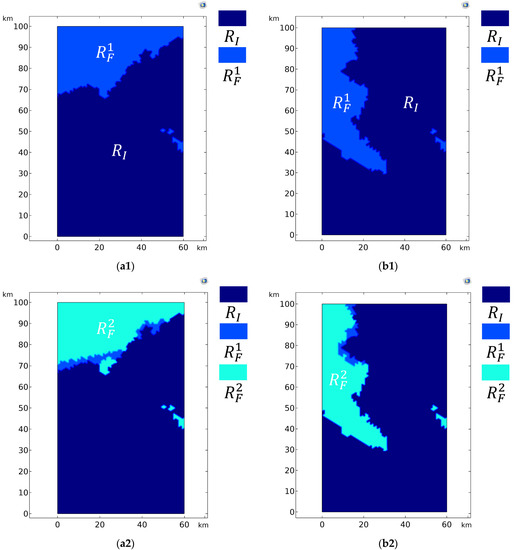
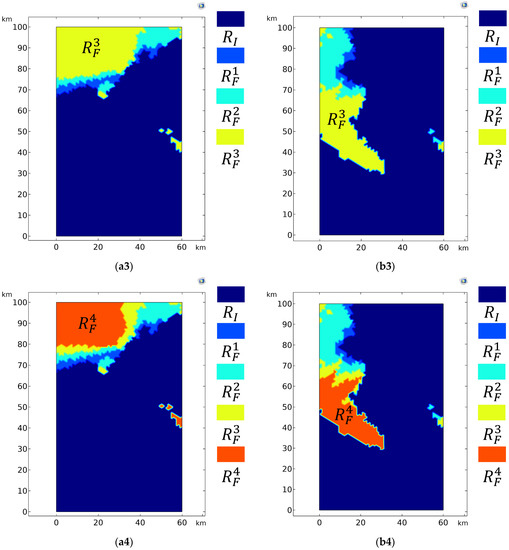
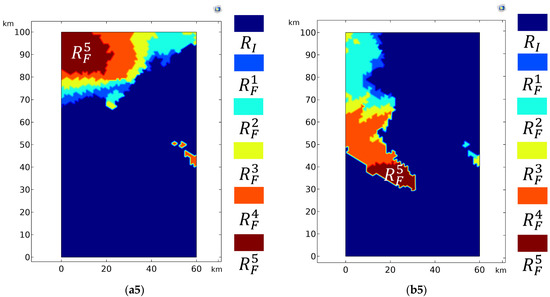
Figure 10.
Feasible regions with different intersection angle ranges for station 1 (a) and station 2 (b). (a1) The feasible region , and infeasible region , with an intersection angle of 60–120°. 346 feasible points; (b1) The feasible region and infeasible region , with an intersection angle of 60–120°. 361 feasible points. The total number of feasible point pairs is 15,642; (a2) The feasible region and infeasible region with an intersection angle of 65–115°. 301 feasible points; (b2) The feasible region and infeasible region with an intersection angle of 65–115°. 337 feasible points. The total number of feasible point pairs is 12,102; (a3) The feasible region and infeasible region with an intersection angle of 70–110°. 235 feasible points; (b3) The feasible region and infeasible region with an intersection angle of 70–110°. 237 feasible points. The total number of feasible point pairs is 7828; (a4) The feasible region and infeasible region with an intersection angle of 75–105°. 169 feasible points; (b4) The feasible region and infeasible region with an intersection angle of 75–105°. 174 feasible points. The total number of feasible point pairs is 3730; (a5) The feasible region and infeasible region with an intersection angle of 80–100°. 80 feasible points; (b5) The feasible region and infeasible region with an intersection angle of 80–100°. 61 feasible points. The total number of feasible point pairs is 655; The infeasible region remains unchanged, while the feasible regions are .
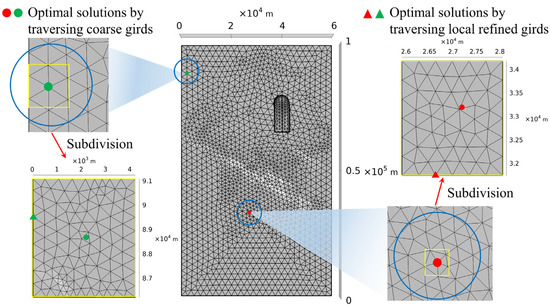
Figure 11.
The optimal solutions and details of local refinement. Here, we discretize 125 local nodes with 210 triangular units and 61 nodes with 96 triangular units.
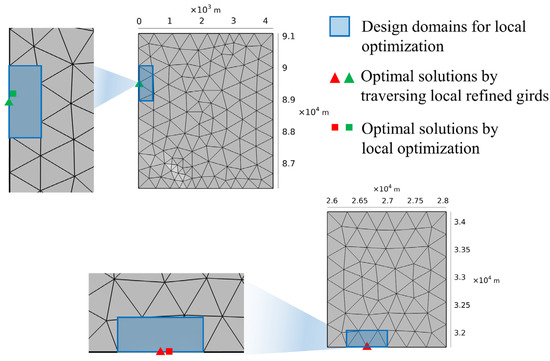
Figure 12.
The design domains and location information for the optimal stations.

Table 1.
Optimal station locations and values of objective function based on traversing coarse grids, local refinement, and local optimization.
When the optimal station locations are achieved, the optimal value of the objective function and the distribution of the intersection angle on the boundary of the observation airspace can also be calculated, as presented in Figure 13. By evaluating the objective function value obtained using traversing coarse grids and local optimization, the optimal value decreases by 7.13%. Therefore, local optimization is an effective method that can be used to improve the measurement precision. The algorithm proposed in this paper demonstrates efficient computation capabilities, having an ability to imply fast computing, as the computing time in MATLAB is approximately 13 s for the whole process.
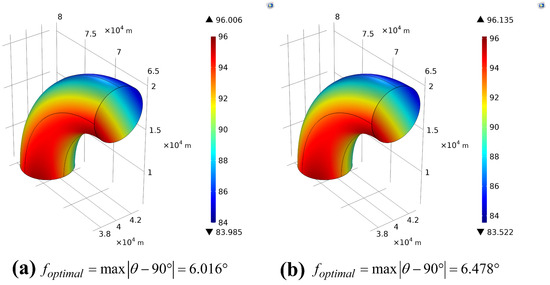
Figure 13.
Optimal intersection angle distribution on the boundary of the observation airspace based on traversing coarse grids (a) and local optimization (b).
5.2. Relay Measurement with Multiple Stations
In a shooting range, two stations are usually assigned to complete the measurement tasks for a certain section of the flight trajectory. For long-distance targets, it is difficult to track the target for the entire flight trajectory when using only two stations due to the limitations in the maximum observation distance , the elevation angle , and the intersection angle . Therefore, in order to complete the measurement tasks more effectively and improve the measurement accuracy, it is usually necessary to use multiple stations. This section focuses on the relay measurement techniques that utilize three or four photoelectric theodolite stations. The basic concept remains the same, even when using more than four stations.
The relay measurement concept can be classified into two modes. The traditional mode involves determining the flight sections according to the target’s flight path, such as assigning the section as the encounter section and the section as the active section. Each measurement section needs to be measured using two stations. In this mode, we can divide the flight sections into segments and separately compute them using the method presented in this paper; the relay station is then set at the intersection of the feasible areas of the two corresponding measurement sections. Subsequently, the optimal station positions are determined based on the results of each flight section. This mode is characterized by its simplicity and low computational requirements. However, it may not always find the global optimal solution under the pre-defined observation subregions.
In the second relay mode, the measurement section is unknown, and only the observation airspace to be measured is given. If we assume that we have stations, the sub-region that can be observed using 1, 2 photoelectric theodolite stations is , the sub-region that can be observed using 2, 3 stations is , etc., as the sub-regions have the following relationship:
The objective function is as follows:
Here, is the intersection angle of stations and .
5.2.1. Relay Measurement of Three Stations
The utilization of relay stations involves the implementation of all constraints within the observation airspace for relay measurement of three stations. The constraint conditions are in accordance with those outlined in Section 5.1 and the objective function in Equation (18). The main difference lies in the expansion of the station arrangement region and the scope of the observation airspace. Discretization of the station arrangement region and observation airspace can be seen in Figure 14. Feasible regions and point pairs with intersection angle ranges of 60–120°, along with optimal station locations based on the traditional relay and the second relay modes, are shown in Figure 15 and Figure 16, and the optimal intersection angle distributions on the boundary of the observation airspace and the relay strategy of the two modes are shown in Figure 17 and Figure 18, respectively. Local optimization is also adopted to improve the precision of station arrangement, though we do not show the computation details.
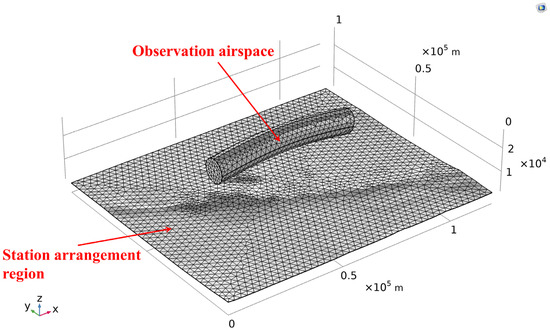
Figure 14.
Discretization of the relay measurement. We discretized 2019 nodes and 595 nodes for station arrangement region and observation airspace, respectively, in this example.
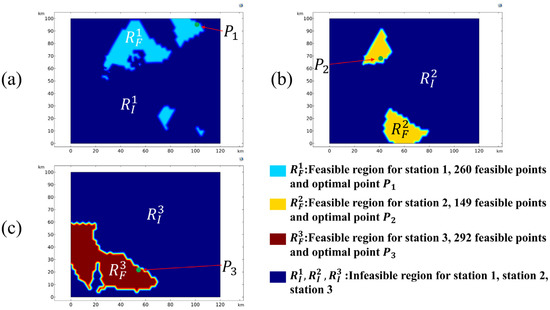
Figure 15.
Feasible regions of station 1 (a), station 2 (b), and station 3 (c), with intersection angle in the range of 60–120° and optimal station locations of the traditional relay mode for relay measurement taken at three stations. The total number of feasible point pairs is 271,462.
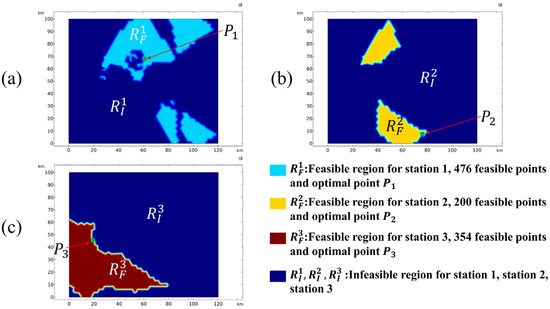
Figure 16.
Feasible regions of station 1 (a), station 2 (b), and station 3 (c) with an intersection angle range of 60–120° and optimal station locations of the second relay mode for relay measurement of three stations. The total number of feasible point pairs is 880,490.
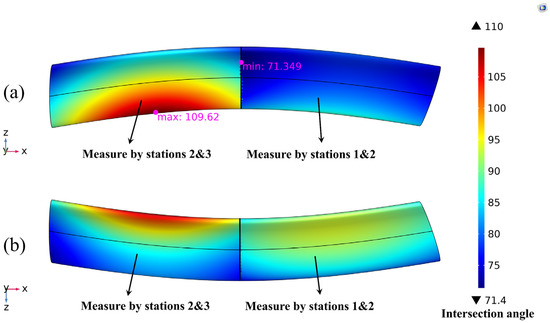
Figure 17.
Optimal intersection angle distributions on the boundary of the observation airspace, as well as the relay strategy of the traditional relay mode for relay measurement of three stations from y-axis positive direction (a) and y-axis negative direction (b), respectively. The global optimal value of the objective function is 19.632.
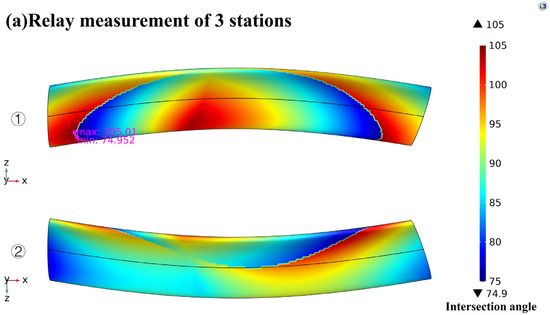
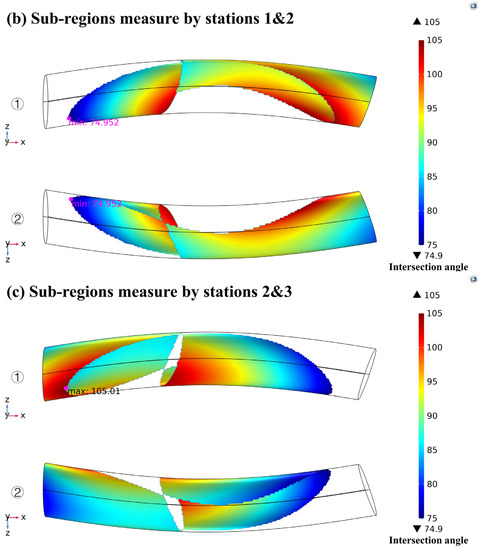
Figure 18.
Optimal intersection angle distributions on the boundary of the observation airspace (a), and the relay strategy (b,c) of the second relay mode for relay measurement of three stations from y-axis positive direction (1) and y-axis negative direction (2), respectively. The global optimal value of objective function is 15.048.
In this example, the optimal relay method may not be limited to relaying only once through the traditional mode; rather, it involves additional relay measurements. The comparison between the optimal location stations and values of the objective function of the two modes is shown in Table 2. Compared to the traditional relay mode, the optimal value of the objective function of the second relay mode decreases by 23.16%.

Table 2.
Locations and optimal values of the two relay modes for relay measurements taken at three stations.
5.2.2. Relay Measurement of Four Stations
The relay measurement method used for four photoelectric theodolite stations is the same as the method employed for relay measurements taken at three stations, though the intersection angle ranges of the two modes are set at 70–110° and 75–105°, respectively. The parameters used in the provided example are consistent with those listed in Section 5.2.1. The feasible regions of the two relay modes are shown in Figure 19 and Figure 20, and the optimal intersection angle distributions on the boundary of the observation airspace, and the measurement strategies of the two relay modes are shown in Figure 21 and Figure 22, respectively. The comparison between the optimal location stations and the values of objective function of the two modes is shown in Table 3. Compared to the traditional relay mode, the optimal value of the objective function for the second relay mode decreases by 44.31%.
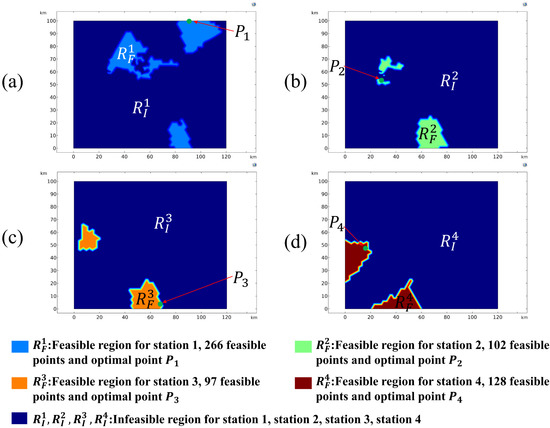
Figure 19.
Feasible regions with intersection angle ranges of 70–110° and optimal station locations of the traditional relay mode for relay measurement of four stations. The total number of feasible point pairs is 350,617.
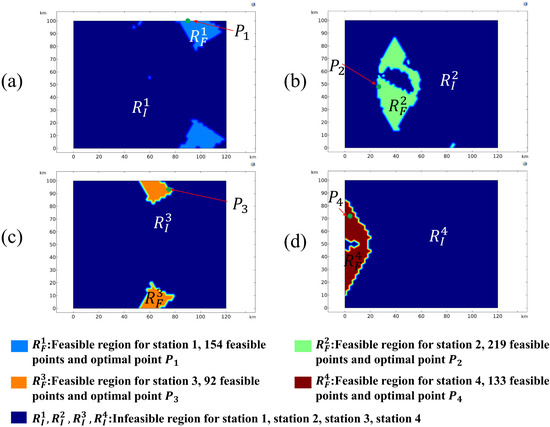
Figure 20.
Feasible regions with intersection angle ranges of 75–105° and optimal station locations of the second relay mode for relay measurements taken at four stations. The total number of feasible point pairs is 1,954,438.
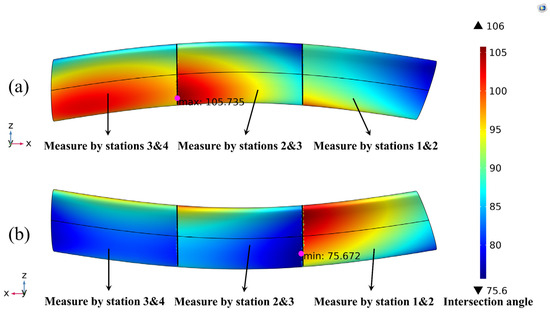
Figure 21.
Optimal intersection angle distributions on the boundary of the observation airspace, as well as the relay strategy of the traditional relay mode for relay measurement of four stations from y-axis positive direction (a) and y-axis negative direction (b), respectively. The global optimal value of objective function is 15.735.
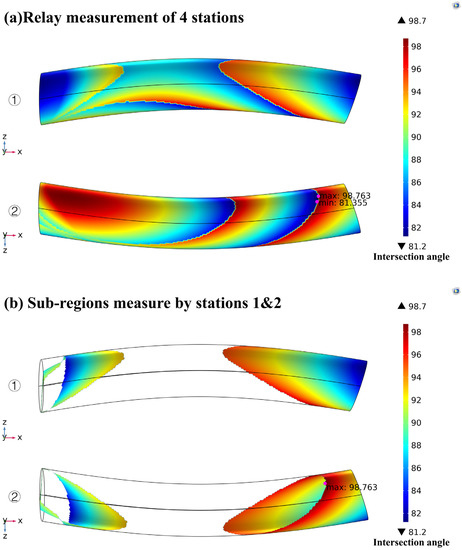
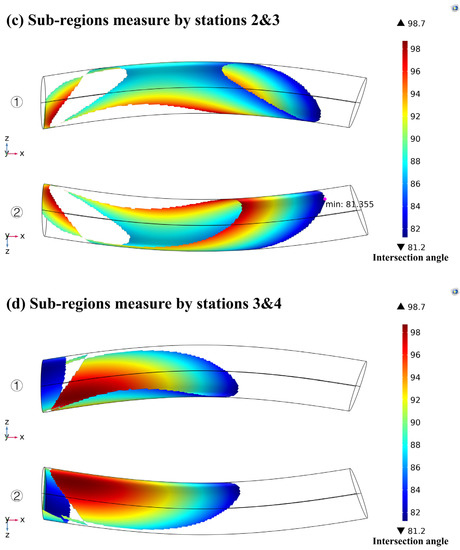
Figure 22.
Optimal intersection angle distributions on the boundary of the observation airspace (a), as well as relay strategy (b–d) of the second relay mode for relay measurement of four stations from y-axis positive direction (1) and y-axis negative direction (2), respectively. The global optimal value of objective function is 8.763.

Table 3.
Locations and optimal values of the two relay modes for relay measurements taken at four stations.
6. Conclusions
This paper presents a numerical algorithm usable to find the global optimal solution to the station arrangement optimization problem of photoelectric theodolite using traversal algorithm. According to the problem’s specific characteristics, the computational efficiency of the algorithm is notably enhanced by utilizing the Euclidean distance matrix to calculate the intersection angle and reducing the dimension of the observation airspace. The station arrangement optimization model proposed in this paper has valuable practical application, and a couple of design constraints based on actual terrain were considered in this study. Numerical examples demonstrate the model’s effectiveness and can perform relay measurement computation. Furthermore, the efficiency can be further augmented if parallel computing is implemented.
Author Contributions
Conceptualization, Z.M. and Z.L.; methodology, Z.M.; software, Z.M.; validation, Z.M., Z.L. and C.W.; formal analysis, Z.M.; investigation, Z.M.; resources, Y.L.; data curation, Z.L.; writing—original draft preparation, Z.M.; writing—review and editing, C.W.; visualization, Z.L.; supervision, Z.L.; project administration, Y.L.; funding acquisition, Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study did not require ethical approval.
Informed Consent Statement
Not applicable. The study did not involve humans.
Data Availability Statement
The data presented in this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Binghua, H.; Heng, W.; Hongli, H. A New Method of Trajectory Accurate Measurement by Single Photoelectric Theodolite. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 4939–4943. [Google Scholar]
- Haomiao, L.; Wei, W.; Bile, W. Research on theodolite auto-collimation technique based on visual image analysis. In Proceedings of the 2017 IEEE 2nd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 December 2017; pp. 150–153. [Google Scholar]
- Li, M. Concept Research on Stations Arrangement of Active Measurement System for More, Small, Rapid and Dark Objects; Chinese Academy of Sciences: Beijing, China, 2011. [Google Scholar]
- Bishop, A.N.; Fidan, B.; Anderson, B.D.O.; Pathirana, P.N.; Dogancay, K. Optimality Analysis of Sensor-Target Geometries in Passive Localization: Part 2—Time-of-Arrival Based Localization. In Proceedings of the 2007 3rd International Conference on Intelligent Sensors, Sensor Networks and Information, Melbourne, VIC, Australia, 6 March 2007; pp. 13–18. [Google Scholar]
- Zhong, Y.; Wu, X.Y.; Huang, S.C. Geometric dilution of precision for bearing-only passive location in three-dimensional space. Electron. Lett. 2015, 51, 518–519. [Google Scholar] [CrossRef]
- Xiu, J.J.; He, Y.; Wang, G.H.; Xiu, J.H.; Tang, X.M. Constellation of multisensors in bearing-only location system. IEE Proc.-Radar Sonar Navig. 2005, 152, 215–218. [Google Scholar] [CrossRef]
- Bai, J.; Wang, G.H.; Wang, N.; Xu, H. Study on Optimum Cut Angles in Bearing-only Location Systems. Acta Aeronaut. Astronaut. Sin. 2009, 30, 298–304. [Google Scholar]
- Yang, B.; Scheuing, J. Cramer-Rao bound and optimum sensor array for source localization from time differences of arrival. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Philadelphia, PA, USA, 23–23 March 2005; Volume 4, pp. iv/961–iv/964. [Google Scholar]
- Rui, L.; Ho, K.C. Elliptic localization: Performance study and optimum receiver placement. IEEE Trans. Signal Process. 2014, 62, 4673–4688. [Google Scholar] [CrossRef]
- Elhoseny, M.; Tharwat, A.; Farouk, A.; Hassanien, A.E. K-coverage model based on genetic algorithm to extend WSN lifetime. IEEE Sens. Lett. 2017, 1, 1–4. [Google Scholar] [CrossRef]
- Zameni, M.; Rezaei, A.; Farzinvash, L. Two-phase node deployment for target coverage in rechargeable WSNs using genetic algorithm and integer linear programming. J. Supercomput. 2021, 77, 4172–4200. [Google Scholar] [CrossRef]
- Hurley, S.; Khan, M.I. Netted radar: Network communications design and optimisation. Ad Hoc Netw. 2011, 9, 736–751. [Google Scholar] [CrossRef]
- Guo, L.; Zhu, Y.; Di, Y. Optimization of photoelectric theodolite station distribution based on GA. Chin. J. Sci. Instrum. 2010, 31, 741–746. [Google Scholar]
- Yang, L.; Xiong, J.; Jian, C. Method of Optimal Deployment for Radar Netting Based on Detection Probability. In Proceedings of the 2009 International Conference on Computational Intelligence and Software Engineering, Wuhan, China, 11–13 December 2009; pp. 1–5. [Google Scholar]
- Yi, J.; Wan, X.; Leung, H. Receiver placement in multistatic passive radars. In Proceedings of the 2015 IEEE Radar Conference (RadarCon), Arlington, VA, USA, 10–15 May 2015; pp. 0876–0879. [Google Scholar]
- Lin, F.; Chiu, P.L. A near-optimal sensor placement algorithm to achieve complete coverage-discrimination in sensor networks. IEEE Commun. Lett. 2005, 9, 43–45. [Google Scholar]
- Zhang, H.; Zhang, S.; Bu, W. A clustering routing protocol for energy balance of wireless sensor network based on simulated annealing and genetic algorithm. Int. J. Hybrid Inf. Technol. 2014, 7, 71–82. [Google Scholar] [CrossRef]
- Zhang, T.; Liang, J.; Yang, Y.; Cui, G.; Kong, L.; Yang, X. Antenna deployment method for multistatic radar under the situation of multiple regions for interference. Signal Process. 2018, 143, 292–297. [Google Scholar] [CrossRef]
- Wang, Y.; Yi, W.; Yang, S.; Mallick, M.; Kong, L. Antenna Placement Algorithm for Distributed MIMO Radar with Distance Constrains. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; pp. 1–6. [Google Scholar]
- Jin, G.; Wang, J.Q.; Wei, N.I. The Three error Axis of Theodolite with the Utilization of the Coordinate to the Variation. Opt. Precis. Eng. 1999, 05, 89–94. [Google Scholar]
- Huang, B.; Li, Z.H.; Tian, X.Z.; Yang, L.; Zhang, P.J.; Chen, B. Modeling and correction of pointing error of space-borne optical imager. Optik 2021, 247, 167998. [Google Scholar] [CrossRef]
- Li, H.; Hu, Y. Correction method for photoelectric theodolite measure error based on BP neural network. In Proceedings of the Intelligent Computing and Information Science: International Conference, ICICIS 2011, Chongqing, China, 8–9 January 2011; Proceedings, Part I. Springer: Berlin/Heidelberg, Germany, 2011; pp. 225–230. [Google Scholar]
- Zhao, L.; Zhu, W.; Zhang, Y.; Sun, J. The method of the system error modification of photoelectric theodolite of T type. In Proceedings of the 2012 International Conference on Optoelectronics and Microelectronics, Florence, Italy, 21–25 September 2012; pp. 384–387. [Google Scholar]
- Calafiore, G. Reliable localization using set-valued nonlinear filters. IEEE Trans. Syst. Man Cybern.—Syst. Hum. 2005, 35, 189–197. [Google Scholar] [CrossRef]
- Jia, T.; Wu, N.-W.; Chen, T. Cramer-Rao lower bounds of position estimation in a photoelectric theodolite-based network. Opto-Electron. Eng. 2005, 07, 4–6+18. [Google Scholar]
- Farina, A. Target tracking with bearings-only measurements. Signal Process. 1999, 78, 61–78. [Google Scholar] [CrossRef]
- Fisher, P.F.; Tate, N.J. Causes and consequences of error in digital elevation models. Prog. Phys. Geogr. 2006, 30, 467–489. [Google Scholar] [CrossRef]
- Holmes, K.W.; Chadwick, O.A.; Kyriakidis, P.C. Error in a USGS 30-meter digital elevation model and its impact on terrain modeling. J. Hydrol. 2000, 233, 154–173. [Google Scholar] [CrossRef]
- Alfakih, A.Y.; Charron, P.; Piccialli, V.; Wolkowicz, H. Euclidean Distance Matrices, Semidefinite Programming, and Sensor Network Localization. Port. Math. 2011, 68, 53–102. [Google Scholar] [CrossRef] [PubMed]
- Dokmanic, I.; Parhizkar, R.; Ranieri, J.; Vetterli, M. Euclidean Distance Matrices: A Short Walk Through Theory, Algorithms and Applications. IEEE Signal Process. Mag. 2015, 32, 12–30. [Google Scholar] [CrossRef]
- Drusvyatskiy, D.; Krislock, N.; Voronin, Y.L.; Wolkowicz, H. Noisy Euclidean distance realization: Robust facial reduction and the Pareto frontier. Mathematics 2015, 27, 2301–2331. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).