Abstract
In the last three decades, light’s orbital angular momentum (OAM) has been of great interest because it has unique characteristics that make it sought after in many research fields, especially in optical communications. To address the exponentially increasing demands for higher data rates and capacity in optical communication systems, OAM has emerged as an additional degree of freedom for multiplexing and transmitting multiple independent data streams within a single spatial mode using the spatial division multiplexing (SDM) technology. Innumerable research findings have proven to scale up the channel capacity of communication links by a very high order of magnitude, allowing it to circumvent the reaching of optical fiber’s non-linear Shannon limit. This review paper provides a background and overview of OAM beams, covering the fundamental concepts, the various OAM generators, and the recent experimental and commercial applications of the OAM-SDM multiplexing technique in optical communications.
1. Introduction
The technological boom over the past few decades has resulted in the exponential growth of global internet users to over five billion as of the second quarter of the year 2022 [1]. This number has already matched Cisco’s projection for 2023 [2]. This surge has inherently caused the need for better ways to improve the channel capacity of the various communication links used by the devices of internet users such as the usage of high-bandwidth applications [3], high-definition video conferencing contributed by remote working, an increasing number of heavily used social media apps, distributed computing systems, sensor networks, and cloud-based services to name a few. This has unabatedly resulted in the quest to find a solution to the exponential traffic growth on communication networks which is generally believed, based on information theory [4] to be approaching the non-linear Shannon limit [5,6]. Charles Kao’s [7] 2009 physics Nobel-prize-winning research published that single-mode silica-based optical fibers are the future of communications; however, over the years, its scalability is fast running out—this is commonly called a “capacity crunch”, indicating that the capacity limits of the transmission channels are approaching. The implication is that when the current communication channels reach their maximum capacity, more optical cables will be required to be installed to cope with the increasing demand [8]. However, this may not be the best option because upgraded fiber will not even be able to address system capacity scaling issues [9]. Hence, additional ways to multiplex with the existing techniques for a higher channel capacity are required. In the optical communications research community, this problem opened the need to adopt multiplexing techniques such as orbital angular momentum (OAM) and space division multiplexing (SDM) which allows information to be carried simultaneously in multiple modes, theoretically infinite, and which can also be easily adapted with the currently existing technologies.
Recently, Allen et al. [10] discovered that a Laguerre Gaussian (LG) laser mode has twisted phase fronts with a well-defined orbital angular momentum (OAM) of per photon where is the azimuthal mode index also known as OAM mode ranging from ±1 to infinity, acting as the integral multiple of the reduced Planck’s constant . The helical shape and orthogonality of OAM beams are major differentiating characteristics that make it applicable in many unique ways such as in optical tweezers [11,12], atomic manipulation [13,14,15], nanoscale microscopy [16,17,18,19], wireless communication [20], information encoding [21], quantum information processing [22], data storage [23,24,25], and optical communication, which is the main interest of this review.
The bandwidth/capacity of a communication system is determined by the number of orthogonal modes that are available for information to be encoded. This makes orthogonal beams such as OAM beams the best bet as they can be encoded with information and multiplexed with existing multiplexing techniques for an additional degree of freedom to boost the data capacity of transmission channels. Orbital angular momentum multiplexing is a subset of space division multiplexing (SDM), which sees how separately distinguished modes such as OAM modes can be used as alternatives to other multiplexing techniques. Winzer’s report [26] in Figure 1 also shows that SDM technology will be adopted for the desired systems capacities in the next decades. Interestingly, OAM multiplexing has been named as one of the promising technologies for the multi-terabyte per second (Tb/s) and 6G networks [27] and is expected to provide superior performance to the 5G ecosystem.
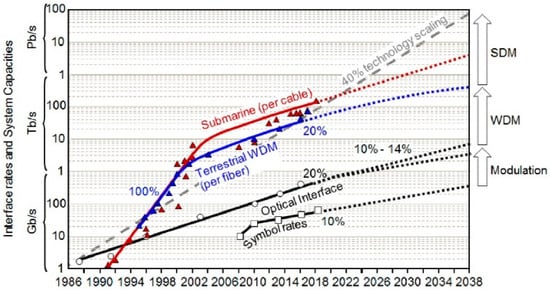
Figure 1.
The long-term evolution/trend of commercial optical transmission systems over the past 30 years and extrapolations for the next 15 years [26] with the assumption that the technology continues to grow at a 40% scale according to the historic trend [9]. Reprinted from ref. [26].
The ever-increasing demands for higher data capacities and additional degrees of freedom in optical communications have driven the evolution of communication channels across various modulation and multiplexing technologies over the years [28,29,30]. Multiplexing allows the simultaneous transmission of combined signals through a single channel with the aim of increasing the capacity of the communication system. In optical communication systems, information is encoded in light signals and transmitted through optical fiber or free space. Light signals have several physical dimensions which can be modulated and multiplexed. The dimensions are time, amplitude/phase, wavelength/frequency, polarization, and spatial dimension. Since the origin of multiplexing [31,32], these dimensions have been explored in several multiplexing techniques (shown in Figure 2) to improve the bandwidth of communication channels, including the following: the amplitude/phase dimension for quadrature amplitude modulation QAM [33,34], which transmits information by combining the phase and amplitude of a carrier wave; time for time-division multiplexing TDM, which is one of the earliest multiplexing techniques used in optical communications [35,36] where several independent signals are transmitted through a channel of different timeslots; polarization for polarization-division multiplexing PDM [37], a multiplexing method which combines two linear and orthogonally polarized signals over the same carrier frequency and doubling the system capacity; the wavelength/frequency for wavelength/frequency-division multiplexing WDM/FDM [38,39] where multiple signals of different wavelength/frequency are transmitted over a single channel; and spatial multiplexing (SM) also known as space-division multiplexing (SDM), termed the next frontier in optical communication [40,41], which uses the multiplicity of spatially separated/unique orthogonal modes (such as OAM modes) to transmit multiple optical data. In multiplexing, the orthogonality of the transmitted signals in the various dimensions is paramount [42]. It ensures that the uniquely separated signals can be multiplexed, transmitted, and demultiplexed without impacting the performance of the transmitted information on each signal.
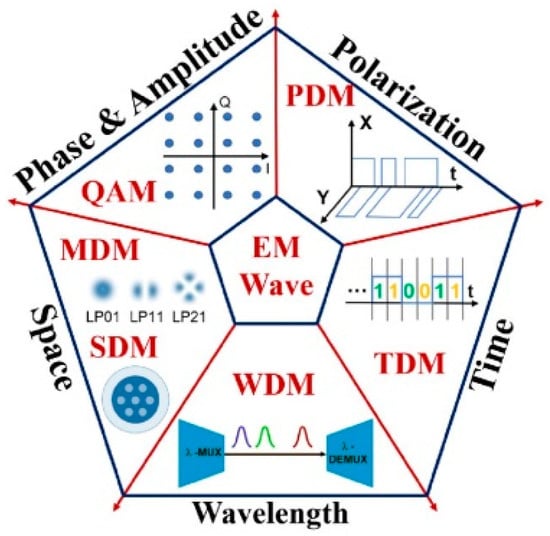
Figure 2.
Multiplexing and modulation techniques in optical communications. (TDM: time-division multiplexing; WDM: wavelength-division multiplexing; SDM: space-division multiplexing; MDM: space-division multiplexing; QAM: quadrature amplitude modulation; PDM: polarization-division multiplexing. Reprinted from ref. [43].
This review is a valuable resource for individuals new to the OAM field and seeking a concise overview and accessible summary of the vast existing literature. It makes the complex concepts of OAM more understandable to a broader audience and offers an extensive awareness of the potential of OAM as a crucial technology for achieving greater channel capacity in future communication networks.
Roadmap of the Review
This review addresses readers who want to have general knowledge about orbital angular momentum and its role in scaling channel capacity and meeting the escalating capacity demands of future communication systems. First, the background of OAM is introduced along with its physical characteristics and connection to the helical phase structure of light, emphasizing their special qualities and potential to boost communication capacity.
Next, the various approaches used to generate OAM modes are addressed. These methods consist of the spatial-generating method and the fiber-generating methods. We also look at their comparisons, advantages, and disadvantages. Furthermore, we discuss how the generated OAM can be detected and how they propagate. The experimental breakthroughs and demonstrations of OAM multiplexing in SDM with other multiplexing techniques such as PDM and WDM are reported. Moreover, a highlight is given about the foundational elements of SDM, such as multicore fibers, and few-mode fibers, and how they enhance channel capacity, spectral efficiency, and increase data rates. Lastly, the necessity for OAM-compatible devices and the recently commercialized OAM-SDM products and devices are mentioned.
2. Background of OAM
According to Maxwell [44], the fundamental property of an electromagnetic wave is energy and momentum. It has a linear momentum and an angular momentum when the particle moves at a position from the origin. The difference between angular momentum and linear momentum is that angular momentum, a vector quantity, has a rotation or spin about an axis and a clear direction in which it acts. For an electromagnetic wave, angular momentum in the z direction requires a component of linear momentum in the x, y plane, a light beam with a transverse momentum component. The linear momentum density is related to the angular momentum density ϳ through where is the medium dielectric permittivity, and E and B are the electric and magnetic fields, respectively. Hence, it follows that the angular momentum of an EM wave propagating in the z-direction requires a component of the electric and/or magnetic field also moving in the z-direction.
By 1936, Beth demonstrated [45] Poynting’s theory [46] of the rotation of circularly polarized light beams transmitted through a half-wave plate. He noticed that the wave plate reversed the handiness of the transmitted polarized light, hence also reversing the angular momentum of the light beam. The change in the light’s angular momentum resulted in a torque τ, a change in angular momentum with respect to time, which caused the wave plate to rotate. In modern physics where momentum per photon is considered, this change in handedness or spin in the left and right directions is known as spin angular momentum (SAM) with the value ±ħ, where ± is the handedness of the circular polarization and ħ is the Planck’s constant, a conserved quantity. Beth believed that a photon should be able to carry a more complex angular momentum which would result in a much greater momentum transfer of ħ as in the case of circularly polarized light.
2.1. OAM in High-Order Transmission
During the high-order transmission experiment, Charles G. Darwin [47] considered a light emitted at a short radius from the atomic orbit and found that the linear momentum of the emitted photon resulted in an extra torque τ on the atomic orbit. This torque is now called the orbital angular momentum (OAM). Orbital angular momentum arises when beams move in a non-perpendicular direction to the propagation axis. In geometric optics approximation, the light which makes up the OAM beams is skewed. Skewed rays are rays that travel through an optical fiber without passing through the axis of the optical fiber. OAM has independent states per photon, being an integer. The signs indicate the handedness with respect to the beam direction where − signifies the clockwise direction and + signifies the anticlockwise direction.
When a particle rotates about position r it is said to have angular momentum; hence, a particle at a position r revolving/spinning around the orbit of an atom is said to possess an orbital angular momentum mvr = n() where m is the mass of the particle, v is the velocity, r is the radius of the orbital, () is the unit of the energy quanta, and n is an integer. Bohr proposed that as an electron absorbs more energy n, it gains more orbital angular momentum [48]. The same has been said of a photon, according to Poynting, that must be accompanied by an angular momentum as it transforms from linear polarization to a circularly polarized light.
2.2. The Total Angular Momentum of a Photon with OAM
For over 200 years, the spin angular momentum (SAM) property of light which is associated with circular polarization has been extensively investigated. Initial reasoning from Cohen-Tannoudji et al. [49] and Nishijima in 1965 [50] was that it was meaningless to separate the angular momentum of a photon into the spin and orbital parts and [51] also pointed out that not all light waves can possess orbital and spin angular momentum. In 1992, 30 years ago, four researchers working in a quantum optics lab debunked this when they theoretically identified these two distinct properties in a photon. It was shown in [52] that the spin angular momentum and orbital angular momentum are well-defined and separately measurable quantities of a photon. In theory, the OAM beams have an unlimited degree of freedom and enhance information-carrying capacity in both classical and quantum optical communications.
Hence, it is now generally accepted that the total angular momentum J of a photon consists of both SAM, the intrinsic component of the photon which is associated with wave polarization, and OAM, the extrinsic component that represents the spatial distribution of the electromagnetic wave/photon:
With SAM and OAM defined, respectively, by:
and are the electric field and the magnetic field, respectively, is the vacuum permittivity, and is the speed of light. The i-superscripted symbols denote the Cartesian components of the corresponding vectors. The conservation of total angular momentum assumes that without the presence of external forces, no energy of the wave is lost as it propagates. The OAM property of a photon can be multiplexed with the polarization property (SAM) of the same photon, which is independent of OAM, to increase channel capacity. Table 1 summarizes the properties of SAM and OAM.

Table 1.
Overview of SAM and OAM features. represents the number of states the circularly polarized waves have whereas is the azimuthal mode index/OAM mode ranging from 1 to infinity . It indicates the number of independent twists ( phase shift in the azimuthal direction) that a beam possesses. ± indicates the handedness of the beams; − signifies that that beam is propagating in a clockwise direction and + signifies the anticlockwise direction.
2.3. Laguerre-Gaussian Modes
Twisted light beams are a new type of laser beam that have separate OAM modes, also known as Laguerre-Gaussian (LG) modes. Laguerre-Gaussian modes are the most common form of a helically phased beam. Each mode is differentiated by the number of spirals or twists it possesses as in Figure 3.
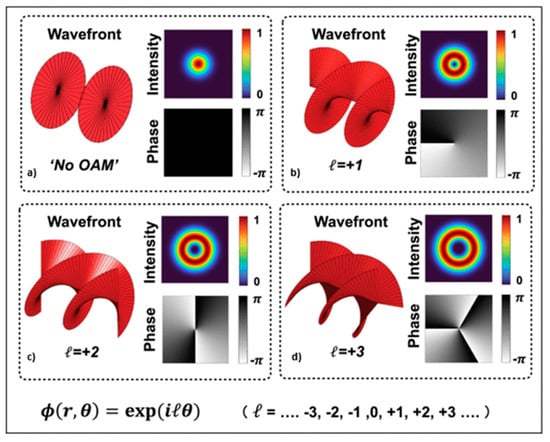
Figure 3.
Wavefront, phase profile, and intensity profiles of OAM beams. (a) l = 0. This is a Gaussian beam with a donut-shaped intensity profile and no twist/OAM in the wavefront; (b) l = 1, which has one twist per wavelength; (c) l = 2, which has two twists per wavelength; (d) l = 3, which has three twists per wavelength. Helical beams (b–d) are all orthogonal to each other with each traveling in the anticlockwise direction indicated by the + sign. These beams can carry independent information on the same transmission and channel frequency. Reprinted from ref. [53].
Allen et al. stated that the amplitude of a Laguerre-Gaussian mode has an azimuthal dependence of and that the Laguerre polynomial distributions of amplitude possess well-defined orbital angular momenta where p is the radial dependence and l is the azimuthal dependence. When p = 0 and l ≠ 0, the LG beam is called which is more applicable in micromanipulation [54]. The intensity profile of a Laguerre-Gaussian beam varies with p and l. When p and l are zero (0), one has a Gaussian intensity profile, a spot, but as the l value increases or decreases, the intensity profiles are seen as an optical vortex indicated by the dark centers surrounded by bright annular rings of helical beams. The higher the p-value, the more rings or intensity profiles as seen in Figure 4.
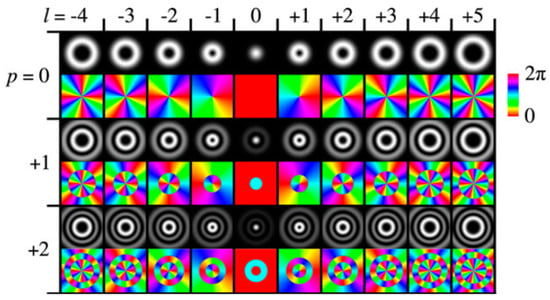
Figure 4.
Intensities (the rings) and phase profiles of LG modes. In each row, the azimuthal index l increases from left to right whereas the radial index p increases from top to bottom. When p = 0 and l = 0, this represents a Gaussian mode (a spot) whereas other modes represent modes. For higher values of l, the beam will have phase fronts that look like intertwined spirals. Reprinted from ref. [55].
The expression for the electric field amplitude of a single LG mode is given by
The coefficient is obtained at the requirement that every mode transmits the same amount of power. is the generalized Laguerre polynomial given by . Where p is the number of radial nodes in the intensity distribution, l is the azimuthal mode number/index giving an OAM of per photon, w(z) is the beam radius, k is the free space wave number, signifies the Rayleigh range. In terms of their intensity cross-section, an LG mode with comprises concentric rings with a zero intensity on the axis [56]. Sjöholm [57] stated that the reason for using the absolute value of ( in the Laguerre polynomial and the amplitude part as seen in Equation (2) is that the Laguerre polynomials are only defined for and that having the amplitude to the power of −l would result in infinite amplitude as tends to 0.
3. Generation of OAM Beams
OAM or vortex beams in the optical domain can be generated in free space using spatial-generating devices and in optical fibers using fiber-generating devices.
3.1. Spatial-Generating Methods
OAM is usually generated by manipulating the spatial phase structure of the electric field of an electromagnetic wave [58]. A spatial device with a specially designed surface structure is used to imprint a phase profile on the electric field of a propagating plane light wave as it passes through the device. The resulting beam has a spiral or helical phased structure because of the spatial variation in the phase. A structured light wave can also be generated when an external magnetic field interacts with the light wave on a carbon nanotube [59]. When a magnetic field is applied to an optical device made from magneto-optical materials and a light wave is passed through, the refractive index of the wave becomes altered and this also changes the spatial phase distribution of the light [60,61].
The spatial-generating methods include the use of spatial devices such as cylindrical lenses [62,63,64,65,66], spiral phase plates [67,68,69,70,71,72,73,74], Phase holograms [75,76,77,78,79,80,81], spatial light modulators [82,83,84,85,86,87,88], and q-plates [89,90,91,92].
Allen’s experiment established high-order Hermite-Gaussian (HG) modes are transformed into a helically phased beam with an azimuthal dependence exp(−ilφ), a phase singularity or vortex at the center. The conversion process is performed in various optical materials known as mode converters shown in Figure 5. A fundamental transverse mode (a Gaussian beam, ) emitted from a laser, makes a small angle as it passes through the optical medium. This gives a twist to the resulting beam called the Laguerre-Gaussian beam [93].
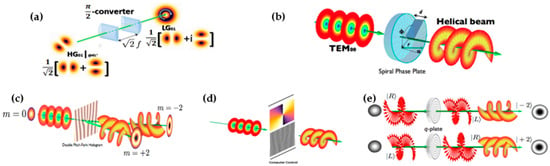
Figure 5.
Exemplification of OAM spatial generation techniques: (a) Cylindrical lens which was used by Allen et al. to transform HG modes to LG modes with OAM and a phase singularity at the center; (b) spiral phase plate is the simplest converter. It has spiral phase distribution which converts a plane Gaussian beam of a particular wavelength into an OAM beam that has a spiral wavefront; (c) phase hologram with the use of forked diffraction grating, an OAM beam is formed as it passes through the forked grating. The number of forks determines the OAM number of the beam generated; (d) spatial light modulator uses the molecules in their liquid crystal to deflect and give a twist to the incident plane beam; (e) Q-plates are inhomogeneous birefringent devices that convert Gaussian beams to OAM beams.
It is important to note that distance and coherence length of propagation have significant effects on the propagation and generation of a vortex beam. As the vortices propagate farther or as the coherence length decreases, a vortex of an opposite sign is formed, resulting in two vortices in space; however, this does not affect the properties of the vortex beam, making it potentially useful in optical communications [94].
It should also be noted that these methods are plagued with disadvantages such as large volume space requirement by the spatial devices, high insertion loss due to the high refractive index difference at the interphase where the incident plane wave is being converted to OAM beams, a limited number of OAM beams created per time, and a high cost of fabrication of the optical materials as new materials need to be fabricated for the desired OAM number. Table 2 features a comparison of the different spatial OAM generation methods.

Table 2.
Comparison of the spatial generation techniques of OAM.
Still in the spatial domain, generating OAM beams at the nanoscale is of significant interest for various applications in nanophotonics [95,96] and optical device miniaturization [97]. Recent developments in the creation and detection of optical vortex as well as some of its applications are observed in photonic integrated circuits [98,99,100,101,102,103], micro-ring resonators [104,105,106,107,108,109,110,111], metamaterials [112,113,114,115,116,117,118,119,120], plasmonic nanostructures [121,122,123,124], and metasurfaces [125,126,127,128], which offer precise control over the phase, amplitude, and polarization of light at the nanoscale. By engineering the meta-atoms on a metasurface, it is possible to design them to introduce a tailored phase gradient, resulting in the generation of OAM beams. Metasurfaces can be fabricated with various materials, including plasmonic nanostructures or dielectric resonators, allowing for efficient manipulation of light and generation of OAM beams at the nanoscale.
In general, at the time of writing this review, it suffices to say that the spatial-generating methods have many limitations in the fabrication of the devices and cost among others, and cannot be commercialized profitably; hence, other methods need to be embraced.
3.2. Fiber-Generating Methods
The second method of generating OAM modes is the so-called fiber-generating method. This is more advantageous owing to characteristics such as miniaturization, lower insertion loss in fibers, increased transmission distance, higher efficiency, and a reduction in external interference, which is lacking in the spatial generating method [129]. Moreover, owing to the cylindrical shape of fibers, the eigenmode of the incident wave is easily restricted to the cylindrical symmetry of the fiber during conversion into OAM beams.
Conventional optical fibers cannot transmit OAM; hence, new specialized fibers need to be designed to support OAM mode transmission. These specialized fibers, however, require converters listed below and shown in the experimental setups in Figure 6.
- (a)
- Fiber gratings [130] used in FMF [131];
- (b)
- Mode-selective couplers [132] used in both SMF and FMF;
- (c)
- Photonic lanterns [133,134] also used in SMF;
- (d)
- Microstructure optical fibers or photonic crystal fibers (PCF) [135,136,137].
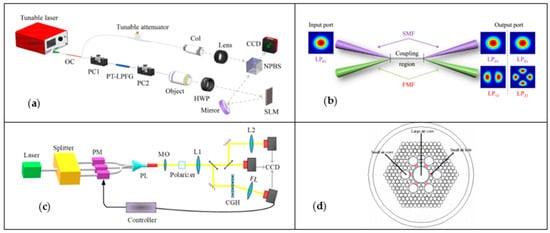
Figure 6.
Experimental setup of OAM generation through fibers. (a) Fiber grating: Experimental setup to generate and detect 4th-order OAM modes by presetting the number of twists before the fabrication of the fiber grating. OC-optical coupler; PC-polarization controller; PT-LPFG—preset twist-long period fiber gratings; HWP-half-wave plate; SLM—spatial light modulator; Col—collimator; NPBS—non-polarization beam splitter. Reprinted from ref. [138]; (b) mode selective couplers which uses a single-mode fiber (SMF) as the input fiber and FMF as the output fiber joined together with fiber optic couplers. The mode coupler ensures that the refractive index of the fundamental Gaussian at the input fiber is retained in the resultant OAM mode at the output fiber. Reprinted from ref. [139]; (c) photonic lanterns: The fundamental mode is emitted from the laser passes through the splitter into the photonic lantern which couples and converts the beam into the desired OAM beam. PM—phase modulators; PL- photonic lantern; CGH—computer-generated hologram; MO—microscope objectives; L1, L2—imaging lenses; FL—Fourier lens. Reprinted from ref. [140]; (d) Photonic crystal fiber. Reprinted from ref. [141].
3.3. Photonic Crystal Fibers (PCF)
Although fibers that support OAM states have had limited success because they have only been able to propagate very short distances and the modal intensity patterns are unstable due to the mode mixing of the eigenmodes [142,143], specially designed microstructure optical fibers (MOFs), also known as photonic crystal fibers (PCF), have shown incredible abilities with flexible and adjustable fiber parameters structure [144]. Most especially, structures comprising air holes [145,146,147,148]. These perform excellently and are easy to manufacture. Some PCF designs with air holes are as follows:
- A circular PCF (C-PCF) supporting 26 OAM modes [149];
- A C-PCF with square air holes in the cladding that supports 46 OAM [150];
- A unique PCF with square and circular air holes (SC-PCF) that support 86 OAM modes [151];
- A pure-silica-based PCF with a central round air hole that supports 114 OAM modes was also designed showing higher effective refractive index difference, lower confinement loss, and non-linear coefficient [152];
- A PCF with an ssk2 dense crown glass ring with optimized central air hole radius and annular region thickness stably transmitted 394 OAM modes [153];
- A total of 84 OAM modes [154], 110 OAM modes [155], and 166 OAM modes [156].
The several results generated through the finite element analysis of the above-listed PCFs show a result of an effective modal index, low/flat dispersion, small and controllable non-linearity, high birefringent, high mode quality, high performance, and avoid mode coupling. These qualities are needed for the best performance in long-distance communication systems and hold a huge promise in high-performance optical communication systems. However, more improvements are seen with PCF designs made with low refractive index rings owing to their easier fabrication/manufacturing [157]. Table 3 highlights the advantages and disadvantages of each fiber-generating method, whereas Table 4 gives a general merit and demerit of the spatial method and fiber method according to their corresponding references in the texts.

Table 3.
Advantages and disadvantages of the fiber-generation technique of OAM.

Table 4.
Advantages and disadvantages of the fiber-generation technique of OAM.
3.4. Measurement of OAM Modes
As much as it is important to generate OAM beams, it is equally important to be able to measure and determine the number of modes an OAM beam possesses for use in diverse applications. The topological charge or OAM mode of a helical or vortex beam can be measured by examining the interference pattern between the beam and a reference beam [158] and the use of a Mach–Zehnder interferometer for higher-order topological charges [159,160]. The OAM of a single photon can also be measured using a computer-generated hologram setup [161]; the fork dislocation of the hologram is used to generate the azimuthal phase dependence of on the incident beam, giving it a helical phase front. To turn the twisted beam back into a plane wave, a reverse hologram is used to focus the helical beam through a pinhole, and it is then detected as a plane phase front. Measurements of the OAM state of a beam with SLM-based annular gratings were also reported in [162] where the number of black fringes and the direction of the diffraction patterns indicate the size and sign of topological charge values, respectively.
These measurements can be completed theoretically and experimentally in close interaction [163]. Theoretical methods involve mathematical simulations and models to understand, predict, and optimize the design parameters for the generation of OAM in light beams. Experimental methods involve physically manipulating light beams with the use of various optical components mentioned in Section 3 to imprint a desired spatial phase structure onto the light beam, resulting in the creation of OAM modes. Theoretical models guide the development of experimental techniques by providing insights into the fundamental principles of OAM generation whereas experimental results inform and validate theoretical models by providing empirical data and feedback for refining theoretical understanding. However, both approaches adhere to the azimuthal symmetry and conservation of angular momentum associated with OAM. Both theoretical and experimental methods essentially contribute to advancing knowledge and applications of OAM in various fields, such as optical communications, imaging, and quantum information processing.
4. Multiplexing of Information-Carrying OAM Beams
When a Gaussian beam encoded with information passes through an optical element such as a spiral phase plate, it acquires an azimuthal phase dependence of and becomes an OAM beam with a helical phase front. Multiple of such OAM beams (), each carrying its own information, can be multiplexed. Each helical beam develops a phase singularity (optical vortex with a bright ring and a dark center) while the wavefront spirals around the optical axis as they propagate. The orbital angular momentum of each OAM beam remains unchanged by its propagation through free space and spherical lenses [164].
The beam with the highest OAM number creates the outermost vortex by wrapping the smaller vortices around itself, whereas the helix with the lowest OAM number is located in the center of the multiplexed vortex structure. As a result, many OAM beams propagate as though they were a single beam.
After their transit through the communication channel, the OAM beam must be converted back to a Gaussian to extract the information contained in them. An inverse spatial element (SPP) with a predetermined charge of is utilized and used for demultiplexing, isolating, and recovering each data-carrying OAM beam at the receiver end to eliminate the azimuthal phase dependence of the OAM beam and its information [165].
Most OAM beam multiplexing was experimentally demonstrated across relatively short distances of less than 1m in the lab often; however, in recent years, several investigations have investigated the possibility of employing OAM beams to create long-distance FSO linkages in the field environment [166,167].
4.1. OAM in Space-Division Multiplexing
Space-division multiplexing is a technology used in optical communication systems to boost capacity and data transmission capabilities by employing various spatial modes within an optical fiber or waveguide. Unlike TDM or WDM, which used time or frequency, SDM exploits the spatial domain to simultaneously transmit many independent data streams. Using fibers as the communication links with the SDM multiplexing techniques, reports show that 2Pbps/fiber was achieved [168,169,170,171,172], half of which has been unrealized with the other multiplexing methods. This is because each spatial path or mod4e in SDM is a separate/independent communication channel; hence, it is extremely useful in improving the capacity of communication systems.
SDM relies on multiplexing spatially separated beam modes such as linearly polarized (LP) modes [173,174,175] and OAM modes [176,177,178]. This is made possible by orthogonality, transverse phase structure, and a helical/twisted phase front of such modes. OAM multiplexing corresponds with mode-division multiplexing (MDM), which is a popular form of SDM multiplexing. MDM can increase the transmission capacity in optical fiber communications due to the orthogonality and theoretically infinite states of OAM modes [179] used in such a technique.
Based on their orthogonality, OAM beams could also be multiplexed with the other multiplexing techniques and transmitted over free space or fiber to increase the data capacity of communication systems by the number of beams transmitted. Likewise, the spectral efficiency is increased because the transmitted beams are in the same frequency range [180]. The first time OAM multiplexing was used for MDM communication links, four different OAM modes were multiplexed on two polarizations in free space in Figure 7a–c. This yielded a data rate of 1.37 Tbit/s [181].
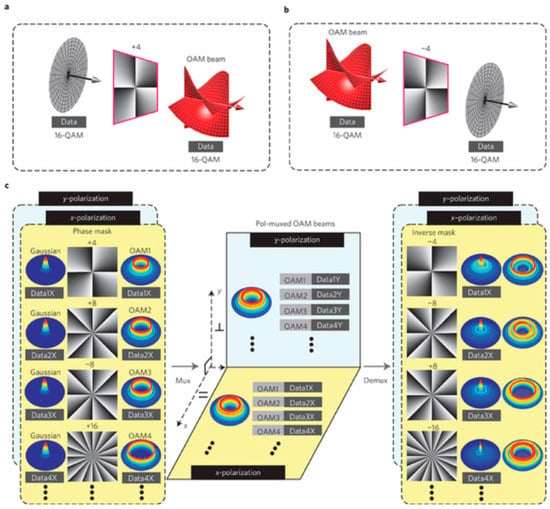
Figure 7.
OAM multiplexing with PDM in free space. (a) Represents the generation of an information-carrying OAM beam after an information-carrying Gaussian has been passed through a spatial element (spiral phase mask) with OAM mode l = 4; (b) signifies the recovery of an information-carrying Gaussian from an information-carrying OAM beam after passing through an inverse spiral phase mask of l = −4; (c) describes the multiplexing and demultiplexing of the polarization multiplexed OAM beams. Reprinted from ref. [181].
In addition to PDM multiplexing, OAM beams can also be multiplexed with WDM to boost the capacity of OAM multiplexed in free space links [182]. In the experiment illustrated in Figure 8a,b, the OAM multiplexed beams and OAM-PDM multiplexed beams, respectively, are carried on the same frequency. Figure 8c depicts how other independent data channels can be sent or received using the other frequencies on the same number of OAM modes N and both polarizations. Because OAM multiplexing and PDM are compatible with WDM in this manner, the aggregated connection capacity is boosted further by M times by using M separate carrier frequencies. Overall, the data rate of the communication link is 2 N M, indicating that OAM is truly an additional degree of freedom to the PDM and WDM techniques. In the experimental setup, a data rate of 100Tbit/s was achieved with 12 OAM modes, two polarizations, and 42 wavelengths.
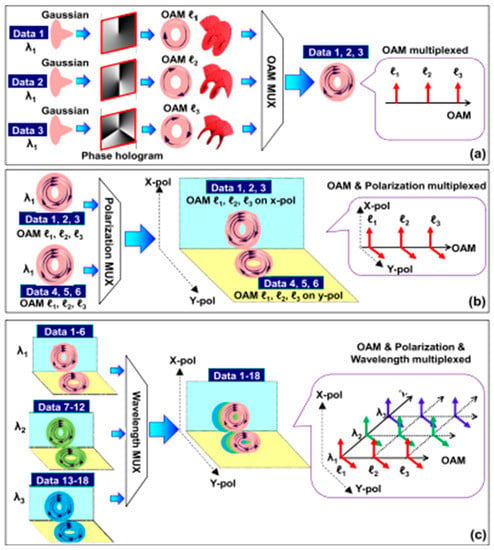
Figure 8.
The idea of boosting channel capacity by combining OAM multiplexing with PDM and WDM. (a) Using OAM beams to multiplex numerous data channels; (b) combination of PDM and OAM multiplexing; (c) a total of 12 OAM modes, 2 polarizations, and 42 wavelengths were multiplexed to reach a 100.8 Tbit/s aggregated data rate by combining OAM multiplexing and PDM with WDM [182].
Aside from OAM modes, the SDM technique can also be used in multi-core fiber (MCF) [183], a fiber that consists of multiple individual cores within a single fiber. The number of cores in the fiber gives the fiber capacity. Moreover, few-mode fiber (FMF) [184], which supports multiple spatial modes within a single core, is employed in SDM. Here, the number of modes supported by the fiber gives the fiber capacity. SDM transmission allows a combination of multiple cores within a single cladding (MCF) or multiple modes in a single core (FMF) [185]. SDM thus positions itself as the multiplexing approach best suited to carry future capacity needs.
The advantages of OAM-based MDM systems are numerous. Apart from increasing the channel capacity and spectral efficiency of communication links due to the several spatial modes accommodated, SDM also provides scalability by enabling the addition of more spatial pathways or modes when the need for more capacity rises, without necessitating substantial changes to the underlying infrastructure. OAM-SDM also simultaneously enables significant reductions in cost-per-bit and increased energy efficiency [186]. Likewise, it will avoid complex multiple-input and multiple-output (MIMO) digital signal processing and overcome intermodal crosstalk and finite modes [187,188,189]. In the multiple-in multiple-out (MIMO) technique, the channel capacity increases in correspondence with the number of transmitting and receiving antennas [190,191], making it a bulky and expensive technique.
Although there are many advantages, the actual application of OAM-based multiplexing is still constrained significantly by crosstalk. Crosstalk between OAM modes can cause interference, poor signal quality, and impose a limit to the number of multiplexable channels [192,193].
4.2. OAM-Compatible Infrastructures and Devices for Scaling
Although OAM-SDM systems are taking the top research attention, Winzer [194] looked at the integration of SDM components into the existing non-SDM infrastructure. Data network designers believe that in order to use the currently embedded fiber structures to scale up the channel capacity and spectral efficiency of communication system, the OAM optical communications research community must come up with compatible new technologies such as devices such as photonics integrated circuits, light sources, (de)modulators, amplifiers, switching devices, OAM filters [195], transmitters, receivers, and signal processing elements which support compact, efficient, cost-effective OAM generation, multiplexing, demultiplexing, and detection [196,197]. Figure 9 shows some of the devices needed to fully scale the OAM-SDM technique.
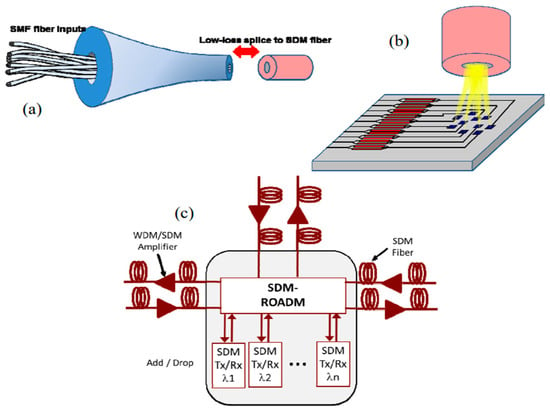
Figure 9.
SDM-compatible devices. (a) Elegantly scalable passive multiplexers, (b) integrated transmitter and receiver arrays providing low-loss coupling to many modes of an SDM fiber, and (c) reconfigurable routing elements that can direct SDM traffic without the need for electronic MIMO in between transmitter and receiver. Reprinted from ref. [198].
In terms of commercialization of the SDM multiplexing technique, an optical lab named “Cailabs” has developed a solution using multi-plane light conversion (MPLC) technology to generate high-order, high-purity OAM beams in free space and fiber [199]. The MPLC technology converts multiplexed modes from SMF inputs by using successive reflections on a single reflective phase plate and a mirror. The technology then converts each input into a given mode within an MMF or free space output. Since each mode represents an additional information channel, this means that there would be an increase in the bandwidth which is the goal of all OAM research. The setup also consists of a demultiplexer which recovers the original signal information. According to the company, their solution overcomes all the other constraints by the other generation techniques featuring a high number of modes (up to 45 modes), optimal crosstalk, low insertion loss level, completely passive, and compatibility with a wide range of wavelengths. It is the only commercial solution that offers OAM-SDM multiplexing at the time of writing this review.
Several commercial enterprises also demonstrated wireless transmission for multiplexed OAM beams [200,201,202], achieving a data rate 100 that of LTE and Wi-Fi. These can be used for next-generation 5G and 6G systems, such as connected cars, virtual reality/augmented reality (VR/AR), high-definition video transmission, and remote medicine.
5. Summary and Outlook
5.1. Summary
This work offers an overview of the orbital angular momentum components of electromagnetic waves and their capabilities in boosting the optical communication channel to meet the growing capacity needs of future technologies. Firstly, the authors reviewed why OAM beams are important, especially in optical communications. The background of OAM was presented and the various methods of generating OAM in space, such as the use of spiral phase plate, cylindrical lens, and others that convert incident Gaussian beams to beams with twisted wavefronts also known as Laguerre-Gaussian mode. The orthogonality of these modes makes them suitable for various applications and makes it possible for them to be multiplexed with the other multiplexing techniques to generate higher channel capacity. Additionally, the authors reviewed how OAM beams are being generated in specialized optical fibers with the use of fiber gratings, couplers, and especially the photonic crystal fibers that support OAM mode transmission needed in high-performance optical communication. Contexts of multiplexing OAM with SDM, PDM, and WDM were also considered.
5.2. Outlook and Future Perspectives
There are still many questions and challenges to be overcome in OAM research. These challenges can be turned into opportunities for the future development and utilization of OAM. It would be interesting to see more research towards the design of efficient cost-effective and compatible multiplexing and demultiplexing devices that would support a large number of OAM-SDM modes [203] including some advances in tunable, compact, and high-power OAM lasers [204,205,206,207]. Multiplexing of OAM and WDM was recently experimented with in a multimode fiber to also improve capacity [208], so this could also be considered to keep pushing the limits and scope of OAM beams. In future research, the development of cutting-edge fibers which are fit for SDM and which will also be able to accommodate the next frontier technologies needs to be investigated. Crosstalk between channels is a clear potential drawback that is continuously being addressed [209,210]. An interdisciplinary exploration of OAM in other scientific disciplines can also lead to new discoveries and applications in diverse fields.
With ongoing attempts to investigate and enhance various methodologies, including multicore fibers, few-mode fibers, and OAM-based systems, SDM remains a topic of current study and development. These developments in SDM will help optical communication systems fulfill the goal of introducing OAM as an additional degree of freedom and increasing optical channel capacities. At the current rate of research in the field, it is believed that this feat would be achieved in the near future and commercialization would commence on a huge scale.
Author Contributions
Conceptualization, T.M.O. and P.A.R.; writing—original draft preparation, T.M.O.; writing—review and editing, T.M.O., P.A.R. and M.R.; supervision, P.A.R. and M.R.; funding acquisition, P.A.R. and M.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Portuguese National Funding Agency (FCT-MCTES), UIDB/04559/2020 (LIBPhys), and UIDP/04559/2020 (LIBPhys).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Statista. Internet and Social Media Users in the World 2022. Available online: https://www.statista.com/statistics/617136/digital-population-worldwide/ (accessed on 20 December 2022).
- Cisco Annual Internet Report. White Paper Cisco Public. 2018. Available online: https://www.cisco.com/c/en/us/solutions/collateral/executive-perspectives/annual-internet-report/white-paper-c11-741490.html (accessed on 6 January 2023).
- Cisco Meraki Blog. 5 Apps That Hog Bandwidth on Your Network. Available online: https://meraki.cisco.com/blog/2011/08/5-apps-that-hog-bandwidth-on-your-network/ (accessed on 6 January 2023).
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Ellis, A.D.; Zhao, J.; Cotter, D. Approaching the Non-Linear Shannon Limit. J. Lightwave Technol. 2010, 28, 423–433. [Google Scholar] [CrossRef]
- Essiambre, R.-J.; Kramer, G.; Winzer, P.J.; Foschini, G.J.; Goebel, B. Capacity Limits of Optical Fiber Networks. J. Lightwave Technol. 2010, 28, 662–701. [Google Scholar] [CrossRef]
- Kao, K.; Hockham, G. Dielectric-fibre surface waveguides for optical frequencies. Proc. Inst. Electr. Eng. 1966, 113, 1151–1158. [Google Scholar] [CrossRef]
- Ellis, D.; Suibhne, N.M.; Saad, D.; Payne, D.N. Communication networks beyond the capacity crunch. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 2062. [Google Scholar] [CrossRef]
- Winzer, P.J.; Neilson, D.T. From Scaling Disparities to Integrated Parallelism: A Decathlon for a Decade. J. Lightwave Technol. 2017, 35, 1099–1115. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Padgett, M.; Bowman, R. Tweezers with a twist. Nat. Photonics 2011, 5, 343–348. [Google Scholar] [CrossRef]
- Dholakia, K.; Čižmár, T. Shaping the future of manipulation. Nat. Photonics 2011, 5, 335–342. [Google Scholar] [CrossRef]
- Moretti, D.; Felinto, D.; Tabosa, J.W.R. Storage and manipulation of orbital angular momentum of light in a cold atomic ensemble. In Proceedings of the CLEO/Europe-EQEC 2009-European Conference on Lasers and Electro-Optics and the European Quantum Electronics Conference, Munich, Germany, 14–19 June 2009. [Google Scholar] [CrossRef]
- Liu, X.J.; Liu, X.; Kwek, L.C.; Oh, C.H. Manipulating atomic states via optical orbital angular-momentum. Front. Phys. China 2008, 3, 113–125. [Google Scholar] [CrossRef]
- Toyoda, K.; Miyamoto, K.; Aoki, N.; Morita, R.; Omatsu, T. Using optical vortex to control the chirality of twisted metal nanostructures. Nano Lett. 2012, 12, 3645–3649. [Google Scholar] [CrossRef] [PubMed]
- Tamburini, F.; Anzolin, G.; Umbriaco, G.; Bianchini, A.; Barbieri, C. Overcoming the Rayleigh criterion limit with optical vortices. Phys. Rev. Lett. 2006, 97, 163903. [Google Scholar] [CrossRef]
- Ritsch-Marte, M.; Fürhapter, S.; Jesacher, A.; Bernet, S. Spiral interferometry. Opt. Lett. 2005, 30, 1953–1955. [Google Scholar] [CrossRef]
- Grillo, V.; Harvey, T.R.; Venturi, F.; Pierce, J.S.; Balboni, R.; Bouchard, F.; Gazzadi, G.C.; Frabboni, S.; Tavabi, A.H.; Li, Z.-A.; et al. Observation of nanoscale magnetic fields using twisted electron beams. Nat. Commun. 2017, 8, 689. Available online: https://sci-hub.ru/https://www.nature.com/articles/s41467-017-00829-5 (accessed on 26 January 2023). [CrossRef] [PubMed]
- Noguchi, Y.; Nakayama, S.; Ishida, T.; Saitoh, K.; Uchida, M. Efficient Measurement of the Orbital-Angular-Momentum Spectrum of an Electron Beam via a Dammann Vortex Grating. Phys. Rev. Appl. 2019, 12, 064062. [Google Scholar] [CrossRef]
- Noor, S.K.; Yasin, M.N.M.; Ismail, A.M.; Osman, M.N.; Soh, P.J.; Ramli, N.; Rambe, A.H. A Review of Orbital Angular Momentum Vortex Waves for the Next Generation Wireless Communications. IEEE Access 2022, 10, 89465–89484. [Google Scholar] [CrossRef]
- Lamilla, E.; Sacarelo, C.; Alvarez-Alvarado, M.S.; Pazmino, A.; Iza, P. Optical Encoding Model Based on Orbital Angular Momentum Powered by Machine Learning. Sensors 2023, 23, 2755. [Google Scholar] [CrossRef] [PubMed]
- Nagali, E.; Sciarrino, F. Manipulation of Photonic Orbital Angular Momentum for Quantum Information Processing. In Advanced Photonic Sciences; InTech: London, UK, 2012. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, L.; Zhao, S. Orbital Angular Momentum Multiplexing Holography for Data Storage. IEEE Photonics Technol. Lett. 2023, 35, 179–182. [Google Scholar] [CrossRef]
- Ding, D.S.; Zhang, W.; Zhou, Z.-Y.; Shi, S.; Xiang, G.-Y.; Wang, X.-S.; Jiang, Y.-K.; Shi, B.-S.; Guo, G.-C. Quantum storage of orbital angular momentum entanglement in an atomic ensemble. Phys. Rev. Lett. 2015, 114, 050502. [Google Scholar] [CrossRef]
- Mcmanamon, P.; Vedadi, A.; Willner, A.E.; Choudhary, D.; Montifiore, N.; Harlev, O. High capacity and access rate, data storage using laser communications. Opt. Eng. 2021, 60, 015105. [Google Scholar] [CrossRef]
- Winzer, P.J.; Neilson, D.T.; Chraplyvy, A.R. Fiber-optic transmission and networking: The previous 20 and the next 20 years [Invited]. Opt. Express 2018, 26, 24190. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiao, Y.; Ma, Z.; Xiao, M.; Ding, Z.; Lei, X.; Karagiannidis, G.K.; Fan, P. 6G Wireless Networks: Vision, Requirements, Architecture, and Key Technologies. IEEE Veh. Technol. Mag. 2019, 14, 28–41. [Google Scholar] [CrossRef]
- Akyildiz, F.I.; Kak, A.; Nie, S. 6G and Beyond: The Future of Wireless Communications Systems. IEEE Access 2020, 8, 133995–134030. [Google Scholar] [CrossRef]
- Larsson, E. Communication Systems. 1975. Available online: https://sci-hub.ru/https://commsys.isy.liu.se/MCSY-information-2022.pdf (accessed on 26 May 2023).
- Al-Amri, M.D.; El-Gomati, M.M.; Zubairy, M.S. Optics in Our Time; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Schwartz, M. The Origins of Carrier Multiplexing: Major George Owen Squier and AT&T. IEEE Commun. Mag. 2008, 46, 20–24. [Google Scholar] [CrossRef]
- Squier, G.O. Multiplex Telephony and Telegraphy by Means of Electric Waves Guided by Wires. Proc. Am. Inst. Electr. Eng. 1911, 30, 857–905. [Google Scholar] [CrossRef]
- Hanzo, L.; Webb, W.T.; Keller, T. Single-and Multi-Carrier Quadrature Amplitude Modulation: Principles and Applications for Personal Communications, WLANs and Broadcasting; Wiley: Chichester, UK, 2000. [Google Scholar]
- Modern Quadrature Amplitude Modulation: Principles and Applications for Fixed and Wireless Channels. Available online: https://www.researchgate.net/publication/37530662_Modern_Quadrature_Amplitude_Modulation_Principles_and_applications_for_fixed_and_wireless_channels (accessed on 5 January 2023).
- Tucker, R.S.; Eisenstein, G.; Korotky, S.K. Optical time-division multiplexing for very high bit-rate transmission. J. Lightwave Technol. 1988, 6, 1737–1749. [Google Scholar] [CrossRef]
- Spirit, D.M.; Ellis, A.D.; Barnsley, P.E. Optical Time Division Multiplexing: Systems and Networks. IEEE Commun. Mag. 1994, 32, 56–62. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Yan, L.S.; Pan, Y.; Jiang, L.; Yi, A.L.; Pan, W.; Luo, B. Use of polarization freedom beyond polarizationdivision multiplexing to support high-speed and spectral-efficient data transmission. Light. Sci. Appl. 2017, 6, e16207. [Google Scholar] [CrossRef] [PubMed]
- Brackett, C.A. Dense Wavelength Division Multiplexing Networks: Principles and Applications. IEEE J. Sel. Areas Commun. 1990, 8, 948–964. [Google Scholar] [CrossRef]
- Grobe, K.; Eiselt, M. Wavelength Division Multiplexing: A Practical Engineering Guide. Available online: https://www.perlego.com/book/1001511/wavelength-division-multiplexing-a-practical-engineering-guide-pdf (accessed on 5 January 2023).
- Li, G.; Bai, N.; Zhao, N.; Xia, C. Space-division multiplexing: The next frontier in optical communication. Adv. Opt. Photonics 2014, 6, 413. [Google Scholar] [CrossRef]
- Rademacher, G.; Luís, R.S.; Puttnam, B.J. Space-division multiplexing for optical fiber communications. Optica 2021, 8, 1186–1203. [Google Scholar] [CrossRef]
- Proakis, G.; Salehi, M. Digital Communications; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Li, S.A.; Huang, H.; Pan, Z.; Yin, R.; Wang, Y.; Fang, Y.; Zhang, Y.; Bao, C.; Ren, Y.; Li, Z.; et al. Enabling Technology in High-Baud-Rate Coherent Optical Communication Systems. IEEE Access 2020, 8, 111318–111329. [Google Scholar] [CrossRef]
- Poynting, J.H. XV. On the transfer of energy in the electromagnetic field. Philos. Trans. R. Soc. Lond. 1884, 175, 343–361. [Google Scholar] [CrossRef]
- Beth, R.A. Mechanical Detection and Measurement of the Angular Momentum of Light. Phys. Rev. 1936, 50, 115–125. [Google Scholar] [CrossRef]
- Poynting, J.H. The wave motion of a revolving shaft, and a suggestion as to the angular momentum in a beam of circularly polarised light. Proc. R. Soc. Lond. Ser. A 1909, 82, 560–567. [Google Scholar] [CrossRef]
- Bangham, D.H.; Fakhoury, N. Notes on the theory of radiation. Proc. R. Soc. Lond. Ser. A 1932, 136, 36–52. [Google Scholar] [CrossRef]
- Kragh, H. Niels Bohr and the Quantum Atom; Oxford University Press: Oxford, UK, 2012. [Google Scholar] [CrossRef]
- Cohen-Tannoudji, C.; Dupont-roc, J.; Grynberg, G. Photons and Atoms: Introduction to Quantum Electrodynamics. Choice Rev. Online 1989, 27, 5805. [Google Scholar] [CrossRef]
- Nishijima. Quantum electrodynamics. J. Franklin Inst. 1965, 280, 451–452. [Google Scholar] [CrossRef]
- Zhang, F. An Evanescent Light Wave Can-not Possess a Transverse Spin. J. Mod. Phys. 2019, 10, 459–465. [Google Scholar] [CrossRef]
- van Enk, S.J.; Nienhuis, G. Spin and Orbital Angular Momentum of Photons. Europhys. Lett. (EPL) 1994, 25, 497–501. [Google Scholar] [CrossRef]
- Willner, E.; Song, H.; Zou, K.; Zhou, H.; Su, X. Orbital Angular Momentum Beams for High-Capacity Communications. J. Lightwave Technol. 2023, 41, 1918–1933. [Google Scholar] [CrossRef]
- Cao, J.; Chen, Q.; Guo, H. Creation of a controllable three dimensional optical chain by TEM01 mode radially polarized Laguerre–Gaussian beam. Optik 2013, 124, 2033–2036. [Google Scholar] [CrossRef]
- Nicolas, A.; Veissier, L.; Giacobino, E.; Maxein, D.; Laurat, J. Quantum state tomography of orbital angular momentum photonic qubits via a projection-based technique. New J. Phys. 2015, 17, 033037. [Google Scholar] [CrossRef]
- Yao, M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonics 2011, 3, 161. [Google Scholar] [CrossRef]
- Sjöholm, J.; Palmer, K. Angular Momentum of Electromagnetic Radiation. Fundamental Physics Applied to the Radio Domain for Innovative Studies of Space and Development of New Concepts in Wireless Communications. May 2009. Available online: http://arxiv.org/abs/0905.0190 (accessed on 29 January 2023).
- Bai, X.; Jin, R.; Liu, L.; Geng, J.; Liang, X. Generation of OAM Radio Waves with Three Polarizations Using Circular Horn Antenna Array. Int. J. Antennas Propag. 2015, 2015, 132549. [Google Scholar] [CrossRef]
- Ajiki, H.; Ando, T. Aharonov-Bohm effect in carbon nanotubes. Phys. B Condens. Matter 1994, 201, 349–352. [Google Scholar] [CrossRef]
- García-Merino, J.A.; Mercado-Zúñiga, C.; Hernández-Acosta, M.A.; Aguilar-Pérez, L.A.; Villanueva-Fierro, I.; Hevia, S.A.; Torres-Torres, C. Magnetic frequency identification by quantum interference in magnetoplasmonic carbon/metal nanostructures. Mater. Sci. Eng. B 2021, 266, 115048. [Google Scholar] [CrossRef]
- Hurtado-Aviles, E.A.; Vila, M.; Vilatela, J.J.; Martines-Arano, H.; Bornacelli, J.; García-Merino, J.A.; Cervantes-Sodi, F.; Torres-Torres, C. Structured light using carbon nanostructures driven by Kerr nonlinearities and a magnetic field. Phys. Chem. Chem. Phys. 2022, 24, 1081–1090. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Porfirev, A.P.; Kozlova, E.S. Three different types of astigmatic Hermite-Gaussian beams with orbital angular momentum. J. Opt. 2019, 21, 115601. [Google Scholar] [CrossRef]
- Volyar, A.; Bretsko, M.; Akimova, Y.; Egorov, Y. Measurement of the vortex and orbital angular momentum spectra with a single cylindrical lens. Appl. Opt. 2019, 58, 5748. [Google Scholar] [CrossRef]
- Pan, J.; Shen, Y.; Wan, Z.; Fu, X.; Zhang, H.; Liu, Q. Index-Tunable Structured-Light Beams from a Laser with an Intracavity Astigmatic Mode Converter. Phys. Rev. Appl. 2020, 14, 044048. [Google Scholar] [CrossRef]
- Lu, J.; Cao, C.; Zhu, Z.; Gu, B. Flexible measurement of high-order optical orbital angular momentum with a variable cylindrical lens pair. Appl. Phys. Lett. 2020, 116, 201105. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, W.; Chen, L. Experimental detection of high-order or fractional orbital angular momentum of light based on a robust mode converter. Appl. Phys. Lett. 2016, 108, 111108. [Google Scholar] [CrossRef]
- Massari, M.; Ruffato, G.; Gintoli, M.; Ricci, F.; Romanato, F. Fabrication and characterization of high-quality spiral phase plates for optical applications. Appl. Opt. 2015, 54, 4077. [Google Scholar] [CrossRef]
- Wei, W.; Mahdjoubi, K.; Brousseau, C.; Emile, O. Horn antennas for generating radio waves bearing orbital angular momentum by using spiral phase plate. IET Microw. Antennas Propag. 2016, 10, 1420–1427. [Google Scholar] [CrossRef]
- Stegenburgs, E.; Bertoncini, A.; Trichili, A.; Alias, M.S.; Ng, T.K.; Alouini, M.-S.; Liberale, C.; Ooi, B.S. Near-Infrared OAM Communication Using 3D-Printed Microscale Spiral Phase Plates. IEEE Commun. Mag. 2019, 57, 65–69. [Google Scholar] [CrossRef]
- Hui, X.; Zheng, S.; Hu, Y.; Xu, C.; Jin, X.; Chi, H.; Zhang, X. Ultralow Reflectivity Spiral Phase Plate for Generation of Millimeter-wave OAM Beam. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 966–969. [Google Scholar] [CrossRef]
- Cheng, L.; Hong, W.; Hao, Z. Design and implementation of planar reflection spiral phase plate for beams with orbital angular momentum. Wiley Online Libr. 2017, 11, 260–264. [Google Scholar] [CrossRef]
- Chen, Y.; Zheng, S.; Li, Y.; Hui, X.; Jin, X.; Chi, H.; Zhang, X. A Flat-Lensed Spiral Phase Plate Based on Phase-Shifting Surface for Generation of Millimeter-Wave OAM Beam. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1156–1158. [Google Scholar] [CrossRef]
- Ruffato, G.; Massari, M.; Carli, M.; Romanato, F. Spiral phase plates with radial discontinuities for the generation of multiring orbital angular momentum beams: Fabrication, characterization, and application. Opt. Eng. 2015, 54, 111307. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Logachev, V.I.; Porfirev, A.P. Properties of vortex light fields generated by generalized spiral phase plates. Phys. Rev. A 2020, 101, 043829. [Google Scholar] [CrossRef]
- Sabino, J. Orbital Angular Momentum of Photons: A Tool to Transmit Information, Technico Universidade de Lisboa, Lisboa, Portugal. 2016. Available online: https://fenix.tecnico.ulisboa.pt/downloadFile/844820067125161/Resumo.pdf (accessed on 1 May 2023).
- Fang, X.; Ren, H.; Gu, M. Orbital angular momentum holography for high-security encryption. Nat. Photonics 2019, 14, 102–108. [Google Scholar] [CrossRef]
- Ren, H.; Briere, G.; Fang, X.; Ni, P.; Sawant, R.; Héron, S.; Chenot, S.; Vézian, S.; Damilano, B.; Brändli, V.; et al. Metasurface orbital angular momentum holography. Nat. Commun. 2019, 10, 2986. [Google Scholar] [CrossRef]
- Zambale, G.; Doblado, N.H. OAM Beams from Incomplete Computer Generated Holograms. arXiv 2016, arXiv:1609.01791. [Google Scholar] [CrossRef]
- Zhong-Yi, G.; Shi-Liang, Q.; Zheng-He, S.; Shu-Tian, L. Superposition of orbital angular momentum of photons by a combined computer-generated hologram fabricated in silica glass with femtosecond laser pulses. Chin. Phys. B 2008, 17, 4199–4203. [Google Scholar] [CrossRef]
- Shikder, A.; Nishchal, N.K. Computer Generated Hologram Encryption Using Array of Vortex Beams. In Digital Holography and 3-D Imaging 2022; Optica Publishing Group: Washington, DC, USA, 2022; p. W2A.13. [Google Scholar] [CrossRef]
- Ruffato, G.; Rossi, R.; Massari, M.; Mafakheri, E.; Capaldo, P.; Romanato, F. Design, fabrication and characterization of Computer Generated Holograms for anti-counterfeiting applications using OAM beams as light decoders. Sci. Rep. 2017, 7, 18011. [Google Scholar] [CrossRef]
- Forbes, A.; Dudley, A.; McLaren, M. Creation and detection of optical modes with spatial light modulators. Adv. Opt. Photonics 2016, 8, 200. [Google Scholar] [CrossRef]
- Lian, Y.; Qi, X.; Wang, Y.; Bai, Z.; Wang, Y.; Lu, Z. OAM beam generation in space and its applications: A review. Opt. Lasers Eng. 2022, 151, 106923. [Google Scholar] [CrossRef]
- Thomas, G.M.; Minassian, A.; Damzen, M.J.; Rosales-Guzmán, C.; Ndagano, B.; Forbes, A.; Wu, J.; Liu, Y.; Zhang, D.; Pinnell, J.; et al. Probing the limits of orbital angular momentum generation and detection with spatial light modulators. J. Opt. 2021, 23, 15602–15611. [Google Scholar] [CrossRef]
- Cunha, A.; Figueira, G.; André, P. Enabling the study of photons orbital angular momentum for optical communications: Orbital angular momentum carrying beam modulation and demodulation using twsited nematic liquid crystal spatial light modulators. Opt. Quantum Electron. 2016, 48, 425. [Google Scholar] [CrossRef]
- Khonina, S.N.; Karpeev, S.V.; Butt, M.A. Spatial-light-modulator-based multichannel data transmission by vortex beams of various orders. Sensors 2021, 21, 2988. [Google Scholar] [CrossRef] [PubMed]
- Andersen, M.; Alperin, S.N.; Voitiv, A.A.; Holtzmann, W.G.; Gopinath, J.T.; Siemens, M.E. Characterizing vortex beams from a spatial light modulator with collinear phase-shifting holography. Appl. Opt. 2019, 58, 404. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, J. Arbitrary manipulation of spatial amplitude and phase using phase-only spatial light modulators. Sci. Rep. 2014, 4, 7441. [Google Scholar] [CrossRef] [PubMed]
- Gregg, P.; Mirhosseini, M.; Rubano, A.; Marrucci, L.; Karimi, E.; Boyd, R.; Ramachandran, S. Q-Plates for Switchable Excitation of Fiber OAM Modes. In CLEO: 2015; OSA: Washington, DC, USA, 2015; p. SW4M.3. [Google Scholar] [CrossRef]
- Slussarenko, S.; Murauski, A.; Du, T.; Chigrinov, V.; Marrucci, L.; Santamato, E. Tunable liquid crystal q-plates with arbitrary topological charge. Opt. Express 2011, 19, 4085. [Google Scholar] [CrossRef] [PubMed]
- Marrucci, L. The q-plate and its future. J. Nanophotonics 2013, 7, 078598. Available online: https://sci-hub.ru/https://www.spiedigitallibrary.org/journals/journal-of-nanophotonics/volume-7/issue-1/078598/The-q-plate-and-its-future/10.1117/1.JNP.7.078598.short (accessed on 26 January 2023). [CrossRef]
- Karimi, E.; Piccirillo, B.; Nagali, E.; Marrucci, L.; Santamato, E. Efficient generation and sorting of orbital angular momentum eigenmodes of light by thermally tuned q-plates. Appl. Phys. Lett. 2009, 94, 231124. [Google Scholar] [CrossRef]
- Beijersbergen, M.W.; Allen, L.; van der Veen, H.E.L.O.; Woerdman, J.P. Astigmatic laser mode converters and transfer of orbital angular momentum. Opt. Commun. 1993, 96, 123–132. [Google Scholar] [CrossRef]
- Dong, M.; Yang, Y. Coherent Vortices Properties of Partially Coherent Elegant Laguerre-Gaussian Beams in the Free Space. Opt. Photonics J. 2020, 10, 159–166. [Google Scholar] [CrossRef]
- Ni, J.; Huang, C.; Zhou, L.M.; Gu, M.; Song, Q.; Kivshar, Y.; Qiu, C.W. Multidimensional phase singularities in nanophotonics. Science 2021, 374, eabj0039. [Google Scholar] [CrossRef]
- Li, C.-h.; Maier, S.A. REN Hao-ran Optical vortices in nanophotonics. Chin. Opt. 2021, 14, 792–811. [Google Scholar] [CrossRef]
- Kim, G.; Kim, S.; Kim, H.; Lee, J.; Badloe, T.; Rho, J. Metasurface-empowered spectral and spatial light modulation for disruptive holographic displays. Nanoscale 2022, 14, 4380. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Rusch, L.A.; Shi, W. Silicon Photonic Integrated Circuits for OAM Generation and Multiplexing; CRC Press: Boca Raton, FL, USA, 2021; Available online: https://sci-hub.ru/https://www.taylorfrancis.com/chapters/edit/10.1201/9780429292033-14/silicon-photonic-integrated-circuits-oam-generation-multiplexing-yuxuan-chen-leslie-rusch-wei-shi (accessed on 26 January 2023).
- Rui, G.; Gu, B.; Cui, Y.; Zhan, Q. Detection of orbital angular momentum using a photonic integrated circuit. Sci. Rep. 2016, 6, 28262. [Google Scholar] [CrossRef] [PubMed]
- Kutluyarov, R.; Fatkhiev, D.; Stepanov, I.; Grakhova, E.; Lyubopytov, V.; Sultanov, A. Design and modeling of a photonic integrated device for optical vortex generation in a silicon waveguide. Comput. Opt. 2021, 45, 324–330. [Google Scholar] [CrossRef]
- Song, H.; Zhou, H.; Zou, K.; Zhang, R.; Pang, K.; Song, H.; Su, X.; Minoofar, A.; Hu, N.; Liu, C.; et al. Demonstration of Recovering Orbital-Angular-Momentum Multiplexed Channels Using a Tunable, Broadband Pixel-Array-Based Photonic-Integrated-Circuit Receiver. J. Lightwave Technol. 2022, 40, 1346–1352. Available online: https://sci-hub.ru/https://opg.optica.org/abstract.cfm?uri=jlt-40-5-1346 (accessed on 26 January 2023). [CrossRef]
- Guan, B.; Scott, R.P.; Qin, C.; Fontaine, N.K.; Su, T.; Ferrari, C.; Cappuzzo, M.; Klemens, F.; Keller, B.; Earnshaw, M.; et al. Free-space coherent optical communication with orbital angular, momentum multiplexing/demultiplexing using a hybrid 3D photonic integrated circuit. Opt. Express 2014, 22, 145. [Google Scholar] [CrossRef]
- Alam, M.S.; Gnawali, R.; Hendrickson, J.R.; Beamer, D.; Payne, T.E.; Volk, A.; Agha, I. Photonic Integrated Circuit for Rapidly Tunable Orbital Angular Momentum Generation Using Sb2Se3 Ultra-Low-Loss Phase Change Material. Adv. Opt. Mater. 2022, 10, 2200098. [Google Scholar] [CrossRef]
- Li, S.; Klitis, C.; Nong, Z.; Gao, S.; Sorel, M.; Yu, S.; Cai, X. Orbital Angular Momentum Mode Multiplexer Based on Multimode Micro-Ring Resonator with Angular Gratings. In Proceedings of the 2016 Conference on Lasers and Electro-Optics (CLEO), Washington, DC, USA, 5–10 June 2016; p. STh3E.5. [Google Scholar] [CrossRef]
- Fatkhiev, M.; Lyubopytov, V.S.; Kutluyarov, R.V.; Sultanov, A.K. OAM signal emitter based on a ring resonator. In Optical Technologies for Telecommunications 2019; Burdin, V.A., Andreev, V.A., Morozov, O.G., Bourdine, A.V., Sultanov, A.H., Eds.; SPIE: Washington, DC, USA, 2020; p. 71. [Google Scholar] [CrossRef]
- Lin, W.; Ota, Y.; Arakawa, Y.; Iwamoto, S. An On-chip Full Poincaré Beam Emitter Based on an Optical Micro-ring Cavity. In Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 5–10 May 2019; OSA: Washington, DC, USA, 2019. Paper SW4J.4. [Google Scholar] [CrossRef]
- Zhou, H.; Song, H.; Zhao, Z.; Zhang, R.; Song, H.; Pang, K.; Zou, K.; Liu, C.; Su, X.; Hu, N.; et al. Modal properties of a beam carrying OAM generated by a circular array of multiple ring-resonator emitters. Opt. Lett. 2021, 46, 4722. [Google Scholar] [CrossRef]
- Yuan, G.; Cao, S.; Zhang, P.; Peng, F.; Peng, Z.; Wang, Z. Achieving wide-range photonics applications based on a compact grating-assisted silicon micro-ring resonator. Optik 2019, 183, 887–896. [Google Scholar] [CrossRef]
- Li, S.; Ding, Y.; Guan, X.; Tan, H.; Nong, Z.; Wang, L.; Liu, L.; Zhou, L.; Yang, C.; Yvind, K.; et al. Compact high-efficiency vortex beam emitter based on a silicon photonics micro-ring. Opt. Lett. 2018, 43, 1319. [Google Scholar] [CrossRef]
- Li, S.; Nong, Z.; Wu, X.; Yu, W.; He, M.; Klitis, C.; Zhu, Y.; Gao, S.; Liu, J.; Li, Z.; et al. Orbital angular momentum vector modes (de)multiplexer based on multimode micro-ring. Opt. Express 2018, 26, 29895. [Google Scholar] [CrossRef]
- Stepanov, I.V.; Fatkhiev, D.M.; Lyubopytov, V.S.; Kutluyarov, R.V.; Grakhova, E.P.; Neumann, N.; Khonina, S.N.; Sultanov, A.K. Wavelength-tunable vortex beam emitter based on silicon micro-ring with pn depletion diode. Sensors 2022, 22, 929. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Yan, M.; Xu, B. Formation of orbital angular momentum and focused beams based on chiral double-helical metamaterials. Opt. Mater. 2020, 107, 109962. [Google Scholar] [CrossRef]
- Ma, Q.; Cui, T.J. Information Metamaterials: Bridging the physical world and digital world. PhotoniX 2020, 1, 1. [Google Scholar] [CrossRef]
- Jin, J.; Pu, M.; Wang, Y.; Li, X.; Ma, X.; Luo, J.; Zhao, Z.; Gao, P.; Luo, X. Multi-Channel Vortex Beam Generation by Simultaneous Amplitude and Phase Modulation with Two-Dimensional Metamaterial. Adv. Mater. Technol. 2017, 2, 1600201. [Google Scholar] [CrossRef]
- Chen, R.; Zhou, H.; Moretti, M.; Wang, X.; Li, J. Orbital Angular Momentum Waves: Generation, Detection, and Emerging Applications. IEEE Commun. Surv. Tutor. 2020, 22, 840–868. [Google Scholar] [CrossRef]
- Meng, Z.K.; Shi, Y.; Wei, W.Y.; Zhang, Y.; Li, L. Graphene-based metamaterial transmitarray antenna design for the generation of tunable orbital angular momentum vortex electromagnetic waves. Opt. Mater. Express 2019, 9, 3709. [Google Scholar] [CrossRef]
- Sun, Z.C.; Yan, M.Y.; Xu, B.J. Generation of orbital angular momentum and focused beams with tri-layer medium metamaterial. Chin. Phys. B 2020, 29, 104101. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, Y. Generation of Wideband Tunable Orbital Angular Momentum Vortex Waves Using Graphene Metamaterial Reflectarray. IEEE Access 2018, 6, 5341–5347. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, J.; Li, S.; Willner, A.E. Metamaterials-based broadband generation of orbital angular momentum carrying vector beams. Opt. Lett. 2013, 38, 932. [Google Scholar] [CrossRef]
- Zhao, Z.; Ren, Y.; Xie, G.; Yan, Y.; Li, L.; Huang, H.; Bao, C.; Ahmed, N.; Lavery, M.P.; Zhang, C.; et al. Experimental demonstration of 16-Gbit/s millimeter-wave communications link using thin metamaterial plates to generate data-carrying orbital-angular-momentum beams. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 1392–1397. [Google Scholar] [CrossRef]
- Spektor, G.; Kilbane, D.; Mahro, A.K.; Frank, B.; Ristok, S.; Gal, L.; Kahl, P.; Podbiel, D.; Mathias, S.; Giessen, H.; et al. Revealing the subfemtosecond dynamics of orbital angular momentum in nanoplasmonic vortices. Science 2017, 355, 1187–1191. [Google Scholar] [CrossRef]
- Genevet, P.; Lin, J.; Kats, M.A.; Capasso, F. Holographic Detection of the Orbital Angular Momentum of Light with Plasmonic Photodiodes. Nat. Commun. 2012, 3, 1278. Available online: https://sci-hub.ru/https://www.nature.com/articles/ncomms2293 (accessed on 17 May 2023). [CrossRef] [PubMed]
- Prinz, E.; Hartelt, M.; Spektor, G.; Orenstein, M.; Aeschlimann, M. Orbital Angular Momentum in Nanoplasmonic Vortices. ACS Photonics 2023, 10, 340–367. [Google Scholar] [CrossRef]
- Kim, H.; Park, J.; Cho, S.W.; Lee, S.Y.; Kang, M.; Lee, B. Synthesis and dynamic switching of surface plasmon vortices with plasmonic vortex lens. Nano Lett. 2010, 10, 529–536. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Jiang, L.; Sha, W. Orbital Angular Momentum Generation and Detection by Geometric-Phase Based Metasurfaces. Appl. Sci. 2018, 8, 362. [Google Scholar] [CrossRef]
- Qin, F.; Wan, L.; Li, L.; Zhang, H.; Wei, G.; Gao, S. A Transmission Metasurface for Generating OAM Beams. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 1793–1796. [Google Scholar] [CrossRef]
- Bai, X.; Liang, X.-L.; Jiao, S.; Jin, R.; Kong, F.; Sun, Y.; Wang, G.; Qian, J.; Li, X.; Cao, A.; et al. High-efficiency transmissive programmable metasurface for multimode OAM generation. Adv. Opt. Mater. 2020, 8, 2000570. [Google Scholar] [CrossRef]
- Ahmed, H.; Kim, H.; Zhang, Y.; Intaravanne, Y.; Jang, J.; Rho, J.; Chen, S.; Chen, X. Optical metasurfaces for generating and manipulating optical vortex beams. Nanophotonics 2022, 11, 941–956. [Google Scholar] [CrossRef]
- Ma, M.; Lian, Y.; Wang, Y.; Lu, Z. Generation, Transmission and Application of Orbital Angular Momentum in Optical Fiber: A Review. Front. Phys. 2021, 9, 773505. [Google Scholar] [CrossRef]
- Han, Y.; Liu, Y.G.; Wang, Z.; Huang, W.; Chen, L.; Zhang, H.W.; Yang, K. Controllable all-fiber generation/conversion of circularly polarized orbital angular momentum beams using long period fiber gratings. Nanophotonics 2018, 7, 287–293. [Google Scholar] [CrossRef]
- Yao, S.; Ren, G.; Shen, Y.; Jiang, Y.; Zhu, B.; Jian, S. Tunable Orbital Angular Momentum Generation Using All-Fiber Fused Coupler. IEEE Photonics Technol. Lett. 2018, 30, 99–102. [Google Scholar] [CrossRef]
- Pidishety, S.; Pachava, S.; Gregg, P.; Ramachandran, S.; Brambilla, G.; Srinivasan, B. Orbital angular momentum beam excitation using an all-fiber weakly fused mode selective coupler. Opt. Lett. 2017, 42, 4347. [Google Scholar] [CrossRef] [PubMed]
- Eznaveh, Z.S.; Pachava, S.; Gregg, P.; Ramachandran, S.; Brambilla, G.; Srinivasan, B. Annular Core Photonic Lantern OAM Mode Multiplexer. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 19–23 March 2017; OSA: Washington, DC, USA, 2017. Paper Tu3J.3. [Google Scholar] [CrossRef]
- Eznaveh, Z.S.; Zacarias, J.C.A.; Lopez, J.E.A.; Shi, K.; Milione, G.; Jung, Y.; Thomsen, B.C.; Richardson, D.J.; Fontaine, N.; Leon-Saval, S.G.; et al. Photonic lantern broadband orbital angular momentum mode multiplexer. Opt. Express 2018, 26, 30042. [Google Scholar] [CrossRef] [PubMed]
- Wei, W.; An, N.; Zhang, Z.; Tang, L.; Ding, L.; Li, Y. Design of a microstructure optical fiber supporting 52 vortex beams. Opt. Commun. 2021, 490, 126657. [Google Scholar] [CrossRef]
- Huang, W.; Liu, Y.; Wang, Z.; Zhang, W.; Luo, M.; Liu, X.; Guo, J.; Liu, B.; Lin, L. Generation and excitation of different orbital angular momentum states in a tunable microstructure optical fiber. Opt. Express 2015, 23, 33741. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Zhou, G.; Chen, C.; Zhou, G.; Sheng, Z.; Hou, Z.; Xia, C.A. A novel micro-structured fiber for OAM mode and LP mode simultaneous transmission. J. Opt. 2018, 47, 428–436. [Google Scholar] [CrossRef]
- Chang, W.; Feng, M.; Mao, B.; Wang, P.; Wang, Z.; Liu, Y.-G. All-Fiber Fourth-Order OAM Mode Generation Employing a Long Period Fiber Grating Written By Preset Twist. J. Lightwave Technol. 2022, 40, 4804–4811. [Google Scholar] [CrossRef]
- Wang, T.; Wang, F.; Shi, F.; Pang, F.; Huang, S.; Wang, T.; Zeng, X. Generation of Femtosecond Optical Vortex Beams in All-Fiber Mode-Locked Fiber Laser Using Mode Selective Coupler. J. Lightwave Technol. 2017, 35, 2161–2166. [Google Scholar] [CrossRef]
- Lu, Y.; Jiang, Z.; Liu, W.; Liu, Q.; Jiang, M.; Jiang, K. Orbital angular momentum mode generation system based on photonic lantern. J. Opt. 2019, 21, 125702. [Google Scholar] [CrossRef]
- Arman, H.; Olyaee, S.; Mohebzadeh-Bahabady, A. Gas sensor based on large hollow-core photonic bandgap fiber. IJOP 2015, 9, 99–106. Available online: https://sci-hub.ru/https://ijop.ir/article-1-209-en.html (accessed on 31 March 2023).
- Birks, A.; Witkowska, A.; Leon-Saval, S.G.; Pham, A. All-fiber LP11 mode convertors. Opt. Lett. 2008, 33, 306–308. [Google Scholar] [CrossRef]
- Wong, G.K.L.; Xi, X.M.; Kang, M.S.; Lee, H.W.; Russell, P.S.J. Quantization of orbital angular momentum in helically twisted photonic crystal fiber. In Proceedings of the Frontiers in Optics 2012/Laser Science XXVIII (2012), Rochester, NY, USA, 14–18 October 2012. Paper FTh3C.3. [Google Scholar] [CrossRef]
- Lian, Y.; Yu, Y.; Han, S.; Luan, N.; Wang, Y.; Lu, Z. OAM Beams Generation Technology in Optical Fiber: A Review. IEEE Sens. J. 2022, 22, 3828–3843. [Google Scholar] [CrossRef]
- Russel, P.S.J. Photonic-Crystal Fibers. J. Lightwave Technol. 2006, 24, 4729–4749. [Google Scholar] [CrossRef]
- Russell, P. Photonic Crystal Fibers. Science 2003, 299, 358–362. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, R. Generation of phase singular optical beams in microstructure optical fibers. Opt. Commun. 2018, 428, 15–21. [Google Scholar] [CrossRef]
- Al-Zahrani, F.A.; Kabir, A. Ring-core photonic crystal fiber of terahertz orbital angular momentum modes with excellence guiding properties in optical fiber communication. Photonics 2021, 8, 122. [Google Scholar] [CrossRef]
- Tian, W.; Zhang, H.; Zhang, X.; Xi, L.; Zhang, W.; Tang, X.A. circular photonic crystal fiber supporting 26 OAM modes. Opt. Fiber Technol. 2016, 30, 184–189. [Google Scholar] [CrossRef]
- Bai, X.; Chen, H.; Yang, H. Design of a circular photonic crystal fiber with square air-holes for orbital angular momentum modes transmission. Optik 2018, 158, 1266–1274. [Google Scholar] [CrossRef]
- Yu, Y.; Lian, Y.; Hu, Q.; Xie, L.; Ding, J.; Wang, Y.; Lu, Z. Design of PCF Supporting 86 OAM Modes with High Mode Quality and Low Nonlinear Coefficient. Photonics 2022, 9, 266. [Google Scholar] [CrossRef]
- Liu, Q.; Tai, S.; Lu, W.; Sun, J.; Lv, T.; Liu, C.; Sun, Y.; Lv, J.; Liu, W.; Sun, T.; et al. Design of pure silica-based photonic crystal fiber for supporting 114 OAM modes transmission. J. Opt. 2021, 23, 095701. [Google Scholar] [CrossRef]
- Fu, H.; Zhu, M.; Liu, C.; Yi, Z.; Lv, J.; Yang, L.; Wang, F.; Liu, Q.; Su, W.; Li, X.; et al. Photonic crystal fiber supporting 394 orbital angular momentum modes with flat dispersion, low nonlinear coefficient, and high mode quality. Opt. Eng. 2022, 61, 026111. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, H.; Xu, Z.; Liang, R. A design of novel photonic crystal fiber with low and flattened dispersion for supporting 84 orbital angular momentum modes. Commun. Theor. Phys. 2021, 73, 085501. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, K.; Peng, J.; Deng, J.; Yang, Y.; Ma, J. Circular photonic crystal fiber supporting 110 OAM modes. Opt. Commun. 2018, 429, 189–193. [Google Scholar] [CrossRef]
- Liu, Q.; Tai, S.; Sun, Y.; Han, M.; Wang, J.; Liu, C.; Lv, J.; Wang, S.; Sun, G.; Chu, P.K. Simple ring-structured photonic crystal fiber with low nonlinear coefficients and flat dispersion supporting 166 OAM modes. Opt. Eng. 2022, 61, 076108. [Google Scholar] [CrossRef]
- Wang, W.; Wang, N.; Li, K.; Geng, Z.; Jia, H. A novel dual guided modes regions photonic crystal fiber with low crosstalk supporting 56 OAM modes and 4 LP modes. Opt. Fiber Technol. 2020, 57, 102213. [Google Scholar] [CrossRef]
- Harris, M.; Hill, C.A.; Tapster, P.R.; Vaughan, J.M. Laser modes with helical wave fronts. Phys. Rev. A 1994, 49, 3119–3122. [Google Scholar] [CrossRef] [PubMed]
- Lv, F.; Li, X.; Tai, Y.; Zhang, L.; Nie, Z.; Chen, Q. High-order topological charges measurement of LG vortex beams with a modified Mach–Zehnder interferometer. Optik 2015, 126, 4378–4381. [Google Scholar] [CrossRef]
- Dai, K.; Gao, C.; Zhong, L.; Na, Q.; Wang, Q. Measuring OAM states of light beams with gradually-changing-period gratings. Opt. Lett. 2015, 40, 562–565. [Google Scholar] [CrossRef] [PubMed]
- Leach, J.; Padgett, M.J.; Barnett, S.M.; Franke-Arnold, S.; Courtial, J. Measuring the Orbital Angular Momentum of a Single Photon. Phys. Rev. Lett. 2002, 88, 4. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S.; Wang, J. Measuring Orbital Angular Momentum (OAM) States of Vortex Beams with Annular Gratings. Sci. Rep. 2017, 7, 40781. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Li, X.; Cheng, Y.; Gao, Y.; Fan, B.; Jiang, Y. OAM-Based Multitarget Detection: From Theory to Experiment. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 760–762. [Google Scholar] [CrossRef]
- Yan, Y.; Xie, G.; Lavery, M.P.J.; Huang, H.; Ahmed, N.; Bao, C.; Ren, Y.; Cao, Y.; Li, L.; Zhao, Z. High-capacity millimetre-wave communications with orbital angular momentum multiplexing. Nat. Commun. 2014, 5, 4876. Available online: https://www.nature.com/articles/ncomms5876 (accessed on 26 May 2023). [CrossRef] [PubMed]
- Berkhout, G.C.G.; Lavery, M.P.J.; Courtial, J.; Beijersbergen, M.W.; Padgett, M.J. Efficient sorting of orbital angular momentum states of light. Phys. Rev. 2010, 105, 153601. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, Z.; Liao, P.; Li, L.; Xie, G.; Huang, H.; Zhao, Z.; Yan, Y.; Ahmed, N.; Willner, A.; et al. Experimental characterization of a 400 Gbit/s orbital angular momentum multiplexed free-space optical link over 120 m. Opt. Lett. 2015, 41, 622–625. [Google Scholar] [CrossRef] [PubMed]
- Krenn, M.; Handsteiner, J.; Fink, M.; Fickler, R.; Ursin, R.; Malik, M.; Zeilinger, A. Twisted light transmission over 143 km. Proc. Natl. Acad. Sci. USA 2016, 113, 13648–13653. [Google Scholar] [CrossRef] [PubMed]
- Sakaguchi, J.; Awaji, Y.; Wada, N.; Kanno, A.; Kawanishi, T.; Hayashi, T.; Taru, T.; Kobayashi, T.; Watanabe, M. Space Division Multiplexed Transmission of 109-Tb/s Data Signals Using Homogeneous Seven-Core Fiber. J. Lightwave Technol. 2012, 30, 658–665. [Google Scholar] [CrossRef]
- Sakaguchi, J.; Puttnam, B.J.; Klaus, W.; Awaji, Y.; Wada, N.; Kanno, A.; Kawanishi, T.; Imamura, K.; Inaba, H.; Mukasa, K.; et al. 305 Tb/s Space Division Multiplexed Transmission Using Homogeneous 19-Core Fiber. J. Lightwave Technol. 2013, 31, 554–562. [Google Scholar] [CrossRef]
- Nejabati, R.; Shu, Y.; Puttnam, B.J.; Klaus, W.; Wada, N.; Awaji, Y.; Channegowda, M.; Amaya, N.; Harai, H.; Ou, Y.; et al. First Demonstration of Software Defined Networking (SDN) over Space Division Multiplexing (SDM) Optical Networks. In Proceedings of the 39th European Conference and Exhibition on Optical Communication (ECOC 2013), London, UK, 22–26 September 2013; pp. 1263–1265. [Google Scholar] [CrossRef]
- Sakaguchi, J.; Puttnam, B.J.; Klaus, W.; Awaji, Y.; Wada, N.; Kanno, A.; Kawanishi, T.; Imamura, K.; Inaba, H.; Mukasa, K.; et al. 19-core fiber transmission of 19×100×172-Gb/s SDM-WDM-PDM-QPSK signals at 305Tb/s. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 4–8 March 2012; OSA: Washington, DC, USA, 2012. paper PDP5C.1. [Google Scholar] [CrossRef]
- Puttnam, B.J.; Luis, R.S.; Klaus, W.; Sakaguchi, J.; Delgado Mendinueta, J.-M.; Awaji, Y.; Wada, N.; Tamura, Y.; Hayashi, T.; Hirano, M.; et al. 2.15 Pb/s transmission using a 22 core homogeneous single-mode multi-core fiber and wideband optical comb. In Proceedings of the 2015 European Conference on Optical Communication (ECOC), Valencia, Spain, 27 September–1 October 2015; pp. 1–3. [Google Scholar] [CrossRef]
- Jin, X.Q.; Li, R.; O’Brien, D.C.; Payne, F.P. Linearly polarized mode division multiplexed transmission over ring-index multimode fibres. In Proceedings of the 2013 IEEE Photonics Society Summer Topical Meeting Series, PSSTMS 2013, Waikoloa, HI, USA, 8–10 July 2013; pp. 113–114. [Google Scholar] [CrossRef]
- Karelin, N.; Louchet, H.; Kroushkov, D.; Uvarov, A.; Mingaleev, S.; Koltchanov, I.; Richter, A. Modeling and design framework for SDM transmission systems. In Proceedings of the International Conference on Transparent Optical Networks, Budapest, Hungary, 5–9 July 2015. [Google Scholar] [CrossRef]
- Ryf, R.; Randel, S.; Gnauck, A.H.; Bolle, C.; Essiambre, R.J.; Winzer, P.J.; Peckham, D.W.; McCurdy, A.; Lingle, J. Space-division multiplexing over 10 km of three-mode fiber using coherent 6 × 6 MIMO processing. In Proceedings of the Optical Fiber Communication Conference/National Fiber Optic Engineers Conference 2011, Los Angeles, CA, USA, 6–10 March 2011. Paper PDPB10. [Google Scholar] [CrossRef]
- Rjeb, A.; Fathallah, H.; Machhout, M. OAM Modes in Optical Fibers for Next Generation Space Division Multiplexing (SDM) Systems. In Fiber Optics-Technology and Applications; IntechOpen: London, UK, 2021. [Google Scholar] [CrossRef]
- Saridis, G.M.; Alexandropoulos, D.; Zervas, G.; Simeonidou, D. Survey and evaluation of space division multiplexing: From technologies to optical networks. IEEE Commun. Surv. Tutor. 2015, 17, 2136–2156. [Google Scholar] [CrossRef]
- Fontaine, K. Integrated photonics and components for space-division multiplexing systems. In Proceedings of the 2014 13th International Conference on Optical Communications and Networks, ICOCN 2014, Suzhou, China, 9–10 November 2014. [Google Scholar] [CrossRef]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef]
- Willner, E.; Zhao, Z.; Liu, C.; Zhang, R.; Song, H.; Pang, K.; Manukyan, K.; Song, H.; Su, X.; Xie, G.; et al. Perspectives on advances in high-capacity, free-space communications using multiplexing of orbital-angular-momentum beams. APL Photonics 2021, 6, 030901. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.-Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Huang, H.; Xie, G.; Yan, Y.; Ahmed, N.; Ren, Y.; Yue, Y.; Rogawski, D.; Willner, M.J.; Erkmen, B.I.; Birnbaum, K.M.; et al. 100 Tbit/s Free-Space Data Link Enabled by Three-Dimensional Multiplexing of Orbital Angular Momentum, Polarization, and Wavelength. Opt. Lett. 2014, 39, 197. [Google Scholar] [CrossRef] [PubMed]
- Klaus, W.; Sakaguchi, J.; Puttnam, B.J.; Awaji, Y.; Wada, N.; Kobayashi, T.; Watanabe, M. Free-Space Coupling Optics for Multicore Fibers. IEEE Photonics Technol. Lett. 2012, 24, 1902–1905. [Google Scholar] [CrossRef]
- Weng, Y.; He, X.; Pan, Z. Space division multiplexing optical communication using few-mode fibers. Opt. Fiber Technol. 2017, 36, 155–180. [Google Scholar] [CrossRef]
- Matsuo, S.; Sasaki, Y.; Ishida, I.; Takenaga, K.; Saitoh, K.; Koshiba, M. Recent Progress on Multi-Core Fiber and Few-Mode Fiber. In Proceedings of the Optical Fiber Communication Conference/National Fiber Optic Engineers Conference 2013, Anaheim, CA, USA, 17–21 March 2013; OSA: Washington, DC, USA, 2013; p. 3. [Google Scholar] [CrossRef]
- Winzer, J. Energy-Efficient Optical Transport Capacity Scaling Through Spatial Multiplexing. IEEE Photonics Technol. Lett. 2011, 23, 851–853. [Google Scholar] [CrossRef]
- Zhao, Z.; Ren, Y.; Xie, G.; Ahmed, N.; Ashrafi, N.; Lavery, M.P.J.; Ramachandran, S.; Ashrafi, S.; Willner, A.E.; Molisch, A.F.; et al. Optical communications using orbital angular momentum beams. Adv. Opt. Photonics 2015, 7, 66–106. [Google Scholar] [CrossRef]
- Wu, G.; Wu, G.; Wu, X.; Wu, X.; Gao, S.; Gao, S.; Tu, J.; Tu, J.; Zhou, J.; Sui, Q.; et al. Multi-channel higher-order OAM generation and switching based on a mode selective interferometer. Opt. Express 2022, 30, 25093–25102. [Google Scholar] [CrossRef]
- Erhard, M.; Fickler, R.; Krenn, M.; Zeilinger, A. Twisted photons: New quantum perspectives in high dimensions. Light Sci. Appl. 2017, 7, 17146. [Google Scholar] [CrossRef]
- Molisch, F.; Win, M.Z.; Choi, Y.S.; Winters, J.H. Capacity of MIMO systems with antenna selection. IEEE Trans. Wirel. Commun. 2005, 4, 1759–1771. [Google Scholar] [CrossRef]
- Goldsmith, A.; Jafar, S.; Jindal, N.; Vishwanath, S. Capacity limits of MIMO channels. IEEE J. Sel. Areas Commun. 2003, 21, 684–702. [Google Scholar] [CrossRef]
- Ke, X.; Ning, C.; Wang, J. Crosstalk analysis of orbital angular momentum-multiplexed state under atmospheric turbulence. Infrared Laser Eng. 2018, 47, 1122002. [Google Scholar] [CrossRef]
- Li, S.; Wang, J. Multi-Orbital-Angular-Momentum Multi-Ring Fiber for High-Density Space-Division Multiplexing. IEEE Photonics J. 2013, 5, 7101007. [Google Scholar] [CrossRef]
- Winzer, P.J. Making spatial multiplexing a reality. Nat. Photonics 2014, 8, 345–348. [Google Scholar] [CrossRef]
- Li, W.; Zhao, S. Orbital angular momentum filter based on multiple-beam interference. Opt. Commun. 2019, 430, 98–103. [Google Scholar] [CrossRef]
- Wang, J. Twisted optical communications using orbital angular momentum. Sci. China-Phys. Mech. Astron. 2019, 62, 34201. [Google Scholar] [CrossRef]
- Kareem, F.Q.; Zeebaree, S.R.M.; Dino, H.I.; M Sadeeq, M.A.; Rashid, Z.N.; Hasan, D.A.; Sharif, K.H.A. A Survey of Optical Fiber Communications: Challenges and Processing Time Influences. Asian J. Res. Comput. Sci. 2021, 7, 48–58. [Google Scholar] [CrossRef]
- Richardson, D.J.; Fini, J.M.; Nelson, L.E. Space-division multiplexing in optical fibres. Nat. Photonics 2013, 7, 354–362. [Google Scholar] [CrossRef]
- PROTEUS. Cailabs: Spatial Mode Multiplexer for Use in SDM. Available online: https://www.cailabs.com/en/products/proteus/?hsCtaTracking=fa8c0b4e-2124-464f-b5d4-43f48c442b16%7C7edc995b-d3e2-475c-96de-dc2a40a7dda4 (accessed on 30 March 2023).
- Sasaki, H.; Yagi, Y.; Yamada, T.; Lee, D. Field Experimental Demonstration on OAM-MIMO Wireless Transmission on 28 GHz Band. In Proceedings of the 2019 IEEE Globecom Workshops (GC Wkshps), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–4. [Google Scholar] [CrossRef]
- NEC. NEC Successfully Demonstrates New Digital OAM Mode Multiplexing Transmission: Press Releases. Available online: https://www.nec.com/en/press/201812/global_20181219_02.html (accessed on 18 May 2023).
- Sasaki, H.; Yagi, Y.; Yamada, T.; Semoto, T.; Lee, D. An Experimental Demonstration of over 100 Gbit/s OAM Multiplexing Transmission at a Distance of 100 m on 40 GHz Band. In Proceedings of the 2020 IEEE International Conference on Communications Workshops, Dublin, Ireland, 7–11 June 2020. [Google Scholar] [CrossRef]
- Brunet, C.; Rusch, L.A. Optical fibers for the transmission of orbital angular momentum modes. Opt. Fiber Technol. 2017, 35, 2–7. [Google Scholar] [CrossRef]
- Shen, Y.; Meng, Y.; Fu, X.; Gong, M. Wavelength-tunable Hermite–Gaussian modes and an orbital-angular-momentum-tunable vortex beam in a dual-off-axis pumped Yb: CALGO laser. Opt. Lett. 2018, 43, 291–294. [Google Scholar] [CrossRef]
- Lin, D.; Feng, Y.; Ren, Z.; Richardson, D.J. The generation of femtosecond optical vortex beams with megawatt powers directly from a fiber based Mamyshev oscillator. Nanophotonics 2022, 11, 847–854. [Google Scholar] [CrossRef]
- Forbes, A. Advances in Orbital Angular Momentum Lasers. J. Lightwave Technol. 2022, 41, 2079–2086. [Google Scholar] [CrossRef]
- Geberbauer, J.W.T.; Kerridge-Johns, W.R.; Damzen, M.J. >30 W vortex LG01 or HG10 laser using a mode transforming output coupler. Opt. Express 2021, 29, 29082. [Google Scholar] [CrossRef] [PubMed]
- Shukla, M.; Gupta, S. Joint WDM and OAM Mode Group Multiplexed Transmission Over Conventional Multimode Fiber. IEEE Photonics J. 2023, 15, 7201109. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, S.; Lai, Z.; Li, Y.; Ao, Z.; Li, J.; Tu, J.; Wu, Y.; Liu, W.; Li, Z. Broadband, Low-Crosstalk, and Massive-Channels OAM Modes De/Multiplexing Based on Optical Diffraction Neural Network. Laser Photonics Rev. 2023, 17, 2200536. [Google Scholar] [CrossRef]
- Jian, Y.-H.; Chow, C.-W. Design and analysis of a compact micro-ring resonator signal emitter to reduce the uniformity-induced phase distortion and crosstalk in orbital angular momentum (OAM) division multiplexing. Opt. Express 2023, 31, 810. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).