Interpretation of Localized Surface Plasmonic Resonances of Gold Nanoparticles Covered by Polymeric Coatings
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Details
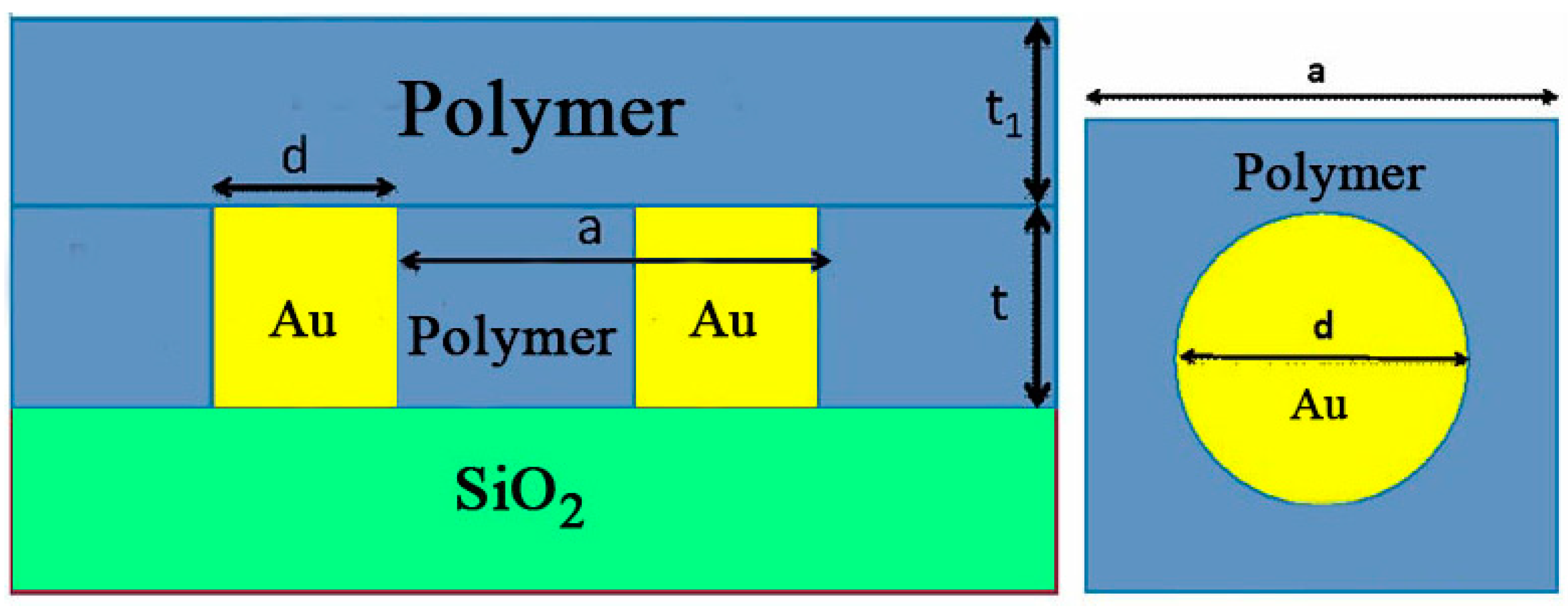
2.2. Theoretical Model
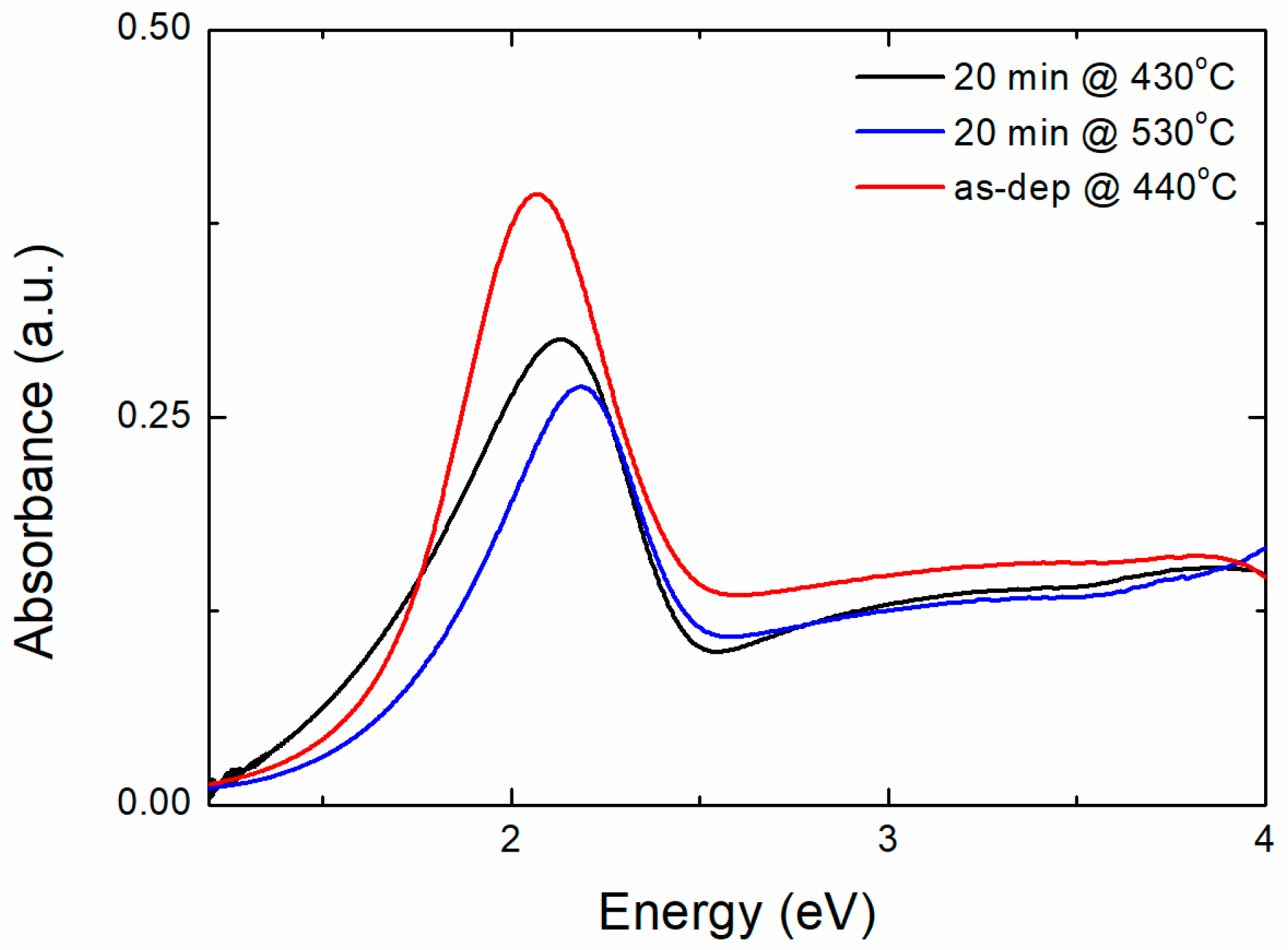
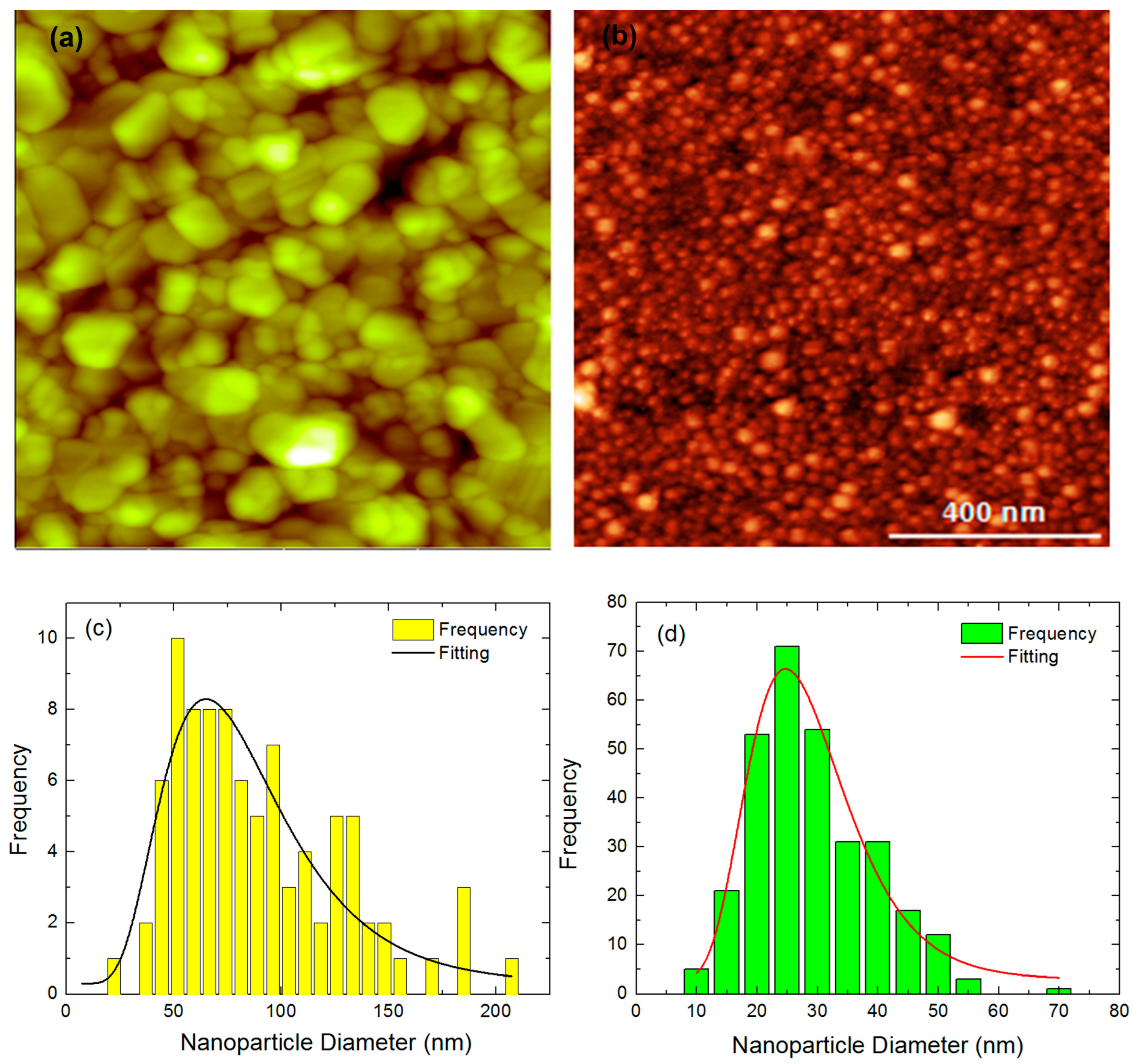
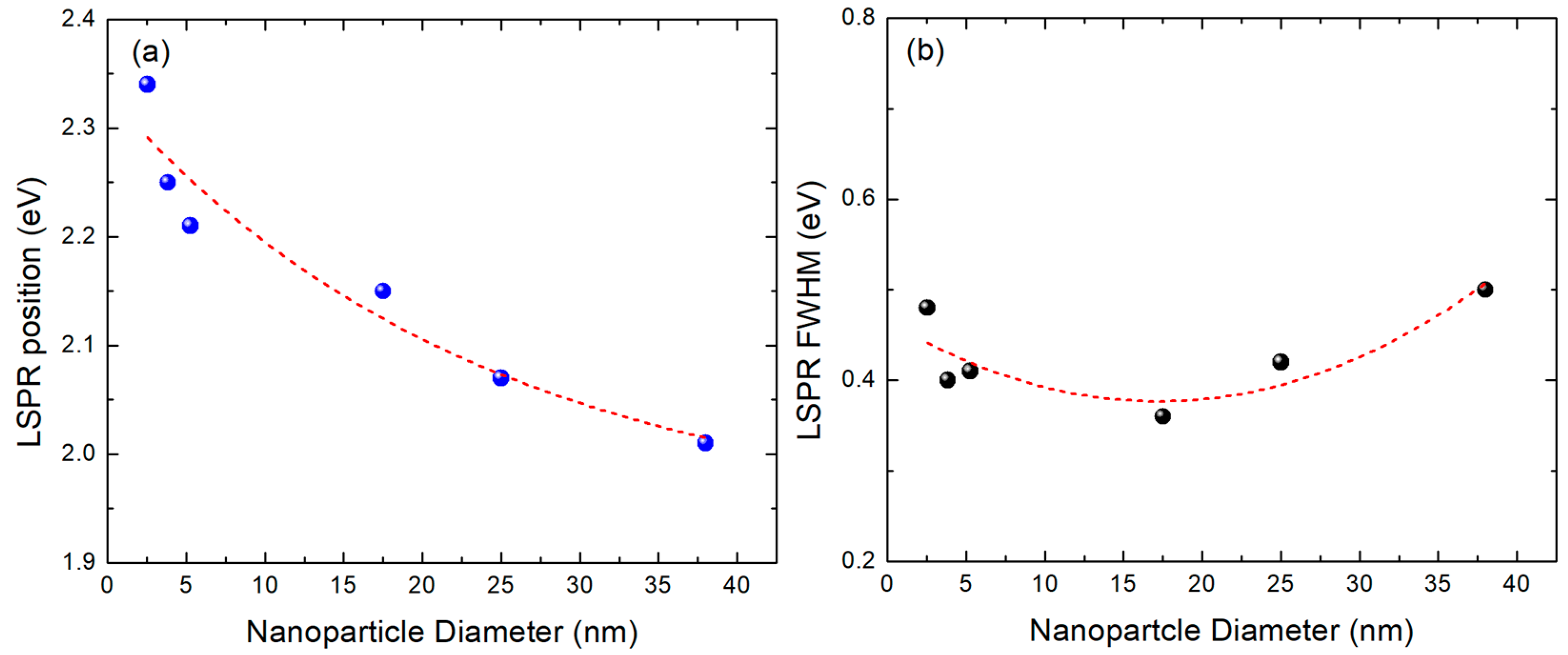
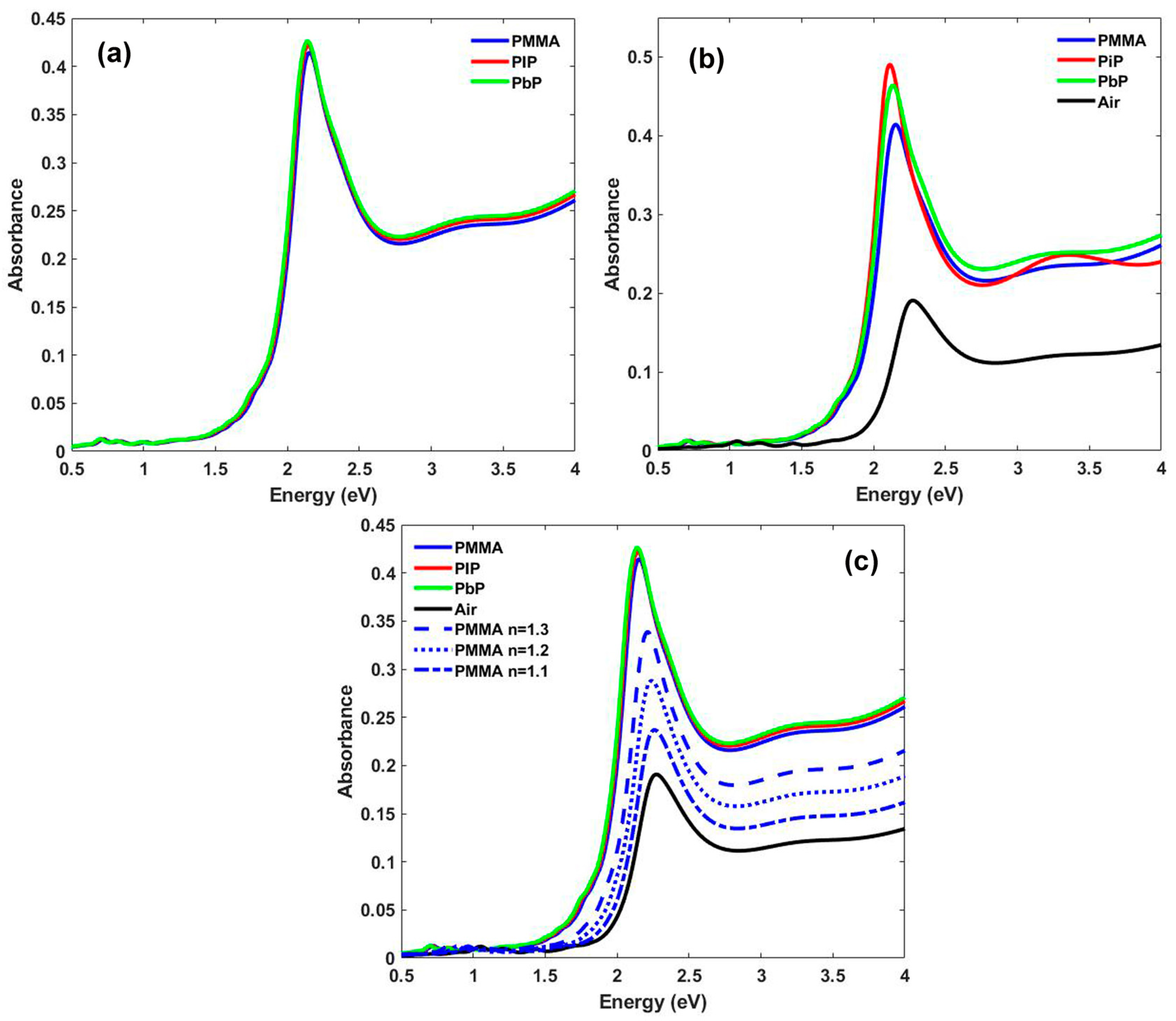
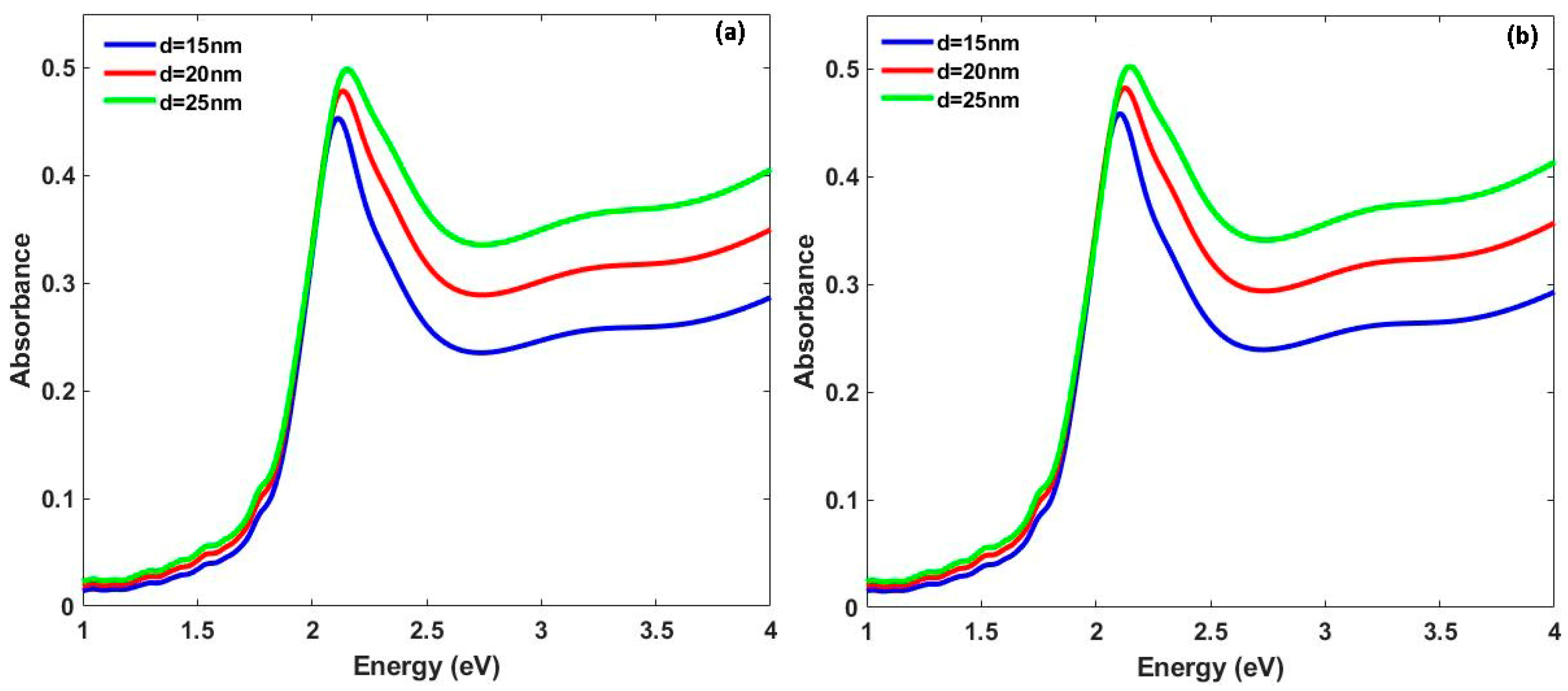
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barbillon, G. Latest Advances in Nanoplasmonics and Use of New Tools for Plasmonic Characterization. Photonics 2022, 9, 112. [Google Scholar] [CrossRef]
- Hutter, E.; Fendler, J.H. Exploitation of localized surface plasmon resonance. Adv. Mater. 2004, 16, 1685–1706. [Google Scholar] [CrossRef]
- Loiseau, A.; Zhang, L.; Hu, D.; Salmain, M.; Mazouzi, Y.; Flack, R.; Liedberg, B.; Boujday, S. Core−Shell Gold/Silver Nanoparticles for Localized Surface Plasmon Resonance-Based Naked-Eye Toxin Biosensing. ACS Appl. Mater. Interfaces 2019, 11, 46462–46471. [Google Scholar] [CrossRef] [PubMed]
- Haes, A.J.; Hall, W.P.; Chang, L.; Klein, W.L.; Van Duyne, R.P. A localized surface plasmon resonance biosensor: First steps toward an assay for Alzheimer’s disease. Nano Lett. 2004, 4, 1029–1034. [Google Scholar] [CrossRef]
- Grammatikopoulos, S.; Pappas, S.D.; Dracopoulos, V.; Poulopoulos, P.; Fumagalli, P.; Velgakis, M.J.; Politis, C. Self-assembled au nanoparticles on heated corning glass by dc magnetron sputtering: Size-dependent surface plasmon resonance tuning. J. Nanoparticle Res. 2013, 15, 1446. [Google Scholar] [CrossRef]
- Xiao, T.; Huang, J.; Wang, D.; Meng, T.; Yang, X. Au and Au-Based nanomaterials: Synthesis and recent progress in electrochemical sensor applications. Talanta 2020, 206, 120210. [Google Scholar] [CrossRef]
- Guo, F.C.; Sun, T.; Cao, F.; Liu, Q.; Ren, Z. Metallic nanostructures for light trapping in energy-harvesting devices. Light Sci. Appl. 2014, 3, e161. [Google Scholar]
- Yang, Q.; Guo, X.; Wang, W.; Zhang, Y.; Xu, S.; Lien, D.H.; Wang, Z.L. Enhancing sensitivity of a single ZnO micro-/nanowire photodetector by piezo-phototronic effect. ACS Nano 2010, 4, 6285–6291. [Google Scholar] [CrossRef]
- Pallavicini, P.; Chirico, G.; Taglietti, A. Harvesting light to produce heat: Photothermal nanoparticles for technological applications and biomedical devices. Chem. Eur. J. 2021, 27, 15361–15374. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Esteban, R.; Borisov, A.G.; Baumberg, J.J.; Nordlander, P.; Lezec, H.J.; Aizpurua, J.; Crozier, K.B. Quantum mechanical effects in plasmonic structures with subnanometre gaps. Nat. Commun. 2016, 7, 11495. [Google Scholar] [CrossRef]
- Beni, A.A.; Jabbari, H. Nanomaterials for Environmental Applications. Results Eng. 2022, 15, 100467. [Google Scholar] [CrossRef]
- Sarychev, A.K.; Ivanov, A.; Lagarkov, A.; Barbillon, G. Light Concentration by Metal-Dilectric Micro-Resonators for SERS Sensing. Materials 2019, 12, 103. [Google Scholar] [CrossRef]
- Faupel, F.; Zaporojtchenko, V.; Strunskus, T.; Elbahri, M. Metal-Polymer Nanocomposites for Functional Applications. Adv. Eng. Mater. 2010, 12, 1177–1190. [Google Scholar] [CrossRef]
- Tokarev, I.; Minko, S. Tunable plasmonic nanostructures from noble metal nanoparticles and stimuli-responsive polymers. Soft Matter 2012, 8, 5980–5987. [Google Scholar] [CrossRef]
- Burtch, N.C.; Heinen, J.; Bennett, T.D.; Dubbeldam, D.; Allendorf, M.D. Mechanical properties in metal–organic frameworks: Emerging opportunities and challenges for device functionality and technological applications. Adv. Mater. 2018, 30, 1704124. [Google Scholar] [CrossRef]
- Heilmann, A. Polymer Films with Embedded Metal Nanoparticles; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Yao, M.; Shen, P.; Liu, Y.; Chen, B.; Guo, W.; Ruan, S.; Shen, L. Performance improvement of polymer solar cells by surface-energyinduced dual plasmon resonance. ACS Appl. Mater. Interfaces 2016, 8, 6183–6189. [Google Scholar] [CrossRef] [PubMed]
- Bernardi, M.; Palummo, M.; Grossman, J.C. Extraordinary Sunlight absorption and one nanometer thick photovoltaics using two-dimensional monolayer materials. Nano Lett. 2013, 13, 3664–3670. [Google Scholar] [CrossRef] [PubMed]
- Venditti, I.; Fratoddi, I.; Russo, M.V.; Bearzotti, A. A nanostructured composite based on polyaniline and gold nanoparticles: Synthesis and gas sensing properties. Nanotechnology 2013, 24, 155503. [Google Scholar] [CrossRef]
- Pan, C.; Dong, L.; Zhu, G.; Niu, S.; Yu, R.; Yang, Q.; Liu, Y.; Wang, Z.L. High-resolution electroluminescent imaging of pressure distribution using a piezoelectric nanowire LED array. Nat. Photonics 2013, 7, 752–758. [Google Scholar] [CrossRef]
- Daniyal, W.M.E.M.M.; Fen, Y.W.; Abdullah, J.; Sadrolhosseini, A.R.; Mahdi, M.A. Design and Optimization of Surface Plasmon Resonance Spectroscopy for Optical Constant Characterization and Potential Sensing Application: Theoretical and Experimental Approaches. Photonics 2021, 8, 361. [Google Scholar] [CrossRef]
- Blattmann, C.O.; Sotiriou, G.A.; Pratsinis, S.E. Rapid synthesis of flexible conductive polymer nanocomposite films. Nanotechnology 2015, 26, 125601. [Google Scholar] [CrossRef]
- Dunklin, J.R.; Forcherio, G.T.; Berry, K.R., Jr.; Roper, D.K. Asymmetric Reduction of Gold Nanoparticles into Thermoplasmonic Polydimethylsiloxane Thin Films. ACS Appl. Mater. Interfaces 2013, 5, 8457–8466. [Google Scholar] [CrossRef] [PubMed]
- Andam, N.; Refki, S.; Ishitobi, H.; Inouye, Y.; Sekkat, Z. Optical Characterization of Ultra-Thin Films of Azo-Dye-Doped Polymers Using Ellipsometry and Surface Plasmon Resonance Spectroscopy. Photonics 2021, 8, 41. [Google Scholar] [CrossRef]
- Dunklin, J.R.; Bodinger, C.; Forcherio, G.T.; Roper, D.K. Plasmonic extinction in gold nanoparticle-polymer films as film thickness and nanoparticle separation decrease below resonant wavelength. J. Nanophotonics 2017, 11, 016002. [Google Scholar] [CrossRef]
- Ye, J.; Verellen, N.; Roy, W.V.; Lagae, L.; Maes, G.; Borghs, G.; Dorpe, P.V. Plasmonic Modes of Metallic Semishells in a Polymer Film. ACS Nano 2010, 4, 1457–1464. [Google Scholar] [CrossRef]
- Kapaklis, V.; Grammatikopoulos, S.; Sordan, R.; Miranda, A.; Traversi, F.; von Känel, H.; Trachylis, D.; Poulopoulos, P.; Politis, C. Nanolithographic Templates Using Diblock Copolymer Films on Chemically Heterogeneous Substrates. J. Nanosci. Nanotechnol. 2010, 10, 6056–6061. [Google Scholar] [CrossRef] [PubMed]
- Gaylord, T.K.; Moharam, M.G. Rigorous coupled-wave analysis of antireflective surface-relief gratings. J. Opt. Soc. Am. A 1986, 3, 1780–1787. [Google Scholar]
- Lee, M.S.L.; Lalanne, P.; Rodier, J.C.; Chavel, P.; Cambril, E.; Chen, Y. Imaging with blazed-binary diffractive elements. J. Opt. A Pure Appl. Opt. 2002, 4, 358. [Google Scholar] [CrossRef]
- Kapaklis, V.; Poulopoulos, P.; Karoutsos, V.; Manouras, T.; Politis, C. Growth of thin Ag films produced by radio frequency magnetron sputtering. Thin Solid Film. 2006, 510, 138–142. [Google Scholar] [CrossRef]
- Garoufalis, C.; Poulopoulos, P.; Bouropoulos, N.; Barnasas, A.; Baskoutas, S. Growth and optical properties of Fe2O3 thin films: A study of quantum confinement effects by experiment and theory. Phys. E Low-Dimens. Syst. Nanostruct. 2017, 89, 67–71. [Google Scholar] [CrossRef]
- Karoutsos, V. Scanning probe microscopy: Instrumentation and applications on thin films and magnetic multilayers. J. Nanosci. Nanotechnol. 2009, 9, 6783–6798. [Google Scholar] [CrossRef]
- Escobar, M.A.; Magana, L.F.; Valenzuela, R. Effect of the grain size distribution on the magnetization curve. J. Appl. Phys. 1985, 57, 2142–2147. [Google Scholar] [CrossRef]
- Vasisht, S.; Shirokoff, J. Preferred orientations in nano nanogold/silica/silicon interfaces. Appl. Surf. Sci. 2010, 256, 4915–4923. [Google Scholar] [CrossRef]
- Scaffardi, L.B.; Pellegri, N.; Sanctis, O.; Tocho, J.O. Sizing gold nanoparticles by optical extinction spectroscopy. Nanotechnology 2005, 16, 158–163. [Google Scholar] [CrossRef]
- Chronis, A.G.; Stamatelatos, A.; Grammatikopoulos, S.; Sigalas, M.M.; Karoutsos, V.; Maratos, D.M.; Lysandrou, S.P.; Trachylis, D.; Politis, C.; Poulopoulos, P. Microstructure and plasmonic behavior of self-assembled silver nanoparticles and nanorings. J. Appl. Phys. 2019, 125, 23106. [Google Scholar] [CrossRef]
- Tsarmpopoulou, M.; Chronis, A.G.; Sigalas, M.; Stamatelatos, A.; Poulopoulos, P.; Grammatikopoulos, S. Calculation of the Localized Surface Plasmon Resonances of Au Nanoparticles Embedded in NiO. Solids 2022, 4, 55–65. [Google Scholar] [CrossRef]
- Stamatelatos, A.; Tsarmpopoulou, M.; Chronis, A.G.; Kanistras, N.; Anyfantis, D.I.; Violagi, E.; Geralis, D.; Sigalas, M.; Poulopoulos, P. Optical interpretation for plasmonic adjustment of nanostructured Ag-NiO thin films. Int. J. Mod. Phys. B 2021, 35, 2150093. [Google Scholar] [CrossRef]
- Stamatelatos, A.; Sousanis, A.; Chronis, D.; Sigalas, M.; Grammatikopoulos, S.; Poulopoulos, P. Analysis of localized surface plasmon resonances in gold nanoparticles surrounded by copper oxides. J. Appl. Phys. 2018, 123, 083103. [Google Scholar] [CrossRef]
- Available online: https://polymerdatabase.com/polymer%20physics/Ref%20Index%20Table%20.html (accessed on 12 February 2022).
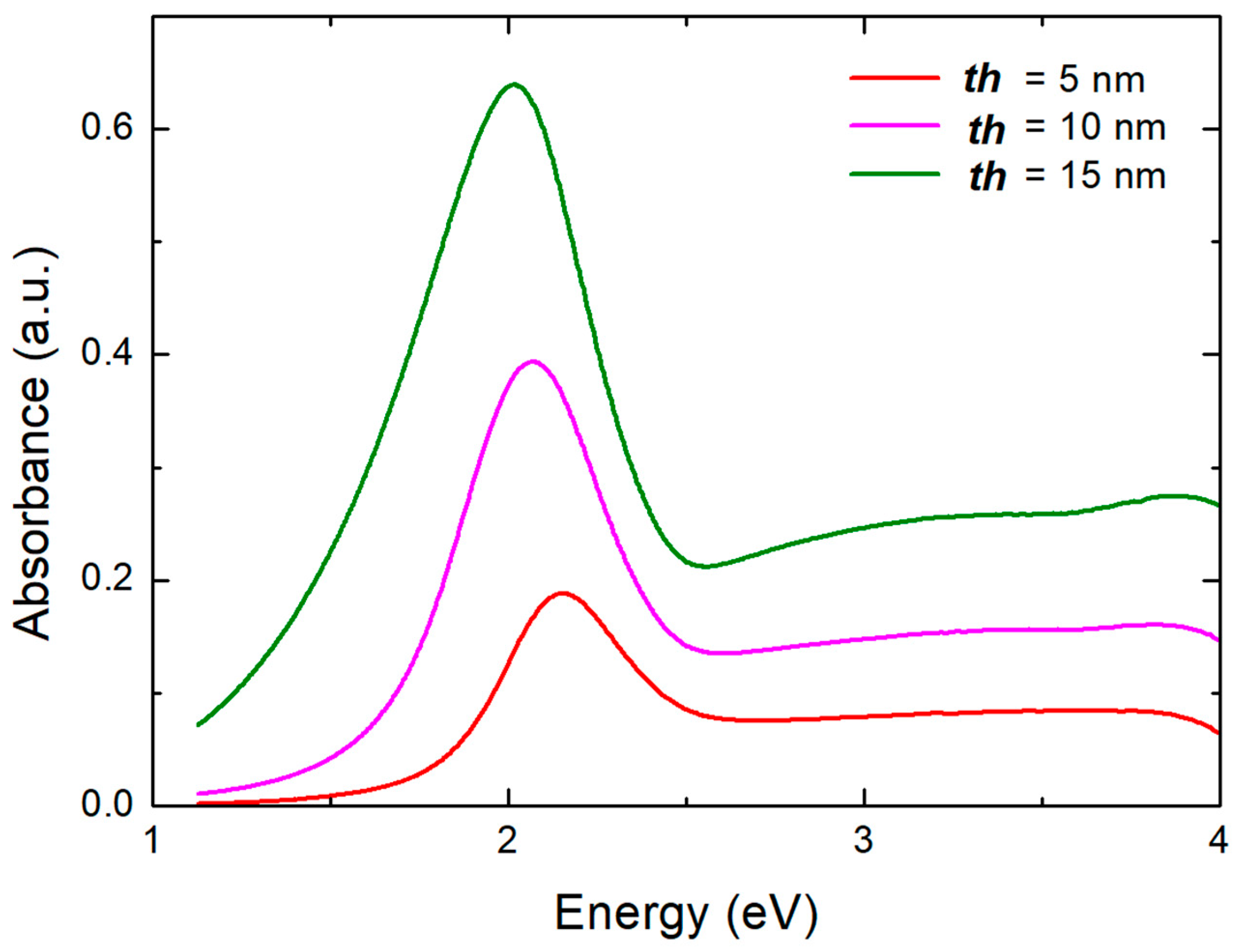
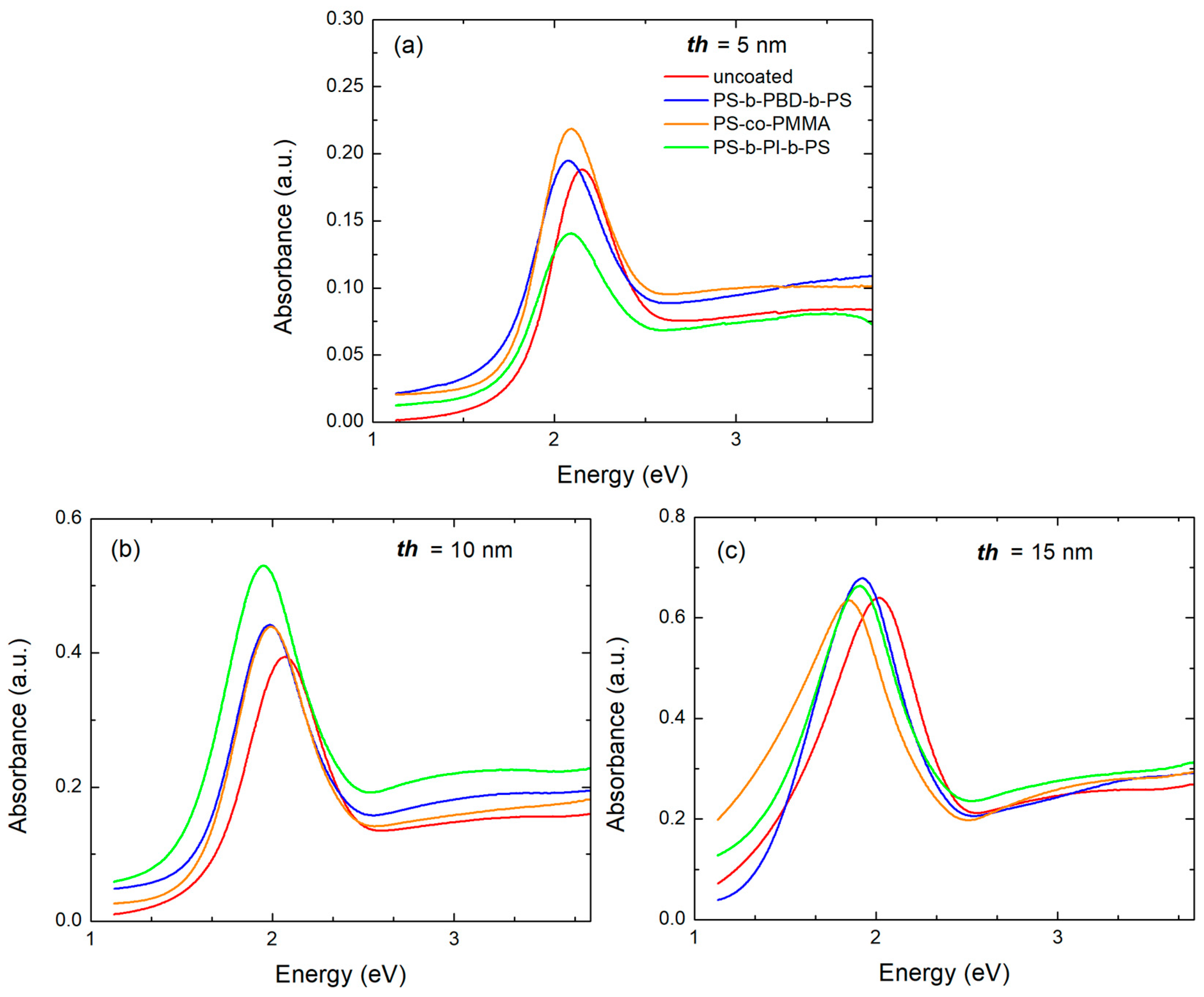
| th (nm) | Coating | LSPR Position (eV) | FWHM (eV) LSPRcoat/LSPRuncoat | |
|---|---|---|---|---|
| 5 | - | 2.15 | 0.36 | 1.0 |
| PS-b-PBD-b-PS | 2.07 | 0.37 | 0.93 | |
| PS-co-PMMA | 2.08 | 0.37 | 1.06 | |
| PS-b-PI-b-PS | 2.08 | 0.38 | 0.68 | |
| 10 | - | 2.07 | 0.42 | 1.0 |
| PS-b-PBD-b-PS | 1.98 | 0.41 | 1.03 | |
| PS-co-PMMA | 1.98 | 0.44 | 1.08 | |
| PS-b-PI-b-PS | 1.94 | 0.45 | 1.23 | |
| 15 | - | 2.01 | 0.50 | 1.0 |
| PS-b-PBD-b-PS | 1.91 | 0.53 | 1.13 | |
| PS-co-PMMA | 1.85 | 0.55 | 0.77 | |
| PS-b-PI-b-PS | 1.90 | 0.50 | 0.94 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stamatelatos, A.; Tsarmpopoulou, M.; Geralis, D.; Chronis, A.G.; Karoutsos, V.; Ntemogiannis, D.; Maratos, D.M.; Grammatikopoulos, S.; Sigalas, M.; Poulopoulos, P. Interpretation of Localized Surface Plasmonic Resonances of Gold Nanoparticles Covered by Polymeric Coatings. Photonics 2023, 10, 408. https://doi.org/10.3390/photonics10040408
Stamatelatos A, Tsarmpopoulou M, Geralis D, Chronis AG, Karoutsos V, Ntemogiannis D, Maratos DM, Grammatikopoulos S, Sigalas M, Poulopoulos P. Interpretation of Localized Surface Plasmonic Resonances of Gold Nanoparticles Covered by Polymeric Coatings. Photonics. 2023; 10(4):408. https://doi.org/10.3390/photonics10040408
Chicago/Turabian StyleStamatelatos, Alkeos, Maria Tsarmpopoulou, Dimitrios Geralis, Alexandros G. Chronis, Vagelis Karoutsos, Dimitrios Ntemogiannis, Dionysios M. Maratos, Spyridon Grammatikopoulos, Mihail Sigalas, and Panagiotis Poulopoulos. 2023. "Interpretation of Localized Surface Plasmonic Resonances of Gold Nanoparticles Covered by Polymeric Coatings" Photonics 10, no. 4: 408. https://doi.org/10.3390/photonics10040408
APA StyleStamatelatos, A., Tsarmpopoulou, M., Geralis, D., Chronis, A. G., Karoutsos, V., Ntemogiannis, D., Maratos, D. M., Grammatikopoulos, S., Sigalas, M., & Poulopoulos, P. (2023). Interpretation of Localized Surface Plasmonic Resonances of Gold Nanoparticles Covered by Polymeric Coatings. Photonics, 10(4), 408. https://doi.org/10.3390/photonics10040408







