Broadband UV Supercontinuum Generation by Three-Color Ionizing Laser Pulses
Abstract
1. Introduction
2. Equations
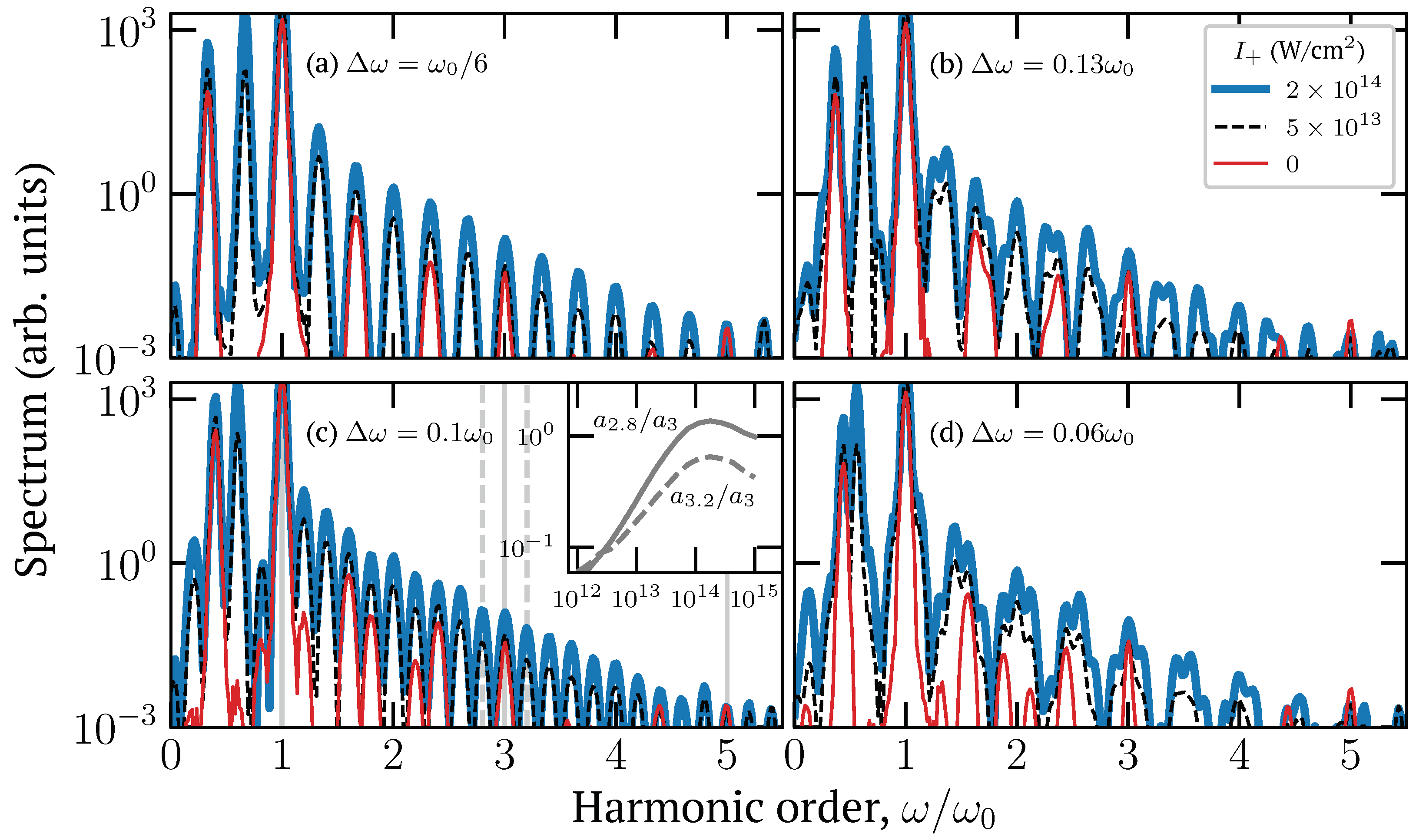
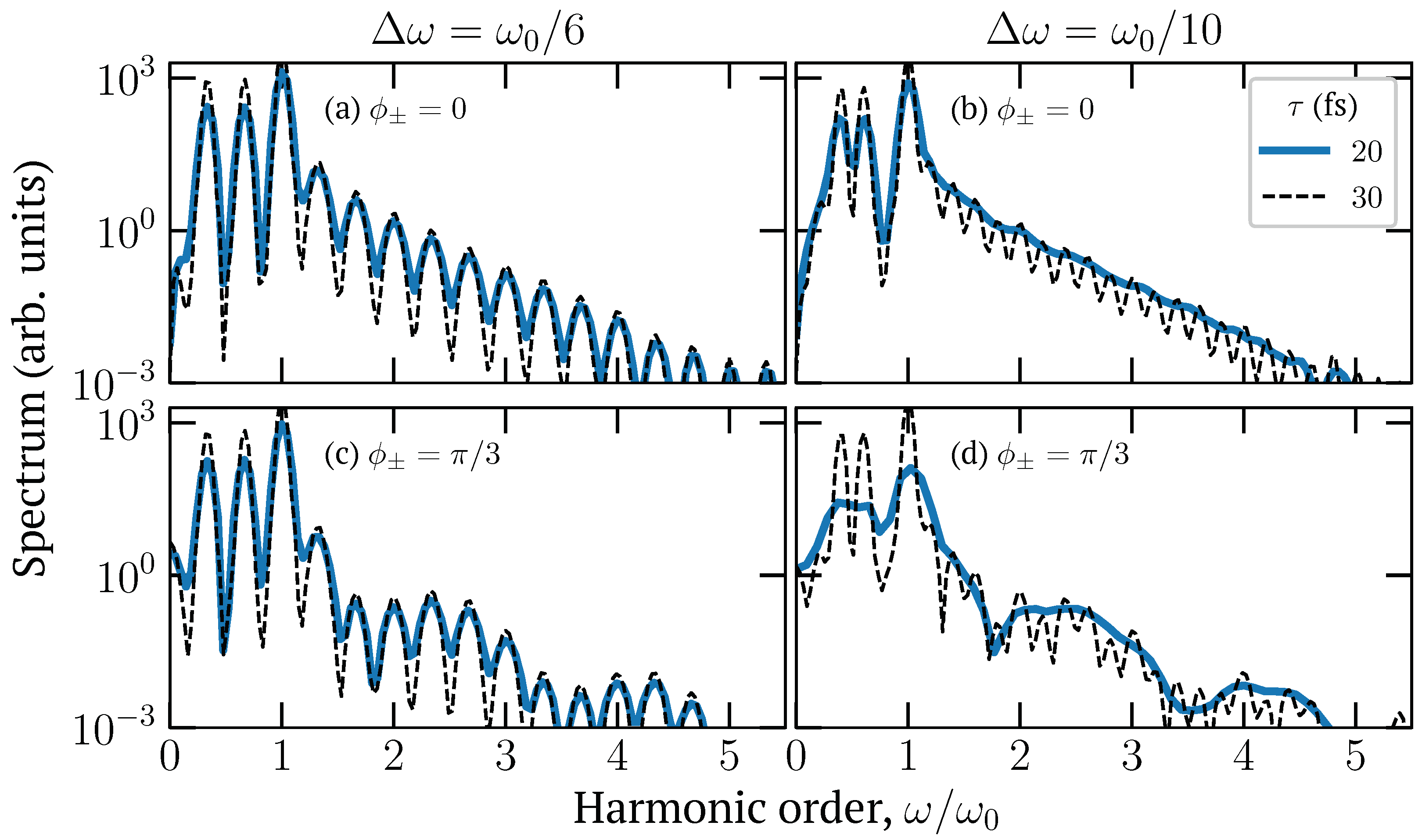
3. Results and Discussion
Smooth Supercontinuum Generation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FWHM | full width at half maximum |
| OPA | optical parametric amplifier |
| TDSE | time-dependent Schrödinger equation |
| UV | ultraviolet |
References
- Koulouklidis, A.D.; Gollner, C.; Shumakova, V.; Fedorov, V.Y.; Pugžlys, A.; Baltuška, A.; Tzortzakis, S. Observation of extremely efficient terahertz generation from mid-infrared two-color laser filaments. Nat. Commun. 2020, 11, 292. [Google Scholar] [CrossRef]
- Nguyen, A.; Kaltenecker, K.; Delagnes, J.C.; Zhou, B.; Cormier, E.; Fedorov, N.; Bouillaud, R.; Descamps, D.; Thiele, I.; Skupin, S.; et al. Wavelength scaling of terahertz pulse energies delivered by two-color air plasmas. Opt. Lett. 2019, 44, 1488–1491. [Google Scholar] [CrossRef] [PubMed]
- Dai, J.; Karpowicz, N.; Zhang, X.C. Coherent polarization control of terahertz waves generated from two-color laser-induced gas plasma. Phys. Rev. Lett. 2009, 103, 023001. [Google Scholar] [CrossRef] [PubMed]
- Vvedenskii, N.V.; Korytin, A.I.; Kostin, V.A.; Murzanev, A.A.; Silaev, A.A.; Stepanov, A.N. Two-color laser-plasma generation of terahertz radiation using a frequency-tunable half harmonic of a femtosecond pulse. Phys. Rev. Lett. 2014, 112, 055004. [Google Scholar] [CrossRef]
- Zhang, L.L.; Wang, W.M.; Wu, T.; Zhang, R.; Zhang, S.J.; Zhang, C.L.; Zhang, Y.; Sheng, Z.M.; Zhang, X.C. Observation of terahertz radiation via the two-color laser scheme with uncommon frequency ratios. Phys. Rev. Lett. 2017, 119, 235001. [Google Scholar] [CrossRef] [PubMed]
- Kostin, V.A.; Laryushin, I.D.; Silaev, A.A.; Vvedenskii, N.V. Ionization-Induced Multiwave Mixing: Terahertz Generation with Two-Color Laser Pulses of Various Frequency Ratios. Phys. Rev. Lett. 2016, 117, 035003. [Google Scholar] [CrossRef]
- Vaičaitis, V.; Balachninaitė, O.; Morgner, U.; Babushkin, I. Terahertz radiation generation by three-color laser pulses in air filament. J. Appl. Phys. 2019, 125, 173103. [Google Scholar] [CrossRef]
- Brunel, F. Harmonic generation due to plasma effects in a gas undergoing multiphoton ionization in the high-intensity limit. J. Opt. Soc. Am. B 1990, 7, 521–526. [Google Scholar] [CrossRef]
- Kostin, V.A.; Vvedenskii, N.V. Generation of Few- and Subcycle Radiation in Midinfrared-to-Deep-Ultraviolet Range During Plasma Production by Multicolor Femtosecond Pulses. Phys. Rev. Lett. 2018, 120, 065002. [Google Scholar] [CrossRef]
- Mitrofanov, A.; Sidorov-Biryukov, D.; Nazarov, M.; Voronin, A.; Rozhko, M.; Shutov, A.; Ryabchuk, S.; Serebryannikov, E.; Fedotov, A.; Zheltikov, A. Ultraviolet-to-millimeter-band supercontinua driven by ultrashort mid-infrared laser pulses. Optica 2020, 7, 15–19. [Google Scholar] [CrossRef]
- Laryushin, I.; Romanov, A. Analysis of Combination Frequencies Arising from the Ionization of Gases by Multicolor Femtosecond Pulses. Photonics 2022, 9, 444. [Google Scholar] [CrossRef]
- Negro, M.; Vozzi, C.; Kovacs, K.; Altucci, C.; Velotta, R.; Frassetto, F.; Poletto, L.; Villoresi, P.; De Silvestri, S.; Tosa, V.; et al. Gating of high-order harmonics generated by incommensurate two-color mid-IR laser pulses. Laser Phys. Lett. 2011, 8, 875. [Google Scholar] [CrossRef]
- Sarantseva, T.; Romanov, A.; Silaev, A.; Vvedenskii, N.; Frolov, M. Waveform retrieving of an isolated attosecond pulse using high-order harmonics generation of the superimposed infrared field. Opt. Express 2021, 29, 38298–38313. [Google Scholar] [CrossRef]
- Liu, S.; Fan, Z.; Lu, C.; Gui, J.; Luo, C.; Wang, S.; Liang, Q.; Zhou, B.; Houard, A.; Mysyrowicz, A.; et al. Coherent control of boosted terahertz radiation from air plasma pumped by a femtosecond three-color sawtooth field. Phys. Rev. A 2020, 102, 063522. [Google Scholar] [CrossRef]
- Kostin, V.A.; Laryushin, I.D.; Vvedenskii, N.V. Generation of Terahertz radiation by multicolor ionizing pulses. JETP Lett. 2020, 112, 77–83. [Google Scholar] [CrossRef]
- Labruyère, A.; Tonello, A.; Couderc, V.; Huss, G.; Leproux, P. Compact supercontinuum sources and their biomedical applications. Opt. Fiber Technol. 2012, 18, 375–378. [Google Scholar] [CrossRef]
- Smith, C.R.; Moltke, A.; Adamu, A.I.; Michieletto, M.; Bowen, P.; Moselund, P.M.; Markos, C.; Bang, O. Low-noise tunable deep-ultraviolet supercontinuum laser. Sci. Rep. 2020, 10, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Lei, H.; Yao, J.; Zhao, J.; Xie, H.; Zhang, F.; Zhang, H.; Zhang, N.; Li, G.; Zhang, Q.; Wang, X.; et al. Ultraviolet supercontinuum generation driven by ionic coherence in a strong laser field. Nat. Commun. 2022, 13, 4080. [Google Scholar] [CrossRef]
- Poudel, C.; Kaminski, C.F. Supercontinuum radiation in fluorescence microscopy and biomedical imaging applications. JOSA B 2019, 36, A139–A153. [Google Scholar] [CrossRef]
- Romanov, A.A.; Silaev, A.A.; Sarantseva, T.S.; Frolov, M.V.; Vvedenskii, N.V. Study of high-order harmonic generation in xenon based on time-dependent density-functional theory. New J. Phys. 2021, 23, 043014. [Google Scholar] [CrossRef]
- Strelkov, V.V. High-order optical processes in intense laser field: Towards nonperturbative nonlinear optics. Phys. Rev. A 2016, 93, 053812. [Google Scholar] [CrossRef]
- Babushkin, I.; Demircan, A.; Morgner, U.; Savel’ev, A. High-order harmonics and supercontinua formed by a weak optical pump in the presence of an extreme terahertz field. Phys. Rev. A 2022, 106, 013115. [Google Scholar] [CrossRef]
- Chung, K.L. A Course in Probability Theory; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Picqué, N.; Hänsch, T.W. Frequency comb spectroscopy. Nat. Photonics 2019, 13, 146–157. [Google Scholar] [CrossRef]
- Lu, J.; Liu, X.; Bruch, A.W.; Zhang, L.; Wang, J.; Yan, J.; Tang, H.X. Ultraviolet to mid-infrared supercontinuum generation in single-crystalline aluminum nitride waveguides. Opt. Lett. 2020, 45, 4499–4502. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Gong, P.; Bai, L.; Xu, X.; Zhang, S.; Sun, Z.; Lin, Z.; Hong, M.; Chen, C.; Luo, J. Beryllium-free Li4Sr (BO3)2 for deep-ultraviolet nonlinear optical applications. Nat. Commun. 2014, 5, 4019. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laryushin, I.; Romanov, A. Broadband UV Supercontinuum Generation by Three-Color Ionizing Laser Pulses. Photonics 2023, 10, 406. https://doi.org/10.3390/photonics10040406
Laryushin I, Romanov A. Broadband UV Supercontinuum Generation by Three-Color Ionizing Laser Pulses. Photonics. 2023; 10(4):406. https://doi.org/10.3390/photonics10040406
Chicago/Turabian StyleLaryushin, Ivan, and Alexander Romanov. 2023. "Broadband UV Supercontinuum Generation by Three-Color Ionizing Laser Pulses" Photonics 10, no. 4: 406. https://doi.org/10.3390/photonics10040406
APA StyleLaryushin, I., & Romanov, A. (2023). Broadband UV Supercontinuum Generation by Three-Color Ionizing Laser Pulses. Photonics, 10(4), 406. https://doi.org/10.3390/photonics10040406




