Adaptive Weighted K-Nearest Neighbor Trilateration Algorithm for Visible Light Positioning
Abstract
1. Introduction
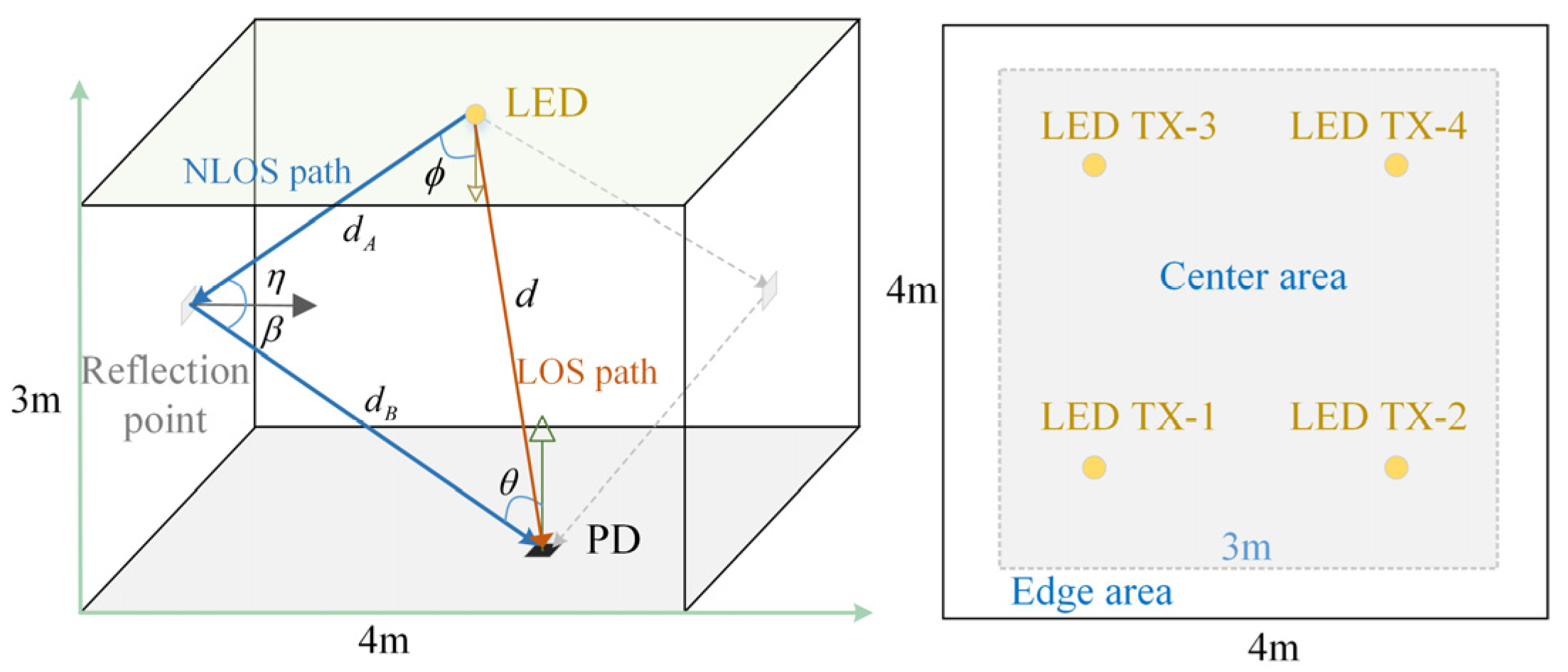
2. System Model
2.1. Optical Wireless Channel Model
2.2. CSI-Based Positioning System Model
2.3. Related Work
2.3.1. Nonlinear LS Estimation Algorithm
2.3.2. Modified WKNN Algorithm
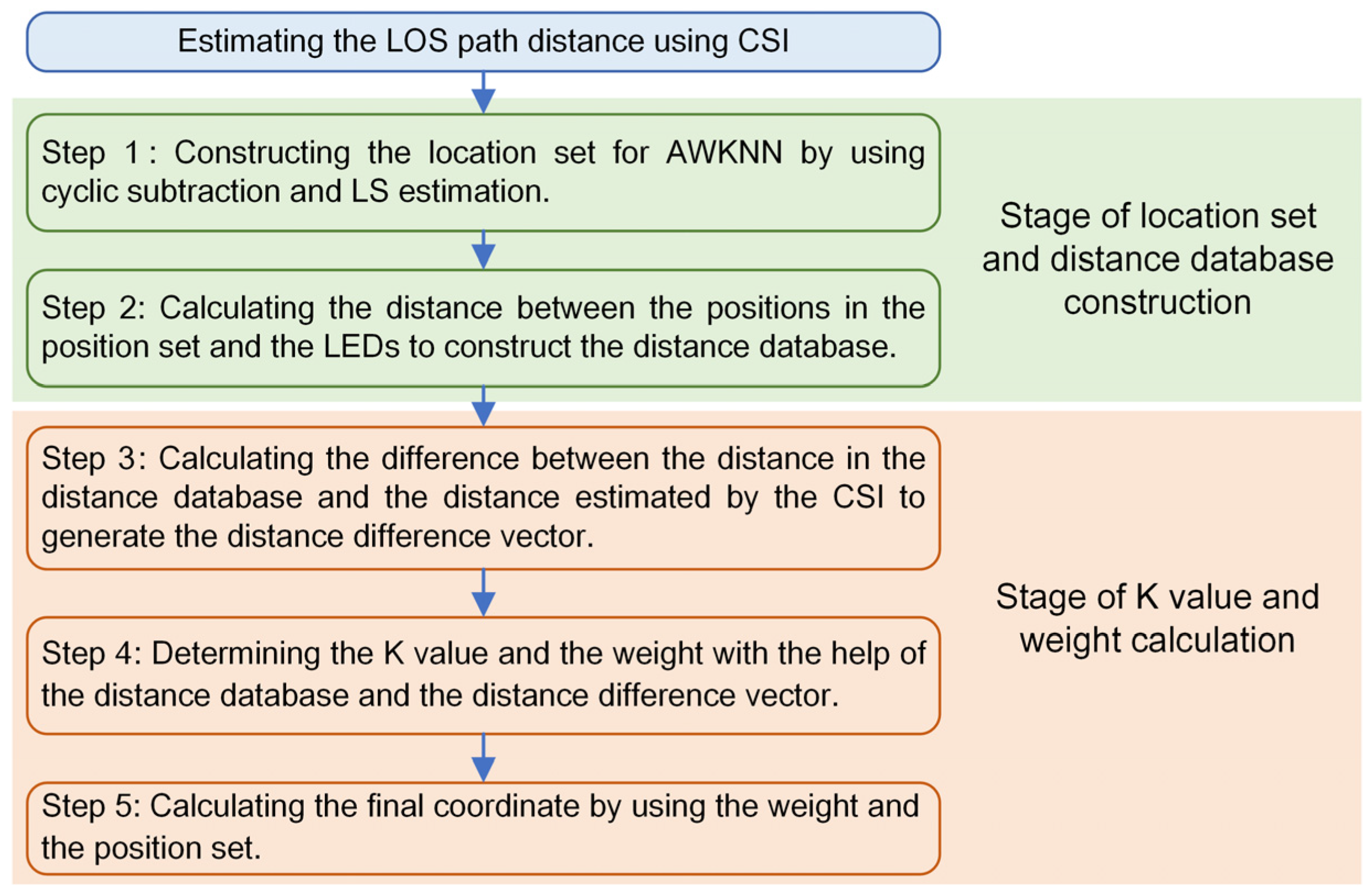
3. AWKNN Method
| Algorithm 1. Determination of the K-value and weight |
| 1: Let be the vector generated by sorting the values in vector from small to large, and the corresponding index vector is defined as . |
| 2: For , iteratively complete the following. |
| (a) Calculate the weight vector , as follows |
| (b) The distance vectors corresponding to the first K values of the index vector are taken from the distance database to generate a new distance matrix , which can be expressed as |
| (c) Calculate the weighted average distance vector of the distance matrix , as follows |
| (d) Calculate the difference between the new distance vector and the estimated horizontal distance vector based on the CSI |
| 3: After the above iterative calculation, the distance difference vector is obtained. The index corresponding to the minimum value in the difference vector is determined as the K value, as follows |
| 4: The weight of the AWKNN is defined as |
4. Results and Discussion
4.1. Simulation Setup
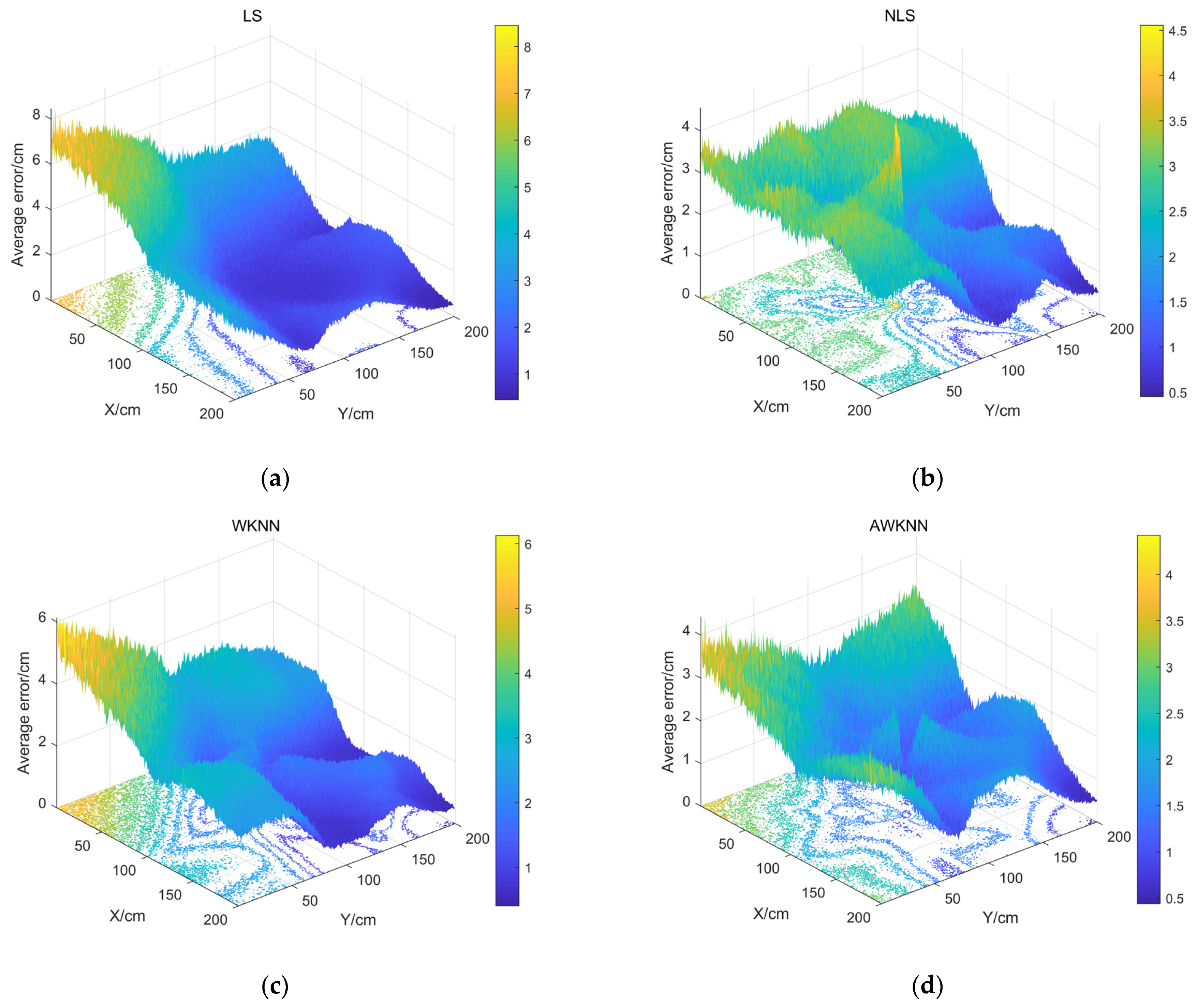
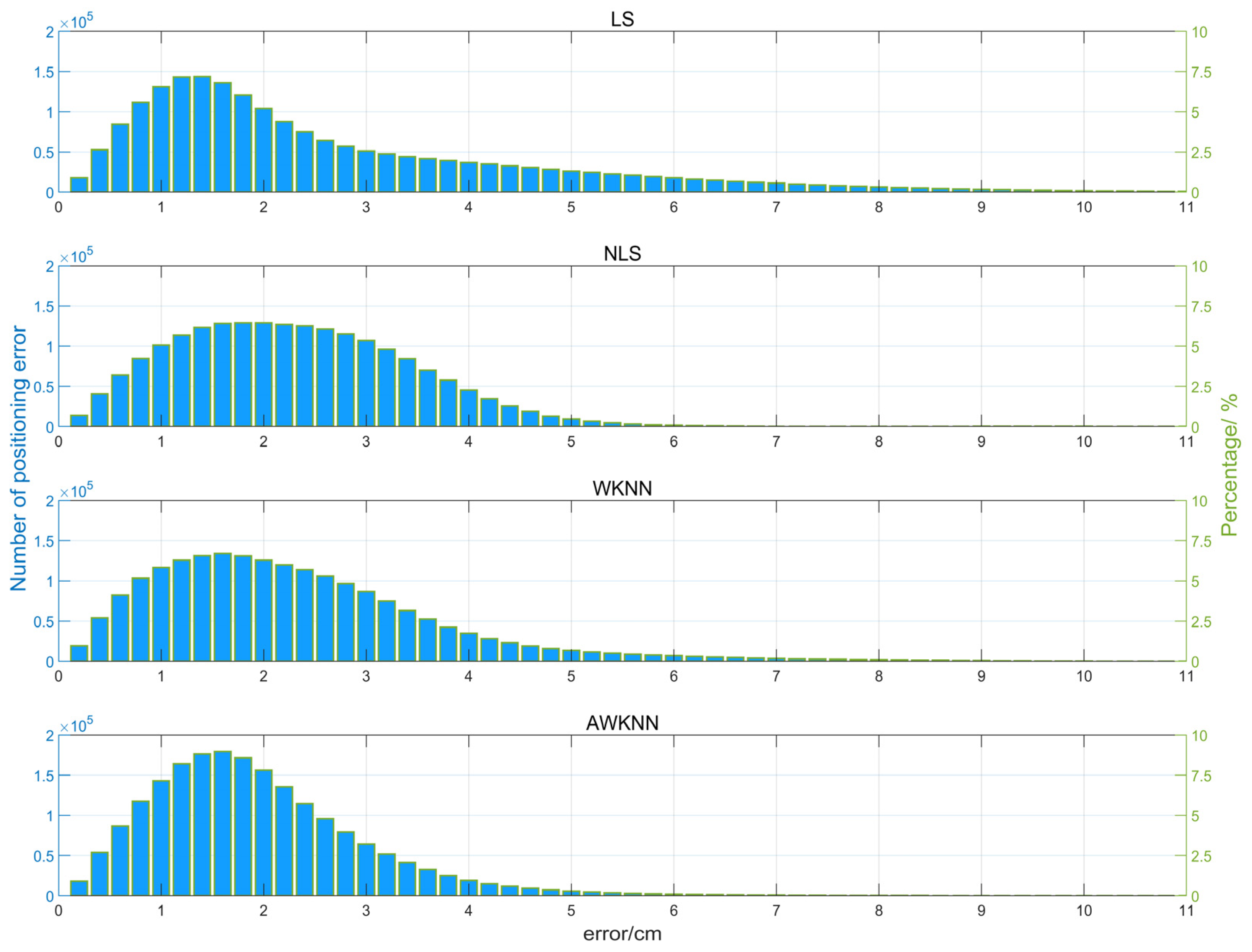
4.2. Performance Evaluation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Farahsari, P.S.; Farahzadi, A.; Rezazadeh, J.; Bagheri, A. A Survey on Indoor Positioning Systems for IoT-Based Applications. IEEE Internet Things J. 2022, 9, 7680–7699. [Google Scholar] [CrossRef]
- Guo, X.; Ansari, N.; Hu, F.; Shao, Y.; Elikplim, N.R.; Li, L. A Survey on Fusion-Based Indoor Positioning. IEEE Commun. Surv. Tutor. 2020, 22, 566–594. [Google Scholar] [CrossRef]
- Zafari, F.; Gkelias, A.; Leung, K.K. A survey of indoor localization systems and technologies. IEEE Commun. Surv. Tutor. 2019, 21, 2568–2599. [Google Scholar] [CrossRef]
- Matheus, L.E.M.; Vieira, A.B.; Vieira, L.F.M.; Vieira, M.A.M.; Gnawali, O. Visible Light Communication: Concepts, Applications and Challenges. IEEE Commun. Surv. Tutor. 2019, 21, 3204–3237. [Google Scholar] [CrossRef]
- Huang, N.; Gong, C.; Luo, J.; Xu, Z. Design and Demonstration of Robust Visible Light Positioning Based on Received Signal Strength. J. Light. Technol. 2020, 38, 5695–5707. [Google Scholar] [CrossRef]
- Martínez-Ciro, R.A.; López-Giraldo, F.E.; Luna-Rivera, J.M.; Ramírez-Aguilera, A.M. An Indoor Visible Light Positioning System for Multi-Cell Networks. Photonics 2022, 9, 146. [Google Scholar] [CrossRef]
- Steendam, H. A 3-D positioning algorithm for AOA-based VLP with an aperture-based receiver. IEEE J. Sel. Areas Commun. 2018, 36, 23–33. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, J. A Novel Three-Dimensional Algorithm Based on Practical Indoor Visible Light Positioning. IEEE Photonics J. 2019, 11, 6101308. [Google Scholar] [CrossRef]
- Du, P.; Zhang, S.; Chen, C.; Alphones, A.; Zhong, W.-D. Demonstration of a Low-Complexity Indoor Visible Light Positioning System Using an Enhanced TDOA Scheme. IEEE Photonics J. 2018, 10, 7905110. [Google Scholar] [CrossRef]
- Meng, X.; Jia, C.; Cai, C.; He, F.; Wang, Q. Indoor High-Precision 3D Positioning System Based on Visible-Light Communication Using Improved Whale Optimization Algorithm. Photonics 2022, 9, 93. [Google Scholar] [CrossRef]
- Bai, L.; Yang, Y.; Feng, C.; Guo, C. Received signal strength assisted perspective-three-point algorithm for indoor visible light positioning. Opt. Express 2020, 28, 28045–28059. [Google Scholar] [CrossRef]
- Liu, X.; Zou, D.; Huang, N.; Wang, Y. An Efficient Iterative Least Square Method for Indoor Visible Light Positioning under Shot Noise. IEEE Photonics J. 2022, 15, 7300910. [Google Scholar] [CrossRef]
- Gu, W.; Aminikashani, M.; Deng, P.; Kavehrad, M. Impact of Multipath Reflections on the Performance of Indoor Visible Light Positioning Systems. J. Light. Technol. 2016, 34, 2578–2587. [Google Scholar] [CrossRef]
- Wang, K.; Liu, Y.; Hong, Z. RSS-based visible light positioning based on channel state information. Opt. Express 2022, 30, 56. [Google Scholar] [CrossRef]
- Bakar, A.; Glass, T.; Tee, H.; Alam, F.; Legg, M. Accurate visible light positioning using multiple-photodiode receiver and machine learning. IEEE Trans. Instrum. Meas. 2021, 70, 7500812. [Google Scholar] [CrossRef]
- Tran, H.Q.; Ha, C. High Precision Weighted Optimum K-Nearest Neighbors Algorithm for Indoor Visible Light Positioning Applications. IEEE Access 2020, 8, 114597–114607. [Google Scholar] [CrossRef]
- Xu, S.; Chen, C.C.; Wu, Y.; Wang, X.; Wei, F. Adaptive Residual Weighted K-Nearest Neighbor Fingerprint Positioning Algorithm Based on Visible Light Communication. Sensors 2020, 20, 4432. [Google Scholar] [CrossRef]
- Lin, D.C.; Chow, C.W.; Peng, C.W.; Hung, T.Y.; Chang, Y.H.; Song, S.H.; Lin, Y.S.; Liu, Y.; Lin, K.H. Positioning unit cell model duplication with residual concatenation neural network (RCNN) and transfer learning for visible light positioning (VLP). J. Light. Technol. 2021, 39, 6366–6372. [Google Scholar] [CrossRef]
- Chen, H.; Han, W.; Wang, J.; Lu, H.; Chen, D.; Jin, J.; Feng, L. High accuracy indoor visible light positioning using a long short term memory-fully connected network based algorithm. Opt. Express 2021, 29, 41109–41120. [Google Scholar] [CrossRef]
- Hsu, L.; Tsai, D.; Chen, H.M.; Chang, Y.; Liu, Y.; Chow, C.; Song, S.; Yeh, C. Using Received-Signal-Strength (RSS) Pre-Processing and Convolutional Neural Network (CNN) to Enhance Position Accuracy in Visible Light Positioning (VLP). In Proceedings of the Optical Fiber Communication Conference (OFC) 2022, San Diego, CA, USA, 6–10 March 2022. [Google Scholar]
- Cao, Z.; Cheng, M.; Yang, Q.; Tang, M.; Liu, D.; Deng, L. Experimental investigation of environmental interference mitigation and blocked LEDs using a memory-artificial neural network in 3D indoor visible light positioning systems. Opt. Express 2021, 29, 33937–33953. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, L. Intelligent and Practical Deep Learning Aided Positioning Design for Visible Light Communication Receivers. IEEE Commun. Lett. 2020, 3, 577–580. [Google Scholar] [CrossRef]
- Liu, R.; Liang, Z.; Yang, K.; Li, W. Machine Learning Based Visible Light Indoor Positioning With Single-LED and Single Rotatable Photo Detector. IEEE Photonics J. 2022, 14, 7322511. [Google Scholar] [CrossRef]
- Wang, K.; Liu, Y.; Hong, Z. A Novel Timing Synchronization Method for DCO-OFDM-Based VLC Systems. IEEE Photon. J. 2021, 13, 7300709. [Google Scholar] [CrossRef]
- Wang, K. Simulation Results of CSI-Based AWKNN; FigShare. Available online: https://figshare.com/articles/dataset/Simulation_Results_of_CSI-Based_AWKNN/22276759 (accessed on 21 December 2022).



| Symbol | Parameter | Value | |
|---|---|---|---|
| room parameters | L × W × H | size of the simulation environment | 4 m × 4 m × 3 m |
| reflectance factor of the wall | 0.33 | ||
| reflective area of each reflection point | 1 cm2 | ||
| transmitter parameters | N | number of LEDs | 4 |
| m | order of Lambertian emission | 2.6 | |
| LED transmit power | 2 W | ||
| receiver parameters | surface area of the PD | 1 cm2 | |
| PD’s responsivity | 0.5 A/W | ||
| PD’s FOV semi-angle | 80° | ||
| optical filter gain | 1 | ||
| concentrator gain | 1 | ||
| noise bandwidth factor | 0.562 | ||
| noise bandwidth factor | 0.0868 | ||
| background current | 5100 μA | ||
| circuit absolute temperature | 295 K | ||
| G | open-loop voltage gain | 10 | |
| fixed capacitance per unit area | 112 pF/cm2 | ||
| FET channel noise factor | 1.5 | ||
| FET transconductance | 30 mS | ||
| system parameters | B | system bandwidth | 125 MHz |
| length of CP | 16 | ||
| length of training symbol | 512 | ||
| number of pilot symbol | 128 | ||
| length of pilot symbol | 32 | ||
| sampling interval of the receiver signal | 4 ns | ||
| M | size of the position set in the NLS and WKNN algorithms | 25 | |
| T | number of iterations in the NLS algorithm | 6 | |
| K | number of nearest neighbors in the WKNN algorithm | 5 |
| Positioning Error | LS | WKNN | NLS | AWKNN | |
|---|---|---|---|---|---|
| Entire room | Mean/cm | 2.58 | 2.21 | 2.20 | 1.84 |
| RMS/cm | 3.27 | 2.62 | 2.47 | 2.13 | |
| Center area | Mean/cm | 1.48 | 1.52 | 1.72 | 1.43 |
| RMS/cm | 1.75 | 1.74 | 1.96 | 1.59 | |
| Edge area | Mean/cm | 3.99 | 3.09 | 2.82 | 2.37 |
| RMS/cm | 4.53 | 3.43 | 2.99 | 2.67 | |
| Method | Time Complexity |
|---|---|
| LS | |
| WKNN | |
| NLS | |
| AWKNN |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; He, Y.; Huang, X.; Hong, Z. Adaptive Weighted K-Nearest Neighbor Trilateration Algorithm for Visible Light Positioning. Photonics 2023, 10, 319. https://doi.org/10.3390/photonics10030319
Wang K, He Y, Huang X, Hong Z. Adaptive Weighted K-Nearest Neighbor Trilateration Algorithm for Visible Light Positioning. Photonics. 2023; 10(3):319. https://doi.org/10.3390/photonics10030319
Chicago/Turabian StyleWang, Kaiyao, Yi He, Xinpeng Huang, and Zhiyong Hong. 2023. "Adaptive Weighted K-Nearest Neighbor Trilateration Algorithm for Visible Light Positioning" Photonics 10, no. 3: 319. https://doi.org/10.3390/photonics10030319
APA StyleWang, K., He, Y., Huang, X., & Hong, Z. (2023). Adaptive Weighted K-Nearest Neighbor Trilateration Algorithm for Visible Light Positioning. Photonics, 10(3), 319. https://doi.org/10.3390/photonics10030319





