Experimental Proof-of-Concept of a Spatial Photonic Switch Based on an Off-Axis Zone Plate in Millimeter Wavelength Range
Abstract
:1. Introduction
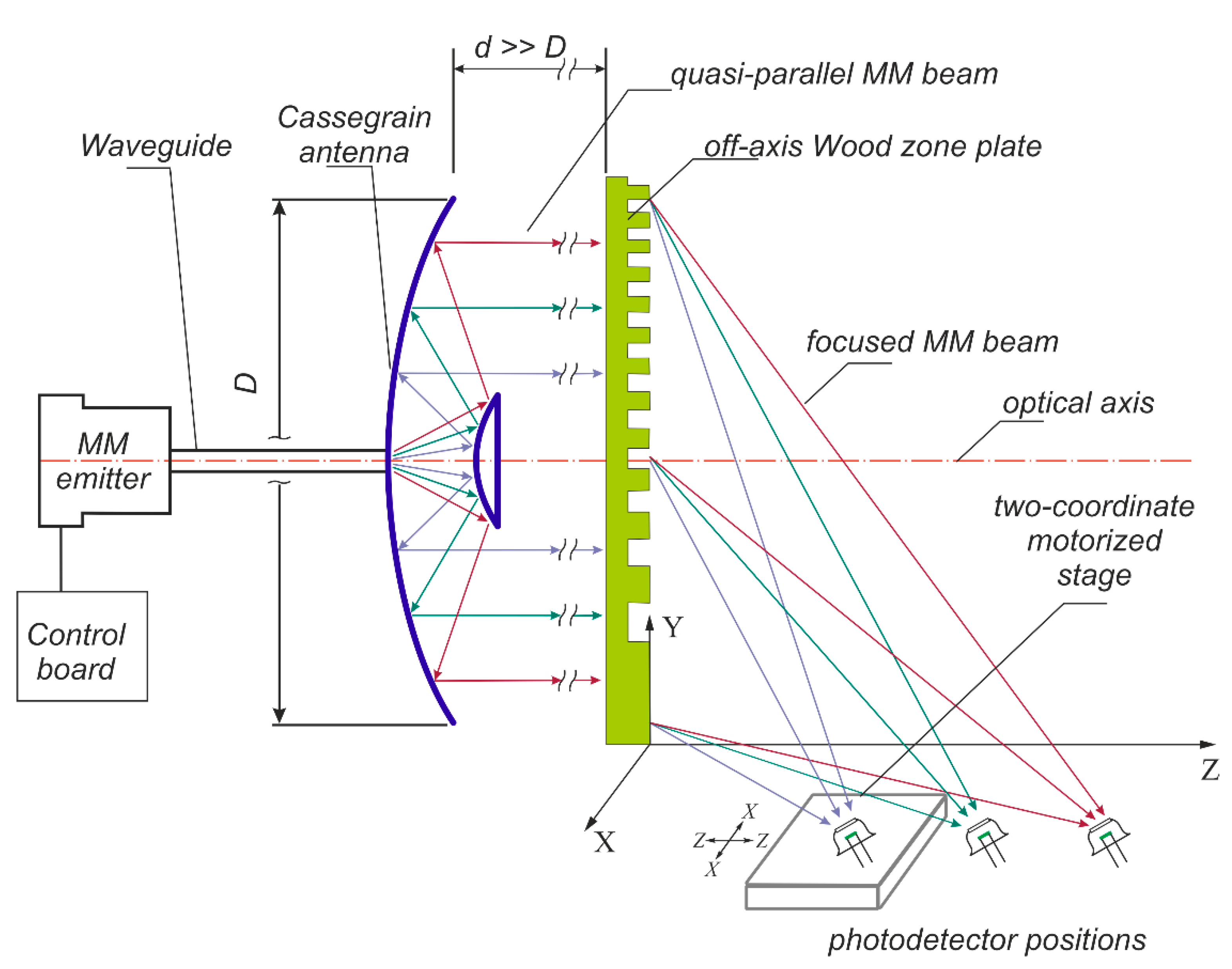
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- El-Bawab, T.S. Optical Switching; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Brunetti, G.; Marocco, G.; Di Benedetto, A.; Giorgio, A.; Armenise, M.N.; Ciminelli, C. Design of a large bandwidth 2 × 2 interferometric switching cell based on a sub-wavelength grating. J. Opt. 2021, 23, 085801. [Google Scholar] [CrossRef]
- Yeow, T.-W.; Law, K.L.E.; Goldenberg, A. MEMS optical switches. IEEE Commun. Mag. 2001, 39, 158–163. [Google Scholar] [CrossRef]
- Neyer, A. Electro-optic X-switch using single-mode Ti:LiNbO3 channel waveguides. Electron. Lett. 1983, 14, 553–554. [Google Scholar] [CrossRef]
- Ikku, Y.; Yokoyama, M.; Ichikawa, O.; Hata, M.; Takenaka, M.; Takagi, S. Low-driving-current InGaAsP photonic-wire optical switches using III-V CMOS photonics platform. Opt. Express 2012, 20, B357–B364. [Google Scholar] [CrossRef] [PubMed]
- Burmeister, E.F.; Mack, J.P.; Poulsen, H.N.; Klamkin, J.; Coldren, L.A.; Blumenthal, D.J.; Bowers, J.E. SOA gate array recirculating buffer for optical packet switching. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 24–28 February 2008; pp. 1–3. [Google Scholar] [CrossRef]
- D’Alessandro, A.; Asquini, R.; Menichella, F.; Ciminelli, C. Realisation and characterisation of a ferroelectric liquid crystal bistable optical switch. Mol. Cryst. Liq. Cryst. 2002, 372, 353–363. [Google Scholar] [CrossRef]
- Tanabe, T.; Notomi, M.; Mitsugi, S.; Shinya, A.; Kuramochi, E. All-optical switches on a silicon chip realized using photonic crystal nanocavities. Appl. Phys. Lett. 2005, 87, 151112. [Google Scholar] [CrossRef]
- Stabile, R.; Albores-Mejia, A.; Rohit, A.; Williams, K.A. Integrated optical switch matrices for packet data networks. Microsyst. Nanoeng. 2016, 2, 15042. [Google Scholar] [CrossRef]
- Cheng, Z.; Ríos, C.; Pernice, W.H.P.; Wright, C.D.; Bhaskaran, H. On-chip photonic synapse. Sci. Adv. 2017, 3, e1700160. [Google Scholar] [CrossRef]
- Cheng, Q.; Bahadori, M.; Glick, M.; Rumley, S.; Bergman, K. Recent advances in optical technologies for data centers: A review. Optica 2018, 5, 1354–1370. [Google Scholar] [CrossRef]
- Virgilio, M.; Witzigmann, B.; Bolognini, G.; Guha, S.; Schroeder, T.; Capellini, G. CMOS-compatible optical switching concept based on strain-induced refractive-index tuning. Opt. Express 2015, 23, 5930–5940. [Google Scholar] [CrossRef]
- Ravel, K.; Koechlin, C.; Prevost, E.; Bomer, T.; Poirier, R.; Tonck, L.; Guinde, G.; Beaumel, M.; Parsons, N.; Enrico, M.; et al. Optical switch matrix development for new concepts of photonic based flexible telecom payloads. In Proceedings of the SPIE 11180, International Conference on Space Optics—ICSO 2018, Chania, Greece, 9–12 October 2018; p. 111803H. [Google Scholar]
- Jia, H.; Yang, S.; Zhou, T.; Shao, S.; Fu, X.; Zhang, L.; Yang, L. WDM-compatible multimode optical switching system-on-chip. Nanophotonics 2019, 8, 889–898. [Google Scholar] [CrossRef]
- Williamson, I.A.D.; Fan, S. Broadband Optical Switch based on an Achromatic Photonic Gauge Potential in Dynamically Modulated Waveguides. Phys. Rev. Appl. 2019, 11, 054035. [Google Scholar] [CrossRef]
- Li, L.; Liu, C.; Peng, H.; Wang, Q. Optical switch based on electrowetting liquid lens. J. Appl. Phys. 2012, 111, 103103. [Google Scholar] [CrossRef]
- Seok, T.J.; Quack, N.; Han, S.; Muller, R.S.; Wu, M.C. Large-scale broadband digital silicon photonic switches with vertical adiabatic couplers. Optica 2016, 3, 64–70. [Google Scholar] [CrossRef]
- Han, S.; Seok, T.J.; Quack, N.; Yoo, B.-W.; Wu, M.C. Large-scale silicon photonic switches with movable directional couplers. Optica 2015, 2, 370–375. [Google Scholar] [CrossRef]
- Han, S.; Seok, T.J.; Yu, K.; Quack, N.; Muller, R.S.; Wu, M.C. Large-scale polarization-insensitive silicon photonic MEMS switches. J. Lightwave Technol. 2018, 36, 1824–1830. [Google Scholar] [CrossRef]
- Seok, T.J.; Luo, J.; Huang, Z.; Kwon, K.; Henriksson, J.; Jacobs, J.; Ochikubo, L.; Muller, R.S.; Wu, M.C. Silicon photonic wavelength cross-connect with integrated MEMS switching. APL Photonics 2019, 4, 100803. [Google Scholar] [CrossRef]
- Yamamoto, N.; Ogawa, T.; Komori, K. Photonic crystal directional coupler switch with small switching length and wide bandwidth. Opt. Express 2006, 14, 1223. [Google Scholar] [CrossRef]
- Strasser, T.A.; Wagener, J.L. Wavelength-selective switches for ROADM applications. IEEE J. Sel. Top. Quantum. Electron. 2010, 16, 1150–1157. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, M.; Xie, Y.; Shi, Y.; Kumar, R.; Panepucci, R.R.; Dai, D. Wavelength-selective 2 × 2 optical switch based on a Ge2Sb2Te5-assisted microring. Photon. Res. 2020, 8, 1171–1176. [Google Scholar] [CrossRef]
- Grujic, K.; Hole, J.P.; Hellesø, O.G.; Wilkinson, J.S. Whispering gallery modes excitation in borosilicate glass microspheres by K+ ion-exchanged channel waveguide coupler. In Proceedings of the SPIE: Photonics West: 8th International Conference on Laser Beam Control and Applications, San José, Costa Rica, 22–26 January 2006. [Google Scholar]
- Işçi, S.; Bilici, T.; Kurt, A.; Serpengüzel, A. Morphology-dependent resonances of optical microsphere resonators for the realization of passive wavelength-division multiplexing components. Opt. Eng. 2004, 43, 1051–1055. [Google Scholar] [CrossRef]
- Geints, Y.; Minin, O.V.; Yue, L.; Minin, I.V. Wavelength-scale photonic space switch proof-of-concept based on photonic hook effect. Ann. Phys. 2021, 533, 2100192. [Google Scholar] [CrossRef]
- Yue, L.; Wang, Z.; Xie, Y.; Geints, Y.; Minin, O.V.; Minin, I.V. Near-field light-bending photonic switch: Physics of switching based on three-dimensional Poynting vector analysis. Photonics 2022, 9, 154. [Google Scholar] [CrossRef]
- Geints, Y.; Minin, I.V.; Minin, O.V. Tailoring ‘photonic hook’ from Janus dielectric microbar. J. Opt. 2020, 22, 065606. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Liu, C.; Wei, H.; Geints, Y.; Karabchevsky, A. Experimental demonstration of a tunable photonic hook by a partially illuminated dielectric microcylinder. Opt. Lett. 2020, 45, 4899–4902. [Google Scholar] [CrossRef]
- Liu, C.; Chung, H.; Minin, O.V.; Minin, I.V. Shaping photonic hook via well-controlled illumination of finite-size graded-index micro-ellipsoid. J. Opt. 2020, 22, 085002. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Golodnikov, D.O. Simple free-space method for measurement of dielectric constant by means of diffractive optics with new capabilities. In Proceedings of the 8th International Conference on Actual Problems of Electronic Instrument Engineering, Novosibirsk, Russia, 26–28 September 2006; pp. 3–8. [Google Scholar]
- Su, H.; Hurd Price, H.; Jing, L.; Tian, Q.; Liu, J.; Qian, K. Janus particles: Design, preparation, and biomedical applications. Mater. Today Bio 2019, 4, 100033. [Google Scholar] [CrossRef]
- Paulish, A.G.; Gusachenko, A.V.; Morozov, A.O.; Dorozhkin, K.V.; Suslyaev, V.I.; Golyashov, V.A.; Minin, O.V.; Minin, I.V. Characterization of tetraaminediphenyl-based pyroelectric detector from visible to millimeter wave ranges. Opt. Eng. 2020, 59, 061612. [Google Scholar] [CrossRef]
- Paulish, A.G.; Gusachenko, A.V.; Morozov, A.O.; Golyashov, V.A.; Dorozhkin, K.V.; Suslyaev, V.I. Sensitivity of the tetraaminodiphenyl based pyroelectric sensor from visible to sub-THz range. Sens. Rev. 2020, 40, 291–296. [Google Scholar] [CrossRef]
- Guo, Y.J.; Barton, S.K. Offset Fresnel zone plate antennas. Int. J. Satell. Commun. 1994, 12, 381–385. [Google Scholar] [CrossRef]
- Monkevich, J.M.; Le Sage, G.P. Design and fabrication of a customdielectric Fresnel multi-zone plate lens antenna using additive manufacturing techniques. IEEE Access 2019, 7, 61452–61460. [Google Scholar] [CrossRef]
- Furlan, W.D.; Ferrando, V.; Monsoriu, J.A.; Zagrajek, P.; Czerwińska, E.; Szustakowski, M. 3D printed diffractive terahertz lenses. Opt. Lett. 2016, 41, 1748–1751. [Google Scholar] [CrossRef]
- Poyanco, J.M.; Pizarro, F.; Rajo-Iglesias, E. Cost-effective wideband dielectric planar lens antenna for millimeter wave applications. Sci. Rep. 2022, 12, 4204. [Google Scholar] [CrossRef] [PubMed]
- Minin, I.V.; Minin, O.V.; Lukianchuk, B.S. Mesotronic era of dielectric photonics. Proc. SPIE 2022, 12152, 89–93. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics; Pergamon Press: New York, NY, USA, 1955. [Google Scholar]
- Pfeiffer, F.; David, C.; van der Veen, J.F.; Bergemann, C. Nanometer focusing properties of Fresnel zone plates described by dynamical diffraction theory. Phys. Rew. B 2006, 73, 245331. [Google Scholar] [CrossRef]
- Fast Detectors (ZBD-F). Available online: https://vadiodes.com/en/zbd (accessed on 12 August 2022).
- Zero-Bias Detector Operational Manual (ZBD, ZBD-F, QOD). Available online: https://www.amtechs.co.jp/product/ea0ce625ff6a2c70bbd3d4bdba61f36757498363.pdf (accessed on 12 August 2022).
- Park, C.H.; Lee, J.H. Formulas of 1/f noise in Schottky barrier diodes under reverse bias. Solid-State Electron. 2012, 69, 85–88. [Google Scholar] [CrossRef]
- Feng, L.; Tetz, K.; Slutsky, B.; Lomakin, V.; Fainman, V. Fourier plasmonics: Diffractive focusing of in-plane surface plasmon polariton waves. Appl. Phys. Lett. 2007, 91, 081101. [Google Scholar] [CrossRef]
- Podbiel, D.; Kahl, P.; Frank, B.; Davis, T.; Giessen, H.; Hoegen, M.; Heringdorf, F. patiotemporal Analysis of an Efficient Fresnel Grating Coupler for Focusing Surface Plasmon Polaritons. ACS Photonics 2019, 6, 600–604. [Google Scholar] [CrossRef]
- Vinogradov, A.P.; Aivazyan, A.V. Scaling theory for homogenization of the Maxwell equations. Phys. Rev. E 1999, 60, 987. [Google Scholar] [CrossRef]

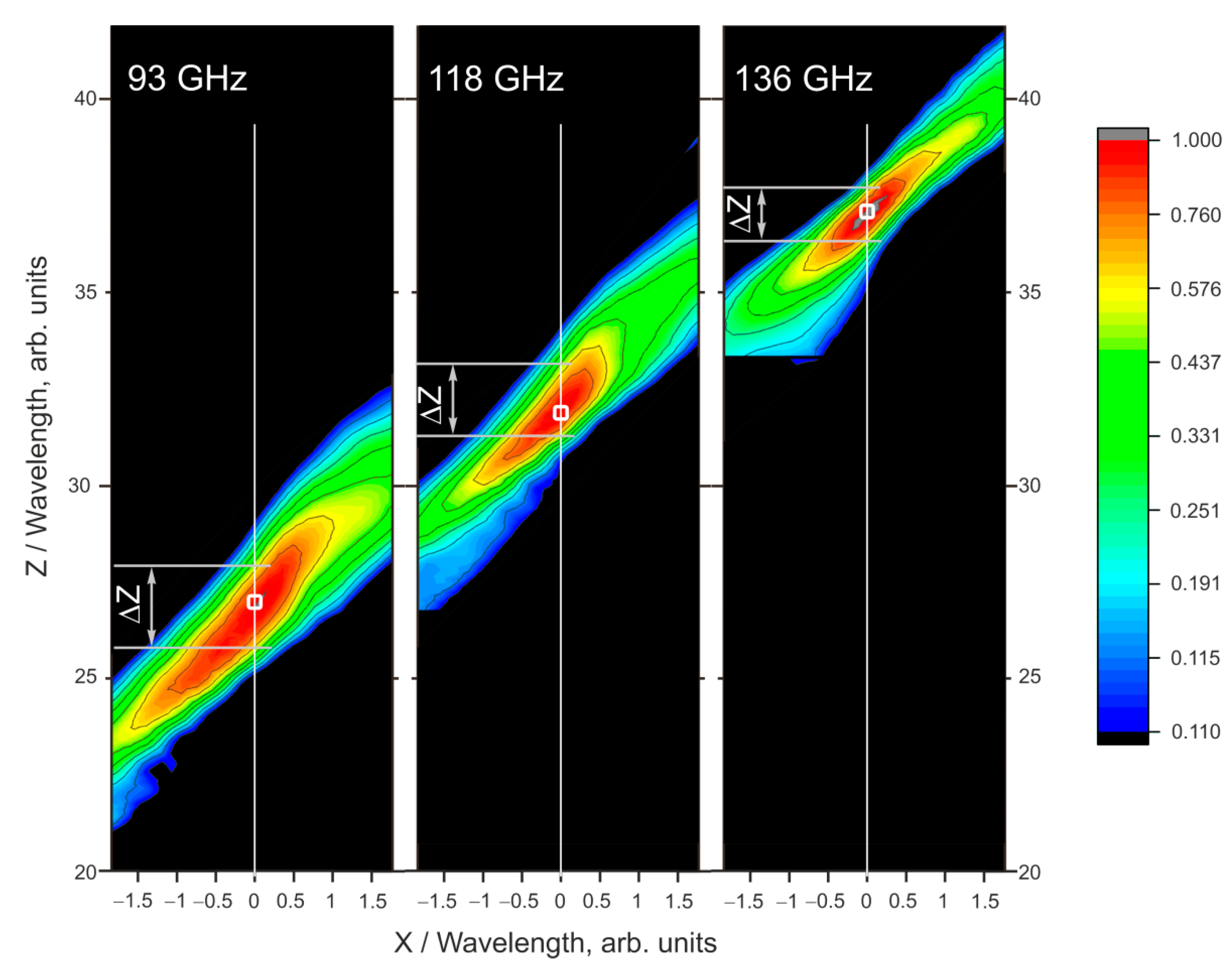
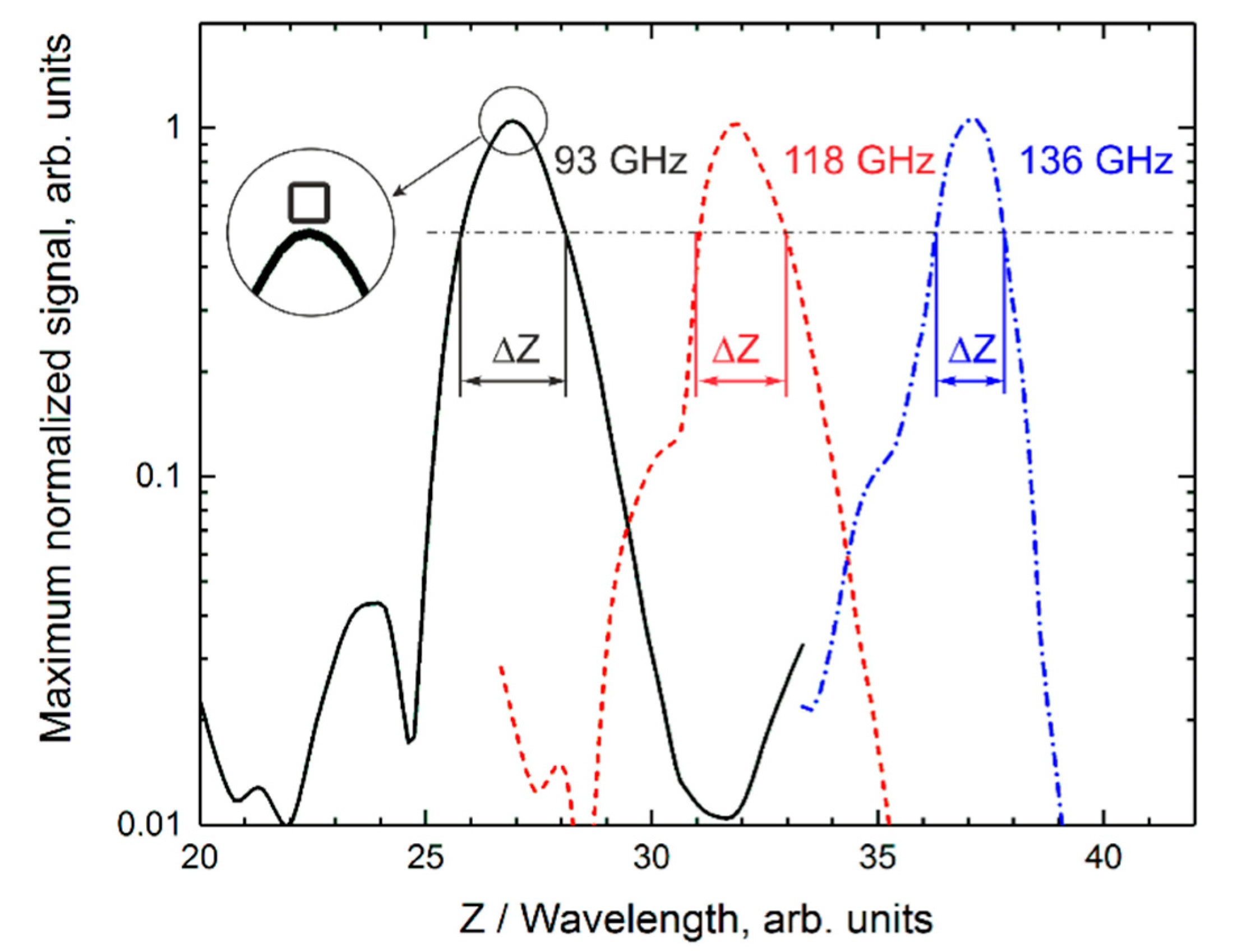
| Frequency (GHz) | Wavelength (mm) | Maximum Coordinate, Z/λ (arb. units) | FWHM, ΔZ/λ (arb. units) | FWHM, ΔZ/Z (%) |
|---|---|---|---|---|
| 93 | 3.23 | 26.9 | 2.29 | 8.5 |
| 118 | 2.54 | 31.8 | 1.86 | 5.8 |
| 136 | 2.21 | 37.1 | 1.56 | 4.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paulish, A.G.; Minin, O.V.; Geints, Y.E.; Minin, I.V. Experimental Proof-of-Concept of a Spatial Photonic Switch Based on an Off-Axis Zone Plate in Millimeter Wavelength Range. Photonics 2022, 9, 670. https://doi.org/10.3390/photonics9100670
Paulish AG, Minin OV, Geints YE, Minin IV. Experimental Proof-of-Concept of a Spatial Photonic Switch Based on an Off-Axis Zone Plate in Millimeter Wavelength Range. Photonics. 2022; 9(10):670. https://doi.org/10.3390/photonics9100670
Chicago/Turabian StylePaulish, Andrey G., Oleg V. Minin, Yuri E. Geints, and Igor V. Minin. 2022. "Experimental Proof-of-Concept of a Spatial Photonic Switch Based on an Off-Axis Zone Plate in Millimeter Wavelength Range" Photonics 9, no. 10: 670. https://doi.org/10.3390/photonics9100670
APA StylePaulish, A. G., Minin, O. V., Geints, Y. E., & Minin, I. V. (2022). Experimental Proof-of-Concept of a Spatial Photonic Switch Based on an Off-Axis Zone Plate in Millimeter Wavelength Range. Photonics, 9(10), 670. https://doi.org/10.3390/photonics9100670






