Plasmonic Metasurfaces for Superposition of Profile-Tunable Tightly Focused Vector Beams and Generation of the Structured Light
Abstract
1. Introduction
2. Basic Principles
3. Theoretical Calculation and Numerical Simulation
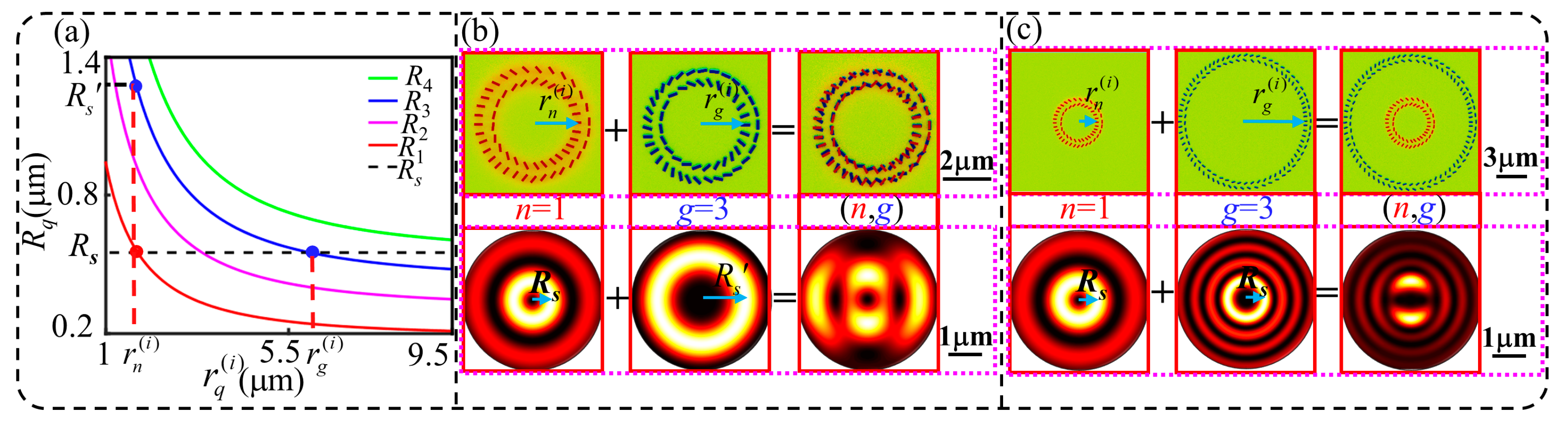
3.1. Design of the Metasurfaces
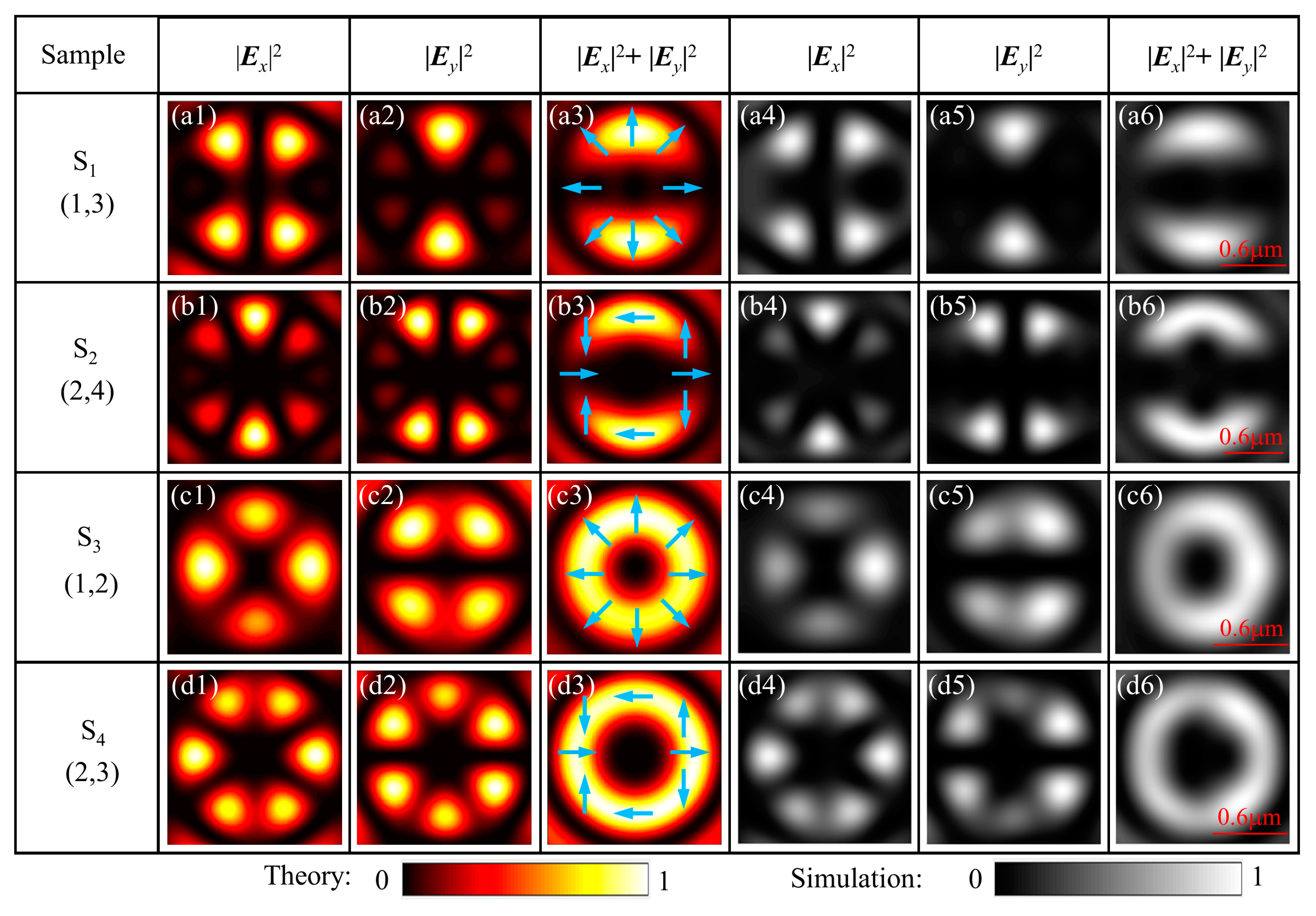
3.2. Calculation of the Superimposed Field of Tightly-Focused VBs
3.3. Analysis of Results
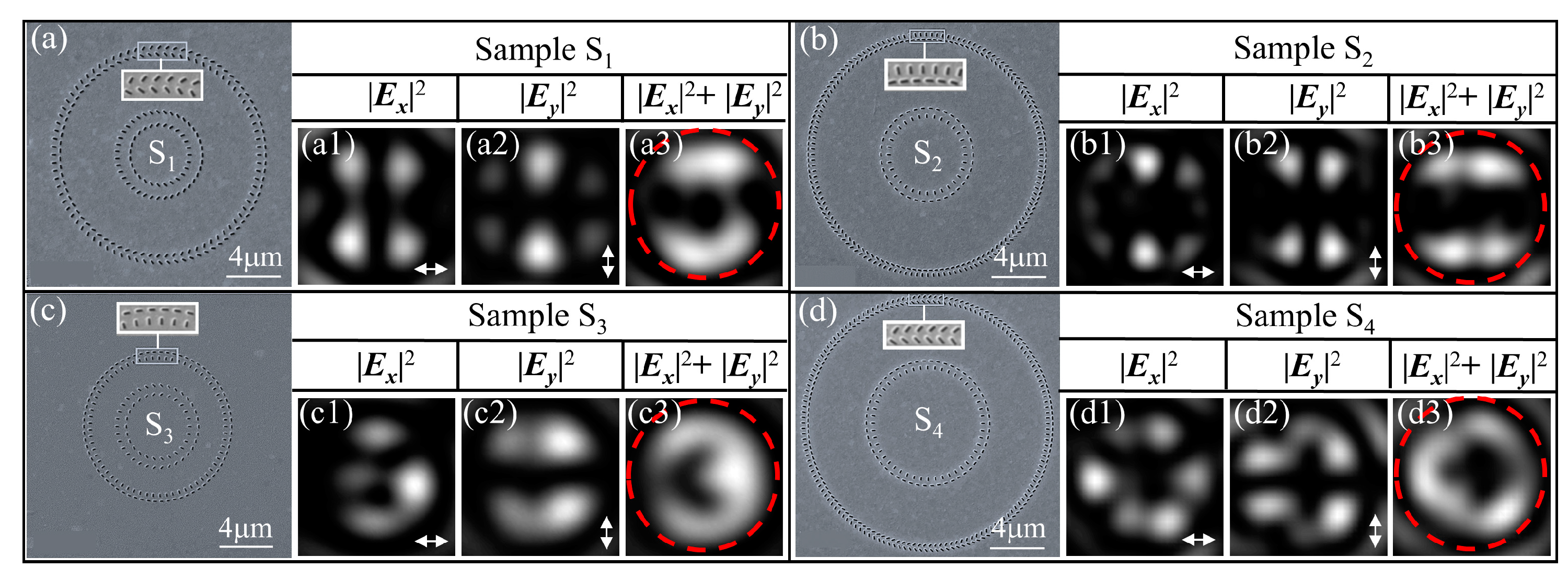
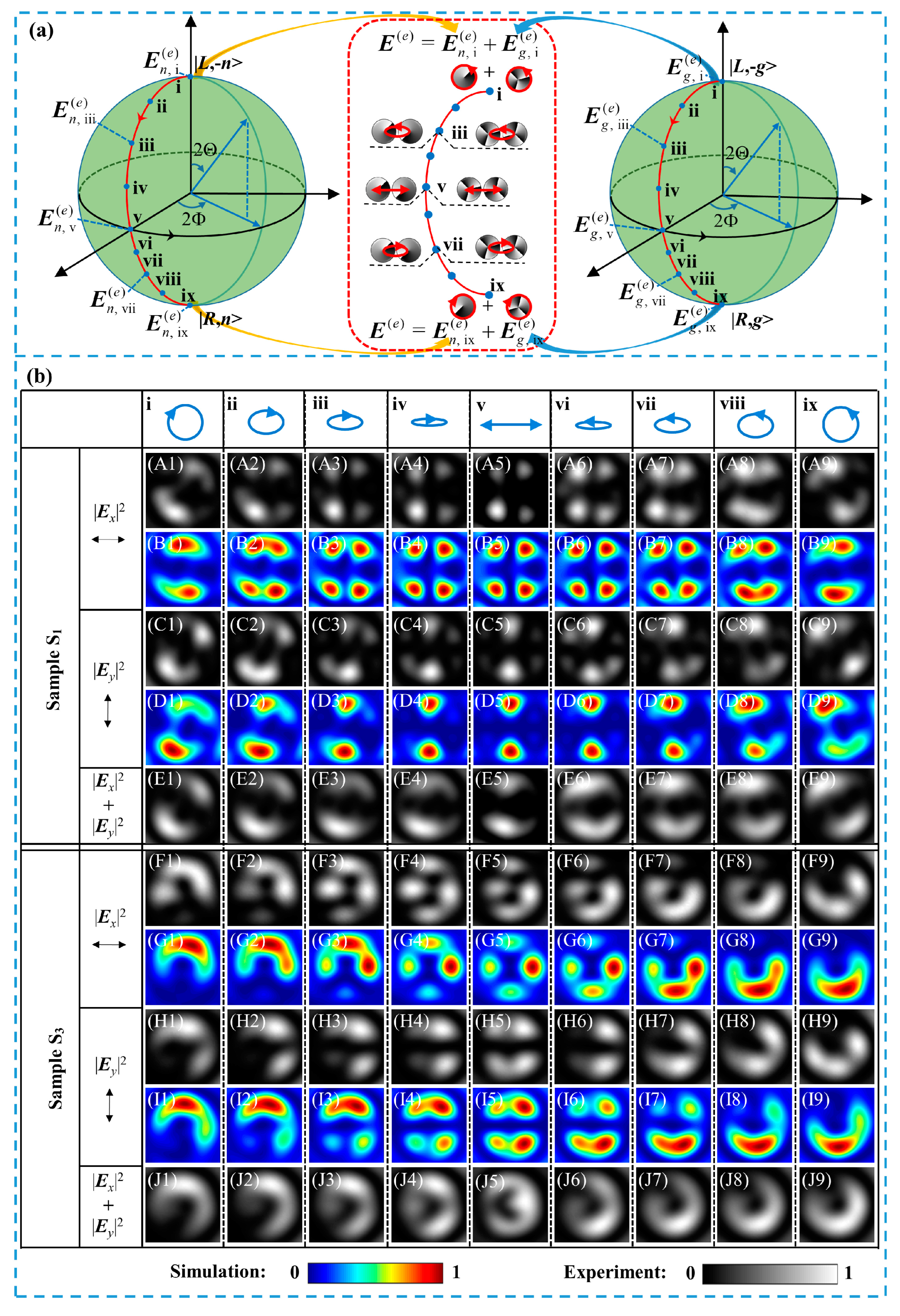
4. Experiment
5. Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, W.T.; Zhu, A.Y.; Capasso, F. Flat optics with dispersion-engineered metasurfaces. Nat. Rev. Mater. 2020, 5, 604–620. [Google Scholar] [CrossRef]
- Ding, F.; Yang, Y.; Deshpande, R.A.; Bozhevolnyi, S.I. A review of gap-surface plasmon metasurfaces: Fundamentals and applications. Nanophotonics 2018, 7, 1129–1156. [Google Scholar] [CrossRef]
- Li, A.; Singh, S.; Sievenpiper, D. Metasurfaces and their applications. Nanophotonics 2018, 7, 989–1011. [Google Scholar] [CrossRef]
- Zang, X.; Ding, H.; Intaravanne, Y.; Chen, L.; Peng, Y.; Xie, J.; Ke, Q.; Balakin, A.V.; Shkurinov, A.P.; Chen, X.; et al. A Multi-Foci Metalens with Polarization-Rotated Focal Points. Laser Photonics Rev. 2019, 13, 1900182. [Google Scholar] [CrossRef]
- Chen, M.K.; Wu, Y.; Feng, L.; Fan, Q.; Lu, M.; Xu, T.; Tsai, D.P. Principles, Functions, and Applications of Optical Meta-Lens. Adv. Opt. Mater. 2021, 9, 2001414. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016, 352, 1190–1194. [Google Scholar] [CrossRef]
- Zhao, R.; Sain, B.; Wei, Q.; Tang, C.; Li, X.; Weiss, T.; Huang, L.; Wang, Y.; Zentgraf, T. Multichannel vectorial holographic display and encryption. Light Sci. Appl. 2018, 7, 95. [Google Scholar] [CrossRef]
- Ren, H.; Briere, G.; Fang, X.; Ni, P.; Sawant, R.; Héron, S.; Chenot, S.; Vézian, S.; Damilano, B.; Brändli, V.; et al. Metasurface orbital angular momentum holography. Nat. Commun. 2019, 10, 2986. [Google Scholar] [CrossRef]
- Kim, I.; Jang, J.; Kim, G.; Lee, J.; Badloe, T.; Mun, J.; Rho, J. Pixelated bifunctional metasurface-driven dynamic vectorial holographic color prints for photonic security platform. Nat. Commun. 2021, 12, 3614. [Google Scholar] [CrossRef]
- Ren, H.; Fang, X.; Jang, J.; Bürger, J.; Rho, J.; Maier, S.A. Complex-amplitude metasurface-based orbital angular momentum holography in momentum space. Nat. Nanotechnol. 2020, 15, 948–955. [Google Scholar] [CrossRef]
- Tseng, M.L.; Jahani, Y.; Leitis, A.; Altug, H. Dielectric Metasurfaces Enabling Advanced Optical Biosensors. ACS Photonics 2021, 8, 47–60. [Google Scholar] [CrossRef]
- Zhang, S.; Wong, C.L.; Zeng, S.; Bi, R.; Tai, K.; Dholakia, K.; Olivo, M. Metasurfaces for biomedical applications: Imaging and sensing from a nanophotonics perspective. Nanophotonics 2021, 10, 259–293. [Google Scholar] [CrossRef]
- Kim, I.; Martins, R.J.; Jang, J.; Badloe, T.; Khadir, S.; Jung, H.-Y.; Kim, H.; Kim, J.; Genevet, P.; Rho, J. Nanophotonics for light detection and ranging technology. Nat. Nanotechnol. 2021, 16, 508–524. [Google Scholar] [CrossRef] [PubMed]
- Rodrigo, D.; Tittl, A.; Ait-Bouziad, N.; John-Herpin, A.; Limaj, O.; Kelly, C.; Yoo, D.; Wittenberg, N.J.; Oh, S.-H.; Lashuel, H.A.; et al. Resolving molecule-specific information in dynamic lipid membrane processes with multi-resonant infrared metasurfaces. Nat. Commun. 2018, 9, 2160. [Google Scholar] [CrossRef] [PubMed]
- Flauraud, V.; Reyes, M.; Paniagua-Domínguez, R.; Kuznetsov, A.I.; Brugger, J. Silicon Nanostructures for Bright Field Full Color Prints. ACS Photonics 2017, 4, 1913–1919. [Google Scholar] [CrossRef]
- Daqiqeh Rezaei, S.; Dong, Z.; You En Chan, J.; Trisno, J.; Ng, R.J.H.; Ruan, Q.; Qiu, C.-W.; Mortensen, N.A.; Yang, J.K.W. Nanophotonic Structural Colors. ACS Photonics 2021, 8, 18–33. [Google Scholar] [CrossRef]
- Sun, S.; Zhou, Z.; Zhang, C.; Gao, Y.; Duan, Z.; Xiao, S.; Song, Q. All-Dielectric Full-Color Printing with TiO2 Metasurfaces. ACS Nano 2017, 11, 4445–4452. [Google Scholar] [CrossRef]
- Yang, W.; Xiao, S.; Song, Q.; Liu, Y.; Wu, Y.; Wang, S.; Yu, J.; Han, J.; Tsai, D.-P. All-dielectric metasurface for high-performance structural color. Nat. Commun. 2020, 11, 1864. [Google Scholar] [CrossRef]
- Sun, S.; Yang, K.-Y.; Wang, C.-M.; Juan, T.-K.; Chen, W.T.; Liao, C.Y.; He, Q.; Xiao, S.; Kung, W.-T.; Guo, G.-Y.; et al. High-Efficiency Broadband Anomalous Reflection by Gradient Meta-Surfaces. Nano Lett. 2012, 12, 6223–6229. [Google Scholar] [CrossRef]
- Lin, D.; Fan, P.; Hasman, E.; Brongersma, M.L. Dielectric gradient metasurface optical elements. Science 2014, 345, 298–302. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef]
- Sun, S.; He, Q.; Xiao, S.; Xu, Q.; Li, X.; Zhou, L. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat. Mater. 2012, 11, 426–431. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Chen, X.; Mühlenbernd, H.; Li, G.; Bai, B.; Tan, Q.; Jin, G.; Zentgraf, T.; Zhang, S. Dispersionless Phase Discontinuities for Controlling Light Propagation. Nano Lett. 2012, 12, 5750–5755. [Google Scholar] [CrossRef]
- Zaman, M.A.; Padhy, P.; Hesselink, L. Solenoidal optical forces from a plasmonic Archimedean spiral. Phys. Rev. A 2019, 100, 013857. [Google Scholar] [CrossRef]
- Tsai, W.-Y.; Huang, J.-S.; Huang, C.-B. Selective Trapping or Rotation of Isotropic Dielectric Microparticles by Optical Near Field in a Plasmonic Archimedes Spiral. Nano Lett. 2014, 14, 547–552. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, R.; Li, X.; Ma, L.; Liu, C.; He, C.; Cheng, C. Radially polarized plasmonic vector vortex generated by a metasurface spiral in gold film. Opt. Express 2017, 25, 32150–32160. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.; Lee, D.; Yang, Y.; Kim, Y.; Rho, J. Reaching the highest efficiency of spin Hall effect of light in the near-infrared using all-dielectric metasurfaces. Nat. Commun. 2022, 13, 2036. [Google Scholar] [CrossRef]
- Luo, W.; Sun, S.; Xu, H.-X.; He, Q.; Zhou, L. Transmissive Ultrathin Pancharatnam-Berry Metasurfaces with nearly 100% Efficiency. Phys. Rev. A 2017, 7, 044033. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, K.; Ratni, B.; Song, Q.; Ding, X.; Wu, Q.; Burokur, S.N.; Genevet, P. Independent phase modulation for quadruplex polarization channels enabled by chirality-assisted geometric-phase metasurfaces. Nat. Commun. 2020, 11, 4186. [Google Scholar] [CrossRef]
- Xiang, Z.; Shen, Z.; Shen, Y. Quasi-perfect vortices generated by Pancharatnam-Berry phase metasurfaces for optical spanners and OAM communication. Sci. Rep. 2022, 12, 1053. [Google Scholar] [CrossRef]
- Ni, J.; Huang, C.; Zhou, L.-M.; Gu, M.; Song, Q.; Kivshar, Y.; Qiu, C.-W. Multidimensional phase singularities in nanophotonics. Science 2021, 374, 418. [Google Scholar] [CrossRef] [PubMed]
- Forbes, A.; de Oliveira, M.; Dennis, M.R. Structured light. Nat. Photonics 2021, 15, 253–262. [Google Scholar] [CrossRef]
- Xie, X.; Chen, Y.; Yang, K.; Zhou, J. Harnessing the Point-Spread Function for High-Resolution Far-Field Optical Microscopy. Phys. Rev. Lett. 2014, 113, 263901. [Google Scholar] [CrossRef]
- Roxworthy, B.J.; Toussaint, K.C. Optical trapping with pi-phase cylindrical vector beams. New J. Phys. 2010, 12, 073012. [Google Scholar] [CrossRef]
- Yuanjie, Y.; Yuxuan, R.; Mingzhou, C.; Yoshihiko, A.; Carmelo, R.-G. Optical trapping with structured light: A review. Adv. Photonics 2021, 3, 034001. [Google Scholar] [CrossRef]
- He, C.; He, H.; Chang, J.; Chen, B.; Ma, H.; Booth, M.J. Polarisation optics for biomedical and clinical applications: A review. Light Sci. Appl. 2021, 10, 194. [Google Scholar] [CrossRef]
- Sit, A.; Bouchard, F.; Fickler, R.; Gagnon-Bischoff, J.; Larocque, H.; Heshami, K.; Elser, D.; Peuntinger, C.; Günthner, K.; Heim, B.; et al. High-dimensional intracity quantum cryptography with structured photons. Optica 2017, 4, 1006–1010. [Google Scholar] [CrossRef]
- Rosales-Guzmán, C.; Bhebhe, N.; Forbes, A. Simultaneous generation of multiple vector beams on a single SLM. Opt. Express 2017, 25, 25697–25706. [Google Scholar] [CrossRef]
- Parigi, V.; D’Ambrosio, V.; Arnold, C.; Marrucci, L.; Sciarrino, F.; Laurat, J. Storage and retrieval of vector beams of light in a multiple-degree-of-freedom quantum memory. Nat. Commun. 2015, 6, 7706. [Google Scholar] [CrossRef]
- Cardano, F.; Massa, F.; Qassim, H.; Karimi, E.; Slussarenko, S.; Paparo, D.; de Lisio, C.; Sciarrino, F.; Santamato, E.; Boyd, R.W.; et al. Quantum walks and wavepacket dynamics on a lattice with twisted photons. Sci. Adv. 2015, 1, e1500087. [Google Scholar] [CrossRef]
- Graham, T.M.; Bernstein, H.J.; Wei, T.-C.; Junge, M.; Kwiat, P.G. Superdense teleportation using hyperentangled photons. Nat. Commun. 2015, 6, 7185. [Google Scholar] [CrossRef] [PubMed]
- Ndagano, B.; Perez-Garcia, B.; Roux, F.S.; McLaren, M.; Rosales-Guzman, C.; Zhang, Y.; Mouane, O.; Hernandez-Aranda, R.I.; Konrad, T.; Forbes, A. Characterizing quantum channels with non-separable states of classical light. Nat. Phys. 2017, 13, 397–402. [Google Scholar] [CrossRef]
- Toninelli, E.; Ndagano, B.; Vallés, A.; Sephton, B.; Nape, I.; Ambrosio, A.; Capasso, F.; Padgett, M.J.; Forbes, A. Concepts in quantum state tomography and classical implementation with intense light: A tutorial. Adv. Opt. Photonics 2019, 11, 67–134. [Google Scholar] [CrossRef]
- Yan, H.; Li, S.; Xie, Z.; Zheng, X.; Zhang, H.; Zhou, B. Design of PANDA ring-core fiber with 10 polarization-maintaining modes. Photonics Res. 2017, 5, 1–5. [Google Scholar] [CrossRef]
- Vasilyeu, R.; Dudley, A.; Khilo, N.; Forbes, A. Generating superpositions of higher–order Bessel beams. Opt. Express 2009, 17, 23389–23395. [Google Scholar] [CrossRef] [PubMed]
- Naidoo, D.; Roux, F.S.; Dudley, A.; Litvin, I.; Piccirillo, B.; Marrucci, L.; Forbes, A. Controlled generation of higher-order Poincaré sphere beams from a laser. Nat. Photonics 2016, 10, 327–332. [Google Scholar] [CrossRef]
- Wan, H.; Wang, J.; Zhang, Z.; Cai, Y.; Sun, B.; Zhang, L. High efficiency mode-locked, cylindrical vector beam fiber laser based on a mode selective coupler. Opt. Express 2017, 25, 11444–11451. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, E.; Zhao, B.; Duan, K. Free-space propagation of guided optical vortices excited in an annular core fiber. Opt. Express 2012, 20, 17904–17915. [Google Scholar] [CrossRef]
- Li, S.; Wang, J. Multi-Orbital-Angular-Momentum Multi-Ring Fiber for High-Density Space-Division Multiplexing. IEEE Photonics J. 2013, 5, 7101007. [Google Scholar] [CrossRef]
- García-García, J.; Rickenstorff-Parrao, C.; Ramos-García, R.; Arrizón, V.; Ostrovsky, A.S. Simple technique for generating the perfect optical vortex. Opt. Lett. 2014, 39, 5305–5308. [Google Scholar] [CrossRef]
- Ostrovsky, A.S.; Rickenstorff-Parrao, C.; Arrizón, V. Generation of the “perfect” optical vortex using a liquid-crystal spatial light modulator. Opt. Lett. 2013, 38, 534–536. [Google Scholar] [CrossRef]
- Vaity, P.; Rusch, L. Perfect vortex beam: Fourier transformation of a Bessel beam. Opt. Lett. 2015, 40, 597–600. [Google Scholar] [CrossRef]
- Dong, M.; Yang, Z.; Chao, Z.; Hua, L.; Cong, W.; Han, Z.; Wending, Z.; Ting, M.; Jianlin, Z. Generation of polarization and phase singular beams in fibers and fiber lasers. Adv. Photonics 2021, 3, 014002. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Y.; Liu, S.; Ma, C.; Han, L.; Cheng, H.; Zhao, J. Generation of perfect vectorial vortex beams. Opt. Lett. 2016, 41, 2205–2208. [Google Scholar] [CrossRef]
- Fu, S.; Gao, C.; Wang, T.; Zhang, S.; Zhai, Y. Simultaneous generation of multiple perfect polarization vortices with selective spatial states in various diffraction orders. Opt. Lett. 2016, 41, 5454–5457. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Chang, C.; Nie, S.; Feng, S.; Ma, J.; Yuan, C. Generation of elliptic perfect optical vortex and elliptic perfect vector beam by modulating the dynamic and geometric phase. Appl. Phys. Lett. 2018, 113, 121101. [Google Scholar] [CrossRef]
- Liu, Y.; Ke, Y.; Zhou, J.; Liu, Y.; Luo, H.; Wen, S.; Fan, D. Generation of perfect vortex and vector beams based on Pancharatnam-Berry phase elements. Sci. Rep. 2017, 7, 44096. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Y.; Ke, Y.; Liu, Y.; Shu, W.; Luo, H.; Wen, S. Generation of arbitrary vector vortex beams on hybrid-order Poincaré sphere. Photonics Res. 2017, 5, 15–21. [Google Scholar] [CrossRef]
- Bao, Y.; Ni, J.; Qiu, C.-W. A Minimalist Single-Layer Metasurface for Arbitrary and Full Control of Vector Vortex Beams. Adv. Mater. 2020, 32, 1905659. [Google Scholar] [CrossRef]
- Wang, E.; Shi, L.; Niu, J.; Hua, Y.; Li, H.; Zhu, X.; Xie, C.; Ye, T. Multichannel Spatially Nonhomogeneous Focused Vector Vortex Beams for Quantum Experiments. Adv. Opt. Mater. 2019, 7, 1801415. [Google Scholar] [CrossRef]
- Zhang, Y.-Q.; Zeng, X.-Y.; Zhang, R.-R.; Zhan, Z.-J.; Li, X.; Ma, L.; Liu, C.-X.; He, C.-W.; Cheng, C.-F. Generation of a plasmonic radially polarized vector beam with linearly polarized illumination. Opt. Lett. 2018, 43, 4208–4211. [Google Scholar] [CrossRef]
- Yue, F.; Wen, D.; Xin, J.; Gerardot, B.D.; Li, J.; Chen, X. Vector Vortex Beam Generation with a Single Plasmonic Metasurface. ACS Photonics 2016, 3, 1558–1563. [Google Scholar] [CrossRef]
- Liu, M.; Huo, P.; Zhu, W.; Zhang, C.; Zhang, S.; Song, M.; Zhang, S.; Zhou, Q.; Chen, L.; Lezec, H.J.; et al. Broadband generation of perfect Poincaré beams via dielectric spin-multiplexed metasurface. Nat. Commun. 2021, 12, 2230. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Xie, Z.; Zhang, M.; Ouyang, X.; Xu, Y.; Cao, Y.; Wang, S.; Zhu, L.; Li, X. Ultra-secure optical encryption based on tightly focused perfect optical vortex beams. Nanophotonics 2022, 11, 1063–1070. [Google Scholar] [CrossRef]
- Shao, W.; Huang, S.; Liu, X.; Chen, M. Free-space optical communication with perfect optical vortex beams multiplexing. Opt. Commun. 2018, 427, 545–550. [Google Scholar] [CrossRef]
- Wang, W.; Wang, P.; Pang, W.; Pan, Y.; Nie, Y.; Guo, L. Evolution Properties and Spatial-Mode UWOC Performances of the Perfect Vortex Beam Subject to Oceanic Turbulence. IEEE Trans. Commun. 2021, 69, 7647–7658. [Google Scholar] [CrossRef]
- Chen, M.; Mazilu, M.; Arita, Y.; Wright, E.M.; Dholakia, K. Dynamics of microparticles trapped in a perfect vortex beam. Opt. Lett. 2013, 38, 4919–4922. [Google Scholar] [CrossRef]
- Han, L.; Liu, S.; Li, P.; Zhang, Y.; Cheng, H.; Zhao, J. Catalystlike effect of orbital angular momentum on the conversion of transverse to three-dimensional spin states within tightly focused radially polarized beams. Phys. Rev. A 2018, 97, 053802. [Google Scholar] [CrossRef]
- Guo, X.; Li, P.; Zhong, J.; Liu, S.; Wei, B.; Zhu, W.; Qi, S.; Cheng, H.; Zhao, J. Tying Polarization-Switchable Optical Vortex Knots and Links via Holographic All-Dielectric Metasurfaces. Laser Photonics Rev. 2020, 14, 1900366. [Google Scholar] [CrossRef]
- Zuo, R.; Liu, W.; Cheng, H.; Chen, S.; Tian, J. Breaking the Diffraction Limit with Radially Polarized Light Based on Dielectric Metalenses. Adv. Opt. Mater. 2018, 6, 1800795. [Google Scholar] [CrossRef]
- Li, Y.; Cao, L.; Wen, Z.; Qin, C.; Yang, J.; Zhang, Z.; Liang, G.; Shang, Z.; Zhang, K.; Zhang, S.; et al. Broadband quarter-wave birefringent meta-mirrors for generating sub-diffraction vector fields. Opt. Lett. 2019, 44, 110–113. [Google Scholar] [CrossRef]
- Lin, J.; Mueller, J.P.B.; Wang, Q.; Yuan, G.; Antoniou, N.; Yuan, X.-C.; Capasso, F. Polarization-Controlled Tunable Directional Coupling of Surface Plasmon Polaritons. Science 2013, 340, 331–334. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Zhang, Y.; Ma, L.; Zeng, X.; Li, X.; Zhan, Z.; Ren, X.; He, C.; Liu, C.; Cheng, C. Nanoscale optical lattices of arbitrary orders manipulated by plasmonic metasurfaces combining geometrical and dynamic phases. Nanoscale 2019, 11, 14024–14031. [Google Scholar] [CrossRef]
- Zeng, X.; Zhang, Y.; Gu, M.; Zhan, Z.; Zhang, R.; Zhang, Y.; Sun, R.; He, C.; Liu, C.; Cheng, C. Arbitrary manipulations of focused higher-order Poincaré beams by a Fresnel zone metasurface with alternate binary geometric and propagation phases. Photonics Res. 2022, 10, 1117–1126. [Google Scholar] [CrossRef]
- Teperik, T.V.; Archambault, A.; Marquier, F.; Greffet, J.J. Huygens-Fresnel principle for surface plasmons. Opt. Express 2009, 17, 17483–17490. [Google Scholar] [CrossRef]
- RefractiveIndex.INFO-Refractive Index Database. Available online: https://refractiveindex.info/ (accessed on 11 March 2023).
- Babar, S.; Weaver, J.H. Optical constants of Cu, Ag, and Au revisited. Appl. Opt. 2015, 54, 477–481. [Google Scholar] [CrossRef]
- Malitson, I.H. Interspecimen Comparison of the Refractive Index of Fused Silica*,†. J. Opt. Soc. Am. 1965, 55, 1205–1209. [Google Scholar] [CrossRef]
- Zhan, Q. Cylindrical vector beams: From mathematical concepts to applications. Adv. Opt. Photonics 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Lu, T.H.; Huang, T.D.; Wang, J.G.; Wang, L.W.; Alfano, R.R. Generation of flower high-order Poincaré sphere laser beams from a spatial light modulator. Sci. Rep. 2016, 6, 39657. [Google Scholar] [CrossRef] [PubMed]
- Milione, G.; Evans, S.; Nolan, D.A.; Alfano, R.R. Higher Order Pancharatnam-Berry Phase and the Angular Momentum of Light. Phys. Rev. Lett. 2012, 108, 190401. [Google Scholar] [CrossRef]



| Sample | S1 | S2 | S3 | S4 |
|---|---|---|---|---|
| (n, g) | (1, 3) | (2, 4) | (1, 2) | (2, 3) |
| Rs | 0.5458 | 0.63 | 0.432 | 0.4844 |
| 1.807 | 2.7983 | 2.3775 | 4.1119 | |
| 2.587 | 3.3993 | 3.041 | 4.5939 | |
| 6.048 | 8.0784 | 5.0731 | 8.978 | |
| 6.448 | 8.4482 | 5.5085 | 9.3415 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Zeng, X.; Gu, M.; Zhang, Y.; Sun, R.; Zhang, Z.; Cui, G.; Zhou, Y.; Cheng, C.; Liu, C. Plasmonic Metasurfaces for Superposition of Profile-Tunable Tightly Focused Vector Beams and Generation of the Structured Light. Photonics 2023, 10, 317. https://doi.org/10.3390/photonics10030317
Li L, Zeng X, Gu M, Zhang Y, Sun R, Zhang Z, Cui G, Zhou Y, Cheng C, Liu C. Plasmonic Metasurfaces for Superposition of Profile-Tunable Tightly Focused Vector Beams and Generation of the Structured Light. Photonics. 2023; 10(3):317. https://doi.org/10.3390/photonics10030317
Chicago/Turabian StyleLi, Lianmeng, Xiangyu Zeng, Manna Gu, Yuqin Zhang, Rui Sun, Ziheng Zhang, Guosen Cui, Yuxiang Zhou, Chuanfu Cheng, and Chunxiang Liu. 2023. "Plasmonic Metasurfaces for Superposition of Profile-Tunable Tightly Focused Vector Beams and Generation of the Structured Light" Photonics 10, no. 3: 317. https://doi.org/10.3390/photonics10030317
APA StyleLi, L., Zeng, X., Gu, M., Zhang, Y., Sun, R., Zhang, Z., Cui, G., Zhou, Y., Cheng, C., & Liu, C. (2023). Plasmonic Metasurfaces for Superposition of Profile-Tunable Tightly Focused Vector Beams and Generation of the Structured Light. Photonics, 10(3), 317. https://doi.org/10.3390/photonics10030317




