Effect of Beam-Steering Angle, Operation Wavelength and Mean Inter-Element Distance on the Side-Lobe Levels of Integrated Optical Phased Arrays under Beam-Steering Operation
Abstract
:1. Introduction
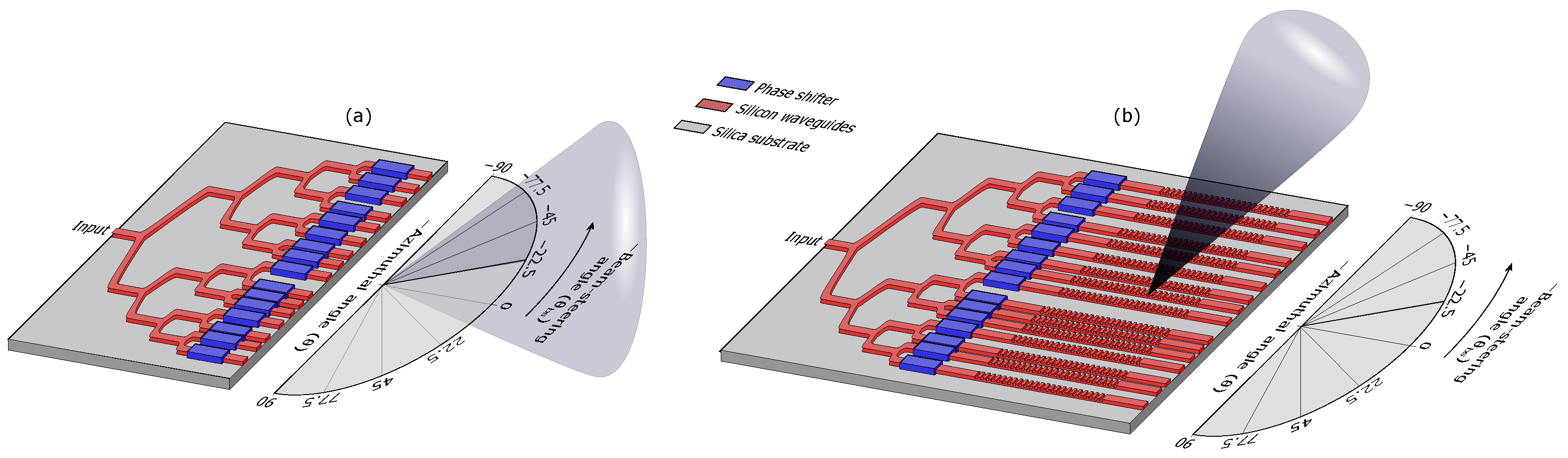
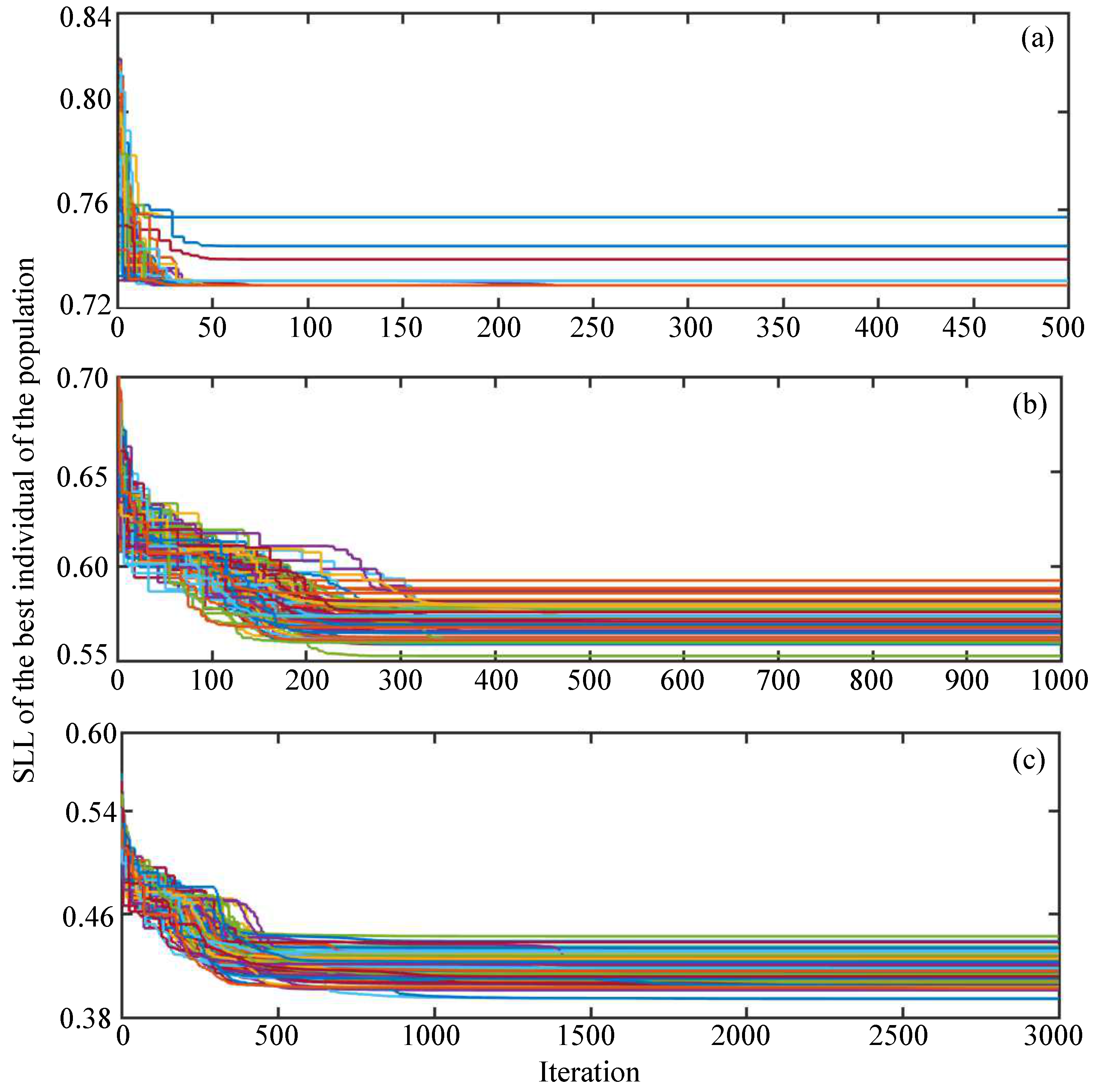
2. Optimization of Element Positions
3. Results
3.1. Effect of Beam-Steering Angle and Operation Wavelength on the Side-Lobe Level
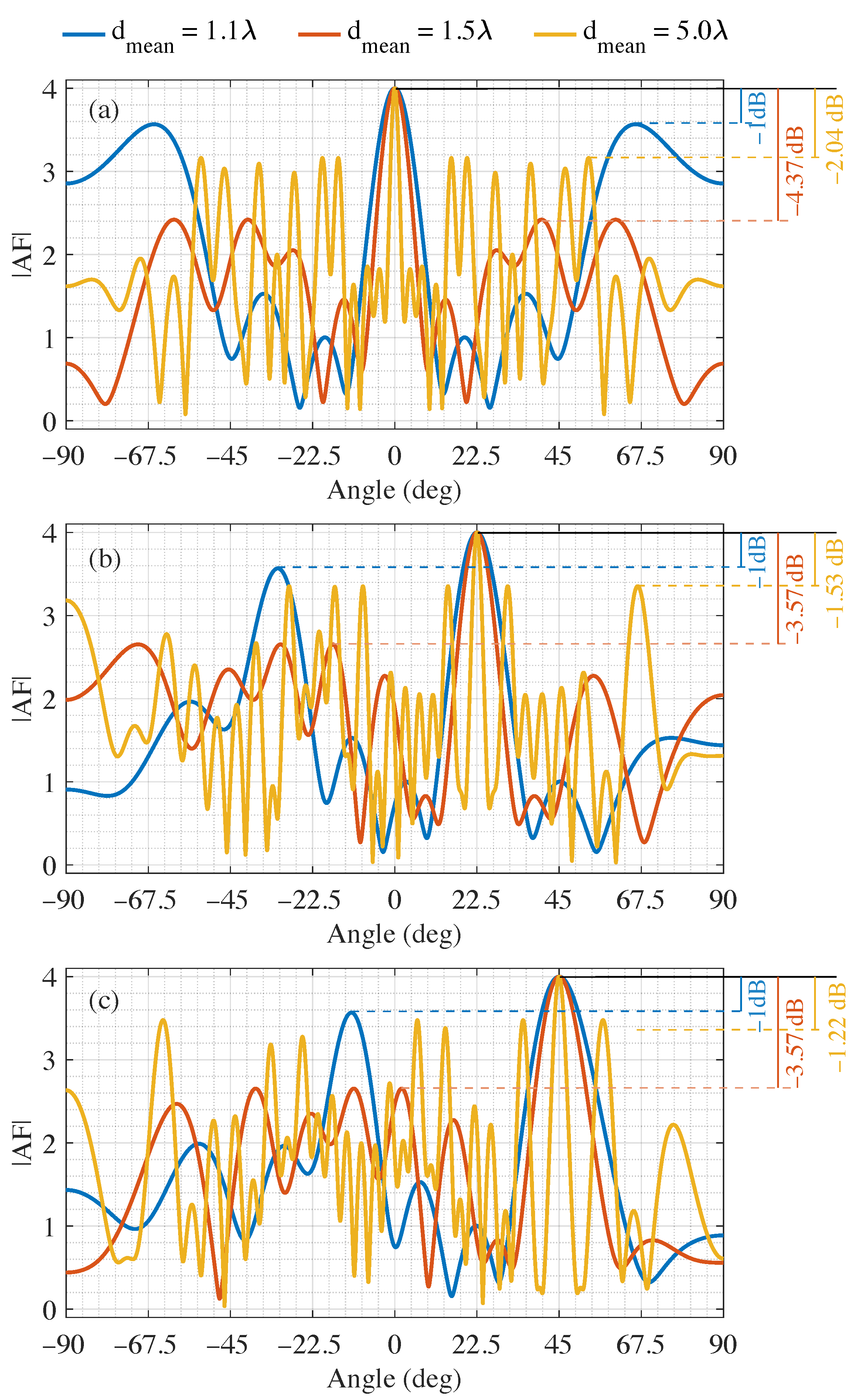
3.2. Effect of the Mean Inter-Element Distance and Beam-Steering Angle on the Side-Lobe Level
3.3. Effect of the Number of Elements and the Average and Minimum Separation on the Side-Lobe Level
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LIDAR | Light detection and ranging |
| OPA | Optical phased array |
| SLL | Side-lobe level |
| AF | Array factor |
| DE | Differential evolution |
References
- Wuytens, P.C.; Skirtach, A.G.; Baets, R. On-chip surface-enhanced Raman spectroscopy using nanosphere-lithography patterned antennas on silicon nitride waveguides. Opt. Express 2017, 25, 12926–12934. [Google Scholar] [CrossRef] [PubMed]
- Poulton, C.V.; Byrd, M.J.; Russo, P.; Timurdogan, E.; Khandaker, M.; Vermeulen, D.; Watts, M.R. Long-range LiDAR and free-space data communication with high-performance optical phased arrays. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1–8. [Google Scholar] [CrossRef]
- Poulton, C.V.; Yaacobi, A.; Cole, D.B.; Byrd, M.J.; Raval, M.; Vermeulen, D.; Watts, M.R. Coherent solid-state LIDAR with silicon photonic optical phased arrays. Opt. Lett. 2017, 42, 4091–4094. [Google Scholar] [CrossRef]
- Bharadwaj, P.; Deutsch, B.; Novotny, L. Optical antennas. Adv. Opt. Photonics 2009, 1, 438–483. [Google Scholar] [CrossRef]
- Krasnok, A.E.; Miroshnichenko, A.E.; Belov, P.A.; Kivshar, Y.S. All-dielectric optical nanoantennas. Opt. Express 2012, 20, 20599–20604. [Google Scholar] [CrossRef] [PubMed]
- Heck, M.J. Highly integrated optical phased arrays: Photonic integrated circuits for optical beam shaping and beam steering. Nanophotonics 2017, 6, 93–107. [Google Scholar] [CrossRef]
- Michaels, A.; Yablonovitch, E. Reinventing the circuit board with integrated optical interconnects. In Proceedings of the CLEO: Science and Innovations, San Jose, CA, USA, 5–10 June 2016. [Google Scholar]
- Sun, X.; Zhang, L.; Zhang, Q.; Zhang, W. Si photonics for practical LiDAR solutions. Appl. Sci. 2019, 9, 4225. [Google Scholar] [CrossRef]
- Pita, J.L.; Aldaya, I.; Santana, O.J.; Dainese, P.; Gabrielli, L.H. Side-lobe level reduction in bio-inspired optical phased-array antennas. Opt. Express 2017, 25, 30105–30114. [Google Scholar] [CrossRef]
- de Souza, B.D.P.; Junior, A.E.F.; Abbade, M.L.F.; Aldaya, I. Side-lobe level reduction in 1D photonic array antennas. In Proceedings of the 2018 SBFoton International Optics and Photonics Conference (SBFoton IOPC), Campinas, Brazil, 8–10 October 2018; pp. 1–4. [Google Scholar]
- Barott, W.C.; Steffes, P.G. Grating lobe reduction in aperiodic linear arrays of physically large antennas. IEEE Antennas Wirel. Propag. Lett. 2008, 8, 406–408. [Google Scholar] [CrossRef]
- Phare, C.T.; Shin, M.C.; Sharma, J.; Ahasan, S.; Krishnaswamy, H.; Lipson, M. Silicon Optical Phased Array with Grating Lobe-Free Beam Formation Over 180 Degree Field of View. In Proceedings of the CLEO: Science and Innovations. Optical Society of America, San Jose, CA, USA, 13–18 May 2018. [Google Scholar]
- Caratelli, D.; Viganó, M.C. Analytical synthesis technique for linear uniform-amplitude sparse arrays. Radio Sci. 2011, 46, 1–6. [Google Scholar] [CrossRef]
- Suárez, S.; Leon Fernandez, G.; Arrebola, M.; Herrán Ontañón, L.F.; Las Heras Andres, F. Experimental validation of linear aperiodic array for grating lobe suppression. Prog. Electromagn. Res. 2012, 26, 193–203. [Google Scholar] [CrossRef]
- Sandi, E.; Zulkifli, F.Y.; Rahardjo, E.T. A Hybrid Technique Using Combinatorial Cyclic Difference Sets and Binomial Amplitude Tapering for Linear Sparse Array Antenna Design. Adv. Electromagn. 2016, 5, 73–79. [Google Scholar] [CrossRef]
- Trucco, A.; Murino, V. Stochastic optimization of linear sparse arrays. IEEE J. Ocean. Eng. 1999, 24, 291–299. [Google Scholar] [CrossRef]
- Khodier, M.M.; Christodoulou, C.G. Linear array geometry synthesis with minimum sidelobe level and null control using particle swarm optimization. IEEE Trans. Antennas Propag. 2005, 53, 2674–2679. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X. Thinning of antenna array via adaptive memetic particle swarm optimization. EURASIP J. Wirel. Commun. Netw. 2017, 2017, 1–7. [Google Scholar] [CrossRef]
- Bray, M.G.; Werner, D.H.; Boeringer, D.W.; Machuga, D.W. Optimization of thinned aperiodic linear phased arrays using genetic algorithms to reduce grating lobes during scanning. IEEE Trans. Antennas Propag. 2002, 50, 1732–1742. [Google Scholar] [CrossRef]
- Hawes, M.B.; Liu, W. Location optimization of robust sparse antenna arrays with physical size constraint. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 1303–1306. [Google Scholar] [CrossRef]
- Hawes, M.B.; Liu, W. Sparse microphone array design for wideband beamforming. In Proceedings of the 2013 18th International Conference on Digital Signal Processing (DSP), Fira, Greece, 1–3 July 2013; pp. 1–5. [Google Scholar]
- Hawes, M.B.; Liu, W. Compressive sensing-based approach to the design of linear robust sparse antenna arrays with physical size constraint. IET Microw. Antennas Propag. 2014, 8, 736–746. [Google Scholar] [CrossRef]
- Raji, M.F.; Zhao, H.; Monday, H.N. Fast optimization of sparse antenna array using numerical Green’s function and genetic algorithm. Int. J. Numer. Model. Electron. Netw. Devices Fields 2019, 33, e2544. [Google Scholar] [CrossRef]
- Li, M.; Wei, H.; Zhao, J.; Tao, Q.; You, Z. A Novel Linear Sparse Array with Reconfigurable Pixel Antenna Elements. Int. J. Antennas Propag. 2020, 2020, 3624563. [Google Scholar] [CrossRef]
- Dib, N.I.; Goudos, S.K.; Muhsen, H. Application of Taguchi’s optimization method and self-adaptive differential evolution to the synthesis of linear antenna arrays. Prog. Electromagn. Res. 2010, 102, 159–180. [Google Scholar] [CrossRef]
- Zhang, F.; Jia, W.; Yao, M. Linear aperiodic array synthesis using differential evolution algorithm. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 797–800. [Google Scholar] [CrossRef]
- Wang, R.Q.; Jiao, Y.C.; Zhang, H.; Zhou, Z. Synthesis of unequally spaced linear arrays using modified differential evolution algorithm. IET Microw. Antennas Propag. 2018, 12, 1908–1912. [Google Scholar] [CrossRef]
- Coman, C.I.; Lager, I.E.; Ligthart, L.P. Design considerations in sparse array antennas. In Proceedings of the European Radar Conference, Manchester, UK, 13–15 September 2006; pp. 72–75. [Google Scholar]
- Zhang, D.; Zhang, F.; Pan, S. Grating-lobe-suppressed optical phased array with optimized element distribution. Opt. Commun. 2018, 419, 47–52. [Google Scholar] [CrossRef]
- Liu, Q.; Lu, Y.; Wu, B.; Jiang, P.; Cao, R.; Feng, J.; Guo, J.; Jin, L. Silicon Optical Phased Array Side Lobe Suppression Based on an Improved Genetic Algorithm. In Proceedings of the 2020 Asia Communications and Photonics Conference (ACP) and International Conference on Information Photonics and Optical Communications (IPOC), Beijing, China, 24–27 October 2020; pp. 1–3. [Google Scholar]
- Du, K.; Wang, R.; Guo, J.; Jiang, R.; Kan, D.; Zhang, Y. Design of a sparse array for a one-dimensional non-uniform optical phased array. JOSA B 2022, 39, 1141–1146. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Qing, A.; Lee, C.K. Differential Evolution in Electromagnetics; Springer: Heidelberg/Berlin, Germany, 2010. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aldaya, I.; Pires de Souza, B.D.; Penchel, R.A.; Pita, J.L.; dos Santos, M.P.; de Oliveira, J.A.; Abbade, M.L.F. Effect of Beam-Steering Angle, Operation Wavelength and Mean Inter-Element Distance on the Side-Lobe Levels of Integrated Optical Phased Arrays under Beam-Steering Operation. Photonics 2023, 10, 1300. https://doi.org/10.3390/photonics10121300
Aldaya I, Pires de Souza BD, Penchel RA, Pita JL, dos Santos MP, de Oliveira JA, Abbade MLF. Effect of Beam-Steering Angle, Operation Wavelength and Mean Inter-Element Distance on the Side-Lobe Levels of Integrated Optical Phased Arrays under Beam-Steering Operation. Photonics. 2023; 10(12):1300. https://doi.org/10.3390/photonics10121300
Chicago/Turabian StyleAldaya, Ivan, Bruna Dias Pires de Souza, Rafael Abrantes Penchel, Julian Leonel Pita, Mirian Paula dos Santos, José Augusto de Oliveira, and Marcelo Luis Francisco Abbade. 2023. "Effect of Beam-Steering Angle, Operation Wavelength and Mean Inter-Element Distance on the Side-Lobe Levels of Integrated Optical Phased Arrays under Beam-Steering Operation" Photonics 10, no. 12: 1300. https://doi.org/10.3390/photonics10121300
APA StyleAldaya, I., Pires de Souza, B. D., Penchel, R. A., Pita, J. L., dos Santos, M. P., de Oliveira, J. A., & Abbade, M. L. F. (2023). Effect of Beam-Steering Angle, Operation Wavelength and Mean Inter-Element Distance on the Side-Lobe Levels of Integrated Optical Phased Arrays under Beam-Steering Operation. Photonics, 10(12), 1300. https://doi.org/10.3390/photonics10121300






