Abstract
Stimulated Brillouin scattering (SBS) is the major factor that limits the maximum optical fiber output power in narrow linewidth applications, which include important fields such as passive optical networks (PONs), high-power fiber amplifiers, and lasers. Great efforts have been dedicated to suppressing the SBS effect and increasing the maximum optical fiber output power. This paper focuses on key fiber-based techniques to suppress SBS. These techniques take advantages of the properties of optical fibers. We present how these properties (electric modes, acoustic modes, and material properties) could be utilized to suppress SBS. The fiber-based techniques are divided into transverse optical fiber design, longitudinal variant fiber design, and external perturbations (strain and temperature) on optical fibers. Transverse optical fiber design focuses on the mechanism electro-acoustic interaction. Large effective area fiber design and acoustic tailoring techniques have been discussed. Longitudinal variant fiber design considers the nonlinear SBS interaction along propagation distance, and various techniques related have been presented. External perturbations (strain and temperature) on optical fibers emphasize on how external static perturbations could modify the SBS effect.
1. Introduction
Brillouin scattering is a type of inelastic scattering, the theoretical grounds of which were first laid out by Brillouin in around 1922. In 1930, the experimental observation of Brillouin scattering in organic liquids was reported by Evgenii Fedorovich Gross [1] right after the observation of Raman scattering [2]. He pointed out that it is due to the acoustic oscillations of molecules. This is the first experimental observation of spontaneous Brillouin scattering. In that process, the incident light wave is transformed into scattered light and an acoustic wave. The scattered wave is downshifted in frequency. Not until the development of interferometric techniques and the invention of lasers [3,4] was the SBS phenomenon observed. In 1964, Garmire E and Townes CH experimentally demonstrated SBS in solids [5]. In the experiment, an intense laser beam was focused to a crystal and the coherent amplification of scattered light was detected. The mechanism of SBS is found due to electrostriction [6].
In 1972, the effect of SBS in optical fibers was first observed by E.P. Ippen and R.H. Stolen [7], which, for the first time, pointed out the limitation in the optical fiber transmission due to SBS. In the same year, R.G. Smith theoretically predicted that SBS would limit the power transmitted through fibers [8]. In the paper, he considered two types of nonlinear scattering processes, SBS and stimulated Raman scattering (SRS), and determined that SBS should determine the maximum power handling capacity of a fiber. Later, further properties of SBS in optical fibers were studied, including electrostrictive contribution [9,10,11,12,13,14], temporal response [15,16], polarization properties [17,18,19], and so on.
After the demonstration of SBS, there has been a lot of work in that realm. SBS has successfully found its applications in various fields, Brillouin amplifiers [20,21], Brillouin lasers [22,23,24,25,26,27,28], phase conjugation [29,30,31], beam combining [32,33,34], pulse compression [35,36], pulse delays [37,38,39], and many others.
In some areas, however, SBS is viewed as undesirable, especially when high-power light with narrow laser linewidths needs be delivered through optical fibers. These areas include PON transmission [40,41,42], high-power fiber lasers, and amplifiers [43,44,45,46]. The schematics of PON is shown in Figure 1. In PON application, light coded with a signal transmits 10 s of kms to reach the optical line terminal (OLT). Splitters are used so that each optical network unit (ONU) can receive a signal. For PON to cover more ONUs, power budget is the key factor, the constraint of which is SBS. Figure 2 shows the schematic of one type of high-power fiber laser; several laser diodes (LDs) are implemented as pump light. For laser to achieve high output power, SBS must be suppressed.
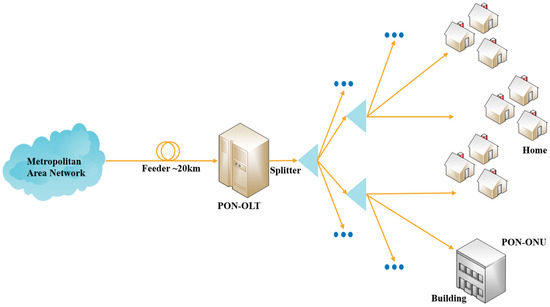
Figure 1.
The Schematics of PON.

Figure 2.
The schematics of one type of high-power fiber laser.
To overcome the effects of SBS on these applications, numerous studies have been explored. In this paper, our focus is on the fiber-based techniques to suppress SBS. Other methods such as using phase-broadening techniques [47,48,49,50,51,52,53,54,55] and optical devices [56,57,58] are beyond the scope of our paper.
This paper is organized as follows. In Section 2, we provide an introduction to the theoretical background of SBS and discuss the rationale for SBS suppression. In Section 3, we present techniques of SBS suppression. The techniques are presented from four categories: transverse optical fiber design, longitudinal variant fiber design, external perturbations (strain and temperature) on optical fibers, and combined methods. We conclude our paper in Section 4.
2. Theoretical Background and Design Rationale
2.1. Theoretical Background of Brillouin Scattering in Optical Fibers
In the modern picture, the process of spontaneous Brillouin scattering is due to the interaction with intermolecular vibrations, or, more accurately, with the phonon spectrum’s acoustic branch [59,60,61]. The process can be viewed as an annihilation of the incident photon (with angular frequency ) and creation of a scattered photon ) and an acoustic phonon . During the interaction, the energy and momentum must be conserved; thus, we have two relations:
where , , and are the corresponding wave vectors of the acoustic phonon, incident photon, and scattered photon. The process is shown in Figure 3.
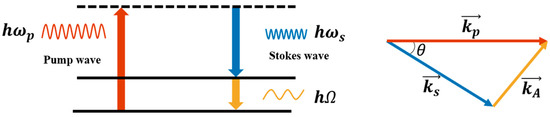
Figure 3.
Diagram of Brillouin scattering energy conservation and momentum conservation.
The acoustic phonon frequency and the wave vector satisfy the dispersion relationship that is shown in Equation (3):
where is the scalar acoustic velocity. Equation (3) shows that the shifting frequency of the scattered light depends on the scattering angle . is maximum in the backward direction and vanishes in the forward direction.
Next, we introduce the mechanism of SBS in the optical fibers. The structure of the step-index optical fiber consists of a core, a cladding, and a coating. The core has a larger refractive index than the cladding. The most widely adopted optical fiber is single-mode fiber (SMF), which typically has a core size of around . SMF allows one spatial mode (two vector modes) transmission in the optical fibers. When the core size becomes larger, more spatial modes can be allowed to transmit in optical fibers. These fibers are called few-mode fiber (FMF) or multimode fiber (MMF), depending on how many spatial modes can be supported. The governing equation for solving the scaler spatial modes of optical fiber can be shown by Equation (4):
where is the transverse Laplacian operator in cylindrical coordinates; is the jth transverse electric mode; is the optical angular frequency; is the optical refractive index; is the light velocity; and is the propagation constant of the jth electric mode. This equation uses the weak guiding approximation and applies to most optical fibers, where the optical fiber’s core index is only slightly larger than the cladding index. In this paper, only the fundamental electric mode is considered. For simplicity, we label the fundamental mode , since the fundamental electric mode profile does not depend on .
When the intensity of the narrow bandwidth light (typically in the fundamental mode) in optical fibers becomes large, SBS could be observed experimentally. The interaction picture could be illustrated in Figure 4. When light (pump wave) is incident on the optical fiber, the backscattered Stokes light (initially from spontaneous Brillouin scattering) interferes with the input pump light and generates an acoustic wave through the effect of electrostriction. The forward propagating acoustic wave acts as a Bragg grating, which scatters even more light in the backward direction. At a steady state, the strength of SBS is nonlinearly dependent on the input power.
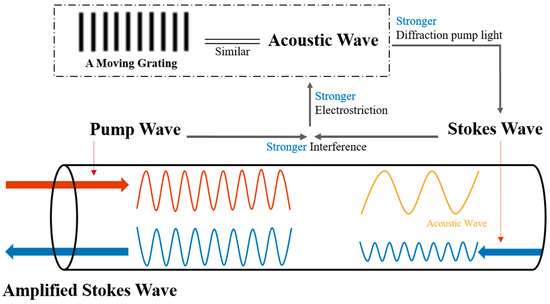
Figure 4.
SBS schematic diagram.
The longitudinal propagating acoustic wave in optical fibers can be described by the following function with static state assumption:
where is the mth transverse profiles of the fundamental acoustic mode; is the longitudinal acoustic velocity profile across the fiber; and is the propagation constant of the acoustic mode. The acoustic mode in the optical fiber can be calculated numerically [62,63,64]. Figure 5 shows the electric mode and acoustic mode under different index profiles (conventional SMF and Corning large effective area fiber). The three lowest order acoustic modes non-dependent on angle are displaced.

Figure 5.
The electric mode and acoustic mode under different profiles. (a) The profiles of the single mode fiber, (b) The profile of Corning large effective area fiber. [Reprinted/Adapted] with permission from [65] © The Optical Society.
The physics to describe the interaction of incident light and SBS light along the uniform optical fiber is described by:
where is the incident pump power; is the SBS power; is the peak SBS efficiency for the acoustic mode; and is the fiber loss. Equation (6) could be solved numerically and the Stokes power can be calculated; this has the physics, meaning that input power is how much power is converted to SBS power at the fiber input. Figure 6 shows the measured dependence of the Stokes power on the input power for various fiber lengths.

Figure 6.
The measured dependence of the Stokes power on the input power for various fiber lengths. [Reprinted/Adapted] with permission from [61] © The Optical Society.
The Brillouin Gain Spectrum (BGS) can be described as
where is the pump frequency; and and are the frequency shift and FWHM width of the mth line in the BGS.
2.2. Fiber-Based Technique of SBS Suppression Rationale
To develop the fiber-based technique that suppresses SBS, the major parameter of concern is the SBS threshold. The SBS threshold is the maximum optical power allowed so that the ratio of over does not exceed a certain threshold value [66]. The threshold value differs from paper to paper though, and the SBS threshold gain in dB still catches the essential physics.
Combined with Functions (6) and (7), the SBS effective gain factor can be expressed as [67]:
where is the SBS effective gain factor; is the fiber effective interaction length; is the laser spectrum; and is the mode effective area.
The SBS threshold using Smith’s condition is described as:
where is the peak Brillouin gain.
where is the effective refractive index of the fiber; is the respective component of the electrostriction tensor; is the incident pump wavelength; and is the mean value of the material density of the fiber.
Equations (8) and (9) provide the guidance for the fiber-based techniques development. Equation (9) provides the guidance of SBS on the longitudinal direction and Equation (8) shed some light on the transverse dimension.
3. Fiber-Based Techniques for SBS Suppression
3.1. Transverse Optical Fiber Design
3.1.1. Large Mode Area Fiber
One idea to suppress SBS is to design optical fibers in terms of a fiber dopant and waveguide structure. In the early days, it was found that dispersion non-shifted fiber has better performance in terms of the SBS threshold than SSMF [68]. Additionally, various studies have been conducted to study the SBS in optical fibers with different core sizes, dopant concentrations, and dopant types. Nori Shibata researched three different core types (pure silica core, GeO2 dopant core, and P2O5 dopant core) with different waveguide structures and tailored the spectrum of SBS [69], which opens the door for future design. Y. Koyamada simulated the BGS by accounting for the contributions from all the acoustic modes along the fiber axis [64]. The model includes how the dopant type and concentration affect the acoustic velocity and refractive index, which is summarized from the empirical data [70,71,72].
One viable technique is to design the optical fibers that have a large mode area (LMA) [73]. From Equation (9), a large effective area has a linear relationship with the SBS threshold. One way to increase the mode effective area is to lower the core refractive index and increase the core diameter. Figure 7 shows the relationship between the core diameter and mode effective area for the GeO2-doped step-index fiber with different numerical aperture (NA). The mode effective area increases when the core diameter exceeds a certain value. Below that value, the core diameter is not large enough to confine the electric mode. However, this method has constraint. The first constraint is that the optical fiber need be single mode. That means, when core diameter increases, the index difference must be decreased. However, the control of the small index steps in the glass manufacturing process can be difficult, which puts a limit to that method. The state-of-the-art conventional large-mode-area (LMA) fibers are generally limited in practice to diameters that are less than [74].
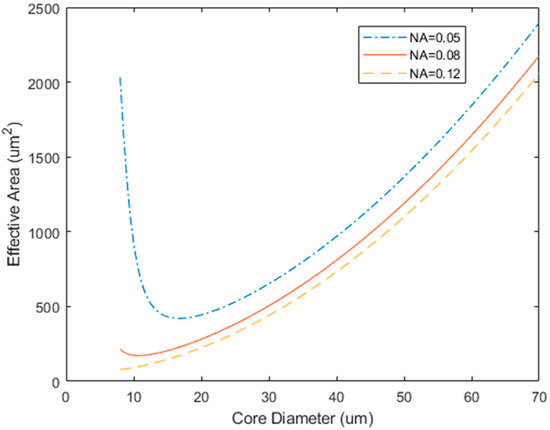
Figure 7.
The relationship between the core diameter and mode effective area.
To further increase the mode effective area, photonic crystal fibers (PCFs) are proposed. PCF is an optical fiber with an ordered array of microscopic airholes running along its length. In such a fiber, the guidance is determined by the geometry of the pattern of air-holes rather than by the material [75]. The introduction of micron-sized air holes in a fiber allows for a more precise control of the effective index of refraction of the cladding. The fabrication method applied is stacking and drawing, which could achieve the high precision of geometric index. Right after the first PCF laser was reported [76], the first LMA PCF laser was demonstrated [77]. Figure 8 shows an optical micrograph of this rod embedded in a PCF preform. The core area is in the middle, which consists of 425 small doped regions. With further fiber structure design and fabrication improvements [74,78,79,80,81], the reported mode effective area has increased significantly. Additionally, the results of LMA fiber lasers have been reported [82,83,84].

Figure 8.
Optical micrograph of the core region of a fiber preform, showing 425 small doped regions within the core. Pitch . [Reprinted/Adapted] with permission from [78] © The Optical Society.
3.1.2. Acoustic Tailoring
Another method is the acoustic tailoring that was proposed by Andrey Kobyakov, etc. [65], who found that the approximation in the derivation of Equation (9) is not necessary for every fiber design. For more complicated fiber geometry, the mode effective area needs be replaced by the acousto-optic effective area , with the expression:
where the angular brackets denote averaging over the transverse cross section of the fiber, and and are the radial profiles of the fundamental electric and mth acoustic modes of the fiber, respectively. In Equation (11), the dependence of the acoustic mode is dropped, since, in the overlap, the integral would be negligible if acoustic modes with angle dependence are considered.
The basic idea is to design special fiber structures that reduce the overlap integral between the fundamental electric mode field and acoustic mode field. To effectively reduce the overlap integral, the radial distribution of the aelectric mode field and acoustic mode field need be different. Since the optical fiber system components are designed for a Gaussian-like mode field, it would be convenient to tailor the acoustic mode field from an engineering point of view. It is not very difficult to find that Equations (4) and (5) are quite similar [85]. The optical refractive index in Equation (4) is similar to in Equation (5); thus, the acoustic refractive index is defined as:
where is the longitudinal velocity in the cladding and is the longitudinal acoustic velocity in the radial dimension.
A higher optical refractive index has the general effect of concentrating the electric field and so does higher acoustic refractive index on the acoustic field. To achieve the goal of reducing the overlap integral, the radial distributions of the optical refractive index and acoustic refractive index need to have different distributions. Table 1 shows how various dopant types affect the optical refractive index and acoustic refractive index. It can be shown that, if the dopant is GeO2, two refractive indices both increase. However, if the dopant is Al2O3, the optical refractive index goes up, while the acoustic refractive index goes down, which is critical for this technique. One design method is proposed by Mingjun Li [86], which is shown in Figure 9. Two types of doping types (GeO2 and Al2O3) are used, with (a) the Al2O3 dopant at the inner core region and the GeO2 dopant at the outer core region; (b) the GeO2 dopant at the inner core region, the Al2O3 dopant at the outer core region; and (c) the Al2O3 dopant at both the inner core and outer core region. The electric mode profile and acoustic mode profile is shown in dashed lines. These two mode profiles are quite different, meaning SBS can be suppressed. The simulation results show that these designs can have roughly 6.7 dB SBS threshold gain vs. the GeO2-doped fibers with same optical refractive profile. This technique does not require the core diameter to be large. The experimental demonstration of the fiber-type design (a) is also fabricated as 12 m for fiber laser application. The SBS threshold gain is measured to be around 6 dB. By further optimizing the overlap integral and fabrication method, improvement has been reported [87,88,89,90]. This technique is critical for SBS suppression.

Table 1.
Trend of optical and acoustic refractive index with different dopants in silica [86].

Figure 9.
Dopant designs for acoustic tailoring. (a) the Al2O3 dopant at the inner core region and the GeO2 dopant at the outer core region, (b) the GeO2 dopant at the inner core region, the Al2O3 dopant at the outer core region, and (c) the Al2O3 dopant at both the inner core and outer core region. [Reprinted/Adapted] with permission from [86] © The Optical Society.
3.2. Longitudinal Variant Fiber Design
From a longitudinal point of view, SBS suppression can also be achieved by introducing longitudinal variant fiber design. The theoretical background of SBS in nonuniform fibers is laid by X.P. Mao, etc. [67], and later revised by S Rae, etc. [91].
3.2.1. Concatenated Optical Fibers
One technique to suppress SBS is to use concatenated fibers. As different fibers have different peak gain spectra, by concatenating different fibers, the total Brillouin backscattered power could be reduced compared with using only one type of fiber. The first experimental result using concatenating fibers was demonstrated by Toshihiko Sugie [92]; 364.3 km of optical fiber transmission was demonstrated and concatenated fibers were used to suppress SBS. The SBS threshold gain was proved to be 3.8 dB. One notable feature of using concatenated fibers is that the forward SBS threshold and backward SBS threshold would be different, which is illustrated in Figure 10. In addition, if two peak Brillouin frequencies of two fibers are separated enough, two frequencies can still be observed [93]. A. Kobyakov, etc., developed and experimentally validated an analytical approach to calculate the SBS threshold in a nonuniform fiber consisting of segments with non-overlapping Brillouin gain spectra [94]. The analytical results allow for the optimization of nonuniform fiber spans in applications where the magnitude of the SBS threshold is critical.

Figure 10.
TheSBS thresholds of the concatenated fibers, (a) concatenation of fiber I and II, (b) concatenation of fiber I and fiber III. A is fiber I + fiber II, indicating that the front segment is fiber I and the backend is II, and same for B, C, D. [Reprinted/Adapted] with permission from [61] © The Optical Society.
3.2.2. Tapered Optical Fibers
Another technique is to fabricate tapered fibers. One method is to engineer the preform so that the fabricated fibers have core variations in the transmission direction. By changing the core diameter of the optical fiber, the peak Brillouin frequency shifts accordingly, which could effectively suppress SBS. The first experiment reported that the outer diameter of the 320 mm preform varied from 30 mm to 23 mm [68]. A 14 km long fiber was drawn, and the comparison experiment showed that the Brillouin gain was reduced by 3.5 dB. Recently, the fiber tapering method for SBS suppression has been widely explored in the realm of high-power amplifiers and lasers [95,96,97,98,99,100,101,102].
3.3. External Perturbations (Temperature and Strain)
Another technique is to apply external perturbations (temperature and strain) on optical fibers. Applying strain distribution and temperature distribution are two different ways to shift the peak Brillouin frequency. They both perturb the fiber preform and distort the fiber refractive index profile, which could shift the peak frequency of SBS. One notable application is Brillouin distributed sensing [103,104,105,106,107], the key to which is to detect local strain or temperature change, hence the local disturbance. In our application, the longitudinal variation along the optical fiber propagation direction due to strain or temperature distribution could be used to suppress SBS.
3.3.1. Temperature Distribution on Optical Fibers
Applying temperature distribution to suppress SBS is mostly used in short length fiber applications, especially high-power lasers or amplifiers from an engineering perspective. The thermal effects on Brillouin scattering has been studied since 1990s [108,109,110]. The effect of how a temperature change shifts the SBS central frequency is modeled by Equation (13) [111]:
where is the peak Brillouin gain; is the center frequency shift of Brillouin gain spectrum due to temperature gradient; and is the temperature.
J. Hansryd, etc., demonstrated the SBS threshold increase for a short, highly nonlinear GeO2-doped fiber by applying different temperature distributions along the fiber [112]. By winding the fiber onto eight spools (100 m) with a temperature difference of 350 °C, an 8 dB increase in the SBS threshold was achieved. Other methods of creating temperature gradient were also demonstrated to be effective in SBS suppression [43,113,114,115].
3.3.2. Strain Distribution on Optical Fibers
Applying strain distribution along the optical fibers could also contribute to SBS suppression, which could be applied to both short and long optical fiber SBS suppression applications. The relationship between the strain and SBS frequency shift on longitudinal direction can be expressed as the following [116]:
where is the strain applied to the fiber, is the strain coefficient of the Brillouin frequency, and is the SBS frequency shift when no strain is applied.
For short-distance applications, various methods could be implemented. One method is to divide the optical fibers into many sections and stretch each section with designed forces so that strain is introduced. Each section serves as an independent element and can be combined to simulate longitudinal strain distribution (stair ramp, triangular, etc.). Using this method, around 8 dB SBS threshold gain were demonstrated for around 500 m fiber [117,118]. Recently, the method of creating arbitrary longitudinal strain distribution was proposed and demonstrated [119]. The schematic of the coiling machine is shown in Figure 11. Fiber stain can be modified by a strain control module that consists of a brake section and force sensor so that the arbitrary strain can be applied to each coil of the fiber. The strain technique has the advantage of convenient implementation, so it has been widely used to suppress SBS [116,120,121,122].
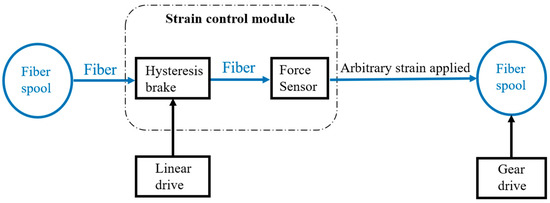
Figure 11.
Schematic of the fiber coiling machine.
When optical fiber is used for transmission application, the methods are limited. This is mainly due to implementation cost. The main method is cabling. The first experiment applying strain distribution to suppress SBS was conducted by N.Yoshizawa, etc. [123]. In their experiment, strain distribution along the propagation distance was implemented by cabling. It was a double-stranded optical unit structure, where the optical fiber section can be stretched or compressed. Transmission over 3.7 km under-sea optical fiber was demonstrated. Compared with traditional fiber, the bandwidth of the SBS spectrum was expanded 2.9 times, which is the demonstration of SBS suppression. Years later, N. Yoshizawa, etc., optimized their cabling method by using a tight-double-helix structure [124,125].
3.4. Combined Techniques
These techniques are in general compatible with each other, thus can be applied in combination to further suppress SBS. Longitudinal variant fiber technique combined with temperature gradient technique [101], longitudinal variant fiber technique with LMA fiber technique [96,97] and acoustic tailoring technique with strain technique [126] were demonstrated.
4. Conclusions
In this paper, we have reviewed fiber-based techniques to suppress SBS. These techniques were developed based on rich properties of optical fibers, which cover electromagnetism, acoustics, and materials. Unfortunately, some important techniques (phase broadening, etc.) are beyond the scope of our paper, though they are equally important. The techniques of SBS suppression have been widely adopted in the fiber laser and fiber communication industry. Researchers are encouraged to further explore new techniques.
Author Contributions
Conceptualization, B.H.; methodology, X.S.; software, J.W.; validation, B.H.; formal analysis, J.W.; investigation, B.H. and J.W.; resources, X.S.; data curation, J.W.; writing—original draft preparation, B.H. and J.W.; writing—review and editing, B.H. and X.S.; visualization, J.W.; supervision, B.H.; project administration, B.H. and X.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gross, E. Change of wave-length of light due to elastic heat waves at scattering in liquids. Nature 1930, 126, 201–202. [Google Scholar] [CrossRef]
- Raman, C.V. A change of wave-length in light scattering. Nature 1928, 121, 619. [Google Scholar] [CrossRef]
- McClung, F.J.; Hellwarth, R.W. Giant optical pulsations from ruby. Appl. Opt. 1962, 1, 103–105. [Google Scholar] [CrossRef]
- Woodbury, E.J.; Ng, W.K.; Co, H.A.; Calif, C.C. Ruby Laser Opeartion in the Near IR. Proc. IRE 1962, 50, 2367. [Google Scholar]
- Chiao, R.Y.; Townes, C.H.; Stoicheff, B.P. Stimulated Brillouin scattering and coherent generation of intense hypersonic waves. Phys. Rev. Lett. 1964, 12, 592. [Google Scholar] [CrossRef]
- Sundar, V.; Newnham, R.E. Electrostriction. In The Electrical Engineering Handbook, 2nd ed.; Dorf, R.C., Ed.; CRC Press: Boca Raton, FL, USA, 1997; pp. 1193–1200. [Google Scholar]
- Ippen, E.P.; Stolen, R.H. Stimulated Brillouin scattering in optical fibers. Appl. Phys. Lett. 1972, 21, 539–541. [Google Scholar] [CrossRef]
- Smith, R.G. Optical power handling capacity of low loss optical fibers as determined by stimulated Raman and Brillouin scattering. Appl. Opt. 1972, 11, 2489–2494. [Google Scholar] [CrossRef]
- Buckland, E.L.; Boyd, R.W. Electrostrictive contribution to the intensity-dependent refractive index of optical fibers. Opt. Lett. 1996, 21, 1117–1119. [Google Scholar] [CrossRef]
- Buckland, E.L. Mode-profile dependence of the electrostrictive response in fibers. Opt. Lett. 1999, 24, 872–874. [Google Scholar] [CrossRef]
- Dianov, E.M.; Sukharev, M.E.; Biriukov, A.S. Electrostrictive response in single-mode ring-index-profile fibers. Opt. Lett. 2000, 25, 390–392. [Google Scholar] [CrossRef]
- Townsend, P.D.; Poustie, A.J.; Hardman, P.J.; Blow, K.J. Measurement of the refractive-index modulation generated by electrostriction-induced acoustic waves in optical fibers. Opt. Lett. 1996, 21, 333–335. [Google Scholar] [CrossRef] [PubMed]
- Buckland, E.L.; Boyd, R.W. Measurement of the frequency response of the electrostrictive nonlinearity in optical fibers. Opt. Lett. 1997, 22, 676–678. [Google Scholar] [CrossRef] [PubMed]
- Melloni, A.; Frasca, M.; Garavaglia, A.; Tonini, A.; Martinelli, M. Direct measurement of electrostriction in optical fibers. Opt. Lett. 1998, 23, 691–693. [Google Scholar] [CrossRef] [PubMed]
- Biryukov, A.S.; Sukharev, M.E.; Dianov, E.M. Excitation of sound waves upon propagation of laser pulses in optical fibers. Quantum Electron. 2002, 32, 765. [Google Scholar] [CrossRef]
- Biryukov, A.S.; Erokhin, S.V.; Kushchenko, S.V.; Dianov, E.M. Electrostriction temporal shift of laser pulses in optical fibers. Quantum Electron. 2004, 34, 1047. [Google Scholar] [CrossRef]
- Van Deventer, M.O.; Boot, A.J. Polarization properties of stimulated Brillouin scattering in single-mode fibers. J. Light. Technol. 1994, 12, 585–590. [Google Scholar] [CrossRef]
- Engan, H.E. Analysis of polarization-mode coupling by acoustic torsional waves in optical fibers. JOSA A 1996, 13, 112–118. [Google Scholar] [CrossRef]
- Imai, Y.; Yoshida, M. Polarization characteristics of fiber-optic SBS phase conjugation. Opt. Fiber Technol. 2000, 6, 42–48. [Google Scholar] [CrossRef]
- Ferreira, M.F.; Rocha, J.F.; Pinto, J.L. Analysis of the gain and noise characteristics of fibre Brillouin amplifiers. Opt. Quant. Electron. 1994, 26, 35–44. [Google Scholar] [CrossRef]
- Schneider, T.; Hannover, D.; Junker, M. Investigation of Brillouin scattering in optical fibers for the generation of millimeter waves. J. Light. Technol. 2006, 24, 295. [Google Scholar] [CrossRef]
- Hill, K.O.; Kawasaki, B.S.; Johnson, D.C. CW Brillouin laser. Appl. Phys. Lett. 1976, 28, 608–609. [Google Scholar] [CrossRef]
- Stokes, L.F.; Chodorow, M.; Shaw, H.J. All-fiber stimulated Brillouin ring laser with submilliwatt pump threshold. Opt. Lett. 1982, 7, 509–511. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.P.; Zarinetchi, F.; Ezekiel, S. Narrow-linewidth stimulated Brillouin fiber laser and applications. Opt. Lett. 1991, 16, 393–395. [Google Scholar] [CrossRef] [PubMed]
- Bayvel, P.; Giles, I.P. Linewidth narrowing in semiconductor laser pumped all-fibre Brillouin ring laser. Electron. Lett. 1989, 4, 260–262. [Google Scholar] [CrossRef]
- Grudinin, I.S.; Matsko, A.B.; Maleki, L. Brillouin lasing with a CaF2 whispering gallery mode resonator. Phys. Rev. Lett. 2009, 102, 043902. [Google Scholar] [CrossRef]
- Pant, R.; Poulton, C.; Choi, D.-Y.; McFarlane, H.; Hile, S.; Li, E.; Thevenaz, L.; Luther-Davies, B.; Madden, S.J.; Eggleton, B.J. On-chip stimulated Brillouin scattering. Opt. Express 2011, 19, 8285–8290. [Google Scholar] [CrossRef]
- Li, J.; Lee, H.; Chen, T.; Vahala, K.J. Characterization of a high coherence, Brillouin microcavity laser on silicon. Opt. Express 2012, 20, 20170–20180. [Google Scholar] [CrossRef]
- Carr, I.D.; Hanna, D.C. Performance of a Nd: YAG oscillator/ampflifier with phase-conjugation via stimulated Brillouin scattering. Appl. Phys. B 1985, 36, 83–92. [Google Scholar] [CrossRef]
- Andreev, N.F.; Khazanov, E.A.; Pasmanik, G.A. Applications of Brillouin cells to high repetition rate solid-state lasers. IEEE J. Quantum Electron. 1992, 28, 330–341. [Google Scholar] [CrossRef]
- Dane, C.B.; Zapata, L.E.; Neuman, W.A.; Norton, M.A.; Hackel, L.A. Design and operation of a 150 W near diffraction-limited laser amplifier with SBS wavefront correction. IEEE J. Quantum Electron. 1995, 31, 148–163. [Google Scholar] [CrossRef]
- Sumida, D.S.; Jones, D.C.; Rockwell, D.A. An 8.2 J phase-conjugate solid-state laser coherently combining eight parallel amplifiers. IEEE J. Quantum Electron. 1994, 30, 2617–2627. [Google Scholar] [CrossRef]
- Kong, H.J.; Lee, J.Y.; Shin, Y.S.; Byun, J.O.; Park, H.S.; Kim, H. Beam Recombination Characteristics in Array Laser Amplification Using Stimulated Brillouin Scattering Phase Conjugation. Opt. Rev. 1997, 4, 277–283. [Google Scholar] [CrossRef]
- Omatsu, T.; Kong, H.J.; Park, S.; Cha, S.; Tsubakimoto, K.; Fujita, N.; Miyanaga, N.; Nakatsuka, M.; Wang, Y.; Lu, Z.; et al. The current trends in SBS and phase conjugation. Laser Part Beams 2012, 30, 117–174. [Google Scholar] [CrossRef]
- Hon, D.T. Pulse compression by stimulated Brillouin scattering. Opt. Lett. 1980, 5, 516–518. [Google Scholar] [CrossRef]
- Xu, X.; Feng, C.; Diels, J.C. Optimizing sub-ns pulse compression for high energy application. Opt. Express 2014, 22, 13904–13915. [Google Scholar] [CrossRef]
- Song, K.Y.; Herráez, M.G.; Thévenaz, L. Observation of pulse delaying and advancement in optical fibers using stimulated Brillouin scattering. Opt. Express 2005, 13, 82–88. [Google Scholar] [CrossRef]
- Herráez, M.G.; Song, K.Y.; Thévenaz, L. Arbitrary-bandwidth Brillouin slow light in optical fibers. Opt. Express 2006, 14, 1395–1400. [Google Scholar] [CrossRef]
- Okawachi, Y.; Bigelow, M.S.; Sharping, J.E.; Zhu, Z.; Schweinsberg, A.; Gauthier, D.J.; Boyd, R.W.; Gaeta, A.L. Tunable all-optical delays via Brillouin slow light in an optical fiber. Phys. Rev. Lett. 2005, 94, 153902. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Zhou, X.; Effenberger, F.; Yan, X.; Peng, G.; Qian, Y.; Ma, Y. Time-and wavelength-division multiplexed passive optical network (TWDM-PON) for next-generation PON stage 2 (NG-PON2). J. Light. Technol. 2012, 31, 587–593. [Google Scholar] [CrossRef]
- Ellis, R.B.; Weiss, F.; Anton, O.M. HFC and PON-FTTH networks using higher SBS threshold singlemode optical fibre. Electron. Lett. 2007, 43, 1–2. [Google Scholar] [CrossRef]
- Tan, A.H.H. Super PON-a fiber to the home cable network for CATV and POTS/ISDN/VOD as economical as a coaxial cable network. J. Light. Technol. 1997, 15, 213–218. [Google Scholar] [CrossRef]
- Kovalev, V.I.; Harrison, R.G. Suppression of stimulated Brillouin scattering in high-power single-frequency fiber amplifiers. Opt. Lett. 2006, 31, 161–163. [Google Scholar] [CrossRef] [PubMed]
- Zervas, M.N.; Codemard, C.A. High power fiber lasers: A review. IEEE J. Quantum Electron. 2014, 20, 219–241. [Google Scholar] [CrossRef]
- Richardson, D.J.; Nilsson, J.; Clarkson, W.A. High power fiber lasers: Current status and future perspectives. JOSA B 2010, 27, B63–B92. [Google Scholar] [CrossRef]
- Fu, S.; Shi, W.; Feng, Y.; Zhang, L.; Yang, Z.; Xu, S.; Zhu, X.; Norwood, R.A.; Peyghambarian, N. Review of recent progress on single-frequency fiber lasers. JOSA B 2017, 34, A49–A62. [Google Scholar] [CrossRef]
- Willems, F.W.; Muys, W.; Leong, J.S. Simultaneous suppression of stimulated Brillouin scattering and interferometric noise in externally modulated lightwave AM-SCM systems. IEEE Photon. Technol. Lett. 1994, 6, 1476–1478. [Google Scholar] [CrossRef]
- Downie, J.D.; Hurley, J. Experimental study of SBS mitigation and transmission improvement from cross-phase modulation in 10.7 Gb/s unrepeatered systems. Opt. Express 2007, 15, 9527–9534. [Google Scholar] [CrossRef]
- Coles, J.B.; Kuo, B.P.P.; Alic, N.; Moro, S.; Bres, C.S.; Boggio, J.C.; Andrekson, P.A.; Karlsson, M.; Radic, S. Bandwidth-efficient phase modulation techniques for stimulated Brillouin scattering suppression in fiber optic parametric amplifiers. Opt. Express 2010, 18, 18138–18150. [Google Scholar] [CrossRef]
- Wu, P.Y.; Lu, H.H.; Ying, C.L.; Li, C.Y.; Su, H.S. An upconverted phase-modulated fiber optical CATV transport system. J. Light. Technol. 2011, 29, 2422–2427. [Google Scholar] [CrossRef]
- Anderson, B.; Robin, C.; Flores, A.; Dajani, I. Experimental study of SBS suppression via white noise phase modulation. SPIE 2014, 8961, 362–368. [Google Scholar]
- Flores, A.; Robin, C.; Lanari, A.; Dajani, I. Pseudo-random binary sequence phase modulation for narrow linewidth, kilowatt, monolithic fiber amplifiers. Opt. Express 2014, 22, 17735–17744. [Google Scholar] [CrossRef] [PubMed]
- Harish, A.V.; Nilsson, J. Optimization of phase modulation formats for suppression of stimulated Brillouin scattering in optical fibers. IEEE J Quantum Electron. 2017, 24, 5100110. [Google Scholar] [CrossRef]
- Kim, D.; Kim, B.G.; Bo, T.; Kim, H. Dither-frequency tuning technique for RSOA-based coherent WDM PON. IEEE Photon. Technol. Lett. 2018, 31, 7–10. [Google Scholar] [CrossRef]
- Yang, Y.; Li, B.; Liu, M.; Huang, X.; Feng, Y.; Cheng, D.; He, B.; Zhou, J.; Nilsson, J. Optimization and visualization of phase modulation with filtered and amplified maximal-length sequence for SBS suppression in a short fiber system: A theoretical treatment. Opt. Express 2021, 29, 16781–16803. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Agrawal, G.P. Suppression of stimulated Brillouin scattering in optical fibers using fiber Bragg gratings. Opt. Express 2003, 11, 3467–3472. [Google Scholar] [CrossRef]
- Takushima, Y.; Okoshi, T. Suppression of stimulated Brillouin scattering using optical isolators. Electron. Lett. 1992, 12, 1155–1157. [Google Scholar] [CrossRef]
- Weßels, P.; Adel, P.; Auerbach, M.; Wandt, D.; Fallnich, C. Novel suppression scheme for Brillouin scattering. Opt. Express 2004, 12, 4443–4448. [Google Scholar] [CrossRef]
- Garmire, E. Perspectives on stimulated Brillouin scattering. NJP 2017, 19, 011003. [Google Scholar] [CrossRef]
- Garmire, E. Stimulated Brillouin review: Invented 50 years ago and applied today. Int. J. Opt. 2018, 2018, 17. [Google Scholar] [CrossRef]
- Kobyakov, A.; Sauer, M.; Chowdhury, D. Stimulated Brillouin scattering in optical fibers. Adv. Opt. Photon. 2010, 2, 1–59. [Google Scholar] [CrossRef]
- Dasgupta, S.; Poletti, F.; Liu, S.; Petropoulos, P.; Richardson, D.J.; Gruner-Nielsen, L.; Herstrom, S. Modeling Brillouin gain spectrum of solid and microstructured optical fibers using a finite element method. J. Light. Technol. 2011, 29, 22–30. [Google Scholar] [CrossRef]
- Dong, L. Formulation of a complex mode solver for arbitrary circular acoustic waveguides. J. Light. Technol. 2010, 28, 3162–3175. [Google Scholar]
- Koyamada, Y.; Sato, S.; Nakamura, S.; Sotobayashi, H.; Chujo, W. Simulating and designing Brillouin gain spectrum in single-mode fibers. J. Light. Technol. 2004, 22, 631. [Google Scholar] [CrossRef]
- Kobyakov, A.; Kumar, S.; Chowdhury, D.Q.; Ruffin, A.B.; Sauer, M.; Bickham, S.R.; Mishra, R. Design concept for optical fibers with enhanced SBS threshold. Opt. Express 2005, 13, 5338–5346. [Google Scholar] [CrossRef] [PubMed]
- Supradeepa, V.R. Stimulated Brillouin scattering thresholds in optical fibers for lasers linewidth broadened with noise. Opt. Express 2013, 21, 4677–4687. [Google Scholar] [CrossRef]
- Mao, X.P.; Tkach, R.W.; Chraplyvy, A.R.; Jopson, R.M.; Derosier, R.M. Stimulated Brillouin threshold dependence on fiber type and uniformity. IEEE Photon. Technol. Lett. 1992, 4, 66–69. [Google Scholar] [CrossRef]
- Shiraki, K.; Ohashi, M.; Tateda, M. Suppression of stimulated Brillouin scattering in a fibre by changing the core radius. Electron. Lett. 1995, 31, 668–669. [Google Scholar] [CrossRef]
- Shibata, N.; Waarts, R.G.; Braun, R.P. Brillouin-gain spectra for single-mode fibers having pure-silica, GeO2-doped, and P2O5-doped cores. Opt. Lett. 1987, 12, 269–271. [Google Scholar] [CrossRef]
- Nikles, M.; Thevenaz, L.; Robert, P.A. Brillouin gain spectrum characterization in single-mode optical fibers. J. Light. Technol. 1997, 15, 1842–1851. [Google Scholar] [CrossRef]
- Lagakos, N.; Bucaro, J.A.; Hughes, R. Acoustic sensitivity predictions of single-mode optical fibers using Brillouin scattering. Appl. Opt. 1980, 19, 3668–3670. [Google Scholar] [CrossRef]
- Shiraki, K.; Ohashi, M. Sound velocity measurement based on guided acoustic-wave Brillouin scattering. IEEE Photon. Technol. Lett. 1992, 4, 1177–1180. [Google Scholar] [CrossRef]
- Broderick, N.G.R.; Offerhaus, H.L.; Richardson, D.J.; Sammut, R.A.; Caplen, J.; Dong, L. Large mode area fibers for high power applications. Opt. Fiber Technol. 1999, 5, 185–196. [Google Scholar] [CrossRef]
- Limpert, J.; Deguil-Robin, N.; Manek-Hönninger, I.; Salin, F.; Röser, F.; Liem, A.; Schreiber, T.; Nolte, S.; Zellmer, A.; Tunnermann, A.; et al. High-power rod-type photonic crystal fiber laser. Opt. Express 2005, 13, 1055–1058. [Google Scholar] [CrossRef] [PubMed]
- Knight, J.C.; Birks, T.A.; Russell, P.S.J.; Atkin, D.M. All-silica single-mode optical fiber with photonic crystal cladding. Opt. Lett. 1996, 21, 1547–1549. [Google Scholar] [CrossRef]
- Wadsworth, W.J.; Knight, J.C.; Reeves, W.H.; Russell, P.S.J.; Arriaga, J. Yb3+-doped photonic crystal fiber laser. Electron. Lett. 2000, 36, 17. [Google Scholar] [CrossRef]
- Wadsworth, W.J.; Knight, J.C.; Russell, P.S.J. Large mode area photonic crystal fiber laser. In Proceedings of the Conference on Lasers and Electro-Optics, Baltimore, MD, USA, 11 May 2001. [Google Scholar]
- Wadsworth, W.J.; Percival, R.M.; Bouwmans, G.; Knight, J.C.; Russell, P.S.J. High power air-clad photonic crystal fiber laser. Opt. Express 2003, 11, 48–53. [Google Scholar] [CrossRef]
- El Hamzaoui, H.; Bouwmans, G.; Cassez, A.; Bigot, L.; Capoen, B.; Bouazaoui, M.; Vanvincq, O.; Douay, M. F/Yb-codoped sol-gel silica glasses: Toward tailoring the refractive index for the achievement of high-power fiber lasers. Opt. Lett. 2017, 42, 1408–1411. [Google Scholar] [CrossRef]
- Golojuch, G.; Urbańczyk, W. Large mode area photonic crystal fibers with high geometrical birefringence. SPIE 2008, 7141, 433–437. [Google Scholar]
- Chen, M.Y. Polarization and leakage properties of large-mode-area microstructured-core optical fibers. Opt. Express 2007, 15, 12498–12507. [Google Scholar] [CrossRef]
- Christensen, S.L.; Papior, S.R.; Johansen, M.M.; Hauge, J.M.; Weirich, J.; Jakobsen, C.; Michieletto, M.; Bondu, M.; Triches, M.; Alkeskjold, T.T.; et al. Photonic crystal fiber technology for monolithic single-mode large-mode-area all-solid amplifier. SPIE 2019, 10897, 255–261. [Google Scholar]
- Kim, Y.G.; Ryu, J.W.; Cha, Y.H.; Park, H.M.; Lim, G.; Han, J.M.; Ko, K.H.; Kim, T.S.; Jeong, D.Y. Maintaining the polarization, temperature and amplification characteristics of a ytterbium-doped rod-type photonic crystal fiber (PCF) amplifier. J. Korean Phys. Soc. 2011, 59, 3182–3187. [Google Scholar] [CrossRef]
- Alkeskjold, T.T.; Laurila, M.; Weirich, J.; Johansen, M.M.; Olausson, C.B.; Lumholt, O.; Noordegraaf, D.; Maack, M.D.; Jakobsen, C. Photonic crystal fiber amplifiers for high power ultrafast fiber lasers. Nanophotonics 2013, 2, 369–381. [Google Scholar] [CrossRef]
- Mamdem, Y.S.; Phéron, X.; Taillade, F.; Jaouën, Y.; Gabet, R.; Lanticq, V.; Moreau, G.; Boukenter, A.; Ouerdane, Y.; Lesoille, S.; et al. Two-dimensional FEM analysis of Brillouin gain spectra in acoustic guiding and antiguiding single mode optical fibers. In Proceedings of the COMSOL Conference 2010, Paris, France, 17 November 2010. [Google Scholar]
- Li, M.J.; Chen, X.; Wang, J.; Gray, S.; Liu, A.; Demeritt, J.A.; Ruffin, A.B.; Crowley, A.M.; Walton, D.T.; Zenteno, L.A. Al/Ge co-doped large mode area fiber with high SBS threshold. Opt. Express 2007, 15, 8290–8299. [Google Scholar] [CrossRef] [PubMed]
- Robin, C.; Dajani, I. Acoustically segmented photonic crystal fiber for single-frequency high-power laser applications. Opt. Lett. 2011, 36, 2641–2643. [Google Scholar] [CrossRef] [PubMed]
- Dragic, P.D. Brillouin suppression by fiber design. In Proceedings of the IEEE Photonics Society Summer Topicals 2010, Playa del Carmen, Mexico, 19–21 July 2010. [Google Scholar]
- Dragic, P.D. Ultra-flat Brillouin gain spectrum via linear combination of two acoustically anti-guiding optical fibres. Electron. Lett. 2012, 48, 1492–1493. [Google Scholar] [CrossRef]
- Dragic, P.D.; Liu, C.H.; Papen, G.C.; Galvanauskas, A. Optical fiber with an acoustic guiding layer for stimulated Brillouin scattering suppression. In Proceedings of the Conference on Lasers and Electro-Optics, Baltimore, MD, USA, 22–27 May 2005; Volume 3, pp. 1984–1986. [Google Scholar]
- Rae, S.; Bennion, I.; Cardwell, M.J. New numerical model of stimulated Brillouin scattering in optical fibers with nonuniformity. Opt. Commun. 1996, 123, 611–616. [Google Scholar] [CrossRef]
- Sugie, T.; Ohkawa, N.; Imai, T.; Ito, T. A 2.5 Gb/s, 364 km CPFSK repeaterless transmission experiment employing an Er-doped fiber amplifier and SBS suppression optical link. In Optical Amplifiers and Their Applications; Optica Publishing Group: Monterey, CA, USA, 1990. [Google Scholar]
- De Oliveira, C.A.S.; Jen, C.K.; Shang, A.; Saravanos, C. Stimulated Brillouin scattering in cascaded fibers of different Brillouin frequency shifts. JOSA B 1993, 10, 969–972. [Google Scholar] [CrossRef]
- Kobyakov, A.; Sauer, M.; Hurley, J.E. SBS threshold of segmented fibers. In Optical Fiber Communication Conference; Optica Publishing Group: Anaheim, CA, USA, 2005. [Google Scholar]
- Patokoski, K.; Rissanen, J.; Noronen, T.; Gumenyuk, R.; Chamorovskii, Y.; Filippov, V.; Toivonen, J. Single-frequency 100 ns/0.5 mJ laser pulses from all-fiber double clad ytterbium doped tapered fiber amplifier. Opt. Express 2019, 27, 31532–31541. [Google Scholar] [CrossRef]
- Lai, W.; Ma, P.; Liu, W.; Huang, L.; Li, C.; Ma, Y.; Zhou, P. 550 W single frequency fiber amplifiers emitting at 1030 nm based on a tapered Yb-doped fiber. Opt. Express 2020, 28, 20908–20919. [Google Scholar] [CrossRef]
- Jiang, W.; Yang, C.; Zhao, Q.; Gu, Q.; Huang, J.; Jiang, K.; Zhou, K.; Feng, Z.; Yang, Z.; Xu, S. 650 W All-Fiber Single-Frequency Polarization-Maintaining Fiber Amplifier Based on Hybrid Wavelength Pumping and Tapered Yb-Doped Fibers. Photonics 2022, 9, 518. [Google Scholar] [CrossRef]
- Huang, L.; Ma, P.; Su, R.; Lai, W.; Ma, Y.; Zhou, P. Comprehensive investigation on the power scaling of a tapered Yb-doped fiber-based monolithic linearly polarized high-peak-power near-transform-limited nanosecond fiber laser. Opt. Express 2021, 29, 761–782. [Google Scholar] [CrossRef] [PubMed]
- Kerttula, J.; Filippov, V.; Chamorovskii, Y.; Golant, K.; Okhotnikov, O.G. Actively Q-switched 1.6-mJ tapered double-clad ytterbium-doped fiber laser. Opt. Express 2010, 18, 18543–18549. [Google Scholar] [CrossRef] [PubMed]
- Kerttula, J.; Filippov, V.; Chamorovskii, Y.; Ustimchik, V.; Golant, K.; Okhotnikov, O.G. Tapered fiber amplifier with high gain and output power. Laser Phys. 2012, 22, 1734–1738. [Google Scholar] [CrossRef]
- Liu, A. Suppressing stimulated Brillouin scattering in fiber amplifiers using nonuniform fiber and temperature gradient. Opt. Express 2007, 15, 977–984. [Google Scholar] [CrossRef]
- Filippov, V.; Chamorovskii, Y.; Kerttula, J.; Golant, K.; Pessa, M.A.; Okhotnikov, O.G. Double clad tapered fiber for high power applications. Opt. Express 2008, 16, 1929–1944. [Google Scholar] [CrossRef]
- Galindez-Jamioy, C.A.; Lopez-Higuera, J.M. Brillouin distributed fiber sensors: An overview and applications. J. Sens. 2012, 2012, 204121. [Google Scholar] [CrossRef]
- Horiguchi, T.; Shimizu, K.; Kurashima, T.; Tateda, M.; Koyamada, Y. Development of a distributed sensing technique using Brillouin scattering. J. Light. Technol. 1995, 13, 1296–1302. [Google Scholar] [CrossRef]
- Bao, X.; Chen, L. Recent Progress in Brillouin Scattering Based Fiber Sensors. Sensors 2011, 11, 4152–4187. [Google Scholar] [CrossRef]
- Soto, M.A.; Thévenaz, L. Modeling and evaluating the performance of Brillouin distributed optical fiber sensors. Opt. Express 2013, 21, 31347–31366. [Google Scholar] [CrossRef]
- Grattan, K.T.V.; Sun, T. Fiber optic sensor technology: An overview. Sens. Actuator A Phys. 2000, 82, 40–61. [Google Scholar] [CrossRef]
- Imai, Y.; Shimada, N. Dependence of stimulated Brillouin scattering on temperature distribution in polarization-maintaining fibers. IEEE Photon. Technol. Lett. 1993, 5, 1335–1337. [Google Scholar] [CrossRef]
- Kurashima, T.; Horiguchi, T.; Tateda, M. Thermal effects of Brillouin gain spectra in single-mode fibers. IEEE Photon. Technol. Lett. 1990, 2, 718–720. [Google Scholar] [CrossRef]
- Kurashima, T.; Horiguchi, T.; Tateda, M. Thermal effects on the Brillouin frequency shift in jacketed optical silica fibers. Appl. Opt. 1990, 29, 2219–2222. [Google Scholar] [CrossRef] [PubMed]
- Hildebrandt, M.; Büsche, S.; Weßels, P.; Frede, M.; Kracht, D. Brillouin scattering spectra in high-power single frequency ytterbium doped fiber amplifiers. Opt. Express 2008, 16, 15970–15979. [Google Scholar] [CrossRef] [PubMed]
- Hansryd, J.; Dross, F.; Westlund, M.; Andrekson, P.A.; Knudsen, S.N. Increase of the SBS threshold in a short highly nonlinear fiber by applying a temperature distribution. J. Light. Technol. 2001, 19, 1691. [Google Scholar] [CrossRef]
- Theeg, T.; Ottenhues, C.; Sayinc, H.; Neumann, J.; Kracht, D. Core-pumped single-frequency fiber amplifier with an output power of 158 W. Opt. Lett. 2016, 41, 9–12. [Google Scholar] [CrossRef] [PubMed]
- Gray, S.; Liu, A.; Walton, D.T.; Wang, J.; Li, M.; Chen, X.; Ruffin, A.B. 502 Watt, single transverse mode, narrow linewidth, bidirectionally pumped Yb-doped fiber amplifier. Opt. Express 2007, 15, 17044–17050. [Google Scholar] [CrossRef]
- Li, W.; Yan, Z.; Ren, S.; Deng, Y.; Chen, Y.; Ma, P.; Liu, W.; Huang, L.; Pan, Z.; Zhou, P.; et al. Confined-doped active fiber enabled all-fiber high-power single-frequency laser. Opt. Lett. 2022, 47, 5024–5027. [Google Scholar] [CrossRef]
- Boggio, J.M.C.; Marconi, J.D.; Fragnito, H.L. Experimental and numerical investigation of the SBS-threshold increase in an optical fiber by applying strain distributions. J. Light. Technol. 2005, 23, 3808–3814. [Google Scholar] [CrossRef]
- Boggio, J.M.C.; Marconi, J.D.; Fragnito, H.L. 8 dB increase of the SBS threshold in an optical fiber by applying a stair ramp strain distribution. In Conference on Lasers and Electro-Optics; Optica Publishing Group: San Francisco, CA, USA, 2004. [Google Scholar]
- Marconi, J.D.; Boggio, J.M.C.; Fragnito, H.L. 7.3 dB increase of the SBS threshold in an optical fiber by applying a strain distribution. In Optical Fiber Communication Conference; Optica Publishing Group: Los Angeles, CA, USA, 2004. [Google Scholar]
- Engelbrecht, R. Analysis of SBS gain shaping and threshold increase by arbitrary strain distributions. J. Light. Technol. 2014, 32, 1689–1700. [Google Scholar] [CrossRef]
- Zhang, L.; Cui, S.; Liu, C.; Zhou, J.; Feng, Y. 170 W, single-frequency, single-mode, linearly-polarized, Yb-doped all-fiber amplifier. Opt. Express 2013, 21, 5456–5462. [Google Scholar] [CrossRef]
- Engelbrecht, R.; Hagen, J.; Schmidt, M. SBS-suppression in variably strained fibers for fiber-amplifiers and fiber-lasers with a high spectral power density. SPIE 2005, 5777, 795–798. [Google Scholar]
- Ma, P.; Tao, R.; Su, R.; Wang, X.; Zhou, P.; Liu, Z. 1.89 kW all-fiberized and polarization-maintained amplifiers with narrow linewidth and near-diffraction-limited beam quality. Opt. Express 2016, 24, 4187–4195. [Google Scholar] [CrossRef] [PubMed]
- Yoshizawa, N.; Horiguchi, T.; Kurashima, T. Proposal for stimulated Brillouin scattering suppression by fibre cabling. Electron. Lett. 1991, 27, 1100–1101. [Google Scholar] [CrossRef]
- Yoshizawa, N. Nine-dB expansion of Brillouin gain bandwidth by applying ±0.35% strain distribution to fiber by cabling. In Optical Fiber Communication Conference; Optica Publishing Group: San Jose, CA, USA, 1992. [Google Scholar]
- Yoshizawa, N.; Imai, T. Stimulated Brillouin scattering suppression by means of applying strain distribution to fiber with cabling. J. Light. Technol. 1993, 11, 1518–1522. [Google Scholar] [CrossRef]
- Khudyakov, M.M.; Tsvetkov, S.V.; Kosolapov, A.F.; Bubnov, M.M.; Lobanov, A.S.; Lipatov, D.S.; Guryanov, A.N.; Likhachev, M.E. Combined Method for SBS Suppression in High Numerical Aperture Single-Mode Optical Fibers. IEEE Photon. Technol. Lett. 2022, 34, 1069–1072. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).