Comprehensive Analysis of Copper Plasma: A Laser-Induced Breakdown Spectroscopic Approach
Abstract
1. Introduction
2. Materials and Methods
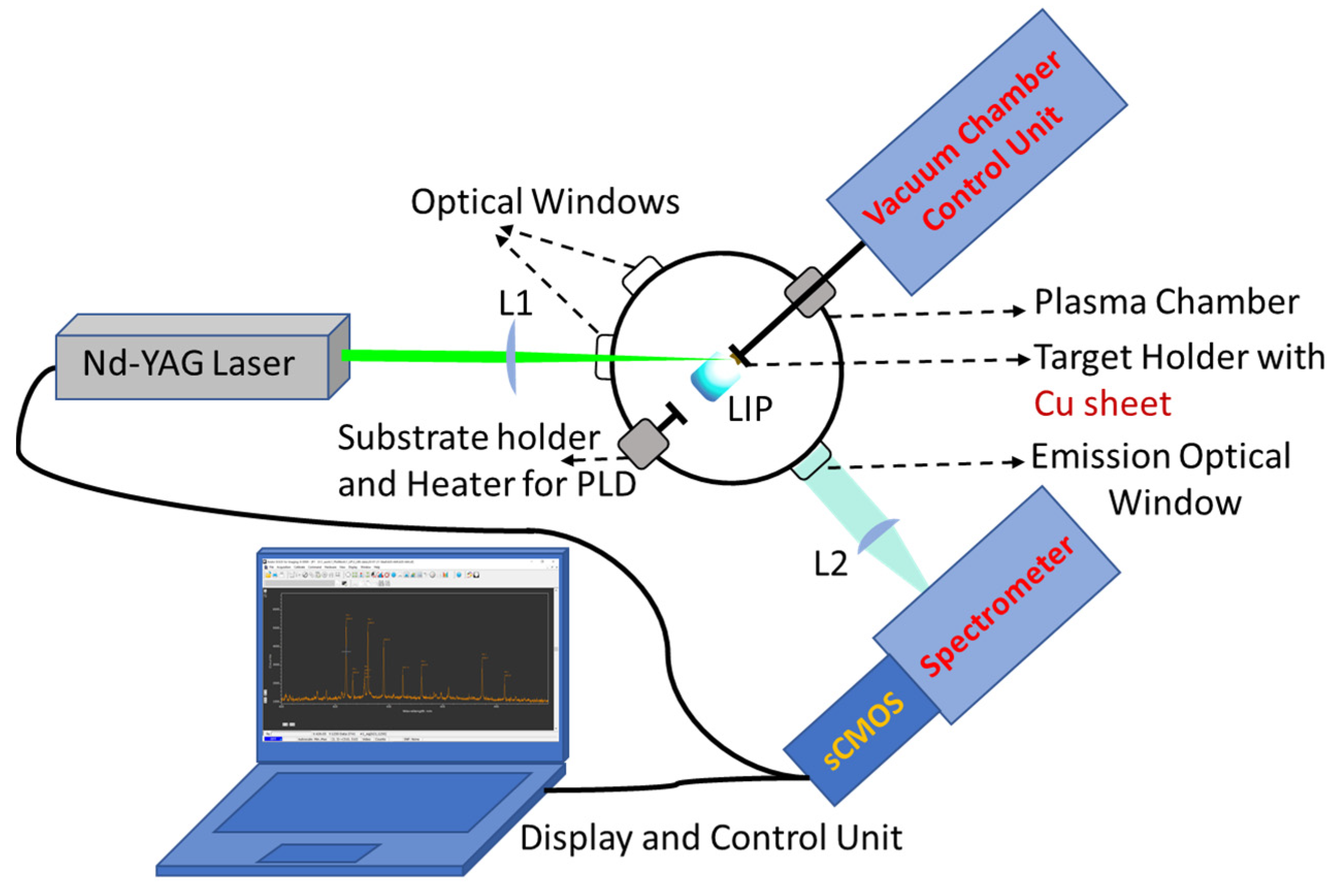
2.1. Instrumentation
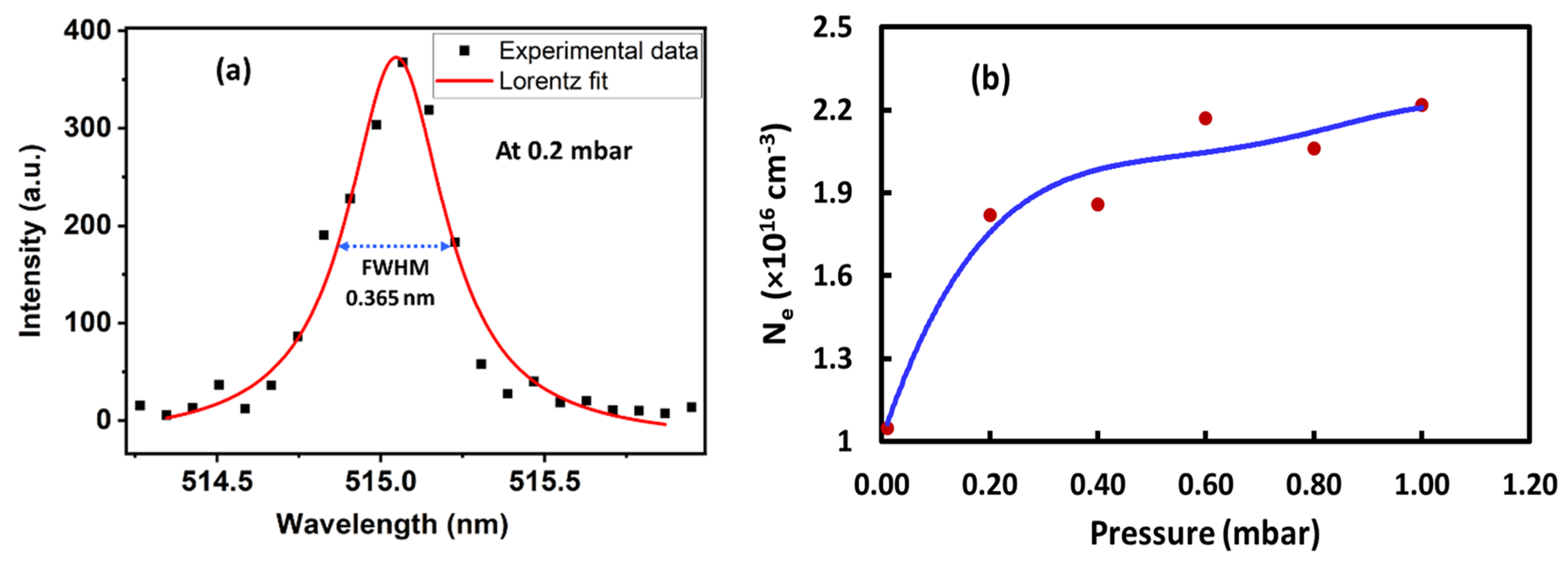
2.2. Plasma Parameters
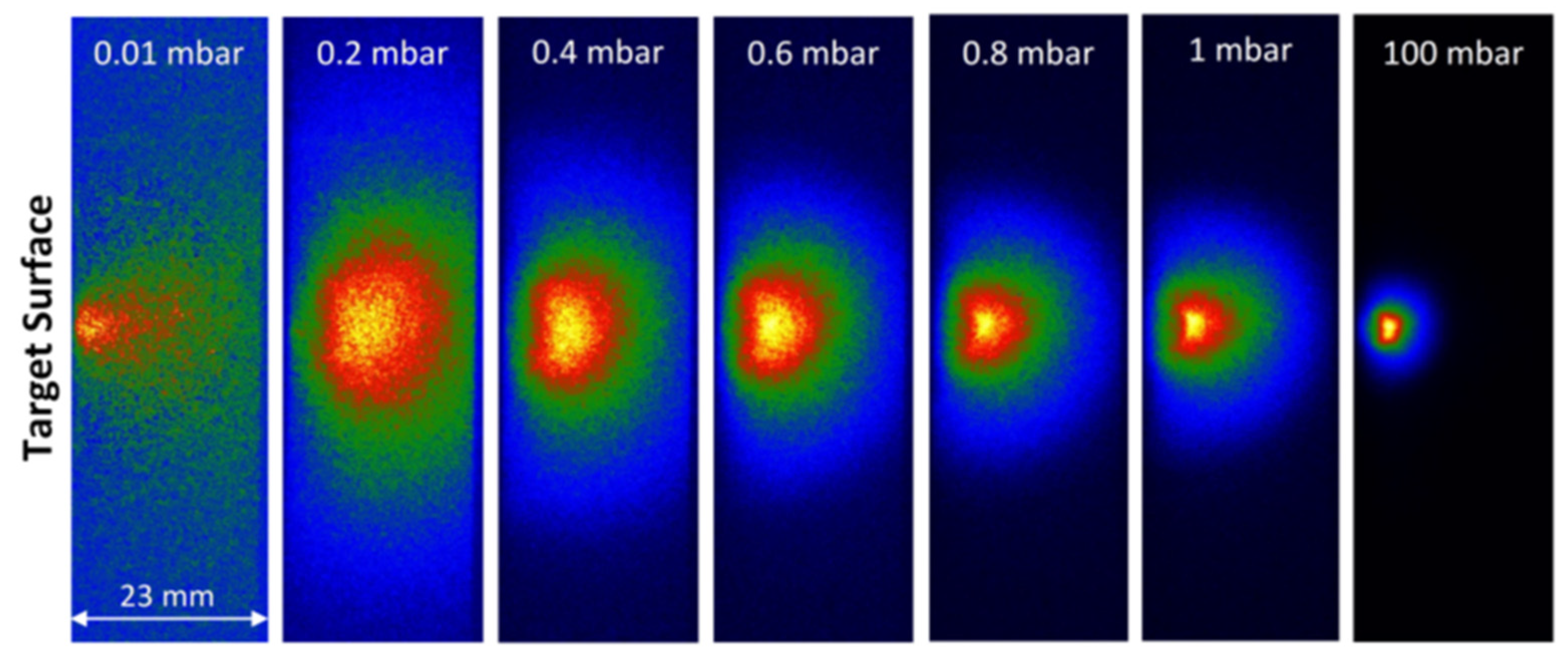
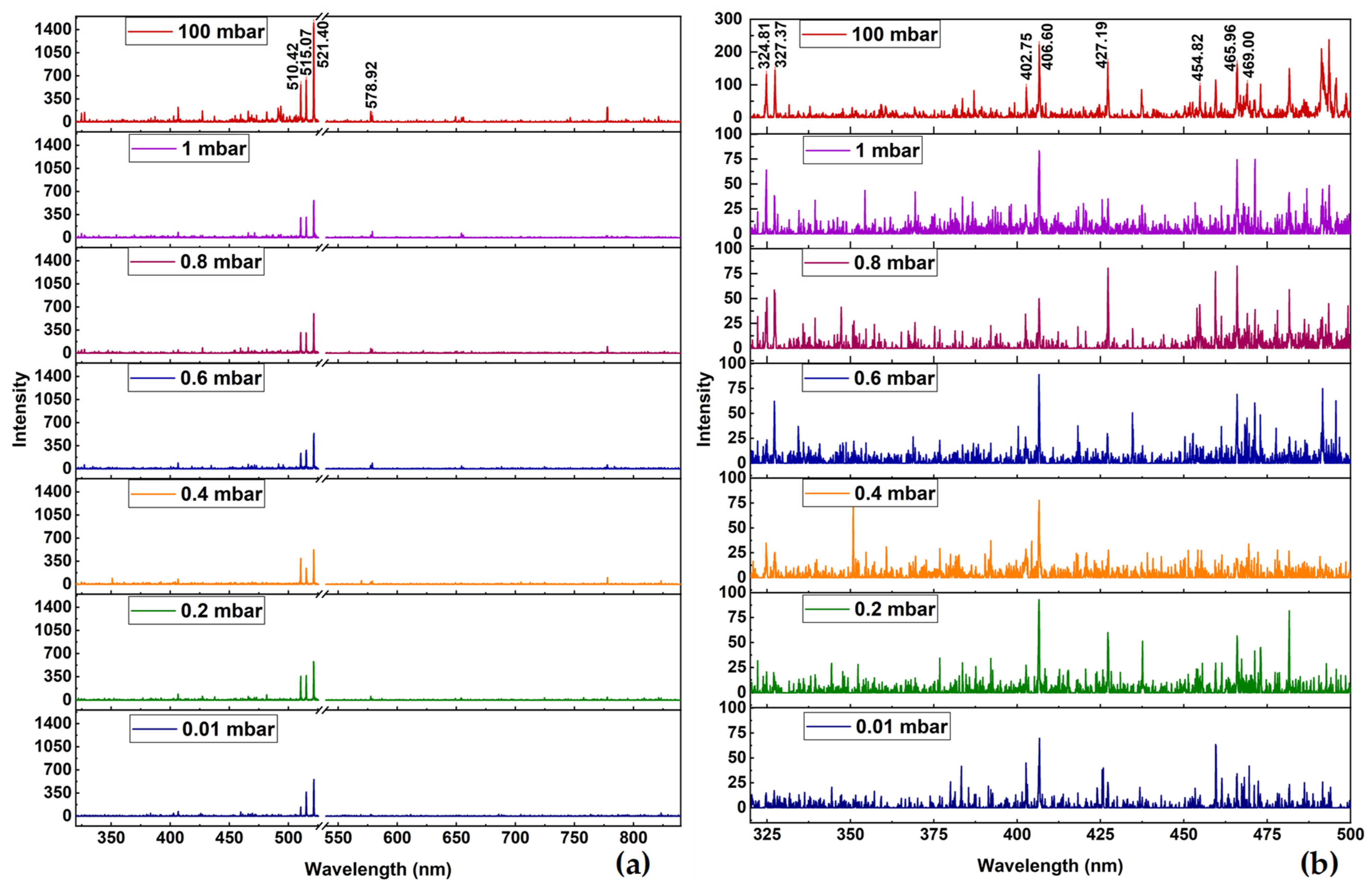
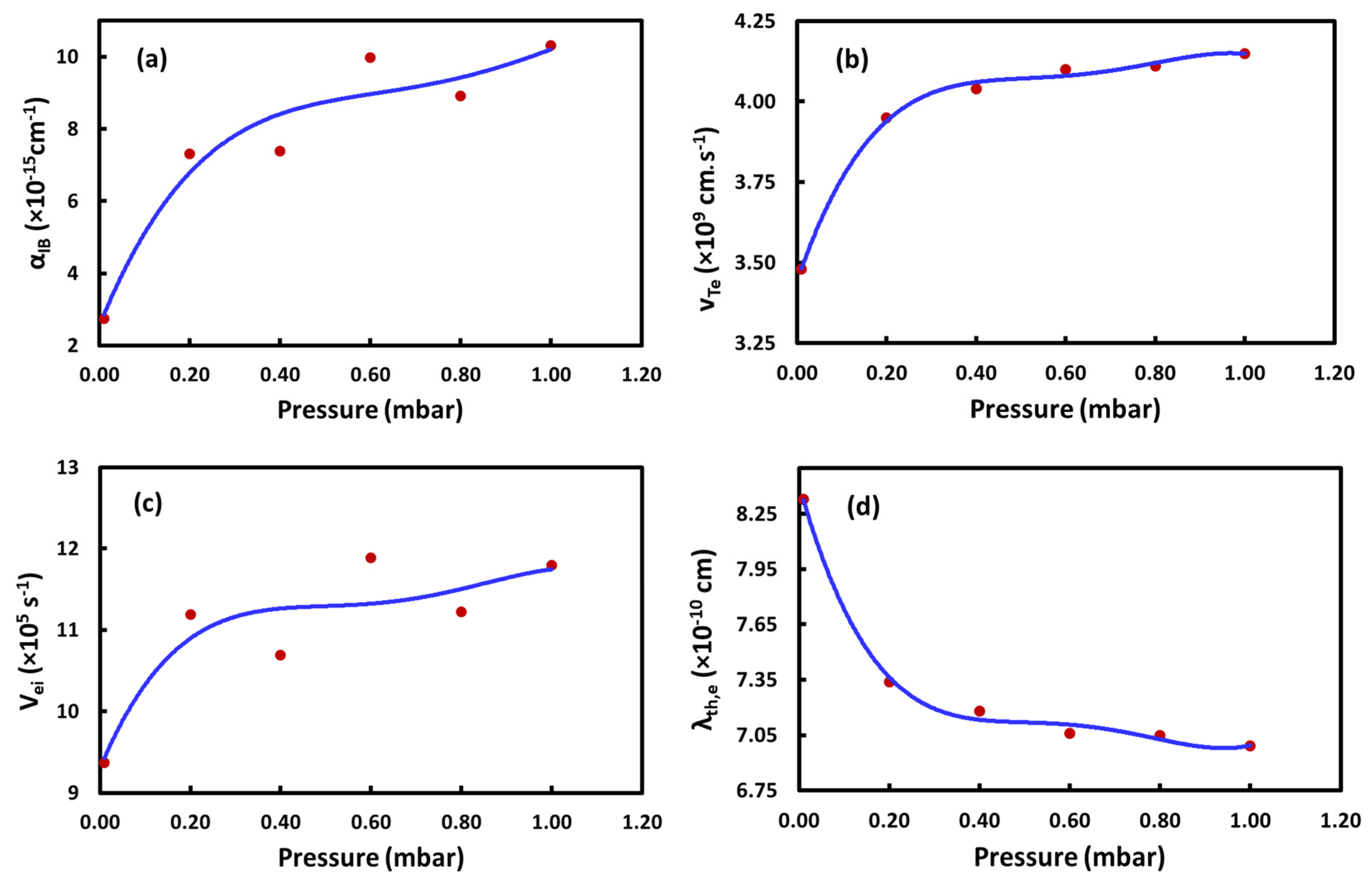
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cremers, D.A.; Radziemski, L.J. History and Fundamentals of LIBS. In Laser-Induced Breakdown Spectroscopy (LIBS); Miziolek, A.W., Palleschi, V., Schechter, I., Eds.; Cambridge University Press: Cambridge, UK, 2006; Volume 9780521852, pp. 1–39. ISBN 9780511541261. [Google Scholar]
- Noll, R. Laser-Induced Breakdown Spectroscopy; Springer Berlin Heidelberg: Berlin, Heidelberg, 2012; ISBN 978-3-642-20667-2. [Google Scholar]
- Kanyinda Jean-Noëla, M.; Tshamala Arthurb, K.; Jean-Marcc, B. LIBS Technology and Its Application: Overview of the Different Research Areas. J. Environ. Sci. Public Heal. 2020, 04, 134–149. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, Y.; Chen, Y.; Zhangcheng, Y.; Zhuo, Z.; Li, L. Online Detection of Halogen Atoms in Atmospheric VOCs by the LIBS-SPAMS Technique. Opt. Express 2020, 28, 22844. [Google Scholar] [CrossRef]
- Zhou, Z.; Ge, Y.; Liu, Y. Real-Time Monitoring of Carbon Concentration Using Laser-Induced Breakdown Spectroscopy and Machine Learning. Opt. Express 2021, 29, 39811. [Google Scholar] [CrossRef]
- Ye, Y.; Wan, E.; Sun, Z.; Zhang, X.; Zhang, Z.; Liu, Y. Online Detection and Source Tracing of Crop Straw Burning. J. Laser Appl. 2022, 34, 042049. [Google Scholar] [CrossRef]
- Kochuev, D.A.; Voznesenskaya, A.A.; Galkin, A.F.; Khorkov, K.S.; Chernikov, A.S.; Chkalov, R. V Influence of Laser-Induced Plasma Parameters on the Formation of Laser-Induced Surface-Periodic Structures. J. Phys. Conf. Ser. 2021, 2077, 012009. [Google Scholar] [CrossRef]
- Lachko, I.M.; Volkov, R.V.; Golishnikov, D.M.; Gordienko, V.M.; Dzhidzhoev, M.S.; Mar’in, B.V.; Mikheev, P.M.; Savel’ev, A.B.; Uryupina, D.S.; Shashkov, A.A. Control of Femtosecond Laser Plasma Parameters by Surface Contaminants Cleaning with Preceding Laser Pulse. In Proceedings of the Volume 5482, Laser Optics 2003: Superintense Light Fields and Ultrafast Processes, St. Petersburg, Russia, 30 June–4 July 2003; pp. 102–111. [Google Scholar]
- Ojeda-G-P, A.; Döbeli, M.; Lippert, T. Influence of Plume Properties on Thin Film Composition in Pulsed Laser Deposition. Adv. Mater. Interfaces 2018, 5, 1701062. [Google Scholar] [CrossRef]
- Escobar-Alarcón, L.; Arrieta, A.; Camps, E.; Romero, S.; Fernandez, M.; Haro-Poniatowski, E. Influence of the Plasma Parameters on the Properties of Aluminum Oxide Thin Films Deposited by Laser Ablation. Appl. Phys. A 2008, 93, 605–609. [Google Scholar] [CrossRef]
- Radziemski, L.J.; Cremers, D.A. Laser-Induced Plasmas and Applications; Marcel Dekker: New York, NY, USA, 1989; ISBN 9780511541261. [Google Scholar]
- Diwakar, P.K.; Hahn, D.W. Study of Early Laser-Induced Plasma Dynamics: Transient Electron Density Gradients via Thomson Scattering and Stark Broadening, and the Implications on Laser-Induced Breakdown Spectroscopy Measurements. Spectrochim. Acta Part B At. Spectrosc. 2008, 63, 1038–1046. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Gurlui, S.; Bulai, G.; Nica, P.; Agop, M.; Focsa, C. Langmuir Probe Investigation of Transient Plasmas Generated by Femtosecond Laser Ablation of Several Metals: Influence of the Target Physical Properties on the Plume Dynamics. Appl. Surf. Sci. 2017, 417, 108–118. [Google Scholar] [CrossRef]
- Krebs, H.-U.; Weisheit, M.; Faupel, J.; Süske, E.; Scharf, T.; Fuhse, C.; Störmer, M.; Sturm, K.; Seibt, M.; Kijewski, H.; et al. Pulsed Laser Deposition (PLD)—A Versatile Thin Film Technique. In Advances in Solid State Physics; Springer: Berlin, Germany, 2003; pp. 505–518. [Google Scholar]
- Richter, A. Characteristic Features of Laser-Produced Plasmas for Thin Film Deposition. Thin Solid Films 1990, 188, 275–292. [Google Scholar] [CrossRef]
- Kumar, N.; Dash, S.; Tyagi, A.K.; Raj, B. Dynamics of Plasma Expansion in the Pulsed Laser Material Interaction. Sadhana 2010, 35, 493–511. [Google Scholar] [CrossRef]
- Sarkar, A.; Shah, R.V.; Alamelu, D.; Aggarwal, S.K. Studies on the Ns-IR-Laser-Induced Plasma Parameters in the Vanadium Oxide. J. At. Mol. Opt. Phys. 2011, 2011, 1–7. [Google Scholar] [CrossRef]
- Harilal, S.S.; Bindhu, C.V.; Issac, R.C.; Nampoori, V.P.N.; Vallabhan, C.P.G. Electron Density and Temperature Measurements in a Laser Produced Carbon Plasma. J. Appl. Phys. 1997, 82, 2140–2146. [Google Scholar] [CrossRef]
- Harilal, S.S.; Phillips, M.C.; Froula, D.H.; Anoop, K.K.; Issac, R.C.; Beg, F.N. Optical Diagnostics of Laser-Produced Plasmas. arXiv 2022, arXiv:2201.08783. [Google Scholar]
- Hussain Shah, S.K.; Iqbal, J.; Ahmad, P.; Khandaker, M.U.; Haq, S.; Naeem, M. Laser Induced Breakdown Spectroscopy Methods and Applications: A Comprehensive Review. Radiat. Phys. Chem. 2020, 170, 108666. [Google Scholar] [CrossRef]
- Pasquini, C.; Cortez, J.; Silva, L.M.C.; Gonzaga, F.B. Laser Induced Breakdown Spectroscopy. J. Braz. Chem. Soc. 2007, 18, 463–512. [Google Scholar] [CrossRef]
- Hafez, M.A.; Khedr, M.A.; Elaksher, F.F.; Gamal, Y.E. Characteristics of Cu Plasma Produced by a Laser Interaction with a Solid Target. Plasma Sources Sci. Technol. 2003, 12, 185–198. [Google Scholar] [CrossRef]
- Griem, H.R. Principles of Plasma Spectroscopy; Cambridge University Press: Cambridge, UK, 1997; ISBN 9780521455046. [Google Scholar]
- McWhirter, R.W.P.; Richard, H. Plasma Diagnostic Techniques; Huddlestone, R.H., Leonard, S.L., Eds.; Academic Press: New York, NY, USA, 1965. [Google Scholar]
- Liu, H.C.; Mao, X.L.; Yoo, J.H.; Russo, R.E.U. Early Phase Laser Induced Plasma Diagnostics and Mass Removal during Single-Pulse Laser Ablation of Silicon. Spectrochim. Acta Part B At. Spectrosc. 1999, 54, 1607–1624. [Google Scholar] [CrossRef]
- Fikry, M.; Tawfik, W.; Omar, M.M. Investigation on the Effects of Laser Parameters on the Plasma Profile of Copper Using Picosecond Laser Induced Plasma Spectroscopy. Opt. Quantum Electron. 2020, 52, 249. [Google Scholar] [CrossRef]
- Gornushkin, I.B.; King, L.A.; Smith, B.W.; Omenetto, N.; Winefordner, J.D. Line Broadening Mechanisms in the Low Pressure Laser-Induced Plasma. Spectrochim. Acta Part B At. Spectrosc. 1999, 54, 1207–1217. [Google Scholar] [CrossRef]
- Colón, C.; Alonso-Medina, A.; Herrán-Martínez, C. Spectroscopic Study of a Laser-Produced Lead Plasma: Experimental Atomic Transition Probabilities for Pb III Lines. J. Phys. B At. Mol. Opt. Phys. 1999, 32, 3887–3897. [Google Scholar] [CrossRef]
- Shaikh, N.M.; Rashid, B.; Hafeez, S.; Jamil, Y.; Baig, M.A. Measurement of Electron Density and Temperature of a Laser-Induced Zinc Plasma. J. Phys. D. Appl. Phys. 2006, 39, 1384–1391. [Google Scholar] [CrossRef]
- Sarkar, A.; Singh, M. Laser-Induced Plasma Electron Number Density: Stark Broadening Method versus the Saha–Boltzmann Equation. Plasma Sci. Technol. 2017, 19, 025403. [Google Scholar] [CrossRef]
- Search, H.; Journals, C.; Contact, A.; Iopscience, M.; Address, I.P. Characteristics of Excimer Laser Induced Plasma from an Aluminum Target by Spectroscopic Study Characteristics of Excimer Laser Induced Plasma from an Aluminum Target by Spectroscopic Study. Jpn. J. Appl. Phys. 1999, 2958, 18–24. [Google Scholar]
- Gibbon, P. Introduction to Plasma Physics. In Proceedings of the 2014 CAS-CERN Accelerator School: Plasma Wake Acceleration, Geneva, Switzerland, 23–29 November 2014; pp. 51–65. [Google Scholar] [CrossRef]
- Chen, F.F. Introduction to Plasma Physics and Controlled Fusion; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-22308-7. [Google Scholar]
- Haq, S.U.; Ahmat, L.; Mumtaz, M.; Shakeel, H.; Mahmood, S.; Nadeem, A. Spectroscopic Studies of Magnesium Plasma Produced by Fundamental and Second Harmonics of Nd:YAG Laser. Phys. Plasmas 2015, 22, 083504. [Google Scholar] [CrossRef]
- Hahn, D.W.; Lunden, M.M. Detection and Analysis of Aerosol Particles by Laser-Induced Breakdown Spectroscopy. Aerosol Sci. Technol. 2000, 33, 30–48. [Google Scholar] [CrossRef]
- Jaspers, R.J.E. Plasma Spectroscopy. Fusion Sci. Technol. 2012, 61, 384–393. [Google Scholar] [CrossRef]
- Unnikrishnan, V.K.; Alti, K.; Kartha, V.B.; Santhosh, C.; Gupta, G.P.; Suri, B.M. Measurements of Plasma Temperature and Electron Density in Laser-Induced Copper Plasma by Time-Resolved Spectroscopy of Neutral Atom and Ion Emissions. Pramana 2010, 74, 983–993. [Google Scholar] [CrossRef]
- NIST Atomic Spectra Database. Available online: http://physics.nist.gov (accessed on 1 January 2021).
- National Academies of Sciences, Engineering, and Medicine. Plasma Science:Enabling Technology, Sustainability, Security, and Exploration; The National Academies Press: Washington, DC, USA, 2021; ISBN 9780309677639. [Google Scholar]
- Konjević, N.; Wiese, W.L. Experimental Stark Widths and Shifts for Spectral Lines of Neutral and Ionized Atoms. J. Phys. Chem. Ref. Data 1990, 19, 1307–1385. [Google Scholar] [CrossRef]
- Konjević, N.; Lesage, A.; Fuhr, J.R.; Wiese, W.L. Experimental Stark Widths and Shifts for Spectral Lines of Neutral and Ionized Atoms (A Critical Review of Selected Data for the Period 1989 Through 2000). J. Phys. Chem. Ref. Data 2002, 31, 819–927. [Google Scholar] [CrossRef]
- Farid, N.; Bashir, S.; Mahmood, K. Effect of Ambient Gas Conditions on Laser-Induced Copper Plasma and Surface Morphology. Phys. Scr. 2012, 85, 015702. [Google Scholar] [CrossRef]
- Wiesemann, K. A Short Introduction to Plasma Physics. arXiv 2014, arXiv:1404.0509. [Google Scholar]
- Stenson, E.V.; Horn-Stanja, J.; Stoneking, M.R.; Pedersen, T.S. Debye Length and Plasma Skin Depth: Two Length Scales of Interest in the Creation and Diagnosis of Laboratory Pair Plasmas. J. Plasma Phys. 2017, 83, 595830106. [Google Scholar] [CrossRef]
- Umstadter, D. Review of Physics and Applications of Relativistic Plasmas Driven by Ultra-Intense Lasers. Phys. Plasmas 2001, 8, 1774. [Google Scholar] [CrossRef]



| Atom/Ion | Observed λ (nm) | Aij (s−1) | Ei (eV) | gi | Transitions |
|---|---|---|---|---|---|
| Lower Level ➔ Upper Level | |||||
| Cu I | 324.81 | 1.395 × 108 | 3.816692 | 4 | 3d104p ➔ 3d104s |
| Cu I | 327.21 | 1.376 × 108 | 3.785898 | 2 | 3d104p ➔ 3d104s |
| Cu I | 402.51 | 1.90 × 107 | 6.867196 | 4 | 3d105d ➔ 3d104p |
| Cu I | 406.6 | 2.10 × 107 | 6.867646 | 6 | 3d105d ➔ 3d104p |
| Cu I | 427.27 | 3.45 × 107 | 7.737027 | 8 | 3d94s(3D)5s ➔ 3d9(2D)4s4p(3P°) |
| Cu I | 453.38 | 2.12 × 107 | 7.883492 | 4 | 3d94s(3D)5s ➔3d9(2D)4s4p(3P°) |
| Cu I | 465.96 | 3.80 × 107 | 7.737027 | 8 | 3d94s(3D)5s ➔ 3d9(2D)4s4p(3P°) |
| Cu I | 471.33 | 5.5 × 106 | 7.737027 | 8 | 3d94s(3D)5s ➔ 3d9(2D)4s4p(3P°) |
| Cu I | 510.42 | 2.0 × 106 | 3.816692 | 4 | 3d104p ➔ 3d94s2 |
| Cu I | 515.07 | 6.0 × 107 | 6.191175 | 4 | 3d104p ➔ 3d104d |
| Cu I | 521.48 | 7.5 × 107 | 6.192025 | 6 | 3d104p ➔ 3d104d |
| Cu I | 522.36 | 1.50 × 107 | 6.191175 | 4 | 3d104p ➔ 3d104d |
| Cu I | 578.92 | 1.65 × 106 | 3.785898 | 2 | 3d104p ➔ 3d94s2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ajith, A.; Swapna, M.N.S.; Cabrera, H.; Sankararaman, S.I. Comprehensive Analysis of Copper Plasma: A Laser-Induced Breakdown Spectroscopic Approach. Photonics 2023, 10, 199. https://doi.org/10.3390/photonics10020199
Ajith A, Swapna MNS, Cabrera H, Sankararaman SI. Comprehensive Analysis of Copper Plasma: A Laser-Induced Breakdown Spectroscopic Approach. Photonics. 2023; 10(2):199. https://doi.org/10.3390/photonics10020199
Chicago/Turabian StyleAjith, Asokan, Mohanachandran Nair Sindhu Swapna, Humberto Cabrera, and Sankaranarayana Iyer Sankararaman. 2023. "Comprehensive Analysis of Copper Plasma: A Laser-Induced Breakdown Spectroscopic Approach" Photonics 10, no. 2: 199. https://doi.org/10.3390/photonics10020199
APA StyleAjith, A., Swapna, M. N. S., Cabrera, H., & Sankararaman, S. I. (2023). Comprehensive Analysis of Copper Plasma: A Laser-Induced Breakdown Spectroscopic Approach. Photonics, 10(2), 199. https://doi.org/10.3390/photonics10020199







