Abstract
We analyze schemes of high-fidelity multi-qubit CNOT and CNOT gates for alkali metal neutral atoms used as qubits. These schemes are based on the electromagnetically induced transparency and Rydberg blockade. The fidelity of homonuclear multi-qubit CNOT gate based on Rydberg blockade was limited by the undesirable interaction between the target atoms and by the coupling laser intensity. We propose overcoming these limits by using strong heteronuclear dipole–dipole interactions via Förster resonances for control and target atoms, while the target atoms are coupled by a weaker van der Waals interaction. We optimized the gate performance in order to achieve higher fidelity, while keeping the coupling laser intensity as small as possible in order to improve the experimental feasibility of the gate schemes. We also considered the optimization of the schemes of the CNOT gates, where the fidelity is affected by the relation between the control–control, control–target and target–target interaction energies. Our numeric simulations confirm that the fidelity of the CNOT gate (single control and four target atoms) can be up to 99.3% and the fidelity of the CNOT (two control and two target atoms) is up to 99.7% for the conditions which are experimentally feasible.
1. Introduction
Notable progress in quantum computing in recent years has resulted in first demonstrations of quantum supremacy with superconducting qubits and photons [,,]. Ultracold ions and atoms remain promising platforms for a scalable quantum computer []. The advantage of ultracold atoms is the potential to create quantum registers of thousands of identical qubits on a micrometer scale []. A substantial improvement of two-qubit gate fidelity in quantum registers based on single trapped atoms has been recently demonstrated [,,,]. Quantum simulations of complex problems of many-body physics and correlated quantum phases of matter can be performed using two-dimensional arrays of hundreds of Rydberg atoms in optical tweezers [,]. However, the fidelity of two-qubit gates for neutral atoms still remains limited. These gates use temporary excitation of atoms into Rydberg states []. The dipole moments of Rydberg atoms scale as [], where n is the principal quantum number. Ground-state atoms do not interact at distances of few microns, but Rydberg atoms do. Therefore the dipole-dipole interaction of Rydberg atoms can be used for implementation of two-qubit gates and creation of entanglement []. The experimentally demonstrated schemes of two-qubit gates are based on the effect of Rydberg blockade: when two atoms are located at short interatomic distance, they cannot be excited simultaneously to Rydberg states by narrow-band laser radiation [,,,,].
Multi-qubit gates with many target qubits can provide a remarkable speed-up of quantum algorithms. Realization of geometric and swap gates with atomic qubits using antiblockade was discussed in Refs. [,,]. Schemes for multi-control and multi-target gates based on microwave dressing were proposed in Refs. [,,]. A single-step implementation of the three-qubit controlled gates with Rydberg atoms was reported []. Also, the realization of a two-qubit controlled-PHASE (C) gate via single-modulated-pulse off-resonant modulated driving embedded in a two-photon transition for Rb atoms with high-fidelity entanglement to be 0.980(7) was recently reported [].
Quantum error correction schemes are of essential importance for quantum information processing with neutral atoms. A scheme for fault-tolerant quantum computing based on surface codes was proposed by Auger et al. []. This scheme requires parallel implementation of multiqubit CNOT (where N is a number of target atoms) gates with a single control atom and N target atoms, which are used as ancillary qubits, as shown in Figure 1a. Recently, a surface code with an atomic quantum processor was experimentally demonstrated []. The non-local connectivity between qubits was achieved by coherent transport of qubits in two dimensions and between multiple zones.
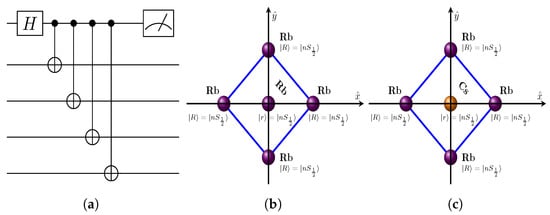
Figure 1.
(a) Scheme of generation of multi-atom entangled GHZ-state using a sequence of CNOT gates applied to different target atoms. Firstly, we apply Hadamard gate H on the control atom and do measurement after performing the CNOT gates. (b,c) Scheme of spatial configurations of Rb and Cs atoms for implementation of the CNOT gate in the case of (b) symmetric homonuclear interaction of Rb atoms and (c) asymmetric heteronuclear interaction between Cs control atom and four Rb target atoms.
Multi-qubit gates can be built using Rydberg blockade and electromagnetically-induced transparency (EIT) []. EIT is a quantum interference phenomenon that can be observed by two optical fields (probe and control lasers) tuned to interact with quantum states of atoms []. The transmission of a weak probe field is enhanced in the presence of a strong (near-)resonant coupling field []. Several groups studied EIT with Rydberg states theoretically [,] and experimentally [,,]. From the original proposal [] it is clear that implementation of high-fidelity multi-qubit quantum gates based on EIT requires large coupling Rabi frequencies (of order of GHz) for transition between low excited and Rydberg states [], which is difficult to achieve in the experiment. For lower values of the coupling Rabi frequency, the fidelity of parallel CNOT gates becomes substantially limited by the interaction between the target atoms. It is possible to suppress the interaction between the target atoms while keeping strong interaction between control and target atoms by using the dipole-dipole interactions via Förster resonances and asymmetric excitation of control and target atoms to different Rydberg states. Moreover, creation of heteronuclear atomic arrays [] provides both extended control over the interatomic interaction and reduced error rates during readout of qubit states. The heteronuclear atomic species were first entangled in the experiment by Zeng et al. []. A two-dimensional array of two isotopes of Rb atoms was recently demonstrated []. An experimental implementation of a dual-element atomic array with individual control of single Rb and Cs atoms with negligible crosstalk between the two atomic species was recently reported []. There are also related experimental studies of ultracold dense trapped samples of over 1000 of Rb Cs molecules in rovibrational ground state with full nuclear hyperfine state control by protocols of stimulated Raman adiabatic passage (STIRAP) with efficiencies of 90% [,]. Rydberg blockade between a single Rb atom and a single RbCs molecule was recently demonstrated []. A mixture of heteronuclear Li and Cs atomic clouds was studied in Ref. [].
In the present work we optimize the performance of a parallel CNOT gate based on Rydberg blockade and EIT in order to reduce the required coupling Rabi frequency for transitions between low excited and Rydberg states and improve the overall gate fidelity. With decrease of the coupling Rabi frequency the target-target interaction deteriorates the gate performance []. When both control and target atoms are excited to identical Rydberg states [symmetric homonuclear interaction, as shown in Figure 1b], it is not possible to tune the control-target and target-target interactions independently. However, if the control and target atoms are excited to different Rydberg states [asymmetric homonuclear or heteronuclear interaction, which is illustrated in Figure 1c], it is possible to meet the conditions of Förster resonance [,] for control-target interaction and to keep target-target interaction in the van der Waals regime. That allows substantial suppression of the target-target interaction and obtaining higher fidelity of parallel CNOT gate at moderate coupling Rabi frequencies of 100–200 MHz, which can be readily achieved in modern experiments for tightly focused laser beams.
While working on this manuscript we became aware of a foremost experimental work [] demonstrating the considered EIT gate protocol for two-qubits, verifying the ability to perform a native CNOT gate. The authors managed to achieve a loss corrected gate fidelity of , and prepared an entangled Bell state with by trapping individually a pair of Cs atoms separated by .
The paper is organized as follows: in Section 2 we describe the scheme of multi-qubit CNOT gate and the physical model used for our numeric simulation of the gate performance. In Section 3, we discuss the properties of the asymmetric homonuclear and heteronuclear Förster interactions. In Section 4, we investigate the influence of the parameters of atomic states and laser fields, Förster interaction channels, and gate duration on the gate fidelity in homonuclear symmetric and heteronuclear asymmetric configurations. In Section 5, we extend our approach to implement a CNOT gate with two control and two target atoms and calculate its fidelity for heteronuclear configuration. Analysis of gate errors due to spontaneous emissions is given in Section 6. In Appendix A, the model of the atomic system is described taking into account multiple Rydberg interaction channels. Results of calculations are compared with the single-channel model. In Appendix B, a model of multi-intermediate hyperfine states of the target atom is formulated.
2. Scheme of Rydberg EIT CNOT Gate
The scheme of multiqubit CNOT gate, proposed in Ref. [], is shown in Figure 2a. The gate operation can be understood as following: (i) If the control atom is initially in the ground state , the first -pulse does not change its quantum state. The Raman transfer between states and is inhibited due to the interaction with intensive resonant coupling radiation with Rabi frequency , as shown in Figure 2b. The fidelity of blocking the population transfer is determined by the value of coupling Rabi frequency . (ii) If the control atom is initially prepared in the ground state , then it will be excited to the Rydberg state by the first laser pulse . The interaction between control and target atoms will shift the energy levels of the target atoms by a value of where denotes kth target atom, and will make the coupling radiation off-resonant for the transition between intermediate excited and Rydberg state of the target atoms, as shown in Figure 2c. Thus, the conditions for EIT are not met anymore, and the Raman population transfer between the states and becomes possible. In the ideal limit of a blockade regime, the Rydberg states of the target atoms are never populated.
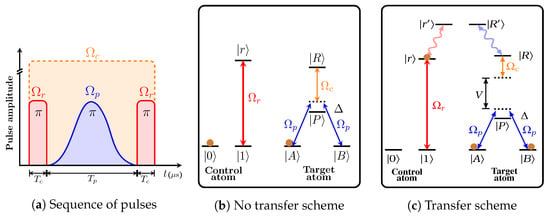
Figure 2.
(a) Sequence of laser pulses for Rydberg EIT gate. couples intermediate excited state and Rydberg state of the target atom. Two-photon smooth Raman pulse couples logical states of the target atoms and of the target atom. Laser pulses excite and de-excite Rydberg states of control atom; (b) Scheme of CNOT gate operation in the regime of blocked population transfer (the control atom in ground state ). No population transfer between states and is allowed; (c) Scheme of CNOT gate operation in the transfer regime. The ground state of control atom is coupled to the Rydberg state by a -pulse . The ground states of the target atom and are coupled to the intermediate state by a smooth Raman -pulse , and the intermediate state is coupled to the Rydberg state by resonant laser radiation with Rabi frequency . The dipole-dipole interaction between control and target atoms results from coupling of Rydberg states and to and , respectively.
It is shown in Ref. [] that the following conditions for CNOT gate are satisfied:
We considered several spatial configurations for target atoms, which are illustrated in Figure 3. The control atom is at the origin. The target atoms are equally displaced from the control atom. For (), the target atoms are placed on the vertices’ of an isosceles triangle (square) where the distance between the nearest target atoms is .
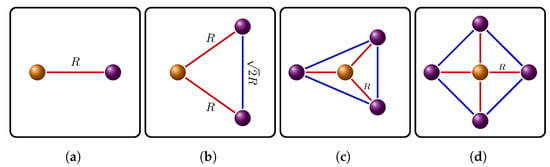
Figure 3.
Spatial configurations of control and target atoms. The control atom is at the origin. Here is the quantization axis and R is the interatomic distance between the control and the target atoms for linear configurations (a) with single target atom, (b) with two target atoms; (c) Triangular configuration with three target atoms equally displaced from the control atom. The coordinates of the target atoms are , , and ; (d) Rectangular configuration with four target atoms. The coordinates of the target atoms are , , , and .
The interaction of the control atom with radiation in the rotating wave approximation (RWA) is described by the Hamiltonian in basis of , and as
where ℏ is Planck’s constant, and is a sharp pulse which couples the Rydberg state with and is applied for . Explicitly is defined as following
The interaction of the target atom with radiation for an inverted Y configuration of the atomic energy levels is described by the Hamiltonian in basis of , , , and as
where is a smooth Raman -pulse that couples the ground states of the Rb target atom and to the intermediate state (For Cs atoms, the long-lived ground states, and intermediate state of the target atoms are , and , respectively.) with . Here is the detuning from the resonance with the intermediate state , as shown in Figure 2. Explicitly is defined as following
The value is a constant Rabi frequency which couples the intermediate state with Rydberg state [see Figure 2b].
The model Hamiltonian of the combined system with single control atom and N target atoms can be written as
where with dimensions and with dimensions are the identity matrices acting on the control atom, and on the ensemble of target atoms, respectively. is the Hamiltonian describing the ensemble of target atoms. can be written in the following form
where
The third and fourth terms of Equation (7) are the terms describing the interaction between control and target atoms, and the interaction between the target atoms, respectively. In Section 3, we show how to calculate the interaction energies in homonuclear and heteronuclear architectures.
In our simulations, we choose the maximum value of the Raman pulse and the detuning . The Raman pulse is applied for a duration . Also, we adopted an approach of a non-Hermitian Hamiltonian to consider the finite lifetime of Rydberg state of control atom by adding the term to Equation (3) and the finite lifetime of the intermediate states of target atoms by adding the term to Equation (5) where and are the decay rates of Rydberg and intermediate excited states, respectively.
Following the original work [], in Figure 4 we illustrate the dependence of the probability of blocking the population transfer as a function of the ratio between and . In this case, the control atom is not excited to Rydberg state. Therefore, there is no interaction between control and target atoms. As clearly seen in Figure 4a, for in the EIT regime [] the transfer between ground states of the target atom is blocked. The time dependence of the population transfer is shown in Figure 4b–d. At low value of the population transfer becomes allowed [Figure 4b]. In the intermediate case of relatively small , the state is temporarily depopulated, but finally the system returns to the initial state [see Figure 4c]. At very high values the system mostly remains in the state [see Figure 4d]. Although the regime of strong coupling is advantageous for maximum gate probability transfer, it requires high coupling Rabi frequencies of order of hundreds of MHz or GHz which are difficult to achieve experimentally for highly excited Rydberg states due to the drop of transition matrix elements for ground-Rydberg laser excitation as . Therefore, the intermediate values of are of interest for experimental implementation. Similar behavior of probability transfer is observed for larger number of target atoms.
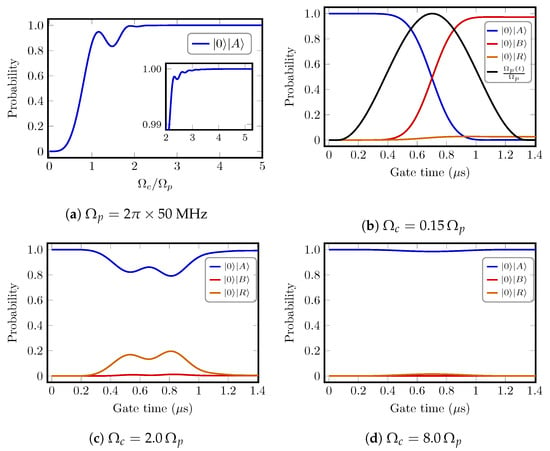
Figure 4.
(a) The dependence of the probability of blocking the population transfer on the ratio between and . The inset shows the behavior of the population of initial state in the region when it is close to 1. (b–d) Time dependence of the population of the collective states (solid-blue curve) and (solid-red curve) for the case of blocked population transfer during CNOT gate for (b) ; (c) and (d) . The solid-orange curve illustrates the population transfer to the Rydberg state of the target atom in the case of blocked population transfer between logical states.
Müller et al. [] analyzed the effect of target-target interactions in the three-qubit GHZ state for three target atoms while considering the control-target interaction to be constant and varying the target-target interaction. This two-dimensional configuration is not relevant to the typical experimental conditions, since changing the values of the target-target interaction requires varying the interatomic distance between target atoms, which also results in change of the distance between the control and target atoms in all possible spatial configurations of atomic ensembles. In our following simulations, we varied the interatomic distances for several spatial configurations, which are illustrated in Figure 3. In Appendix A, we developed an analogous model for the one described in this section, where the coupling between many Rydberg states in considered.
3. Homonuclear and Heteronuclear Interaction Energy
Our approach is based on the additional control of the energy of interatomic dipole-dipole interactions using Förster resonances between two distinguishable atoms, which were studied in Ref. []. A Förster resonance [] means that the energies of two collective states of two Rydberg atoms coupled by dipole-dipole interaction are equal. This enhances the probability of the population transfer between the collective two-body states which is equivalent to energy transfer between interacting atoms [,,]. Förster resonance is employed to compromise the choice of selected Rydberg states. The interaction between atoms lies in two different regimes: dipole-dipole regime (d-d) where interaction energy can be described as or van der Waals regime (vdW) where []. Recently, software packages [,] facilitated the calculations of interaction energies between alkali and alkaline earth atoms. We used Alkali Rydberg Calculator (ARC) [] to calculate the interaction energy of two alkali atoms in Rydberg states (here n is the principal quantum number, ℓ is orbital angular momentum number, j is the total angular momentum number, and is the projection of the total angular momentum on the quantization z-axis) for homonuclear and heteronuclear configurations. We also calculated the Le Roy radius [] which is the internuclear distance between two interacting atoms at which the theory of Le Roy-Bernstein is satisfied, and the interaction potential can be approximated by charge independent atomic distributions. This radius sets the minimum limit of the interatomic distance where our calculations of the interaction energies are valid. As shown in Figure 3, we considered the quantization z-axis perpendicular to the interatomic axis, which is the general case for all spatial configurations which are studied in this work. As shown in Section 2, we investigated the performance of CNOT gate based on EIT with a single control atom for different number of target atoms for homonuclear and heteronuclear configurations. The target atoms are identical in all cases.
3.1. Heteronuclear Architecture
We consider a Cs atom excited from the ground state to Rydberg state as control qubit (as described in Section 2), and spatially ordered Rb atoms as target qubits. The intermediate state of target atoms is coupled to Rydberg state . Due to the interaction between these two atoms the Rydberg states in both atoms will be coupled to other neighboring Rydberg state(s) [see Figure 2c]. The most dominant interaction channel, as shown in Appendix A, is
The asymmetric interaction between these two atoms lies in the regime of dipole-dipole interaction. The interaction Hamiltonian between control and target atoms can be written as []
where is a dipole-dipole interaction coefficient for the target atom j separated from the control atom by distance , is the angle between the quantization axis and the interatomic axis. The energy defect is the energy difference between the collective two-atom Rydberg states for the dominant interaction channel. The collective state is defined as
where is the excited Rydberg state of the target atom, and is the set of all basis states of any target atom with dimensions .
In this architecture, all target atoms are identical, and they interact in the vdW regime. The Hamiltonian describing their interaction can be written as
where is van der Waals coefficient calculated by fitting the model function with the calculated energy level using ARC function getC6fromLevelDiagram for rStart = , rStop = 20 , and minStateContribution = 0. The interatomic distance between different target atoms . The set of all basis states of the control atom with . The collective state where
3.2. Homonuclear Architecture
The case when all interacting atoms are the same atomic species (Rb), all interactions are in the vdW regime, since all atoms all excited to the same Rydberg state and the interaction is in the vdW regime. The control-target Hamiltonian in this case will be in the following form
and the target-target interaction Hamiltonian will be the same as given in Equation (13) for Rb atoms. For Cs homonuclear interaction with all atoms are excited to the same Rydberg state , the van der Waals coefficient .
In Figure 5a, we show the dependence of the dipole-dipole interaction coefficient for Cs and Rb atoms excited to Rydberg states, on the angle between quantization z-axis and the interatomic axis for two different cases of the projection of the total angular momentum on the quantization z-axis. We have which does not meet the maximum value of interaction energies but for using negative projection of the Rydberg state of Cs atom strengths the interaction. The interaction between the two atoms vanish at the magic angle , and .
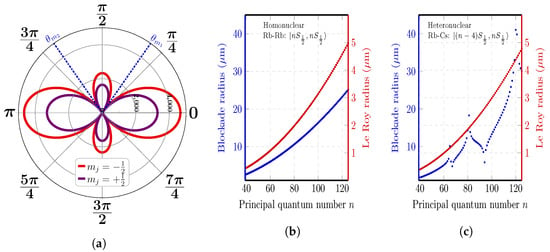
Figure 5.
(a) The dipole-dipole interaction coefficient (.) as a function of the angle between the interatomic axis and the quantization axis for the heteronuclear interaction between Rb and Cs . Red curve (Violet curve) represent the projection of the total angular momentum on z-axis () for the most dominant interaction channel. (b,c) The evolution of blockade radius (blue curve) and Le Roy radius (red curve) as a function of the principal quantum number n for homonuclear interaction of two Rb atoms and heteronuclear interaction between Rb and Cs atoms, respectively. Local minima of blockade radius of the heteronuclear interaction of pair states can be attributed to principal quantum numbers where the dipole-dipole couplings to different pair states compensate each other.
In Figure 5b,c, we show the evolution of blockade radius (dotted-blue curve) and Le Roy radius (dotted-red curve) as a function of the principal quantum number n of the excited Rydberg state for homonuclear interaction between two Rb atoms excited symmetrically to Rydberg states and the heteronuclear interaction between Rb and Cs atom excited asymmetrically to Rydberg states , and , respectively. It is noted that for homonuclear interactions with symmetric Rydberg states, the evolution of blockade radius is steady while being fluctuant for the asymmetric heteronuclear (or homonuclear) interactions. For Rb atom excited to Rydberg state interacting with Cs atom excited to Rydberg state , the value of blockade radius reaches local maxima. Local maxima points are repeated also at , and 122 (the principal quantum number corresponding to the Rydberg state of Cs atom). Local minima points (, and 94) can be imputed to principal quantum numbers where the dipole-dipole couplings of these pair states counteract each other. The evolution of Le Roy radius is steady in both cases.
4. Fidelity of Multiqubit Entangled States
Fidelity is a measure of the closeness of two arbitrary quantum states. We employed the standard definition [] of fidelity between arbitrary states and of a quantum system as
where we considered as the calculated density matrix after performing a partial trace over the subspace of computational states of control and target atoms, and is the density matrix of the multi-qubit entangled state . We numerically calculated the density operator of the system when it was initially prepared in the superposition of the computational ground states of control atom, which results in simultaneous blocking and transferring operations where . The case when corresponds to a two-qubit Bell state, while for we end in a GHZ-state, which is a useful resource in quantum computing and cryptography []. For , we have four computational states and . Generally, the total number of basic computational states in Rydberg blockade of CNOT gate is equal to from the total states, where is the number of states in control (target) atom.
In our simulations, we consider different configurations of the control and target atoms to be either Rb (Rb) or Cs (Cs). We have taken decay rates and of the Rydberg state of the control atom and the intermediate state of the target atoms , respectively, from the data of ARC []. The lifetime of Rb state (first excited state of Rb) is while for Rb state the lifetime is s. The lifetime of Cs (first excited state of Cs) of the target atom is , while for Cs state we have . Since lifetimes of higher excited states of target atoms are much longer, in the following calculations we consider Rb and Cs states as the intermediate state of the target atom. The Rydberg excitation schemes through these intermediate states were experimentally demonstrated in Refs. [,]. In Section 6, we justify this choice of the intermediate state .
4.1. Homonuclear Architecture
In this section, we study the gate performance for the case when control and target atoms are same atomic species, which can be either Rb or Cs. There are two different scenarios of homonuclear interaction: (i) symmetric interaction , when both control and target atoms are excited to the same Rydberg state, and (ii) asymmetric interaction , when the control atom is excited to one Rydberg state with principal quantum number n, and the target atoms are excited to a different Rydberg state with principal quantum number . Note that in the latter case, the interaction between the target atoms is also symmetric (the quantum states of target atoms are identical)—Symmetric interaction channel . Figure 6 is a contour plot of fidelity of entangled states as a function of interatomic distance between control and target atoms () and the ratio where we considered Rb Rydberg states of control and target atoms with lifetime . In the case of only one target atom it is possible to achieve high fidelity for a wide range of interatomic distances and moderate values of , since the target-target interaction does not exist in this case. Considering schemes with more target atoms , the fidelity for drops at small interatomic distances because of the increase of the influence of strong target-target interactions. The optimum interatomic distance is found to be around . For target atoms, the fidelity for very high values of Rabi frequency at as in Figure 6d.
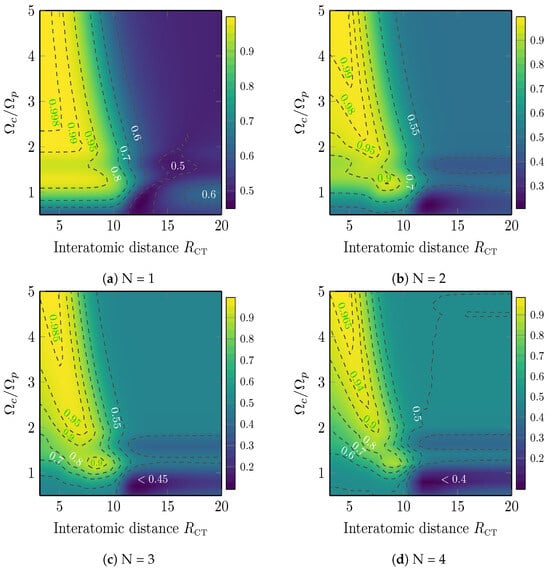
Figure 6.
Contour plot of the fidelity of entangled states as a function of interatomic distance () and coupling Rabi frequency , for homonuclear symmetric interaction of Rb atoms for different spatial configurations of target atoms see [Figure 3].
In principle, it is also possible to consider asymmetric homonuclear interactions () to achieve high fidelities by reducing target-target interaction compared to control-target interaction. This case will be considered in a future work.
4.2. Heteronuclear Architecture
The contour plot of the fidelity of entangled states in heteronuclear configuration is shown in Figure 7 as a function of interatomic distance R () and the ratio . This case corresponds to asymmetric heteronuclear interaction between control and target atoms, while the target atoms interact in the vdW regime. The control Cs atom is excited to Rydberg state with lifetime and Rb target atoms are excited to Rydberg state . Heteronuclear configuration is clearly advantageous in terms of fidelity comparing to the symmetric homonuclear configuration, shown in Figure 6. The regime of a CNOT gate with one target atom for the selected range of interatomic distances , as shown in Figure 7a, is governed purely by dipole-dipole interaction and allows to achieve fidelity for . With increase of the number of target atoms , the maximum obtained fidelity slightly drops, similarly to the homonuclear case. The fidelity within the region and . This justifies the advantage of heteronuclear configuration for implementation of multiqubit CNOT gates. Moreover, the two-species architecture is useful for improvement of readout without cross-talk when the state of a Rb data qubit is not affected by measurements performed by resonant light scattering by ancillary Cs atoms [], which was recently demonstrated experimentally for arbitrary two-dimensional arrays of Rb and Cs atoms [].
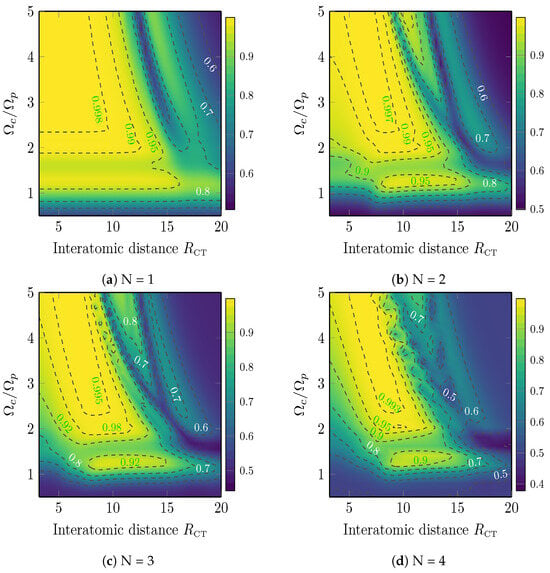
Figure 7.
Contour plot of fidelity as a function of interatomic distance () and coupling Rabi frequency , for the case of heteronuclear asymmetric interaction of Cs control atom in state and Rb target atoms in state for different spatial configurations of target atoms [see Figure 3].
5. Scheme of Rydberg EIT CNOT
The proposals for implementation of CNOT/CZ gates with many control and many target atoms have been limited to gates with either many control atoms and single target atoms, or to single control atom and many target atoms. The most general case for arbitrary number of control and many target atoms has not been studied extensively. Recently, such schemes were proposed in several theoretical approaches [,,]. Young et al. [] designed a protocol which uses microwave dressing to implement multi-qubit gates with many control and many target atoms. This protocol reduces intraspecies interaction energies and maximizes the interspecies interaction energies, leading to asymmetric blockade, which simplifies the state preparation and enhances the speed of quantum algorithms and reduces the need for fault-tolerant error correction schemes. In this section, we modify the previously studied CNOT scheme based on EIT in order to implement a four-qubit gate with two control and two target atoms (CNOT gate) [see Figure 8a] simultaneously by proposing an asymmetric sequence of laser pulses acting on control atoms. We consider the following sequence [see the scheme in Figure 8b]:
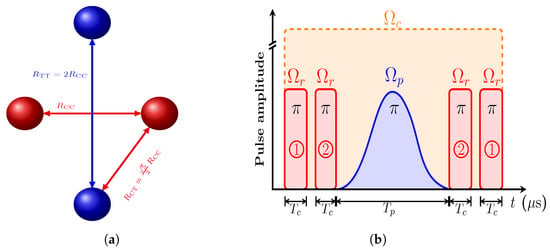
Figure 8.
(a) Scheme of spatial configurations of homonuclear/heteronuclear interactions for the implementation of CNOT gate. The atoms are located on the vertices of a rhombus with perpendicular diagonals and . () is the interatomic distance between control (target) atoms. (b) The sequence of laser pulses to perform CNOT gate.
- We apply -pulses to excite the control atoms from ground state to highly excited Rydberg state in sequence.
- Then we apply smooth Raman laser pulse to couple the ground states of the target atoms and , simultaneously, to the intermediate dark state .
- Finally, we apply pulses to return the control atoms from highly excited Rydberg state to ground state in reversed sequence applied in step 1.
By applying this sequence of laser pulses, it is possible to efficiently implement the following gates by properly tuning the system parameters:
The system dynamics for the case of only one control atom excited to the Rydberg state and the second control atom remaining in the ground state [i.e., or ] corresponds to the previously considered cases for homonuclear symmetric and for heteronuclear configurations in Figure 6b and Figure 7b, respectively.
The architecture of this gate becomes possible if the qubits satisfy the following conditions: (1) Cs control atoms are excited to Rydberg state where their dominant interaction regime is vdW i.e., , (2) Rb target atoms are excited to Rydberg state and similarly their dominant interaction regime is vdW i.e., , (3) The regime of interaction between control Cs and target Rb atoms, is dipole-dipole interaction i.e., .
In Figure 9a,b, we plot the contours of fidelity when the system is initially prepared in the superposition of ground states on control atoms, while the target atoms are in states : with gate duration of . The total number of computational basis states for a scheme with k control atoms interacting with N target atoms is equal to . In Figure 9a, we consider all possible interaction between control and target atoms. The maximum achieved fidelity is for a high value of Rabi frequency for . It is also noticed a sharp drop in fidelity for which can be a result of the interaction between control atoms, since in this regime interaction between target atoms almost vanishes as seen in Figure 9c. In Figure 9b, we study a non-realistic case where we neglected the interaction between control atoms, which can be compared with the case of CNOT in Figure 7b, considering the different spatial arrangements. The maximum value of fidelity becomes possible for a wider range of intratomic distances. This case proves that the destructive pattern in system dynamics is a direct result of .
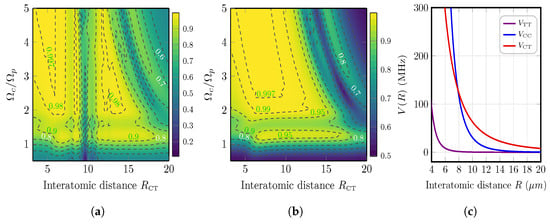
Figure 9.
Contour plot of fidelity for the case of heteronuclear interaction of Cs control atom in state and Rb target atoms in state as a function of the interatomic distance and the ratio . The system is initially prepared in state . , and gate duration . (a) ; (b) ; (c) The evolution of interaction energies as a function of the interatomic distances according to the considered spatial arrangement in Figure 8a.
6. Gate Errors
In this section we discuss the effect of finite lifetimes, and the role of the excitation through different intermediate states and of the spatial arrangement of target atoms on the fidelity for of CNOT and CNOT gates.
CNOT—In Figure 10a,b, we plot the fidelity as a function of interatomic distance between Cs control and Rb target atoms for CNOT gate for , and , respectively, with , , and total gate time . Solid (dashed) curve represents the case of excitation of the target atoms through the second (first) resonance level of the intermediate state (). It is clear that using the second resonance level enhanced the obtained fidelity for CNOT (CNOT) to be () at , compared with () for excitation through the first resonance level.
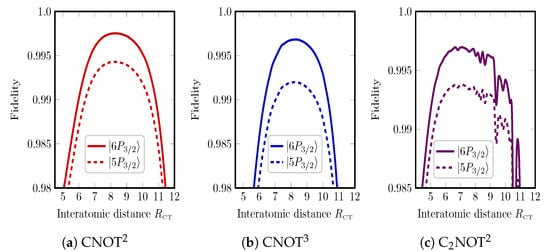
Figure 10.
Investigating the source of error resulting from exciting the target atom from ground state through the first of the second resonance level of intermediate state for different configurations: (a) CNOT, (b) CNOT, and (c) CNOT gates. We plot the evolution of fidelity as a function of the interatomic distance taking into account the finite lifetimes of excited states. Solid (dashed) curves represent the case of intermediate state of the Rb target atoms to be () [see main text]. , .
CNOT—In Figure 10c, we plot the fidelity of multi-control and multi-target CNOT gate as a function of interatomic distance between Cs control and Rb target atoms with total gate time . Solid (Dashed) curve represents the case of excitation of the two target atoms through the second (first) resonance level of the intermediate state () which shows a possible fidelity () at .
In our model, we considered the time gap between excitation and de-excitation of Rydberg state on the control atom to be (s) caused by the pulse sequence which is typically required by a Rydberg blockade gate can cause an expected atom loss, not only for control atom but also for the ensemble of target atoms, which can also a source of errors for implementing the physical system in experiment. In [], the authors reported their findings in constructing a native CNOT gate based on optimizing smooth Gaussian-shaped pulses.
In Figure 11, we show the effect of spatial arrangement and the number of target atoms on the obtained fidelity of CNOT gate for Rabi frequency for two different values of . It is clear that the spatial arrangement of target atoms around the control atom slightly changes the fidelity according to their trapping positions. We also show that the heteronuclear architecture can be advantageous in terms of fidelity as a value for arrays with .
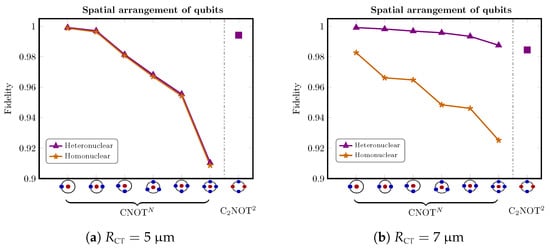
Figure 11.
The fidelity for different spatial arrangement of qubits in CNOT (CNOT) gate for and interatomic distance in (a), in (b).
7. Conclusions
We studied the performance of the multi-qubit CNOT gates based on EIT and Rydberg blockade. Our simulations confirm the advantages of heteronuclear architecture of the atomic quantum registers for suppression of the undesirable target-target interactions which limit the performance of multi-qubit gates. We have shown that in the configuration of single control and four target atoms which is most suitable for surface codes it is possible to achieve the fidelity of multi-qubit CNOT gate above 99% which opens the way to fast quantum error correction schemes with neutral atoms.
Author Contributions
Conceptualization, A.M.F. and I.I.B.; methodology, I.I.B.; application, P.X. and S.B.; software, A.M.F.; investigation, A.M.F.; writing—A.M.F.; writing—review and editing, I.I.B.; visualization, A.M.F.; supervision, I.I.R.; project administration, I.I.B.; funding acquisition, I.I.B., I.I.R. and P.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Russian Science Foundation (Grant No. 23-42-00031) https://rscf.ru/project/23-42-00031/ (accessed on 16 November 2023). A. Farouk is funded by the joint executive educational program between Egypt and Russia (EGY-6544/19). P. Xu acknowledges funding support from the National Key Research and Development Program of China (Grant №2021YFA1402001), the Youth Innovation Promotion Association CAS №Y2021091.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Datasets supporting the plots within this manuscript are available through Zenodo []. Further information is available from the corresponding author.
Acknowledgments
We thank Mark Saffman for helpful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Model of Multiple Rydberg Interaction Channels
In this Appendix, we consider that effect of multiple Rydberg interaction channels due to coupling of initially excited colective two-atom Rydberg state to numerous neighboring collective two-atom states through dipole-dipole interaction. This problem is well described in [], and its formalism is limitedly adopted in [,]. In Ref. [], the authors showed that for implementation of Toffoli gate with homonuclear architecture using main interaction channel for dipole blockade the effect of other interaction channels (e.g., ) can be neglected.
As in Figure A1, we will consider the state which is coupled to a set of other Rydberg states with and for different values of total angular momentum j and of the projection of the total angular momentum on the quantization z-axis , as we show in Table A1, where is the range of variation of principal quantum number n. and are integers . We limited our calculations here for for the interaction channel . The control-target interaction Hamiltonian in Equation (11), can be straightforwardly modified to include coupling to many other Rydberg states.
Energy defect is the energy difference between any two states for the interaction channel ,
where is the energy of atomic state with respect to the center of gravity of the hyperfine-split states.
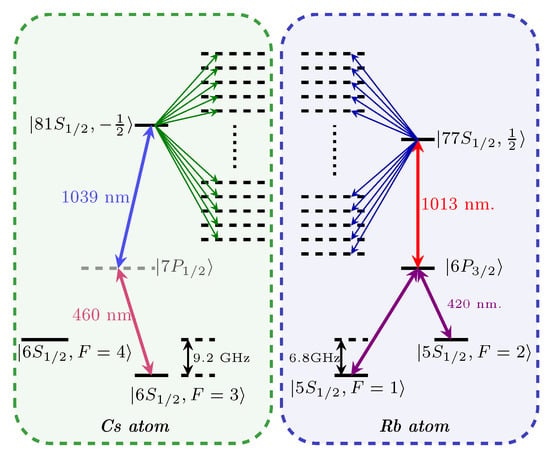
Figure A1.
Hyperfine structure of the collective atomic energy levels with control Cs atom and target Rb atom and laser-induced transitions between ground and Rydberg states.

Table A1.
The calculated dipole-dipole coefficient (), the energy defect (), the van der Waals () interaction coefficients for: Table (above), the heteronuclear asymmetric interaction channels with and for Cs and Rb atoms, respectively. Table (below), the corresponding homonuclear symmetric interaction channels for Rb atoms. () is the driving transition field that couples (). is the dimensionless coupling strength factor. If , then the leakage from the resonantly coupled state can be suppressed. We limited the results of heteronuclear interaction to be and and considered the corresponding interaction channels for the homonuclear interactions. , . The values are taken from ARC using functions getDipoleMatrixElement, and getEnergy.
Table A1.
The calculated dipole-dipole coefficient (), the energy defect (), the van der Waals () interaction coefficients for: Table (above), the heteronuclear asymmetric interaction channels with and for Cs and Rb atoms, respectively. Table (below), the corresponding homonuclear symmetric interaction channels for Rb atoms. () is the driving transition field that couples (). is the dimensionless coupling strength factor. If , then the leakage from the resonantly coupled state can be suppressed. We limited the results of heteronuclear interaction to be and and considered the corresponding interaction channels for the homonuclear interactions. , . The values are taken from ARC using functions getDipoleMatrixElement, and getEnergy.
| Rb | Cs | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 76 | 1 | 81 | 1 | ||||||||||
| 2 | 77 | 1 | 80 | 1 | ||||||||||
| 3 | 77 | 1 | 80 | 1 | 4570 | |||||||||
| 4 | 78 | 1 | 79 | 1 | ||||||||||
| 5 | 78 | 1 | 79 | 1 | ||||||||||
| Rb | Rb | |||||||||||||
| 1 | 76 | 1 | 76 | 1 | ||||||||||
| 2 | 77 | 1 | 77 | 1 | ||||||||||
| 3 | 77 | 1 | 77 | 1 | ||||||||||
| 4 | 78 | 1 | 78 | 1 | ||||||||||
| 5 | 78 | 1 | 78 | 1 | ||||||||||
The dipole-dipole coefficient can be calculated for specific interaction channel by considering the dipole matrix element . Adopting the notation and for the initial and final Rydberg states, respectively. and the van der Waals coefficient can be calculated from the following forms ( is the permittivity of free space):
with a cross-over between these two-regimes occurs at radius . In Table A1, we show the values of , and for different interaction channels.
For the interaction with many target atoms, the target-target interaction Hamiltonian in Equation (13) can be written to include more Rydberg states.
The values of and for the symmetric homonuclear interaction between Rb atoms are given in Table A1 [below]. The dimensions of the system with many Rydberg states substantially increases. The system dimensions are written as , where is the number of considered other coupled Rydberg states for N of target atoms.
In Figure A2, we show the contour plots of fidelity as a function of interatomic distance and using the model of coupling of the initially excited Rydberg state to many other Rydberg states for and 2. It is clearly seen that the coupling to other Rydberg states does not result in significant changes to the value of the calculated fidelity compared to their results shown in Figure 7a,b, where only single interaction channel was considered. The difference in fidelities between these models is of order ∼ for , and of order ∼ for .
Figure A2.
(a) The contour plots of fidelity for implementing CNOT gate using multi-Rydberg model as a function of and for (a) , (b) .
For greater number of target atoms with using many Rydberg states results in substantial increase of the dimension of the model, which makes calculations difficult. Therefore we limited to a single-channel model in our calculations. The situation is the same for many control atoms. Dongmin et al. [], demonstrated that non-resonant couplings between the identical Rydberg states for control atoms in Toffoli gates can be regarded as weak leakage error. We checked our model for a wider range of and higher values for the heteronuclear control-target interaction, and got the same conclusion.
Appendix B. Model of Multi EIT Gate via 6P3/2
The authors in [] considered a multi-level EIT model of a cesium target atom for excitation via the intermediate state. To consider the multi-hyperfine states of the second resonance intermediate state of rubidium atoms, we will consider the target atom Hamiltonian
where are the different hyperfine states of the intermediate state [see Figure A3a], is the Raman detuning, is the detuning from the intermediate state . is the detuning of the individual hyperfine states, with , , , and [,]. and are the Raman and Rabi laser pulses [see the main text]. , and , are the angular factors for dipole moments.
Figure A3.
(a) Scheme of energy levels of Rb target atom. (b) Dependence of the fidelity of the transfer gate on two-photon Raman detuning. (c) Dependence of the fidelity of the blocking gate on the two-photon Rydberg detuning.
The hyperfine structure of the intermediate excited state is a source of additional gate errors. In Ref. [] this question has been explicitly studied and analytical expressions for the differential Stark shifts of Raman transitions have been obtained. The level structure of target Rb atom is shown in Figure A3a. The Raman transition goes through two interaction channels with different Rabi frequencies
The couplings and lead to the additional light shifts of the energy levels. However, these time-dependent light shifts can be compensated by an additional two-photon Raman detuning, as shown in Figure A3a. The numerically calculated dependence of the fidelity of the transfer gate on Raman detuning is shown in Figure A3b. By proper choice of the detuning it is possible to reduce the error due to additional light shifts below .
The light shifts also affect the fidelity of the blocking gate which can be compensated by using an additional detuning of the coupling radiation. The numerically calculated dependence of the fidelity of the blocking gate on Rydberg detuning is shown in Figure A3c. We fixed MHz which provides the maximum fidelity of the transfer gate in Figure 1b. Here it is also possible to reduce the error of the blocking gate due to the additional light shifts below .
Another source of errors can be undesirable Rydberg excitation through different excitation pathways. The excitation of state is suppressed due to selection rules if the clock states and are selected as logical states. However, off-resonant Rydberg excitation through is possible. For low coupling Rabi frequencies Rydberg states are temporarily excited when the blocking gate protocol is implemented. The decay of Rydberg states is taken into account in our model. The influence of the other excitation pathways through different states can be substantially suppressed using optical pumping to the clock states and .
References
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef]
- Wu, Y.; Bao, W.S.; Cao, S.; Chen, F.; Chen, M.C.; Chen, X.; Chung, T.H.; Deng, H.; Du, Y.; Fan, D.; et al. Strong quantum computational advantage using a superconducting quantum processor. Phys. Rev. Lett. 2021, 127, 180501. [Google Scholar] [CrossRef] [PubMed]
- Zhong, H.S.; Deng, Y.H.; Qin, J.; Wang, H.; Chen, M.C.; Peng, L.C.; Luo, Y.H.; Wu, D.; Gong, S.Q.; Su, H.; et al. Phase-programmable Gaussian boson sampling using stimulated squeezed light. Phys. Rev. Lett. 2021, 127, 180502. [Google Scholar] [CrossRef]
- Morgado, M.; Whitlock, S. Quantum simulation and computing with Rydberg-interacting qubits. AVS Quantum Sci. 2021, 3, 023501. [Google Scholar] [CrossRef]
- Graham, T.; Song, Y.; Scott, J.; Poole, C.; Phuttitarn, L.; Jooya, K.; Eichler, P.; Jiang, X.; Marra, A.; Grinkemeyer, B.; et al. Multi-qubit entanglement and algorithms on a neutral-atom quantum computer. Nature 2022, 604, 457. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Y.; Xu, P.; He, X.; Liu, Y.; Liu, M.; Wang, J.; Papoular, D.; Shlyapnikov, G.; Zhan, M. Entangling two individual atoms of different isotopes via Rydberg blockade. Phys. Rev. Lett. 2017, 119, 160502. [Google Scholar] [CrossRef]
- Levine, H.; Keesling, A.; Semeghini, G.; Omran, A.; Wang, T.T.; Ebadi, S.; Bernien, H.; Greiner, M.; Vuletić, V.; Pichler, H.; et al. Parallel implementation of high-fidelity multiqubit gates with neutral atoms. Phys. Rev. Lett. 2019, 123, 170503. [Google Scholar] [CrossRef] [PubMed]
- Graham, T.; Kwon, M.; Grinkemeyer, B.; Marra, Z.; Jiang, X.; Lichtman, M.; Sun, Y.; Ebert, M.; Saffman, M. Rydberg-mediated entanglement in a two-dimensional neutral atom qubit array. Phys. Rev. Lett. 2019, 123, 230501. [Google Scholar] [CrossRef] [PubMed]
- Evered, S.J.; Bluvstein, D.; Kalinowski, M.; Ebadi, S.; Manovitz, T.; Zhou, H.; Li, S.H.; Geim, A.A.; Wang, T.T.; Maskara, N.; et al. High-fidelity parallel entangling gates on a neutral atom quantum computer. arXiv 2023, arXiv:2304.05420. [Google Scholar] [CrossRef]
- Scholl, P.; Schuler, M.; Williams, H.J.; Eberharter, A.A.; Barredo, D.; Schymik, K.N.; Lienhard, V.; Henry, L.P.; Lang, T.C.; Lahaye, T.; et al. Quantum simulation of 2D antiferromagnets with hundreds of Rydberg atoms. Nature 2021, 595, 233–238. [Google Scholar] [CrossRef]
- Ebadi, S.; Wang, T.T.; Levine, H.; Keesling, A.; Semeghini, G.; Omran, A.; Bluvstein, D.; Samajdar, R.; Pichler, H.; Ho, W.W.; et al. Quantum phases of matter on a 256-atom programmable quantum simulator. Nature 2021, 595, 227–232. [Google Scholar] [CrossRef]
- Gallagher, T. Rydberg atoms. Rep. Prog. Phys. 1988, 51, 143. [Google Scholar] [CrossRef]
- Singer, K.; Stanojevic, J.; Weidemüller, M.; Côté, R. Long-range interactions between alkali Rydberg atom pairs correlated to the ns–ns, np–np and nd–nd asymptotes. J. Phys. At. Mol. Opt. Phys. 2005, 38, S295. [Google Scholar] [CrossRef]
- Jaksch, D.; Cirac, J.; Zoller, P.; Rolston, S.; Côté, R.; Lukin, M. Fast quantum gates for neutral atoms. Phys. Rev. Lett. 2000, 85, 2208. [Google Scholar] [CrossRef]
- Lukin, M.D.; Fleischhauer, M.; Cote, R.; Duan, L.; Jaksch, D.; Cirac, J.I.; Zoller, P. Dipole blockade and quantum information processing in mesoscopic atomic ensembles. Phys. Rev. Lett. 2001, 87, 037901. [Google Scholar] [CrossRef] [PubMed]
- Urban, E.; Johnson, T.A.; Henage, T.; Isenhower, L.; Yavuz, D.; Walker, T.; Saffman, M. Observation of Rydberg blockade between two atoms. Nat. Phys. 2009, 5, 110–114. [Google Scholar] [CrossRef]
- Gaëtan, A.; Miroshnychenko, Y.; Wilk, T.; Chotia, A.; Viteau, M.; Comparat, D.; Pillet, P.; Browaeys, A.; Grangier, P. Observation of collective excitation of two individual atoms in the Rydberg blockade regime. Nat. Phys. 2009, 5, 115–118. [Google Scholar] [CrossRef]
- Isenhower, L.; Urban, E.; Zhang, X.; Gill, A.; Henage, T.; Johnson, T.A.; Walker, T.; Saffman, M. Demonstration of a neutral atom controlled-NOT quantum gate. Phys. Rev. Lett. 2010, 104, 010503. [Google Scholar] [CrossRef]
- Su, S.L.; Li, W. Dipole-dipole interaction driven antiblockade of two Rydberg atoms. Phys. Rev. A 2021, 104, 033716. [Google Scholar] [CrossRef]
- Wu, J.L.; Wang, Y.; Han, J.X.; Feng, Y.K.; Su, S.L.; Xia, Y.; Jiang, Y.; Song, J. One-step implementation of Rydberg-antiblockade SWAP and controlled-SWAP gates with modified robustness. Photonics Res. 2021, 9, 814–821. [Google Scholar] [CrossRef]
- Wu, J.L.; Wang, Y.; Han, J.X.; Su, S.L.; Xia, Y.; Jiang, Y.; Song, J. Unselective ground-state blockade of Rydberg atoms for implementing quantum gates. Front. Phys. 2022, 17, 22501. [Google Scholar] [CrossRef]
- Khazali, M.; Mølmer, K. Fast multiqubit gates by adiabatic evolution in interacting excited-state manifolds of Rydberg atoms and superconducting circuits. Phys. Rev. X 2020, 10, 021054. [Google Scholar] [CrossRef]
- Young, J.T.; Bienias, P.; Belyansky, R.; Kaufman, A.M.; Gorshkov, A.V. Asymmetric blockade and multiqubit gates via dipole-dipole interactions. Phys. Rev. Lett. 2021, 127, 120501. [Google Scholar] [CrossRef]
- Li, M.; Li, J.Y.; Guo, F.Q.; Zhu, X.Y.; Liang, E.; Zhang, S.; Yan, L.L.; Feng, M.; Su, S.L. Multiple-Qubit CkUm Logic Gates of Rydberg Atoms via Optimized Geometric Quantum Operations. Ann. Der Phys. 2022, 534, 2100506. [Google Scholar] [CrossRef]
- Sun, L.N.; Yan, L.L.; Su, S.L.; Jia, Y. One-Step Implementation of Time-Optimal-Control Three-Qubit Nonadiabatic Holonomic Controlled Gates in Rydberg Atoms. Phys. Rev. Appl. 2021, 16, 064040. [Google Scholar] [CrossRef]
- Fu, Z.; Xu, P.; Sun, Y.; Liu, Y.Y.; He, X.D.; Li, X.; Liu, M.; Li, R.B.; Wang, J.; Liu, L.; et al. High-fidelity entanglement of neutral atoms via a Rydberg-mediated single-modulated-pulse controlled-phase gate. Phys. Rev. A 2022, 105, 042430. [Google Scholar] [CrossRef]
- Auger, J.M.; Bergamini, S.; Browne, D.E. Blueprint for fault-tolerant quantum computation with Rydberg atoms. Phys. Rev. A 2017, 96, 052320. [Google Scholar] [CrossRef]
- Bluvstein, D.; Levine, H.; Semeghini, G.; Wang, T.T.; Ebadi, S.; Kalinowski, M.; Keesling, A.; Maskara, N.; Pichler, H.; Greiner, M.; et al. A quantum processor based on coherent transport of entangled atom arrays. Nature 2022, 604, 451–456. [Google Scholar] [CrossRef] [PubMed]
- Müller, M.; Lesanovsky, I.; Weimer, H.; Büchler, H.; Zoller, P. Mesoscopic Rydberg gate based on electromagnetically induced transparency. Phys. Rev. Lett. 2009, 102, 170502. [Google Scholar] [CrossRef]
- Fleischhauer, M.; Imamoglu, A.; Marangos, J.P. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 2005, 77, 633. [Google Scholar] [CrossRef]
- Ji, Z.; Jiao, Y.; Xue, Y.; Hao, L.; Zhao, J.; Jia, S. Distinction of electromagnetically induced transparency and Autler-Towners splitting in a Rydberg-involved ladder-type cold atom system. Opt. Express 2021, 29, 11406–11415. [Google Scholar] [CrossRef] [PubMed]
- Pritchard, J.D.; Maxwell, D.; Gauguet, A.; Weatherill, K.J.; Jones, M.; Adams, C.S. Cooperative atom-light interaction in a blockaded Rydberg ensemble. Phys. Rev. Lett. 2010, 105, 193603. [Google Scholar] [CrossRef] [PubMed]
- Weimer, H.; Müller, M.; Lesanovsky, I.; Zoller, P.; Büchler, H.P. A Rydberg quantum simulator. Nat. Phys. 2010, 6, 382–388. [Google Scholar] [CrossRef]
- Peyronel, T.; Firstenberg, O.; Liang, Q.Y.; Hofferberth, S.; Gorshkov, A.V.; Pohl, T.; Lukin, M.D.; Vuletić, V. Quantum nonlinear optics with single photons enabled by strongly interacting atoms. Nature 2012, 488, 57–60. [Google Scholar] [CrossRef] [PubMed]
- Baur, S.; Tiarks, D.; Rempe, G.; Dürr, S. Single-photon switch based on Rydberg blockade. Phys. Rev. Lett. 2014, 112, 073901. [Google Scholar] [CrossRef]
- Gorniaczyk, H.; Tresp, C.; Bienias, P.; Paris-Mandoki, A.; Li, W.; Mirgorodskiy, I.; Büchler, H.; Lesanovsky, I.; Hofferberth, S. Enhancement of Rydberg-mediated single-photon nonlinearities by electrically tuned Förster resonances. Nat. Commun. 2016, 7, 12480. [Google Scholar] [CrossRef] [PubMed]
- Beterov, I.; Saffman, M. Rydberg blockade, Förster resonances, and quantum state measurements with different atomic species. Phys. Rev. A 2015, 92, 042710. [Google Scholar] [CrossRef]
- Sheng, C.; Hou, J.; He, X.; Wang, K.; Guo, R.; Zhuang, J.; Mamat, B.; Xu, P.; Liu, M.; Wang, J.; et al. Defect-free arbitrary-geometry assembly of mixed-species atom arrays. Phys. Rev. Lett. 2022, 128, 083202. [Google Scholar] [CrossRef]
- Singh, K.; Anand, S.; Pocklington, A.; Kemp, J.T.; Bernien, H. Dual-Element, Two-Dimensional Atom Array with Continuous-Mode Operation. Phys. Rev. X 2022, 12, 011040. [Google Scholar] [CrossRef]
- Takekoshi, T.; Reichsöllner, L.; Schindewolf, A.; Hutson, J.M.; Le Sueur, C.R.; Dulieu, O.; Ferlaino, F.; Grimm, R.; Nägerl, H.C. Ultracold dense samples of dipolar RbCs molecules in the rovibrational and hyperfine ground state. Phys. Rev. Lett. 2014, 113, 205301. [Google Scholar] [CrossRef]
- Molony, P.K.; Gregory, P.D.; Ji, Z.; Lu, B.; Köppinger, M.P.; Le Sueur, C.R.; Blackley, C.L.; Hutson, J.M.; Cornish, S.L. Creation of Ultracold 87Rb133Cs Molecules in the Rovibrational Ground State. Phys. Rev. Lett. 2014, 113, 255301. [Google Scholar] [CrossRef]
- Guttridge, A.; Ruttley, D.K.; Baldock, A.C.; González-Férez, R.; Sadeghpour, H.; Adams, C.; Cornish, S.L. Observation of Rydberg blockade due to the charge-dipole interaction between an atom and a polar molecule. Phys. Rev. Lett. 2023, 131, 013401. [Google Scholar] [CrossRef]
- Tung, S.K.; Parker, C.; Johansen, J.; Chin, C.; Wang, Y.; Julienne, P.S. Ultracold mixtures of atomic 6 Li and 133 Cs with tunable interactions. Phys. Rev. A 2013, 87, 010702. [Google Scholar] [CrossRef]
- Walker, T.G.; Saffman, M. Consequences of Zeeman degeneracy for the van der Waals blockade between Rydberg atoms. Phys. Rev. A 2008, 77, 032723. [Google Scholar] [CrossRef]
- Beterov, I.; Hamzina, G.; Yakshina, E.; Tretyakov, D.; Entin, V.; Ryabtsev, I. Adiabatic passage of radio-frequency-assisted förster resonances in Rydberg atoms for two-qubit gates and the generation of bell states. Phys. Rev. A 2018, 97, 032701. [Google Scholar] [CrossRef]
- McDonnell, K.; Keary, L.F.; Pritchard, J.D. Demonstration of a Quantum Gate Using Electromagnetically Induced Transparency. Phys. Rev. Lett. 2022, 129, 200501. [Google Scholar] [CrossRef]
- Förster, T.; Sinanoglu, O. Modern Quantum Chemistry; Academic Press: New York, NY, USA, 1965; Volume 3, pp. 93–137. [Google Scholar]
- Saffman, M.; Walker, T. Analysis of a quantum logic device based on dipole-dipole interactions of optically trapped Rydberg atoms. Phys. Rev. A 2005, 72, 022347. [Google Scholar] [CrossRef]
- Ryabtsev, I.; Tretyakov, D.; Beterov, I.; Entin, V. Observation of the Stark-tuned Förster resonance between two Rydberg atoms. Phys. Rev. Lett. 2010, 104, 073003. [Google Scholar] [CrossRef]
- Tretyakov, D.; Beterov, I.; Yakshina, E.; Entin, V.; Ryabtsev, I.; Cheinet, P.; Pillet, P. Observation of the Borromean three-body Förster resonances for three interacting Rb Rydberg atoms. Phys. Rev. Lett. 2017, 119, 173402. [Google Scholar] [CrossRef]
- Browaeys, A.; Lahaye, T. Many-body physics with individually controlled Rydberg atoms. Nat. Phys. 2020, 16, 132–142. [Google Scholar] [CrossRef]
- Šibalić, N.; Pritchard, J.D.; Adams, C.S.; Weatherill, K.J. ARC: An open-source library for calculating properties of alkali Rydberg atoms. Comput. Phys. Commun. 2017, 220, 319–331. [Google Scholar] [CrossRef]
- Weber, S.; Tresp, C.; Menke, H.; Urvoy, A.; Firstenberg, O.; Büchler, H.P.; Hofferberth, S. Tutorial: Calculation of Rydberg interaction potentials. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 133001. [Google Scholar] [CrossRef]
- Le Roy, R.J. Long-Range Potential Coefficients from RKR Turning Points: C6 and C8 for B ()-State Cl2, Br2, and I2. Can. J. Phys. 1974, 52, 246–256. [Google Scholar] [CrossRef]
- Yu, D.; Wang, H.; Liu, J.M.; Su, S.L.; Qian, J.; Zhang, W. Multiqubit Toffoli gates and optimal geometry with Rydberg atoms. Phys. Rev. Appl. 2022, 18, 034072. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computing and Cuantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Hillery, M.; Bužek, V.; Berthiaume, A. Quantum secret sharing. Phys. Rev. A 1999, 59, 1829. [Google Scholar] [CrossRef]
- Cong, I.; Levine, H.; Keesling, A.; Bluvstein, D.; Wang, S.T.; Lukin, M.D. Hardware-efficient, fault-tolerant quantum computation with Rydberg atoms. Phys. Rev. X 2022, 12, 021049. [Google Scholar] [CrossRef]
- Li, R.; Qian, J.; Zhang, W. Proposal for practical Rydberg quantum gates using a native two-photon excitation. Quantum Sci. Technol. 2023, 8, 035032. [Google Scholar] [CrossRef]
- Farouk, A.M.; Beterov, I.; Xu, P.; Bergamini, S.; Ryabtsev, I. Data for: Parallel Implementation of CNOTN and C2NOT2 Gates via Homonuclear and Heteronuclear Forster Interactions of Rydberg Atoms; Zenodo: Newton, NJ, USA, 2023. [Google Scholar] [CrossRef]
- Saffman, M.; Walker, T.G.; Mølmer, K. Quantum information with Rydberg atoms. Rev. Mod. Phys. 2010, 82, 2313. [Google Scholar] [CrossRef]
- Ponciano-Ojeda, F.; Hernández-Gómez, S.; López-Hernández, O.; Mojica-Casique, C.; Colín-Rodríguez, R.; Ramírez-Martínez, F.; Flores-Mijangos, J.; Sahagún, D.; Jáuregui, R.; Jiménez-Mier, J. Observation of the 5p3/2→6p3/2 electric-dipole-forbidden transition in atomic rubidium using optical-optical double-resonance spectroscopy. Phys. Rev. A 2015, 92, 042511. [Google Scholar] [CrossRef]
- Ramírez-Martínez, F.; Ponciano-Ojeda, F.S.; Hernández-Gómez, S.; Del Angel, A.; Mojica-Casique, C.; Hoyos-Campo, L.M.; Flores-Mijangos, J.; Sahagún, D.; Jáuregui, R.; Jiménez-Mier, J.I. Use of an electric-dipole forbidden transition to optically probe the Autler Townes effect. arXiv 2019, arXiv:1909.01293. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).