Tight Focusing of Circular Partially Coherent Radially Polarized Circular Airy Vortex Beam
Abstract
:1. Introduction
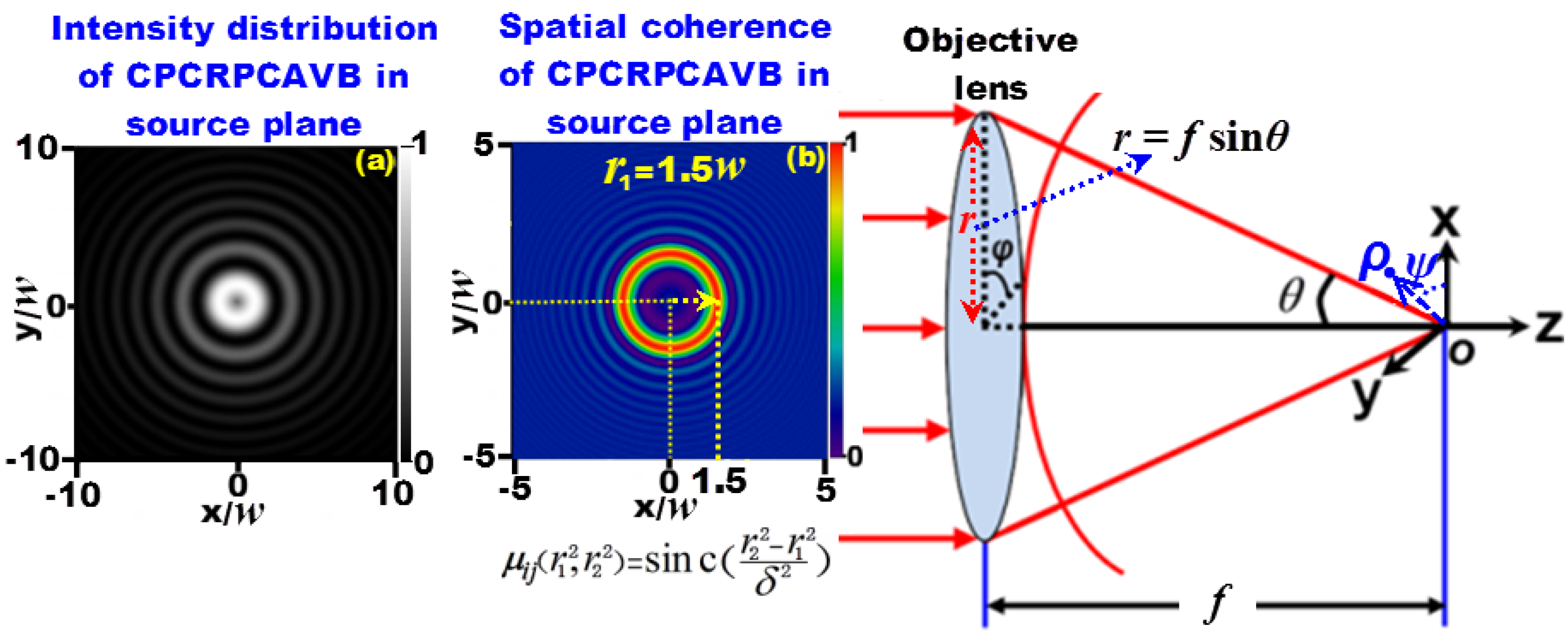
2. Theoretical Analysis
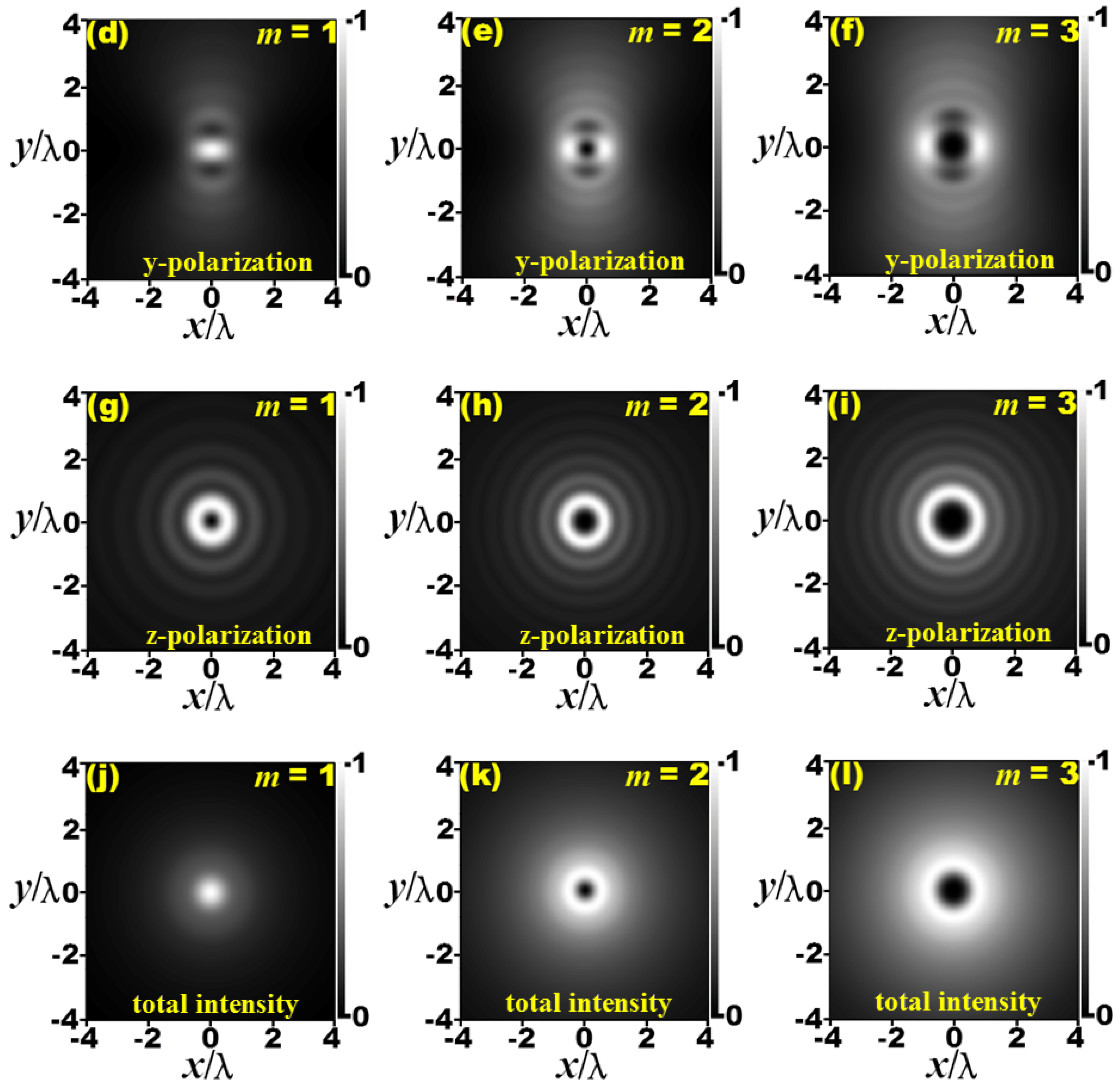
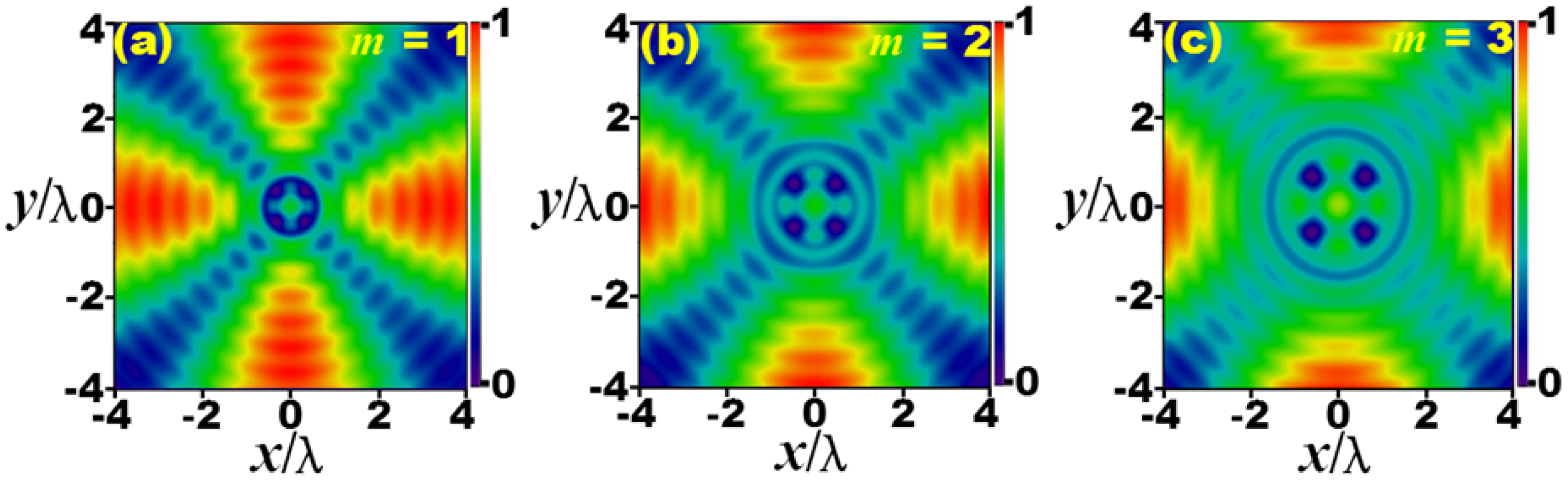
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, X.; Liu, L.; Peng, X.; Liu, L.; Wang, F.; Gao, Y.; Cai, Y. Partially coherent vortex beam with periodical coherence properties. J. Quant. Spectrosc. Radiat. Transf. 2019, 222, 138–144. [Google Scholar] [CrossRef]
- Wang, F.; Cai, Y.; Dong, Y.; Korotkova, O. Experimental generation of a radially polarized beam with controllable spatial coherence. Appl. Phys. Lett. 2012, 100, 051108. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, J.; Yuan, Y.; Wang, F.; Cai, Y. Theoretical and experimental studies of a rectangular Laguerre–Gaussian-correlated Schell-model beam. Appl. Phys. B Laser Opt. 2016, 122, 31. [Google Scholar] [CrossRef]
- Piquero, G.; Santarsiero, M.; Martínez-Herrero, R.; de Sande, J.C.G.; Alonzo, M.; Gori, F. Partially coherent sources with radial coherence. Opt. Lett. 2018, 43, 2376–2379. [Google Scholar] [CrossRef]
- Cui, S.; Chen, Z.; Zhang, L.; Pu, J. Experimental generation of nonuniformly correlated partially coherent light beams. Opt. Lett. 2013, 38, 4821–4824. [Google Scholar] [CrossRef]
- Pang, Z.; Zhao, D. Partially coherent dual and quad airy beams. Opt. Lett. 2019, 44, 4889–4892. [Google Scholar] [CrossRef]
- Zhou, X.; Pang, Z.; Zhao, D. Partially coherent pearcey–gauss beams. Opt. Lett. 2020, 45, 5496–5499. [Google Scholar] [CrossRef]
- Yonglei, L.; Zhen, D.; Yahong, C.; Yangjian, C. Research advances of partially coherent beams with novel coherence structures: Engineering and applications. Opto-Electron. Eng. 2022, 49, 220178-1–220178-28. [Google Scholar]
- Kuskov, V.; Banakh, V. Partially coherent beam focusing based on atmospheric backscatter signals. Atmos. Ocean. Opt. 2022, 35, 226–231. [Google Scholar] [CrossRef]
- Dai, S.; Zheng, X.; Zhao, S. Designing diffractive optical elements for shaping partially coherent beams by proximity correction. Opt. Express 2023, 31, 14464–14472. [Google Scholar] [CrossRef]
- Guo, L.; Chen, Y.; Liu, X.; Liu, L.; Cai, Y. Vortex phase-induced changes of the statistical properties of a partially coherent radially polarized beam. Opt. Express 2016, 24, 13714–13728. [Google Scholar] [CrossRef]
- Lu, X.; Zhao, C.; Shao, Y.; Zeng, J.; Konijnenberg, S.; Zhu, X.; Popov, S.; Urbach, H.P.; Cai, Y. Phase detection of coherence singularities and determination of the topological charge of a partially coherent vortex beam. Appl. Phys. Lett. 2019, 114, 201106. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, J.; Gbur, G.; Korotkova, O. Evolution of the orbital angular momentum flux density of partially coherent vortex beams in atmospheric turbulence. Front. Phys. 2022, 10, 1073662. [Google Scholar] [CrossRef]
- Ding, P.; Pu, J. Coherence and coherence vortex embedded in partially coherent Gaussian beam background during propagation. Opt. Commun. 2023, 545, 129696. [Google Scholar] [CrossRef]
- Liu, X.; Shen, Y.; Liu, L.; Wang, F.; Cai, Y. Experimental demonstration of vortex phase-induced reduction in scintillation of a partially coherent beam. Opt. Lett. 2013, 38, 5323–5326. [Google Scholar] [CrossRef]
- Yu, J.; Huang, Y.; Wang, F.; Liu, X.; Gbur, G.; Cai, Y. Scintillation properties of a partially coherent vector beam with vortex phase in turbulent atmosphere. Opt. Express 2019, 27, 26676–26688. [Google Scholar] [CrossRef]
- Efremidis, N.K.; Christodoulides, D.N. Abruptly autofocusing waves. Opt. Lett. 2010, 35, 4045–4047. [Google Scholar] [CrossRef]
- Dev, V.; Reddy, A.N.K.; Ustinov, A.V.; Khonina, S.N.; Pal, V. Autofocusing and self-healing properties of aberration laser beams in a turbulent media. Phys. Rev. Appl. 2021, 16, 014061. [Google Scholar] [CrossRef]
- Lu, W.; Chen, H.; Liu, S.; Lin, Z. Circular Airy beam with an arbitrary conical angle beyond the paraxial approximation. Phys. Rev. A 2022, 105, 043516. [Google Scholar] [CrossRef]
- Qiu, Z.; Cao, B.; Li, T.; Shen, D.; Huang, K.; Zhang, X.; Lu, X. The abruptly auto-braiding property of the Bessel beam superimposed with circular Airy beam. Opt. Laser Technol. 2022, 148, 107715. [Google Scholar] [CrossRef]
- Li, T.; Sun, M.; Song, J.; Zhang, N.; Tong, X.; Li, D.; Ma, X.; Zhang, X.; Huang, K.; Lu, X. Vortex phase-induced properties of a partially coherent radially polarized circular Airy beam. Opt. Express 2021, 29, 41552–41567. [Google Scholar] [CrossRef]
- Li, T.; Li, D.; Zhang, X.; Huang, K.; Lu, X. Partially coherent radially polarized circular Airy beam. Opt. Lett. 2020, 45, 4547–4550. [Google Scholar] [CrossRef]
- Santarsiero, M.; Martínez-Herrero, R.; Maluenda, D.; de Sande, J.C.G.; Piquero, G.; Gori, F. Partially coherent sources with circular coherence. Opt. Lett. 2017, 42, 1512–1515. [Google Scholar] [CrossRef]
- Ding, C.; Koivurova, M.; Turunen, J.; Pan, L. Self-focusing of a partially coherent beam with circular coherence. J. Opt. Soc. Am. A 2017, 34, 1441–1447. [Google Scholar] [CrossRef]
- Sundaram, C.M.; Prabakaran, K.; Anbarasan, P.M.; Rajesh, K.B.; Musthafa, A.M. Creation of super long transversely polarized optical needle using azimuthally polarized multi Gaussian beam. Chin. Phys. Lett. 2016, 33, 064203. [Google Scholar] [CrossRef]
- Lin, H.; Zhou, X.; Chen, Z.; Sasaki, O.; Li, Y.; Pu, J. Tight focusing properties of a circular partially coherent Gaussian beam. J. Opt. Soc. Am. A 2018, 35, 1974–1980. [Google Scholar]
- Kotlyar, V.V.; Stafeev, S.S.; O’faolain, L.; Soifer, V.A. Tight focusing with a binary microaxicon. Opt. Lett. 2011, 36, 3100–3102. [Google Scholar] [CrossRef]
- Chen, K.; Ma, Z.Y.; Hu, Y.Y. Tightly focused properties of a partially coherent radially polarized power-exponent-phase vortex beam. Chin. Phys. B 2023, 32, 024208. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Stafeev, S.S.; Nalimov, A.G.; Rasouli, S. Tightly focusing vector beams containing V-point polarization singularities. Opt. Laser Technol. 2022, 145, 107479. [Google Scholar] [CrossRef]
- Chen, Z.; Hua, L.; Pu, J. Tight focusing of light beams: Effect of polarization, phase, and coherence. In Progress in Optics; Elsevier: Amsterdam, The Netherlands, 2012; Volume 57, pp. 219–260. [Google Scholar]
- Lindfors, K.; Friberg, A.T.; Setälä, T.; Kaivola, M. Degree of polarization in tightly focused optical fields. J. Opt. Soc. Am. A 2005, 22, 561–568. [Google Scholar] [CrossRef]
- Xu, H.F.; Zhang, Z.; Qu, J.; Huang, W. The tight focusing properties of Laguerre-Gaussian-correlated Schell-model beams. J. Mod. Opt. 2016, 63, 1429–1437. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, Z.; Wang, H.; Huang, C.; He, Z.; Zeng, J.; Chen, F.; Yu, C.; Li, Y.; Chen, H.; Pu, J.; et al. Tight Focusing of Circular Partially Coherent Radially Polarized Circular Airy Vortex Beam. Photonics 2023, 10, 1279. https://doi.org/10.3390/photonics10111279
Wan Z, Wang H, Huang C, He Z, Zeng J, Chen F, Yu C, Li Y, Chen H, Pu J, et al. Tight Focusing of Circular Partially Coherent Radially Polarized Circular Airy Vortex Beam. Photonics. 2023; 10(11):1279. https://doi.org/10.3390/photonics10111279
Chicago/Turabian StyleWan, Zhihao, Haifeng Wang, Cheng Huang, Zhimin He, Jun Zeng, Fuchang Chen, Chaoqun Yu, Yan Li, Huanting Chen, Jixiong Pu, and et al. 2023. "Tight Focusing of Circular Partially Coherent Radially Polarized Circular Airy Vortex Beam" Photonics 10, no. 11: 1279. https://doi.org/10.3390/photonics10111279
APA StyleWan, Z., Wang, H., Huang, C., He, Z., Zeng, J., Chen, F., Yu, C., Li, Y., Chen, H., Pu, J., & Lin, H. (2023). Tight Focusing of Circular Partially Coherent Radially Polarized Circular Airy Vortex Beam. Photonics, 10(11), 1279. https://doi.org/10.3390/photonics10111279



