Abstract
We present our experimental results of two-photon laser excitation 5S1/2→5P3/2→nS1/2 of Rb atoms to Rydberg nS1/2 states with a homemade 480 nm laser in the second excitation step. In an experiment with cold Rb atoms, we excited the 42S1/2 state and detected Rydberg atoms with a selective-field-ionization (SFI) detector that provides single-atom resolution. The resonance line shapes well agreed with numerical simulations in a three-level theoretical model. We also studied the multiatom spectra of Rydberg excitation of mesoscopic atom ensembles which are of interest to quantum information processing. In the experiment with hot Rb atoms, we first excited the 30S1/2 state and observed a narrow Rydberg EIT resonance. Its line shape also agreed well with theory. Then, we performed a similar experiment with the higher 41S1/2 state and observed the Autler–Townes splitting of the EIT resonance in the presence of a microwave field, which was in resonance with the microwave transition 41S→41P3/2. This allowed us to measure the average strength of the microwave field and, thus, demonstrate the operation of a Rydberg microwave sensor. We may conclude that the developed homemade laser at 480 nm substantially extends our capabilities for further experiments on quantum information and quantum sensing with Rydberg atoms.
1. Introduction
Highly excited Rydberg atoms with the principal quantum number n >> 1 have many unique properties compared to low-excited atoms: large electron orbit radius (~n2), large dipole moments of transitions between neighboring states (~n2), strong long-range interactions (~n4–n11), long radiative lifetimes (~n3–n5), huge polarizabilities (~n7), etc. [1]. Laser and microwave spectroscopy of Rydberg atoms can reveal these properties through observing the quantum interference, dephasing, shifts or broadenings of microwave and optical resonances in Rydberg atoms. Single Rydberg atoms can be detected using the selective field ionization (SFI) technique or optically via resonant fluorescence. The control of long-range interactions between Rydberg atoms using laser and microwave radiation, as well as using external electric and magnetic fields, forms the basis for quantum information processing with neutral trapped atoms [2,3,4,5,6]. Rydberg atoms can also be used as high-precision and compact sensors of the dc and ac electric fields using electromagnetically induced-transparency (EIT) resonances at Rydberg excitation of Rb and Cs atoms in vapor cells [7,8].
Rydberg states of alkali-metal atoms can be excited from ground state via resonant laser radiation in various ways. In Rb atoms (Figure 1a), it is possible to implement one-photon excitation on the 5S1/2→nP transitions at 297 nm [9], two-photon excitation 5S1/2→5P3/2→nS,nD with the 780 nm radiation at the first step and 480 nm at the second step [10,11,12,13,14,15,16], or three-photon excitation 5S1/2→5P3/2→6S1/2→nP1/2,3/2 with 780 nm radiation at the first step, 1367 nm at the second step, and 743 nm at the third step [17,18,19,20]. In our paper [21] we have shown theoretically that the three-photon laser excitation of Rydberg states using three different laser beams can be arranged in a starlike geometry that simultaneously eliminates the recoil effect and Doppler broadening. Compared to one- and two-photon laser excitation, this approach provides a much narrower line width and longer coherence time for both cold atom samples and hot vapors, if the intermediate one-photon resonances of the three-photon transition are detuned by more than the respective single-photon Doppler widths. This was confirmed recently in an experiment on three-photon excitation 6S1/2→6P3/2→9S1/2→423/2 in a Cs vapor cell [22], where three-photon EIT resonance was 30 times narrower than the ordinary two-photon resonance 6S1/2→6P3/2→nS,nD [23].
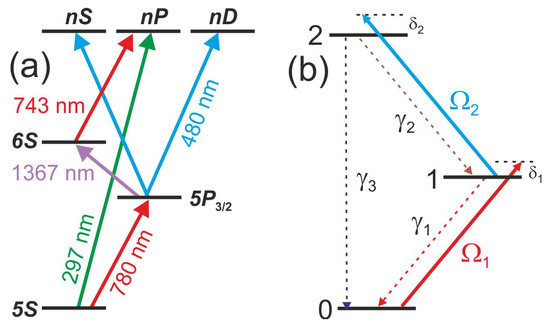
Figure 1.
(a) Scheme of the one-, two-, and three-photon laser excitation of Rydberg states in Rb atoms. (b) A three-level model for the two-photon laser excitation of Rydberg states from ground state 0 to Rydberg state 2 through intermediate state 1.
Therefore, in our previous experiments [17,18,19,20], we used three-photon laser excitation 5S1/2→5P3/2→6S1/2→nP1/2,3/2 of cold Rb Rydberg atoms in magneto-optical and optical dipole traps. However, due to the selection rules, it allowed us to excite only nP Rydberg states, so all our previous experiments on Rydberg interactions and microwave spectroscopy were performed with Rb(nP) atoms.
Two-photon Rydberg excitation is much simpler in experimental realization, as only two highly stable lasers are required. At large detuning of the intermediate level, it is possible to obtain narrow Rydberg excitation resonances for coherent spectroscopy of Rydberg cold atom gases [13,14] and Rabi population oscillations for the implementation of two-qubit quantum gates with single atoms in arrays of optical dipole traps [12,15,16]. Rydberg EIT resonances are widely used to study Rydberg interactions [23] and sense electric fields [7,8,22,24]. We also note that the recoil effect and Doppler shift can be partially canceled at two-photon excitation if counterpropagating laser beams at 780 and 480 nm are used [5,25].
In this paper, we report our first experimental results on the two-photon laser excitation 5S1/2→5P3/2→nS with a homemade 480 nm laser in the second excitation step, which provides the excitation of nS and nD Rydberg states in Rb atoms. We demonstrate this excitation in a Rb magneto-optical trap (MOT) with SFI detection of single Rydberg atoms and in a Rb vapor cell with electromagnetically induced transparency (EIT) detection. This substantially extends our capabilities for further experiments on quantum information and quantum sensing with Rydberg atoms. One of the novelties of MOT experiments is our ability to study multiatom Rydberg excitation spectra of mesoscopic ensembles with a definite number of atoms N = 1–5 due to single-atom resolution of our SFI detector based on a channeltron electron multiplier.
2. Theory of Two-Photon Rydberg Excitation
A three-level theoretical model for the two-photon laser excitation of Rydberg states is shown in Figure 1b. We denote the 5S1/2 ground state to be state 0, 5P3/2 intermediate state to be state 1, and the final nS or nD Rydberg state to be state 2. For each intermediate one-photon transition j = 1, 2 we specify the respective Rabi frequencies (here, dj are dipole moments of one-photon transitions and Ej are electric-field amplitudes of the linearly polarized light fields) and detunings δj. The total detuning δ = δ1 + δ2 from the two-photon transition 0→2 is supposed to be small, while δj are supposed to be large in order to not populate intermediate state 1.
In the absence of spontaneous relaxation, the Schrödinger equation gives for the time evolution of probability amplitudes aj of states j = 0–2 in the rotating wave approximation:
Amplitudes a0 and a2 are slowly varying variables at the two-photon Rabi frequency, while a1 is a small but rapidly oscillating value due to large detuning δ1. We can therefore make the replacement in order to decompose it into a slowly varying part and a rapidly oscillating exponent. Substituting this replacement into Equation (1) and neglecting the small term containing , we finally obtain the population of Rydberg state at two-photon laser excitation to be
where is the two-photon Rabi frequency, and is the power shift of the two-photon resonance. The power shift occurs at transitions and due to the interaction with the far-detuned laser radiations. Equation (2) demonstrates two important features: the presence of the power shift and the possibility of coherent Rabi population oscillations. However, the Rabi oscillations in Equation (2) occur for an infinitely long time, which is obviously not the case in real experiments. The oscillations should be depleting at least due to the spontaneous decay of the excited states 1 and 2.
We now consider a more realistic theoretical model, which takes into account the spontaneous decay of excited levels 1 and 2. In the three-level approximation of Figure 1b, this decay can be taken into account through introducing spontaneous transitions at rates γ1, γ2, γ3. Rate γ1 = 3.7 × 107 s−1 corresponds to the direct spontaneous transition in a Rb atom and is determined by the inverse lifetime of the intermediate state 5P3/2. Rate γ2 corresponds to all possible channels of the spontaneous decay of a Rydberg state to the state 5P3/2, including both a direct transition and transitions through all possible intermediate Rydberg states populated during the spontaneous decay of an initial Rydberg state and under the action of blackbody radiation [26]. Similarly, rate γ3 corresponds to all channels of spontaneous decay into the ground state 5S1/2. Since it is virtually impossible to take into account all channels of the decay of a Rydberg state in equations, we assumed that rates γ2 and γ3 are the same and equal to one half of the inverse effective lifetime of a Rydberg state τR at an ambient temperature of 300 K [26].
To calculate the excitation spectrum of Rydberg state 2 using the three-level model of Figure 1b, we should apply equations for a density matrix ρij. It is impossible to find an analytical solution for Rydberg state population ρ22 at arbitrary Rabi frequencies and detunings. Therefore, the problem should be solved numerically in the general case.
However, in our paper [17], we have shown that we can find a relatively simple solution for coherent three-photon excitation at sufficiently large detunings of the intermediate levels. It should be analogous with the solution for a two-level system with relaxation. During coherent three-photon excitation, only the ground and Rydberg states are populated, and the population at a resonance oscillates between them at three-photon Rabi frequency.
The same conclusion can be applied to the two-photon transition at sufficiently large detuning of the intermediate level. In a certain approximation, the three-level system in Figure 1b should be equivalent to the two-level system with relaxation, where the upper-level relaxation rate γ = γ2 + γ3 is the inverse lifetime of the Rydberg state. In the effective two-level system, an approximated analytical calculation of the population of excited state is possible for the cases of weak (Ω << γ) or strong (Ω >> γ) excitation. In our paper [17], we obtained the following analytical solutions:
A comparison of Equation (4) with simpler Equation (2) for the model without relaxation shows that Equation (2) can be applied at short interaction times (γt << 1). At longer interaction times (γt >> 1), Rabi oscillations become damped and the population approaches a stationary value. A comparison of Equations (3) and (4) with the results of exact numerical calculations demonstrates that they are applicable in all cases except for Ω ~ γ and have a good accuracy at Ω < 3γ and Ω > 3γ. These formulas are useful for prompt calculations of the excitation probability, a transition spectrum, and the time evolution of population and can be used to analyze various limiting cases. For Equations (3) and (4) to be applied to an analytical description of the spectrum of coherent two-photon excitation, we should assume Ω = Ω1Ω2/(2δ1) (two-photon Rabi frequency) and γ = γ2 + γ3 (inverse lifetime of a Rydberg state) and make the substitution δ → δ − δ0 to take into account the power shift of two-photon resonance.
We have also calculated the exact analytical expression for the steady-state solution of the density matrix equations in the model of Figure 1. It is valid for any detunings and Rabi frequencies in this model. However, it is difficult to analyze this exact expression due to its complicated form. Below, we consider only two limiting cases.
In the case of weak two-photon excitation (Ω1, Ω2 << γ1), the steady-state solution is
This solution is interesting as it describes the interference effect of electromagnetically induced transparency (EIT) at two-photon Rydberg excitation [27]. If we set δ2 = 0 and scan δ1 across the two-photon resonance, we will observe two superimposed Lorentz profiles—one with the width γ1 and another with the width γ2 + γ3. As in Rydberg atoms, we typically have γ1 >> γ2 + γ3; the very narrow peak with the width γ = γ2 + γ3 corresponds to Rydberg EIT peak. This peak is of great interest, as it is used in Rydberg sensors of electric fields. For example, it splits, due to the Autler–Townes effect, into two peaks in the presence of a microwave field resonant to a transition between neighboring Rydberg states, and this splitting gives a direct measure of the microwave field strength [7,8,28].
In the case of large intermediate detuning (Ω1, Ω2, γ1 << δ1), the steady-state solution is
Here, the resonance width is given not only by the radiative width γ = γ2 + γ3 of the Rydberg state, but also adds some part of γ1 due to the small population of the intermediate level and due to the power broadening on the order of Ω.
Finally, if the line widths Γ1 and Γ2 of the two lasers are nonzero, they should add to the total line width of the two-photon resonance and reduce its amplitude in Equation (6). In numerical calculations, we take the laser line widths into account through adding additional decay rates Γ1/2 or Γ2/2 to the appropriate nondiagonal elements (coherences) of the density matrix, as described in our paper [17]. This model of taking into account the laser line width is called a phase diffusion model, and it describes the case where laser radiation has random phase fluctuations but has no amplitude fluctuations [29]. We note that the laser radiation spectrum in this model has a Lorentzian shape, which is characteristic of semiconductor lasers; however, other types of lasers can have a Gaussian profile with a more rapid decrease in wings. Therefore, the excitation spectra of Rydberg states calculated in terms of this model can differ from the experimental data in resonance wings.
3. Experimental Results and Their Comparison with Theory
The key elements to implement the two-photon Rydberg excitation scheme 5S1/2→5P3/2→nS,nD are narrowband tunable laser sources at the 780 nm and 480 nm wavelengths. They should provide the line widths and frequency stabilities below 1 MHz. In addition, the blue 480 nm laser should be tunable in the range of 479–485 nm to excite various Rydberg states and should deliver enough optical power (>50 mW), since the transition probability on the second step drops as n−3 when n increases. While the 780 nm lasers are widely available from many manufacturers, the 480 nm lasers with the above parameters are currently provided only by Toptica (Germany) as the TA-SHG Pro model. The latter is rather expensive and not always available in laboratories.
Therefore, we have designed and built a homemade 480 nm laser, which provides the required tunability, line width, and power. It is based on a 960 nm master external-cavity diode laser, semiconductor tapered amplifier, intracavity second harmonic generator with LBO nonlinear crystal, output acousto-optical modulator and frequency-locking electronics to lock its frequency to an external highly stable ultralow expansion glass (ULE) resonator. More details of this laser will be published elsewhere. In the first excitation step at 780 nm, we use a Toptica DL Pro laser locked to saturation absorption resonances in a Rb vapor cell.
Below we describe our first experiments on two-photon excitation in a Rb magneto-optical trap with the SFI detection of single Rydberg atoms and in a Rb vapor cell with the EIT detection.
3.1. Experiment with Cold Rb Atoms in a Magneto-Optical Trap
The experiments were performed with cold 85Rb atoms captured into a magneto-optical trap (MOT), which is shown in Figure 2a. The atoms are cooled using three orthogonal pairs of light waves with a wavelength of 780 nm. The cooling and repumping lasers are tuned to the closed transition 5S1/2(F = 3)→5P3/2(F = 4) and the transition 5S1/2(F = 2)→5P3/2(F = 3), respectively. A cloud of ~106 cold atoms 0.5–1 mm in size with a temperature of 100–200 μK is formed at the trap center.
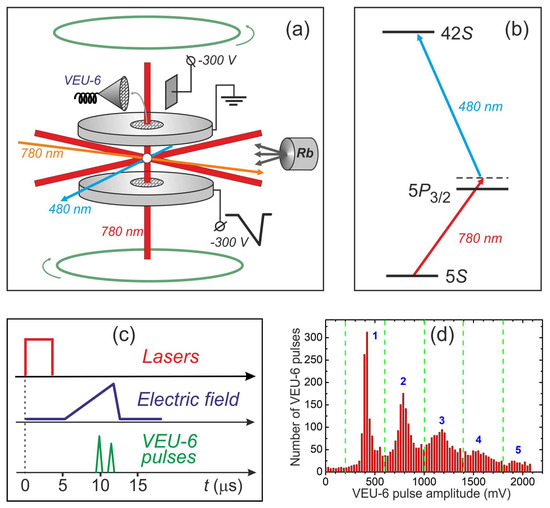
Figure 2.
(a) Scheme of the experiment with cold Rydberg 85Rb atoms in a magneto-optical trap. Rydberg atoms are excited in a small volume of a cold atom cloud and detected using selective field ionization (SFI). (b) Scheme of coherent two-photon laser excitation 5S1/2 → 5P3/2 → 42S1/2 of Rb Rydberg atoms with δ1 = +200 MHz detuning at the first step. (c) Timing diagram of laser and electric pulses. (d) Histogram of the output pulses of the channel electron multiplier VEU-6, which detects electrons formed via SFI. The observed peaks correspond to N = 1–5 detected Rydberg atoms.
The cold Rb atoms were excited to a Rydberg state 42S according to the two-photon scheme 5S1/2 → 5P3/2 → 42S1/2 (Figure 2b). The radiation from the first- and second-step lasers is fed to the MOT through single-mode optical fibers. At the exit from the optical fibers, they are collimated and then focused on the cloud of cold atoms in the geometry of beams crossed at a right angle (Figure 2a) with a waist diameter of ~20 μm. The synchronized 780 nm and 480 nm laser pulses have a repetition rate of 5 kHz.
The Rydberg atoms are excited in the space between two plates of stainless steel, producing a uniform electric field (Figure 2a). The electric field is used for Stark spectroscopy and the detection of Rydberg atoms using the SFI method. The atoms are detected with a repetition rate of 5 kHz when an ionizing electric field sweep pulse with a rise time of 2–3 μm is switched on (Figure 2c). The electrons produced via SFI are accelerated by the electric field, fly through the metal grid of the upper plate, and are directed into the input horn of the VEU-6 channel electron multiplier by the deflecting electrode. The pulsed signals from its output are processed by a box-car integrator and a computer. The number of electrons detected per laser pulse is determined according to the number of Rydberg atoms in the excitation region and the total electron detection efficiency [30]. In our experiments, the detection efficiency reaches 70% [19].
Figure 2d shows a histogram of the amplitudes of VEU-6 output pulses. Several peaks corresponding to different numbers of detected Rydberg atoms, N = 1–5, can be seen on this histogram. The integrated amplitude (area) of each of the peaks is described using a Poisson distribution and depends on the mean number of detected atoms per laser pulse. After each laser pulse, the data acquisition system measured the VEU-6 output pulse amplitude, then determined the number of detected atoms from the premeasured histogram (Figure 2d), sorted the signals according to the number of atoms N, and calculated the two-photon laser excitation probability of a Rydberg state after the accumulation of data in 103–104 laser pulses.
Our experiments on two-photon Rydberg excitation spectroscopy were performed in the MOT switched off in advance for a short time. For this purpose, acousto-optic modulators were installed on all the cooling laser beams, which switched them off for 20 μs, and were switched on again after the measurement. The MOT gradient magnetic field was not switched off during our measurements, but its influence was minimized through adjusting the position of the excitation volume to the point of zero magnetic field. This was controlled via the absence of Zeeman splitting of microwave transitions between Rydberg states according to our method from Ref. [31]. This allowed us to have a high laser pulse repetition rate (5 kHz) and to trace the change in the signals from Rydberg atoms in real time on the oscilloscope screen and in the computer-based data acquisition system.
Figure 3a,b show two examples of the experimental records (blue dots) of the spectra of two-photon laser excitation 5S1/2 → 5P3/2 → 42S1/2 of Rb Rydberg atoms at t = 4 µs interaction time; the power of the 780 nm radiation P1 = 1.5 µW, and the power of the 480 nm radiation (a) P2 = 0.266 mW and (b) P2 = 0.4 mW. The frequency scale is set according to the frequency of a digital synthesizer used in the frequency locking system of the 480 nm laser. The green curves in these figures are the results of numerical simulations that best fit the experimental data. The main fitting parameters are the Rabi frequency of the second step Ω2 and the unknown number N0 = 16 of the ground-state atoms in the laser excitation volume. The other parameters correspond to the experimental ones. The model also takes into account the measured line widths of the two lasers, Γ1/(2π) = 100 kHz and Γ2/(2π) = 500 kHz, and the residual Doppler broadenings of the two transitions at the atom temperature T = 150 µK. Figure 3a,b demonstrate that theory fits the experimental line shapes of the observed two-photon resonance 5S1/2 → 5P3/2 → 42S1/2 well.
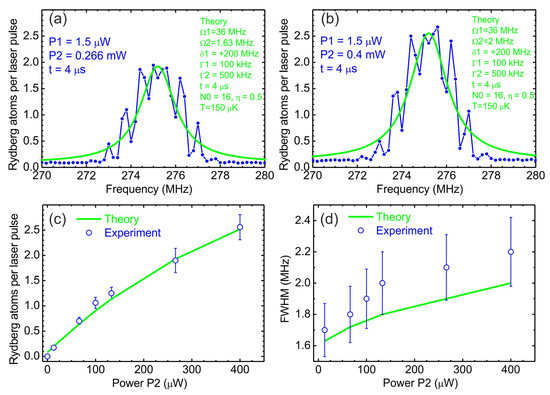
Figure 3.
Examples of the experimental records (blue dots) of the spectra of two-photon laser excitation 5S1/2 → 5P3/2 → 42S1/2 of Rb Rydberg atoms at 4 µs interaction time; the power of the 780 nm radiation P1 = 1.5 µW and the power of the 480 nm radiation (a) P2 = 0.266 mW and (b) P2 = 0.4 mW. The green curves are the results of numerical simulations that best fit the experimental data. (c) Measured dependence of the two-photon resonance height (open circles) on the 480 nm radiation power P2 and its comparison with numerical simulation (green solid curve). (d) Measured dependence of the two-photon resonance FWHM (open circles) on the 480 nm radiation power P2 and its comparison with numerical simulation (green solid curve).
Besides the powers P2 used in Figure 3a,b, we also recorded the two-photon spectra at other powers and measured dependences of the height and full width at half maximum (FWHM) of the resonance on P2.
Figure 3c shows the measured dependence of the two-photon resonance height (open circles) on the 480 nm radiation power P2 and its comparison with numerical simulation (green solid curve). At P2 < 150 µW, the dependence is linear, while at higher power, it tends to start saturating. This figure demonstrates a very good agreement between the experiment and theory at all laser powers, thus confirming the validity of the theoretical model used.
Figure 3d shows the measured dependence of the two-photon resonance FWHM (open circles) on the 480 nm radiation power P2 and its comparison with numerical simulation (green solid curve). Here we see that, at small laser powers, the experimental line width is about 1.7 MHz, and it is close to the theoretical value 1.6 MHz. This value is contributed from the total line width of the two lasers (0.6 MHz), Fourier width of the 4 µs laser pulse (0.25 MHz), and residual Doppler broadening (~0.8 MHz). Upon increasing the power P2 in Figure 3d, the resonance broadens due to the power broadening effect and reaches the experimental width of 2.2 MHz at P2 = 0.4 mW, which corresponds to the two-photon Rabi frequency 0.18 MHz according to theory. The above width of 2.2 MHz, however, is greater than the value of 2 MHz given by theory. We attribute this minor discrepancy to the used diffusion model used to the laser line widths into account, which is not perfectly valid for the resonance wings.
It was already mentioned that, after each laser pulse, we sorted out measured channeltron signals according to the number of detected Rydberg atoms N = 1–5, according to the histogram of Figure 2d. Therefore, we were able to record multiatom laser excitation spectra of the mesoscopic ensembles with definite number of Rydberg atoms N. As it was shown in our previous papers on three-photon laser excitation [18,19], for noninteracting Rydberg atoms, measured multiatom spectra SN are given in theory by the statistical formula
where ρ22 is the theoretical excitation spectrum of a single atom, η is the detection efficiency of the SFI detector, and N0 is the total number of Rb atoms in the laser excitation volume. The experimental and theoretical spectra shown in Figure 3a,b are in fact given by the sum of the multiatom spectra
which corresponds to the mean number of Rydberg atoms detected per laser pulse.
In Figure 4, we present the comparison of the experimental records of multiatom two-photon laser excitation spectra SN (blue curves) with the spectra calculated from Equation (7) for non-interacting atoms at N0 ≈ 16 and η = 0.5 (green curves). Figure 4a–d correspond to the excitation spectrum of Figure 3a at P2 = 0.266 mW, and Figure 4e–h correspond to the excitation spectrum of Figure 3b at P2 = 0.4 mW. Columns N = 1 to N = 4 are excitation spectra SN for mesoscopic ensembles with a certain number of Rydberg atoms, N = 1–4. Their sum gives the total measured signals S shown in Figure 3a,b.
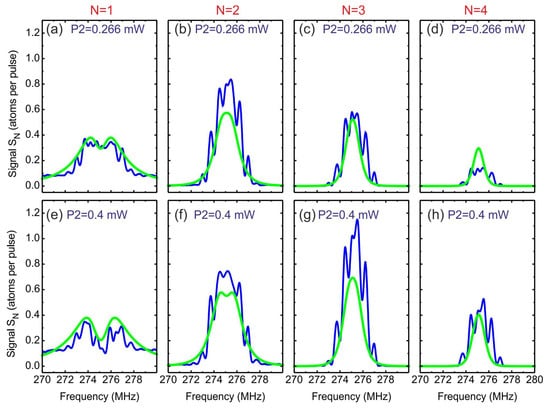
Figure 4.
Comparison of the experimental records of multiatom two-photon laser excitation spectra SN for the Rydberg state 42S1/2 (blue curves) with the spectra calculated from Equation (7) for non-interacting atoms at N0 ≈ 16 and η = 0.5 (green curves): (a–d) for the excitation spectrum of Figure 3a at P2 = 0.266 mW; (e–h) for the excitation spectrum of Figure 3b at P2 = 0.4 mW. Columns N = 1 to N = 4 are excitation spectra SN for mesoscopic ensembles with a certain number of Rydberg atoms, N = 1–4. Their sum gives total measured signals S shown in Figure 3a,b.
In Figure 4e, we see that one-atom spectrum S1 has a prominent dip in its center. This dip is a purely statistical effect: the probability of exciting and detecting more than one atom is larger than the probability of exciting and detecting a single atom. In the case of two atoms (spectrum S2), there is no prominent dip, but the resonance peak has a plateau, which is also due to the reduced probability of exciting two atoms in the resonance center. For a larger number of atoms (multi-atom spectra), the dip and plateau are absent. A weaker dip is also observed in the one-atom spectrum in Figure 4a at the lower two-photon Rabi frequency and, therefore, at lower excitation probability.
The multiatom excitation spectra of Figure 4 are an essentially new result of our study. Such spectra are of interest for quantum information processing with neutral atoms. In particular, the dipole blockade effect can be observed in mesoscopic ensembles of cold atoms excited to Rydberg states [2] if the interaction energy of Rydberg atoms exceeds the excitation resonance width (generally, the Rabi frequency). In the case of complete dipole blockade, only one atom from the entire mesoscopic ensemble can be excited to a Rydberg state, because for a larger number of atoms the collective energy levels are shifted relative to the frequency of unperturbed excitation resonance. This should lead to a radical change in the spectra presented in Figure 4: only the one-atom signal (N = 1) is retained, whereas all other multiatom resonances disappear. Their incomplete disappearance may indicate incomplete dipole blockade. The change in the resonance amplitude ratio, according to Equation (7), allows one to determine the degree of completeness of dipole blockade under specific experimental conditions. In our previous experiments on three-photon excitation we have observed such a partial dipole blockade for high Rydberg nP3/2 states [20]. In Figure 4 some differences between theory and experiments may also be caused by partial dipole blockade, but this should be a subject of our further studies.
From the results of this first experiment with cold Rb atoms we may conclude that the developed homemade laser at 480 nm mainly satisfies the requirements for its basic parameters, especially stability and line width. The observed two-photon resonance width of ~2 MHz indicates the coherence time of ~0.5 µs, which is good enough for the first experiment. However, in the future experiments on quantum information processing and two-qubit quantum gates we will need to realize high-contrast Rabi oscillations with much longer coherence time, so we have to reduce the laser line widths. Our work on this subject is in progress.
3.2. Experiment with Hot Rb Atoms in a Vapor Cell
The experiments were performed with hot 85Rb atoms in a vapor cell with natural isotope abundance and without buffer gas (Figure 5). The cell temperature is stabilized using a heater at T = 56 °C that corresponds to the number density of Rb atoms 2.5 × 1011 cm−3. The cell diameter is 3 cm and the length is 6.5 cm.
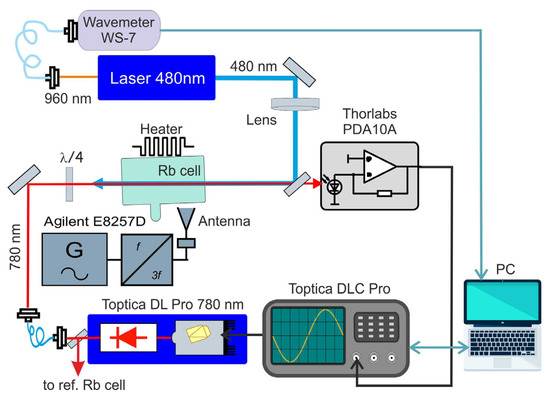
Figure 5.
Scheme of the experiment with hot Rydberg 85Rb atoms in a vapor cell. Rb atoms are excited to a Rydberg state nS according to the two-photon scheme 5S1/2 → 5P3/2 → nS1/2. The radiations from the first- and second-step lasers are counterpropagating in the cell to observe the Rydberg EIT resonance on the top of the Doppler profile upon scanning the frequency of the 780 nm radiation. The measured signal is the transmission of the 780 nm radiation.
Rb atoms are excited to Rydberg nS states according to the two-photon scheme 5S1/2 → 5P3/2 → nS1/2. The radiations from the first- and second-step lasers are counterpropagating in the cell to observe the Rydberg EIT resonance on the top of the Doppler profile upon scanning the frequency of the 780 nm radiation. The frequency of the 480 nm radiation is locked to the ULE cavity. The 780 nm laser beam diameter is set by the collimator to be about 300–600 μm. This radiation was circularly polarized as we have found that this increases the EIT resonance contrast. The 480 nm beam is linearly polarized and focused by a long-focus lens to increase its intensity. The beam diameter at the Rb cell entrance is about 400 μm and at the cell exit is about 80 μm. The measured signal is the transmission of the 780 nm radiation versus the 780 nm radiation frequency.
Figure 6a shows the experimental record (blue curve) of the spectrum of EIT resonance at two-photon laser excitation 5S1/2 → 5P3/2 → 30S1/2 of Rb Rydberg atoms in a vapor cell at the power of the 780 nm radiation P1 = 54 µW and the power of the 480 nm radiation P2 = 56 mW. The detuning δ1 is the detuning of the 780 nm radiation from the closed hyperfine transition 5S1/2(F = 3)→5P3/2(F = 4) in atoms with zero velocity. The green curve is the reference record of the Doppler profile when the 480 nm radiation is switched off. The narrow EIT peak appears on the Doppler profile only in the presence of the 480 nm radiation. It is shifted by δ1 = −100 MHz from the center of the Doppler profile due to nonzero detuning δ2 = +100 MHz of this radiation from the exact resonance 5P3/2 → 30S1/2 in atoms with zero velocity.
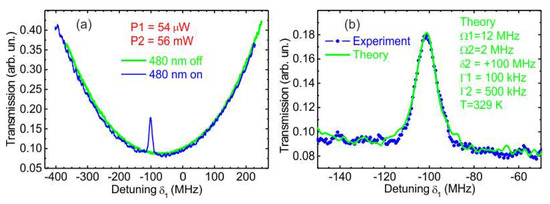
Figure 6.
(a) Experimental record (blue curve) of the spectra of EIT resonance at two-photon laser excitation 5S1/2 → 5P3/2 → 30S1/2 of Rb Rydberg atoms in a vapor cell at the power of the 780 nm radiation P1 = 54 µW and the power of the 480 nm radiation P2 = 56 mW. Detuning δ1 is the detuning of the 780 nm radiation from the closed hyperfine transition 5S1/2(F = 3)→5P3/2(F = 4). The green curve is the reference record of the Doppler profile at the 480 nm radiation switched off. (b) Zoomed view of the experimental EIT resonance (blue dots) having the FWHM of 11.2 MHz. The solid green curve is the best fit from the theoretical calculation with the parameters specified on the right.
Figure 6b shows the zoomed view of the experimental EIT resonance (blue dots). It has nearly Lorentz line shape with the FWHM of 11.2 MHz. This width is typical for the experiments on two-photon excitation in Rb cells [7,8]. The green solid line in Figure 6b is the result of a numerical simulation that best fits the experimental data. The main fitting parameters were the Rabi frequencies of the first and second steps Ω1 and Ω2, and the detuning δ2 of the second-step laser. These were found to be close to the experimental ones. The model also takes into account the measured line widths of the two lasers Γ1/(2π) = 100 kHz and Γ2/(2π) = 500 kHz.
Compared to the theoretical model for cold Rb atoms, in this numerical simulation we had to make the averaging over broad Maxwell velocity distribution of atoms in Rb vapor cell at T = 329 K (the total Doppler broadening is 600 MHz). The velocity averaging was performed for the steady-state analytical solution that we obtained initially for a frozen atom. The averaged theoretical value was the imaginary part of the density matrix element ρ01, which is proportional to the absorption coefficient of the 780 nm radiation measured in the experiment. It is seen that velocity averaging broadens the EIT resonance from ~2 MHz in cold atoms to ~10 MHz in hot atoms. Figure 6b demonstrates a very good agreement between theory and experiment for the EIT resonance line shape and width.
Finally, we have performed an experiment on sensing the microwave field with the Autler–Townes (AT) splitting of the Rydberg EIT resonance. The scheme of transitions in this experiment is shown in Figure 7a. The 41S1/2 Rydberg state is populated via two-photon laser excitation. The microwave field at 58.17 GHz is tuned in resonance with the transition 41S1/2→41P3/2. The AT splitting in the microwave field should be observed if the Rabi frequency of the microwave transition exceeds the width of the EIT resonance.
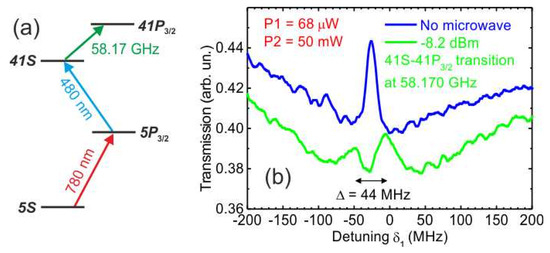
Figure 7.
(a) Scheme of transitions in the experiment on observing the Autler–Townes (AT) splitting of the EIT resonance in the microwave field. The 41S1/2 state is populated via two-photon laser excitation. The microwave field at 58.17 GHz is tuned in resonance with the transition 41S→41P3/2. (b) Experimental records of the EIT resonance at two-photon laser excitation 5S1/2 → 5P3/2 → 41S1/2 of Rb Rydberg atoms in a vapor cell at the power of the 780 nm radiation P1 = 68 µW and the power of the 480 nm radiation P2 = 50 mW: blue curve—without the microwave radiation; green curve—with the microwave radiation at its power −8.2 dBm at the output of the generator Agilent E8257D. The observed AT splitting is Δ = 44 ± 3 MHz.
Figure 7b shows the experimental records of the EIT resonance at two-photon laser excitation 5S1/2 → 5P3/2 → 41S1/2 of Rb Rydberg atoms in a vapor cell at the power of the 780 nm radiation P1 = 68 µW and the power of the 480 nm radiation P2 = 50 mW. The blue curve is the EIT resonance without the microwave radiation. Its FWHM is 16 MHz, which is larger than 11.2 MHz for the 30S1/2 state. This is presumably due to larger intensity of the 780 nm radiation used to compensate for the decrease in the laser excitation probability of the higher 41S1/2 state. The green curve is the EIT resonance with the microwave radiation switched on at its power −8.2 dBm at the output of the generator Agilent E8257D. The actual strength of the microwave field inside Rb cell is unknown and it should be determined from the observed AT splitting Δ = 44 ± 3 MHz in Figure 7b.
In theory [28,32], the observed AT splitting Δ of the Rydberg EIT resonance is described by the formulas
where λ1 and λ2 are wavelengths of radiations at the first and the second steps of the two-photon laser excitation, and ΩMW is the Rabi frequency of the microwave transition. In our experiment we scan δ1, so the calculated from Equation (9) microwave Rabi frequency is ΩMW/(2π) = 72 ± 5 MHz. The Rabi frequency is given by the formula
where dMW is the dipole moment of the microwave transition, and EMW is the amplitude of the microwave field to be measured.
The dipole moments of microwave transitions between Rydberg states can be calculated with high precision due to the quasiclassical motion of the Rydberg electron [26,33]. The numerically calculated dipole moment of the 41S→41P3/2 transition is 776 a.u. for linearly polarized microwave radiation. Then, from Equation (10), we finally obtain EMW = 7.2 ± 0.5 V/m.
Our first experiment, reported in this paper, thus confirms that Rydberg atom-based sensors can provide an absolute measurement of microwave field strength and can potentially become a new SI standard for such measurements, as proposed and demonstrated previously in Refs. [34,35]. We note, however, that in our experiment, the wavelength of the 58.17 GHz radiation is 5 mm, while the Rb cell size is several centimeters. Hence, the observed AT splitting corresponds to some average value of the microwave field strength along the laser beams in the Rb cell. This averaging reduces the heights and broadens the AT-split EIT resonances in Figure 6b. Our numerical simulations for the perfectly homogeneous microwave field have shown that the heights and widths of the split resonances should be the same as for the EIT resonance without a microwave field. This suggests that in our further experiments on Rydberg EIT sensing, we should use a miniature, millimeter-sized Rb cell to provide local measurements of the microwave field.
4. Discussion
In this paper, we presented our first experimental results on the two-photon laser excitation 5S1/2→5P3/2→nS1/2 of Rb atoms to Rydberg nS1/2 states with a homemade 480 nm laser in the second excitation step. We have demonstrated this excitation for cold Rb atoms in a magneto-optical trap with the SFI detection of single Rydberg atoms and for hot Rb atoms in a vapor cell with electromagnetically induced transparency (EIT) detection.
In the experiment with cold Rb atoms, we excited the 42S1/2 state. The two-photon resonance of the 1.7–2.2 MHz width was observed depending on the laser power at the second excitation step. The resonance line shapes agreed well with numerical simulations in a three-level theoretical model, especially for the resonance height. Theory also took into account the nonzero laser line widths and residual Doppler broadening. We note that our simplified model does not consider the magnetic sublevels of atomic states, as more complex models do [36], but it nevertheless produces a reasonable agreement within the experiment. We have also studied multiatom Rydberg excitation spectra of mesoscopic atom ensembles, measured with a selective-field-ionization detector that provides single-atom resolution. Such spectra are an essentially new result, which is of interest for quantum information processing with neutral atoms. It can reveal the presence of the full or partial dipole blockade effect at Rydberg excitation of mesoscopic atom ensembles.
In the experiment with hot Rb atoms, we first excited the 30S1/2 state and observed a narrow Rydberg EIT resonance of 11.2 MHz width on the background of a broad Doppler profile. Its line shape also agreed well with theory, which used velocity averaging. Then, we carried out a similar experiment with the higher 41S1/2 state and observed Autler–Townes splitting of the EIT resonance in the presence of a microwave field, which was in resonance with the microwave transition 41S→41P3/2. This allowed us to measure the average strength of the microwave field and, thus, demonstrate the operation of a Rydberg microwave sensor.
From the results of the above experiments, we may conclude that the developed homemade laser at 480 nm mainly satisfies the requirements for its basic parameters, especially stability and line width. This substantially extends our capabilities for further experiments on quantum information and quantum sensing with Rydberg atoms.
Author Contributions
Conducting experiments—D.B.T. and V.M.E.; methodology and software—I.I.B. and E.A.Y.; building a homemade 480 nm laser—Y.Y.P.; building electronics—V.G.G.; theory, data analysis and writing—I.I.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation, grant number 23-12-00067, https://rscf.ru/project/23-12-00067/ (accessed on 15 May 2023).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gallagher, T.F. Rydberg Atoms; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Lukin, M.D.; Fleischhauer, M.; Cote, R.; Duan, L.M.; Jaksch, D.; Cirac, J.I.; Zoller, P. Dipole Blockade and Quantum Information Processing in Mesoscopic Atomic Ensembles. Phys. Rev. Lett. 2001, 87, 037901. [Google Scholar] [CrossRef] [PubMed]
- Saffman, M.; Walker, T.G.; Mølmer, K. Quantum information with Rydberg atoms. Rev. Mod. Phys. 2010, 82, 2313–2363. [Google Scholar] [CrossRef]
- Ryabtsev, I.I.; Beterov, I.I.; Tretyakov, D.B.; Entin, V.M.; Yakshina, E.A. Spectroscopy of cold rubidium Rydberg atoms for applications in quantum information. Phys. Usp. 2016, 59, 196–208. [Google Scholar] [CrossRef]
- Saffman, M. Quantum computing with atomic qubits and Rydberg interactions: Progress and challenges. J. Phys. B 2016, 49, 202001. [Google Scholar] [CrossRef]
- Henriet, L.; Beguin, L.; Signoles, A.; Lahaye, T.; Browaeys, A.; Reymond, G.-O.; Jurczak, C. Quantum computing with neutral atoms. Quantum 2020, 4, 327. [Google Scholar] [CrossRef]
- Holloway, C.L.; Gordon, J.A.; Schwarzkopf, A.; Anderson, D.A.; Miller, S.A.; Thaicharoen, N.; Raithel, G. Sub-wavelength imaging and field mapping via electromagnetically induced transparency and Autler-Townes splitting in Rydberg atoms. Appl. Phys. Lett. 2014, 104, 244102. [Google Scholar] [CrossRef]
- Fan, H.Q.; Kumar, S.; Daschner, R.; Kübler, H.; Shaffer, J.P. Subwavelength microwave electric-field imaging using Rydberg atoms inside atomic vapor cells. Opt. Lett. 2014, 39, 3030–3033. [Google Scholar] [CrossRef]
- Thoumany, P.; Hänsch, T.; Stania, G.; Urbonas, L.; Becker, T. Optical spectroscopy of rubidium Rydberg atoms with a 297 nm frequency-doubled dye laser. Opt. Lett. 2009, 34, 1621–1623. [Google Scholar] [CrossRef]
- Cubel, T.; Teo, B.K.; Malinovsky, V.S.; Guest, J.R.; Reinhard, A.; Knuffman, B.; Berman, P.R.; Raithel, G. Coherent population transfer of ground-state atoms into Rydberg states. Phys. Rev. A 2005, 72, 023405. [Google Scholar] [CrossRef]
- Reetz-Lamour, M.; Deiglmayr, J.; Amthor, T.; Weidemüller, M. Rabi oscillations between ground and Rydberg states and van der Waals blockade in a mesoscopic frozen Rydberg gas. New J. Phys. 2008, 10, 045026. [Google Scholar] [CrossRef]
- Johnson, T.A.; Urban, E.; Henage, T.; Isenhower, L.; Yavuz, D.D.; Walker, T.G.; Saffman, M. Rabi Oscillations between Ground and Rydberg States with Dipole-Dipole Atomic Interactions. Phys. Rev. Lett. 2008, 100, 113003. [Google Scholar] [CrossRef] [PubMed]
- Viteau, M.; Radogostowicz, J.; Chotia, A.; Bason, M.G.; Malossi, N.; Fuso, F.; Ciampini, D.; Morsch, O.; Ryabtsev, I.I.; Arimondo, E. Ion detection in the photoionization of a Rb Bose-Einstein condensate. J. Phys. B 2010, 43, 155301. [Google Scholar] [CrossRef]
- Nipper, J.; Balewski, J.B.; Krupp, A.T.; Butscher, B.; Löw, R.; Pfau, T. Highly Resolved Measurements of Stark-Tuned Förster Resonances between Rydberg Atoms. Phys. Rev. Lett. 2012, 108, 113001. [Google Scholar] [CrossRef] [PubMed]
- de Léséleuc, S.; Barredo, D.; Lienhard, V.; Browaeys, A.; Lahaye, T. Analysis of imperfections in the coherent optical excitation of single atoms to Rydberg states. Phys. Rev. A 2018, 97, 053803. [Google Scholar] [CrossRef]
- Levine, H.; Keesling, A.; Semeghini, G.; Omran, A.; Wang, T.T.; Ebadi, S.; Bernien, H.; Greiner, M.; Vuletić, V.; Pichler, H.; et al. Parallel Implementation of High-Fidelity Multiqubit Gates with Neutral Atoms. Phys. Rev. Lett. 2019, 123, 170503. [Google Scholar] [CrossRef] [PubMed]
- Entin, V.M.; Yakshina, E.A.; Tretyakov, D.B.; Beterov, I.I.; Ryabtsev, I.I. Spectroscopy of the three-photon laser excitation of cold Rubidium Rydberg atoms in a magneto-optical trap. J. Exp. Theor. Phys. 2013, 116, 721–731. [Google Scholar] [CrossRef]
- Yakshina, E.A.; Tretyakov, D.B.; Entin, V.M.; Beterov, I.I.; Ryabtsev, I.I. Three-photon laser excitation of mesoscopic ensembles of cold rubidium Rydberg atoms. Quantum Electron. 2018, 48, 886–893. [Google Scholar] [CrossRef]
- Yakshina, E.A.; Tretyakov, D.B.; Entin, V.M.; Beterov, I.I.; Ryabtsev, I.I. Observation of the Dipole Blockade Effect in Detecting Rydberg Atoms by the Selective Field Ionization Method. J. Exp. Theor. Phys. 2020, 130, 170–182. [Google Scholar] [CrossRef]
- Beterov, I.I.; Yakshina, E.A.; Tretyakov, D.B.; Alyanova, N.V.; Skvortsova, D.A.; Suliman, G.; Zagirov, T.R.; Entin, V.M.; Ryabtsev, I.I. Three-photon laser excitation of single Rydberg rubidium atoms in an optical dipole trap. J. Exp. Theor. Phys. 2023, 137, 246–253. [Google Scholar] [CrossRef]
- Ryabtsev, I.I.; Beterov, I.I.; Tretyakov, D.B.; Entin, V.M.; Yakshina, E.A. Doppler- and recoil-free laser excitation of Rydberg states via three-photon transitions. Phys. Rev. A 2011, 84, 053409. [Google Scholar] [CrossRef]
- Bohaichuk, S.M.; Ripka, F.; Venu, V.; Christaller, F.; Liu, C.; Schmidt, M.; Kübler, H.; Shaffer, J.P. A Three-Photon Rydberg Atom-Based Radio Frequency Sensing Scheme with Narrow Linewidth. arXiv 2023, arXiv:2304.07409. [Google Scholar] [CrossRef]
- Jiao, Y.-C.; Han, X.-X.; Yang, Z.-W.; Zhao, J.-M.; Jia, S.-T. Electromagnetically Induced Transparency in a Cold Gas with Strong Atomic Interactions. Chin. Phys. Lett. 2016, 33, 123201. [Google Scholar] [CrossRef]
- Sedlacek, J.A.; Schwettmann, A.; Kübler, H.; Löw, R.; Pfau, T.; Shaffer, J.P. Microwave electrometry with Rydberg atoms in a vapour cell using bright atomic resonances. Nat. Phys. 2012, 8, 819–824. [Google Scholar] [CrossRef]
- Sautenkov, V.A.; Saakyan, S.A.; Bobrov, A.A.; Vilshanskaya, E.V.; Zelener, B.B.; Zelener, B.V. Differential two-photon spectroscopy for nondestructive temperature measurements of cold light atoms in a magneto-optical trap. J. Opt. Soc. Am. B 2018, 35, 1546–1551. [Google Scholar] [CrossRef]
- Beterov, I.I.; Ryabtsev, I.I.; Tretyakov, D.B.; Entin, V.M. Quasiclassical calculations of blackbody-radiation-induced depopulation rates and effective lifetimes of Rydberg nS, nP, and nD alkali-metal atoms with n ≤ 80. Phys. Rev. A 2009, 79, 052504. [Google Scholar] [CrossRef]
- Mohapatra, A.K.; Jackson, T.R.; Adams, C.S. Coherent optical detection of highly excited Rydberg states using electromagnetically induced transparency. Phys. Rev. Lett. 2007, 98, 113003. [Google Scholar] [CrossRef] [PubMed]
- Stelmashenko, E.F.; Klezovich, O.A.; Baryshev, V.N.; Tishchenko, V.A.; Blinov, I.Y.; Palchikov, V.G.; Ovsyannikov, V.D. Measuring the Electric Field Strength of Microwave Radiation at the Frequency of the Radiation Transition Between Rydberg States of Atoms 85Rb. Opt. Spectrosc. 2020, 128, 1067–1073. [Google Scholar] [CrossRef]
- Agarwal, G.S. Exact Solution for the Influence of Laser Temporal Fluctuations on Resonance Fluorescence. Phys. Rev. Lett. 1976, 37, 1383–1386. [Google Scholar] [CrossRef]
- Ryabtsev, I.I.; Tretyakov, D.B.; Beterov, I.I.; Entin, V.M. Effect of finite detection efficiency on the observation of the dipole-dipole interaction of a few Rydberg atoms. Phys. Rev. A 2007, 76, 012722. [Google Scholar] [CrossRef]
- Tretyakov, D.B.; Beterov, I.I.; Entin, V.M.; Ryabtsev, I.I.; Chapovsky, P.L. Investigation of cold rubidium Rydberg atoms in a magneto-optical trap. J. Exp. Theor. Phys. 2009, 108, 374–383. [Google Scholar] [CrossRef]
- Fancher, C.T.; Scherer, D.R.; St. John, M.C.; Schmittberger Marlow, B.L. Rydberg Atom Electric Field Sensors for Communications and Sensing. IEEE Trans. Quantum Eng. 2021, 2, 3501313. [Google Scholar] [CrossRef]
- Ovsiannikov, V.D.; Glukhov, I.L.; Nekipelov, E.A. Rates of blackbody radiation-induced transitions from Rydberg states of alkali atoms. J. Phys. B 2011, 44, 195010. [Google Scholar] [CrossRef]
- Holloway, C.L.; Simons, M.T.; Kautz, M.D.; Haddab, A.H.; Gordon, J.A.; Crowley, T.P. A quantum-based power standard: Using Rydberg atoms for a SI-traceable radio-frequency power measurement technique in rectangular waveguides. Appl. Phys. Lett. 2018, 113, 094101. [Google Scholar] [CrossRef]
- Anderson, D.A.; Sapiro, R.E.; Raithel, G. A self-calibrating SI-traceable broadband Rydberg atom-based radio-frequency electric field probe and measurement instrument. IEEE Trans. Antennas Propag. 2021, 69, 5931–5941. [Google Scholar] [CrossRef]
- Gerasimov, L.V.; Yusupov, R.R.; Moiseevsky, A.D.; Vybornyi, I.; Tikhonov, K.S.; Kulik, S.P.; Straupe, S.S.; Sukenik, C.I.; Kupriyanov, D.V. Coupled dynamics of spin qubits in optical dipole microtraps: Application to the error analysis of a Rydberg-blockade gate. Phys. Rev. A 2022, 106, 042410. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).