An Angle Precision Evaluation Method of Rotary Laser Scanning Measurement Systems with a High-Precision Turntable
Abstract
:1. Introduction
2. Measurement Model and Error Analysis of wMPS
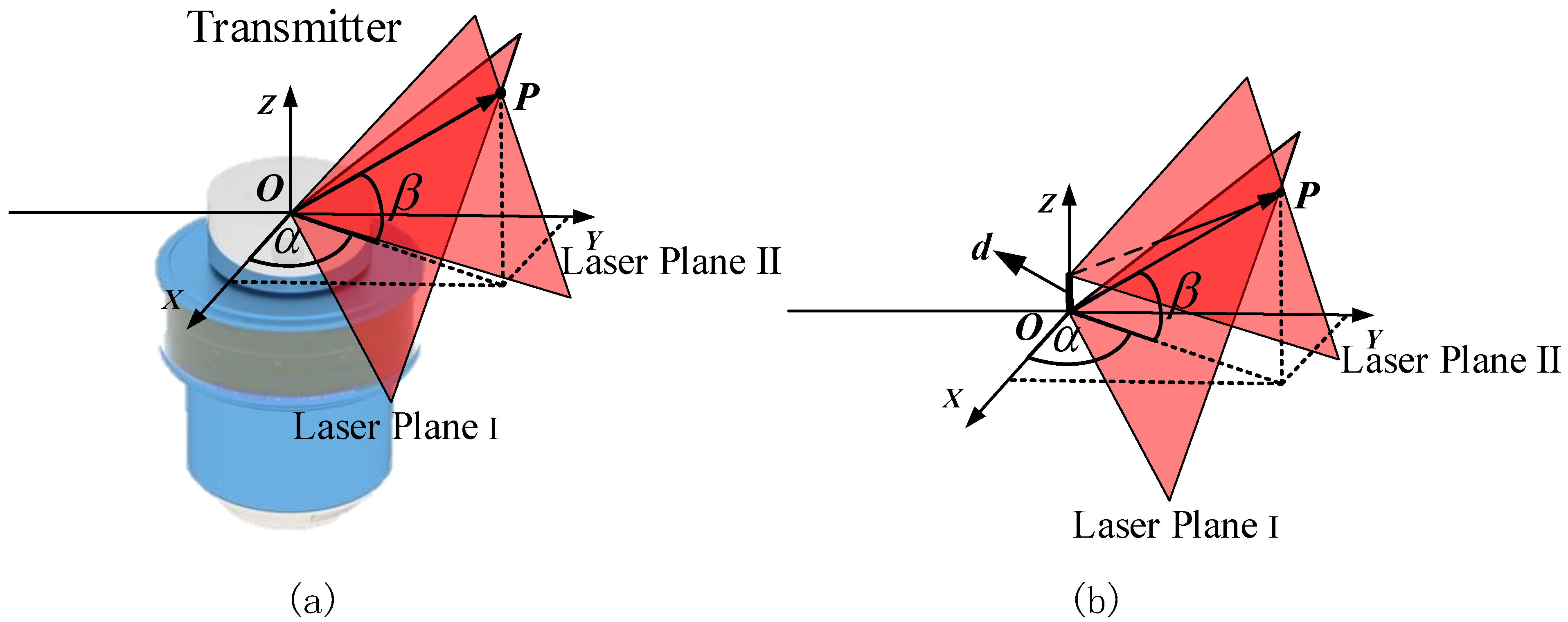
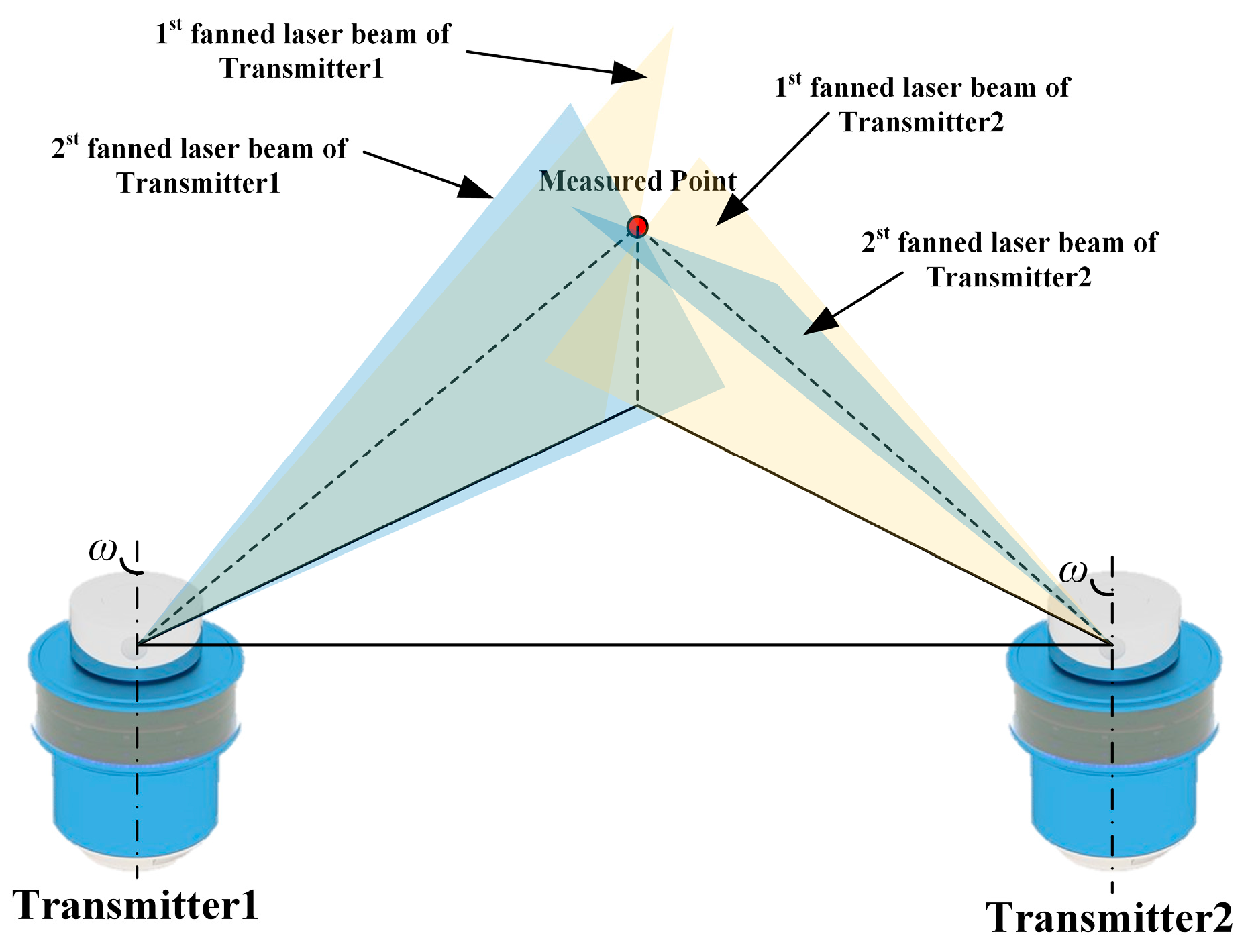
2.1. Measuring Principle of wMPS
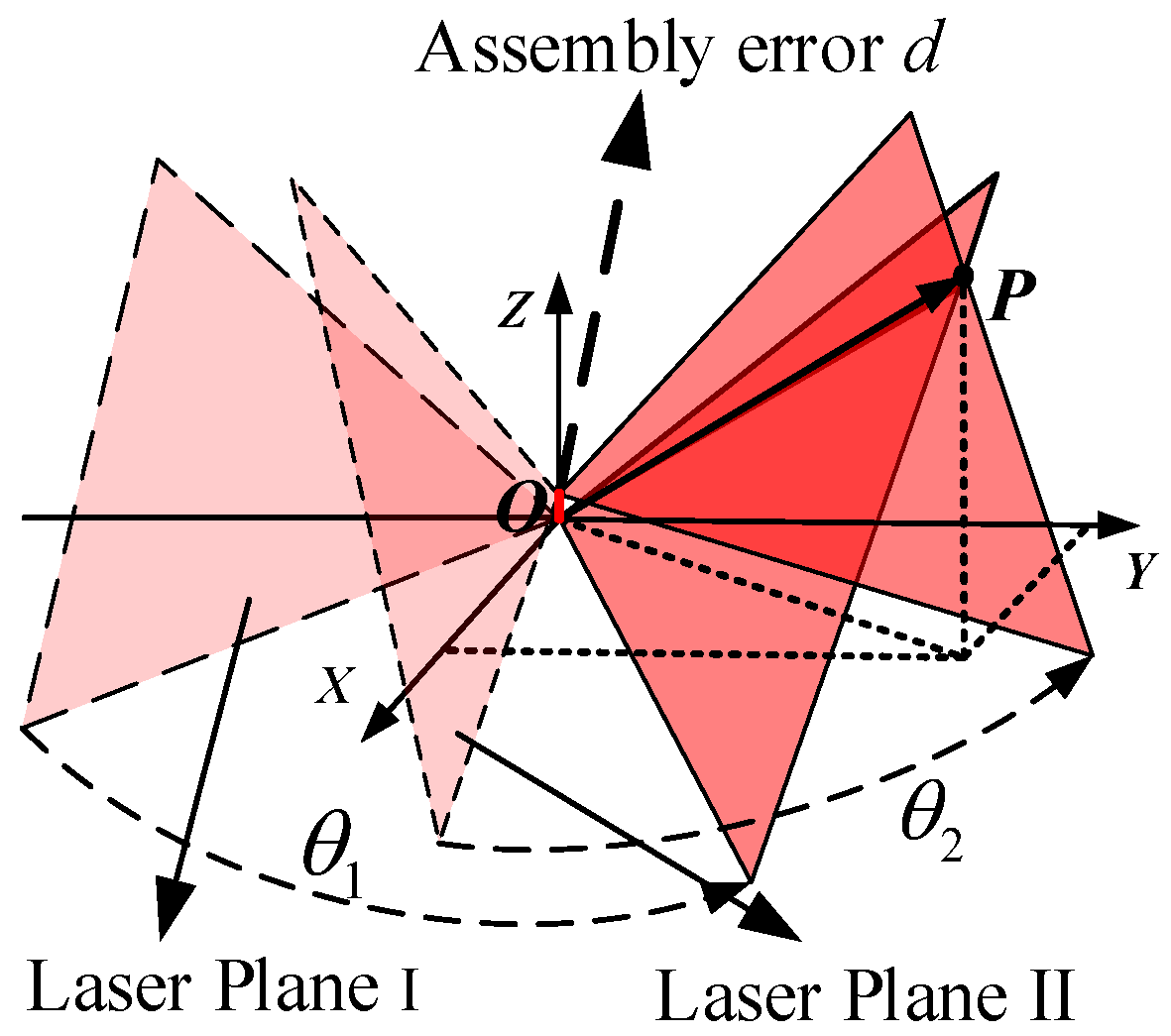
2.2. The Effect of Assembly Error on Vertical and Horizontal Angle
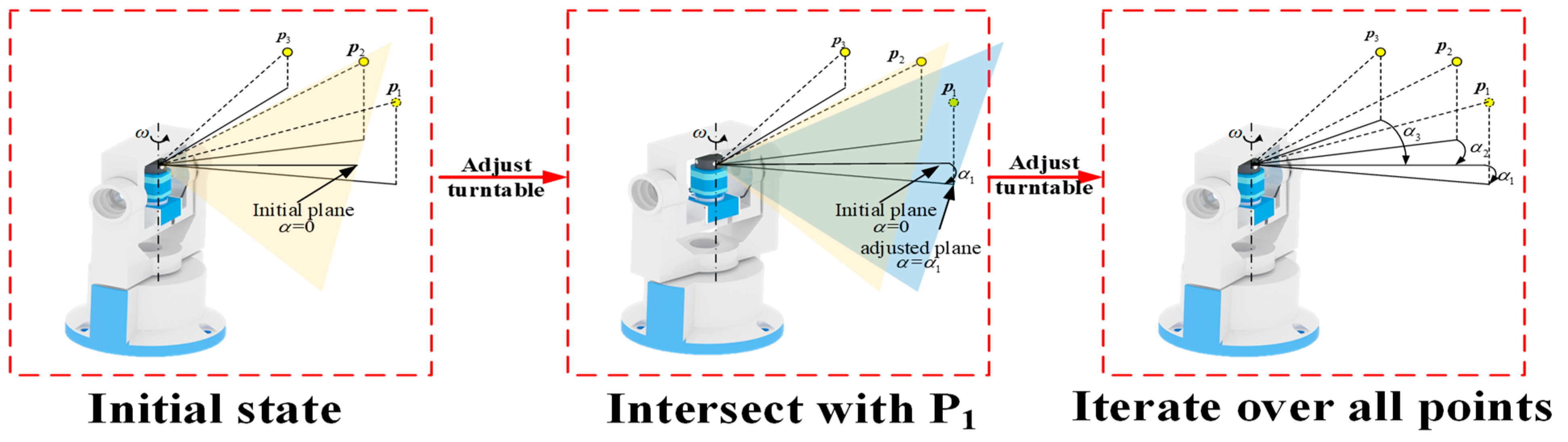
2.3. Establishment of the Evaluation Reference
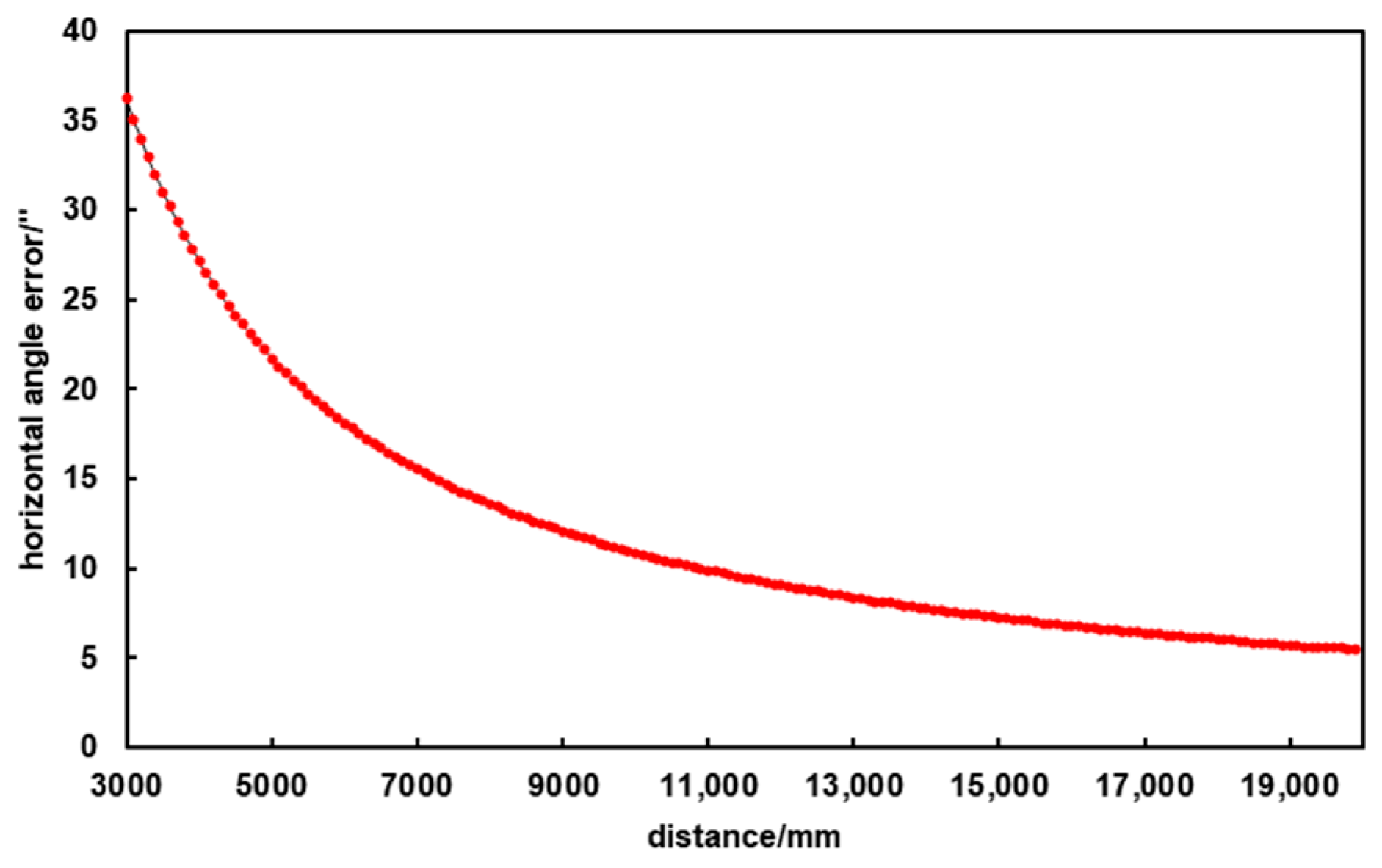
3. Simulations and Analysis
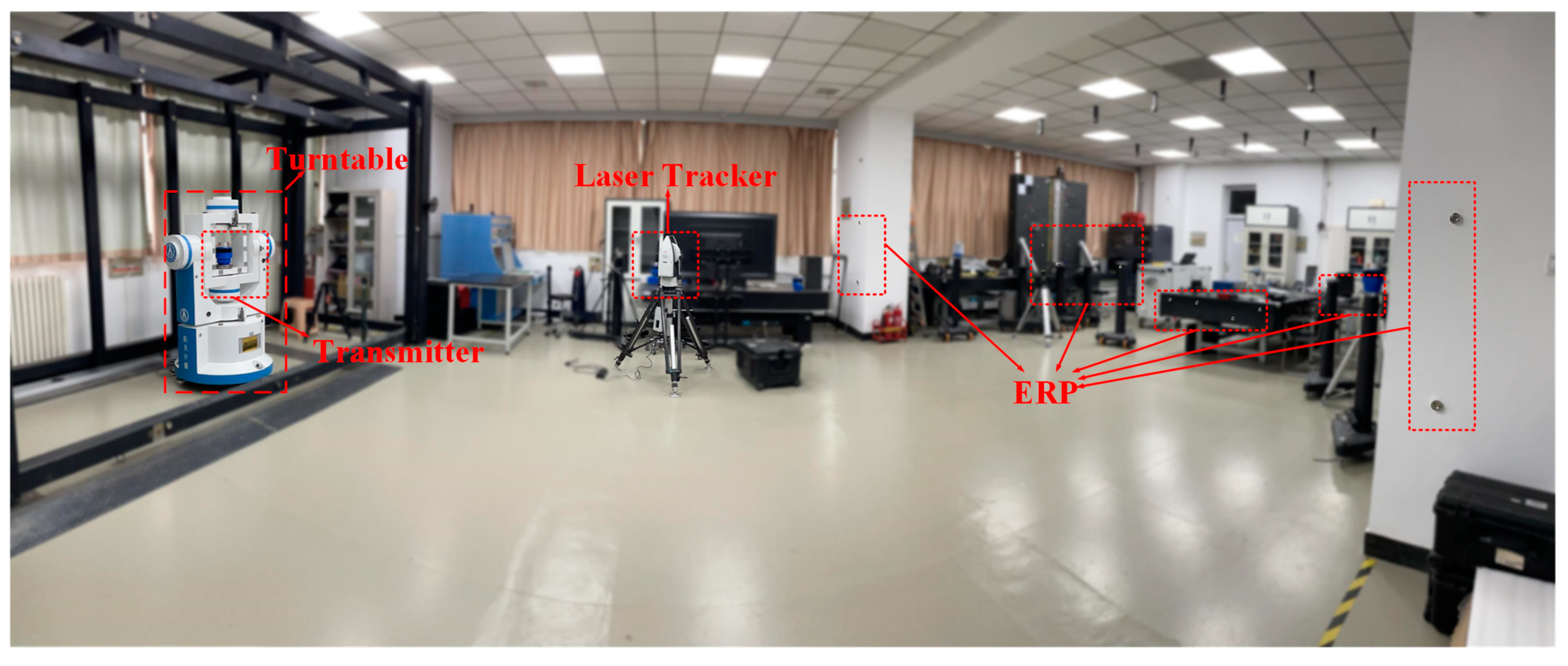
4. Experiments
4.1. Evaluation of the Repeatability of the wMPS Transmitter
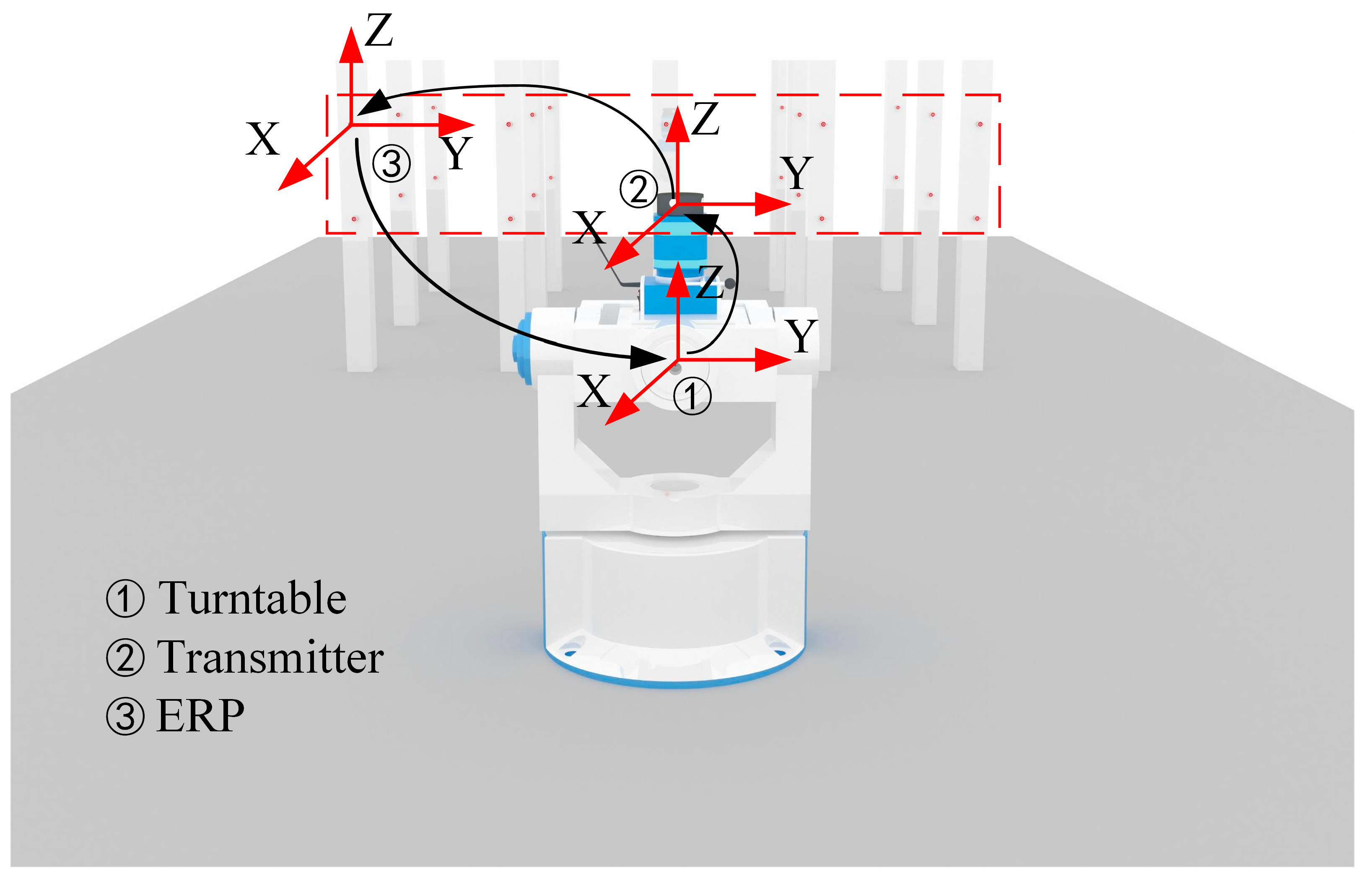
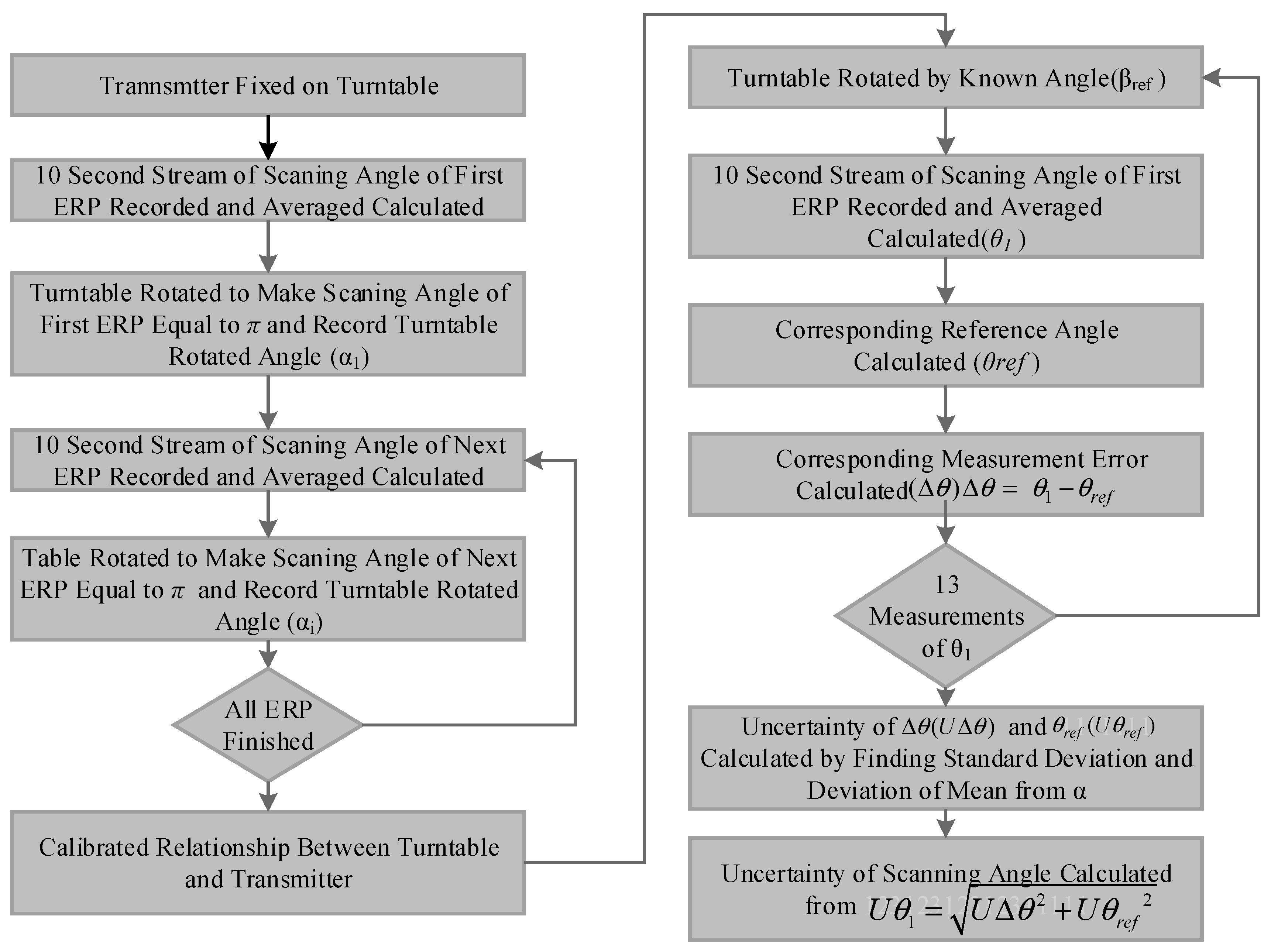
4.2. Calibration Progress of the Relationship between the Transmitter and Turntable
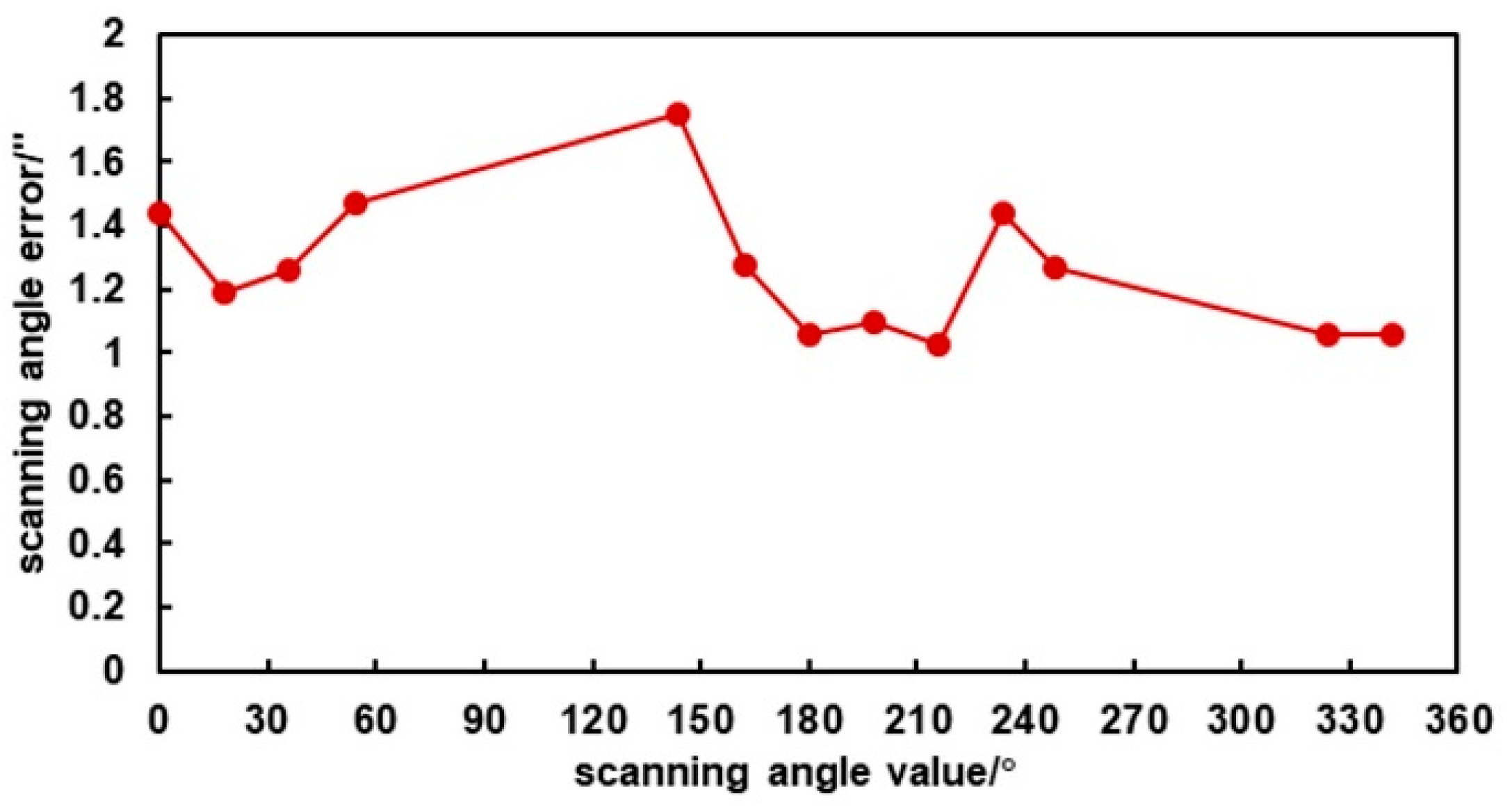
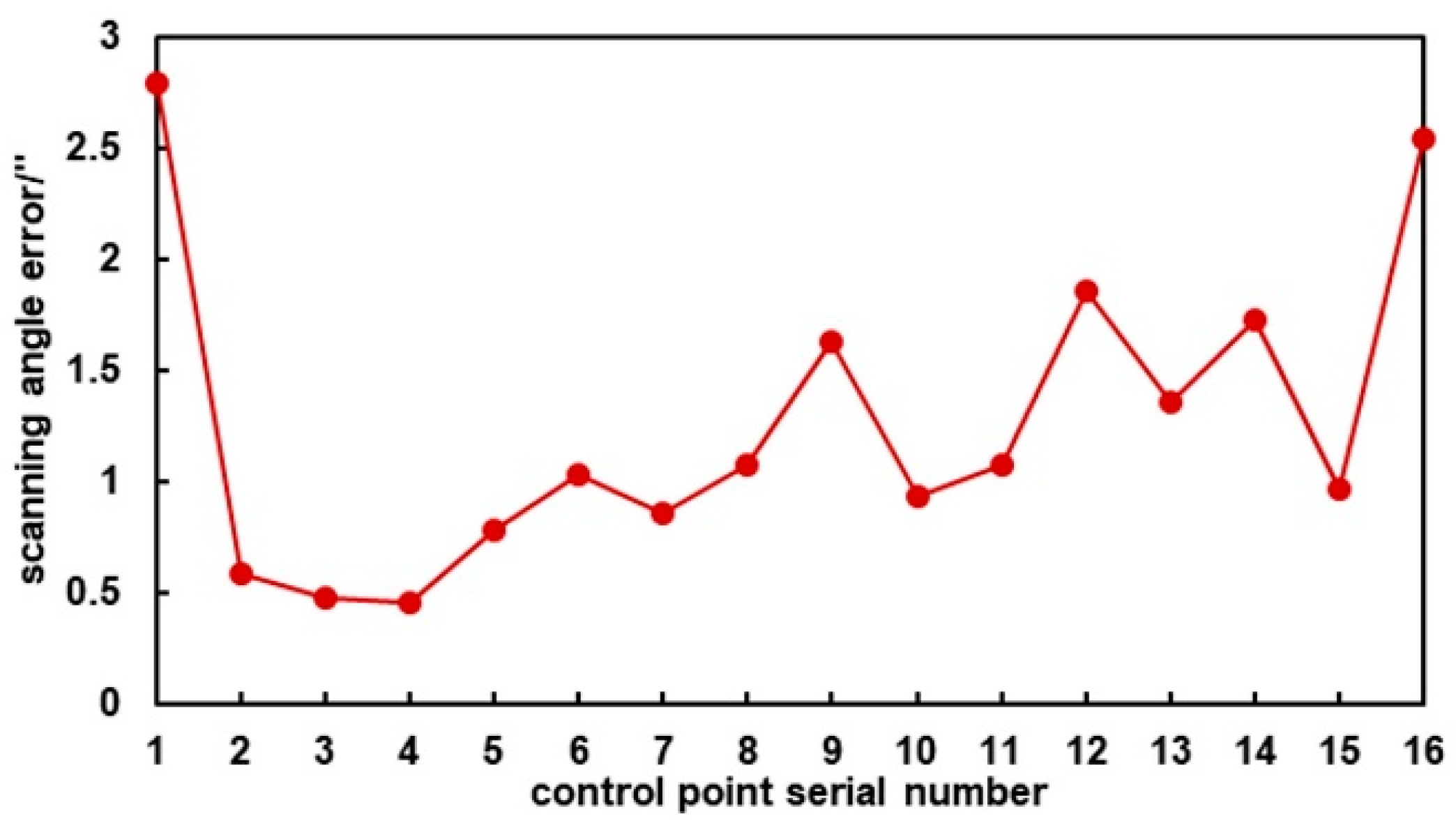
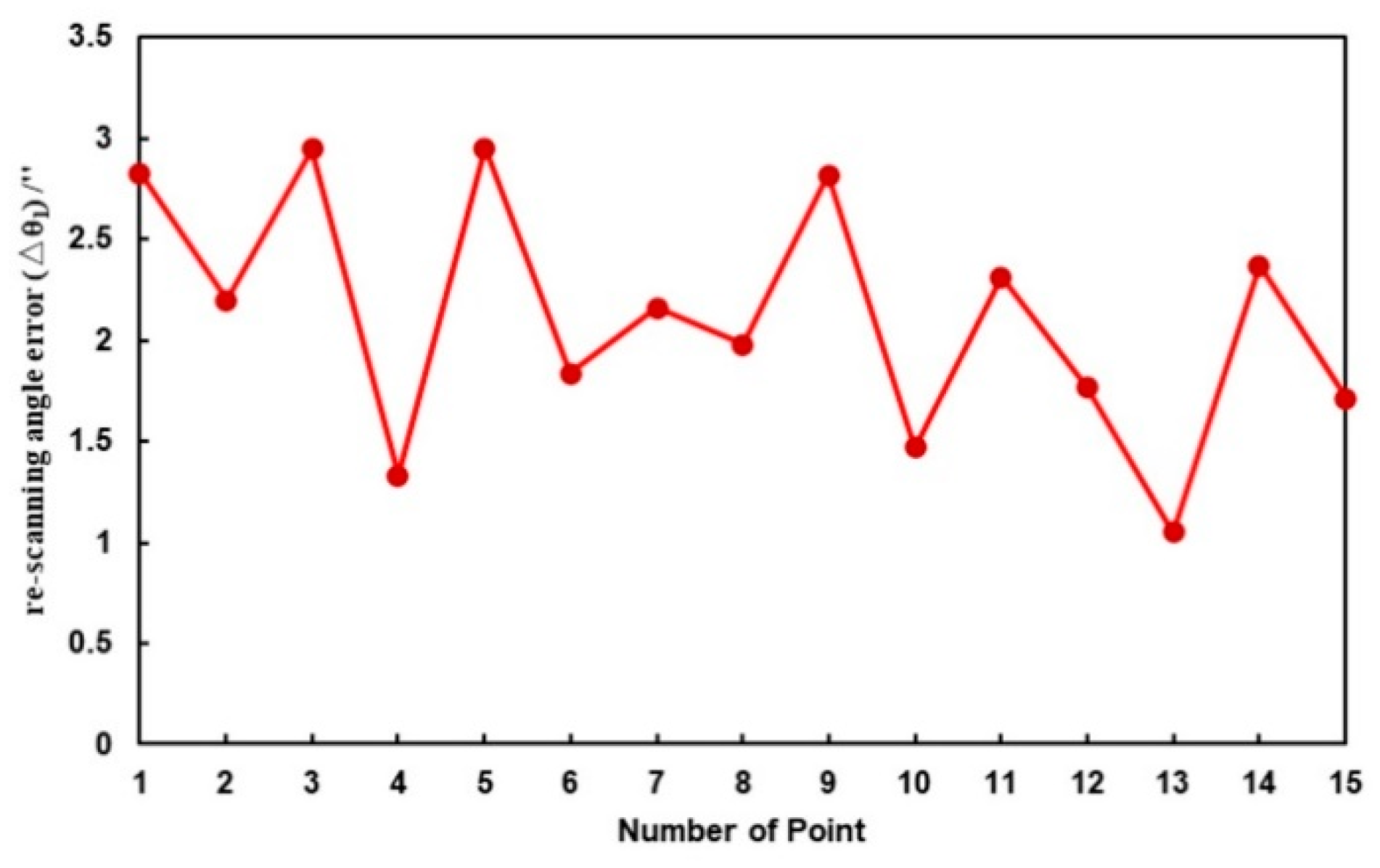
4.3. Evaluation of Scanning Angle Error in Different Positions
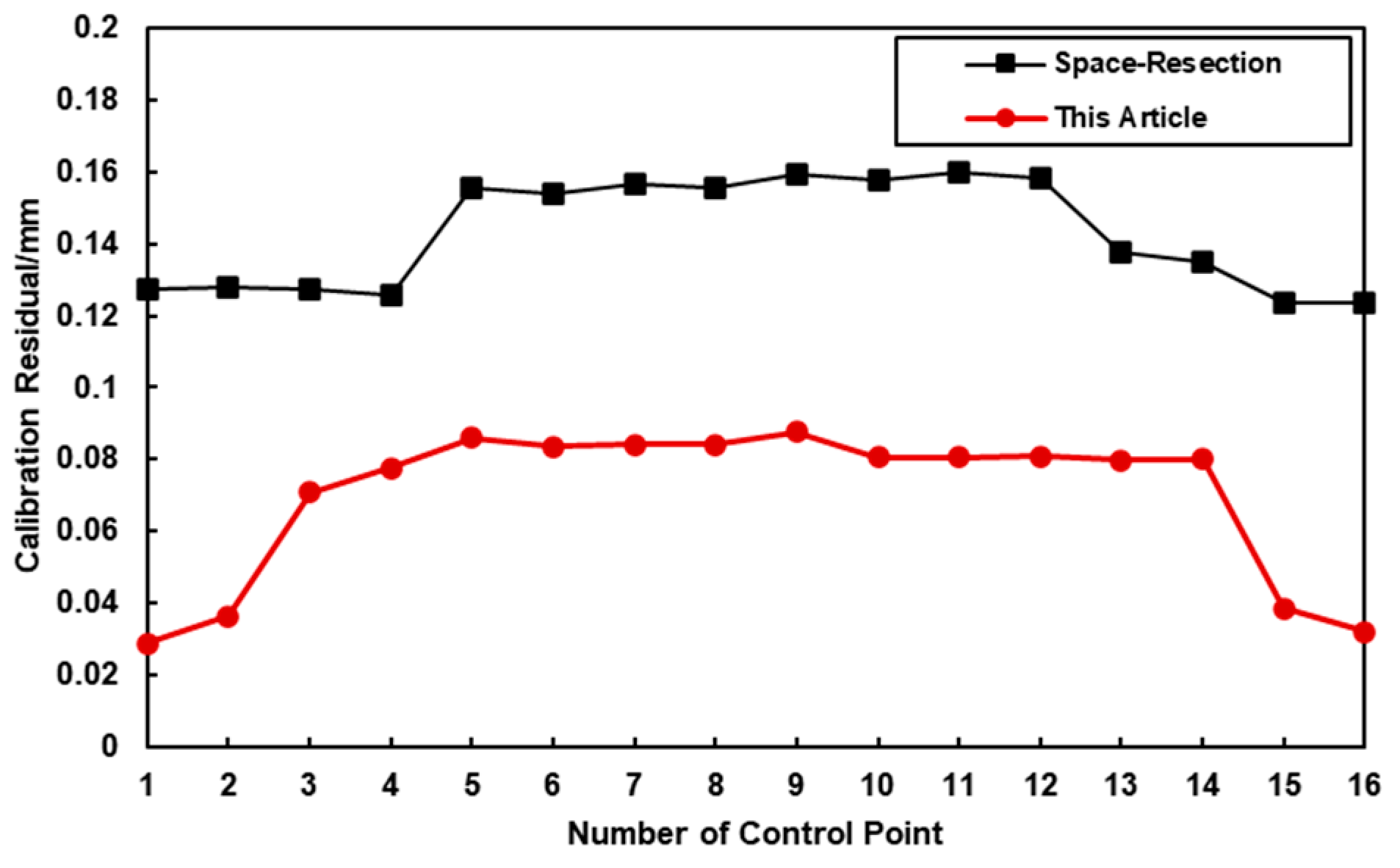
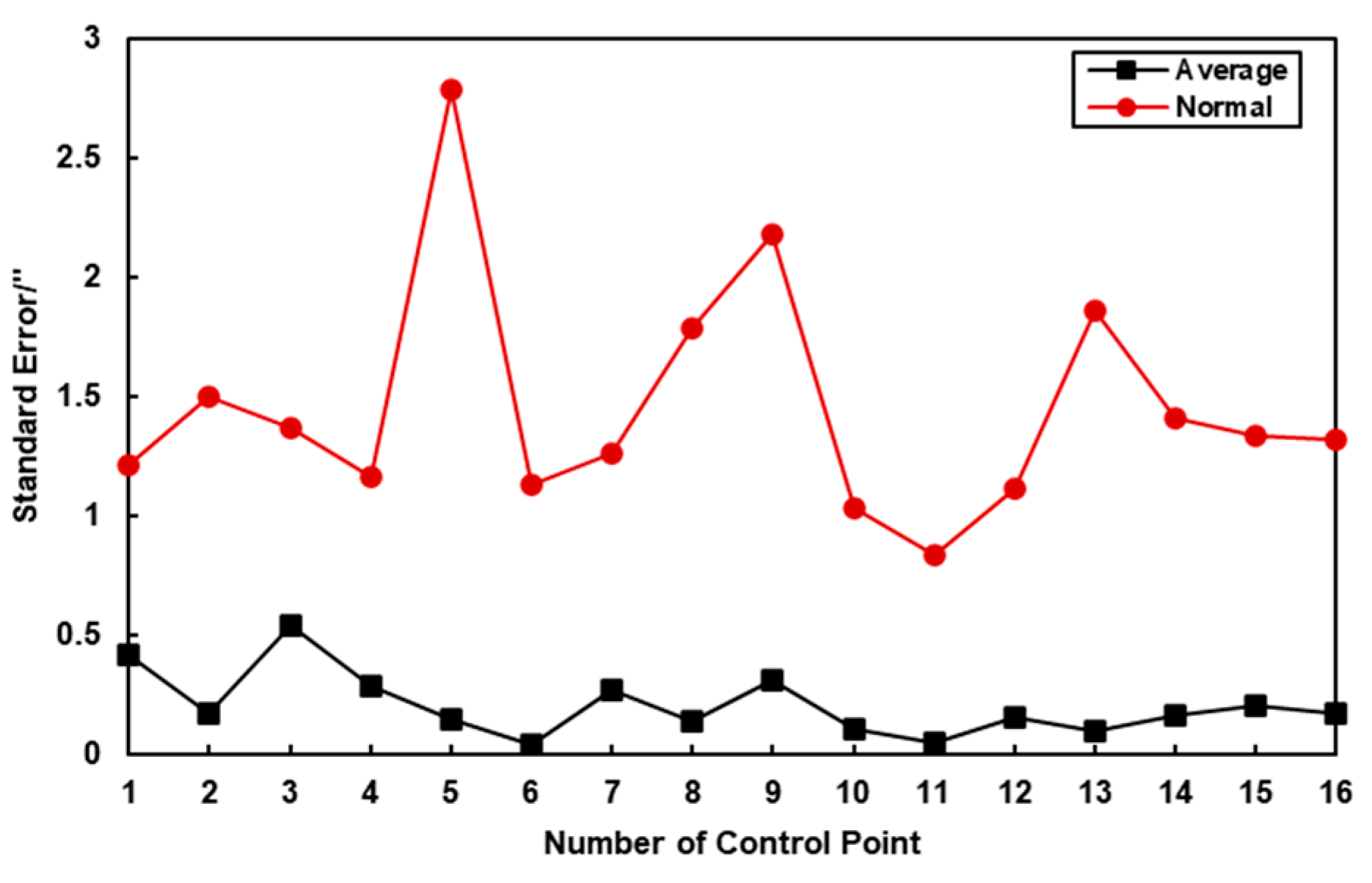
4.4. Verification by Coordinate Measurement
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fan, K.-C.; Chen, L.-C. Special Issue on Precision Dimensional Measurements. Appl. Sci. 2019, 9, 3314. [Google Scholar] [CrossRef]
- Schmitt, R.H.; Peterek, M.; Morse, E.; Knapp, W.; Galetto, M.; Hartig, F.; Goch, G.; Hughes, B.; Forbes, A.; Estler, W.T. Advances in Large-Scale Metrology—Review and future trends. CIRP Ann. 2016, 65, 643–665. [Google Scholar] [CrossRef]
- Franceschini, F.; Galetto, M.; Maisano, D.; Mastrogiacomo, L. Large-scale dimensional metrology (LSDM): From tapes and theodolites to multi-sensor systems. Int. J. Precis. Eng. Manuf. 2014, 15, 1739–1758. [Google Scholar]
- Franceschini, F.; Galetto, M.; Maisano, D.; Mastrogiacomo, L.; Pralio, B. Distributed Large-Scale Dimensional Metrology: New Insights; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Hao, Q.; Zhang, Y.; Fan, S.; Jiang, P.; Yin, H.; Xu, D. A novel three-dimensional coordinate positioning algorithm based on factor graph. IEEE Access 2020, 8, 207167–207180. [Google Scholar]
- Maisano, D.A.; Mastrogiacomo, L. Determining the extrinsic parameters of a network of large-volume metrology sensors of different types. Precis. Eng. 2022, 74, 316–333. [Google Scholar] [CrossRef]
- Muelaner, J.E.; Wang, Z.; Jamshidi, I.; Maropoulos, P.G.; Mileham, A.R.; Hughes, E.B.; Forbes, A.B. Study of the uncertainty of angle measurement for a rotary-laser automatic theodolite (R-LAT). Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2009, 223, 217–229. [Google Scholar] [CrossRef]
- Zhao, J.; Ren, Y.; Lin, J.; Yin, S.; Zhu, J. Study on verifying the angle measurement performance of the rotary-laser system. Opt. Eng. 2018, 57, 044106. [Google Scholar] [CrossRef]
- Qiang, H.; Hongliang, Y.; Dingjie, X.; Bo, Z. Research on the IGPS device error and its influence of positioning accuracy. In Proceedings of the 2017 Forum on Cooperative Positioning and Service (CPGPS), Harbin, China, 19–21 May 2017; pp. 294–299. [Google Scholar]
- Muelaner, J.E.; Wang, Z.; Martin, O.; Jamshidi, J.; Maropoulos, P.G. Verification of the indoor GPS system, by comparison with calibrated coordinates and by angular reference. J. Intell. Manuf. 2012, 23, 2323–2331. [Google Scholar] [CrossRef]
- Schmitt, R.; Nisch, S.; Schnberg, A.; Demeester, F.; Renders, S. Performance evaluation of iGPS for industrial applications. In Proceedings of the 2010 International Conference on Indoor Positioning and Indoor Navigation, Zurich, Switzerland, 15–17 September 2010. [Google Scholar]
- Su, W.; Guo, J.; Liu, Z.; Jia, K. An intrinsic parameter calibration method for R-LAT system based on CMM. Int. J. Adv. Manuf. Technol. 2022, 120, 3155–3165. [Google Scholar] [CrossRef]
- American National Standards Institute. Performance Evaluation of Laser-Based Spherical Coordinate Measurement Systems; American Society of Mechanical Engineers: New York, NY, USA, 2006. [Google Scholar]
- Hughes, B.; Forbes, A.; Lewis, A.; Sun, W.; Veal, D.; Nasr, K. Laser tracker error determination using a network measurement. Meas. Sci. Technol. 2011, 22, 045103. [Google Scholar] [CrossRef]
- Icasio-Hernández, O.; Bellelli, D.A.; Vieira, L.H.B.; Cano, D.; Muralikrishnan, B. Validation of the network method for evaluating uncertainty and improvement of geometry error parameters of a laser tracker. Precis. Eng. 2021, 72, 664–679. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Muralikrishnan, B.; Hernandez, O.I.; Shakarji, C.; Sawyer, D. Performance evaluation of laser trackers using the network method. Measurement 2020, 165, 108165. [Google Scholar] [CrossRef]
- Predmore, C.R. Bundle adjustment of multi-position measurements using the Mahalanobis distance. Precis. Eng. 2010, 34, 113–123. [Google Scholar] [CrossRef]
- More, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. Lect. Notes Math. 1978, 630, 105–116. [Google Scholar]
- Lin, J.R.; Sun, J.L.; Yang, L.H.; Zhang, R.; Ren, Y.J. Modeling and Optimization of Rotary Laser Surface for Large-Scale Optoelectronic Measurement System. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Xiong, C.; Bai, H. Calibration of Large-Scale Spatial Positioning Systems Based on Photoelectric Scanning Angle Measurements and Spatial Resection in Conjunction with an External Receiver Array. Appl. Sci. 2020, 10, 925. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Lin, J.; Shi, S.; Shao, K.; Zhu, J. An Angle Precision Evaluation Method of Rotary Laser Scanning Measurement Systems with a High-Precision Turntable. Photonics 2023, 10, 1224. https://doi.org/10.3390/photonics10111224
Zhang R, Lin J, Shi S, Shao K, Zhu J. An Angle Precision Evaluation Method of Rotary Laser Scanning Measurement Systems with a High-Precision Turntable. Photonics. 2023; 10(11):1224. https://doi.org/10.3390/photonics10111224
Chicago/Turabian StyleZhang, Rao, Jiarui Lin, Shendong Shi, Kunpeng Shao, and Jigui Zhu. 2023. "An Angle Precision Evaluation Method of Rotary Laser Scanning Measurement Systems with a High-Precision Turntable" Photonics 10, no. 11: 1224. https://doi.org/10.3390/photonics10111224
APA StyleZhang, R., Lin, J., Shi, S., Shao, K., & Zhu, J. (2023). An Angle Precision Evaluation Method of Rotary Laser Scanning Measurement Systems with a High-Precision Turntable. Photonics, 10(11), 1224. https://doi.org/10.3390/photonics10111224




