Optical Phased Array-Based Laser Beam Array Subdivide Pixel Method for Improving Three-Dimensional Imaging Resolution
Abstract
:1. Introduction
2. Methods
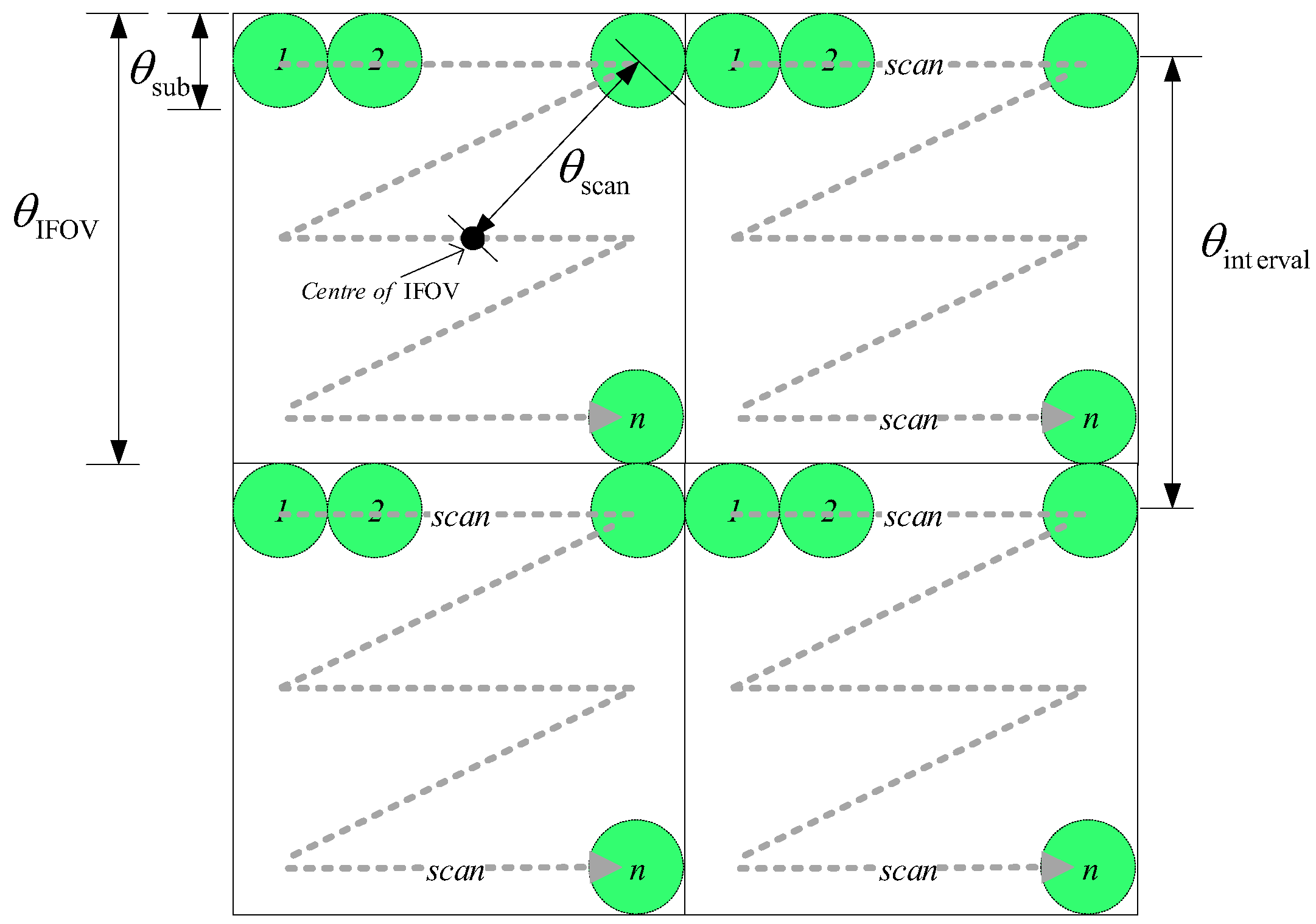
2.1. Fundamentals of the Beam Array Scanning Method for Improving Spatial Resolution
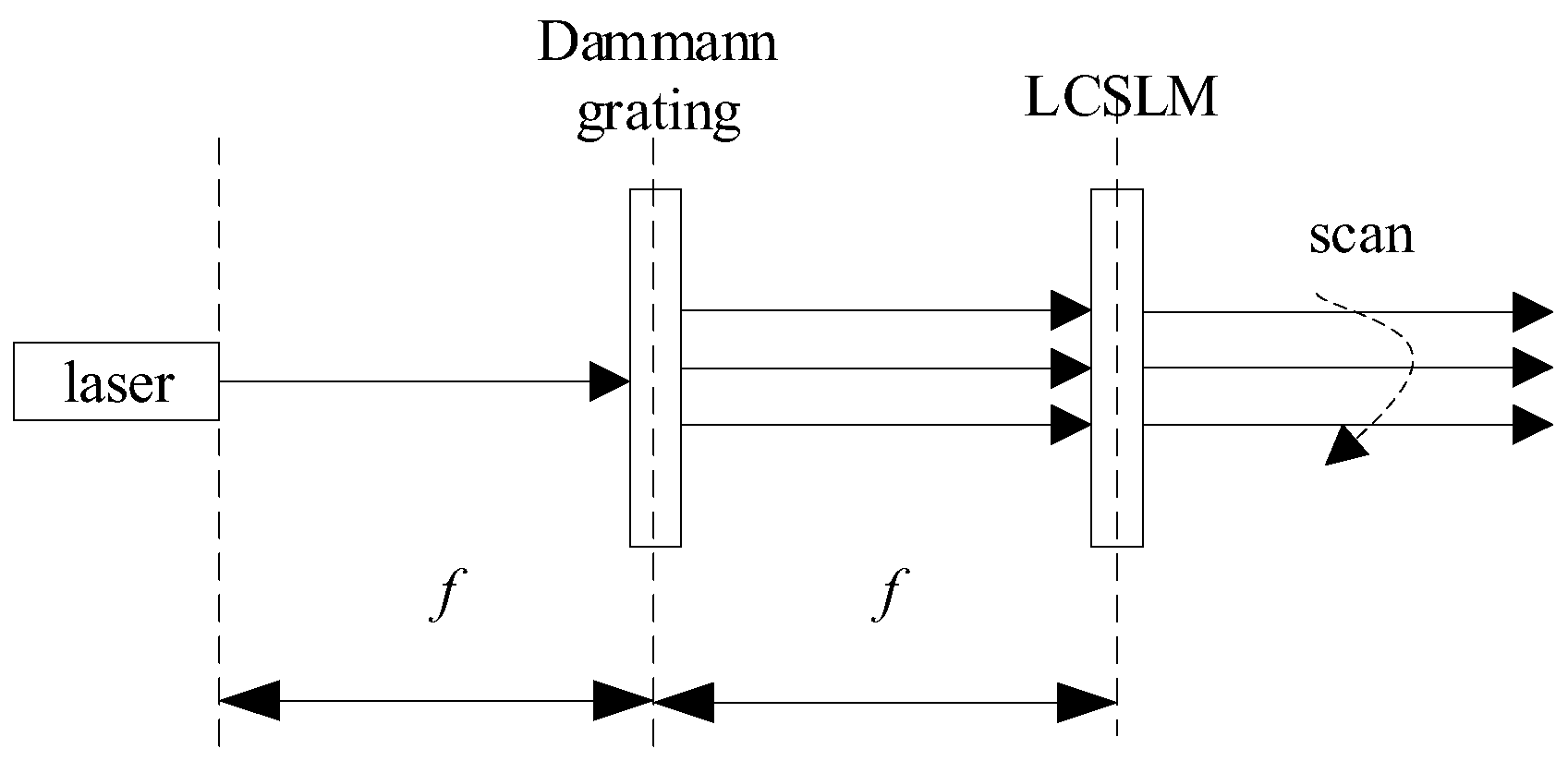
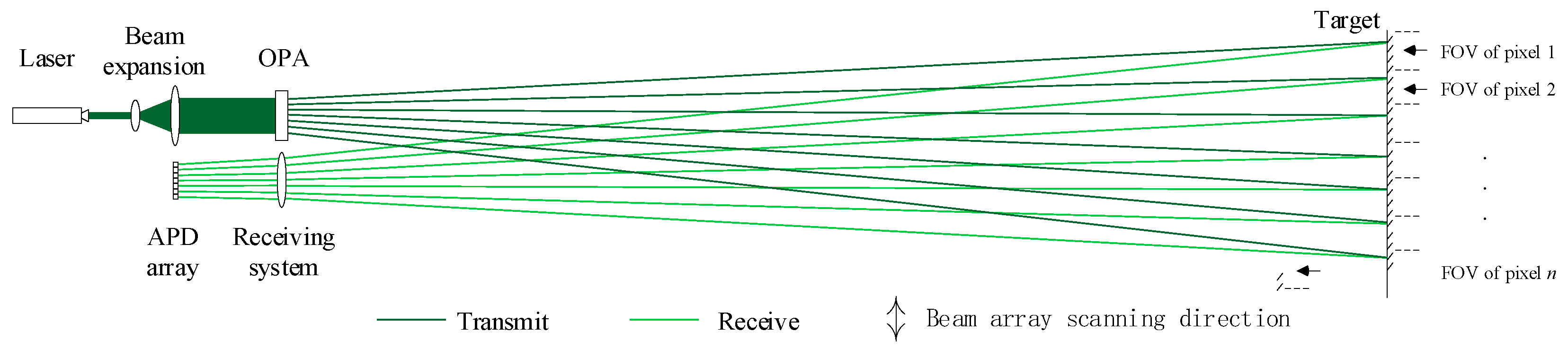
2.2. Optical Phased Array Beam Array Generation and Scanning Methods
2.2.1. Principle of Optical Phased Array Beam Control
2.2.2. Modulation Phase Design
Beam Array Generation Phase Design
Beam Array Scanning Phase Design
3. Simulation and Analysis
3.1. Beam Control Method Simulation
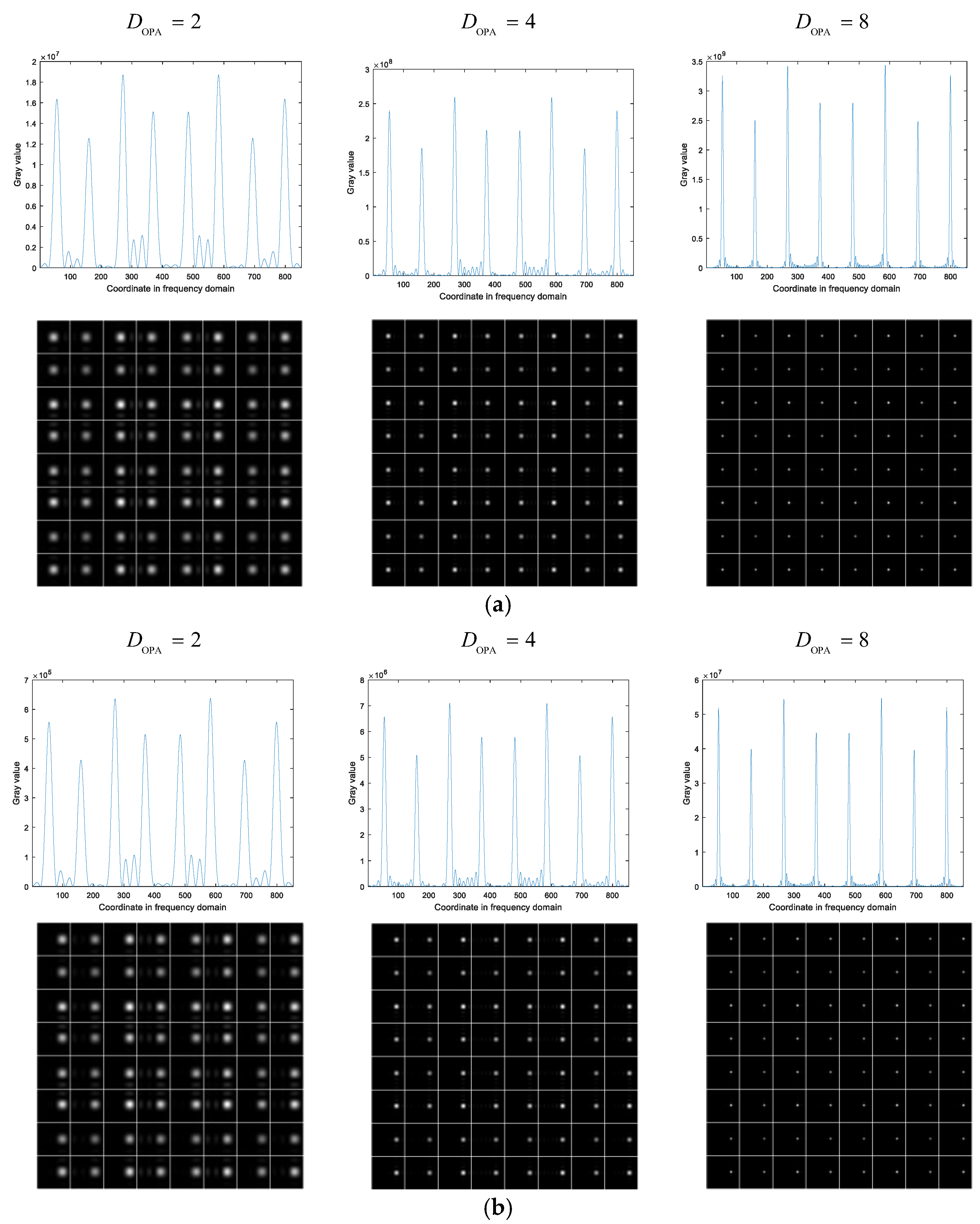
3.1.1. Simulation Results
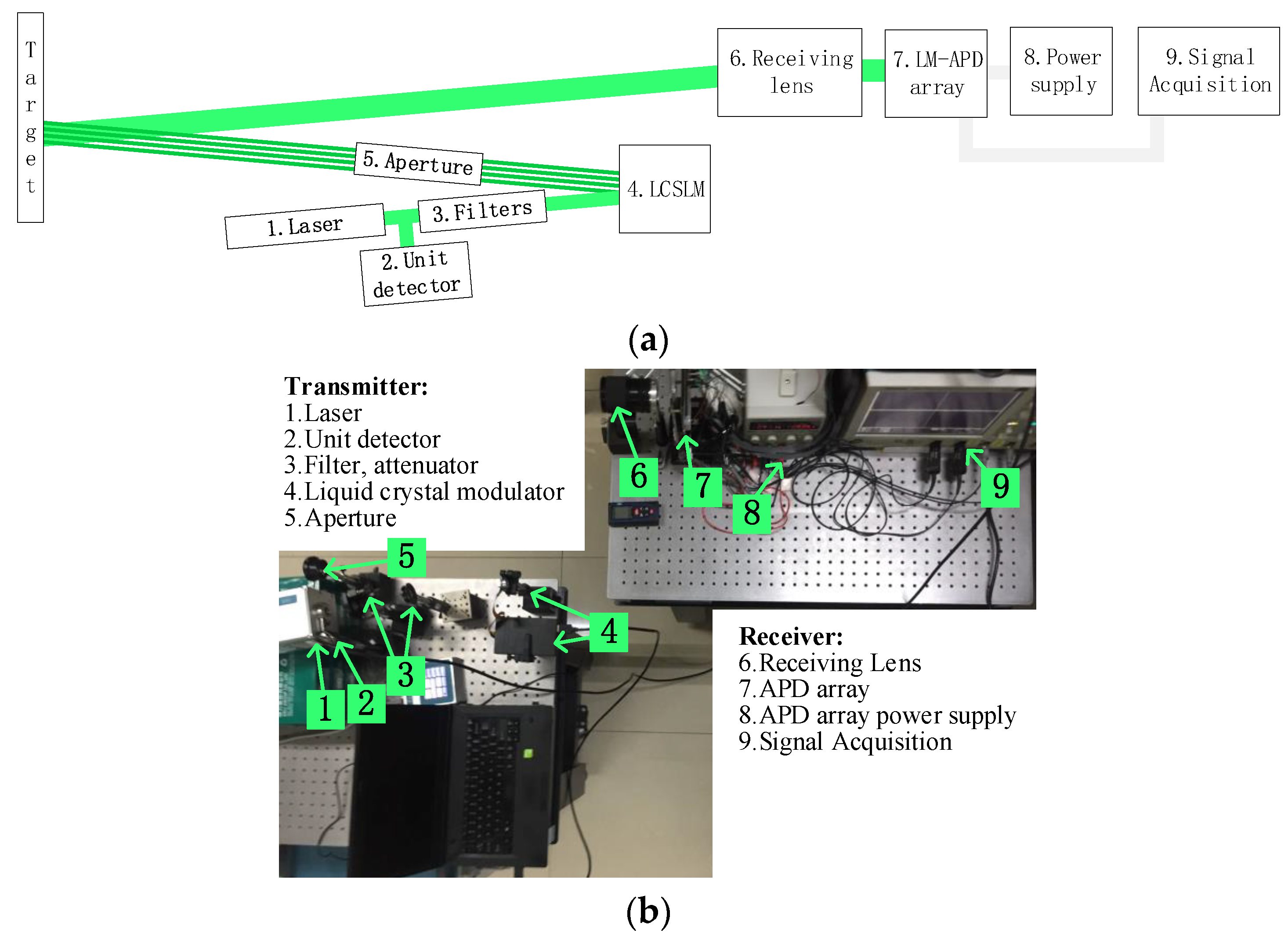
3.1.2. Experiment Results
3.2. Performance Analysis
3.2.1. Field of View
3.2.2. Spatial Resolution
3.2.3. Number of Sampling Points
3.2.4. Beam Energy Uniformity
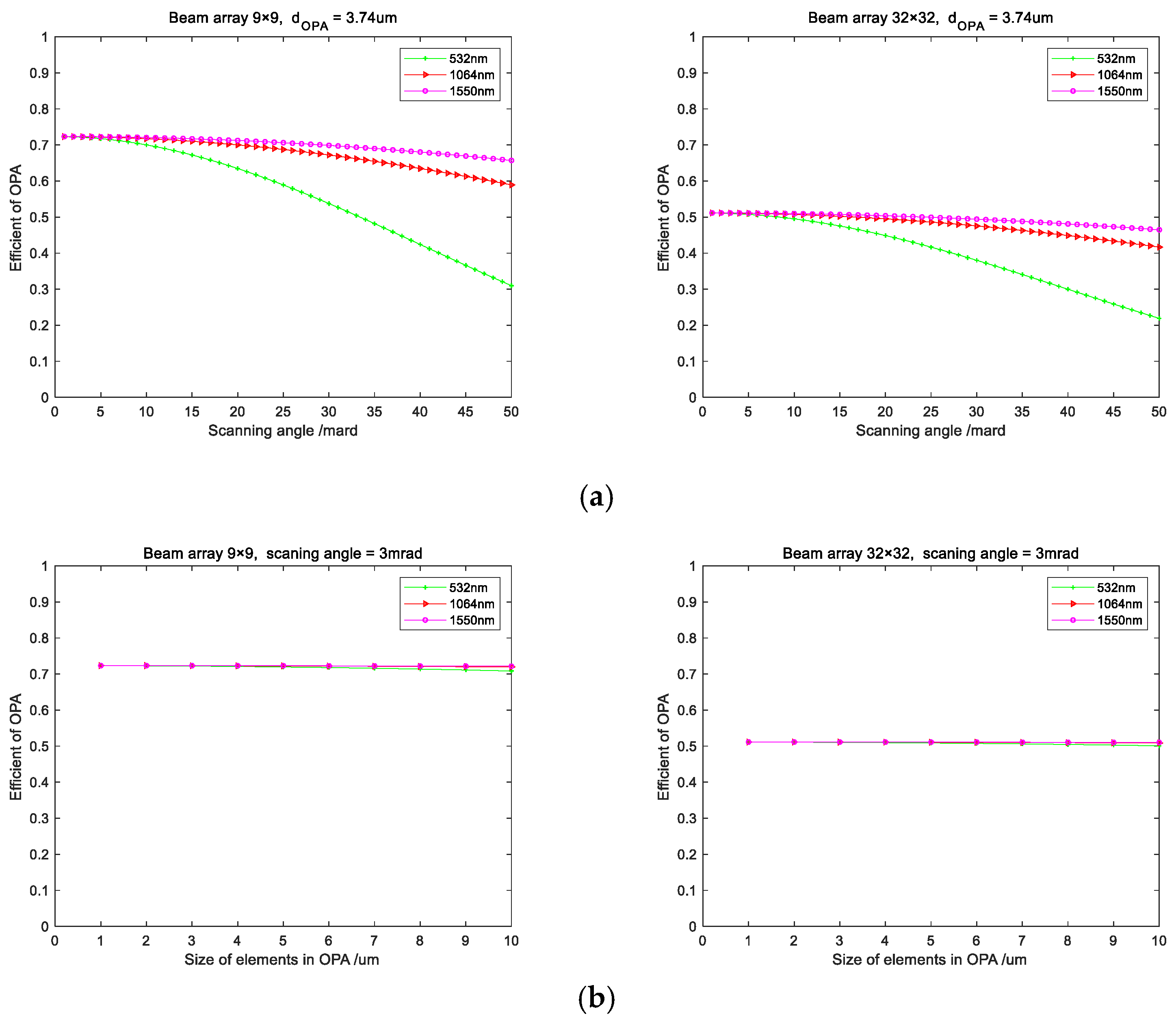
3.2.5. Energy Efficiency
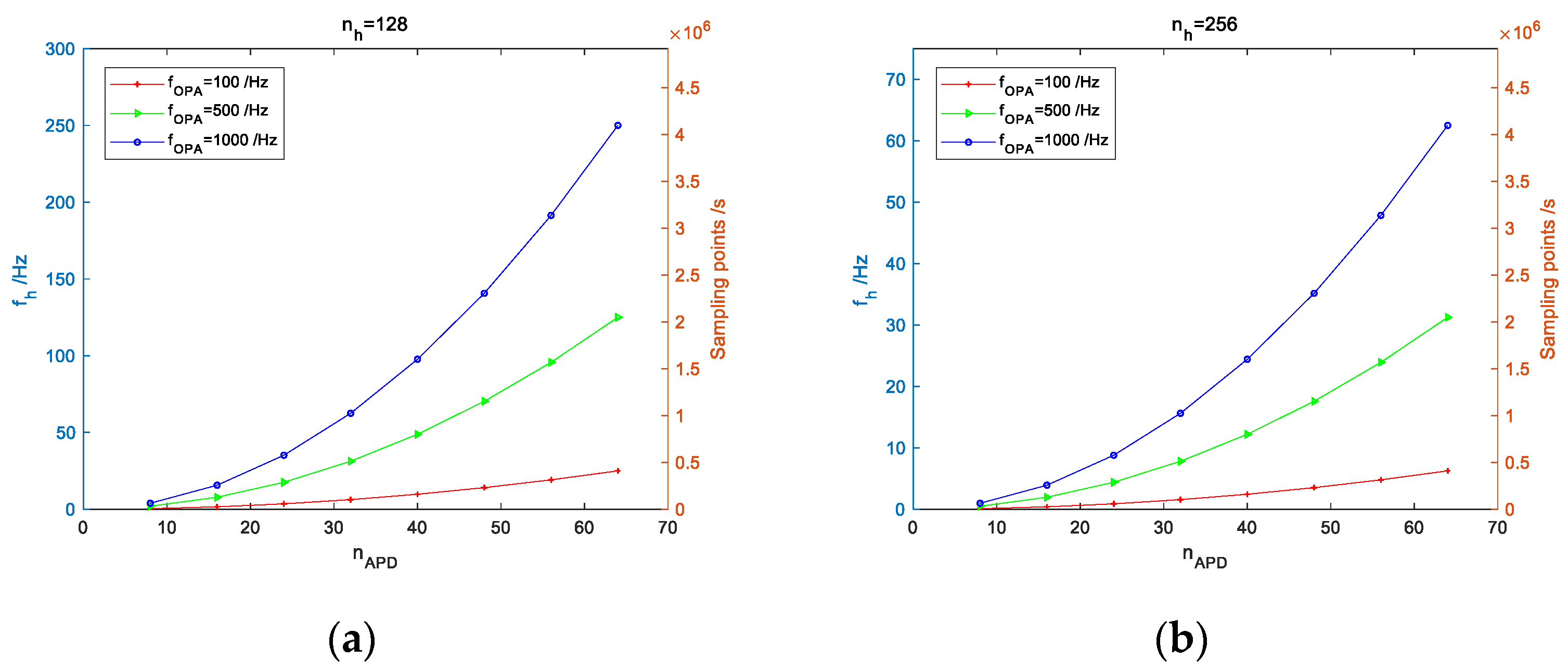
3.2.6. Imaging Frame Rate
3.2.7. Phase Modulation Devices
4. Results
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chang, L.; Liu, J.; Chen, Z.; Bai, J.; Shu, L. Stereo Vision-Based Relative Position and Attitude Estimation of Non-Cooperative Spacecraft. Aerospace 2021, 8, 230. [Google Scholar] [CrossRef]
- Haarlammert, T.; Kwiatkowski, A. Threat detection, identification and optical counter measures for space-based applications. In Proceedings of the High-Power Lasers and Technologies for Optical Countermeasures, Berlin, Germany, 5–8 September 2022; SPIE: Bellingham, WA, USA; Volume 12273, pp. 33–49. [Google Scholar]
- Sornsin, B.A.; Short, B.W. Global shutter solid state flash lidar for spacecraft navigation and docking applications. In Proceedings of the Laser Radar Technology and Applications XXIV, Baltimore, MD, USA, 14–18 April 2019; SPIE: Bellingham, WA, USA; Volume 11005, pp. 229–240. [Google Scholar]
- Pensado, E.A.; de Santos, L.M.G.; Sanjurjo-Rivo, M.; Jorge, H.G. Deep Learning Based Target Pose Estimation Using LiDAR Measurements in Active Debris Removal Operations. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 5658–5670. [Google Scholar] [CrossRef]
- Negri, R.B.; Prado, A.F.; Chagas, R.A.; de Moraes, R.V. Autonomous Rapid Exploration in Close-Proximity of an Asteroid. arXiv 2022, arXiv:2208.03378. [Google Scholar]
- Jin, C.F.; Wang, Y.; Cao, L.; Yu, M.; Liu, L.; Zhao, Y. Design of fiber-array image laser radar system. Opto-Electron. Eng. 2012, 39, 115. [Google Scholar]
- Zhou, G.; Zhou, X.; Yang, J.; Tao, Y.; Nong, X.; Baysal, O. Flash Lidar sensor using fiber-coupled APDs. IEEE Sens. J. 2015, 15, 4758–4768. [Google Scholar] [CrossRef]
- Ito, K.; Niclass, C.; Aoyagi, I.; Matsubara, H.; Soga, M.; Kato, S.; Maeda, M.; Kagami, M. System Design and Performance Characterization of a MEMS-Based Laser Scanning Time-of-Flight Sensor Based on a 256 × 64-pixel Single-Photon Imager. IEEE Photonics J. 2013, 5, 6800114. [Google Scholar] [CrossRef]
- Zhao, W.; Han, S. Cramer-Rao Lower Bound for the Range Accuracy of 3D Flash Imaging Lidar System. Trans. Beijing Inst. Technol. 2014, 34, 501–505. [Google Scholar]
- Amzajerdian, F.; Roback, V.E.; Bulyshev, A.E.; Brewster, P.F.; Carrion, W.A.; Pierrottet, D.F.; Hines, G.D.; Petway, L.B.; Barnes, B.W.; Noe, A.M. Imaging flash LIDAR for safe landing on solar system bodies and spacecraft rendezvous and docking. In Proceedings of the Laser Radar Technology and Applications XX; and Atmospheric Propagation XII, Baltimore, MD, USA, 20–24 April 2015; SPIE: Bellingham, WA, USA; Volume 9465, p. 946502. [Google Scholar]
- Heinrichs, R.; Aull, B.F.; Marino, R.M.; Fouche, D.G.; McIntosh, A.K.; Zayhowski, J.J.; Stephens, T.; O’Brien, M.E.; Albota, M.A. Three-dimensional laser radar with APD arrays. In Proceedings of the Laser Radar Technology and Applications VI, Orlando, FL, USA, 16–20 April 2001; SPIE: Bellingham, WA, USA; Volume 4377. [Google Scholar]
- Zhang, Y.; Cao, X.; Wu, L.; Zhang, S.; Zhao, Y. Experimental research on small scale risley prism scanning imaging laser radar system. Chin. J. Lasers 2013, 40, 0814001. [Google Scholar] [CrossRef]
- Sun, J. Three-Dimensional Laser Imaging System and Method Based on APD Array. China Patent CN105242281A, 13 January 2016. [Google Scholar]
- Li, Z.; Wu, E.; Pang, C.; Du, B.; Tao, Y.; Peng, H.; Zeng, H.; Wu, G. Multi-beam single-photon-counting three-dimensional imaging lidar. Opt. Express 2017, 25, 10189–10195. [Google Scholar] [CrossRef]
- Chen, Y.; He, Y.; Luo, Y. Pulsed Three-dimensional imaging lidar system based on Geiger-mode APD array. Chin. J. Lasers 2023, 50, 0210001. [Google Scholar]
- Kang, Y.; Xue, R.; Li, L. Coaxial scanning three-dimensional imaging based on SPAD array. Laser Optoelectron. Prog. 2021, 10, 1011024. [Google Scholar]
- Xie, S.; Zhao, Y.; Wang, Y.; Lv, H.; Jia, X. Microscanning laser imaging technology based on Geiger-mode APD array. Infrared Laser Eng. 2018, 12, 1206010. [Google Scholar]
- Wu, C.; Liu, C.; Han, X. Design of waveguide optical phased array ladar receiving system. Infrared Laser Eng. 2016, 10, 1030003. [Google Scholar]
- Yu, X.; Yao, Y.; Xu, Z. Laser imaging optical system design with a shared aperture employing APD array. Chin. Opt. 2016, 3, 349–356. [Google Scholar]
- Wang, S.; Huayan, S.; Guo, H. Application of dot-matrix illumination of liquid crystal phase space light modulator in 3D imaging of APD array. In Proceedings of the Nanophotonics Australasia 2017, Melbourne, Australia, 10–13 December 2017; SPIE: Bellingham, WA, USA; Volume 10456. [Google Scholar]
- Calò, G.; Bellanca, G.; Barbiroli, M.; Fuschini, F.; Serafino, G.; Bertozzi, D.; Tralli, V.; Petruzzelli, V. Design of reconfigurable on-chip wireless interconnections through Optical Phased Arrays. Opt. Express 2021, 29, 31212–31228. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Peng, Z.; Fu, Y. Diffraction transfer function and its calculation of classic diffraction formula. Opt. Commun. 2007, 280, 243–248. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, J.; Sui, X.; Cao, C.; Yan, Z.; Wu, Z. Array beam laser three-dimensional imaging technology. Infrared Laser Eng. 2019, 48, 606001. [Google Scholar] [CrossRef]














Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Yuan, G.; Wang, K.-P.; Sun, G.-D.; Liu, L.; Li, L.; Zhang, B.; Quan, L. Optical Phased Array-Based Laser Beam Array Subdivide Pixel Method for Improving Three-Dimensional Imaging Resolution. Photonics 2023, 10, 1360. https://doi.org/10.3390/photonics10121360
Wang S, Yuan G, Wang K-P, Sun G-D, Liu L, Li L, Zhang B, Quan L. Optical Phased Array-Based Laser Beam Array Subdivide Pixel Method for Improving Three-Dimensional Imaging Resolution. Photonics. 2023; 10(12):1360. https://doi.org/10.3390/photonics10121360
Chicago/Turabian StyleWang, Shuai, Gang Yuan, Kun-Peng Wang, Guang-De Sun, Lei Liu, Ling Li, Bing Zhang, and Lin Quan. 2023. "Optical Phased Array-Based Laser Beam Array Subdivide Pixel Method for Improving Three-Dimensional Imaging Resolution" Photonics 10, no. 12: 1360. https://doi.org/10.3390/photonics10121360
APA StyleWang, S., Yuan, G., Wang, K.-P., Sun, G.-D., Liu, L., Li, L., Zhang, B., & Quan, L. (2023). Optical Phased Array-Based Laser Beam Array Subdivide Pixel Method for Improving Three-Dimensional Imaging Resolution. Photonics, 10(12), 1360. https://doi.org/10.3390/photonics10121360




