Reconstructing Depth Images for Time-of-Flight Cameras Based on Second-Order Correlation Functions
Abstract
:1. Introduction
2. Basic Theories and Principles
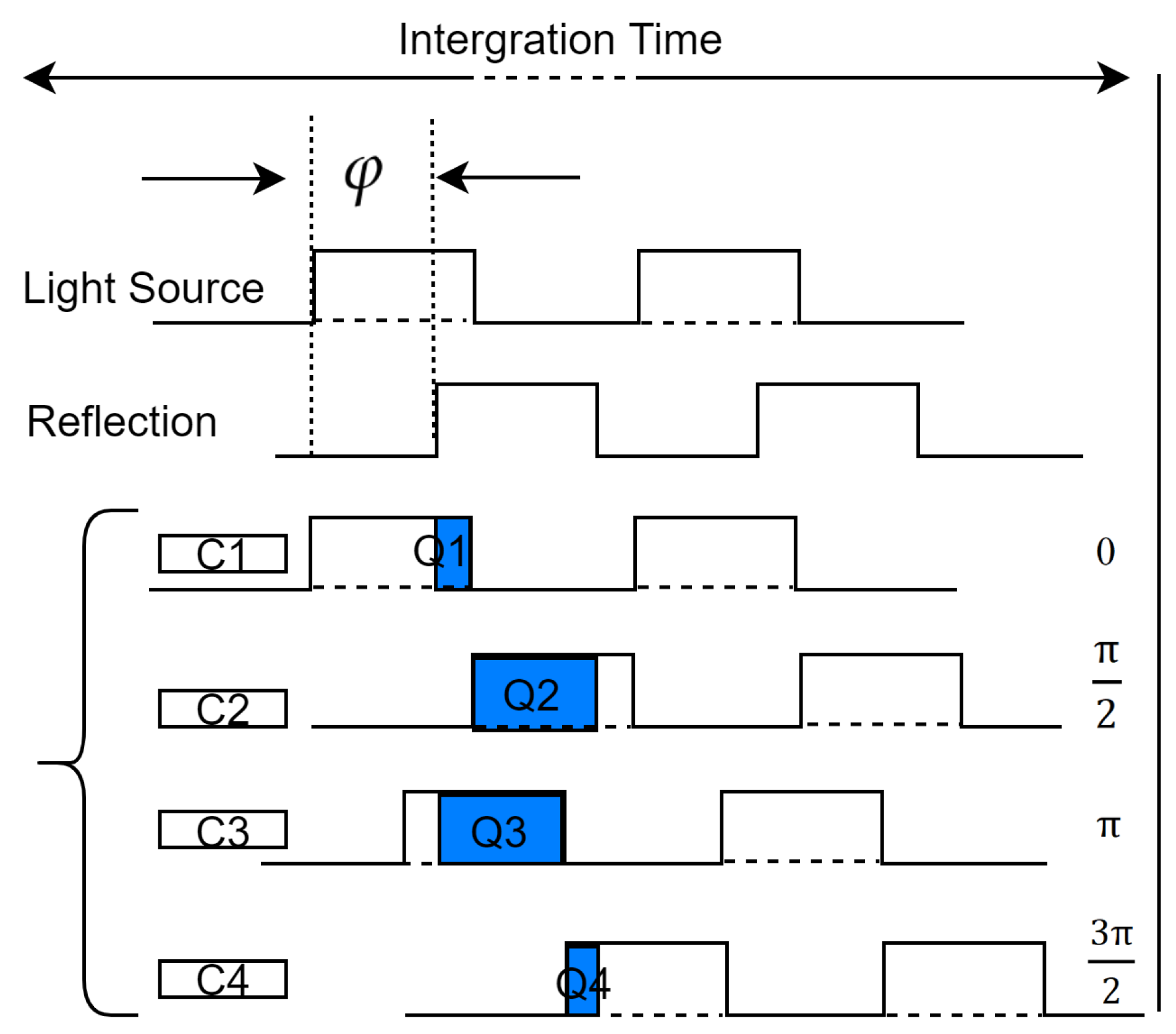
2.1. Ranging Principle of ToF Cameras
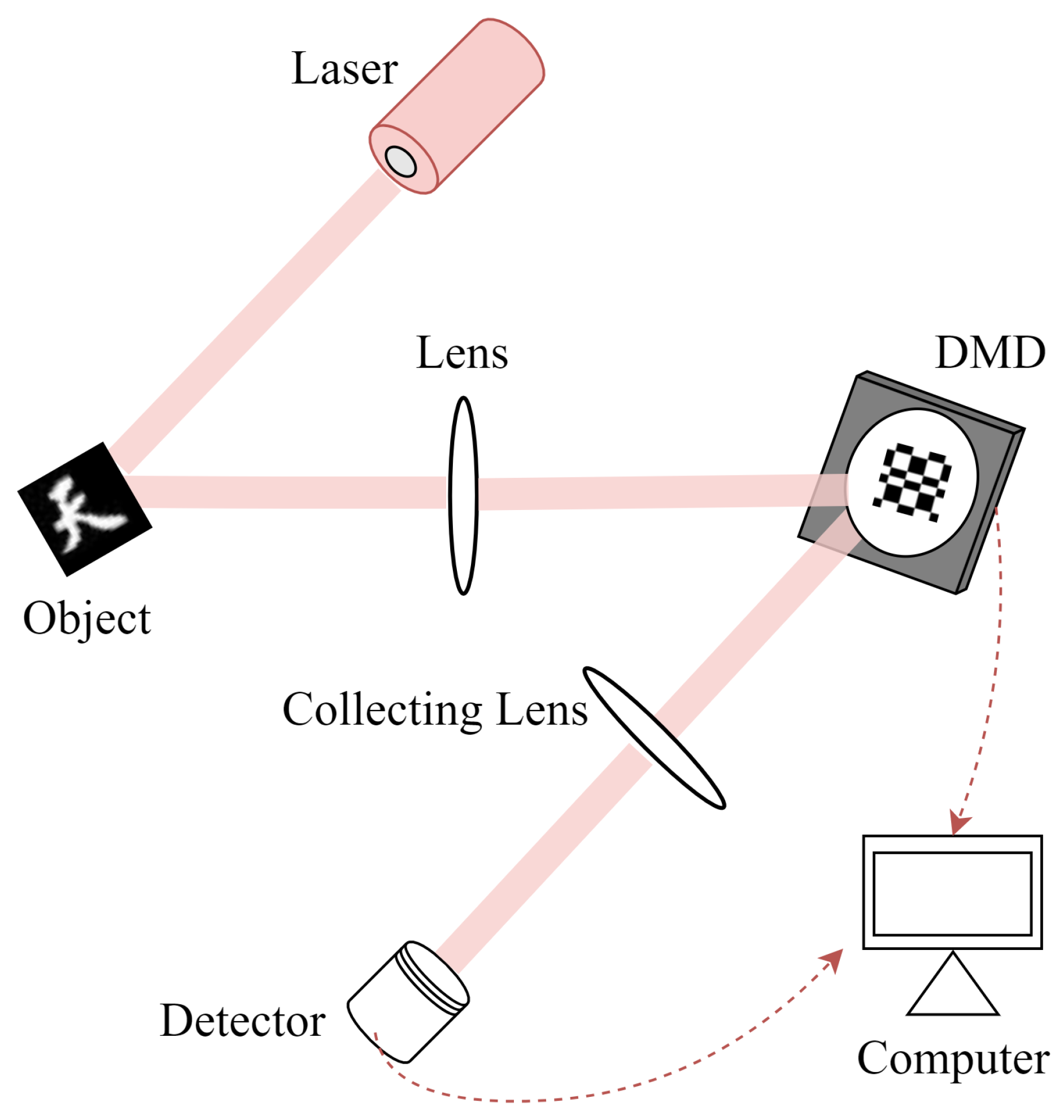
2.2. CGI via a ToF Camera
2.3. Image Reconstruction Algorithm Based on the U-Net Framework
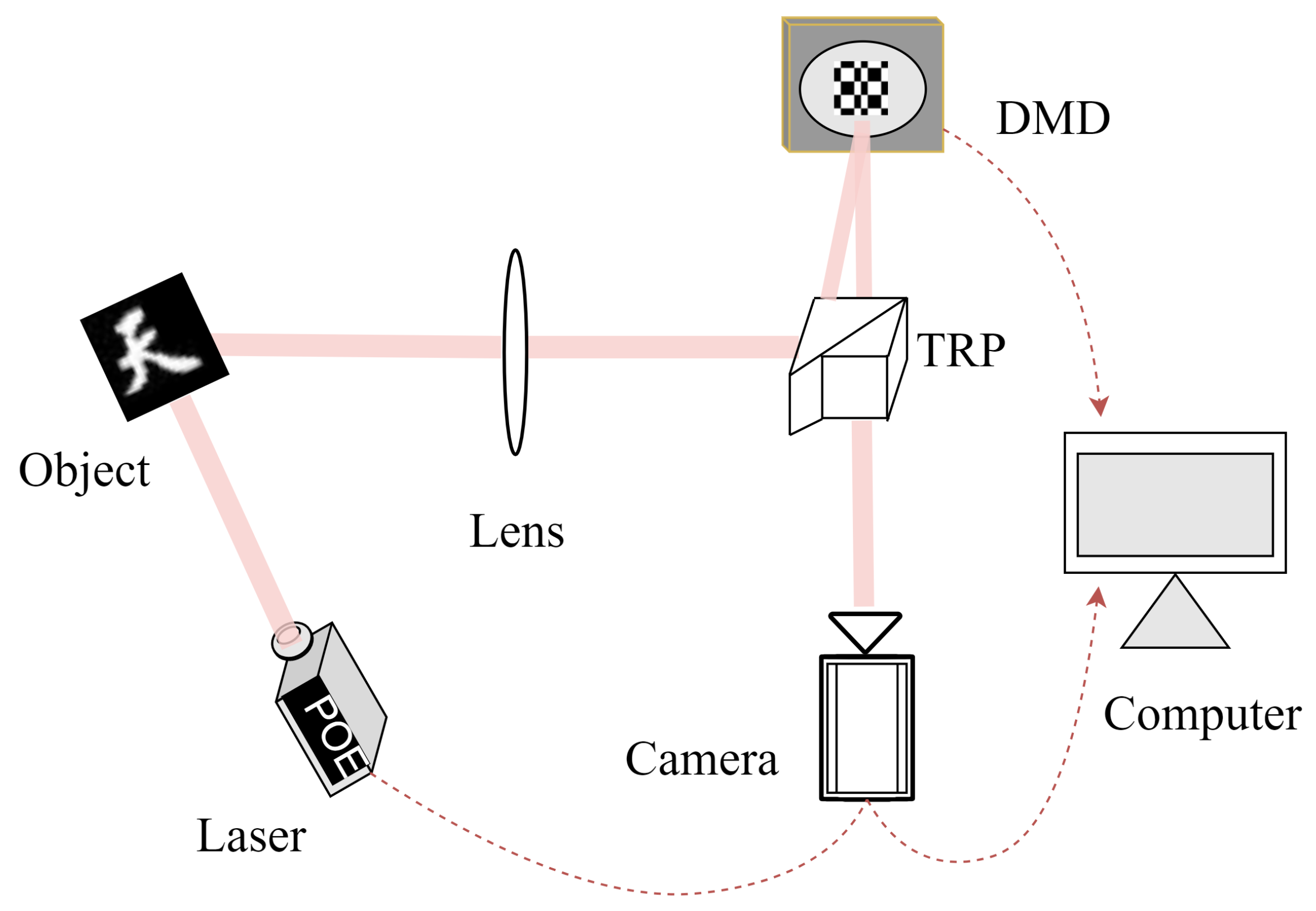
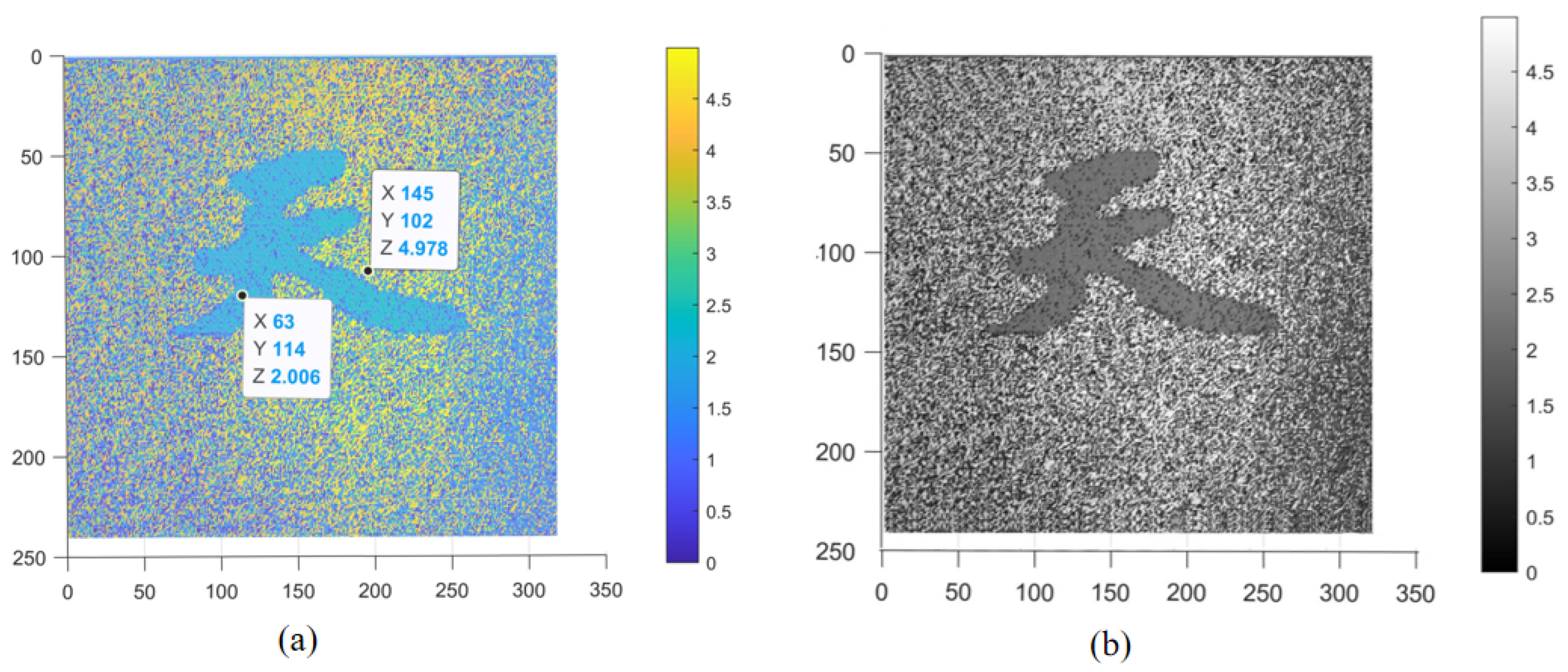
3. Experimental Scheme and Analysis of Results
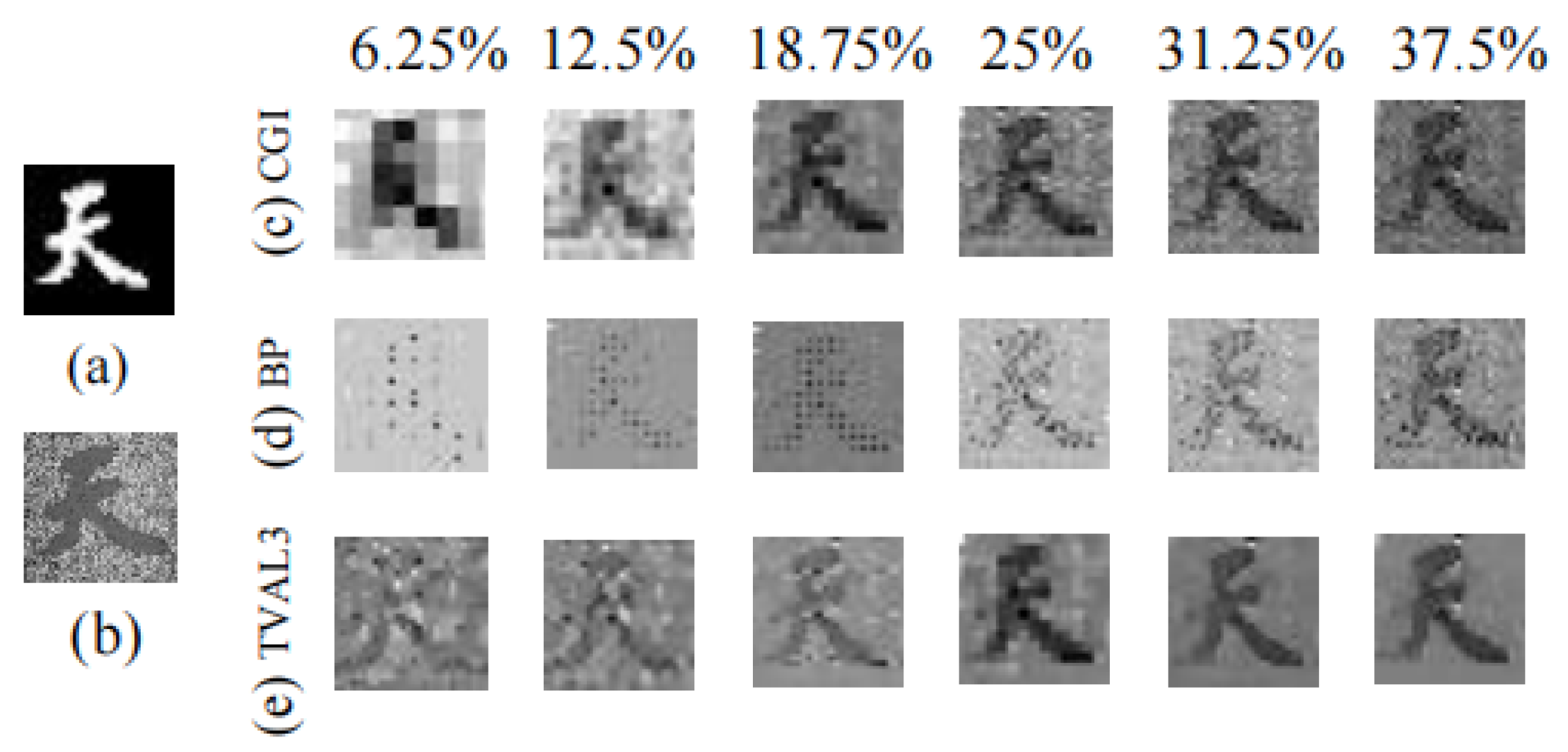
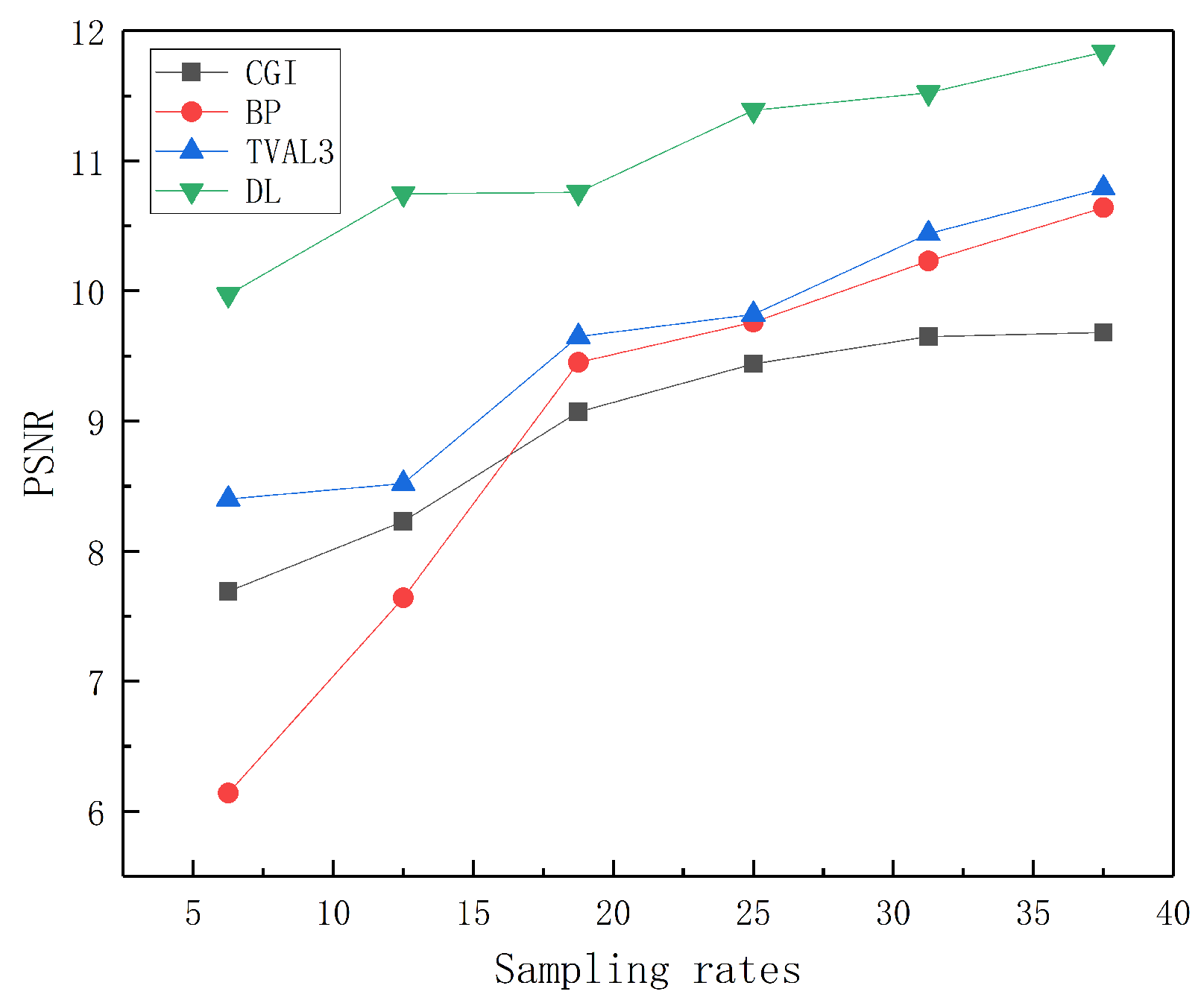
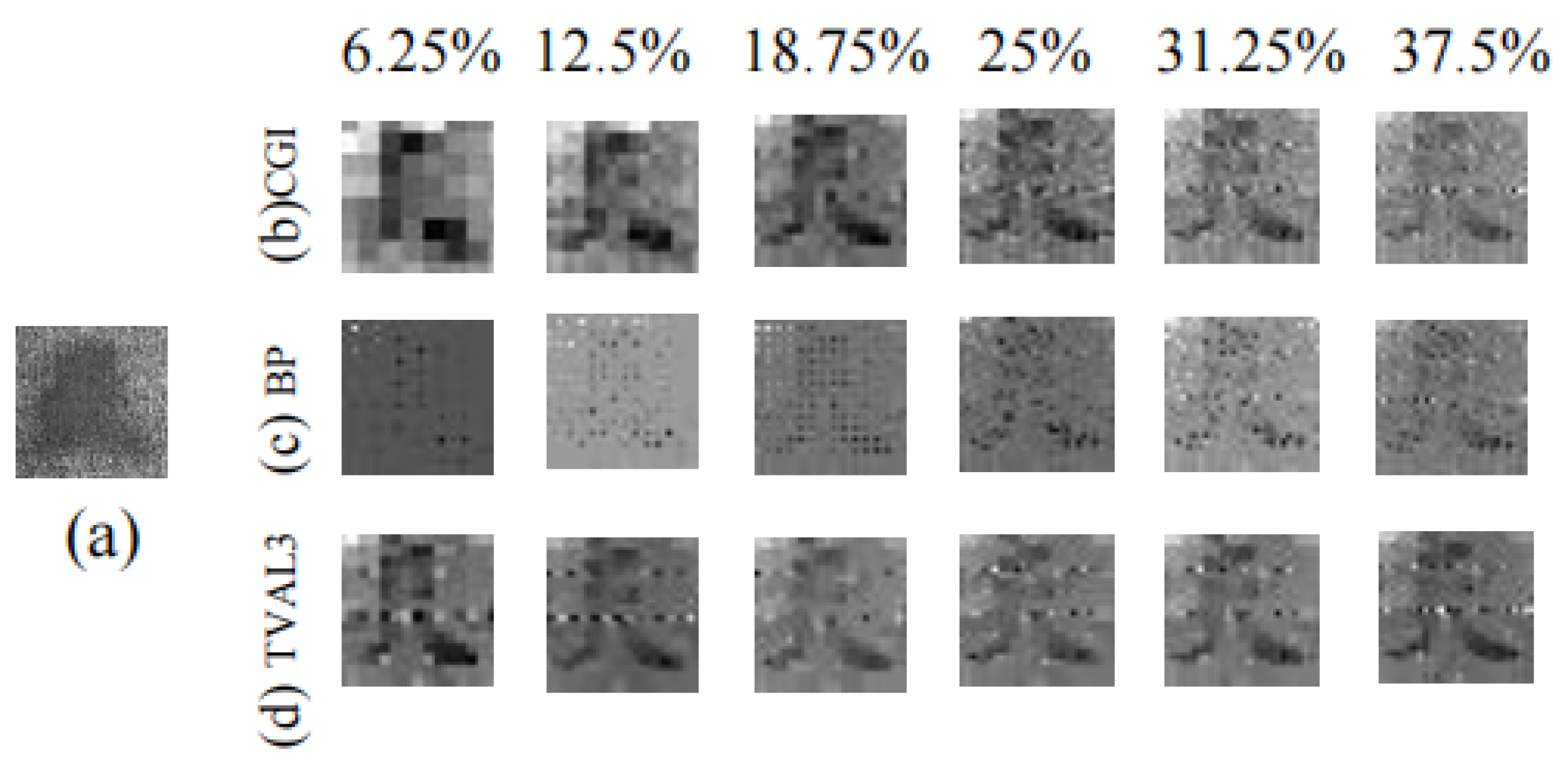
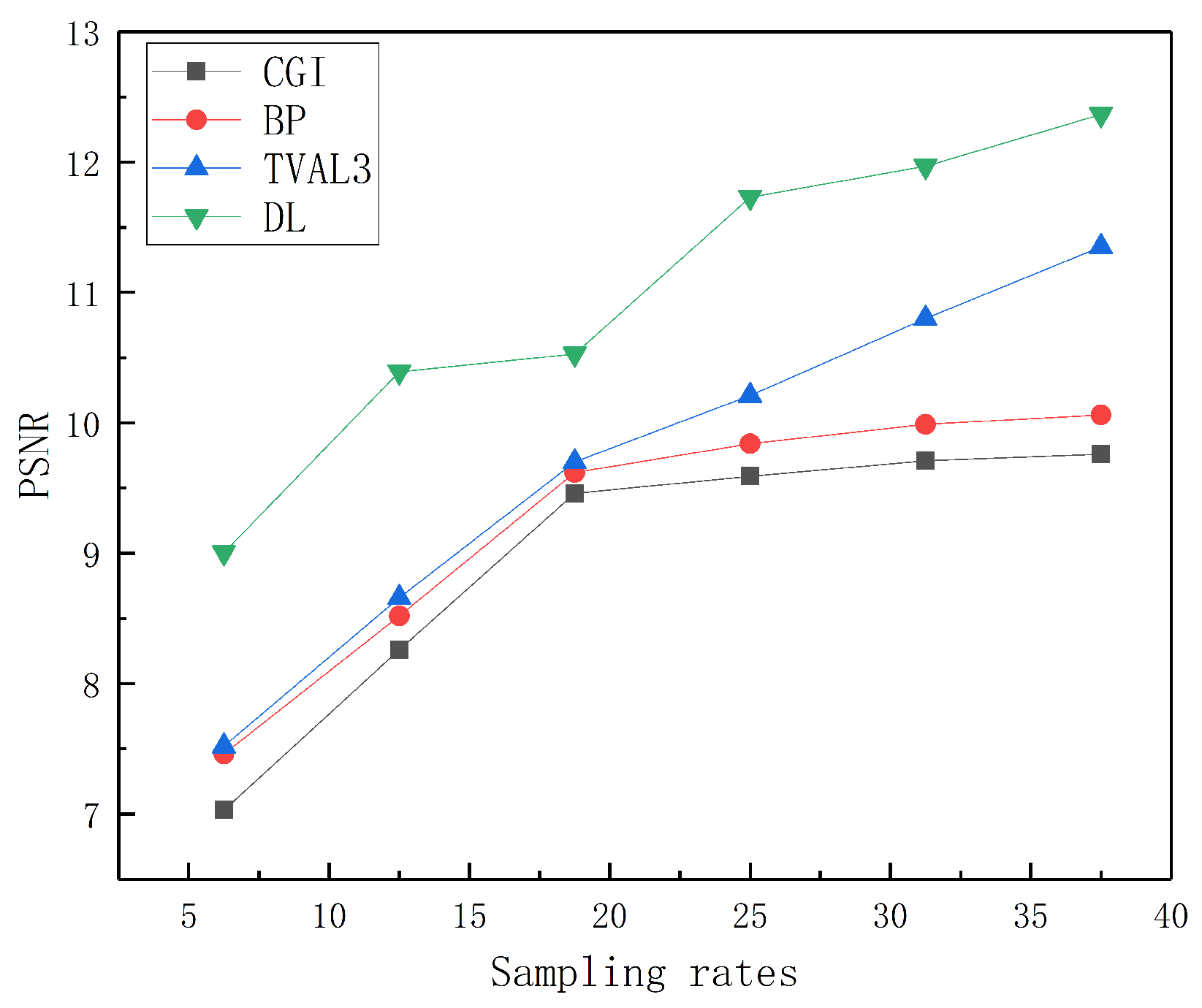
3.1. Recovering Depth Images Using Different Methods
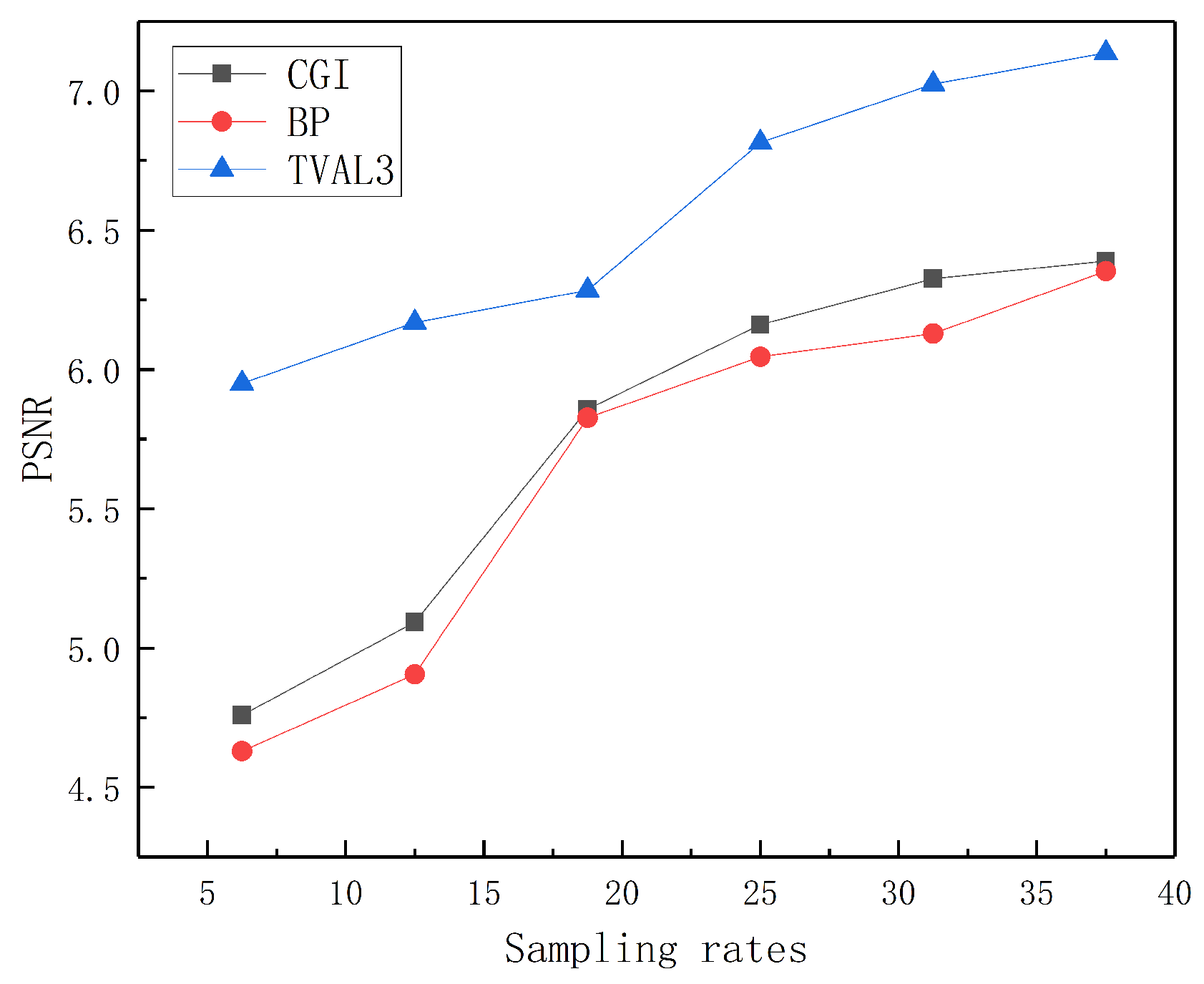
3.2. Recovering Depth Images Using Different Methods through Scattering Media
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Szeliski, R. Computer Vision: Algorithms and Applications; Springer Nature: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Zhang, S.; Huang, P.S. Novel method for structured light system calibration. Opt. Eng. 2006, 45, 083601. [Google Scholar] [CrossRef]
- Soltanlou, K.; Latifi, H. Three-dimensional imaging through scattering media using a single pixel detector. Appl. Opt. 2019, 58, 7716–7726. [Google Scholar] [CrossRef]
- Geng, J. Structured-light 3D surface imaging: A tutorial. Adv. Opt. Photonics 2011, 3, 128–160. [Google Scholar] [CrossRef]
- Salvi, J.; Fernandez, S.; Pribanic, T.; Llado, X. A state of the art in structured light patterns for surface profilometry. Pattern Recognit. 2010, 43, 2666–2680. [Google Scholar] [CrossRef]
- Zuo, C.; Huang, L.; Zhang, M.; Chen, Q.; Asundi, A. Temporal phase unwrapping algorithms for fringe projection profilometry: A comparative review. Opt. Lasers Eng. 2016, 85, 84–103. [Google Scholar] [CrossRef]
- Bhandari, A.; Raskar, R. Signal processing for time-of-flight imaging sensors: An introduction to inverse problems in computational 3-D imaging. IEEE Signal Process. Mag. 2016, 33, 45–58. [Google Scholar] [CrossRef]
- Park, J.; Kim, H.; Tai, Y.W.; Brown, M.S.; Kweon, I. High quality depth map upsampling for 3D-TOF cameras. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 1623–1630. [Google Scholar] [CrossRef]
- Sun, M.J.; Edgar, M.P.; Gibson, G.M.; Sun, B.; Radwell, N.; Lamb, R.; Padgett, M.J. Single-pixel three-dimensional imaging with time-based depth resolution. Nat. Commun. 2016, 7, 12010. [Google Scholar] [CrossRef]
- Howland, G.A.; Lum, D.J.; Ware, M.R.; Howell, J.C. Photon counting compressive depth mapping. Opt. Express 2013, 21, 23822–23837. [Google Scholar] [CrossRef] [PubMed]
- Kirmani, A.; Colaço, A.; Wong, F.N.; Goyal, V.K. Exploiting sparsity in time-of-flight range acquisition using a single time-resolved sensor. Opt. Express 2011, 19, 21485–21507. [Google Scholar] [CrossRef] [PubMed]
- Sun, B.; Edgar, M.P.; Bowman, R.; Vittert, L.E.; Welsh, S.; Bowman, A.; Padgett, M.J. 3D computational imaging with single-pixel detectors. Science 2013, 340, 844–847. [Google Scholar] [CrossRef]
- Velten, A.; Wu, D.; Jarabo, A.; Masia, B.; Barsi, C.; Joshi, C.; Lawson, E.; Bawendi, M.; Gutierrez, D.; Raskar, R. Femto-photography: Capturing and visualizing the propagation of light. ACM Trans. Graph. (ToG) 2013, 32, 1–8. [Google Scholar] [CrossRef]
- Heide, F.; Hullin, M.B.; Gregson, J.; Heidrich, W. Low-budget transient imaging using photonic mixer devices. ACM Trans. Graph. (ToG) 2013, 32, 1–10. [Google Scholar] [CrossRef]
- Peters, C.; Klein, J.; Hullin, M.B.; Klein, R. Solving trigonometric moment problems for fast transient imaging. ACM Trans. Graph. (ToG) 2015, 34, 1–11. [Google Scholar] [CrossRef]
- Kirmani, A.; Hutchison, T.; Davis, J.; Raskar, R. Looking around the corner using transient imaging. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 159–166. [Google Scholar] [CrossRef]
- Velten, A.; Willwacher, T.; Gupta, O.; Veeraraghavan, A.; Bawendi, M.G.; Raskar, R. Recovering three-dimensional shape around a corner using ultrafast time-of-flight imaging. Nat. Commun. 2012, 3, 745. [Google Scholar] [CrossRef]
- Heide, F.; Xiao, L.; Heidrich, W.; Hullin, M.B. Diffuse mirrors: 3D reconstruction from diffuse indirect illumination using inexpensive time-of-flight sensors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3222–3229. [Google Scholar] [CrossRef]
- O’Toole, M.; Heide, F.; Xiao, L.; Hullin, M.B.; Heidrich, W.; Kutulakos, K.N. Temporal frequency probing for 5D transient analysis of global light transport. ACM Trans. Graph. (ToG) 2014, 33, 1–11. [Google Scholar] [CrossRef]
- Wu, D.; Wetzstein, G.; Barsi, C.; Willwacher, T.; O’Toole, M.; Naik, N.; Dai, Q.; Kutulakos, K.; Raskar, R. Frequency analysis of transient light transport with applications in bare sensor imaging. In Proceedings of the Computer Vision—ECCV 2012: 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; Proceedings, Part I 12. Springer: Berlin/Heidelberg, Germany, 2012; pp. 542–555. [Google Scholar] [CrossRef]
- Heide, F.; Heidrich, W.; Hullin, M.; Wetzstein, G. Doppler time-of-flight imaging. ACM Trans. Graph. (ToG) 2015, 34, 1–11. [Google Scholar] [CrossRef]
- Heide, F.; Xiao, L.; Kolb, A.; Hullin, M.B.; Heidrich, W. Imaging in scattering media using correlation image sensors and sparse convolutional coding. Opt. Express 2014, 22, 26338–26350. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, J.H. Computational ghost imaging. Phys. Rev. A 2008, 78, 061802. [Google Scholar] [CrossRef]
- Pittman, T.B.; Shih, Y.; Strekalov, D.; Sergienko, A.V. Optical imaging by means of two-photon quantum entanglement. Phys. Rev. A 1995, 52, R3429. [Google Scholar] [CrossRef] [PubMed]
- Ferri, F.; Magatti, D.; Gatti, A.; Bache, M.; Brambilla, E.; Lugiato, L.A. High-resolution ghost image and ghost diffraction experiments with thermal light. Phys. Rev. Lett. 2005, 94, 183602. [Google Scholar] [CrossRef]
- Cheng, J. Ghost imaging through turbulent atmosphere. Opt. Express 2009, 17, 7916–7921. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, Z.; Tang, Z. Experimental study on anti-disturbance ability of underwater ghost imaging. Laser Optoelectron. Prog. 2021, 58, 611002. [Google Scholar] [CrossRef]
- Takhar, D.; Laska, J.N.; Wakin, M.B.; Duarte, M.F.; Baron, D.; Sarvotham, S.; Kelly, K.F.; Baraniuk, R.G. A new compressive imaging camera architecture using optical-domain compression. Proc. Comput. Imaging IV 2006, 6065, 43–52. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Duarte, M.F.; Davenport, M.A.; Takhar, D.; Laska, J.N.; Sun, T.; Kelly, K.F.; Baraniuk, R.G. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 2008, 25, 83–91. [Google Scholar] [CrossRef]
- Katz, O.; Bromberg, Y.; Silberberg, Y. Compressive ghost imaging. Appl. Phys. Lett. 2009, 95, 131110. [Google Scholar] [CrossRef]
- Katkovnik, V.; Astola, J. Compressive sensing computational ghost imaging. JOSA A 2012, 29, 1556–1567. [Google Scholar] [CrossRef]
- Yu, W.K.; Li, M.F.; Yao, X.R.; Liu, X.F.; Wu, L.A.; Zhai, G.J. Adaptive compressive ghost imaging based on wavelet trees and sparse representation. Opt. Express 2014, 22, 7133–7144. [Google Scholar] [CrossRef]
- Chen, Z.; Shi, J.; Zeng, G. Object authentication based on compressive ghost imaging. Appl. Opt. 2016, 55, 8644–8650. [Google Scholar] [CrossRef] [PubMed]
- Song, X.; Dai, Y.; Qin, X. Deep depth super-resolution: Learning depth super-resolution using deep convolutional neural network. In Proceedings of the Computer Vision—ACCV 2016: 13th Asian Conference on Computer Vision, Taipei, Taiwan, 20–24 November 2016; Revised Selected Papers, Part IV 13. Springer: Berlin/Heidelberg, Germany, 2017; pp. 360–376. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Ranzato, M.; Boureau, Y.L.; Cun, Y. Sparse feature learning for deep belief networks. In NeurIPS Proceedings: Advances in Neural Information Processing Systems 20 (NIPS 2007); Curran Associates: San Jose, CA, USA, 2007. [Google Scholar]
- Tao, Q.; Li, L.; Huang, X.; Xi, X.; Wang, S.; Suykens, J.A. Piecewise linear neural networks and deep learning. Nat. Rev. Methods Prim. 2022, 2, 42. [Google Scholar] [CrossRef]
- Lyu, M.; Wang, W.; Wang, H.; Wang, H.; Li, G.; Chen, N.; Situ, G. Deep-learning-based ghost imaging. Sci. Rep. 2017, 7, 17865. [Google Scholar] [CrossRef]
- He, Y.; Wang, G.; Dong, G.; Zhu, S.; Chen, H.; Zhang, A.; Xu, Z. Ghost imaging based on deep learning. Sci. Rep. 2018, 8, 6469. [Google Scholar] [CrossRef]
- Shimobaba, T.; Endo, Y.; Nishitsuji, T.; Takahashi, T.; Nagahama, Y.; Hasegawa, S.; Sano, M.; Hirayama, R.; Kakue, T.; Shiraki, A.; et al. Computational ghost imaging using deep learning. Opt. Commun. 2018, 413, 147–151. [Google Scholar] [CrossRef]
- Barbastathis, G.; Ozcan, A.; Situ, G. On the use of deep learning for computational imaging. Optica 2019, 6, 921–943. [Google Scholar] [CrossRef]
- Nah, S.; Hyun Kim, T.; Mu Lee, K. Deep multi-scale convolutional neural network for dynamic scene deblurring. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3883–3891. [Google Scholar] [CrossRef]
- Wang, C.; Mei, X.; Pan, L.; Wang, P.; Li, W.; Gao, X.; Bo, Z.; Chen, M.; Gong, W.; Han, S. Airborne near infrared three-dimensional ghost imaging lidar via sparsity constraint. Remote Sens. 2018, 10, 732. [Google Scholar] [CrossRef]
- Mei, X.; Wang, C.; Pan, L.; Wang, P.; Gong, W.; Han, S. Experimental demonstration of vehicle-borne near infrared three-dimensional ghost imaging LiDAR. In Proceedings of the 2019 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 5–10 May 2019; pp. 1–2. [Google Scholar] [CrossRef]
- Li, Z.P.; Huang, X.; Jiang, P.Y.; Hong, Y.; Yu, C.; Cao, Y.; Zhang, J.; Xu, F.; Pan, J.W. Super-resolution single-photon imaging at 8.2 kilometers. Opt. Express 2020, 28, 4076–4087. [Google Scholar] [CrossRef]
- Li, Z.P.; Ye, J.T.; Huang, X.; Jiang, P.Y.; Cao, Y.; Hong, Y.; Yu, C.; Zhang, J.; Zhang, Q.; Peng, C.Z.; et al. Single-photon imaging over 200 km. Optica 2021, 8, 344–349. [Google Scholar] [CrossRef]
- Foix, S.; Alenya, G.; Torras, C. Lock-in time-of-flight (ToF) cameras: A survey. IEEE Sens. J. 2011, 11, 1917–1926. [Google Scholar] [CrossRef]
- Lange, R.; Seitz, P. Solid-state time-of-flight range camera. IEEE J. Quantum Electron. 2001, 37, 390–397. [Google Scholar] [CrossRef]
- Kolb, A.; Barth, E.; Koch, R. ToF-sensors: New dimensions for realism and interactivity. In Proceedings of the 2008 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Anchorage, AK, USA, 23–28 June 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Oggier, T.; Lehmann, M.; Kaufmann, R.; Schweizer, M.; Richter, M.; Metzler, P.; Lang, G.; Lustenberger, F.; Blanc, N. An all-solid-state optical range camera for 3D real-time imaging with sub-centimeter depth resolution (SwissRanger). Proc. Opt. Des. Eng. 2004, 5249, 534–545. [Google Scholar] [CrossRef]
- Li, L. Time-of-Flight Camera—An Introduction; Texas Instruments, Technical White Paper; Texas Instruments: Dallas, TX, USA, 2014; p. SLOA190B. [Google Scholar]
- Liu, S.; Meng, X.; Yin, Y.; Wu, H.; Jiang, W. Computational ghost imaging based on an untrained neural network. Opt. Lasers Eng. 2021, 147, 106744. [Google Scholar] [CrossRef]
- Wang, F.; Wang, C.; Chen, M.; Gong, W.; Zhang, Y.; Han, S.; Situ, G. Far-field super-resolution ghost imaging with a deep neural network constraint. Light. Sci. Appl. 2022, 11, 1. [Google Scholar] [CrossRef]
- Lin, J.; Yan, Q.; Lu, S.; Zheng, Y.; Sun, S.; Wei, Z. A Compressed Reconstruction Network Combining Deep Image Prior and Autoencoding Priors for Single-Pixel Imaging. Photonics 2022, 9, 343. [Google Scholar] [CrossRef]
- Wang, C.H.; Li, H.Z.; Bie, S.H.; Lv, R.B.; Chen, X.H. Single-Pixel Hyperspectral Imaging via an Untrained Convolutional Neural Network. Photonics 2023, 10, 224. [Google Scholar] [CrossRef]
- Li, F.; Zhao, M.; Tian, Z.; Willomitzer, F.; Cossairt, O. Compressive ghost imaging through scattering media with deep learning. Opt. Express 2020, 28, 17395–17408. [Google Scholar] [CrossRef]
- Rizvi, S.; Cao, J.; Hao, Q. Deep learning based projector defocus compensation in single-pixel imaging. Opt. Express 2020, 28, 25134–25148. [Google Scholar] [CrossRef] [PubMed]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.-L.; Ao, L.; Zheng, J.; Sun, Z.-B. Reconstructing Depth Images for Time-of-Flight Cameras Based on Second-Order Correlation Functions. Photonics 2023, 10, 1223. https://doi.org/10.3390/photonics10111223
Wang T-L, Ao L, Zheng J, Sun Z-B. Reconstructing Depth Images for Time-of-Flight Cameras Based on Second-Order Correlation Functions. Photonics. 2023; 10(11):1223. https://doi.org/10.3390/photonics10111223
Chicago/Turabian StyleWang, Tian-Long, Lin Ao, Jie Zheng, and Zhi-Bin Sun. 2023. "Reconstructing Depth Images for Time-of-Flight Cameras Based on Second-Order Correlation Functions" Photonics 10, no. 11: 1223. https://doi.org/10.3390/photonics10111223
APA StyleWang, T.-L., Ao, L., Zheng, J., & Sun, Z.-B. (2023). Reconstructing Depth Images for Time-of-Flight Cameras Based on Second-Order Correlation Functions. Photonics, 10(11), 1223. https://doi.org/10.3390/photonics10111223




