Spectral Characterization of Two-Photon Interference between Independent Sources
Abstract
:1. Introduction
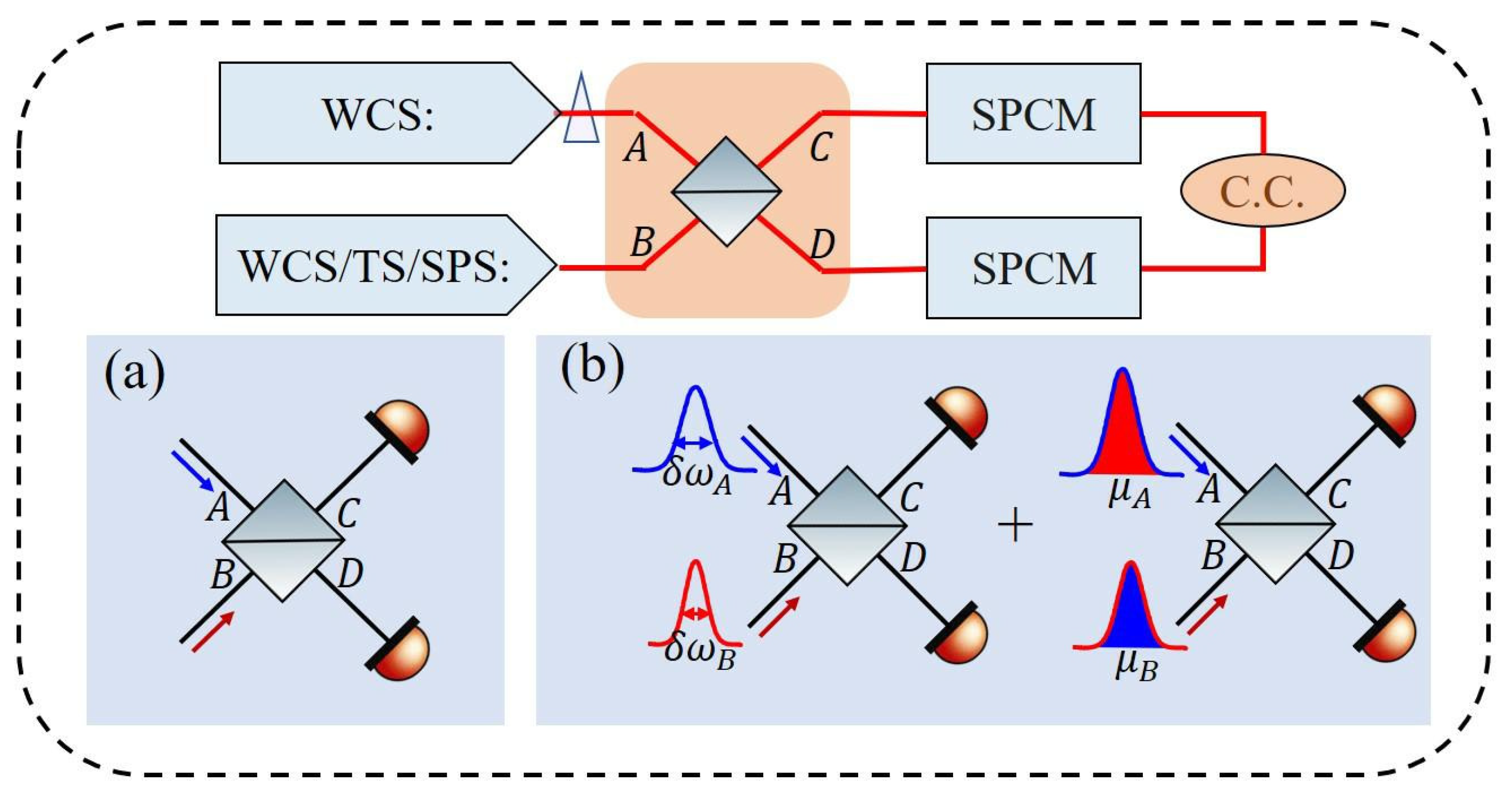
2. Theoretical Model
2.1. Single-Mode Photons with an Average Photon Number
2.2. Photons with Spatiotemporal Modes
3. Interference between Different Sources
3.1. Two Weak Coherent States
3.2. Weak Coherent State and Thermal State
3.3. Single-Photon State and Weak Coherent State
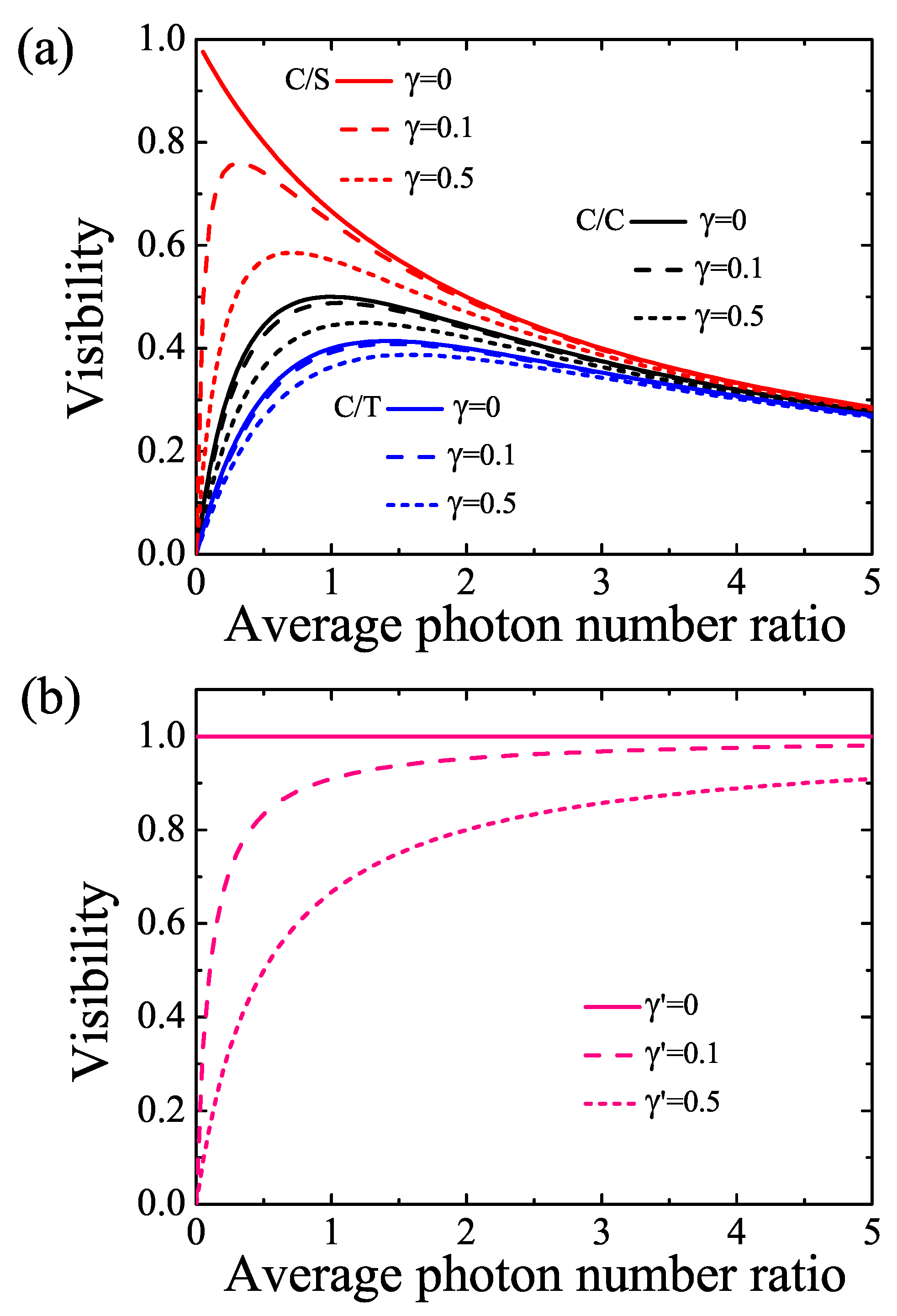
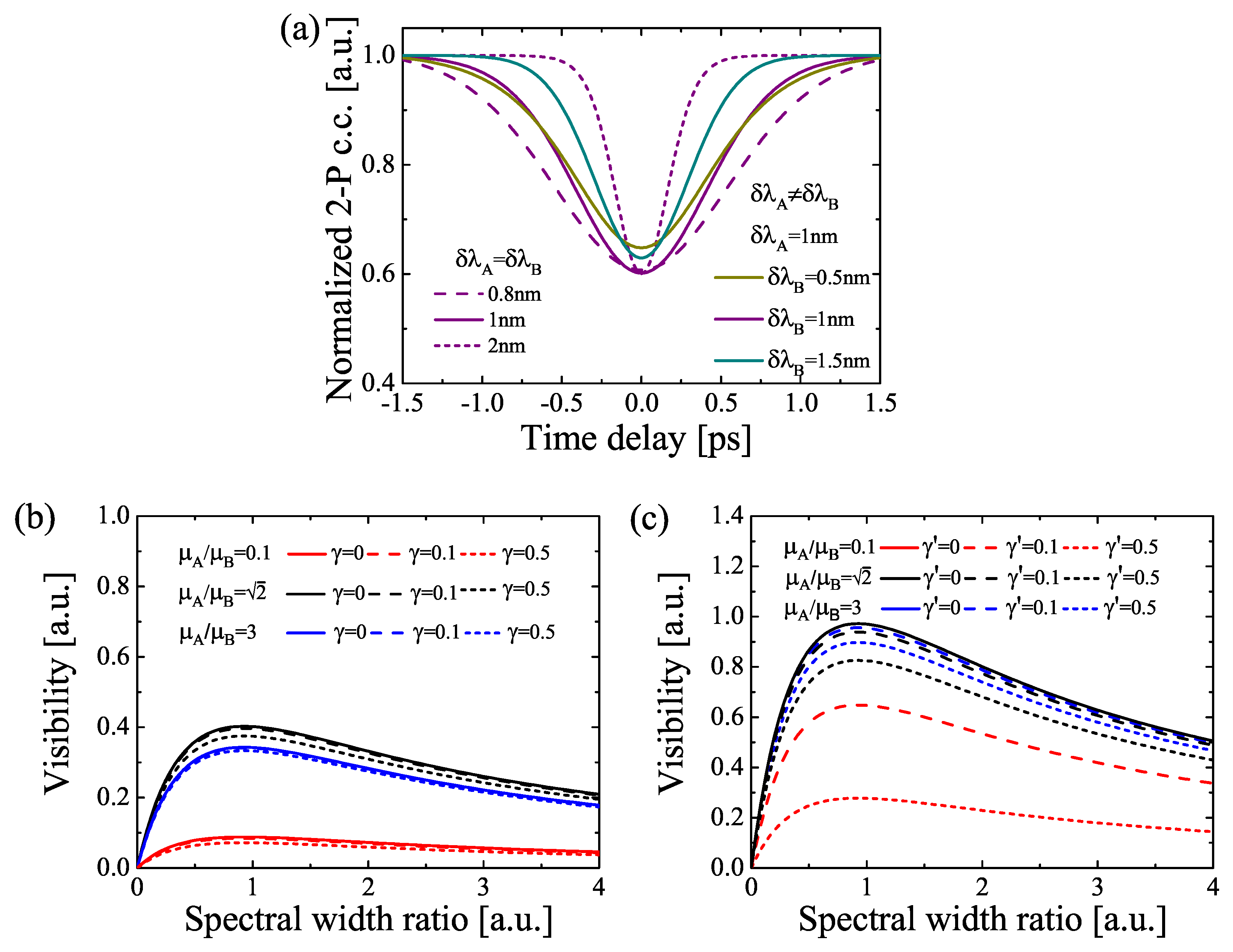
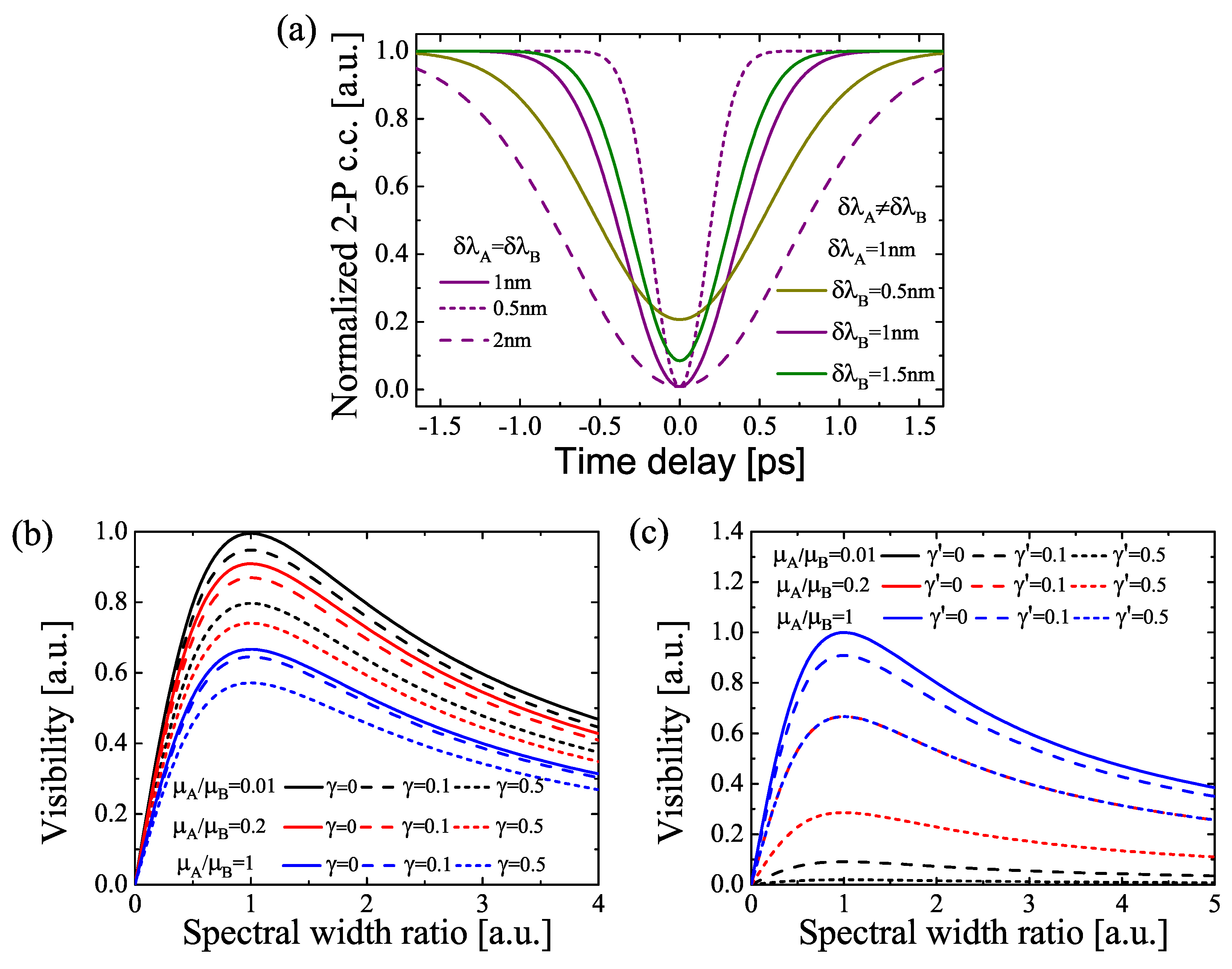
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BS | beam splitter |
| SPDC | spontaneous parametric down-conversion |
| HOM | Hong–Ou–Mandel |
| WCS | weak coherent state |
| TS | thermal state |
| SPS | single-photon state |
| FWHM | full width of half maximum |
References
- Hong, C.K.; Ou, Z.Y.; Mandel, L. Measurement of subpico-second time intervals between two photons by interference. Phys. Rev. Lett. 1987, 59, 2044–2046. [Google Scholar] [CrossRef]
- Bouchard, F.; Sit, A.; Zhang, Y.; Fickler, R.; Miatto, F.M.; Yao, Y.; Sciarrino, F.; Karimi, E. Two-photon interference: The Hong-Ou-Mandel effect. Rep. Prog. Phys. 2021, 84, 012402. [Google Scholar] [CrossRef]
- Reiserer, A. Cavity-based quantum networks with single atoms and optical photons. Rev. Mod. Phys. 2015, 87, 1379. [Google Scholar] [CrossRef]
- Lo, H.; Curty, M.; Qi, B. Measurement-Device-Independent Quantum Key Distribution. Phys. Rev. Lett. 2012, 108, 130503. [Google Scholar] [CrossRef]
- Curty, M.; Xu, F.; Cui, W.; Lim, C.; Tamaki, K.; Lo, H. Finite-key analysis for measurement-device-independent quantum key distribution. Nat. Commun. 2014, 5, 3732. [Google Scholar] [CrossRef]
- Xie, Y.; Lu, Y.; Weng, C.; Cao, X.; Jia, Z.; Bao, Y.; Wang, Y.; Fu, Y.; Yin, H.; Chen, Z. Breaking the Rate-Loss Bound of Quantum Key Distribution with Asynchronous Two-Photon Interference. PRX Quantum 2022, 3, 020315. [Google Scholar] [CrossRef]
- Zhou, L.; Lin, J.; Xie, Y.; Lu, Y.; Jing, Y.; Yin, H.; Yuan, Z. Experimental Quantum Communication Overcomes the Rate-Loss Limit without Global Phase Tracking. Phys. Rev. Lett. 2023, 130, 250801. [Google Scholar] [CrossRef]
- Wehner, S.; Elkouss, D.; Hanson, R. Quantum internet: A vision for the road ahead. Science 2018, 362, eaam9288. [Google Scholar] [CrossRef]
- Langenfeld, S.; Thomas, P.; Morin, O.; Rempe, G. Quantum Repeater Node Demonstrating Unconditionally Secure Key Distribution. Phys. Rev. Lett. 2021, 126, 230506. [Google Scholar] [CrossRef]
- Wei, S.H.; Jing, B.; Zhang, X.Y.; Liao, J.Y.; Yuan, C.Z.; Fan, B.Y.; Lyu, C.; Zhou, D.L.; Wang, Y.; Deng, G.W.; et al. Towards Real-World Quantum Networks: A Review. Laser Photonics Rev. 2022, 16, 2100219. [Google Scholar] [CrossRef]
- Rarity, J.G.; Tapster, P.R.; Loudon, R. Non-classical interference between independent sources. J. Opt. B Quantum Semiclassical Opt. 2005, 7, S171–S175. [Google Scholar] [CrossRef]
- Pittman, T.B.; Franson, J.D. Violation of Bell’s Inequality with Photons from Independent Sources. Phys. Rev. Lett. 2003, 90, 240401. [Google Scholar] [CrossRef]
- Patel, R.B.; Bennett, A.J.; Farrer, I.; Nicoll, C.A.; Ritchie, D.A.; Andrew, J. Two-photon interference of the emission from electrically tunable remote quantum dots. Nat. Photonics 2010, 4, 632–635. [Google Scholar] [CrossRef]
- Vural, H.; Portalupi, S.L.; Maisch, J.; Kern, S.; Weber, J.H.; Jetter, M.; Wrachtrup, J.; Gerhardt, R.L.I.; Michler, P. Two-photon interference in an atom-quantum dot hybrid system. Optica 2018, 5, 367–373. [Google Scholar] [CrossRef]
- Gerber, S.; Rotter, D.; Hennrich, M.; Blatt, R.; Rohde, F.; Schuck, C.; Almendros, M.; Gehr, R.; Dubin, F.; Eschner, J. Quantum interference from remotely trapped ions. New J. Phys. 2009, 11, 013032. [Google Scholar] [CrossRef]
- Toyoda, K.; Hiji, R.; Noguchi, A.; Urabe, S. Hong-Ou-Mandel interference of two phonons in trapped ions. Nature 2015, 527, 74–77. [Google Scholar] [CrossRef]
- Windhager, A.; Suda, M.; Pacher, C.; Peev, M.; Poppe, A. Quantum interference between a single-photon Fock state and a coherent state. Opt. Commun. 2011, 284, 1907–1912. [Google Scholar] [CrossRef]
- Jin, R.B.; Zhang, J.; Shimizu, R.; Matsuda, N.; Mitsumori, Y.; Kosaka, H.; Edamatsu, K. High-visibility nonclassical interference between intrinsically pure heralded single photons and photons from a weak coherent field. Phys. Rev. A 2011, 83, 031805. [Google Scholar] [CrossRef]
- Liu, J.B.; Zheng, H.; Chen, H.; Zhou, Y.; Li, F.L.; Xu, Z. The first and second-order temporal interference between thermal and laser light. Opt. Express 2015, 23, 11868–11878. [Google Scholar] [CrossRef]
- Schofield, R.C.; Clear, C.; Hoggarth, R.A.; Major, K.D.; McCutcheon, D.P.S.; Clark, A.S. Photon indistinguishability measurements under pulsed and continuous excitation. Phys. Rev. Res. 2022, 4, 013037. [Google Scholar] [CrossRef]
- Kim, H.; Kwon, O.; Moon, H. Two photon interferences of weak coherent lights. Sci. Rep. 2021, 11, 20555. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wei, K.; Xu, F. Generalized Hong-Ou-Mandel quantum interference with phase-randomized weak coherent states. Phys. Rev. A 2020, 101, 033823. [Google Scholar] [CrossRef]
- Kim, Y.S.; Slattery, O.; Kuo, P.S.; Tang, X. Two-photon interference with continuous-wave multimode coherent light. Opt. Express 2014, 22, 3611–3620. [Google Scholar] [CrossRef] [PubMed]
- Moschandreou, E.; Garcia, J.I.; Rollick, B.J.; Qi, B.; Pooser, R.; Siopsis, G. Experimental study of Hong-Ou-Mandel interference using independent phase randomized weak coherent states. J. Light. Technol. 2018, 36, 3752–3759. [Google Scholar] [CrossRef]
- Valente, P.; Lezama, A. Probing single-photon state tomography using phase-randomized coherent states. J. Opt. Soc. Am. B 2017, 34, 924. [Google Scholar] [CrossRef]
- Kim, H.; Kim, D.; Park, J.; Moon, H.S. Hong-Ou-Mandel interference of two independent continuous-wave coherent photons. Photon. Res. 2020, 8, 1491–1495. [Google Scholar] [CrossRef]
- Aragoneses, A.; Islam, N.T.; Eggleston, M.; Lezama, A.; Kim, J.; Gauthier, D.J. Bounding the outcome of a two-photon interference measurement using weak coherent states. Opt. Lett. 2018, 43, 3806–3809. [Google Scholar] [CrossRef]
- Mahdavifar, M.; Rafsanjani, S.M.H. Violating Bell inequality using weak coherent states. Opt. Lett. 2021, 46, 5998–6001. [Google Scholar] [CrossRef]
- Jin, R.B.; Wakui, K.; Shimizu, R.; Benichi, H.; Miki, S.; Yamashita, T.; Terai, H.; Wang, Z.; Fujiwara, M.; Sasaki, M. Nonclasscial interference between independent intrinsically pure single photons at telecom wavelength. Phys. Rev. A 2013, 87, 063801. [Google Scholar] [CrossRef]
- Mosley, P.J.; Lundeen, J.S.; Smith, B.J.; Wasylczyk, P.; U’ren, A.B.; Silberhorn, C.; Walmsley, I.A. Heralded Generation of Ultrafast Single Photons in Pure Quantum States. Phys. Rev. Lett. 2008, 100, 133601. [Google Scholar] [CrossRef]
- Thekkadath, G.S.; Bell, B.A.; Patel, R.B.; Kim, M.S.; Walmsley, I.A. Measuring the Joint Spectral Mode of Photon Pairs Using Intensity Interferometry. Phys. Rev. Lett. 2022, 128, 023601. [Google Scholar] [CrossRef] [PubMed]
- Yuan, X.; Zhang, Z.; Lvtkenhaus, N.; Ma, X. Simulating single photons with realistic photon sources. Phys. Rev. A 2016, 94, 062305. [Google Scholar] [CrossRef]
- Navarrete, A.; Wang, W.; Xu, F.; Curty, M. Characterizing multi-photon quantum interference with practical light sources and threshold single-photon detectors. New J. Phys. 2018, 20, 043018. [Google Scholar] [CrossRef]
- Picque, N.; Hansch, T.W. Photon level broadband spectroscopy and interferometry with two frequency combs. Proc. Natl. Acad. Sci. USA 2020, 117, 26688–26691. [Google Scholar] [CrossRef] [PubMed]
- Ren, X.; Xu, B.; Fei, Q.; Liang, Y.; Ge, J.; Wang, X.; Huang, K.; Yan, M.; Zeng, H. Single-Photon Counting Laser Ranging With Optical Frequency Combs. IEEE Photonics Technol. Lett. 2021, 33, 27–30. [Google Scholar] [CrossRef]
- Hu, H.; Ren, X.; Wen, Z.; Li, X.; Liang, Y.; Yan, M.; Wu, E. Single-Pixel Photon-Counting Imaging Based on Dual-Comb Interferometry. Nanomaterials 2021, 11, 1379. [Google Scholar] [CrossRef]
- Branczyk, A.M. Hong-Ou-Mandel Interference. arXiv 2017, arXiv:1711.00080. [Google Scholar]
- Legero, T.; Wilk, T.; Kuhn, A.; Rempe, G. Time-resolved two-photon quantum interference. Appl. Phys. B 2003, 77, 797–802. [Google Scholar] [CrossRef]
- Silva, T.F.; Amaral, G.C.; Vitoreti, D.; Tempor, G.P.; Weid, J.P. Spectral characterization of weak coherent state sources based on two-photon interference. J. Opt. Soc. Am. B 2015, 32, 545–549. [Google Scholar] [CrossRef]
- Cassemiro, K.N.; Laiho, K.; Silberhorn, C. Accessing the purity of a single photon by the width of the Hong-Ou-Mandel interference. New J. Phys. 2010, 12, 113052. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, L.; Xu, A.; Zhang, Y. Spectral Characterization of Two-Photon Interference between Independent Sources. Photonics 2023, 10, 1125. https://doi.org/10.3390/photonics10101125
Duan L, Xu A, Zhang Y. Spectral Characterization of Two-Photon Interference between Independent Sources. Photonics. 2023; 10(10):1125. https://doi.org/10.3390/photonics10101125
Chicago/Turabian StyleDuan, Lifeng, Aojie Xu, and Yun Zhang. 2023. "Spectral Characterization of Two-Photon Interference between Independent Sources" Photonics 10, no. 10: 1125. https://doi.org/10.3390/photonics10101125
APA StyleDuan, L., Xu, A., & Zhang, Y. (2023). Spectral Characterization of Two-Photon Interference between Independent Sources. Photonics, 10(10), 1125. https://doi.org/10.3390/photonics10101125



