Parallel CV-QRNG with Strict Entropy Evaluation

Abstract

Continuous-variable quantum random number generators (CV-QRNGs) have promising application prospects thanks to their advantages such as high detection bandwidth, robustness of system, and integratability. In major CV-QRNGs, the generation of random numbers is based on homodyne detection and discretization of the quadrature fluctuations of the EM fields. Any defectiveness in physical realization may leak information correlated with the generated numbers and the maximal amount of randomness that can be extracted in presence of such side-information is evaluated by the so-called quantum conditional min-entropy. The parallel CV-QRNG overcomes the rate bottleneck of the previous serial type scheme. As a type of device-trusted QRNG, its security needs to be better guaranteed based on self-testing or monitoring that can be rigorously enforced. In this work, four sideband modes of vacuum state within 1.6 GHz detection bandwidth were extracted parallelly as the entropy source, and 16-bit analog-to-digital conversion in each channel was realized. Without making any ideal assumptions, the transfer function of the homodyne and quantization system was measured based on beat method to calibrate the evaluation of the min-entropy. Based on the rigorous entropy evaluation with a hash security parameter of ${\epsilon }_{hash}$ = 2⁻¹¹⁰, a real-time generation rate of 7.25 Gbps was finally achieved.

1. Introduction

With the rapid development of information technology, secure communication and cryptographic systems are playing an increasingly important role in information security, social life, and engineering applications. As the key of information encryption technology, a random number generator fundamentally determines the privacy and security of communication systems, and has been widely used in many fields such as high-speed secure communication, radar ranging, financial security, and so on [1,2,3]. The above applications require the random encryption keys to be unpredictable or irreproducible, but most of the current commercial random number generators are mainly based on algorithmic complexity, generating bit sequences that appear random and even pass the statistical test of randomness. However, these random sequences actually have pattern recoverability, and with increasing computer arithmetic power, algorithmic encryption schemes are at risk of being hacked and deciphered [4,5]. QRNGs are based on the intrinsic uncertainty of quantum physics, and have information-theory provable randomness and security.

In the last decade, numerous investigations into QRNG have been performed theoretically and experimentally. To date, kinds of quantum entropy sources have been explored to yield quantum random numbers, including photon arrival time [6,7,8], single photon branching path [9,10,11], laser phase noise [12,13], photon number statistics [14], continuous-variable (CV) quadrature fluctuations of quantum state [15,16,17], and so on. Among the various schemes, the QRNG with CV quadrature fluctuations of quantum state has a promising prospect of application [18,19,20,21]. In the CV-QRNG scheme, the theoretical model of quantum entropy source and quantum measurement process can be fully established [22,23] and the side-information introduced by nonideal factors in the actual implementation can be quantitatively evaluated. Meanwhile, the CV-QRNG has been widely studied and rapidly developed thanks to its advantages of easy preparation of quantum states, broad detection bandwidth, strong system robustness and integratability [24].

On the other hand, according to trusted degree of device security, many QRNG schemes can be classified into three categories: device-independent [25,26], semi-device-independent [27], and device-trusted QRNGs [28,29,30]. Device-independent QRNG makes as few assumptions as possible about the system, and is based on high-efficiency quantum measurement and entanglement to achieve loophole-free Bell inequality measurements; however, it has difficulty being practical in a short time due to its harsh experimental condition, low generation rate, and high cost [31]. Semi-device-independent QRNGs introduce complete trust in either the source or the detection, or vice versa, who represent an intermediate solution to achieve a comparatively high level of practicality [32,33,34]. Fully trusted QRNGs, including all the commercial ones, exploit trusted environments for the preparation and measurement of the quantum states from which the random numbers are extracted. This represents the most suitable QRNG scheme for real-world applications because it is most probable to build compact and fast generators in this script [35].

Among various QRNG schemes, device-trusted CV-QRNG has been leading the way in terms of production rate. The parallel QRNG scheme proposed by our research group overcomes the rate bottleneck existing in previous serial-type CV-QRNGs and reaches a real-time generation rate of 8.25 Gbps, which provides a scalability to the CV-QRNG scheme and can enhance the production rate multiply [20]. However, due to the very nature of device-trusted QRNG, any hidden side channel in the trusted environment compromises the unpredictability of the generated numbers. Previous schemes always make ideal assumptions about the measurement system, and ignore the effects of nonideal factors such as local oscillator noise, imperfect interference, limited quantum efficiency of photodiodes, frequency dependent gain of amplifiers, low-pass filter loss, and analog bandwidth of analog-to-digital converter (ADC) [36]. Such an ideal assumption is not rigorous, and classical noise can be controlled by the eavesdropper and becomes an attacked channel introducing side-information [37,38].

In this work, we propose a rigorous self-testing parallel CV-QRNG scheme. Without making any ideal assumptions about the detection and digitization system of the vacuum state quadrature fluctuation, and based on the measurement of the transfer function of the system, the quantum noise entropy content contained in the raw random numbers is calibrated rigorously. Previously, a transfer function approach for system characterization was proposed to establish a metrological-grade certification for vacuum-based QRNG [39]. In this work, the optical and electronic noises introduced by the side-information channel during continuous running of the QRNG are quantized based on transfer function measurement in a prolonged operation. The transfer function fluctuates within a certain range due to realistic system disturbance and the min-entropy is rigorously evaluated according to the lower limiting of the reconstructed power spectrum against side-information attacks in practical applications. Specific periodogram method and corresponding parameters in the power spectrum reconstruction are discussed and decided upon. By applying this operation to each component of the four parallel channels of the QRNG, a real-time rate of 7.25 Gbps against side-information with a hash security parameter of 2⁻¹¹⁰ is realized. This work lays a solid foundation for the practical application of the device-trusted CV-QRNG.

2. Theories and Methods

For a practical QRNG scheme, the security of random numbers is based on the description of the entropy source model and entropy content assessment; the more explicit and reliable the entropy source model, the stricter the assessment of quantum noise entropy content, and the safer the QRNG will be. The quantum noise entropy of the CV-QRNG originates from the quantum state quadrature fluctuations. However, in the actual system, besides quantum noise, classical fluctuation due to nonideal characteristics of physical implementation contributes to the total entropy, that is, these excess noises make the error of power spectrum estimation and lead to the overestimation of the quantum noise entropy content of the random signal. We calibrate the entropy source detection power spectrum by measuring the TF of homodyne and digitization system of the parallel CV-QRNG to give a rigorous evaluation of its min-entropy lower bound, which provides a safety guarantee for high-speed stable generation of quantum random numbers.

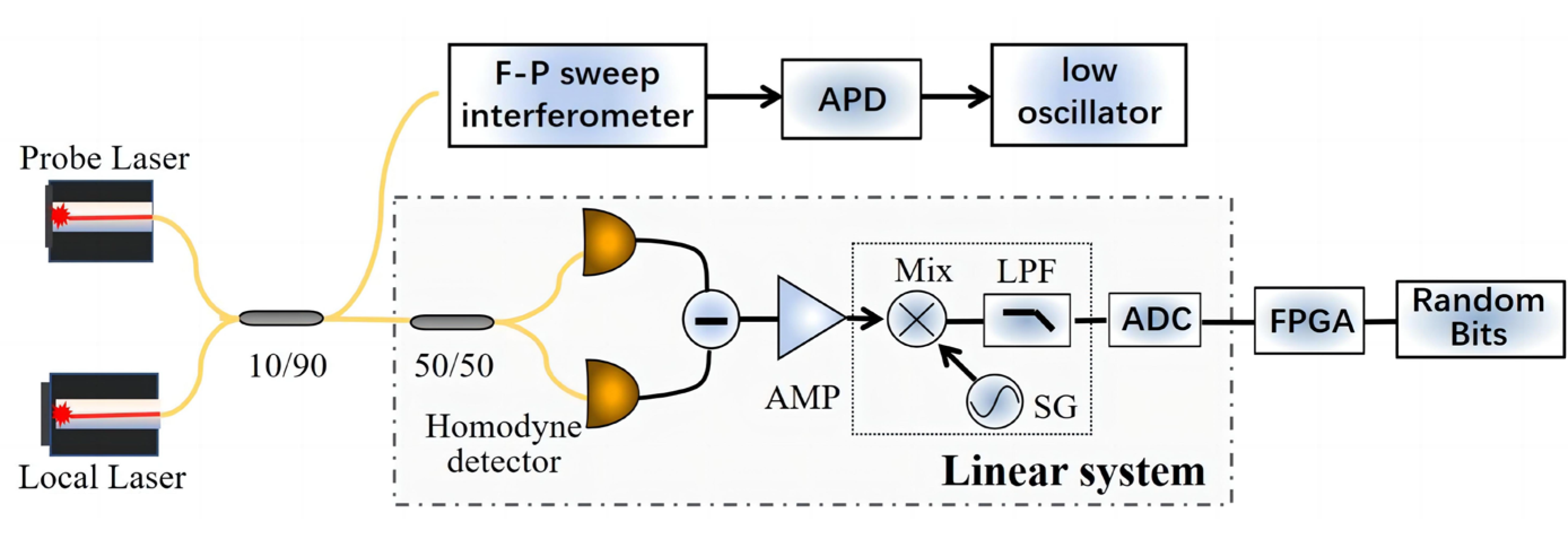
The transfer function (TF) is normally used to characterize the input–output characteristic of a linear system in frequency domain. Technically, TF of a linear system is normally measured based on radio-frequency signals that traverse the analysis frequency bandwidth. Here, this method is migrated into the generation system of random sequence in CV-QRNG. The principle of TF measurement is shown in Figure 1, including the quantum state homodyne measurement, sideband-mode extraction, and ADC discretization. The whole is dealt with as a linear system, which is rational since each component included is a linear unit here. The measured TF includes the effects of all nonideal factors on the accuracy of quantum state measurement, such as local oscillator noise, beam splitter nonideal balance, diode quantum efficiency, finite common mode rejection ratio, ADC noise, and so on. The system TF is expressed as

$$TF\left(v_s\right)=\frac{P_{out}\left(v_s\right)}{P_{in}\left(v_s\right)}$$

(1)

where $P_{in/out}\left(v_s\right)$ denotes the probe power at different analyzed frequencies. Here, the probe is a coherent state generated by beating between a probe laser and the LO. The probe laser is injected through the channel of vacuum state in the case of vacuum-based CV-QRNG. If the detection system in the dashed box shown in Figure 1 is a classical input–output system, the beat signal can just work as a probe. Since the homodyne here is a quantum detection device, the root mean square power of the beat signal works as the probe for the measurement of quadratures of the vacuum state [39]. When the probe attends, the photoelectric signal output from the homodyne system is

$$\widehat{q}=TF\left(v_s\right)\cdot \left({\alpha }_{v_s}\cdot \delta \widehat{x}+\widehat{N}\right)$$

(2)

in which ${\alpha }_{v_s}\cdot \delta \widehat{x}$ is a coherent state and also vacuum state quadrature scaled with the coherent state amplitude ${\alpha }_{v_s}$, which is determined by the probe laser power. At high signal-to-noise ratios, the quadrature of the beat signal is purely a function of the coherent state amplitude because the classical noise $\widehat{N}$ is weak relative to coherent amplitude for a high-frequency sideband mode, which is actually the quantum entropy source of a CV-QRNG and extracted based on a mixed-down system, shown with a dotted line box in Figure 1.

In this way, the TF of the linear system is obtained by studying only the relationship between the system input and output without making any assumptions about the system interior. At each analysis, the $TF\left(v_s\right)$ is determined by normalizing the beat power to the probe power, and the power spectrum density of the vacuum quadrature fluctuations is obtained by multiplying $TF\left(v_s\right)$ with the shot noise energy contained in 1 Hz bandwidth. We reconstruct the power spectrum within the homodyne detection bandwidth based on the beat method, and make the beat signal scan each analysis frequency within the homodyne bandwidth by controlling the probe laser frequency.

For the generation of beat signal, the probe laser and the LO should have similar line-width, and the line-width of the two lasers should be narrow enough to ensure that the coherence time of the beat signal is greater than the response time of the detector. The complex amplitude of the photoelectric field of an ideal laser can be expressed as

$$E\left(t\right)=Ecos\left(\omega t+\phi \right)$$

(3)

where E denotes the amplitude of the field, $\omega$ the frequency of the photoelectric field, and $\phi$ the phase of the photoelectric field. When the photoelectric field complex amplitudes $E_1\left(t\right)$ and $E_2\left(t\right)$ of two laser beams enter the photodetector at the same time,

$$\begin{array}{ll}{\left[E_1\left(t\right)+E_2\left(t\right)\right]}^2& =E_1{}^{2}co{s}^2\left({\omega }_{1}t+{\phi }_1\right)+E_2{}^{2}co{s}^2\left({\omega }_{2}t+{\phi }_2\right)+\frac{1}{2}{E}_1{E}_{2}cos\left[({\omega }_1+{\omega }_2\right)t+\left({\phi }_1+{\phi }_2\right)]\\ & +\frac{1}{2}{E}_1{E}_{2}cos\left[({\omega }_1-{\omega }_2\right)t+\left({\phi }_1-{\phi }_2\right)]\end{array}$$

(4)

Since the BHD used here has a bandwidth of 1.6 GHz, the frequency of the beat signal should be lower than 1.6 GHz. Only the component $1/2E_1{E}_{2}cos\left[({\omega }_1-{\omega }_2\right)t+\left({\phi }_1-{\phi }_2\right)]$ in Equation (4) is likely to be close to the response frequency of the photodetector. From the first-order derivative of the relationship between frequency and wavelength,

$$dV=\frac{C}{{\lambda }^2}d\lambda ,$$

(5)

it can be seen that in order to make the frequency difference between the two lasers within 1.6 GHz, the wavelength difference between the two laser beams should be less than 12.8 pm.

Furthermore, for measuring the TF at each frequency appropriately, it needs to be ensured that there are no additional errors introduced due to the inconformity of the line shape of the beat signal when the probe laser wavelength is adjusted for changing the beat signal frequency. In our experiments, LO and probe lasers are both Lorentzian, and the output line shape of a single Lorentzian laser is

$$g_1\left(v_{ }\right)=\frac{\mathsf{\Delta }{v}_{ }}{{(v_{ }-v_i)}^2+{(\frac{\mathsf{\Delta }{v}_{ }}{2})}^2}$$

(6)

$v$ represents frequency, $v_i$ is the central frequency of the Lorentz function, which is the frequency at which the output light intensity reaches its maximum value, $\mathsf{\Delta }{v}_i$ is the linewidth of the laser, and the beat line pattern of the two lasers is the convolution of the individual line patterns of the two lasers:

$$\begin{array}{cc}& g_{beat}\left(v_{ }\right)=g_1{(v_{ })}^{*}{g}_2\left(v_{ }\right)=\\ & \frac{8\pi \mathsf{\Delta }{v}_1[\mathsf{\Delta }{v}_2((4\left(v_{ }-v_1-v_2{)}^2+\mathsf{\Delta }{v}_1^2-\mathsf{\Delta }{v}_2^2\right)Abs\left[\mathsf{\Delta }{v}_1\right]+\left(4\left(v_{ }-v_1-v_2{)}^2-\mathsf{\Delta }{v}_1^2+\mathsf{\Delta }{v}_2^2\right)Abs\left[\mathsf{\Delta }{v}_2\right]\right)}{(4{(v_{ }-v_1-v_2)}^2+\left(\mathsf{\Delta }{v}_1-\mathsf{\Delta }{v}_2{)}^2\right)(4{(v_{ }-v_1-v_2)}^2+\left(\mathsf{\Delta }{v}_1+\mathsf{\Delta }{v}_2{)}^2\right)Abs\left[\mathsf{\Delta }{v}_1\left]Abs\right[\mathsf{\Delta }{v}_2\right]}\end{array}$$

(7)

The center wavelength of the LO laser is 1550 nm, and the linewidth is 325 kHz. The center wavelength of the probe laser is 1550 nm, and the linewidth is 800 kHz. According to Equation (7) the beat signal line shape is simulated and the result is shown in Figure 2.

From Figure 2, it can be concluded that when the wavelength of the probe field is changed, the center frequency of beat signal is changed correspondingly, but its line shape can remain unchanged. In this way, the possibility of introducing errors from linear shape variations of probe is eliminated.

3. Experiments and Results

3.1. Experimental Setup and Scheme

Experimentally, we constructed the parallel CV-QRNG at the first phase [20], and then coupled the TF measurement part of the quantum noise measurement and quantification system into the experimental setup. The experimental setup diagram is shown in Figure 3. In the parallel CV-QRNG, the LO with a wavelength of 1550 nm provided by a single-mode semiconductor continuous wave laser (ROI, LP1550Y) and vacuum field are combined in the PBS1 to achieve spatial coincidence, resulting in interference in the same polarization direction after PBS2. The interfered field transmitted vertically by PBS2 is divided into two parts with the same power by the half-wave plate and PBS3, which are coupled into two photodiodes of a 1.6 GHz balanced homodyne detector (BHD, Thorlabs, BPD480C-AC).

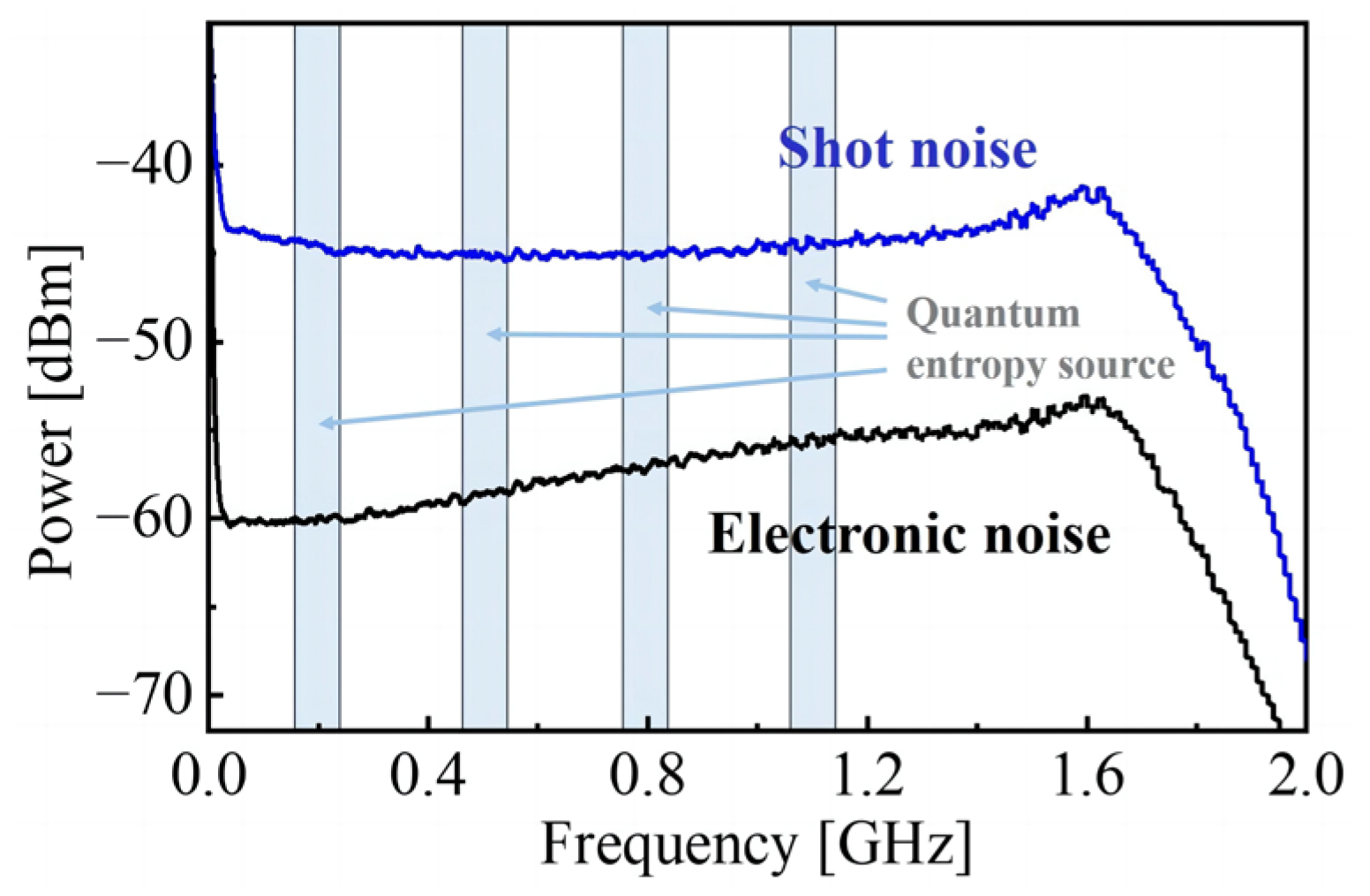
Firstly, the noise power spectrum of BHD measurements is recorded by a spectral analyzer (N9010A, Agilent Technologies Inc., Santa Clara, CA, USA). As shown in Figure 4, classical noise in the photocurrents is rejected effectively over the whole detection band with an SNR above 10 dB. Based on the moderate processing power of our FPGA (xc7k325t, Xilinx Inc., San Jose, CA, USA), after optimizing logical resources, we extract four quantum sideband frequency modes with bandwidths of 98 MHz within the measurement bandwidth. The signal outcome from the BHD is evenly divided into four parts via a power splitter and mixed with rf signals of different frequencies transmitted by SG through a mixer. After low-pass filtering, four subentropy sources in sideband mode are obtained.

The first component is mixed down with a 200 MHz rf signal and then passes through a low-pass filter of 98 MHz cutoff frequency. In this way, the subentropy source is defined as a composite quantum state centered around 200 MHz relative to the optical carrier with a bandwidth of 98 MHz. The second, third, and fourth parts are independently mixed with rf signals of 500 MHz, 800 MHz, and 1100 MHz, and also filtered with a filter of 98 MHz. The four sideband frequency modes of the vacuum state work together to contribute quantum randomness to the QRNG. A 250 MSa/s, 16-bit analog-to-digital converter (ADC) is used to transform the analog signals from each path into binary random sequences. The Toeplitz hash extractor is used in the post-processing stage. The extraction ratio of true number numbers from the original data is based on the leftover hash lemma [40].

When the TF is measured, a probe laser (Eblana Photonics, Dublin, Ireland, EP1550-DM-B), instead of the vacuum state, is injected in the random numbers generation system as shown in Figure 3. The probe laser initially passes through an HWP, and then reflects into PBS1 via a reflector with a PZT attached. The spatial consistency with the LO light results in interference in the same polarization direction in PBS2. Part of the interfered fields is reflected by PBS2 and coupled into the scanning FP interferometers. The oscilloscope receives the FP output signal to monitor the beat signal. On the other hand, the interfered field transmitted vertically by PBS2 is divided into two parts with the same power by the half-wave plate and PBS3, which are coupled into two PDs of a 1.6 GHz balanced homodyne detector (BHD, Thorlabs, Newton, NJ, USA, BPD480C-AC). The time series of beat signals is obtained through differential amplification, mixed filtering, and ADC quantization.

We use a spectrometer with high resolution (AQ6370C, YOKOGAWA) to monitor the wavelength difference between the probe laser and the LO. At the same time, an FP interferometer is employed to monitor the relative frequencies of the two laser beams. The free spectral region (FSR) of the FP cavity needs to be larger than the frequency tuning range of the probe laser to avoid interference artifacts, that is, the interference peaks of the two laser beams overlap and the actual frequency difference is an integer multiple of the FSR of the FP cavity. The FP interferometer we used has an FSR of 3.75 GHz and a fineness of 200.

In addition, when generating the beat signal, one needs to pay attention to the phenomenon where the two laser beams are partially annihilated. For instance, if the linewidth difference between the two laser beams is too large, the beat signal will only reflect the characteristics of the laser with narrow linewidth. That is, the laser linewidth should be as similar as possible or at least maintained at the equal magnitude. At the same time, the necessary conditions for generating the beat signal are high-frequency stability of the two lasers themselves and small drift of the laser output frequency. To satisfy these requirements, we chose an LO laser with a linewidth of 325 kHz and a typical wavelength stability value of 1.5 pm. For the probe laser, we chose a laser with a linewidth of 800 kHz and a wavelength adjustment step of 1 pm by controlling its current source.

3.2. Generation and Reconstruction of Beat Signals

Experimentally, firstly, we adjust the spatial coincidence of the two laser beams. Then, the wavelength difference between the two laser beams is observed through the spectrometer, and the probe laser wavelength is adjusted to close to the LO as much as possible, at least with a wavelength difference below 12.8 pm, as discussed in the Section 2. At the same time, the modes overlap is monitored through the FP interferometer. The typical wavelength proximity observed using the spectrometer is shown in Figure 5a, and the overlap of the two laser modes monitored through the FP is shown in Figure 5b.

Then the beat signal in the frequency domain is employed as a probe to explore the TF of the homodyne and ADC system in the random number generation scheme. By adjusting the frequency of the signal beam while keeping the other laser’s frequency constant, the frequency of the probe, that is, the beat signal, can be controlled. The fluctuations caused by the instability of the current source and temperature control source are one order of magnitude smaller than those caused by LO laser fluctuations. Therefore, we ignore the former and depend on the probe laser minimum adjustment step to collect data within the detector bandwidth. Due to the wavelength jitter of the LO laser, the beat signal of the driving current value of the probe laser fluctuates within 180 MHz. Based on the minimum adjustment step size, we can collect data under up to 13 different driving current values, covering the entire 1.6 GHz homodyne detection bandwidth.

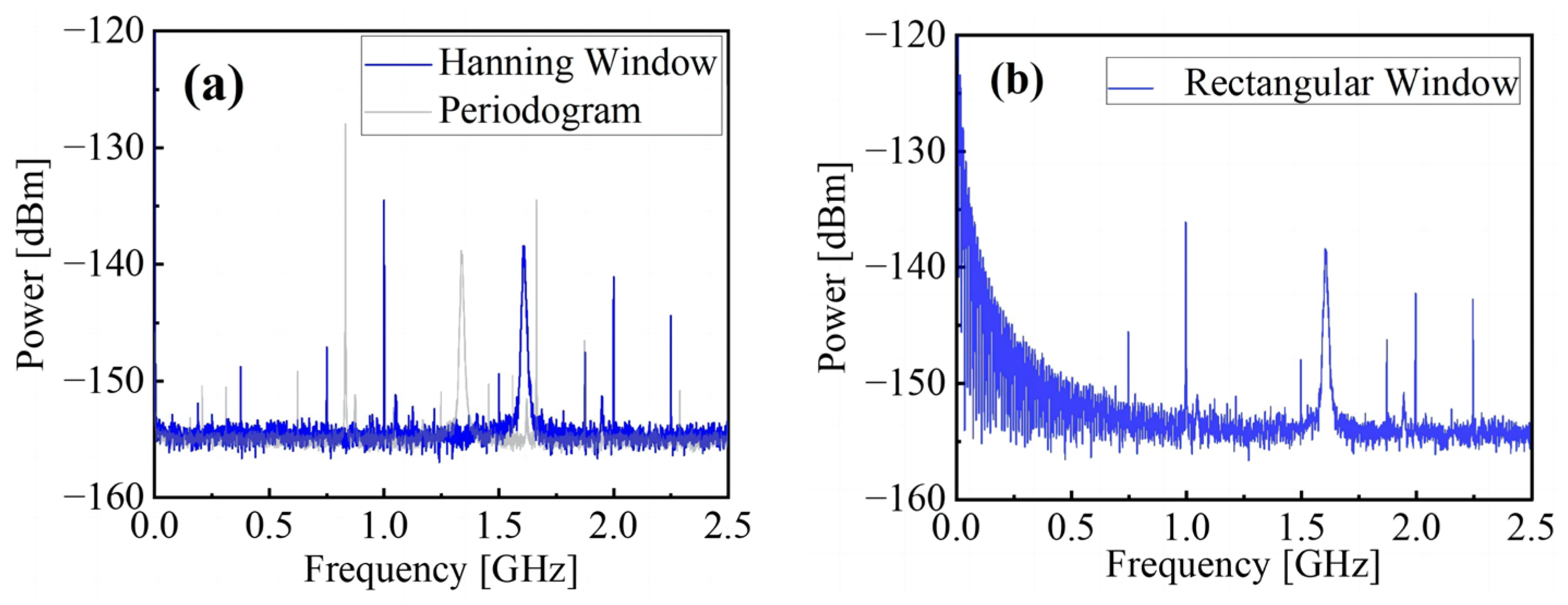
For the beat signal at each frequency section, signal output from each ADC is collected and transformed into frequency-domain by utilizing the Welch method. For the employment of the Welch method, window function, the number of segments, and the resolution are three factors that need to be optimum to obtain an accurate power spectrum estimation. The effects of different window functions (such as rectangular window, Bartlett or Triangular window, Hanning window, Hamming window) on the reconfiguration of the beat signals are compared when the experimental data are processed. Figure 6 shows the power spectra of the beat signals reconstructed based on the two most representative window functions, rectangular and Hanning. The noise level at the low frequency for the rectangular window function is high. In comparison, the Hanning window has a better effect on the noise suppression at low frequencies and has a high resolution; however, there are still some noise peaks that exceed the beat signal in amplitude (still better than typical estimation methods—periodogram), so further adjustment is needed.

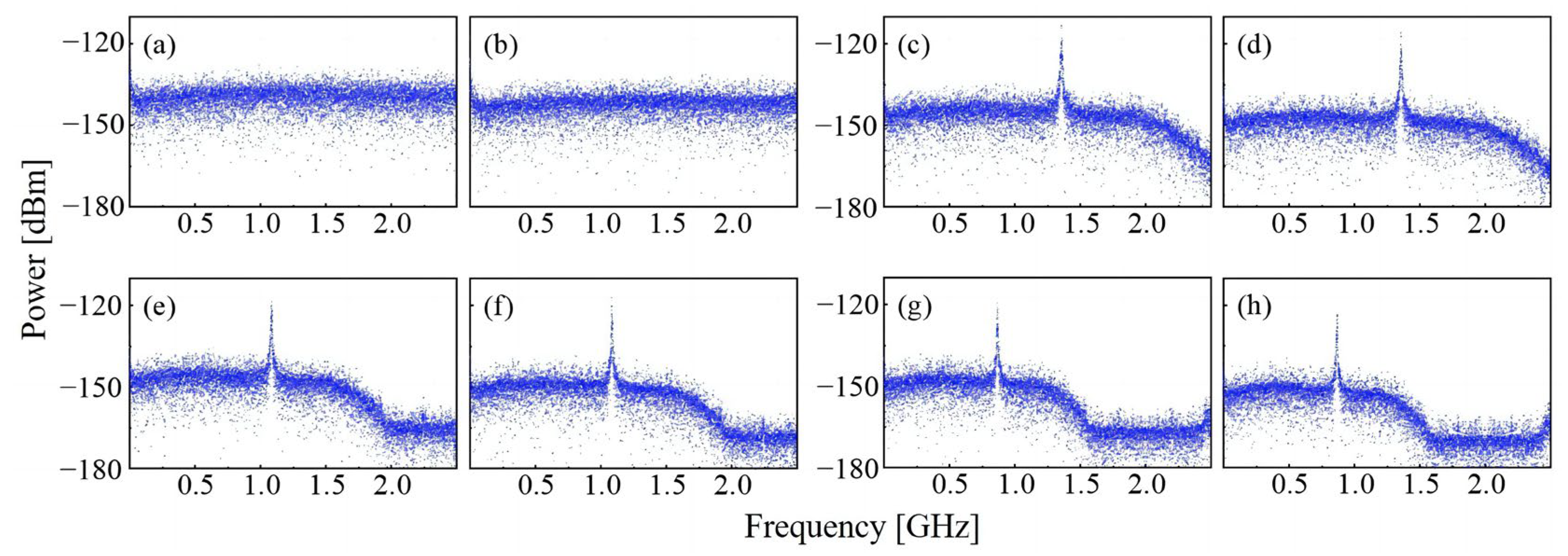
We investigated the impact of different segmentation numbers on power spectrum estimation while allowing for partial overlap between adjacent data segments to reduce the level of the sidelobe and, thus, reduce variance. The differences between the power spectra of continuous time intervals can reveal the instantaneous changes in signal characteristics, such as frequency and amplitude, during these time intervals. Therefore, the difference between adjacent power spectra can be utilized to reveal, in detail, the development trend of instantaneous signal characteristics over time. We found that when the segmentation number is less than 10 or greater than 70, the resolution is insufficient. Therefore, our research mainly focuses on the number of segments between 10 and 70. We divide the sample data of the 1.1 GHz beat signal into 20, 40, 50, and 63 segments, and compare the effect when the differences between adjacent segments are at 1/2 and 1/4 of the total number of segments; the results are shown in Figure 7.

As shown in Figure 7, when the total number of segments is 20, no obvious beat peak can be seen, which indicates that the power spectrum estimation performance is poor. When the data are divided into 40, 50, and 63 segments, there are obvious beat peaks at frequencies around 1.4 GHz, 1.1 GHz, and 800 MHz, respectively, which proves that the number of segments is reasonable at this time; however, the center frequency of the beat peak will shift at different segment numbers. The best value of the number of segments is when the frequency of the beat peak estimated by Welch is consistent with the frequency of the beat peak estimated by the periodogram method without segments, and this frequency is also consistent with the measurement result of the spectrum analyzer. Based on the above discussion, for the 10⁷ data collected at a sampling rate of 250 MSa/s and a depth of 16 bit, we determined the following power spectrum estimation parameters: 50 segments, 50% overlap rate, and Hanning window as the window function to complete the spectrum estimation.

3.3. Experimental Calibration of Power Spectrum of Vacuum Fluctuations

Finally, we progress to the phase of reconstruction of the power spectrum of the beat signal. Firstly, the output time series through the homodyne and ADC system are collected and converted back to decimal voltage values. By adjusting the current of the probe laser, the frequency of the beat signal is changed to span the entire detection bandwidth. According to the minimum adjustment step of the current source, we can collect beat signal data of 13 current values within the detection bandwidth of 1.6 GHz. Due to the influence of the wavelength stability of the local oscillator laser, the beat signal of each current value will fluctuate among a range of about 180 MHz, as shown in Figure 8b.

In order to study the changes in entropy content of random number generators in practical applications, we collected beat signals of QRNG under continuous running (over six hours) and found that the peak value of the beat signal at the same frequency fluctuates within a certain range as well, which should be induced by instabilities in instruments such as LO lasers, balance detectors, and current amplifiers, as well as the impact of environmental variables. In addition, it can be found that the peak value of the beat signal appears to significantly decrease with increasing frequency (Figure 8a), indicating that the quantum entropy content in the detection bandwidth gradually decreases with increasing frequency. This trend is the same as that of the vacuum noise power spectrum (Figure 4) measured by the above spectrum analyzer.

Then, the TF of the four sideband modes is measured separately. Due to the fluctuation of the beat frequency signal for each current value within the range of approximately 180 MHz, we only need to continuously collect the beat signal at a fixed current value to obtain the beat signals of all frequencies in sideband mode, and the beat signal powers are normalized to the probe laser power to obtain the TF in all sideband modes. The obtained calibration power spectrum is as follows:

It can be concluded from Figure 9b that the power spectral density of vacuum fluctuations in the 200 MHz sideband mode is reduced by 8–11.5 dB compared with the original power spectral density, and the other sideband modes are basically the same. The next steps are to compare the original power spectrum with the vacuum fluctuation power spectrum, obtain the signal variance, conditional signal variance, and conditional excess noise variance, and rigorously calibrate the min-entropy lower bound after considering quantum side-information.

3.4. Min-Entropy Lower Bound against Quantum Side-Information

In practice, ADC maps the continuous variables Χ into discrete and bounded variables $\overline{x}$ with a bin size $\mathsf{\Delta }x$. The min-entropy lower bound considering the side-information E can be obtained by optimizing the ADC dynamics range [41,42]:

$$H_{min}(\overline{x}|\mathrm{E}{)}_{\rho }\gtrsim -log\left(\frac{\mathsf{\Delta }x}{g}\frac{\sqrt{2}\left(2n+1\right)}{\sqrt{\pi }\left(4n+3\right)}\right)$$

(8)

where $g$ is the gain factor and$n$ is the average photon number. Now we can use TF to calibrate the vacuum fluctuation power spectrum to obtain the minimum entropy with quantum and classical side-information. We denote the power spectral density reconstructed by the Welch method as f(λ), assuming that T is the runtime of the experiment, and measure N signals at a regular time intervals of δt = T/N. The power spectral density computed from the measured data is a function of N discrete frequencies, denoted as ${\omega }_{ j}$, taking values between 2π/T and 2πN/T. The discrete variable${\lambda }_j$ ≡ T${\omega }_{ j}$/N can be set, which can be approximated by the continuous variable $\lambda$ taking values with domain [0,2π]. Then signal variance ${\sigma }^2$ can be expressed as [43] follows:

$${\sigma }^2={{\displaystyle \int }}_0^{2\pi }\frac{d\lambda }{2\pi }f\left(\lambda \right)$$

(9)

Due to the limited detection bandwidth, the signal $X_t$ and the excess noise $U_t$ will be correlated with previous time values at time t. To remove these effects, we replace the signal variance with conditional signal variance ${\sigma }_X^2$ that is not dependent on previous time values, ${\sigma }_X^2$ denoted as [43] follows:

$${\sigma }_X^2=\frac{1}{2\pi e}{2}^{{{\displaystyle \int }}_0^{2\pi }\frac{d\lambda }{2\pi }log\left[2\mathsf{\pi }{f}_x\left(\lambda \right)\right]}$$

(10)

Similarly, the conditional vacuum fluctuation noise variance ${\sigma }_v^2$ is

$${\sigma }_v^2=\frac{1}{2\pi e}{2}^{{{\displaystyle \int }}_0^{2\pi }\frac{d\lambda }{2\pi }log\left[2\mathsf{\pi }{f}_{vac}\left(\lambda \right)\right]}$$

(11)

Then the conditional excess noise variance ${\sigma }_u^2={\sigma }_X^2-{\sigma }_v^2$, the calculated signal variance, conditional signal variance, and conditional excess noise variance are 3.78 × 10⁵, 3.21 × 10⁵, and (2.72~2.99) × 10⁵. We use this to complete the derivation of the min-entropy lower bound and obtain the following relationship: $g^2\equiv {\sigma }_X^2-{\sigma }_u^2$ and $n=\frac{1}{2}\left(\frac{{\sigma }^2}{{\sigma }_X^2-{\sigma }_u^2}-1\right)$ [39].

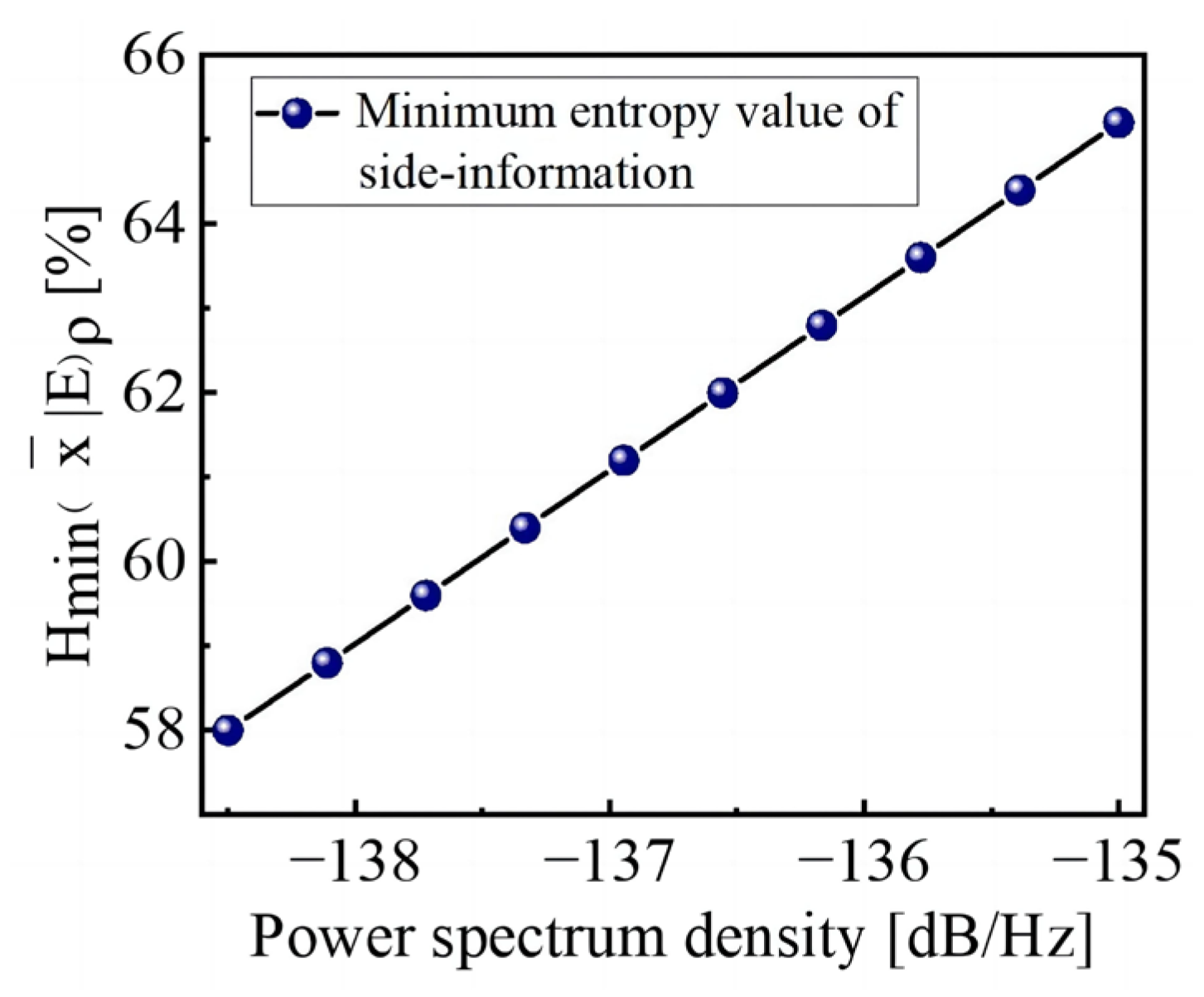
From Figure 10, it can be seen that in the 200 MHz sideband mode, the calibrated entropy rate fluctuates between 58% and 65%, which is smaller than the entropy evaluation results of our previous random number generation scheme [20] because the current scheme does not rely on the ideal assumption of the device, which ensures that the generated random numbers have sufficient security. In addition, when QRNG is continuously running in different working cycles, due to changes in equipment performance and environmental variables, the fluctuation range of the vacuum fluctuation power spectrum exceeds 3.5 dB, which leads to a min-entropy fluctuation of over 7% after considering quantum side-information. To ensure that random numbers are not affected by quantum side-information noise, we take the most conservative result (58%) for the min-entropy with the side-information to complete the generation of random numbers.

3.5. Parallel Real-Time QRNG Based on Min-Entropy with Quantum Side-Information

The min-entropy of the four sideband modes is conservatively 9.33 bit, 9.14 bit, 8.99 bit, and 8.9 bit, respectively. Using the Toeplitz matrix to process original random bits with a sequence length of $y$, a secure random number with a sequence length of $x$ can be extracted based on the leftover hash lemma [40], as follows:

$$x\le y\times H_{min}(\overline{x}|\mathrm{E}{)}_{\rho }-{log}_2{}_{\begin{array}{c}\\ \end{array}}\frac{1}{{\epsilon }_{hash}{}^2}$$

(12)

On the one hand, very large block sizes of random numbers are often required to reduce the finite-size effects to a sufficiently low level for security claim in in quantum key distribution [5]. On the other hand, ${\epsilon }_{hash}$ grows with the number of times QRNG is run with the same seed for the Toeplitz extractor [44]. We set the ${\epsilon }_{hash}$to a conservative value of 2⁻¹¹⁰, which is much smaller than our previous scheme’s 2⁻⁵⁰ [20]. In this case, in order to achieve a higher generation rate, the $y$ in our Toeplitz matrix was extended from 512 to 2048. It can be easily concluded from Equation (12) that as y increases, the length x of the extracted sequence will also increase by the same amount under the same safety parameter, and a higher extraction rate will be obtained. After considering strict entropy evaluation and strict hash security parameter selection, the final Toeplitz matrix sizes for 200 MHz, 500 MHz, 800 MHz, and 1100 MHz sideband modes are 960 × 2048, 928 × 2048, 928 × 2048, and 896 × 2048, respectively, and the final extraction rates of quantum random numbers are 46.9%, 45.3%, 45.3%, and 43.8%, respectively. Finally, we generate quantum random numbers in real time at a rate of 7.25 Gbps.

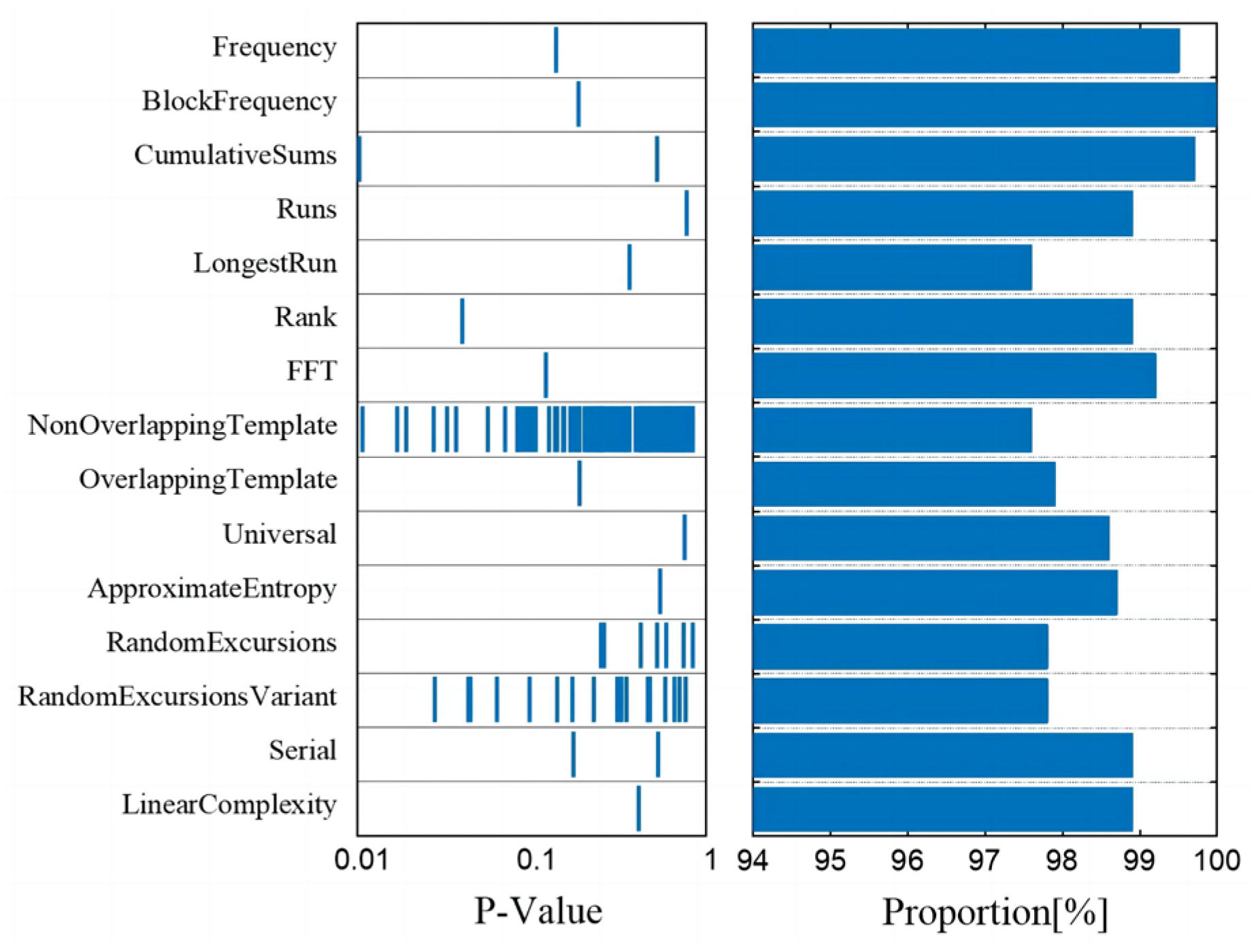
Finally, three representative random number tests are selected to check the generated random numbers: NIST, Diehard, and TestU01 [45,46,47]. For the US National Standard NIST Randomness Test, at a significance level of a = 0.01, the P-values of all 15 tests were greater than 0.01, and all test items passed, as shown in Figure 11.

For the Diehard and TestU01 tests, the P-values of each test are much larger than 0.01. The generated quantum random numbers have also passed all testing projects and once again verified that the random numbers generated by this real-time quantum random number generation scheme have good randomness, as shown in Figure 12.

4. Discussion and Conclusions

It is worth noting that the hash security parameter is far from the ultimate determinant of the failure probability for a QRNG against quantum side-information, while this is the case in the current implementation. Further analysis is needed to extend the security certification with a metrological approach based on quantifying the parallel QRNG’s security in terms of experimentally accessible parameters; details can be found in Ref. [39] for reference.

In conclusion, we proposed a rigorous self-testing parallel CV-QRNG scheme. Without making any ideal assumptions about the homodyne detection and digitization system of the vacuum state quadrature fluctuation, the quantum noise entropy content contained in the raw random numbers was rigorously calibrated based on the measurement of the TF of the system. Four independent subentropy sources were prepared within the 1.6 GHz homodyne bandwidth. A 250 MSa/s, 16-bit ADC quantization and parallel real-time Toeplitz hash post-processing were performed in an FPGA. Based on the rigorous min-entropy evaluation and a high hash security parameter ${\epsilon }_{hash}$ = 2⁻¹¹⁰, the real-time quantum random numbers were generated with a rate of 7.25 Gbps processing, which meets the security and speed requirements in practical applications. This work lays a solid foundation for the practical application of the device-trusted CV-QRNG.