Full-Vectorial Light Propagation Simulation of Optimized Beams in Scattering Media
Abstract
:1. Introduction
2. Simulation Method
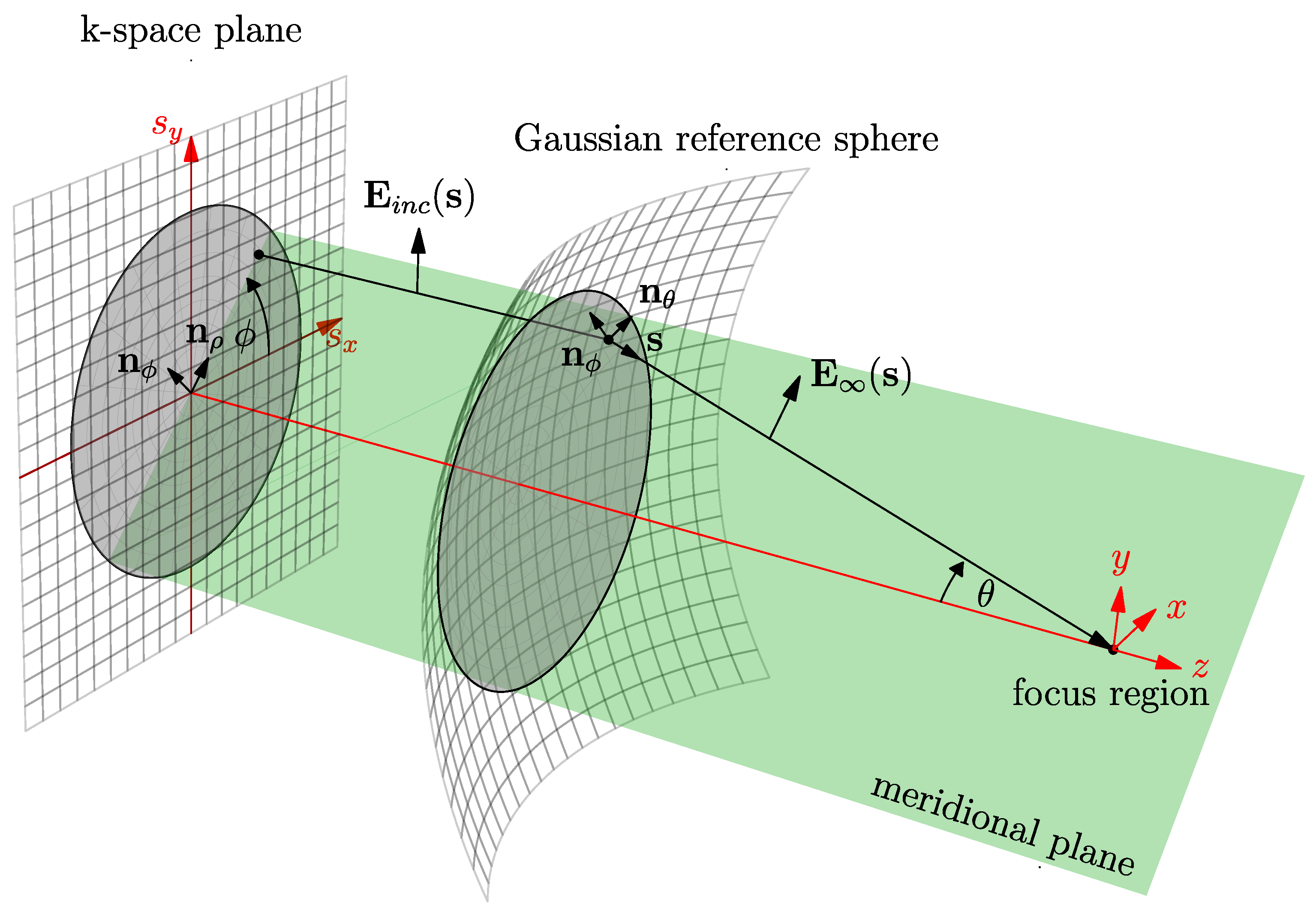
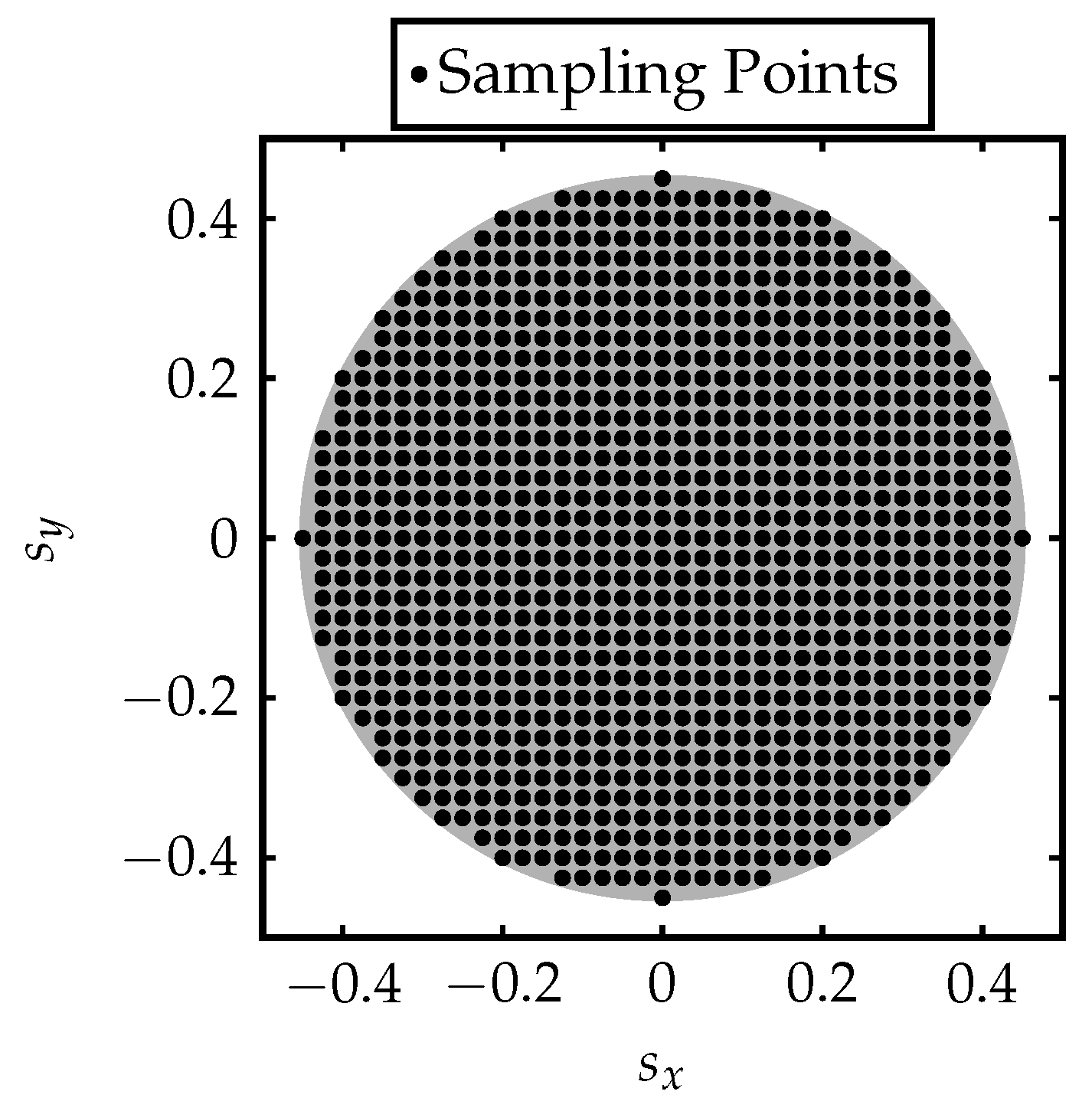
2.1. Two-Step Beam Synthesis Method
2.2. Phase Optimization Techniques
2.3. Scattering Medium and System Specifications
3. Results
3.1. Scattering of a Focused Beam by the Turbid Medium
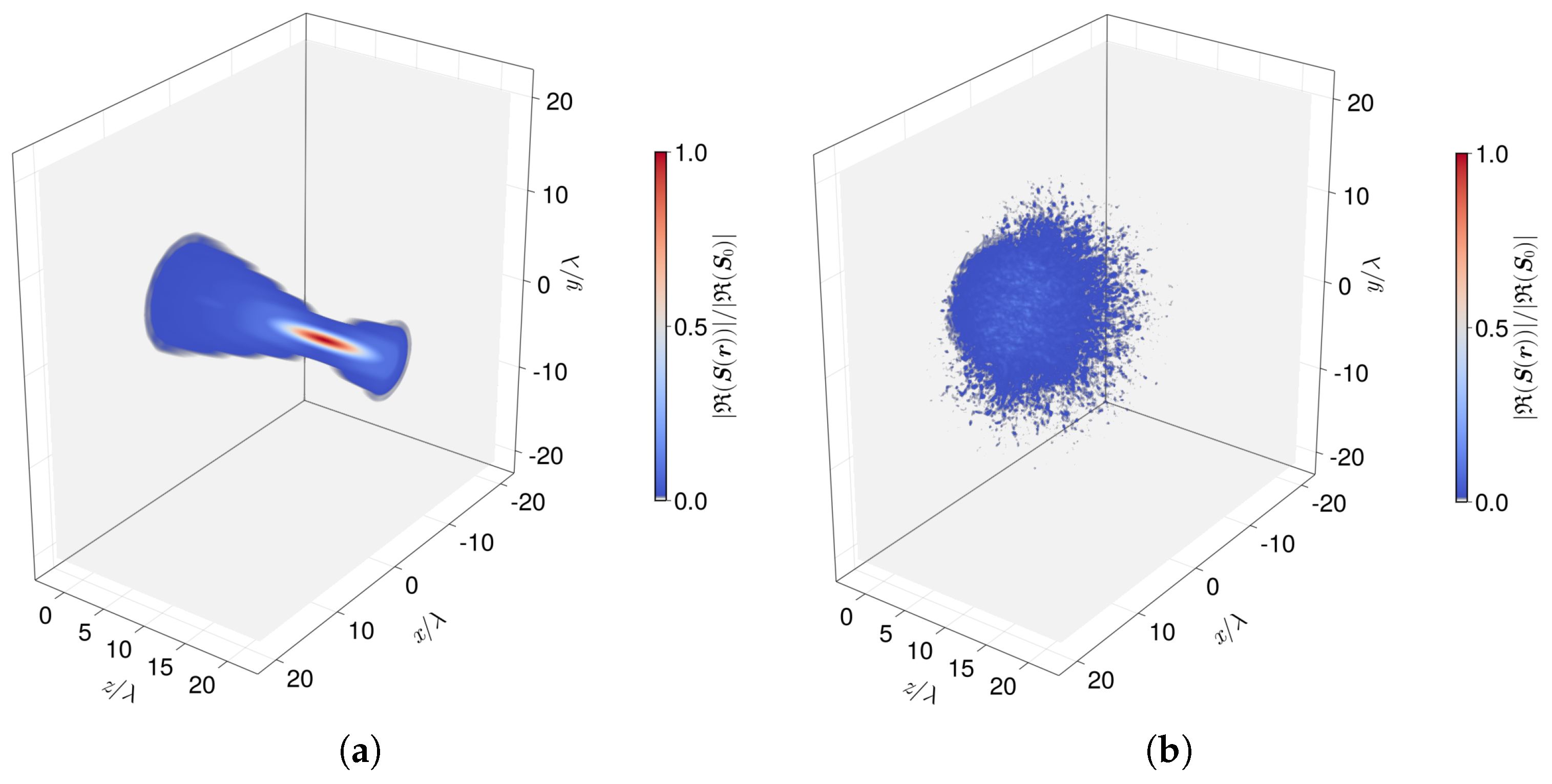
3.2. Phase Optimization to Enhance the Focus Energy Density
3.3. Phase Optimization to Enhance the Absolute Value of the Focus Poynting Vector
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhu, D.; Larin, K.V.; Luo, Q.; Tuchin, V.V. Recent progress in tissue optical clearing. Laser Photonics Rev. 2013, 7, 732–757. [Google Scholar] [CrossRef]
- Durduran, T.; Choe, R.; Baker, W.B.; Yodh, A.G. Diffuse optics for tissue monitoring and tomography. Rep. Prog. Phys. 2010, 73, 076701. [Google Scholar] [CrossRef] [PubMed]
- Gigan, S. Optical microscopy aims deep. Nat. Photonics 2017, 11, 14–16. [Google Scholar] [CrossRef]
- Vellekoop, I.M.; Mosk, A. Focusing coherent light through opaque strongly scattering media. Opt. Lett. 2007, 32, 2309–2311. [Google Scholar] [CrossRef] [PubMed]
- Mosk, A.P.; Lagendijk, A.; Lerosey, G.; Fink, M. Controlling waves in space and time for imaging and focusing in complex media. Nat. Photonics 2012, 6, 283–292. [Google Scholar] [CrossRef]
- Maurer, C.; Jesacher, A.; Bernet, S.; Ritsch-Marte, M. What spatial light modulators can do for optical microscopy. Laser Photonics Rev. 2011, 5, 81–101. [Google Scholar] [CrossRef]
- Bifano, T. MEMS deformable mirrors. Nat. Photonics 2011, 5, 21–23. [Google Scholar] [CrossRef]
- Ren, Y.X.; Lu, R.D.; Gong, L. Tailoring light with a digital micromirror device. Ann. Der Phys. 2015, 527, 447–470. [Google Scholar] [CrossRef]
- Kubby, J.; Gigan, S.; Cui, M. Wavefront Shaping for Biomedical Imaging; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Galaktionov, I.; Nikitin, A.; Samarkin, V.; Sheldakova, J.; Kudryashov, A.V. Laser beam focusing through the scattering medium-low order aberration correction approach. In Proceedings of the Unconventional and Indirect Imaging, Image Reconstruction, and Wavefront Sensing 2018, San Diego, CA, USA, 22–23 August 2018; Volume 10772, pp. 259–272. [Google Scholar]
- Paudel, H.P.; Stockbridge, C.; Mertz, J.; Bifano, T. Focusing polychromatic light through scattering media. In Mems Adaptive Optics VII; SPIE: Bellingham, WA, USA, 2013; Volume 8617, pp. 82–88. [Google Scholar]
- Gigan, S.; Katz, O.; De Aguiar, H.B.; Andresen, E.R.; Aubry, A.; Bertolotti, J.; Bossy, E.; Bouchet, D.; Brake, J.; Brasselet, S.; et al. Roadmap on wavefront shaping and deep imaging in complex media. J. Phys. Photonics 2022, 4, 042501. [Google Scholar] [CrossRef]
- Vellekoop, I.M. Feedback-based wavefront shaping. Opt. Express 2015, 23, 12189–12206. [Google Scholar] [CrossRef]
- Yaqoob, Z.; Psaltis, D.; Feld, M.S.; Yang, C. Optical phase conjugation for turbidity suppression in biological samples. Nat. Photonics 2008, 2, 110–115. [Google Scholar] [CrossRef]
- Yoon, J.; Lee, K.; Park, J.; Park, Y. Measuring optical transmission matrices by wavefront shaping. Opt. Express 2015, 23, 10158–10167. [Google Scholar] [CrossRef] [PubMed]
- Popoff, S.; Lerosey, G.; Fink, M.; Boccara, A.C.; Gigan, S. Image transmission through an opaque material. Nat. Commun. 2010, 1, 81. [Google Scholar] [CrossRef] [PubMed]
- Horstmeyer, R.; Ruan, H.; Yang, C. Guidestar-assisted wavefront-shaping methods for focusing light into biological tissue. Nat. Photonics 2015, 9, 563–571. [Google Scholar] [CrossRef] [PubMed]
- Martelli, F.; Tiziano, B.; Del Bianco, S.; André, L.; Alwin, K. Light Propagation Through Biological Tissue and Other Diffusive Media: Theory, Solutions, and Validations; SPIE: Bellingham, WA, USA, 2022. [Google Scholar]
- Bender, N.; Yamilov, A.; Goetschy, A.; Yılmaz, H.; Hsu, C.W.; Cao, H. Depth-targeted energy delivery deep inside scattering media. Nat. Phys. 2022, 18, 309–315. [Google Scholar] [CrossRef]
- Tseng, S.H.; Yang, C. 2-D PSTD Simulation of optical phase conjugation for turbidity suppression. Opt. Express 2007, 15, 16005–16016. [Google Scholar] [CrossRef] [PubMed]
- Ott, F.; Fritzsche, N.; Kienle, A. Numerical simulation of phase-optimized light beams in two-dimensional scattering media. JOSA A 2022, 39, 2410–2421. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Li, J.; He, S.; Wang, L.V. Angular-spectrum modeling of focusing light inside scattering media by optical phase conjugation. Optica 2019, 6, 250–256. [Google Scholar] [CrossRef]
- Thendiyammal, A.; Osnabrugge, G.; Knop, T.; Vellekoop, I.M. Model-based wavefront shaping microscopy. Opt. Lett. 2020, 45, 5101–5104. [Google Scholar] [CrossRef]
- Wolf, E. Electromagnetic diffraction in optical systems-I. An integral representation of the image field. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1959, 253, 349–357. [Google Scholar]
- Richards, B.; Wolf, E. Electromagnetic diffraction in optical systems, II. Structure of the image field in an aplanatic system. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1959, 253, 358–379. [Google Scholar]
- Novotny, L.; Hecht, B. Principles of Nano-Optics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Çapoğlu, İ.R.; Taflove, A.; Backman, V. Computation of tightly-focused laser beams in the FDTD method. Opt. Express 2013, 21, 87–101. [Google Scholar] [CrossRef] [PubMed]
- Krüger, B.; Brenner, T.; Kienle, A. Solution of the inhomogeneous Maxwell’s equations using a Born series. Opt. Express 2017, 25, 25165–25182. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W. Introduction to Fourier Optics; Roberts and Company Publishers: Englewood, CO, USA, 2005. [Google Scholar]
- Popoff, S.M.; Lerosey, G.; Carminati, R.; Fink, M.; Boccara, A.C.; Gigan, S. Measuring the transmission matrix in optics: An approach to the study and control of light propagation in disordered media. Phys. Rev. Lett. 2010, 104, 100601. [Google Scholar] [CrossRef] [PubMed]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Mogensen, P.K.; Riseth, A.N. Optim: A mathematical optimization package for Julia. J. Open Source Softw. 2018, 3, 615. [Google Scholar] [CrossRef]
- BlackBoxOptim.jl. Available online: https://web.archive.org/web/20230326084433/https://github.com/robertfeldt/BlackBoxOptim.jl (accessed on 29 May 2023).
- Danisch, S.; Krumbiegel, J. Makie.jl: Flexible high-performance data visualization for Julia. J. Open Source Softw. 2021, 6, 3349. [Google Scholar] [CrossRef]
- Ishimaru, A. Wave Propagation and Scattering in Random Media; Academic Press: New York, NY, USA, 1978; Volume 2. [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Elmaklizi, A.; Schäfer, J.; Kienle, A. Simulating the scanning of a focused beam through scattering media using a numerical solution of Maxwell’s equations. J. Biomed. Opt. 2014, 19, 071404. [Google Scholar]
- Elmaklizi, A.; Reitzle, D.; Brandes, A.; Kienle, A. Penetration depth of focused beams in highly scattering media investigated with a numerical solution of Maxwell’s equations in two dimensions. J. Biomed. Opt. 2015, 20, 065007. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ott, F.; Fritzsche, N.; Kienle, A. Full-Vectorial Light Propagation Simulation of Optimized Beams in Scattering Media. Photonics 2023, 10, 1068. https://doi.org/10.3390/photonics10101068
Ott F, Fritzsche N, Kienle A. Full-Vectorial Light Propagation Simulation of Optimized Beams in Scattering Media. Photonics. 2023; 10(10):1068. https://doi.org/10.3390/photonics10101068
Chicago/Turabian StyleOtt, Felix, Niklas Fritzsche, and Alwin Kienle. 2023. "Full-Vectorial Light Propagation Simulation of Optimized Beams in Scattering Media" Photonics 10, no. 10: 1068. https://doi.org/10.3390/photonics10101068
APA StyleOtt, F., Fritzsche, N., & Kienle, A. (2023). Full-Vectorial Light Propagation Simulation of Optimized Beams in Scattering Media. Photonics, 10(10), 1068. https://doi.org/10.3390/photonics10101068




