Polarimetric Images of Biological Tissues Based on the Arrow Decomposition of Mueller Matrices
Abstract
1. Introduction
- depolarization, which can be globally characterized by means of the depolarization index (or degree of polarimetric purity) [7], the polarization entropy [9], the depolarization power [8], the first and second Lorentz depolarization indices [10], the overall purity index [11], etc., while the detailed information on depolarization can be characterized by the indices of polarimetric purity [12,13];
- retardance, whose characterization for general Mueller matrices requires a criterion to define both the entrance and exit retardance vectors.
2. Theoretical Background
3. Arrow-Form-Inspired Parameterization of the Information Contained in a Mueller Matrix
- the three parameters determining the entrance retarder;
- the three parameters determining the exit retarder;
- the MIC of M (which coincides with that of );
- the three parameters determining the diattenuation vector D of M, or, alternatively, the three parameters determining the diattenuation vector of ;
- the three parameters determining the polarizance vector P of M, or, alternatively, the three parameters determining the polarizance vector of ;
- the three indices of polarimetric purity of M (which coincide with those of ).
4. Materials and Methods
4.1. Experimental Setup Description: Complete Image Mueller Matrix Polarimeter
4.2. Sample Description and Preparation
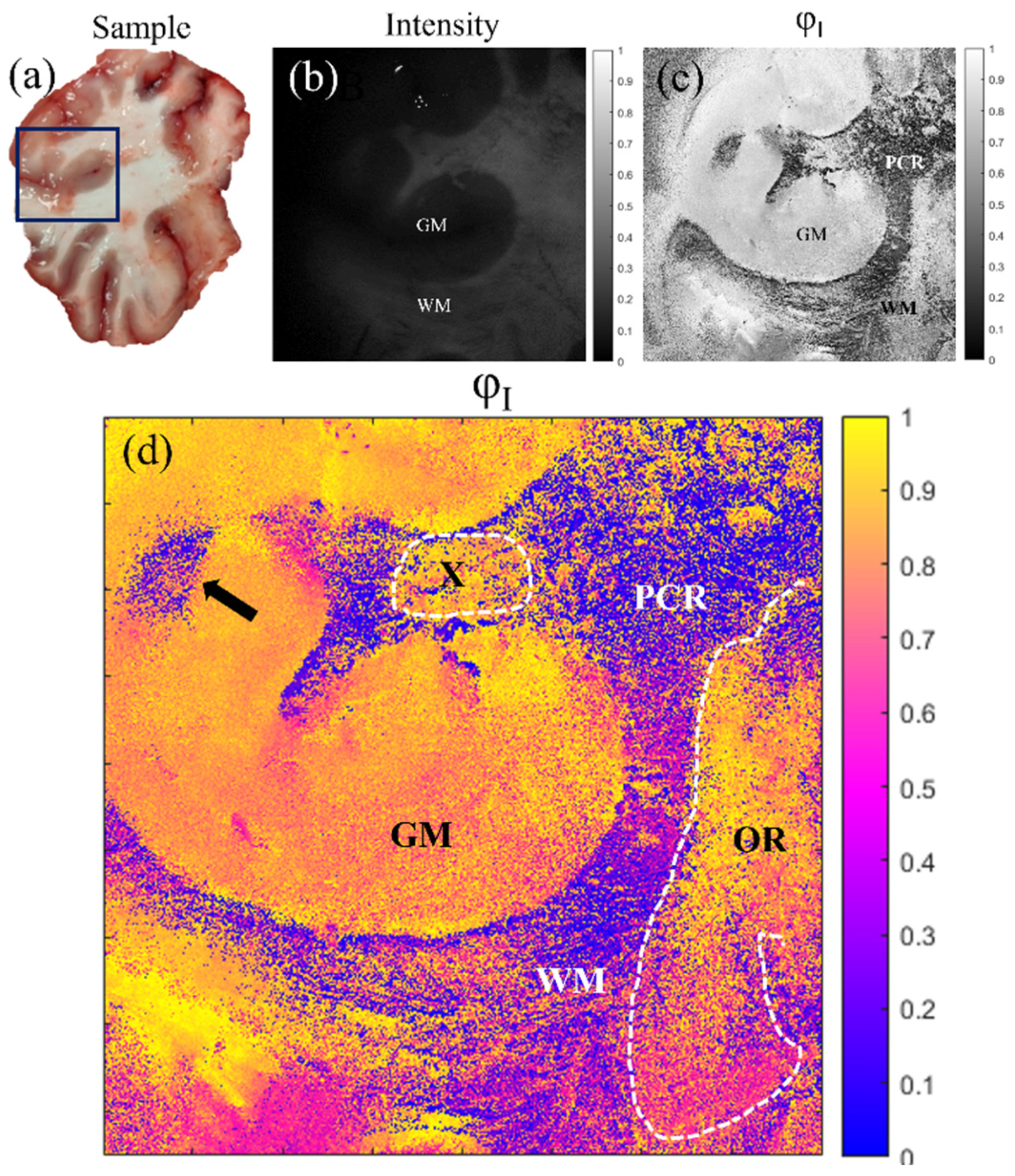
5. Application of the Mueller Matrix Parameterization to Polarimetric Imaging of Biological Tissues
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Goldstein, D.H. Polarized Light, Revised and Expanded; CRC Press: Boca Raton, FL, USA, 2003; ISBN 9780203911587. [Google Scholar]
- Gil, J.J.; Ossikovski, R. Polarized Light and the Mueller Matrix Approach; CRC Press: New York, NY, USA, 2022; ISBN 9780367815578. [Google Scholar]
- Chipman, R.A. Polarimetry. In Handbook of Optics II; McGraw-Hill: New York, NY, USA, 1995; Chapter 22. [Google Scholar]
- Sheppard, C.J.R.; Bendandi, A.; Le Gratiet, A.; Diaspro, A. Eigenvectors of Polarization Coherency Matrices. J. Opt. Soc. Am. A 2020, 37, 1143. [Google Scholar] [CrossRef] [PubMed]
- Ignatenko, D.N.; Shkirin, A.V.; Lobachevsky, Y.P.; Gudkov, S.V. Applications of Mueller Matrix Polarimetry to Biological and Agricultural Diagnostics: A Review. Appl. Sci. 2022, 12, 5258. [Google Scholar] [CrossRef]
- Li, J.; Liao, R.; Guan, C.; Wang, H.; Zhuo, Z.; Zeng, Y.; Ma, H. Particulate Mueller Matrix Polarimetry. Opt. Laser. Technol. 2023, 158, 108780. [Google Scholar] [CrossRef]
- Gil, J.J.; Bernabeu, E. Depolarization and Polarization Indices of an Optical System. Opt. Acta Int. J. Opt. 1986, 33, 185–189. [Google Scholar] [CrossRef]
- Lu, S.-Y.; Chipman, R.A. Interpretation of Mueller Matrices Based on Polar Decomposition. J. Opt. Soc. Am. A 1996, 13, 1106. [Google Scholar] [CrossRef]
- Cloude, S. Group Theory and Polarisation Algebra. Optik 1986, 75, 26–36. [Google Scholar]
- Ossikovski, R. Alternative Depolarization Criteria for Mueller Matrices. J. Opt. Soc. Am. A 2010, 27, 808. [Google Scholar] [CrossRef]
- Tariq, A.; Li, P.; Chen, D.; Lv, D.; Ma, H. Physically Realizable Space for the Purity-Depolarization Plane for Polarized Light Scattering Media. Phys. Rev. Lett. 2017, 119, 033202. [Google Scholar] [CrossRef]
- San José, I.; Gil, J.J. Invariant Indices of Polarimetric Purity: Generalized Indices of Purity for n × n Covariance Matrices. Opt. Commun. 2011, 284, 38–47. [Google Scholar] [CrossRef]
- Ossikovski, R.; Vizet, J. Eigenvalue-Based Depolarization Metric Spaces for Mueller Matrices. J. Opt. Soc. Am. A 2019, 36, 1173. [Google Scholar] [CrossRef]
- Van Eeckhout, A.; Lizana, A.; Garcia-Caurel, E.; Gil, J.J.; Sansa, A.; Rodríguez, C.; Estévez, I.; González, E.; Escalera, J.C.; Moreno, I.; et al. Polarimetric Imaging of Biological Tissues Based on the Indices of Polarimetric Purity. J. Biophotonics 2018, 11, e201700189. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez, C.; Garcia-Caurel, E.; Garnatje, T.; Serra i Ribas, M.; Luque, J.; Campos, J.; Lizana, A. Polarimetric Observables for the Enhanced Visualization of Plant Diseases. Sci. Rep. 2022, 12, 14743. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.; Qadir, M.; Khalid, A.; Ashraf, S.; Ahmad, I. Characterization of Cervical Tissue Using Mueller Matrix Polarimetry. Lasers Med. Sci. 2023, 38, 46. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, I.; Gribble, A.; Ikram, M.; Pop, M.; Vitkin, A. Polarimetric Assessment of Healthy and Radiofrequency Ablated Porcine Myocardial Tissue. J. Biophotonics 2016, 9, 750–759. [Google Scholar] [CrossRef]
- Canabal-Carbia, M.; Rodriguez, C.; Estévez, I.; Van Eeckout, A.; González-Arnay, E.; García-Caurel, E.; Garnatje, T.; Lizana, A.; Campos, J. Enhancing Biological Tissue Structures Visualization through Polarimetric Parameters. In Proceedings of the SPIE 1238205, San Francisco, CA, USA, 28 January–2 February 2023; p. 16. [Google Scholar] [CrossRef]
- Borovkova, M.; Trifonyuk, L.; Ushenko, V.; Dubolazov, O.; Vanchulyak, O.; Bodnar, G.; Ushenko, Y.; Olar, O.; Ushenko, O.; Sakhnovskiy, M.; et al. Mueller-Matrix-Based Polarization Imaging and Quantitative Assessment of Optically Anisotropic Polycrystalline Networks. PLoS ONE 2019, 14, e0214494. [Google Scholar] [CrossRef]
- Clark, A.G.; Vignjevic, D.M. Modes of Cancer Cell Invasion and the Role of the Microenvironment. Curr. Opin. Cell Biol. 2015, 36, 13–22. [Google Scholar] [CrossRef]
- Wood, M.F.G.; Ghosh, N.; Wallenburg, M.A.; Li, S.-H.; Weisel, R.D.; Wilson, B.C.; Li, R.-K.; Vitkin, I.A. Polarization Birefringence Measurements for Characterizing the Myocardium, Including Healthy, Infarcted, and Stem-Cell-Regenerated Tissues. J. Biomed. Opt. 2010, 15, 047009. [Google Scholar] [CrossRef]
- Hogan, B.T.; Ushenko, V.A.; Syvokorovskaya, A.-V.; Dubolazov, A.V.; Vanchulyak, O.Y.; Ushenko, A.G.; Ushenko, Y.A.; Gorsky, M.P.; Tomka, Y.; Kuznetsov, S.L.; et al. 3D Mueller Matrix Reconstruction of the Optical Anisotropy Parameters of Myocardial Histopathology Tissue Samples. Front. Phys. 2021, 9, 737866. [Google Scholar] [CrossRef]
- Palevitz, B.A.; Hepler, P.K. Cellulose Microfibril Orientation and Cell Shaping in Developing Guard Cells of Allium: The Role of Microtubules and Ion Accumulation. Planta 1976, 132, 71–93. [Google Scholar] [CrossRef]
- Wang, L.V.; Coté, G.L.; Jacques, S.L. Special Section Guest Editorial. J. Biomed. Opt. 2002, 7, 278. [Google Scholar] [CrossRef]
- Peyvasteh, M.; Dubolazov, A.; Popowv, A.; Ushenko, A.; Ushenko, Y.; Meglinski, I. Two-point Stokes vector diagnostic approach for characterization of optically anisotropic biological tissues. J. Phys. D Appl. Phys. 2020, 53, 395401. [Google Scholar] [CrossRef]
- Ghosh, N.; Vitkin, I.A. Tissue Polarimetry: Concepts, Challenges, Applications, and Outlook. J. Biomed. Opt. 2011, 16, 110801. [Google Scholar] [CrossRef] [PubMed]
- Borovkova, M.; Peyvasteh, M.; Dubolazov, O.; Ushenko, Y.; Ushenko, V.; Bykov, A.; Deby, S.; Rehbinder, J.; Novikova, T.; Meglinski, I. Complementary Analysis of Mueller-Matrix Images of Optically Anisotropic Highly Scattering Biological Tissues. J. Eur. Opt. Soc.-Rapid Publ. 2018, 14, 20. [Google Scholar] [CrossRef]
- Shtein, I.; Shelef, Y.; Marom, Z.; Zelinger, E.; Schwartz, A.; Popper, Z.A.; Bar-On, B.; Harpaz-Saad, S. Stomatal Cell Wall Composition: Distinctive Structural Patterns Associated with Different Phylogenetic Groups. Ann. Bot. 2017, 119, 1021–1033. [Google Scholar] [CrossRef] [PubMed]
- Ali, Z.; Mahmood, T.; Shahzad, A.; Iqbal, M.; Ahmad, I. Assessment of Tissue Pathology Using Optical Polarimetry. Lasers Med. Sci. 2022, 37, 1907–1919. [Google Scholar] [CrossRef] [PubMed]
- Badieyan, S.; Ameri, A.; Razzaghi, M.R.; Rafii-Tabar, H.; Sasanpour, P. Mueller Matrix Imaging of Prostate Bulk Tissues; Polarization Parameters as a Discriminating Benchmark. Photodiagnosis Photodyn. Ther. 2019, 26, 90–96. [Google Scholar] [CrossRef] [PubMed]
- Van Eeckhout, A.; Garcia-Caurel, E.; Ossikovski, R.; Lizana, A.; Rodríguez, C.; González-Arnay, E.; Campos, J. Depolarization Metric Spaces for Biological Tissues Classification. J. Biophotonics 2020, 13, e202000083. [Google Scholar] [CrossRef]
- Ivanov, D.; Dremin, V.; Borisova, E.; Bykov, A.; Novikova, T.; Meglinski, I.; Ossikovski, R. Polarization and Depolarization Metrics as Optical Markers in Support to Histopathology of Ex Vivo Colon Tissue. Biomed. Opt. Express 2021, 12, 4560. [Google Scholar] [CrossRef]
- Pierangelo, A.; Benali, A.; Antonelli, M.-R.; Novikova, T.; Validire, P.; Gayet, B.; De Martino, A. Ex-Vivo Characterization of Human Colon Cancer by Mueller Polarimetric Imaging. Opt. Express 2011, 19, 1582. [Google Scholar] [CrossRef]
- Rodríguez, C.; Van Eeckhout, A.; Ferrer, L.; Garcia-Caurel, E.; González-Arnay, E.; Campos, J.; Lizana, A. Polarimetric Data-Based Model for Tissue Recognition. Biomed. Opt. Express 2021, 12, 4852. [Google Scholar] [CrossRef]
- Wan, J.; Dong, Y.; Xue, J.-H.; Lin, L.; Du, S.; Dong, J.; Yao, Y.; Li, C.; Ma, H. Polarization-Based Probabilistic Discriminative Model for Quantitative Characterization of Cancer Cells. Biomed. Opt. Express 2022, 13, 3339. [Google Scholar] [CrossRef] [PubMed]
- Canabal-Carbia, M.; Van Eeckhout, A.; Rodríguez, C.; González-Arnay, E.; Estévez, I.; Gil, J.J.; García-Caurel, E.; Ossikovski, R.; Campos, J.; Lizana, A. Depolarizing Metrics in the Biomedical Field: Vision Enhancement and Classification of Biological Tissues. J. Innov. Opt. Health Sci. 2023, 2330004, 1–17. [Google Scholar] [CrossRef]
- Chue-Sang, J.; Holness, N. Use of Mueller Matrix Colposcopy in the Characterization of Cervical Collagen Anisotropy. J. Biomed. Opt. 2018, 23, 1. [Google Scholar] [CrossRef] [PubMed]
- Sprenger, J.; Murray, C.; Lad, J.; Jones, B.; Thomas, G.; Nofech-Mozes, S.; Khorasani, M.; Vitkin, A. Toward a Quantitative Method for Estimating Tumour-Stroma Ratio in Breast Cancer Using Polarized Light Microscopy. Biomed. Opt. Express 2021, 12, 3241. [Google Scholar] [CrossRef]
- Ramella-Roman, J.C.; Saytashev, I.; Piccini, M. A Review of Polarization-Based Imaging Technologies for Clinical and Preclinical Applications. J. Opt. 2020, 22, 123001. [Google Scholar] [CrossRef]
- Trifonyuk, L.; Sdobnov, A.; Baranowski, W.; Ushenko, V.; Olar, O.; Dubolazov, A.; Pidkamin, L.; Sidor, M.; Vanchuliak, O.; Motrich, A.; et al. Differential Mueller Matrix Imaging of Partially Depolarizing Optically Anisotropic Biological Tissues. Lasers Med. Sci. 2020, 35, 877–891. [Google Scholar] [CrossRef]
- Van Eeckhout, A.; Garcia-Caurel, E.; Garnatje, T.; Escalera, J.C.; Durfort, M.; Vidal, J.; Gil, J.J.; Campos, J.; Lizana, A. Polarimetric Imaging Microscopy for Advanced Inspection of Vegetal Tissues. Sci. Rep. 2021, 11, 3913. [Google Scholar] [CrossRef]
- Van Eeckhout, A.; Garcia-Caurel, E.; Garnatje, T.; Durfort, M.; Escalera, J.C.; Vidal, J.; Gil, J.J.; Campos, J.; Lizana, A. Depolarizing Metrics for Plant Samples Imaging. PLoS ONE 2019, 14, e0213909. [Google Scholar] [CrossRef]
- Savenkov, S.N.; Muttiah, R.S.; Oberemok, E.A.; Priezzhev, A.V.; Kolomiets, I.S.; Klimov, A.S. Measurement and Interpretation of Mueller Matrices of Barley Leaves. Quantum Elec. 2020, 50, 55–60. [Google Scholar] [CrossRef]
- Al Bugami, B.; Su, Y.; Rodríguez, C.; Lizana, A.; Campos, J.; Durfort, M.; Ossikovski, R.; Garcia-Caurel, E. Characterization of Vine, Vitis Vinifera, Leaves by Mueller Polarimetric Microscopy. Thin Solid Films 2023, 764, 139594. [Google Scholar] [CrossRef]
- Rodríguez, C.; Van Eeckhout, A.; Garcia-Caurel, E.; Lizana, A.; Campos, J. Automatic Pseudo-Coloring Approaches to Improve Visual Perception and Contrast in Polarimetric Images of Biological Tissues. Sci. Rep. 2022, 12, 18479. [Google Scholar] [CrossRef] [PubMed]
- Patty, C.H.L.; Luo, D.A.; Snik, F.; Ariese, F.; Buma, W.J.; ten Kate, I.L.; van Spanning, R.J.M.; Sparks, W.B.; Germer, T.A.; Garab, G.; et al. Imaging Linear and Circular Polarization Features in Leaves with Complete Mueller Matrix Polarimetry. Biochim. Biophys. Acta (BBA) Gen. Subj. 2018, 1862, 1350–1363. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Núñez, O.; Schucht, P.; Hewer, E.; Novikova, T.; Pierangelo, A. Polarimetric Visualization of Healthy Brain Fiber Tracts under Adverse Conditions: Ex Vivo Studies. Biomed. Opt. Express 2021, 12, 6674. [Google Scholar] [CrossRef] [PubMed]
- Schucht, P.; Lee, H.R.; Mezouar, H.M.; Hewer, E.; Raabe, A.; Murek, M.; Zubak, I.; Goldberg, J.; Kovari, E.; Pierangelo, A.; et al. Visualization of White Matter Fiber Tracts of Brain Tissue Sections With Wide-Field Imaging Mueller Polarimetry. IEEE Trans. Med. Imaging 2020, 39, 4376–4382. [Google Scholar] [CrossRef]
- Ushenko, V.A.; Hogan, B.T.; Dubolazov, A.; Piavchenko, G.; Kuznetsov, S.L.; Ushenko, A.G.; Ushenko, Y.O.; Gorsky, M.; Bykov, A.; Meglinski, I. 3D Mueller Matrix Mapping of Layered Distributions of Depolarisation Degree for Analysis of Prostate Adenoma and Carcinoma Diffuse Tissues. Sci. Rep. 2021, 11, 5162. [Google Scholar] [CrossRef]
- Ahmad, I.; Khaliq, A.; Iqbal, M.; Khan, S. Mueller Matrix Polarimetry for Characterization of Skin Tissue Samples: A Review. Photodiagnosis Photodyn. Ther. 2020, 30, 101708. [Google Scholar] [CrossRef]
- Du, E.; He, H.; Zeng, N.; Sun, M.; Guo, Y.; Wu, J.; Liu, S.; Ma, H. Mueller Matrix Polarimetry for Differentiating Characteristic Features of Cancerous Tissues. J. Biomed. Opt. 2014, 19, 076013. [Google Scholar] [CrossRef]
- Kupinski, M.; Boffety, M.; Goudail, F.; Ossikovski, R.; Pierangelo, A.; Rehbinder, J.; Vizet, J.; Novikova, T. Polarimetric Measurement Utility for Pre-Cancer Detection from Uterine Cervix Specimens. Biomed. Opt. Express 2018, 9, 5691. [Google Scholar] [CrossRef]
- Van Eeckhout, A.; González, E.; Escalera, J.C.; Moreno, I.; Campos, J.; Zhang, H.; Ossikovski, R.; Lizana, A.; Garcia-Caurel, E.; Gil, J.J.; et al. Indices of Polarimetric Purity to Enhance the Image Quality in Biophotonics Applications. In Proceedings of the SPIE 10685, Strasbourg, France, 22–26 April 2018; p. 9. [Google Scholar] [CrossRef]
- Ushenko, V.; Sdobnov, A.; Syvokorovskaya, A.; Dubolazov, A.; Vanchulyak, O.; Ushenko, A.; Ushenko, Y.; Gorsky, M.; Sidor, M.; Bykov, A.; et al. 3D Mueller-Matrix Diffusive Tomography of Polycrystalline Blood Films for Cancer Diagnosis. Photonics 2018, 5, 54. [Google Scholar] [CrossRef]
- Ushenko, V.A.; Hogan, B.T.; Dubolazov, A.; Grechina, A.V.; Boronikhina, T.V.; Gorsky, M.; Ushenko, A.G.; Ushenko, Y.O.; Bykov, A.; Meglinski, I. Embossed Topographic Depolarisation Maps of Biological Tissues with Different Morphological Structures. Sci. Rep. 2021, 11, 3871. [Google Scholar] [CrossRef]
- Gil, J.J. Transmittance Constraints in Serial Decompositions of Depolarizing Mueller Matrices: The Arrow Form of a Mueller Matrix. J. Opt. Soc. Am. A 2013, 30, 701–707. [Google Scholar] [CrossRef]
- Gil, J.J.; San José, I. Reduced Form of a Mueller Matrix. J. Mod. Opt. 2016, 63, 1579–1583. [Google Scholar] [CrossRef]
- Ossikovski, R. Analysis of Depolarizing Mueller Matrices through a Symmetric Decomposition. J. Opt. Soc. Am. A 2009, 26, 1109. [Google Scholar] [CrossRef] [PubMed]
- Xing, Z.-F. On the Deterministic and Non-Deterministic Mueller Matrix. J. Mod. Opt. 1992, 39, 461–484. [Google Scholar] [CrossRef]
- Robson, B.A. The Theory of Polarization Phenomena; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Sekera, Z. Scattering Matrices and Reciprocity Relationships for Various Representations of the State of Polarization. J. Opt. Soc. Am. 1966, 56, 1732. [Google Scholar] [CrossRef]
- Schönhofer, A.; Kuball, H.-G. Symmetry Properties of the Mueller Matrix. Chem. Phys. 1987, 115, 159–167. [Google Scholar] [CrossRef]
- Gil, J.J. Components of Purity of a Mueller Matrix. J. Opt. Soc. Am. A 2011, 28, 1578. [Google Scholar] [CrossRef]
- Gil, J.J. Invariant Quantities of a Mueller Matrix under Rotation and Retarder Transformations. J. Opt. Soc. Am. A 2016, 33, 52–58. [Google Scholar] [CrossRef]
- Gil, J.J. Physical Quantities Involved in a Mueller Matrix. In Proceedings of the SPIE 9853, Baltimore Chenault, MD, USA, 17–21 April 2016; p. 985302. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Ustin, S. Leaf Optical Properties; Cambridge University Press: Cambridge, UK, 2019; ISBN 9781108686457. [Google Scholar]
- Mustafa, F.H.; Jaafar, M.S. Comparison of Wavelength-Dependent Penetration Depths of Lasers in Different Types of Skin in Photodynamic Therapy. Indian J. Phys. 2013, 87, 203–209. [Google Scholar] [CrossRef]
- Peinado, A.; Lizana, A.; Vidal, J.; Iemmi, C.; Campos, J. Optimization and Performance Criteria of a Stokes Polarimeter Based on Two Variable Retarders. Opt. Express 2010, 18, 9815. [Google Scholar] [CrossRef]
- Peinado, A. Analysis, Optimization and Implementation of a Variable Retardance Based Polarimeter; Universitat Autònoma de Barcelona: Barcelona, Spain, 2014. [Google Scholar]
- De Silva, N.; Lumyong, S.; Hyde, K.D.; Bulgakov, T.; Philips, A.J.L.; Yan, J. Mycosphere Essays 9: Defining Biotrophs and Hemibiotrophs. Mycosphere 2016, 7, 545–559. [Google Scholar] [CrossRef]
- Szabó, M.; Csikász-Krizsics, A.; Dula, T.; Farkas, E.; Roznik, D.; Kozma, P.; Deák, T. Black Rot of Grapes (Guignardia bidwellii)—A Comprehensive Overview. Horticulturae 2023, 9, 130. [Google Scholar] [CrossRef]
- Ullrich, C.I.; Kleespies, R.G.; Enders, M.; Koch, E. Biology of the Black Rot Pathogen, Guignardia bidwellii, Its Development in Susceptible Leaves of Grapevine Vitis Vinifera. J. Kulturflanzen 2009, 61, 82–90. [Google Scholar]
- Kuo, K.; Hoch, H.C. The Parasitic Relationship between Phyllosticta Ampelicidaand Vitis Vinifera. Mycologia 1996, 88, 626–634. [Google Scholar] [CrossRef]
- Sommart, U.; Rukachaisirikul, V.; Trisuwan, K.; Tadpetch, K.; Phongpaichit, S.; Preedanon, S.; Sakayaroj, J. Tricycloalternarene Derivatives from the Endophytic Fungus Guignardia Bidwellii PSU-G11. Phytochem. Lett. 2012, 5, 139–143. [Google Scholar] [CrossRef]
- Rosin, N.L.; Agabalyan, N.; Olsen, K.; Martufi, G.; Gabriel, V.; Biernaskie, J.; Di Martino, E.S. Collagen Structural Alterations Contribute to Stiffening of Tissue after Split-Thickness Skin Grafting. Wound Repair Regen. 2016, 24, 263–274. [Google Scholar] [CrossRef]
- Chen, P.; Wang, A.; Haynes, W.; Landao-Bassonga, E.; Lee, C.; Ruan, R.; Breidahl, W.; Shiroud Heidari, B.; Mitchell, C.A.; Zheng, M. A Bio-Inductive Collagen Scaffold That Supports Human Primary Tendon-Derived Cell Growth for Rotator Cuff Repair. J. Orthop. Transl. 2021, 31, 91–101. [Google Scholar] [CrossRef]
- Charvet, C.J. Mapping Human Brain Pathways: Challenges and Opportunities in the Integration of Scales. Brain Behav. Evol. [CrossRef]
- Agrawal, A.; Kapfhammer, J.P.; Kress, A.; Wichers, H.; Deep, A.; Feindel, W.; Sonntag, V.K.H.; Spetzler, R.F.; Preul, M.C. Josef Klingler’s Models of White Matter Tracts: Influences on Neuroanatomy, Neurosurgery, and Neuroimaging. Neurosurgery 2011, 69, 238–254. [Google Scholar] [CrossRef]
- Wang, H.; Black, A.J.; Zhu, J.; Stigen, T.W.; Al-Qaisi, M.K.; Netoff, T.I.; Abosch, A.; Akkin, T. Reconstructing Micrometer-Scale Fiber Pathways in the Brain: Multi-Contrast Optical Coherence Tomography Based Tractography. Neuroimage 2011, 58, 984–992. [Google Scholar] [CrossRef]
- Felger, L.; Rodríguez-Núñez, O.; Gros, R.; Maragkou, T.; McKinley, R.; Moriconi, S.; Murek, M.; Zubak, I.; Novikova, T.; Pierangelo, A.; et al. Robustness of the Wide-Field Imaging Mueller Polarimetry for Brain Tissue Differentiation and White Matter Fiber Tract Identification in a Surgery-like Environment: An Ex Vivo Study. Biomed. Opt. Express 2023, 14, 2400. [Google Scholar] [CrossRef]
- Mandonnet, E.; Sarubbo, S.; Petit, L. The Nomenclature of Human White Matter Association Pathways: Proposal for a Systematic Taxonomic Anatomical Classification. Front. Neuroanat. 2018, 12, 94. [Google Scholar] [CrossRef] [PubMed]
- Helmchen, F.; Denk, W. Deep Tissue Two-Photon Microscopy. Nat. Methods 2005, 2, 932–940. [Google Scholar] [CrossRef] [PubMed]
- Arano-Martinez, J.A.; Martínez-González, C.L.; Salazar, M.I.; Torres-Torres, C. A Framework for Biosensors Assisted by Multiphoton Effects and Machine Learning. Biosensors 2022, 12, 710. [Google Scholar] [CrossRef] [PubMed]
- Raja, H.; Akram, M.U.; Hassan, T.; Ramzan, A.; Aziz, A.; Raja, H. Glaucoma Detection Using Optical Coherence Tomography Images: A Systematic Review of Clinical and Automated Studies. IETE J. Res. 2022, 1–21. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gil, J.J.; San José, I.; Canabal-Carbia, M.; Estévez, I.; González-Arnay, E.; Luque, J.; Garnatje, T.; Campos, J.; Lizana, A. Polarimetric Images of Biological Tissues Based on the Arrow Decomposition of Mueller Matrices. Photonics 2023, 10, 669. https://doi.org/10.3390/photonics10060669
Gil JJ, San José I, Canabal-Carbia M, Estévez I, González-Arnay E, Luque J, Garnatje T, Campos J, Lizana A. Polarimetric Images of Biological Tissues Based on the Arrow Decomposition of Mueller Matrices. Photonics. 2023; 10(6):669. https://doi.org/10.3390/photonics10060669
Chicago/Turabian StyleGil, José J., Ignacio San José, Mónica Canabal-Carbia, Irene Estévez, Emilio González-Arnay, Jordi Luque, Teresa Garnatje, Juan Campos, and Angel Lizana. 2023. "Polarimetric Images of Biological Tissues Based on the Arrow Decomposition of Mueller Matrices" Photonics 10, no. 6: 669. https://doi.org/10.3390/photonics10060669
APA StyleGil, J. J., San José, I., Canabal-Carbia, M., Estévez, I., González-Arnay, E., Luque, J., Garnatje, T., Campos, J., & Lizana, A. (2023). Polarimetric Images of Biological Tissues Based on the Arrow Decomposition of Mueller Matrices. Photonics, 10(6), 669. https://doi.org/10.3390/photonics10060669





