All-Dielectric Dual-Band Metamaterial Absorber Based on Ring Nanocavity in Visible Region for Sensing Applications
Abstract
1. Introduction
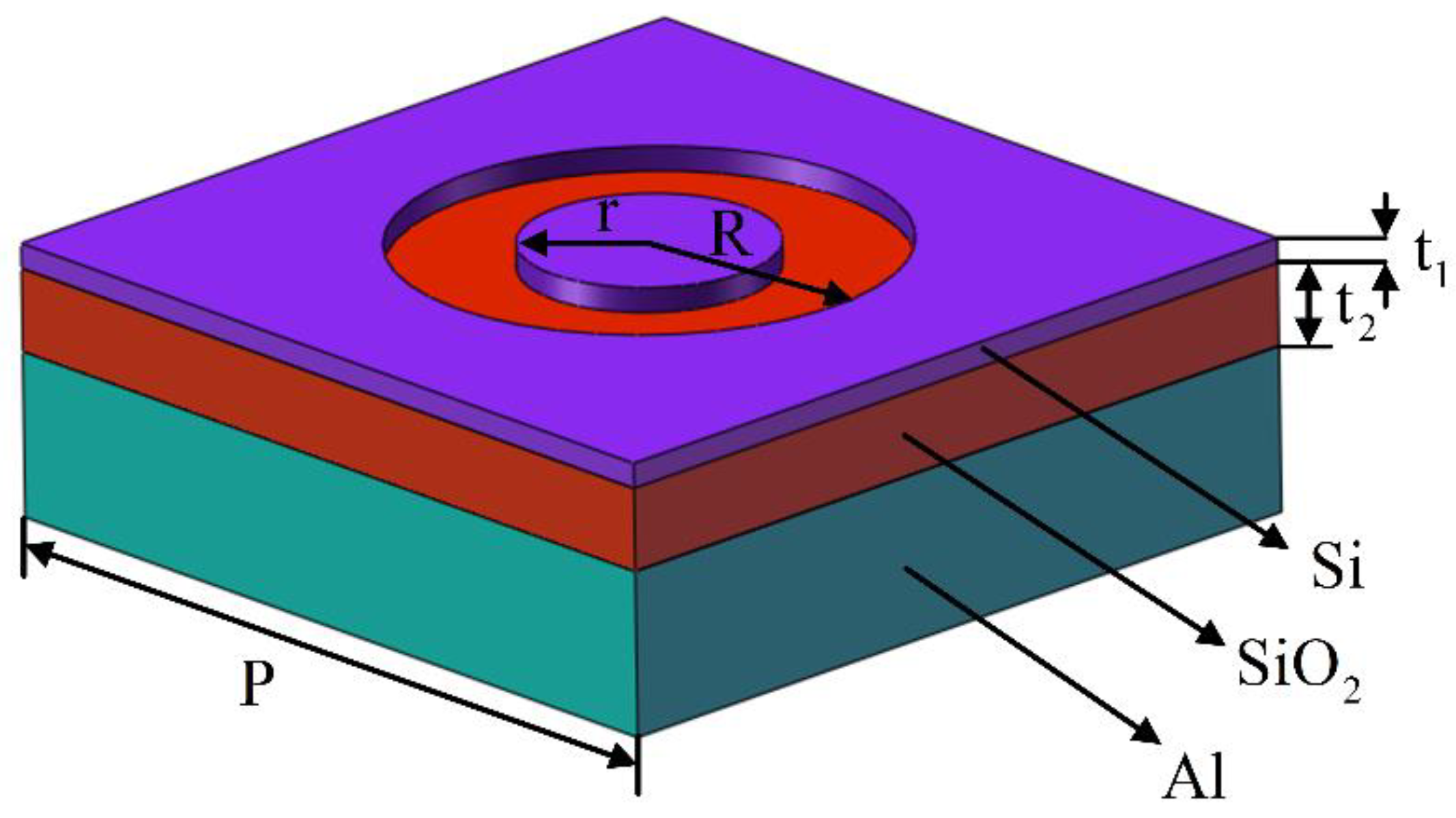
2. Materials and Structure
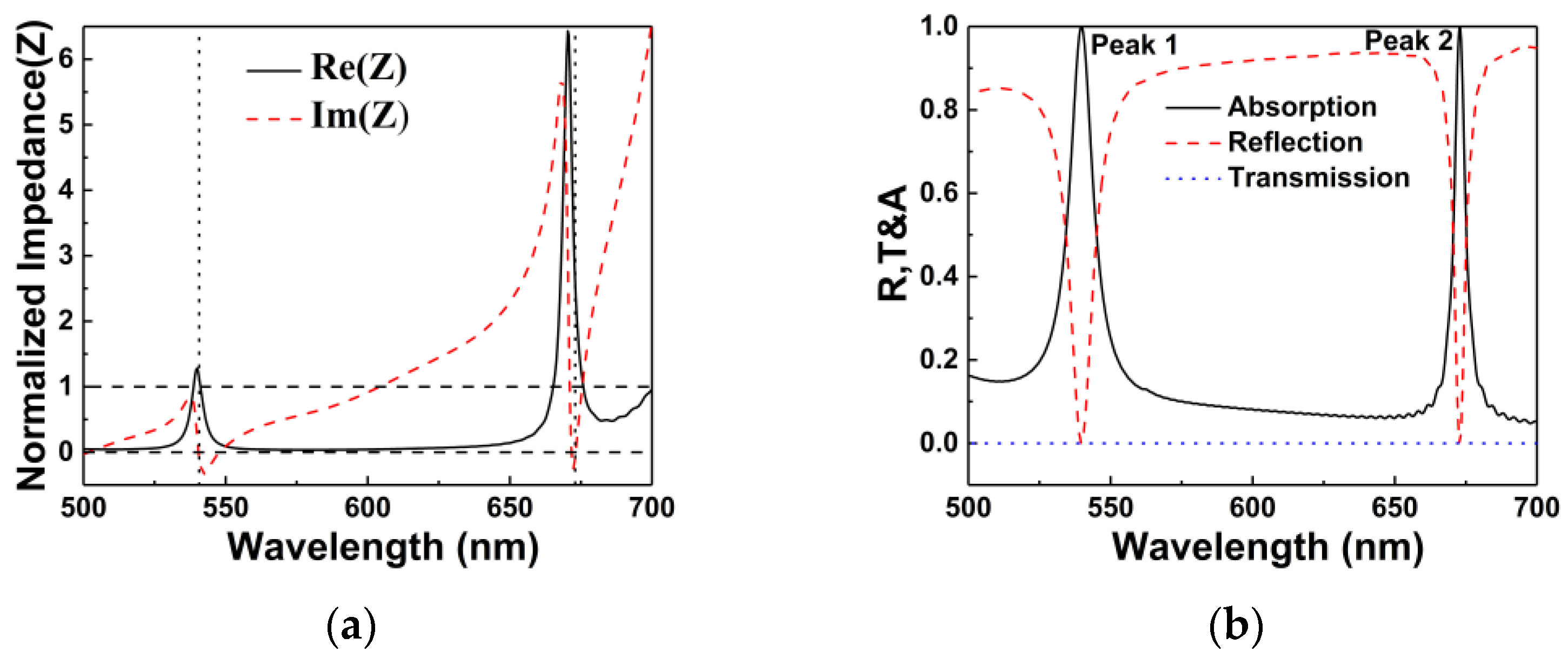
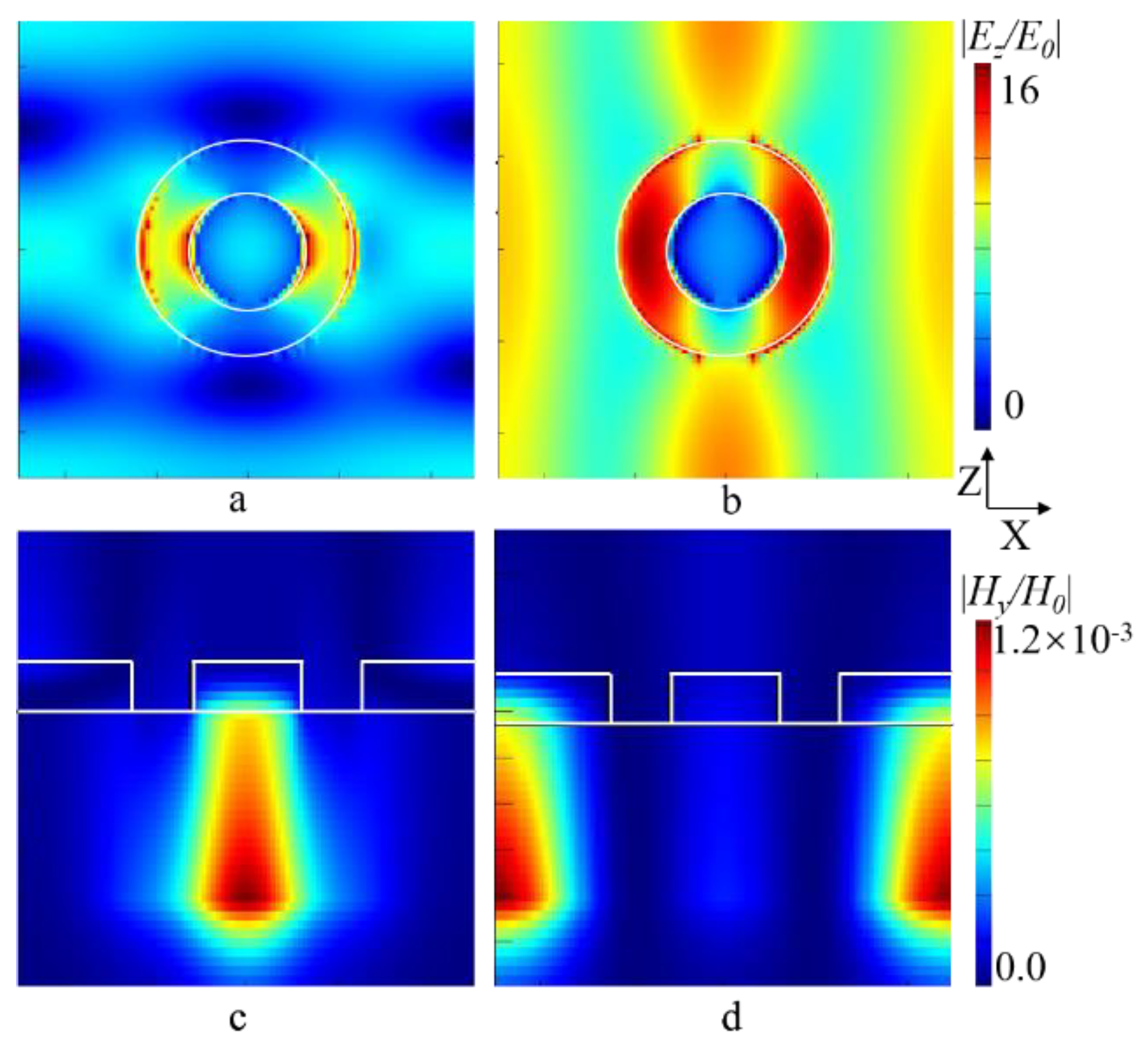
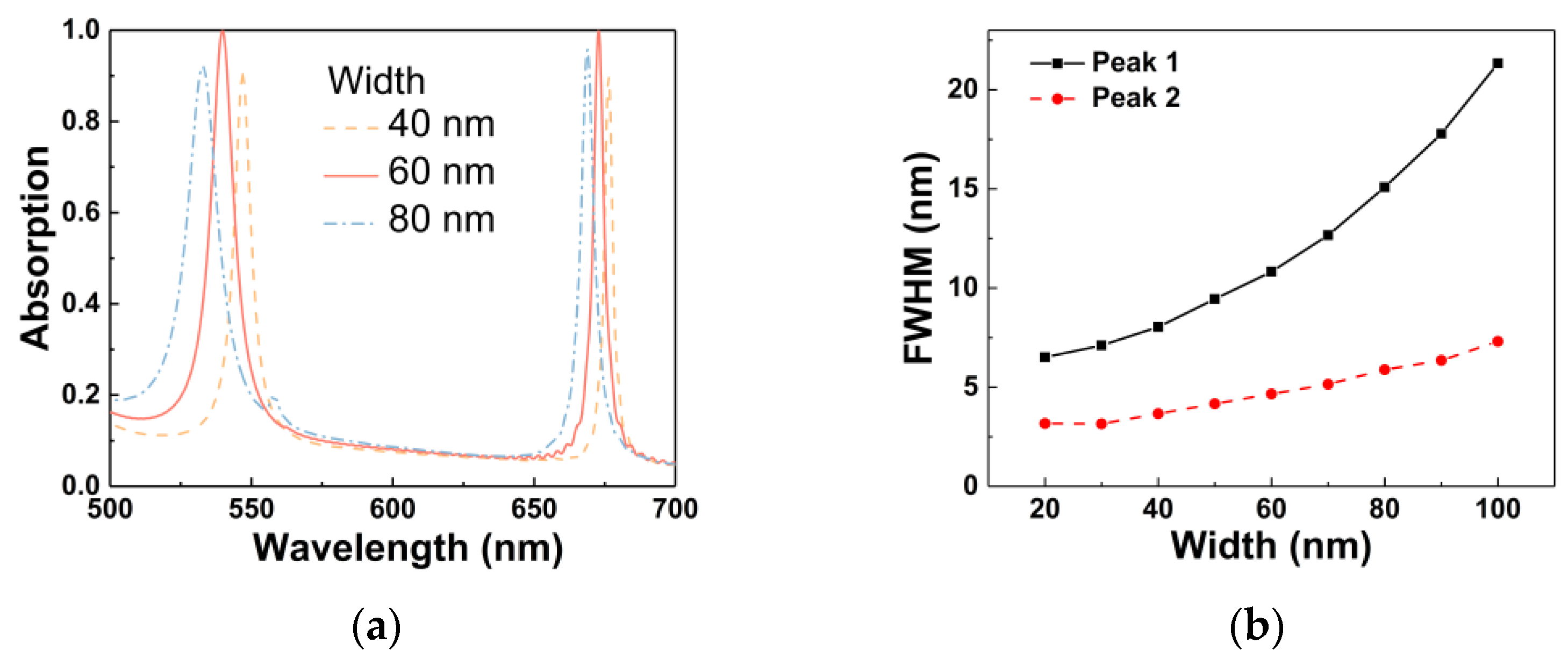
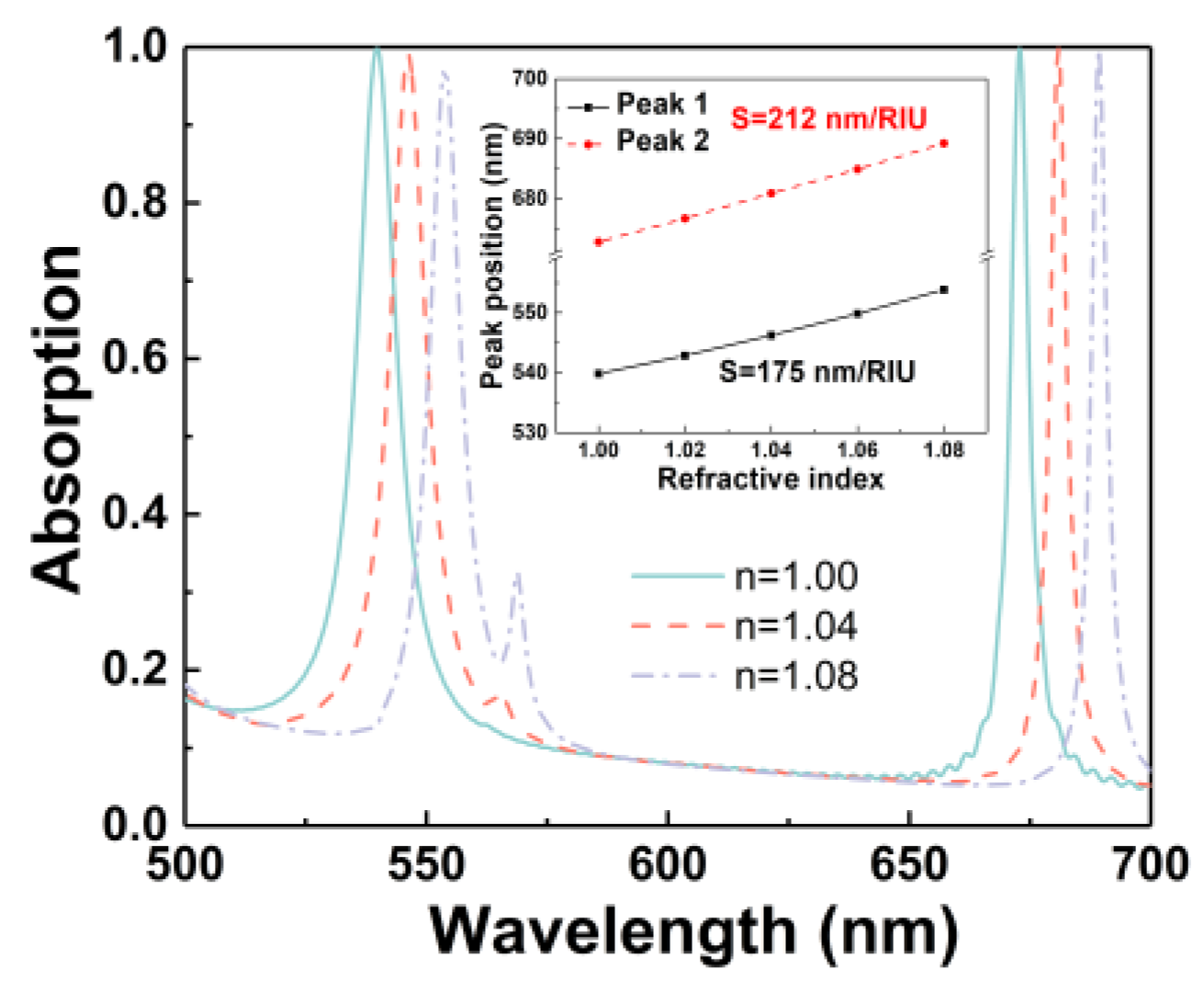
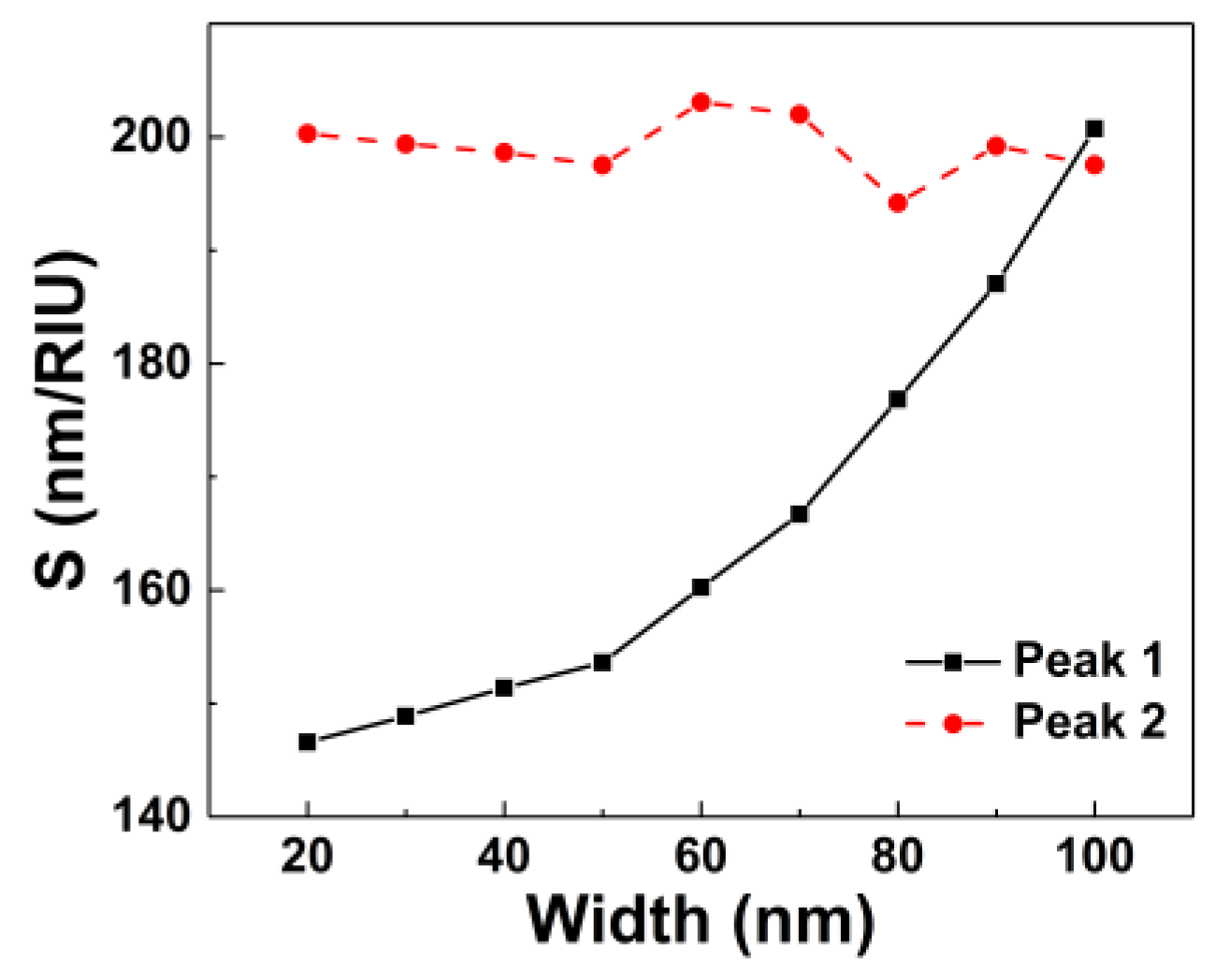
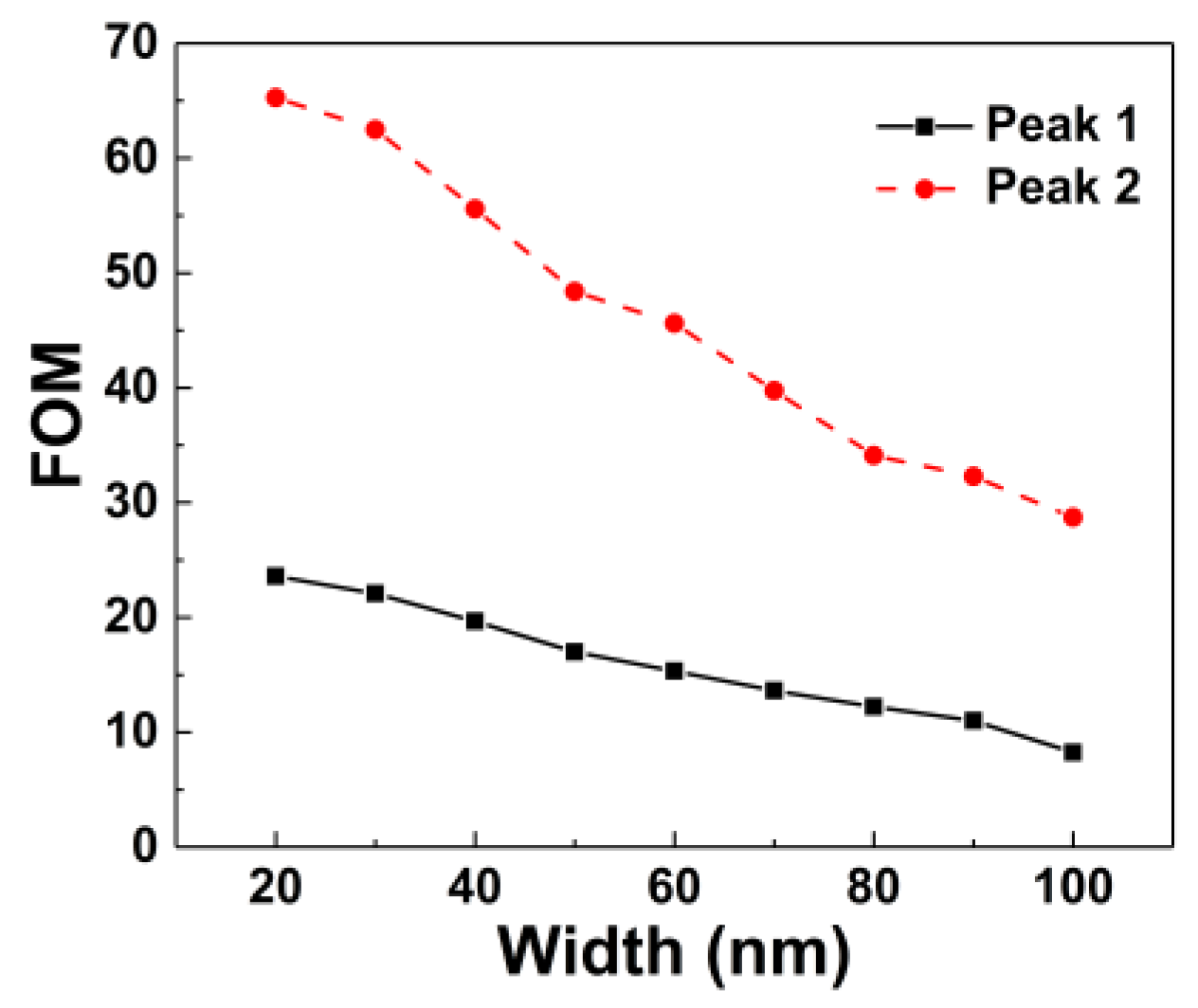
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yan, X.T.; Tang, W.; Liu, J.F.; Wang, M.; Gao, X.X.; Cui, T.J. Glide symmetry for mode control and significant suppression of coupling in dual-strip SSPP transmission lines. Adv. Photonics 2021, 3, 026001. [Google Scholar] [CrossRef]
- Xu, Z.; Chang, J.; Tong, J.; Sievenpiper, D.F.; Cui, T.J. Near-field chiral excitation of universal spin-momentum locking transport of edge waves in microwave metamaterials. Adv. Photonics 2022, 4, 046004. [Google Scholar] [CrossRef]
- Ma, T.; Huang, Q.; He, H.; Zhao, Y.; Lin, X.; Lu, Y. All-dielectric metamaterial analogue of electromagnetically induced transparency and its sensing application in terahertz range. Opt. Express 2019, 27, 16624–16634. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Mesch, M.; Weiss, T.; Hentschel, M.; Giessen, H. Infrared Perfect Absorber and Its Application as Plasmonic Sensor. Nano Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef] [PubMed]
- Tong, L.; Wei, H.; Zhang, S.; Xu, H. Recent Advances in Plasmonic Sensors. Sensors 2014, 14, 7959–7973. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.-Z.; Ren, F.-F.; Ye, J.; Lu, H.; Liang, L.; Huang, X.; Liu, M.; Shadrivov, I.V.; Powell, D.A.; Yu, G.; et al. Electrically tunable terahertz metamaterials with embedded large-area transparent thin-film transistor arrays. Sci. Rep. 2016, 6, 23486. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.-Z.; Shi, Y.-T.; Ye, J.; Ren, F.-F.; Shadrivov, I.V.; Lu, H.; Liang, L.; Hu, X.; Jin, B.; Zhang, R.; et al. A terahertz Controlled-NOT gate based on asymmetric rotation of polarization in chiral metamaterials. Adv. Opt. Mater. 2017, 5, 1700108. [Google Scholar] [CrossRef]
- Ramm, A. Does negative refraction make a perfect lens? Phys. Lett. A 2008, 372, 6518–6520. [Google Scholar] [CrossRef][Green Version]
- Cui, T.J. Microwave metamaterials—From passive to digital and programmable controls of electromagnetic waves. J. Opt. 2017, 19, 084004. [Google Scholar] [CrossRef]
- Wang, X.; Ding, W.; Zhu, H.; Liu, C.; Liu, Y. Tunable broadband, wide-angle, and polarization-dependent perfect infrared absorber based on planar structure containing phase-change material. Appl. Opt. 2018, 57, 8915–8920. [Google Scholar] [CrossRef]
- Kajtár, G.; Kafesaki, M.; Economou, E.; Soukoulis, C.M. Theoretical model of homogeneous metal–insulator–metal perfect multi-band absorbers for the visible spectrum. J. Phys. D Appl. Phys. 2016, 49, 055104. [Google Scholar] [CrossRef]
- Norouzi-Razani, A.; Rezaei, P. Broadband polarization insensitive and tunable terahertz metamaterial perfect absorber based on the graphene disk and square ribbon. Micro Nanost. 2022, 163, 107153. [Google Scholar] [CrossRef]
- Qing, Y.M.; Ma, H.F.; Cui, T.J. Tailoring anisotropic perfect absorption in monolayer black phosphorus by critical coupling at terahertz frequencies. Opt. Express 2018, 26, 32442–32450. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; He, M.; Dong, Z.; Wang, Y.; Ni, B. Design of tunable dual-band terahertz perfect absorber base on graphene. Results Phys 2022, 40, 105860. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect metamaterial absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Shen, Y.; Gu, L.; Li, Y.; Deng, X.; Wei, Z.; Xu, J.; Cao, J. Optical strong coupling in hybrid metal-graphene metamaterial for terahertz sensing*. Chin. Phys. B 2021, 30, 118702. [Google Scholar] [CrossRef]
- Li, G.; Shen, Y.; Xiao, G.; Jin, C. Double-layered metal grating for high-performance refractive index sensing. Opt. Express 2015, 23, 8995–9003. [Google Scholar] [CrossRef]
- Si, J.N.; Dong, Z.W.; Yu, X.Y.; Deng, X.X. Tunable polarization-independent dual-band coherent perfect absorber based on metal-graphene nanoring structure. Opt. Express 2018, 26, 21768–21777. [Google Scholar] [CrossRef]
- Cole, M.A.; Powell, D.A.; Shadrivov, I.V. Strong terahertz absorption in all-dielectric Huygens’ metasurfaces. Nanotechnology 2016, 27, 424003. [Google Scholar] [CrossRef]
- Zhong, Y.; Du, L.; Liu, Q.; Zhu, L.; Meng, K.; Zou, Y.; Zhang, B. Ultrasensitive specific sensor based on all-dielectric metasurfaces in the terahertz range. RSC Adv. 2020, 10, 33018–33025. [Google Scholar] [CrossRef]
- Wang, Y.; Han, Z.; Du, Y.; Qin, J. Ultrasensitive terahertz sensing with high-Q toroidal dipole resonance governed by bound states in the continuum in all-dielectric metasurface. Nanophotonics 2021, 10, 1295–1307. [Google Scholar] [CrossRef]
- Ye, J.; Van Dorpe, P. Improvement of Figure of Merit for Gold Nanobar Array Plasmonic Sensors. Plasmonics 2011, 6, 665–671. [Google Scholar] [CrossRef]
- Ye, H.-Y.; Huang, X.-Q.; Wen, K.-H.; Xue, J.-C.; Zhou, J.-Y.; Meng, Z.-M. Near-infrared narrow plasmonic resonances for high-performance optical sensing in a sodium-based nanograting. Results Phys. 2022, 38, 105566. [Google Scholar] [CrossRef]
- Danilov, A.; Tselikov, G.; Wu, F.; Kravets, V.G.; Ozerov, I.; Bedu, F.; Grigorenko, A.N.; Kabashin, A.V. Ultra-narrow surface lattice resonances in plasmonic metamaterial arrays for biosensing applications. Biosens. Bioelectron. 2018, 104, 102–112. [Google Scholar] [CrossRef]
- Huang, L.; Xu, L.; Mohsen, R. Pushing the limit of high-Q mode of a single dielectric nanocavity. Adv. Photonics 2021, 3, 16004. [Google Scholar] [CrossRef]
- Bozhevolnyi, S.I.; Sondergaard, T. General properties of slow-plasmon resonant nanostructures: Nano-antennas and resonators. Opt. Express 2007, 15, 10869–10877. [Google Scholar] [CrossRef]
- Becker, J.; Trügler, A.; Jakab, A.; Hohenester, U.; Sönnichsen, C. The Optimal Aspect Ratio of Gold Nanorods for Plasmonic Bio-sensing. Plasmonics 2010, 5, 161–167. [Google Scholar] [CrossRef]
- Xie, Q.; Dong, G.; Wang, B.-X.; Huang, W.-Q. Design of Quad-Band Terahertz Metamaterial Absorber Using a Perforated Rectangular Resonator for Sensing Applications. Nanoscale Res. Lett. 2018, 13, 137. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, L.; Zhang, T. Nanoslit-microcavity-based narrow band absorber for sensing applications. Opt. Express 2015, 23, 20715–20720. [Google Scholar] [CrossRef]
- Yong, Z.; Zhang, S.; Gong, C.; He, S. Narrow band perfect absorber for maximum localized magnetic and electric field enhancement and sensing applications. Sci. Rep. 2016, 6, 24063. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, G.; Fu, G.; Liu, X.; Huang, Z.; Gu, G. All-metal meta-surfaces for narrowband light absorption and high performance sensing. J. Phys. D Appl. Phys. 2016, 49, 445104. [Google Scholar] [CrossRef]
- Li, Y.; An, B.; Jiang, S.; Gao, J.; Chen, Y.; Pan, S. Plasmonic induced triple-band absorber for sensor application. Opt. Express 2015, 23, 17607–17612. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Zhang, B.; Wang, Y.; Zhu, M.; Shao, G. Reduced resonance line-width and enhanced figure of merit in Ag/Si/SiO2 nanopillar array sensors. Results Phys. 2020, 19, 103612. [Google Scholar] [CrossRef]
| References | Wavelength Region | Peak Numbers | Peak Absorption (%) | FOM | FOM* |
|---|---|---|---|---|---|
| [28] | THz | 1 | 60.86 | 101 | - |
| [29] | Infrared | 1 | 95 | 25 | 322 |
| [30] | Infrared | 1 | 99.6 | 110 | 19,000 |
| [31] | Infrared | 2 | 89 | 50 | 1075 |
| [32] | Visible | 3 | >99 | ~55 | 45,367 |
| [33] | Visible | 2 | ~60 | 64.3 | - |
| The work | Visible | 2 | 99.91, 99.96 | 23.6 65.3 | 17,265 59,902 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Zou, M.; Feng, Z.; Ni, B.; Ye, B.; Wang, Y. All-Dielectric Dual-Band Metamaterial Absorber Based on Ring Nanocavity in Visible Region for Sensing Applications. Photonics 2023, 10, 58. https://doi.org/10.3390/photonics10010058
Liu F, Zou M, Feng Z, Ni B, Ye B, Wang Y. All-Dielectric Dual-Band Metamaterial Absorber Based on Ring Nanocavity in Visible Region for Sensing Applications. Photonics. 2023; 10(1):58. https://doi.org/10.3390/photonics10010058
Chicago/Turabian StyleLiu, Fei, Meiling Zou, Zhenjie Feng, Bo Ni, Baisong Ye, and Yunji Wang. 2023. "All-Dielectric Dual-Band Metamaterial Absorber Based on Ring Nanocavity in Visible Region for Sensing Applications" Photonics 10, no. 1: 58. https://doi.org/10.3390/photonics10010058
APA StyleLiu, F., Zou, M., Feng, Z., Ni, B., Ye, B., & Wang, Y. (2023). All-Dielectric Dual-Band Metamaterial Absorber Based on Ring Nanocavity in Visible Region for Sensing Applications. Photonics, 10(1), 58. https://doi.org/10.3390/photonics10010058




