Abstract
The minimization of waveguide crosstalk is a long-standing challenge for optical engineers. Nowadays, the most popular technique to suppress crosstalk is anisotropic nanostructures, realized as subwavelength stripes between waveguides. However, the influence of material anisotropy on the efficiency of such structures remains unknown. In this work, we consider MoS2 waveguides separated by MoS2 stripes because this material has the record value of optical anisotropy. We discover that the use of MoS2 instead of Si results in a several-orders-of-magnitude-larger crosstalk distance. Therefore, we envision that by combining the extraordinary material properties with the known crosstalk-suppression methods, one can make the integration density of photonic devices close to electronics.
1. Introduction
Silicon is a bedrock material of modern photonics owing to its high refractive index and mature fabrication technology [1,2,3]. However, the integration density of photonic components based on silicon is still much less than that of its electronic counterparts [4]. To overcome this gap, researchers have developed inverse design methods [5,6,7,8,9,10,11], which allow one to maximize the performance of photonic structures while keeping their footprint small. This approach proves useful in numerous applications, including demultiplexers, waveguide turns, polarizing beam splitters and photonic waveguide crosshairs, to name just a few [5,6,7,8,9,10,11]. Nonetheless, despite tremendous progress in this area in recent years, silicon still faces the fundamental limitation of diffraction of light. To overcome this problem, multiple works [12,13,14,15,16,17] suggested the use of plasmonic structures, where light is coupled to electronic oscillations. Plasmonics enables subdiffractional light confinement, but at the expense of rising optical losses. The alternative solution is the use of anisotropic structures [18,19,20,21,22], which do not cause additional losses. Anisotropic effective dielectric function provides a unique opportunity to manipulate momentum and skin depth of evanescent waves owing to the generalized total internal reflection law [18]. In addition, this strategy is easily applicable within inverse design techniques. Examples include the introduction of two subwavelength stripes between two adjacent silicon waveguides [23] and the optimization of a varied number of stripes in the work of Yang and colleagues [24]. Likewise, numerous publications investigated uniform grating between waveguides [25,26,27]. Their results reveal an increase of several orders of magnitude in the crosstalk distance, compared to the classical scheme without stripes.
Meanwhile, recent reports [21,28,29,30,31] establish a high refractive index, transparency in the near-infrared and giant optical anisotropy in transition metal dichalcogenides (TMDCs), which are increasingly regarded as photonic materials beyond silicon [32,33,34]. Consequently, the suppression of TMDC waveguide crosstalk via inverse design methods is in high demand. In contrast to silicon, this problem requires taking into account the anisotropic tensor of TMDCs because of their giant optical anisotropy.
In this work, we resolve this challenge using the example of TMDC waveguides, separated by one or more stripes. For an exemplary TMDC, we chose molybdenum disulfide since it has one of the highest refractive indices among transparent photonic materials [21]. Nonetheless, our results are also applicable to all similar TMDCs, such as tungsten disulfide (WS2), tungsten diselenide (WSe2) and molybdenum diselenide (MoSe2).
2. Results
We start with the analysis of a typical structure (Figure 1), consisting of a pair of MoS2 waveguides, placed on top of a silicon oxide substrate. To make waveguides operate in a single-mode regime, we chose the following waveguide dimensions, which support only the fundamental transverse electric (TE) mode (height h = 220 nm, width w = 400 nm) and set the gap between waveguides to d = 400 nm. The relations between the dimension, effective refractive index and difference in effective indices of supermodes are collected in Figure A1 in the Appendix A section. Additionally, we noticed that anisotropy aids in the suppression of all modes except TE, giving anisotropic materials an unexpected advantage because the single-mode regime is preferable to prevent undesired losses and multimode interference [35]. The reason for that is a nonzero projection of the electric field perpendicular to MoS2 layers, where the refractive index is relatively small (n ~ 2.5) for waveguide modes apart from fundamental TE mode. Conversely, fundamental TE mode has an electric field along MoS2 layers, where the refractive index is large (n ~ 4.0).
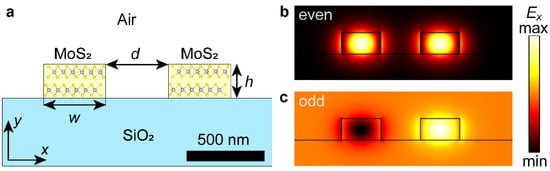
Figure 1.
Structure for optimization. Schematic image of the structure (a) and linear-scale field distribution Ex in the symmetric (b) and antisymmetric mode (c). Note that the orange color in panel c corresponds to zero whereas black and white colors represent negative and positive numbers of maximum absolute value. Waveguide dimensions are h = 220 nm, w = 400 nm and d = 400 nm.
The crosstalk between these waveguides arises as a result of waveguide mode overlap. Accordingly, it generates two supermodes, symmetric (even) and antisymmetric (odd), with propagation constants β+ and β− (Figure 1b). The crosstalk distance L, i.e., the propagation distance required for a mode to transfer from one waveguide to the other one, is given by:
It is convenient to express β+ and β− in terms of effective mode indices n+ and n−:
where λ is the free space wavelength of light. Then, crosstalk distance reads:
Hence, to calculate L, one needs to find n+ and n−, which we performed using the finite element method eigenmode solver implemented in COMSOL Multiphysics software. The initial structure has a crosstalk distance of L0 = 1.59 mm for the standard telecommunication wavelength λ = 1550 nm. This wavelength also belongs to the transparency range of MoS2, where the extinction coefficient k is less than 0.001. Hence, we work under the assumption of negligible optical losses [21].
Next, we try to reduce the crosstalk by placing a single stripe between the waveguides. Since, in practice, waveguides are produced from a planar layer by lithography [36,37], we assume that the stripe height and material composition are identical to the waveguides. It is also worth noting that structure has reflection symmetry; hence, stripes need to be placed symmetrically to achieve the best performance. Therefore, a single stripe should be located in the center between waveguides, as shown in Figure 2a. Figure 2b shows the crosstalk distance as a function of the stripe width w1. The maximum is reached at w1 = 130 nm, with the corresponding L1 = 9.4 mm, which is almost 6-times greater than for the initial configuration without the stripe (Figure 1a). For comparison, silicon waveguides with the same original crosstalk distance have L0 = 1.57 mm (without a stripe) and L1 = 3.16 mm (with a single optimized strip). It implies a several-times enhancement in crosstalk distance for MoS2, compared to silicon. We attribute this fact to the high refractive index (n ~ 4) of MoS2. High refractive index allows for a higher effective mode index of the fundamental mode. It also enhances the effective anisotropy of combined air/MoS2 spacing between waveguides, contributing to the total internal reflection and the decay of the evanescent field outside the waveguides [18,19,20,21,22]. At the same time, giant intrinsic optical anisotropy of MoS2 does not lead to a decrease in the effective mode index since the electric field in TE mode is mainly directed parallel to the atomic planes of MoS2 and, therefore, is weakly influenced by the low out-of-plane component of the refractive index.
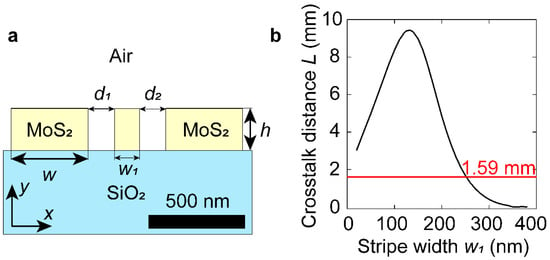
Figure 2.
Single-stripe structure. (a) Schematic view of the optimized structure. (b) Relation between the coupling length and the width of the stripe. The red line stands for coupling length in the initial structure with two waveguides and no additional stripes.
Aiming to further decrease waveguide crosstalk, we study the effect of insertion of two stripes between waveguides on the crosstalk distance. We computed a 2D heatmap (Figure 3) of crosstalk distance as a function of stripe width w1 = w2 (equality required by reflection symmetry) and stripe separation d2 (see the inset in Figure 3). Note that the map is triangular because parameters should satisfy d1 + d2 + d3 + w1 + w2 = 400 nm, equal to the initial gap between waveguides (inset in Figure 3). The absolute maximum in Figure 3 corresponds to L2 = 6.9 m, achieved at w1 = w2 = 44 nm and d2 = 59 nm. Of immediate interest is the significant ratio of L2/L1 ≈ 750 for MoS2. For comparison (Table 1), in the case of uniform stripes (w1 = w2 = d2 = 46 nm), L2/L1 ≈ 100, which is still, by an order of magnitude, higher than for silicon with L2/L1 ≈ 5 [23]. Therefore, our inverse design analysis demonstrates that TMDCs, in particular MoS2, provide an order-of-magnitude-higher integration circuit performance, in our case crosstalk distance, than silicon, despite only 15% higher refractive index.
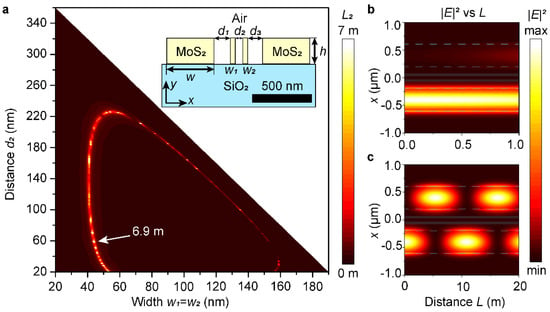
Figure 3.
Two-stripes structure. (a) Dependence of the crosstalk distance L2 on the separation between stripes d2 and their width w1 = w2. White arrow points at the point with the largest crosstalk distance. The inset shows a schematic view of the optimized structure. (b) The electric field intensity distribution versus y and L with a propagation length of 1 m and (c) 20 m. The plots are linear scale. The dashed lines in panels (b,c) show the waveguide edges.

Table 1.
Comparison of the crosstalk distance enhancements with other works.
In light of the recent advances in TMDC fabrication with atomic precision, subwavelength dimensions of the stripes (w1 = w2 = 44 nm and d2 = 59 nm) can be realized with standard lithography techniques [38]. Still, modern synthesis techniques need further development to realize the nanostructures proposed in our work because, to date, researchers have fabricated thick TMDC films using an exfoliation method [27], which yields only, at best, tens of micrometers lateral size [39], so modern synthesis techniques require further development to realize the nanostructures proposed in our work. Nevertheless, the recent advances in molecular beam epitaxy open up prospects for defect-free TMDCs with excellent optical properties on a large scale [40,41].
3. Discussion
In summary, we demonstrated the effect of MoS2 anisotropic optical response on the suppression efficiency of crosstalk between waveguides due to anisotropic nanostructures in the form of subwavelength stripes. We looked at numerous scenarios, including waveguides, separated with one or two stripes and without stripes. According to our calculations, adding even one stripe improves crosstalk by 6-times, while adding two gives an improvement of more than 4000, compared to original waveguides without stripes. This enhancement is 20-times better in comparison to silicon, which we attribute to the high refractive index and optical anisotropy of MoS2. Moreover, we expect a similar situation for other van der Waals (vdW) materials, including WS2, MoSe2 and WSe2, because of their similar dielectric tensor [21,28]. From a wider perspective, with recent advancements in fabrication [42,43,44] and nanostructure processing [33,38,45] of vdW materials, we envisage that our discoveries will be used in the next-generation integrated circuits, where vdW materials will complement or even replace the conventional material platforms, such as silicon [1,2] or gallium phosphide [46,47].
Author Contributions
A.A., V.V. and D.G. suggested and directed the project. D.G., O.M., G.E. and A.V. provided theoretical support. D.G. wrote the original manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
D.G. and G.E. acknowledge the support from the Russian Science Foundation (grant № 22-29-01192).
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
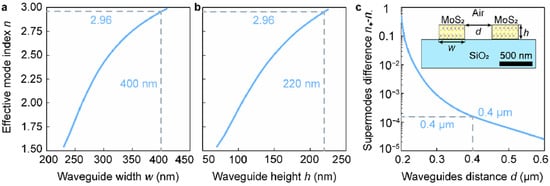
Figure A1.
Dependence of the effective index of the fundamental mode for one waveguide (a) on its width and (b) on its height. (c) Dependence of the difference between the effective indices of symmetric and antisymmetric modes on the distance between the waveguides.
References
- Atabaki, A.H.; Moazeni, S.; Pavanello, F.; Gevorgyan, H.; Notaros, J.; Alloatti, L.; Wade, M.T.; Sun, C.; Kruger, S.A.; Meng, H.; et al. Integrating Photonics with Silicon Nanoelectronics for the next Generation of Systems on a Chip. Nature 2018, 556, 349. [Google Scholar] [CrossRef] [PubMed]
- Bogaerts, W.; Pérez, D.; Capmany, J.; Miller, D.A.B.; Poon, J.; Englund, D.; Morichetti, F.; Melloni, A. Programmable photonic circuits. Nature 2020, 586, 207. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, Y. Recent Progress in the Development of Large-Capacity Integrated Silicon Photonics Transceivers. IEICE Trans. Electron. 2019, E102.C, 357. [Google Scholar] [CrossRef]
- Margalit, N.; Xiang, C.; Bowers, S.M.; Bjorlin, A.; Blum, R.; Bowers, J.E. Perspective on the future of silicon photonics and electronics. Appl. Phys. Lett. 2021, 118, 220501. [Google Scholar] [CrossRef]
- Zhang, J.; Shi, X.; Zhang, Z.; Guo, K.; Yang, J. Ultra-compact, efficient and high-polarization-extinction-ratio polarization beam splitters based on photonic anisotropic metamaterials. Opt. Express 2022, 30, 538–549. [Google Scholar] [CrossRef]
- Shi, X.; Zhang, J.; Fan, W.; Lu, Y.; Peng, N.; Rottwitt, K.; Ou, H. Compact low-birefringence polarization beam splitter using vertical-dual-slot waveguides in silicon carbide integrated platforms. Photonics Res. 2022, 10, A8–A13. [Google Scholar] [CrossRef]
- Su, L.; Piggott, A.Y.; Sapra, N.V.; Petykiewicz, J.; Vučković, J. Inverse Design and Demonstration of a Compact on-Chip Narrowband Three-Channel Wavelength Demultiplexer. ACS Photonics 2018, 5, 301. [Google Scholar] [CrossRef]
- Lu, J.; Vuckovic, J. Nanophotonic computational design. Opt. Express 2013, 21, 13351. [Google Scholar] [CrossRef]
- Huang, J.; Yang, J.; Chen, D.; Bai, W.; Han, J.; Zhang, Z.; Zhang, J.; He, X.; Han, Y.; Liang, L. Implementation of on-chip multi-channel focusing wavelength demultiplexer with regularized digital metamaterials. Nanophotonics 2019, 9, 159. [Google Scholar] [CrossRef]
- Su, L.; Vercruysse, D.; Skarda, J.; Sapra, N.V.; Petykiewicz, J.A.; Vučković, J. Nanophotonic inverse design with SPINS: Software architecture and practical considerations. Appl. Phys. Rev. 2020, 7, 011407. [Google Scholar] [CrossRef]
- Yuan, H.; Huang, J.; Wang, Z.; Zhang, J.; Deng, Y.; Lin, G.; Wu, J.; Yang, J. An ultra-compact dual-channel multimode wavelength demultiplexer based on inverse design. Results Phys. 2021, 27, 104489. [Google Scholar] [CrossRef]
- Bozhevolnyi, S.I.; Volkov, V.S.; Devaux, E.; Laluet, J.-Y.; Ebbesen, T.W. Channel plasmon subwavelength waveguide components including interferometers and ring resonators. Nature 2006, 440, 508. [Google Scholar] [CrossRef] [PubMed]
- Fedyanin, D.Y.; Yakubovsky, D.I.; Kirtaev, R.V.; Volkov, V.S. Ultralow-Loss CMOS Copper Plasmonic Waveguides. Nano Lett. 2016, 16, 362. [Google Scholar] [CrossRef]
- Thomaschewski, M.; Zenin, V.A.; Fiedler, S.; Wolff, C.; Bozhevolnyi, S.I. Plasmonic Lithium Niobate Mach–Zehnder Modulators. Nano Lett. 2022, 22, 6471. [Google Scholar] [CrossRef] [PubMed]
- Teng, D.; Wang, Y.; Xu, T.; Wang, H.; Shao, Q.; Tang, Y. Symmetric Graphene Dielectric Nanowaveguides as Ultra-Compact Photonic Structures. Nanomaterials 2021, 11, 1281. [Google Scholar] [CrossRef] [PubMed]
- Lian, C.; Hu, S.-Q.; Zhang, J.; Cheng, C.; Yuan, Z.; Gao, S.; Meng, S. Integrated Plasmonics: Broadband Dirac Plasmons in Borophene. Phys. Rev. Lett. 2020, 125, 116802. [Google Scholar] [CrossRef]
- Teng, D.; Wang, K. Theoretical Analysis of Terahertz Dielectric–Loaded Graphene Waveguide. Nanomaterials 2021, 11, 210. [Google Scholar] [CrossRef]
- Jahani, S.; Jacob, Z. Transparent subdiffraction optics: Nanoscale light confinement without metal. Optica 2014, 1, 96. [Google Scholar] [CrossRef]
- Jahani, S.; Kim, S.; Atkinson, J.; Wirth, J.C.; Kalhor, F.; Al Noman, A.; Newman, W.D.; Shekhar, P.; Han, K.; Van, V.; et al. Controlling evanescent waves using silicon photonic all-dielectric metamaterials for dense integration. Nat. Commun. 2018, 9, 1893. [Google Scholar] [CrossRef]
- Mia, M.B.; Ahmed, S.Z.; Ahmed, I.; Lee, Y.J.; Qi, M.; Kim, S. Exceptional Coupling in Photonic Anisotropic Metamaterials for Extremely Low Waveguide Crosstalk. Optica 2020, 7, 881. [Google Scholar] [CrossRef]
- Ermolaev, G.A.; Grudinin, D.V.; Stebunov, Y.V.; Voronin, K.V.; Kravets, V.G.; Duan, J.; Mazitov, A.B.; Tselikov, G.I.; Bylinkin, A.; Yakubovsky, D.I.; et al. Giant optical anisotropy in transition metal dichalcogenides for next-generation photonics. Nat. Commun. 2021, 12, 854. [Google Scholar] [CrossRef] [PubMed]
- Ermolaev, G.; Grudinin, D.; Voronin, K.; Vyshnevyy, A.; Arsenin, A.; Volkov, V. Van Der Waals Materials for Subdiffractional Light Guidance. Photonics 2022, 9, 744. [Google Scholar] [CrossRef]
- Khavasi, A.; Chrostowski, L.; Lu, Z.; Bojko, R. Significant Crosstalk Reduction Using All-Dielectric CMOS-Compatible Metamaterials. IEEE Photonics Technol. Lett. 2016, 28, 2787. [Google Scholar] [CrossRef]
- Yang, Y.; Guo, Y.; Huang, Y.; Pu, M.; Wang, Y.; Ma, X.; Li, X.; Luo, X. Crosstalk reduction of integrated optical waveguides with nonuniform subwavelength silicon strips. Sci. Rep. 2020, 10, 4491. [Google Scholar] [CrossRef] [PubMed]
- Bian, Y.; Ren, Q.; Kang, L.; Qin, Y.; Werner, P.L.; Werner, D.H. Efficient Cross-talk Reduction of Nanophotonic Circuits Enabled by Fabrication Friendly Periodic Silicon Strip Arrays. Sci. Rep. 2017, 7, 15827. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Chen, Z.; Wang, H.; Liu, A.; Wang, P.; Lin, T.; Liu, X.; Lv, H. Design of a low-crosstalk half-wavelength pitch nano-structured silicon waveguide array. Opt. Lett. 2019, 44, 3266. [Google Scholar] [CrossRef]
- Wu, H.; Li, C.; Song, L.; Tsang, H.-K.; Bowers, J.E.; Dai, D. Ultra-Sharp Multimode Waveguide Bends with Subwavelength Gratings. Laser Photonics Rev. 2019, 13, 1800119. [Google Scholar] [CrossRef]
- Verre, R.; Baranov, D.G.; Munkhbat, B.; Cuadra, J.; Käll, M.; Shegai, T. Transition metal dichalcogenide nanodisks as high-index dielectric Mie nanoresonators. Nat. Nanotechnol. 2019, 14, 679. [Google Scholar] [CrossRef]
- Ermolaev, G.A.; Stebunov, Y.V.; Vyshnevyy, A.A.; Tatarkin, D.E.; Yakubovsky, D.I.; Novikov, S.M.; Baranov, D.G.; Shegai, T.; Nikitin, A.Y.; Arsenin, A.V.; et al. Broadband optical properties of monolayer and bulk MoS2. NPJ 2D Mater. Appl. 2020, 4, 21. [Google Scholar] [CrossRef]
- Ermolaev, G.; Voronin, K.; Baranov, D.G.; Kravets, V.; Tselikov, G.; Stebunov, Y.; Yakubovsky, D.; Novikov, S.; Vyshnevyy, A.; Mazitov, A.; et al. Topological phase singularities in atomically thin high-refractive-index materials. Nat. Commun. 2022, 13, 2049. [Google Scholar] [CrossRef]
- Munkhbat, B.; Baranov, D.G.; Stührenberg, M.; Wersäll, M.; Bisht, A.; Shegai, T. Self-Hybridized Exciton-Polaritons in Multilayers of Transition Metal Dichalcogenides for Efficient Light Absorption. ACS Photonics 2019, 6, 139. [Google Scholar] [CrossRef]
- Ling, H.; Li, R.; Davoyan, A.R. All van der Waals Integrated Nanophotonics with Bulk Transition Metal Dichalcogenides. ACS Photonics 2021, 8, 721. [Google Scholar] [CrossRef]
- Tselikov, G.I.; Ermolaev, G.A.; Popov, A.A.; Tikhonowski, G.V.; Panova, D.A.; Taradin, A.S.; Vyshnevyy, A.A.; Syuy, A.V.; Klimentov, S.M.; Novikov, S.M.; et al. Transition metal dichalcogenide nanospheres for high-refractive-index nanophotonics and biomedical theranostics. Proc. Natl. Acad. Sci. USA 2022, 119, e2208830119. [Google Scholar] [CrossRef] [PubMed]
- Popkova, A.A.; Antropov, I.M.; Tselikov, G.I.; Ermolaev, G.A.; Ozerov, I.; Kirtaev, R.V.; Novikov, S.M.; Evlyukhin, A.B.; Arsenin, A.V.; Bessonov, V.O.; et al. Nonlinear Exciton-Mie Coupling in Transition Metal Dichalcogenide Nanoresonators. Laser Photonics Rev. 2022, 16, 2100604. [Google Scholar] [CrossRef]
- Li, C.; Liu, D.; Dai, D. Multimode silicon photonics. Nanophotonics 2018, 8, 227. [Google Scholar] [CrossRef]
- Lin, D.; Fan, P.; Hasman, E.; Brongersma, M.L. Dielectric gradient metasurface optical elements. Science 2014, 345, 298. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 2011, 334, 333. [Google Scholar] [CrossRef]
- Munkhbat, B.; Yankovich, A.; Baranov, D.; Verre, R.; Olsson, E.; Shegai, T.O. Transition metal dichalcogenide metamaterials with atomic precision. Nat. Commun. 2020, 11, 4604. [Google Scholar] [CrossRef]
- Frisenda, R.; Niu, Y.; Gant, P.; Muñoz, M.; Castellanos-Gomez, A. Naturally occurring van der Waals materials. NPJ 2D Mater. Appl. 2020, 4, 38. [Google Scholar] [CrossRef]
- Choudhury, T.H.; Zhang, X.; Al Balushi, Z.Y.; Chubarov, M.; Redwing, J.M. Epitaxial Growth of Two-Dimensional Layered Transition Metal Dichalcogenides. Annu. Rev. Mater. Res. 2020, 50, 155–177. [Google Scholar] [CrossRef]
- Ermolaev, G.; El-Sayed, M.; Yakubovsky, D.; Voronin, K.; Romanov, R.; Tatmyshevskiy, M.; Doroshina, N.; Nemtsov, A.; Voronov, A.; Novikov, S.; et al. Optical Constants and Structural Properties of Epitaxial MoS2 Monolayers. Nanomaterials 2021, 11, 1411. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.-K.; Zhang, W.; Lee, Y.-H.; Lin, Y.-C.; Chang, M.-T.; Su, C.-Y.; Chang, C.-S.; Li, H.; Shi, Y.; Zhang, H.; et al. Growth of Large-Area and Highly Crystalline MoS2 Thin Layers on Insulating Substrates. Nano Lett. 2012, 12, 1538. [Google Scholar] [CrossRef] [PubMed]
- Najmaei, S.; Liu, Z.; Zhou, W.; Zou, X.; Shi, G.; Lei, S.; Yakobson, B.I.; Idrobo, J.C.; Ajayan, P.M.; Lou, J. Vapour phase growth and grain boundary structure of molybdenum disulphide atomic layers. Nat. Mater. 2013, 12, 754. [Google Scholar] [CrossRef] [PubMed]
- Dumcenco, D.; Ovchinnikov, D.; Marinov, K.; Lazić, P.; Gibertini, M.; Marzari, N.; Sanchez, O.L.; Kung, Y.-C.; Krasnozhon, D.; Chen, M.-W.; et al. Large-Area Epitaxial Monolayer MoS2. ACS Nano 2015, 9, 4611. [Google Scholar] [CrossRef] [PubMed]
- Munkhbat, B.; Küçüköz, B.; Baranov, D.G.; Antosiewicz, T.J.; Shegai, T.O. Nanostructured Transition Metal Dichalcogenide Multilayers for Advanced Nanophotonics. Laser Photonics Rev. 2022, 2200057. [Google Scholar] [CrossRef]
- Khmelevskaia, D.; Markina, D.I.; Fedorov, V.V.; Ermolaev, G.A.; Arsenin, A.V.; Volkov, V.S.; Goltaev, A.S.; Zadiranov, Y.M.; Tzibizov, I.A.; Pushkarev, A.P.; et al. Directly grown crystalline gallium phosphide on sapphire for nonlinear all-dielectric nanophotonics. Appl. Phys. Lett. 2021, 118, 201101. [Google Scholar] [CrossRef]
- Fedorov, V.V.; Koval, O.Y.; Ryabov, D.R.; Fedina, S.V.; Eliseev, I.E.; Kirilenko, D.A.; Pidgayko, D.A.; Bogdanov, A.A.; Zadiranov, Y.M.; Goltaev, A.S.; et al. Nanoscale Gallium Phosphide Epilayers on Sapphire for Low-Loss Visible Nanophotonics. ACS Appl. Nano Mater. 2022, 5, 8846. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).