A Proper Shape of the Trailing Edge Modification to Solve a Housing Damage Problem in a Gas Turbine Power Plant
Abstract
1. Introduction
2. Theoretical Background
2.1. Aerodynamics
2.2. Structural Dynamics
3. Methodology
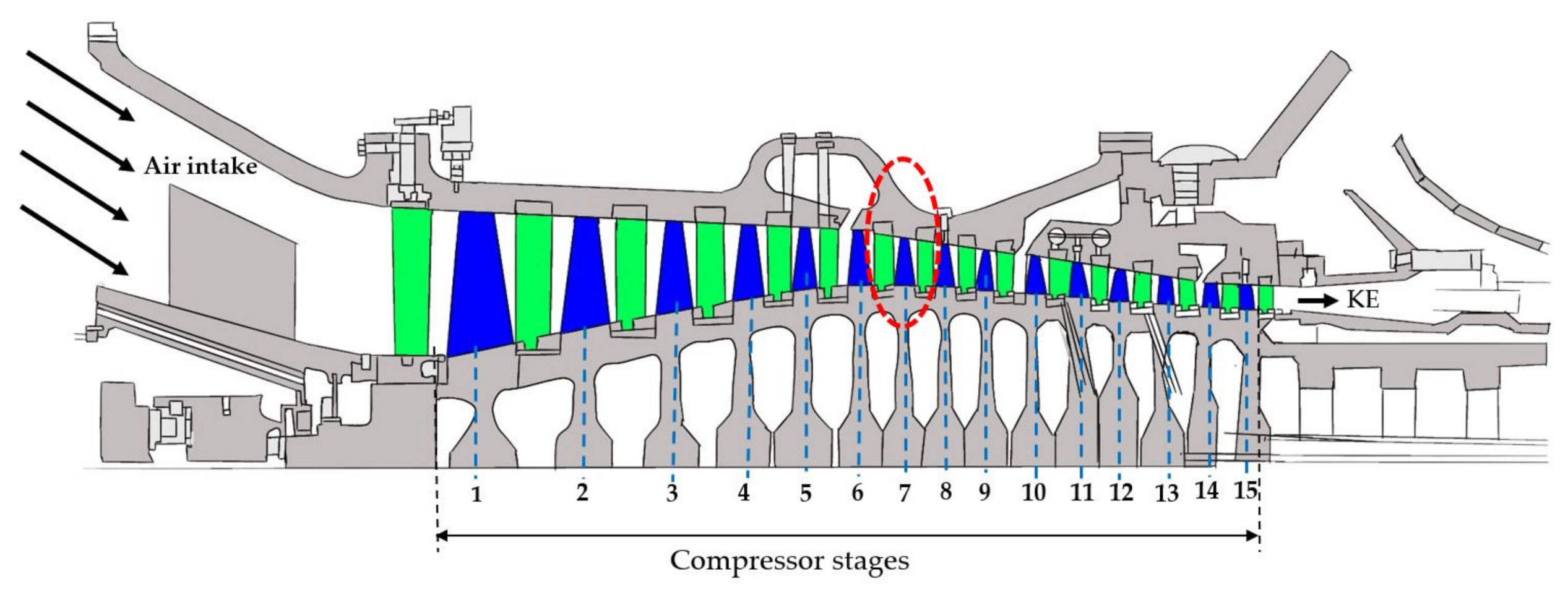
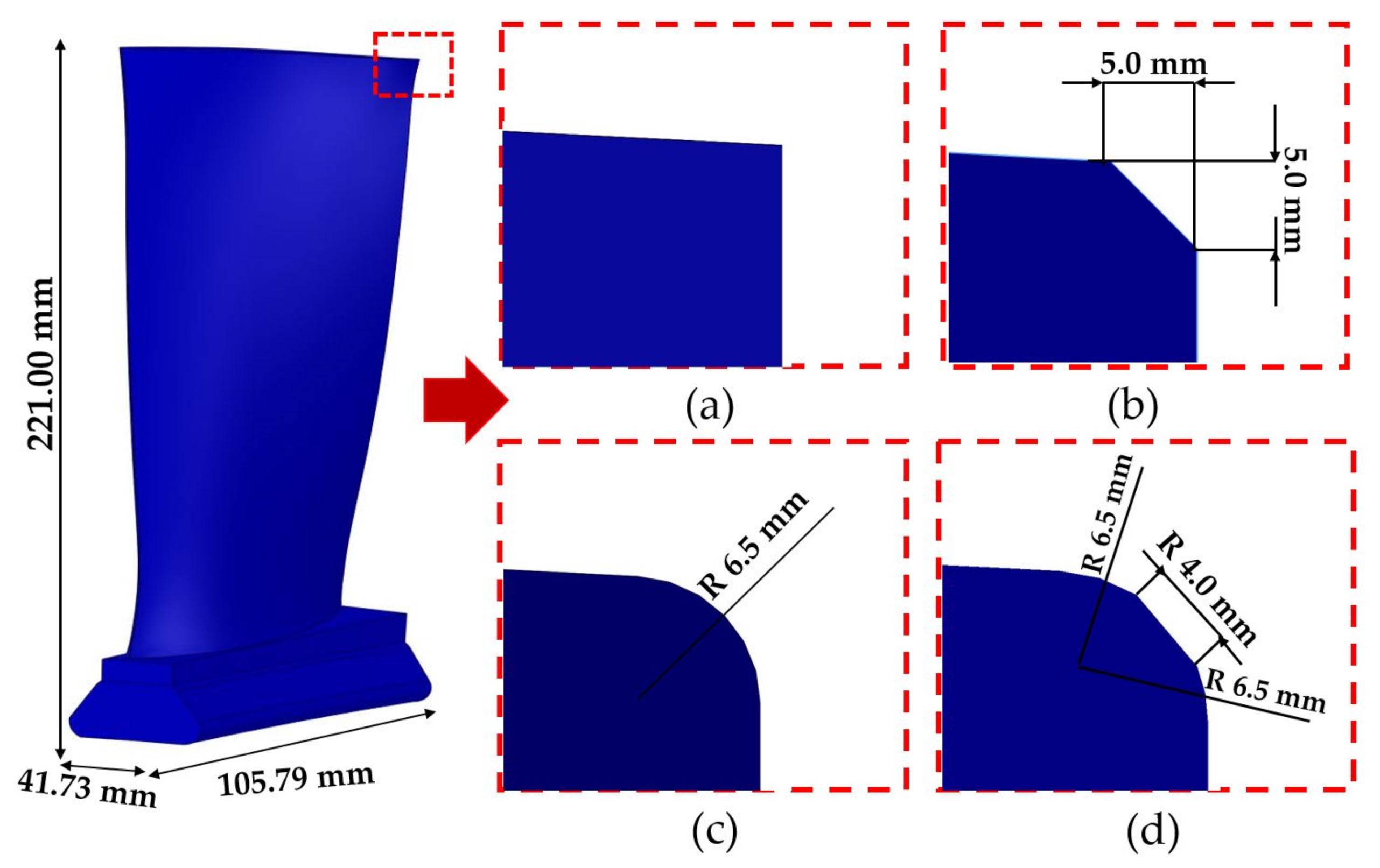
3.1. CB Modification
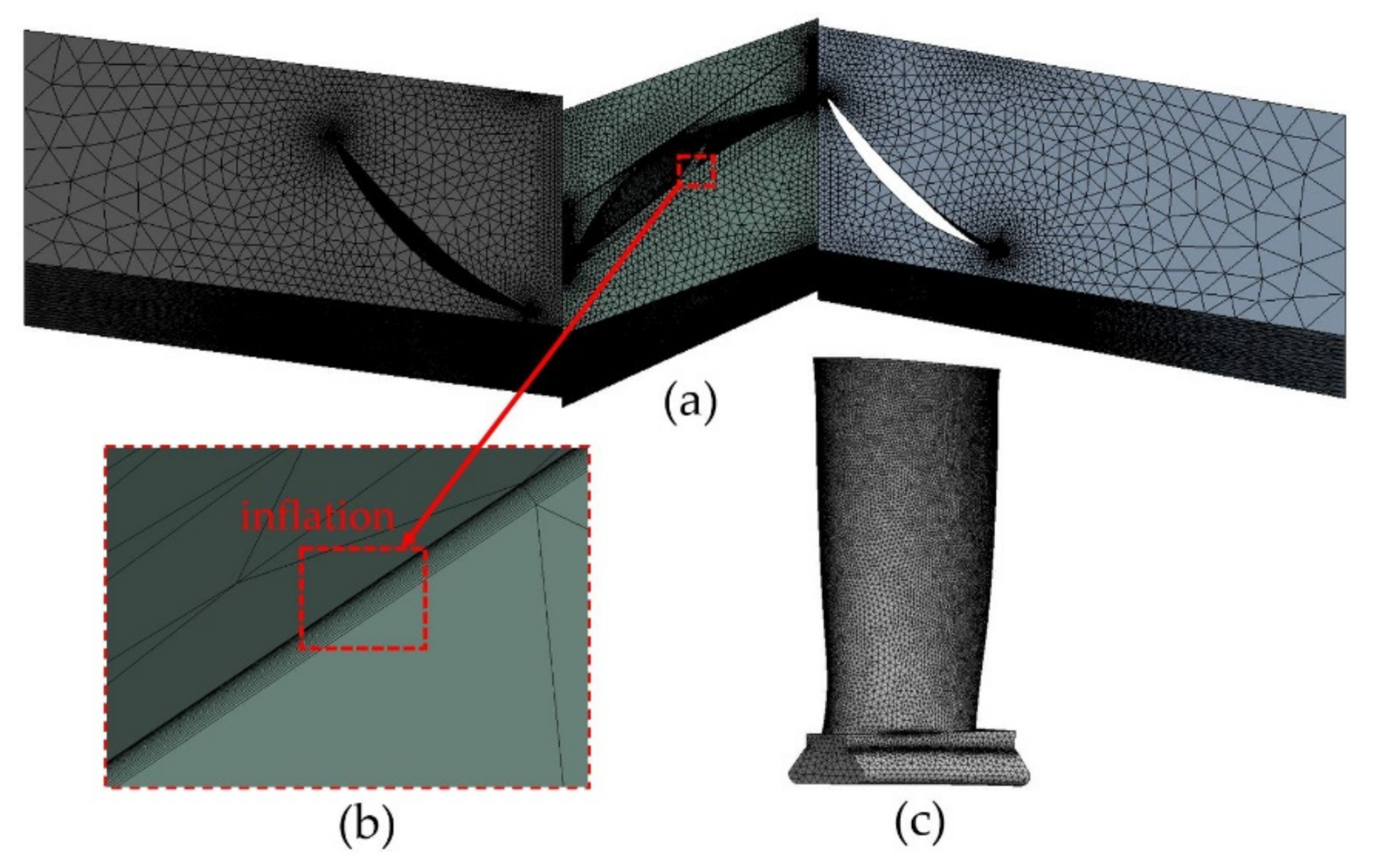
3.2. Models
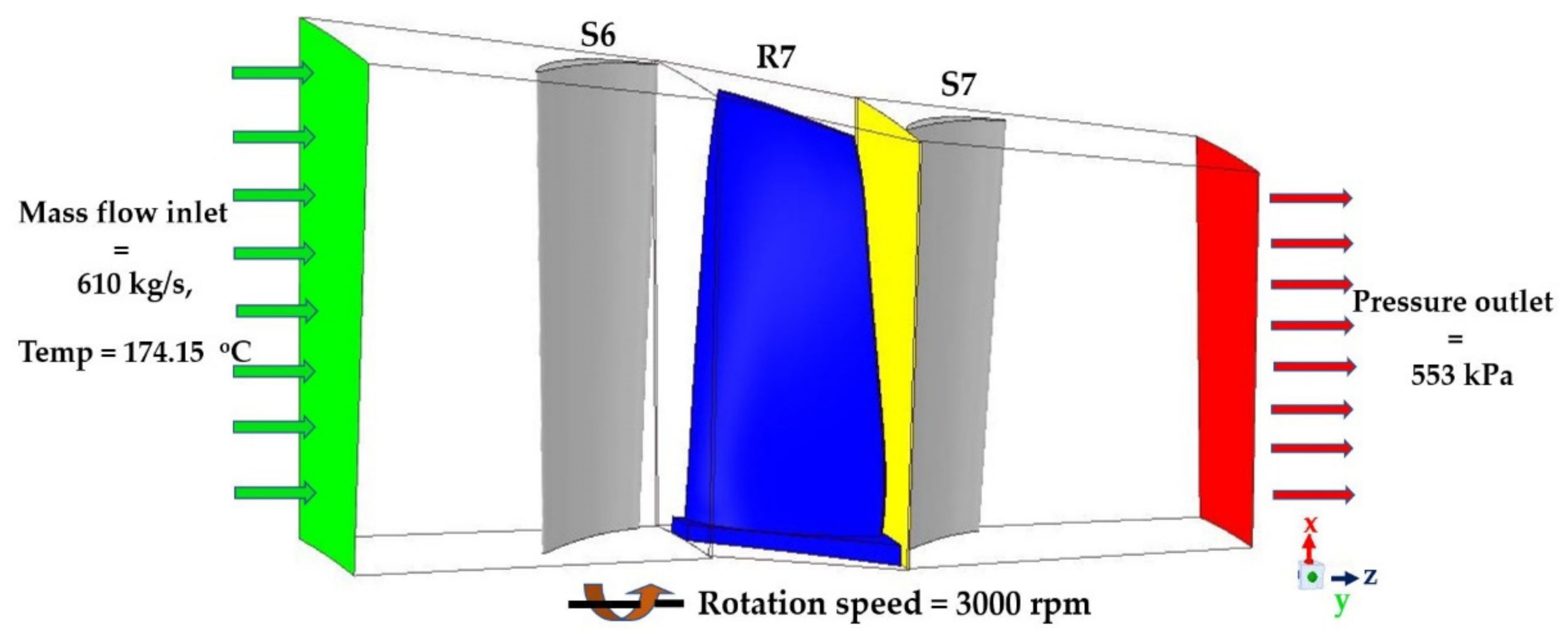
3.3. Boundary Conditions and Software Settings
4. Results and Discussion
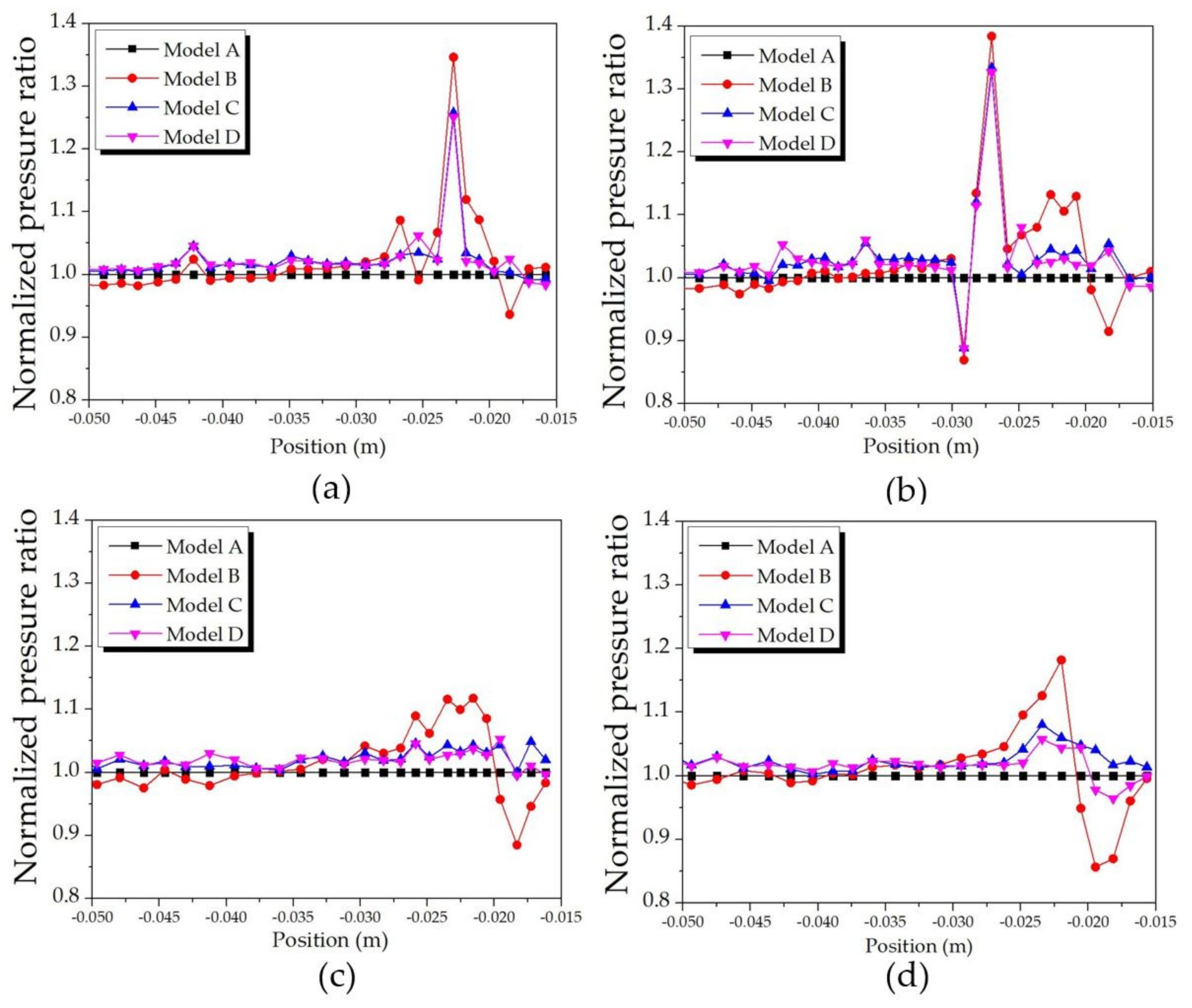
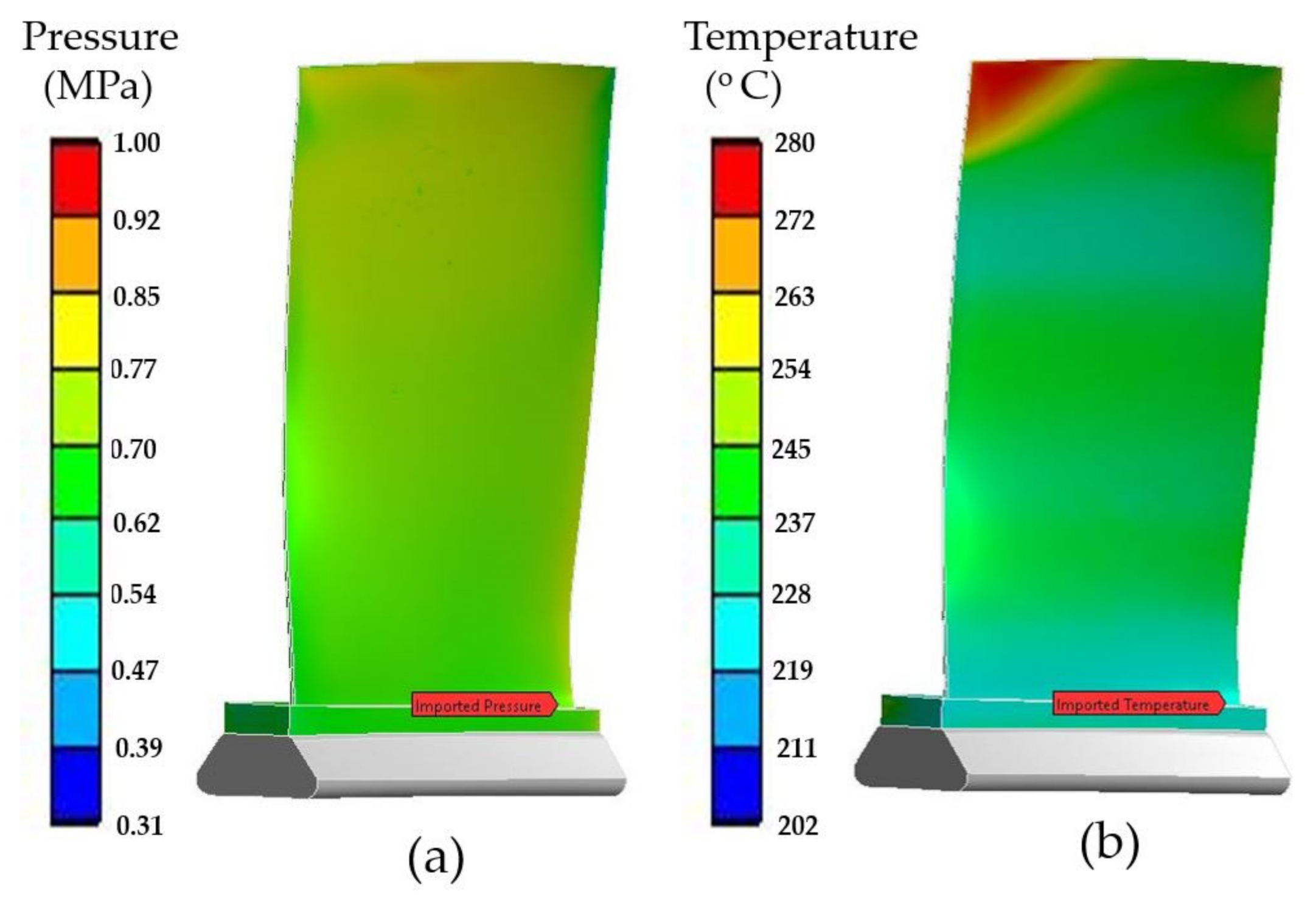
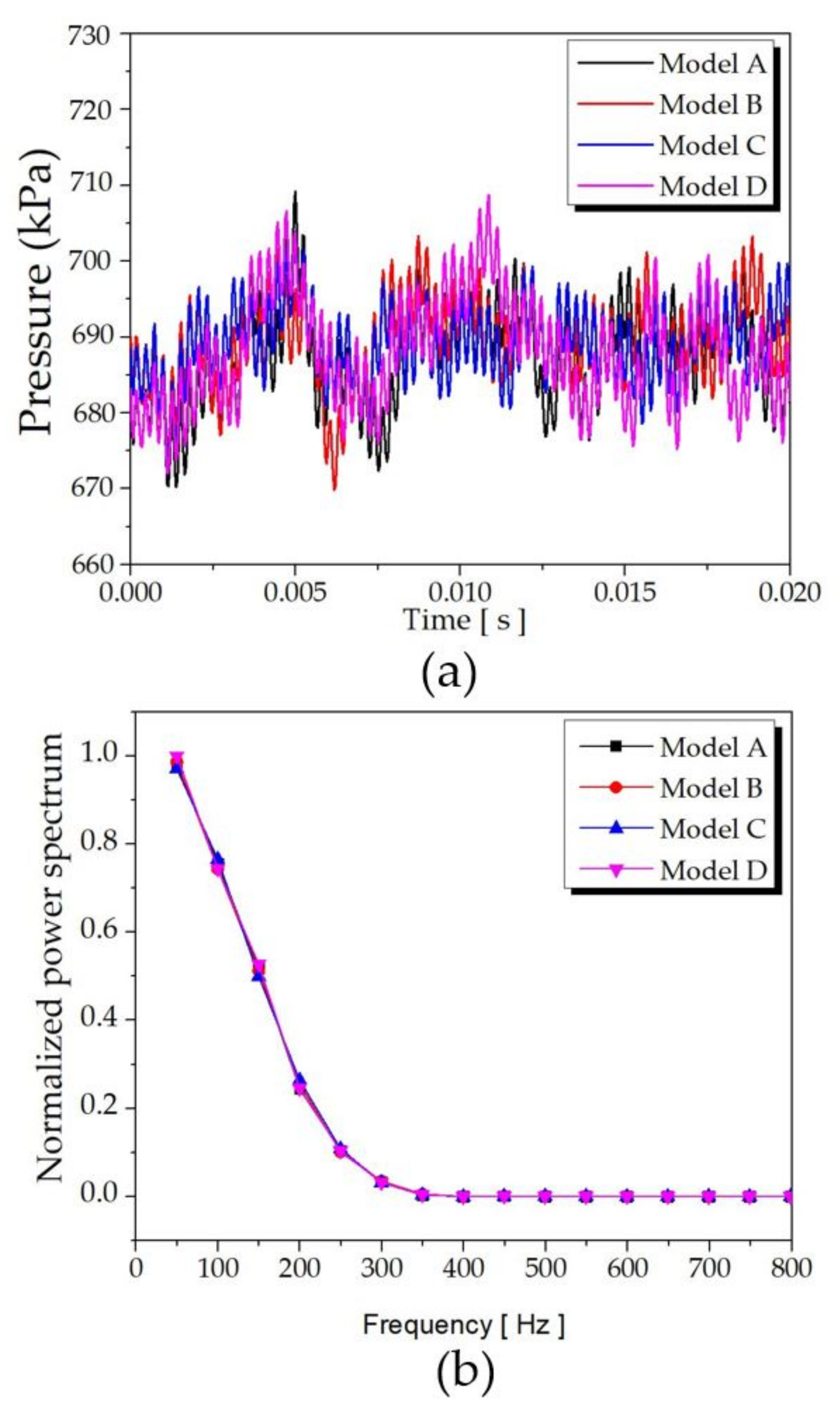
4.1. Aerodynamics
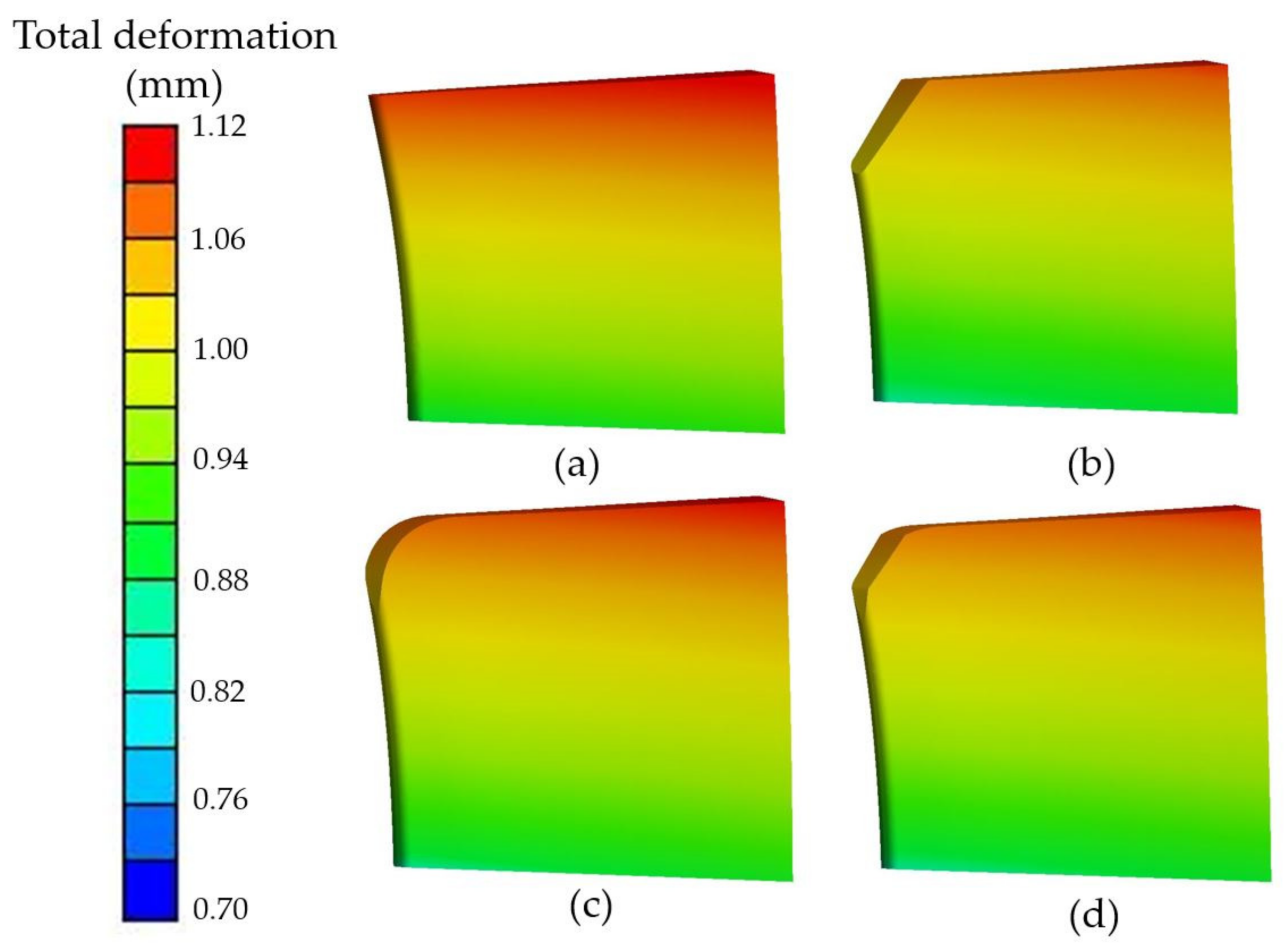
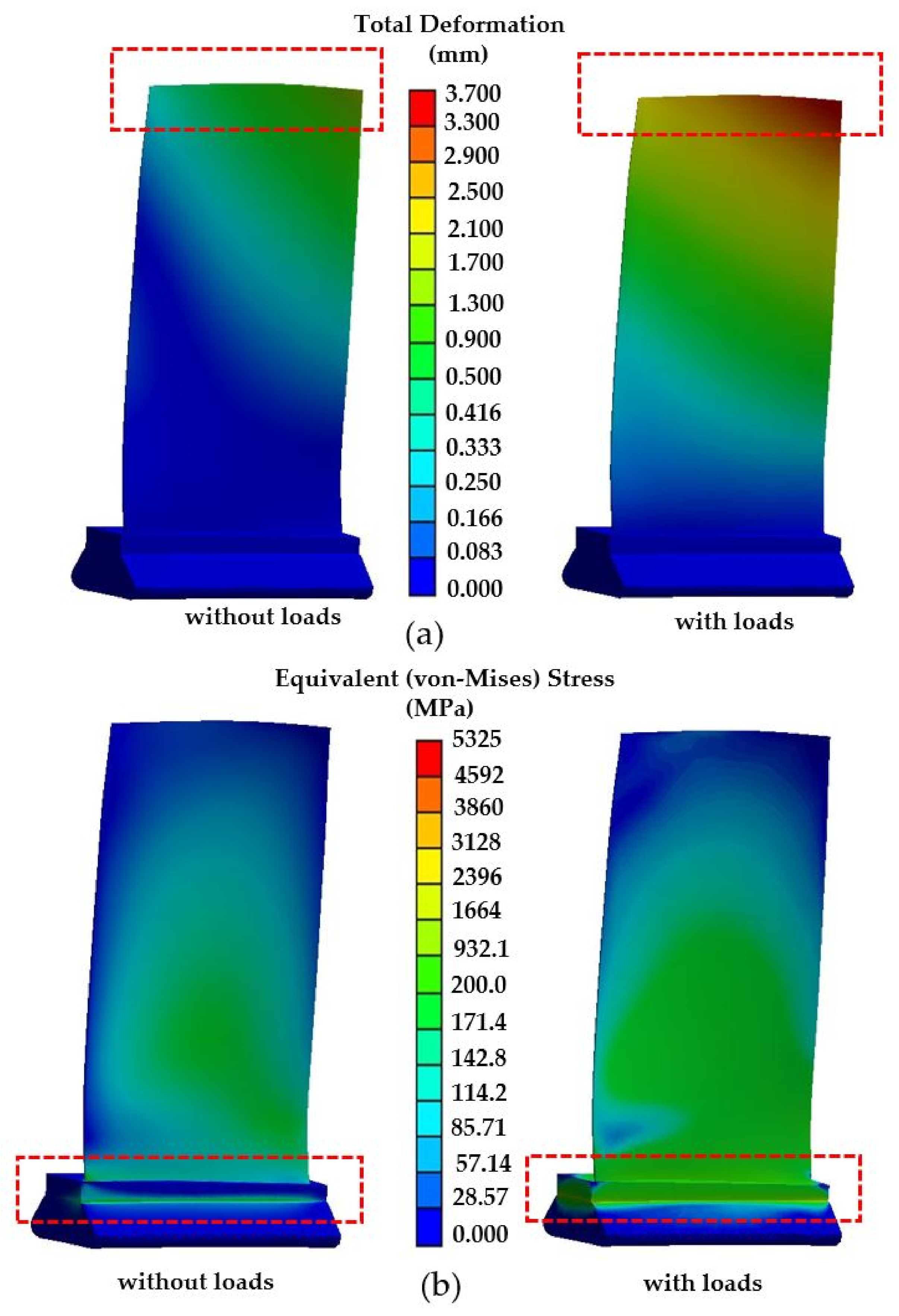
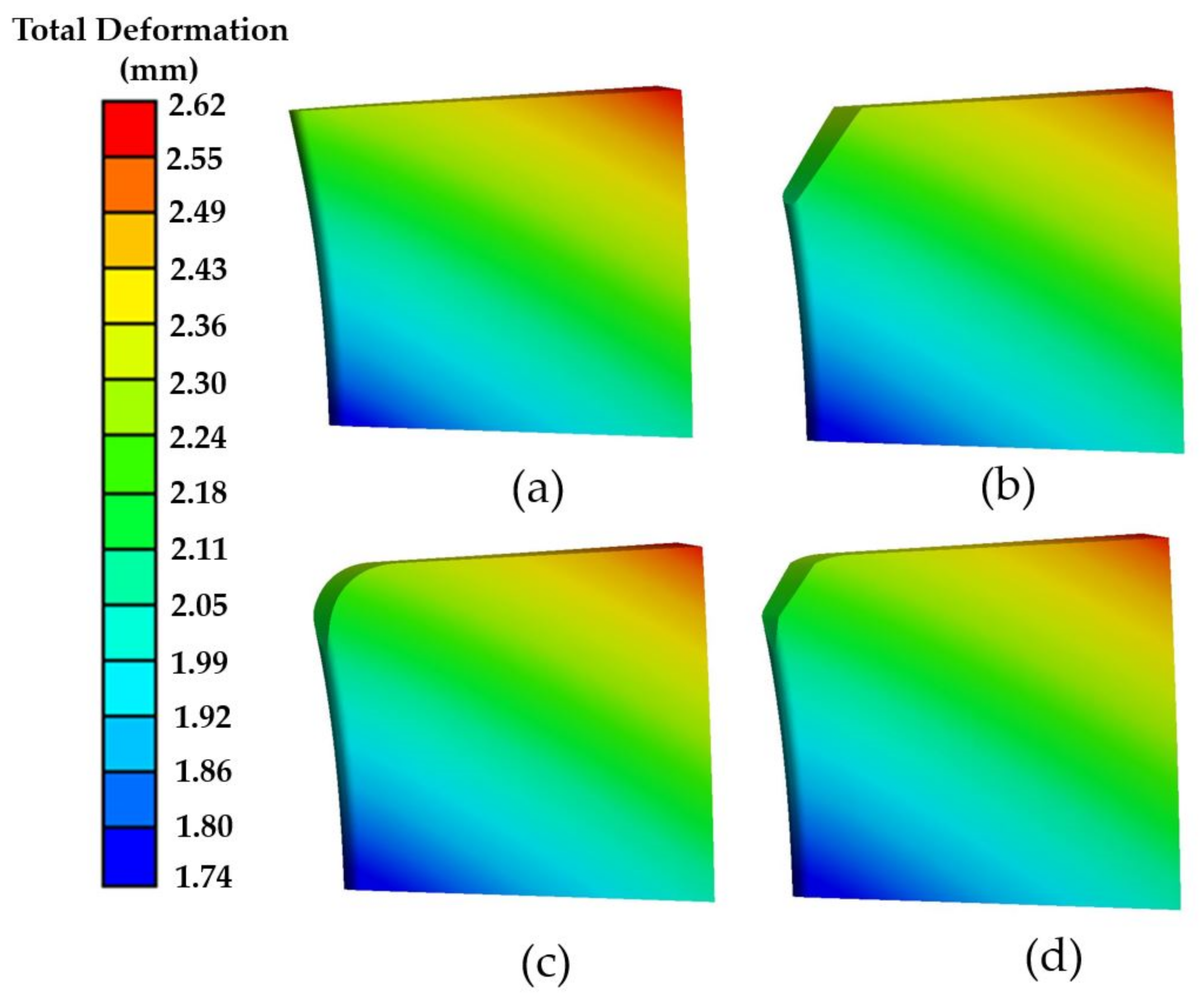
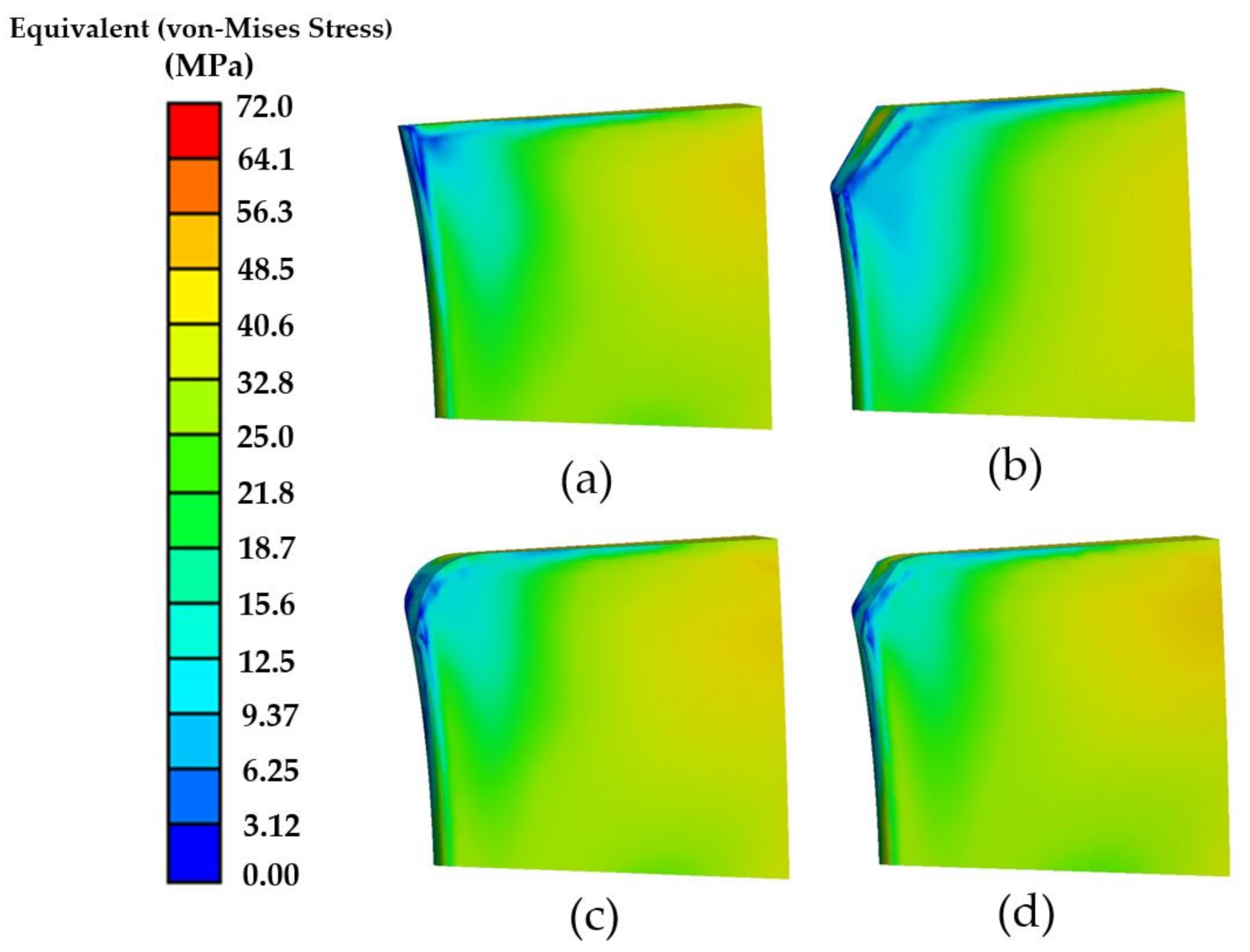
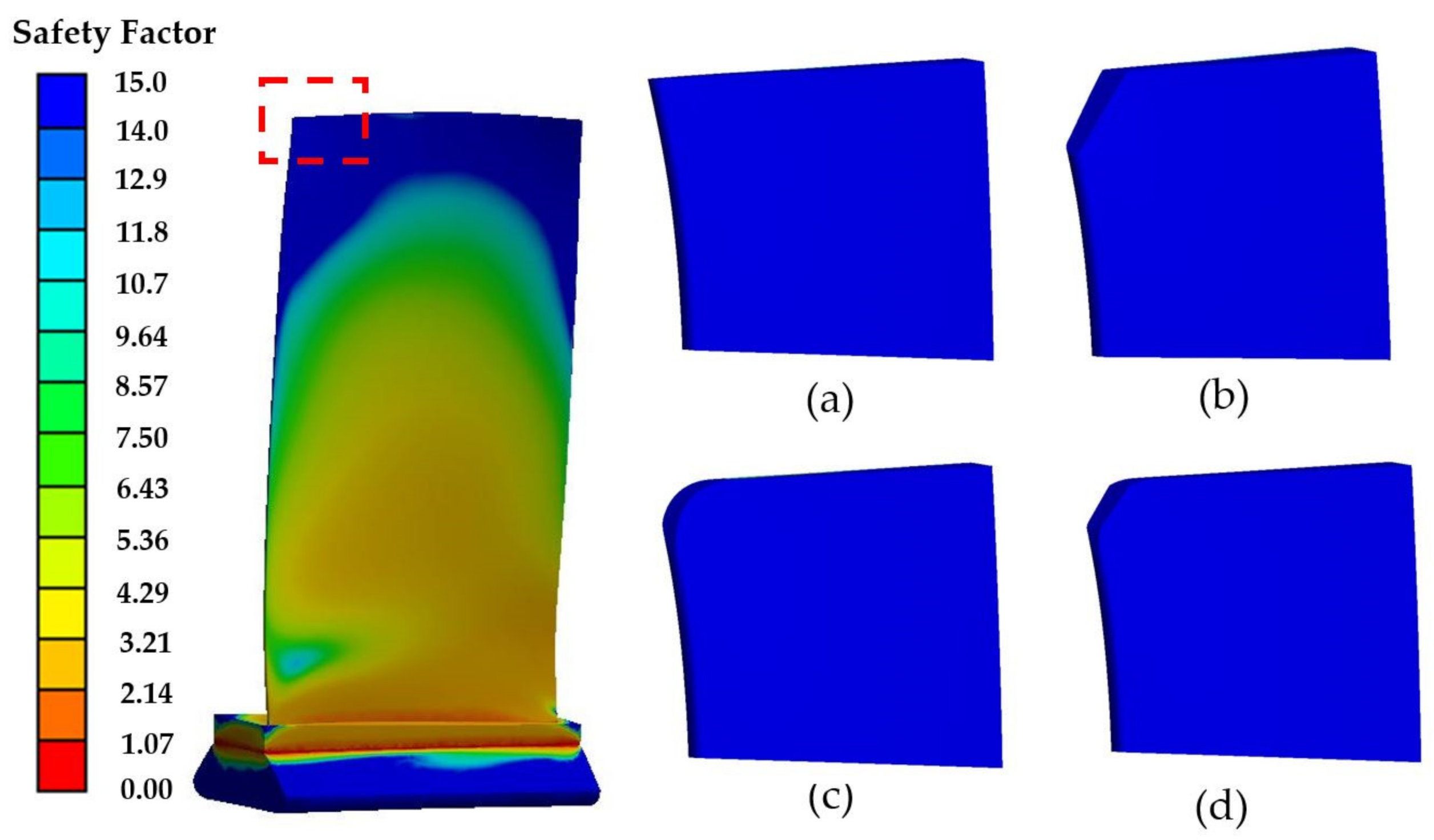
4.2. Structural Dynamics
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 1, 2, and 3 correspond to x, y, and z, respectively | |
| AD | aerodynamics |
| angular frequency (rad/s) | |
| blending function | |
| eddy viscosity (m2/s) | |
| density (kg/m3) | |
| load vector (N) | |
| mean velocity (m/s) | |
| molecular dynamics viscosity (Pa s) | |
| nodal displacement vector (m) | |
| nodal displacement vector (m) | |
| nodal velocity vector (m/s) | |
| pressure (Pa) | |
| shear production of turbulence | |
| source term of energy (N/m2 s) | |
| source term of momentum (N/m3) | |
| specific coefficient for SST k-ω | |
| specific dissipation rate (1/s) | |
| stress tensor (Pa) | |
| structural damping matrix (N s/m) | |
| SD | structural dynamics |
| structural mass matrix (kg) | |
| structural stiffness matrix (N/m) | |
| temperature () | |
| thermal conduction matrix (W/) | |
| thermal conductivity (W/m K) | |
| thermal conduction vector (W) | |
| total enthalpy (J) | |
| turbulent kinetic energy (J/kg) |
References
- Kaewbumrung, M.; Tangsopa, W.; Thongsri, J. Investigation of the Trailing Edge Modification Effect on Compressor Blade Aerodynamics Using SST k-ω Turbulence Model. Aerospace 2019, 6, 48. [Google Scholar] [CrossRef]
- Amoo, L.M. On the design and structural analysis of jet engine fan blade structures. Prog. Aerosp. Sci. 2013, 60, 1–11. [Google Scholar] [CrossRef]
- Heidari, M.; Amini, K. Structural modification of a steam turbine blade. IOP Conf. Ser. Mater. Sci. Eng. 2017, 203, 012007. [Google Scholar] [CrossRef]
- Pugachuk, A.S.; Muller, D.V.; Fominyh, N.K. Development of impellers based on prototypes in microturbine plants. AIP Conf. Proc. 2019, 2141, 030031. [Google Scholar]
- Zhu, M. Design and analysis of steam turbine blades. J. Phys. Conf. Ser. 2019, 1300, 012056. [Google Scholar] [CrossRef]
- NithinKumarK, C.; Tandon, T.; Silori, P.; Shaikh, A. Structural Design and Analysis of Gas Turbine Blade using CAE tools. Int. J. Eng. Res. Technol. 2014, 3, 469–474. [Google Scholar]
- Ujade, G.; Bhambere, M. Review of Structural and Thermal Analysis of Gas Turbine Blade. Int. J. Mech. Eng. Robot. Res. 2014, 3, 347. [Google Scholar]
- Singh, H.P.; Rawat, A.; Manral, A.R.; Kumar, P. Computational analysis of a gas turbine blade with different materials. Mater. Today Proc. 2020. [Google Scholar] [CrossRef]
- Boudounit, H.; Tarfaoui, M.; Saifaoui, D. Modal analysis for optimal design of offshore wind turbine blades. Mater. Today Proc. 2020, 30, 998–1004. [Google Scholar] [CrossRef]
- Boyaraju, G.; Rajasekhar, S.; Sridhar, A.; Rao, J. Thermal analysis of a gas turbine rotor blade. Int. J. Sci. Eng. Adv. Technol. 2015, 3, 1181–1187. [Google Scholar]
- Ngoret, J.K.; Kommula, V.P. Comprehending Occurrence of Premature Failure in Compressor Turbine (CT) Blades for Short-Haul Aircraft Fleet. Int. J. Eng. Res. Afr. 2019, 42, 10–23. [Google Scholar] [CrossRef]
- Kou, H.J.; Lin, J.S.; Fu, X. Dynamic and fatigue compressor blade characteristics during fluid structure interaction: Part Ι-Blade modelling and vibration analysis. Eng. Fail. Anal. 2017, 76, 80–98. [Google Scholar] [CrossRef]
- Zhu, F.-w.; Ding, L.; Huang, B.; Bao, M.; Liu, J.-T. Blade design and optimization of a horizontal axis tidal turbine. Ocean Eng. 2020, 195, 106652. [Google Scholar] [CrossRef]
- Cui, B.; Zhang, C.; Zhang, Y.; Zhu, Z. Influence of Cutting Angle of Blade Trailing Edge on Unsteady Flow in a Centrifugal Pump Under Off-Design Conditions. Appl. Sci. 2020, 10, 580. [Google Scholar] [CrossRef]
- Lu, J.L.; Chu, W.; Zhang, H. Influence of blade tip cutting on axial compressor aerodynamic performance. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2009, 223, 19–29. [Google Scholar] [CrossRef]
- Möller, D.; Jüngst, M.; Holzinger, F.; Brandstetter, C.; Schiffer, H.-P.; Leichtfuß, S. In Numerical Investigation of Tip Clearance Flow Induced Flutter in an Axial Research Compressor. In ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2016. [Google Scholar]
- Halder, P.; Kumar, P.M. Coupled CAD-CFD automated optimization for leading and trailing edge of an axial impulse turbine blade. Ocean Eng. 2020, 213, 107769. [Google Scholar] [CrossRef]
- ANSYS, Inc. Lecture 01: Overview of FSI in Workbench. In ANSYS Fluent Fluid-Structure Interaction (FSI) with ANSYS Mechanical; ANSYS Inc.: Canonsburg, PA, USA, 2016. [Google Scholar]
- ANSYS, Inc. ANSYS 17.1. In ANSYS CFX Introduction; ANSYS Europe Ltd.: Canonsburg, PA, USA, 2017. [Google Scholar]
- ANSYS, Inc. CFX-Solver Theory Guide R19.2; ANSYS Inc.: Canonsburg, PA, USA, 2019. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605.22. [Google Scholar] [CrossRef]
- Puangburee, L.; Busayaporn, W.; Kaewbumrung, M.; Thongsri, J. Evaluation and Improvement of Ventilation System Inside Low-Cost Automation Line to Reduce Particle Contamination. ECTI Trans. Electr. Eng. Electron. Commun. 2020, 18, 35–44. [Google Scholar] [CrossRef][Green Version]
- Santati, S.; Thongsri, J.; Sarntima, P. Modified small-volume jet nebulizer based on CFD simulation and its clinical outcomes in small asthmatic children. J. Healthc. Eng. 2019, 2019, 2524583. [Google Scholar] [CrossRef]
- Tangsopa, W.; Thongsri, J. Development of an industrial ultrasonic cleaning tank based on harmonic response analysis. Ultrasonics 2019, 91, 68–76. [Google Scholar] [CrossRef] [PubMed]
- Tangsopa, W.; Thongsri, J. A Novel Ultrasonic Cleaning Tank Developed by Harmonic Response Analysis and Computational Fluid Dynamics. Metals 2020, 10, 335. [Google Scholar] [CrossRef]
- ANSYS, Inc. ANSYS 2020 R1. In ANSYS Mechanical APDL Theory Reference; ANSYS Europe Ltd.: Canonsburg, PA, USA, 2020. [Google Scholar]
- ANSYS, Inc. Module 07: Modal, Thermal, and Multistep Analysis. In Introduction to ANSYS Mechanical; ANSYS Inc.: Canonsburg, PA, USA, 2016. [Google Scholar]
- Briggs, J.Z.; Parker, T.D. The super 12% Cr Steels. In Source Book on Materials for Evaluated-Temperature Applications; Elihu, F.B., Ed.; American Society for Metals: Geauga County, OH, USA, 1979; p. 121. [Google Scholar]
- Tangsopa, W.; Thongsri, J. A Dual Frequency Ultrasonic Cleaning Tank Developed by Transient Dynamic Analysis. Appl. Sci. 2021, 11, 699. [Google Scholar] [CrossRef]
- Kumar, R.R.; Pandey, K.M. Static Structural and Modal Analysis of Gas Turbine Blade. IOP Conf. Ser. Mater. Sci. Eng. 2017, 225, 012102. [Google Scholar] [CrossRef]


| Model | Fluid Domain | Solid Domain | Total | |||
|---|---|---|---|---|---|---|
| Element | Node | Element | Node | Element | Node | |
| A | 7,223,803 | 2,355,794 | 568,389 | 856,710 | 7,792,192 | 3,212,504 |
| B | 8,484,301 | 2,919,733 | 598,095 | 901,796 | 9,082,396 | 3,821,529 |
| C | 9,068,565 | 3,122,478 | 546,224 | 823,878 | 9,614,789 | 3,946,356 |
| D | 7,059,840 | 2,315,809 | 555,843 | 839,031 | 7,615,683 | 3,154,840 |
| Numerical Parameters | Setting |
|---|---|
| Solvers | Pressure-based |
| Spatial Discretization | High-resolution scheme for the advection term |
| High-resolution scheme for turbulence quantities | |
| Convergence Control | Maximum Iteration 1000 |
| Convergence Criteria | 1.0 × 10−4 |
| Time Scale Control | Auto Timescale |
| Length Scale Option | Conservative |
| Time Scale Factor | Auto Timescale |
| Fluid | Air Ideal Gas |
| Heat Transfer | Total Energy |
| Turbulence | SST k-ω |
| Wall Function | High-speed (compressible) wall heat transfer model |
| Transient Blade Row Model | Profile Transformation |
| Frame Change or Mixing Model | Transient Rotor Stator |
| Pitch Change | Automatic |
| Property | Value |
|---|---|
| Density | 7805 kg/m3 |
| Poisson’s Ratio | 0.195 |
| Shear Modulus | 79,300 MPa |
| Young’s Modulus | 1.896 × 105 MPa |
| Bulk Modulus | 1.037 × 105 MPa |
| Tensile Yield Strength | 1000 MPa |
| Tensile Ultimate Strength | 1580 MPa |
| Thermal Conductivity | |
| 100 °C | 23.9 W/m·°C |
| 350 °C | 26.0 W/m·°C |
| Coefficient of Thermal Expansion | |
| 100 °C | 1.120 × 105 °C−1 |
| 350 °C | 1.147 × 105 °C−1 |
| S-N Curve | 422 Stainless Steel [28] |
| Parameter | Measurement | Simulation | Error |
|---|---|---|---|
| Pressure | 570,000 ± 15% Pa | 619,909 Pa | 8.76% |
| Temperature | 197.0 ± 10% °C | 199.3 °C | 1.17% |
| Model or Parameter | Fz (N) | Fy (N) | Area (m2) | Cl | Cd |
|---|---|---|---|---|---|
| A | 762.945 | 712.282 | 0.0415014 | 0.245 | 0.229 |
| B | 740.563 | 702.746 | 0.0414735 | 0.234 (−3.67%) | 0.227 (−0.87%) |
| C | 744.547 | 701.989 | 0.0414946 | 0.240 (−2.04%) | 0.226 (−1.31%) |
| D | 766.729 | 717.477 | 0.0414903 | 0.250 (+2.04%) | 0.234 (+2.18%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jansaengsuk, T.; Kaewbumrung, M.; Busayaporn, W.; Thongsri, J. A Proper Shape of the Trailing Edge Modification to Solve a Housing Damage Problem in a Gas Turbine Power Plant. Processes 2021, 9, 705. https://doi.org/10.3390/pr9040705
Jansaengsuk T, Kaewbumrung M, Busayaporn W, Thongsri J. A Proper Shape of the Trailing Edge Modification to Solve a Housing Damage Problem in a Gas Turbine Power Plant. Processes. 2021; 9(4):705. https://doi.org/10.3390/pr9040705
Chicago/Turabian StyleJansaengsuk, Thodsaphon, Mongkol Kaewbumrung, Wutthikrai Busayaporn, and Jatuporn Thongsri. 2021. "A Proper Shape of the Trailing Edge Modification to Solve a Housing Damage Problem in a Gas Turbine Power Plant" Processes 9, no. 4: 705. https://doi.org/10.3390/pr9040705
APA StyleJansaengsuk, T., Kaewbumrung, M., Busayaporn, W., & Thongsri, J. (2021). A Proper Shape of the Trailing Edge Modification to Solve a Housing Damage Problem in a Gas Turbine Power Plant. Processes, 9(4), 705. https://doi.org/10.3390/pr9040705









