Hybrid Process Models in Electrochemical Syntheses under Deep Uncertainty
Abstract
1. Introduction
2. Methods
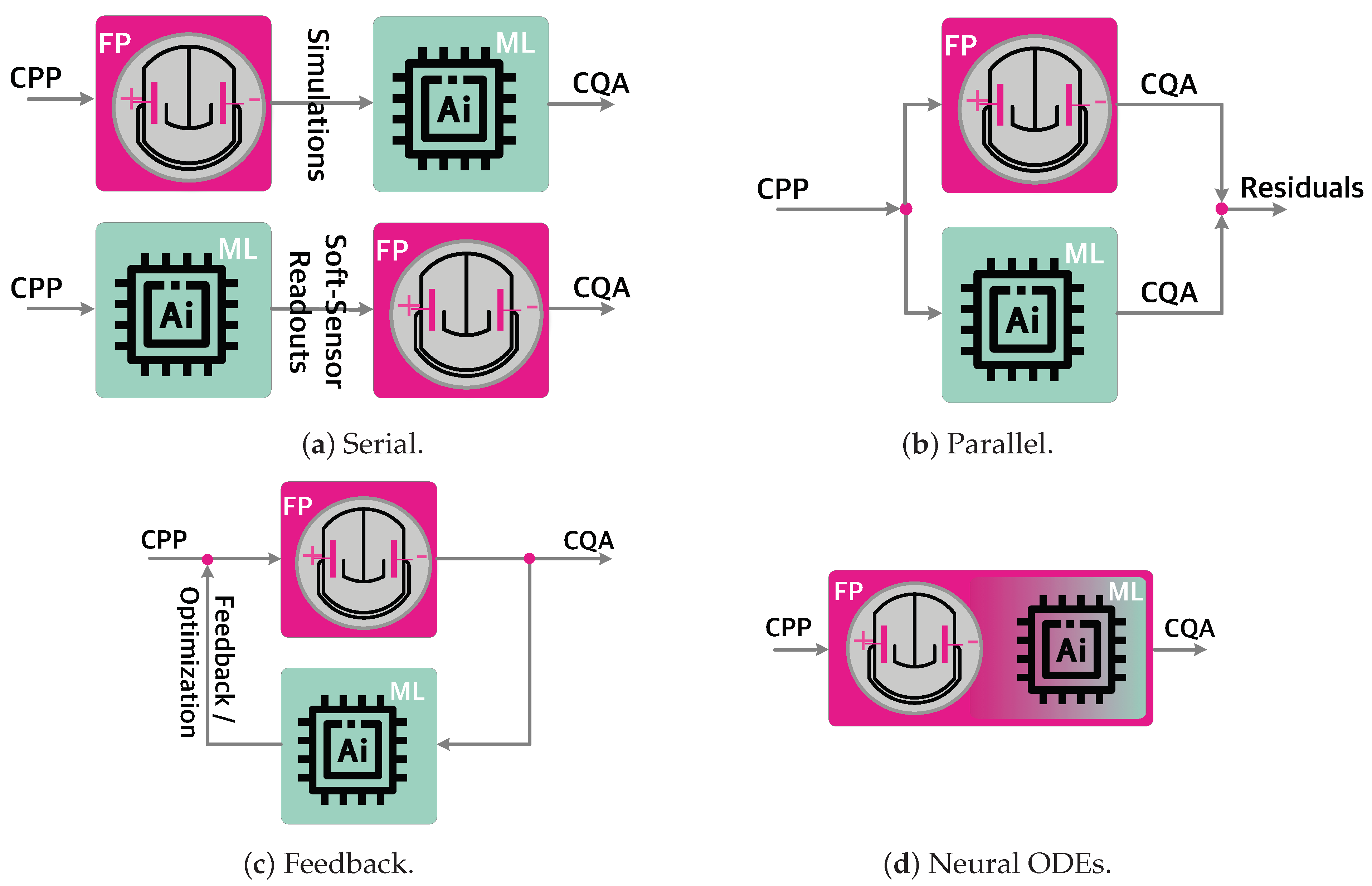
2.1. Hybrid Process Models
2.2. Global Sensitivity Analysis
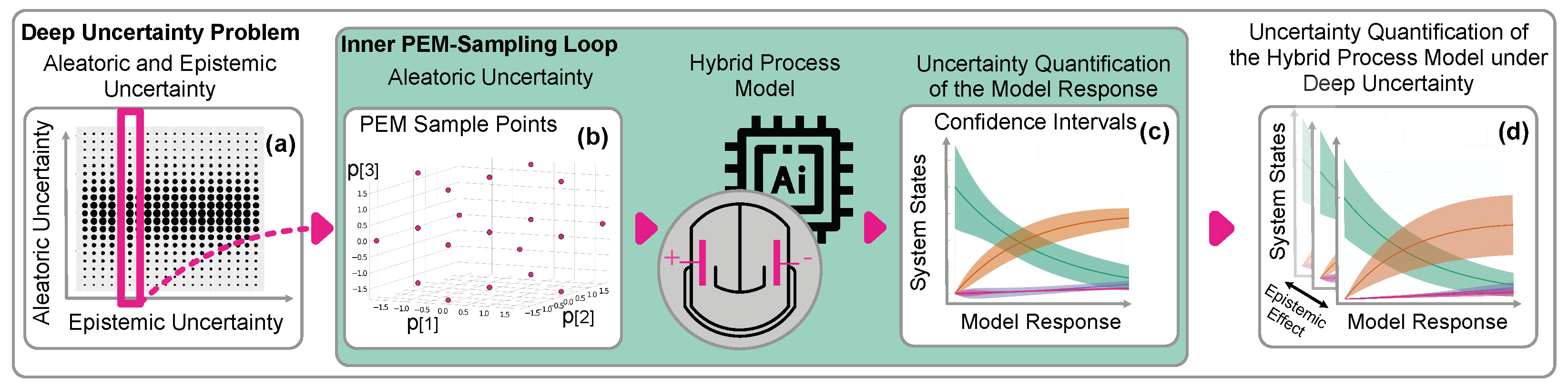
2.3. Deep Uncertainty
2.4. Point Estimate Method
3. Results and Discussion
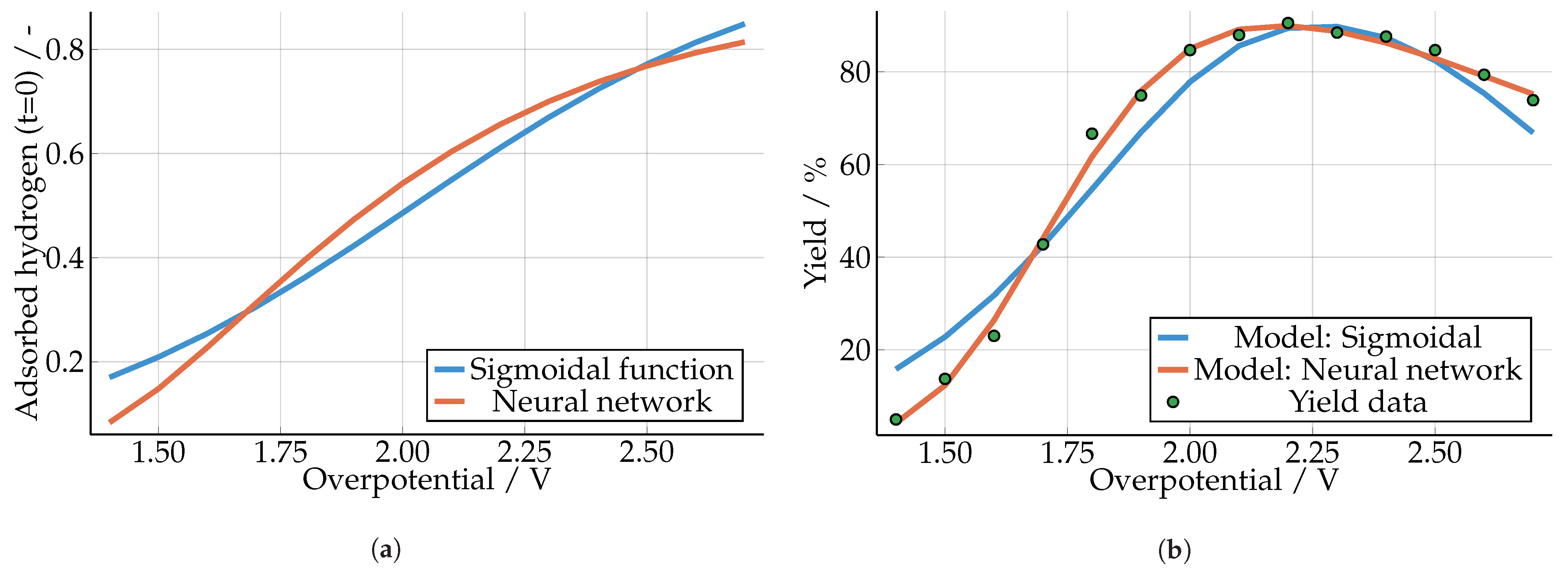
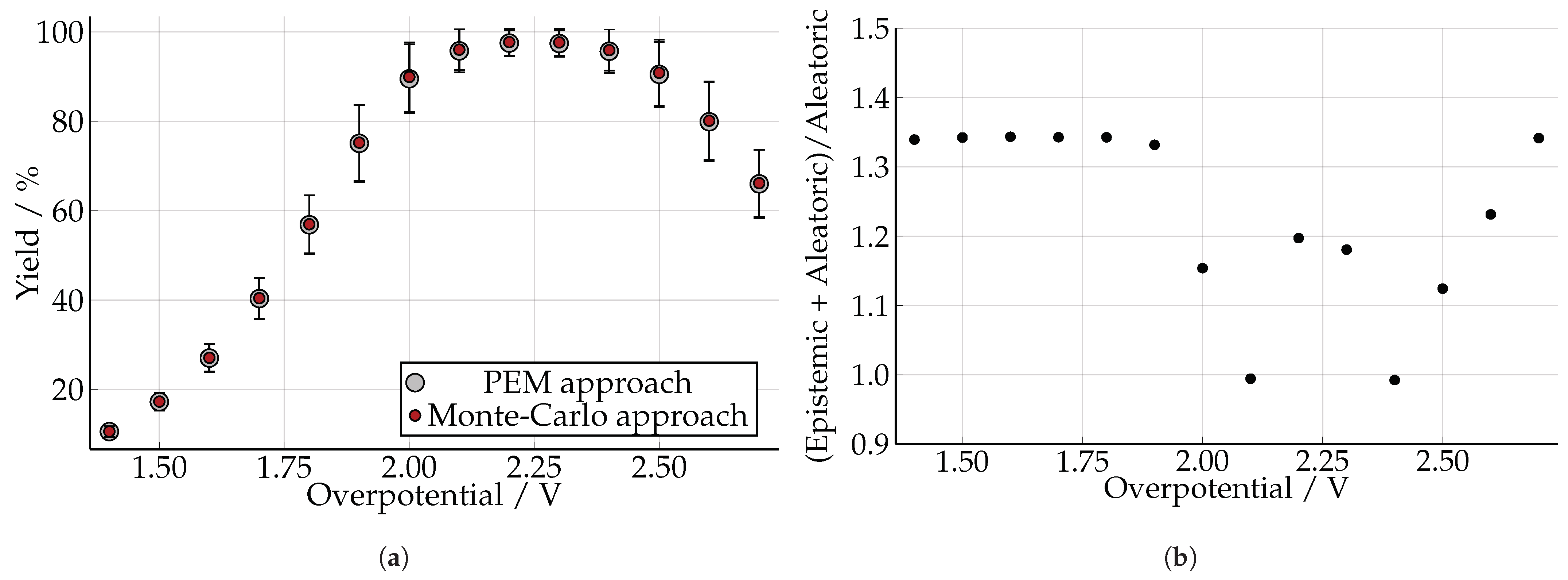
3.1. Furfuryl Alcohol with a Serial Hybrid Model
- The hydrogen fraction of adsorbed hydrogen remains the same during the reaction (continuous reaction and negligible hydrogen evolution).
- There is no formation of additional byproducts such as methyl furan, methyltetrahydrofuran, and tetrahydrofurfuryl alcohol.
- The fraction of the surface area available for the reactions does not change over process time.
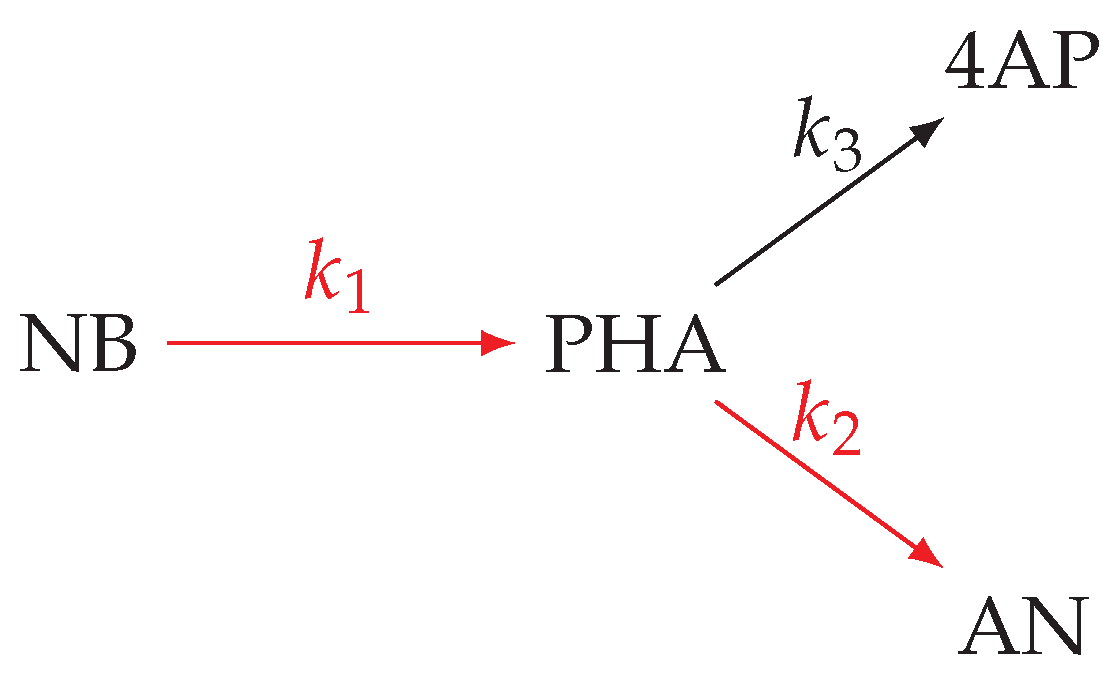
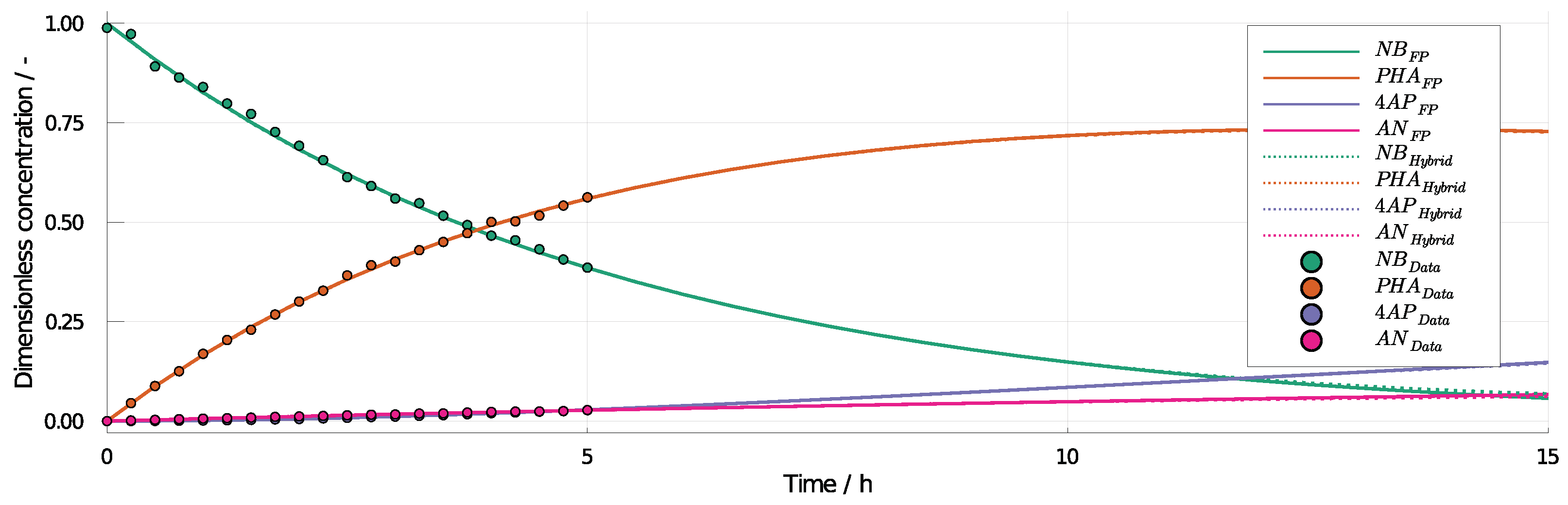
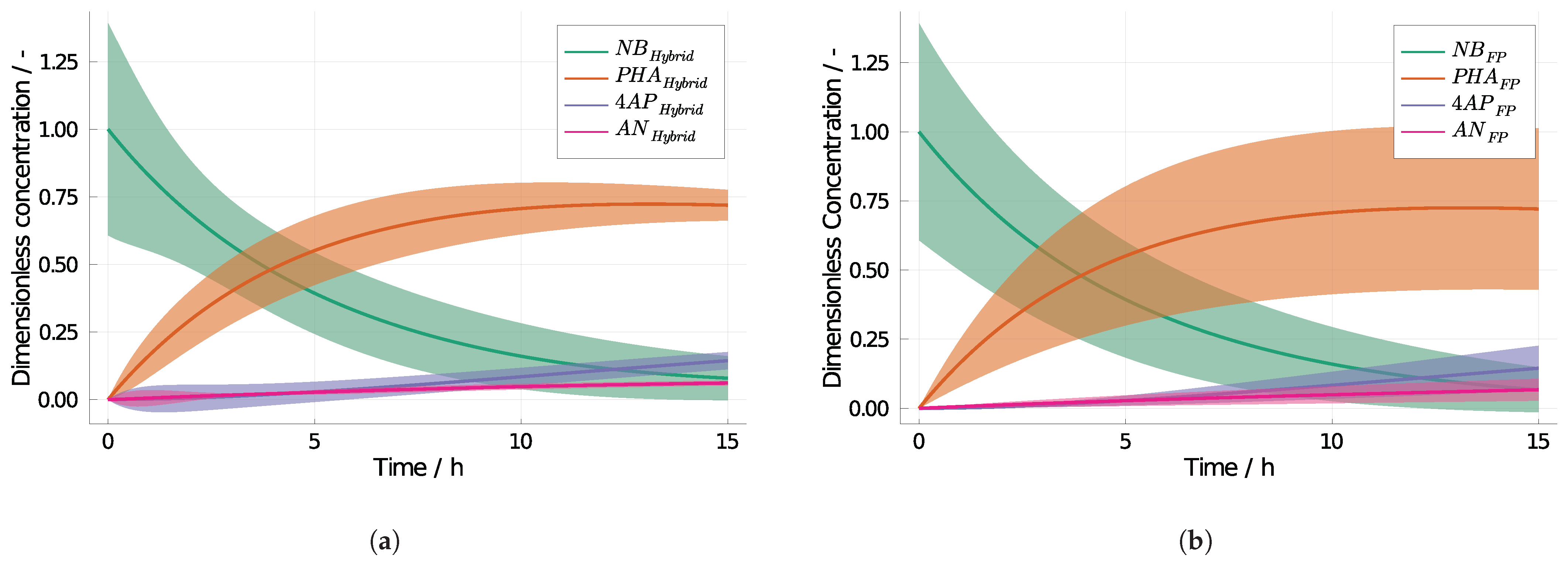
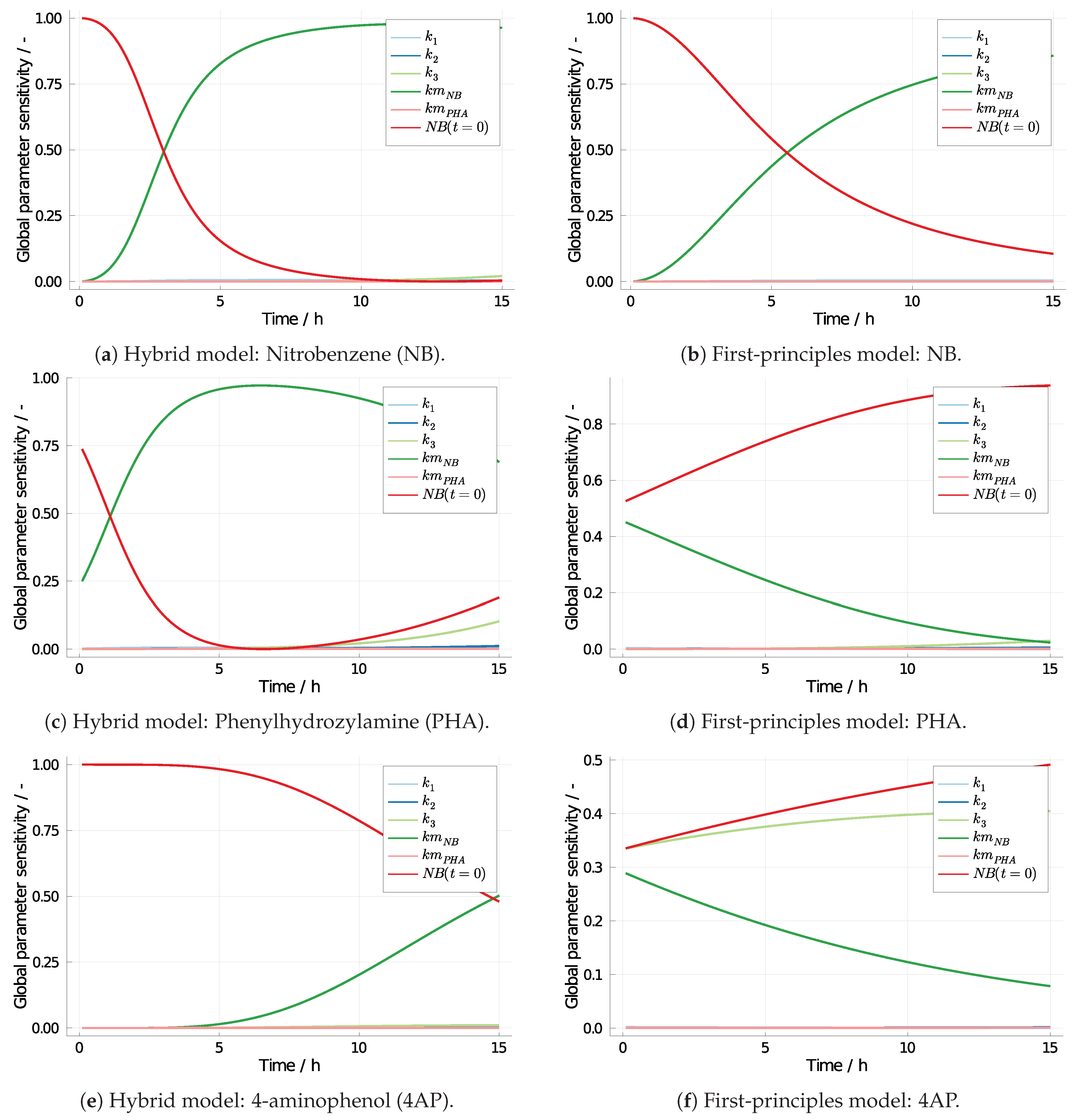
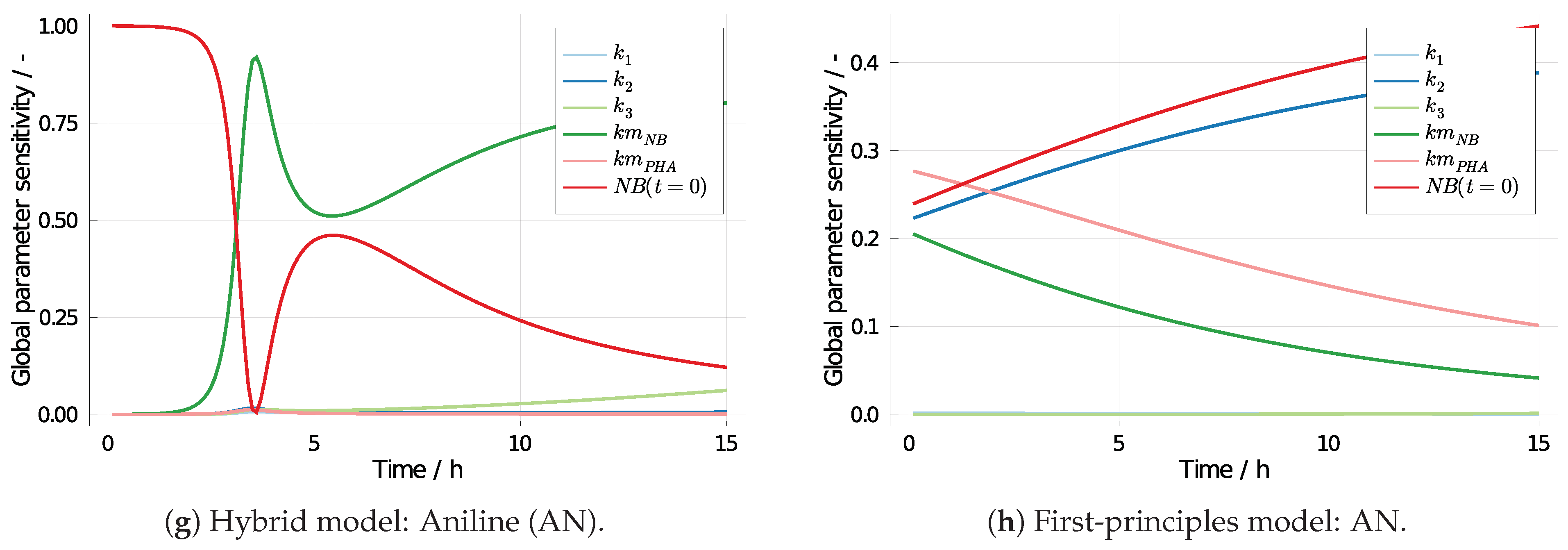
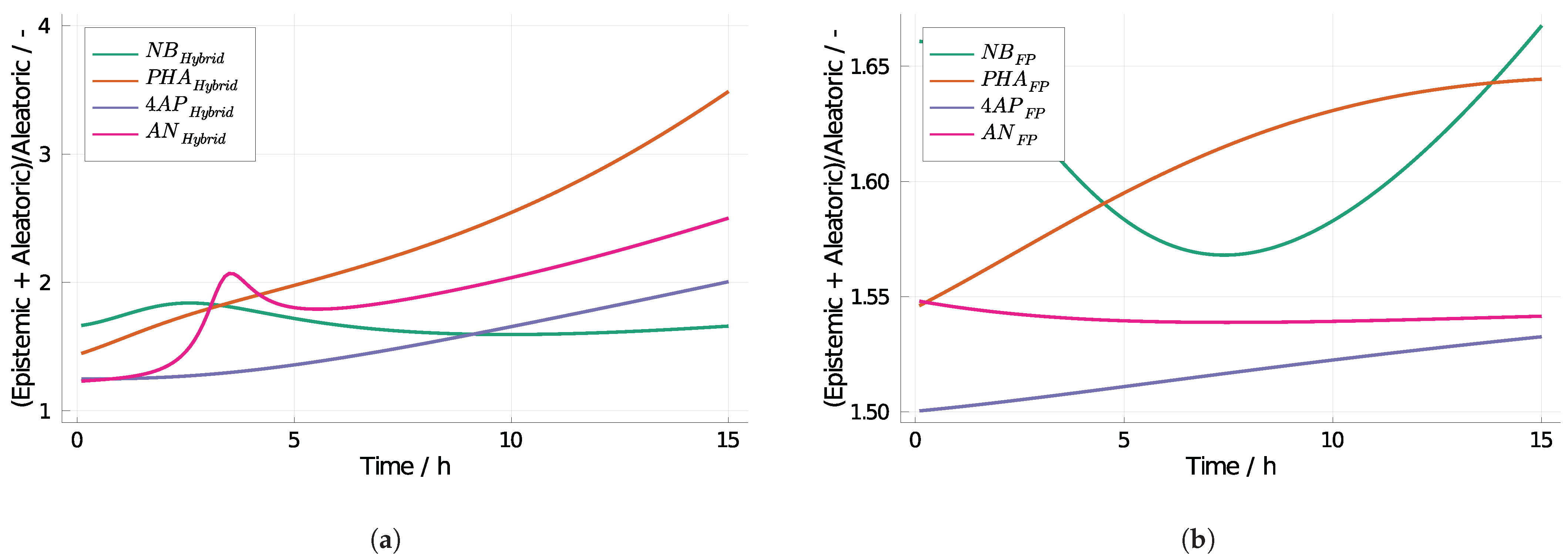
3.2. 4-Aminophenol with Neural Differential Equations
3.3. Computing Effort
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nielsen, R.F.; Nazemzadeh, N.; Sillesen, L.W.; Andersson, M.P.; Gernaey, K.V.; Mansouri, S.S. Hybrid machine learning assisted modelling framework for particle processes. Comput. Chem. Eng. 2020, 140, 106916. [Google Scholar] [CrossRef]
- Schäfer, P.; Caspari, A.; Schweidtmann, A.M.; Vaupel, Y.; Mhamdi, A.; Mitsos, A. The Potential of Hybrid Mechanistic/Data-Driven Approaches for Reduced Dynamic Modeling: Application to Distillation Columns. Chem. Ing. Tech. 2020, 92, 1910–1920. [Google Scholar] [CrossRef]
- Asprion, N.; Böttcher, R.; Pack, R.; Stavrou, M.E.; Höller, J.; Schwientek, J.; Bortz, M. Gray-Box Modeling for the Optimization of Chemical Processes. Chem. Ing. Tech. 2019, 91, 305–313. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, O.; Sampat, C.; Bhalode, P.; Ramachandran, R.; Ierapetritou, M. Digital Twins in Pharmaceutical and Biopharmaceutical Manufacturing: A Literature Review. Processes 2020, 8, 1088. [Google Scholar] [CrossRef]
- Noll, P.; Henkel, M. History and Evolution of Modeling in Biotechnology: Modeling & Simulation, Application and Hardware Performance. Comput. Struct. Biotechnol. J. 2020, 18, 3309–3323. [Google Scholar] [CrossRef]
- Krippl, M.; Dürauer, A.; Duerkop, M. Hybrid modeling of cross-flow filtration: Predicting the flux evolution and duration of ultrafiltration processes. Sep. Purif. Technol. 2020, 248, 117064. [Google Scholar] [CrossRef]
- Cardillo, A.G.; Castellanos, M.M.; Desailly, B.; Dessoy, S.; Mariti, M.; Portela, R.M.C.; Scutella, B.; von Stosch, M.; Tomba, E.; Varsakelis, C. Towards in silico Process Modeling for Vaccines. Trends Biotechnol. 2021. [Google Scholar] [CrossRef]
- Hotvedt, M.; Grimstad, B.; Imsland, L. Identifiability and interpretability of hybrid, gray-box models. arXiv 2020, arXiv:2010.13416. [Google Scholar]
- Feng, J.; Lansford, J.L.; Katsoulakis, M.A.; Vlachos, D.G. Explainable and trustworthy artificial intelligence for correctable modeling in chemical sciences. Sci. Adv. 2020, 6, 1–11. [Google Scholar] [CrossRef]
- Bayer, B.; Striedner, G.; Duerkop, M. Hybrid Modeling and Intensified DoE: An Approach to Accelerate Upstream Process Characterization. Biotechnol. J. 2020, 15, 2000121. [Google Scholar] [CrossRef]
- Kiureghian, A.D.; Ditlevsen, O. Aleatory or epistemic? Does it matter? Struct. Saf. 2009, 31, 105–112. [Google Scholar] [CrossRef]
- Urbina, A.; Mahadevan, S.; Paez, T.L. Quantification of margins and uncertainties of complex systems in the presence of aleatoric and epistemic uncertainty. Reliab. Eng. Syst. Saf. 2011, 96, 1114–1125. [Google Scholar] [CrossRef]
- Zhang, J.; Shields, M.D. On the quantification and efficient propagation of imprecise probabilities resulting from small datasets. Mech. Syst. Signal Process. 2018, 98, 465–483. [Google Scholar] [CrossRef]
- Senge, R.; Bösner, S.; Dembczyński, K.; Haasenritter, J.; Hirsch, O.; Donner-Banzhoff, N.; Hüllermeier, E. Reliable classification: Learning classifiers that distinguish aleatoric and epistemic uncertainty. Inf. Sci. 2014, 255, 16–29. [Google Scholar] [CrossRef]
- Pearce, T.; Leibfried, F.; Brintrup, A.; Zaki, M.; Neely, A. Uncertainty in Neural Networks: Approximately Bayesian Ensembling. arXiv 2018, arXiv:1810.05546. [Google Scholar]
- Hüllermeier, E.; Waegeman, W. Aleatoric and Epistemic Uncertainty in Machine Learning: An Introduction to Concepts and Methods. Mach. Learn. 2019, 110, 1–52. [Google Scholar]
- Salimbeni, H.; Dutordoir, V.; Hensman, J.; Deisenroth, M.P. Deep gaussian processes with importance-weighted variational inference. In Proceedings of the 36th International Conference on Machine Learning, ICML 2019, Long Beach, CA, USA, 9–15 June 2019; pp. 9801–9810. [Google Scholar]
- Faes, M.; Daub, M.; Beer, M. Engineering analysis with imprecise probabilities: A state-of-the-art review on P-boxes. In Proceedings of the 7th Asian-Pacific Symposium on Structural Reliability and its Applications, University of Tokyo, Tokyo, Japan, 5–7 October 2020. [Google Scholar]
- Razavi, S.; Jakeman, A.; Saltelli, A.; Prieur, C.; Iooss, B.; Borgonovo, E.; Plischke, E.; Lo Piano, S.; Iwanaga, T.; Becker, W.; et al. The Future of Sensitivity Analysis: An essential discipline for systems modeling and policy support. Environ. Model. Softw. 2021, 137, 104954. [Google Scholar] [CrossRef]
- Beer, M.; Ferson, S.; Kreinovich, V. Imprecise probabilities in engineering analyses. Mech. Syst. Signal Process. 2013, 37, 4–29. [Google Scholar] [CrossRef]
- Schöbi, R.; Sudret, B. Structural reliability analysis for p-boxes using multi-level meta-models. Probabilistic Eng. Mech. 2017, 48, 27–38. [Google Scholar] [CrossRef]
- Xie, X.; Schenkendorf, R. Robust Process Design in Pharmaceutical Manufacturing under Batch-to-Batch Variation. Processes 2019, 7, 509. [Google Scholar] [CrossRef]
- Schöbi, R.; Sudret, B. Uncertainty propagation of p-boxes using sparse polynomial chaos expansions. J. Comput. Phys. 2017, 339, 307–327. [Google Scholar] [CrossRef]
- Bi, S.; Broggi, M.; Wei, P.; Beer, M. The Bhattacharyya distance: Enriching the P-box in stochastic sensitivity analysis. Mech. Syst. Signal Process. 2019, 129, 265–281. [Google Scholar] [CrossRef]
- Chen, R.T.Q.; Rubanova, Y.; Bettencourt, J.; Duvenaud, D. Neural Ordinary Differential Equations. arXiv 2018, arXiv:1806.07366. [Google Scholar]
- Massaroli, S.; Poli, M.; Park, J.; Yamashita, A.; Asama, H. Dissecting Neural ODEs. arXiv 2020, arXiv:2002.08071. [Google Scholar]
- De Jaegher, B.; Larumbe, E.; De Schepper, W.; Verliefde, A.; Nopens, I. Colloidal fouling in electrodialysis: A neural differential equations model. Sep. Purif. Technol. 2020, 249, 116939. [Google Scholar] [CrossRef]
- Von Stosch, M.; Oliveira, R.; Peres, J.; de Azevedo, S.F. Hybrid semi-parametric modeling in process systems engineering: Past, present and future. Comput. Chem. Eng. 2014, 60, 86–101. [Google Scholar] [CrossRef]
- Qin, S.J.; Chiang, L.H. Advances and opportunities in machine learning for process data analytics. Comput. Chem. Eng. 2019, 126, 465–473. [Google Scholar] [CrossRef]
- Chen, Y.; Ierapetritou, M. A framework of hybrid model development with identification of plant-model mismatch. AIChE J. 2020, 66, 1–16. [Google Scholar] [CrossRef]
- Aykol, M.; Balaji Gopal, C.; Anapolsky, A.; Herring, P.K.; van Vlijmen, B.; Berliner, M.D.; Bazant, M.Z.; Braatz, R.D.; Chueh, W.; Storey, B.D. Perspective—Combining Physics and Machine Learning to Predict Battery Lifetime. J. Electrochem. Soc. 2021. [Google Scholar] [CrossRef]
- Harting, N.; Schenkendorf, R.; Wolff, N.; Krewer, U. State-of-Health identification of Lithium-ion batteries based on Nonlinear Frequency Response Analysis: First steps with machine learning. Appl. Sci. 2018, 8, 821. [Google Scholar] [CrossRef]
- Bhutani, N.; Rangaiah, G.P.; Ray, A.K. First-Principles, Data-Based, and Hybrid Modeling and Optimization of an Industrial Hydrocracking Unit. Ind. Eng. Chem. Res. 2006, 45, 7807–7816. [Google Scholar] [CrossRef]
- Shang, C.; You, F. Data Analytics and Machine Learning for Smart Process Manufacturing: Recent Advances and Perspectives in the Big Data Era. Engineering 2019, 5, 1010–1016. [Google Scholar] [CrossRef]
- Bikmukhametov, T.; Jäschke, J. Combining machine learning and process engineering physics towards enhanced accuracy and explainability of data-driven models. Comput. Chem. Eng. 2020, 138. [Google Scholar] [CrossRef]
- Chen, Z.S.; Zhu, Q.X.; Xu, Y.; He, Y.L.; Su, Q.L.; Chen, Z.S. Integrating virtual sample generation with input-training neural network for solving small sample size problems: Application to purified terephthalic acid solvent system. Soft Comput. 2021, 4. [Google Scholar] [CrossRef]
- Lee, J.H.; Shin, J.; Realff, M.J. Machine learning: Overview of the recent progresses and implications for the process systems engineering field. Comput. Chem. Eng. 2018, 114, 111–121. [Google Scholar] [CrossRef]
- Petsagkourakis, P.; Sandoval, I.O.; Bradford, E.; Zhang, D.; del Rio-Chanona, E.A. Reinforcement learning for batch bioprocess optimization. Comput. Chem. Eng. 2020, 133, 106649. [Google Scholar] [CrossRef]
- Lüthje, J.T.; Schulze, J.C.; Caspari, A.; Mhamdi, A.; Mitsos, A.; Schäfer, P. Adaptive Learning of Hybrid Models for Nonlinear Model Predictive Control of Distillation Columns. arXiv 2020, arXiv:2011.12798. [Google Scholar]
- Chen, R.T.; Rubanova, Y.; Bettencourt, J.; Duvenaud, D.K. Neural ordinary differential equations. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 6571–6583. [Google Scholar]
- Rackauckas, C.; Ma, Y.; Martensen, J.; Warner, C.; Zubov, K.; Supekar, R.; Skinner, D.; Ramadhan, A. Universal differential equations for scientific machine learning. arXiv 2020, arXiv:2001.04385. [Google Scholar]
- Teshima, T.; Tojo, K.; Ikeda, M.; Ishikawa, I.; Oono, K. Universal Approximation Property of Neural Ordinary Differential Equations. arXiv 2020, arXiv:2012.02414. [Google Scholar]
- Arnold, F.; King, R. State–space modeling for control based on physics-informed neural networks. Eng. Appl. Artif. Intell. 2021, 101, 104195. [Google Scholar] [CrossRef]
- Champion, K.; Lusch, B.; Kutz, J.N.; Brunton, S.L. Data-driven discovery of coordinates and governing equations. Proc. Natl. Acad. Sci. USA 2019, 116, 22445–22451. [Google Scholar] [CrossRef]
- Quaghebeur, W.; Nopens, I.; De Baets, B. Incorporating Unmodeled Dynamics Into First-Principles Models Through Machine Learning. IEEE Access 2021, 9, 22014–22022. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A fresh approach to numerical computing. SIAM Rev. 2017, 59, 65–98. [Google Scholar] [CrossRef]
- Innes, M.; Saba, E.; Fischer, K.; Gandhi, D.; Rudilosso, M.C.; Joy, N.M.; Karmali, T.; Pal, A.; Shah, V. Fashionable Modelling with Flux. arXiv 2018, arXiv:1811.01457. [Google Scholar]
- Innes, M. Flux: Elegant Machine Learning with Julia. J. Open Source Softw. 2018. [Google Scholar] [CrossRef]
- Rackauckas, C.; Innes, M.; Ma, Y.; Bettencourt, J.; White, L.; Dixit, V. Diffeqflux.jl-A julia library for neural differential equations. arXiv 2019, arXiv:1902.02376. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Saltelli, A.; Ratto, M.; Tarantola, S.; Campolongo, F. Sensitivity analysis for chemical Models. Chem. Rev. 2005, 105, 2811–2828. [Google Scholar] [CrossRef]
- Joshi, M.; Seidel-Morgenstern, A.; Kremling, A. Exploiting the bootstrap method for quantifying parameter confidence intervals in dynamical systems. Metab. Eng. 2006, 8, 447–455. [Google Scholar] [CrossRef]
- Krausch, N.; Barz, T.; Sawatzki, A.; Gruber, M.; Kamel, S.; Neubauer, P.; Cruz Bournazou, M.N. Monte Carlo Simulations for the Analysis of Non-linear Parameter Confidence Intervals in Optimal Experimental Design. Front. Bioeng. Biotechnol. 2019, 7, 1–16. [Google Scholar] [CrossRef]
- van de Schoot, R.; Depaoli, S.; King, R.; Kramer, B.; Märtens, K.; Tadesse, M.G.; Vannucci, M.; Gelman, A.; Veen, D.; Willemsen, J.; et al. Bayesian statistics and modelling. Nat. Rev. Methods Primers 2021, 1. [Google Scholar] [CrossRef]
- Faes, M.; Daub, M.; Marelli, S.; Patelli, E.; Beer, M. Engineering Analysis with Probability Boxes: A Review on Computational Methods. Preprint submitted to Elsevier. 2021. [Google Scholar]
- Lerner, U.N. Hybrid Bayesian Networks for Reasoning about Complex Systems. Technical Report. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2002. [Google Scholar]
- Schenkendorf, R.; Xie, X.; Rehbein, M.; Scholl, S.; Krewer, U. The Impact of Global Sensitivities and Design Measures in Model-Based Optimal Experimental Design. Processes 2018, 6, 27. [Google Scholar] [CrossRef]
- Laue, V.; Schmidt, O.; Dreger, H.; Xie, X.; Röder, F.; Schenkendorf, R.; Kwade, A.; Krewer, U. Model-Based Uncertainty Quantification for the Product Properties of Lithium-Ion Batteries. Energy Technol. 2019, 8, 1900201. [Google Scholar] [CrossRef]
- Xie, X.; Krewer, U.; Schenkendorf, R. Robust optimization of dynamical systems with correlated random variables using the point estimate method. IFAC-PapersOnLine 2018, 51, 427–432. [Google Scholar] [CrossRef]
- Kwon, Y.; Schouten, K.J.P.; van der Waal, J.C.; de Jong, E.; Koper, M.T.M. Electrocatalytic Conversion of Furanic Compounds. ACS Catal. 2016, 6, 6704–6717. [Google Scholar] [CrossRef]
- Lasia, A. Influence of adsorption of organic compounds and surface heterogeneity on the hydrogen evolution reaction. Can. J. Chem. 1997, 75, 1615–1623. [Google Scholar] [CrossRef]
- Cao, Y.; Noël, T. Efficient Electrocatalytic Reduction of Furfural to Furfuryl Alcohol in a Microchannel Flow Reactor. Org. Process Res. Dev. 2019, 23, 403–408. [Google Scholar] [CrossRef] [PubMed]
- Vaidya, M.J.; Kulkarni, S.M.; Chaudhari, R.V. Synthesis of p-Aminophenol by Catalytic Hydrogenation of p-Nitrophenol. Org. Process Res. Dev. 2003, 7, 1083–6160. [Google Scholar] [CrossRef]
- Tranchant, M.; Serrà, A.; Gunderson, C.; Bertero, E.; García-Amorós, J.; Gómez, E.; Michler, J.; Philippe, L. Efficient and green electrochemical synthesis of 4-aminophenol using porous Au micropillars. Appl. Catal. A Gen. 2020, 602, 117698. [Google Scholar] [CrossRef]
- Bakshi, R.; Fedkiw, P. Optimal time-varying potential control. J. Appl. Electrochem. 1993, 23, 715–727. [Google Scholar] [CrossRef]
- Bakshi, R.; Fedkiw, P. Optimal time-varying cell-voltage control of a parallel-plate reactor. J. Appl. Electrochem. 1994, 24, 1116–1123. [Google Scholar] [CrossRef]
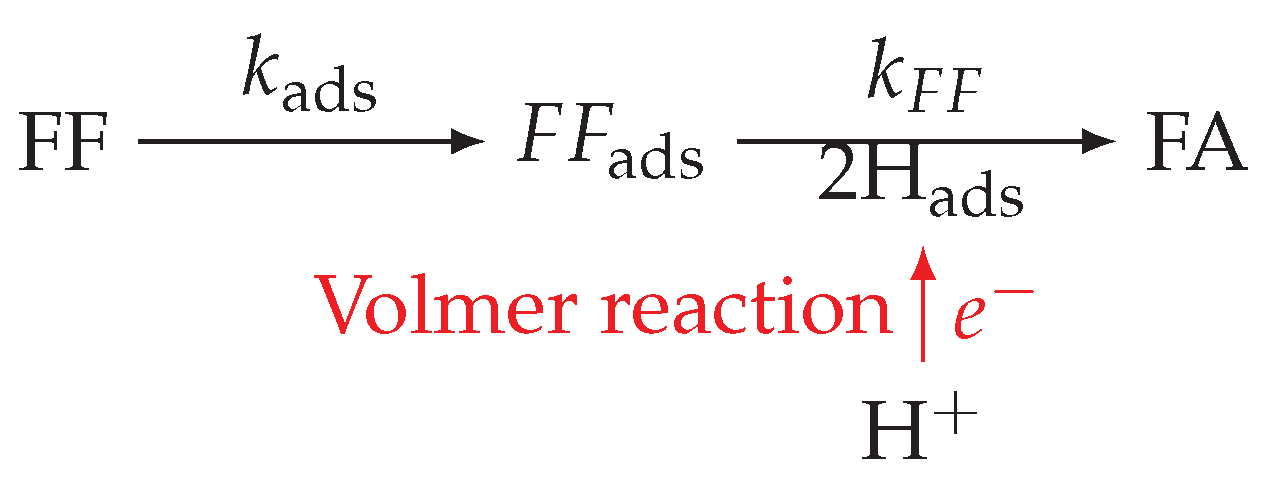
| Parameter | C | |||||
|---|---|---|---|---|---|---|
| Value | 0.5969 | 0 | Equation (17) | |||
| Unit | cm s−1 | s−1 | - | mol cm−3 | mol cm−3 | - |
| Parameter | Mean | Standard Deviation |
|---|---|---|
| [0.5372, 0.6566] | [0.0537, 0.0656] | |
| [5.07 , 6.20 ] | [0.50 , 0.62 ] | |
| C | [1.4 , 1.7 ] | [1.4 , 1.7 ] |
| Parameter | a | ||||||
| Value | 0.693 | 0.398 | 0.02 | 0.5 | |||
| Unit | cm s−1 | cm s−1 | s−1 | - | - | / | |
| Parameter | f | NB (t = 0) | PHA (t = 0) | 4AP (t = 0) | AN (t = 0) | ||
| Value | 38.66 | 1 | 0 | 0 | 0 | ||
| Unit | cm s−1 | cm s−1 | V−1 | - | - | - | - |
| Parameter | Mean | Standard Deviation |
|---|---|---|
| [, ] | [, ] | |
| [, ] | [, ] | |
| [, ] | [, ] | |
| [, ] | [, ] | |
| [, ] | [, ] | |
| [0.8, 1.2] | [0.08, 0.12] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Francis-Xavier, F.; Kubannek, F.; Schenkendorf, R. Hybrid Process Models in Electrochemical Syntheses under Deep Uncertainty. Processes 2021, 9, 704. https://doi.org/10.3390/pr9040704
Francis-Xavier F, Kubannek F, Schenkendorf R. Hybrid Process Models in Electrochemical Syntheses under Deep Uncertainty. Processes. 2021; 9(4):704. https://doi.org/10.3390/pr9040704
Chicago/Turabian StyleFrancis-Xavier, Fenila, Fabian Kubannek, and René Schenkendorf. 2021. "Hybrid Process Models in Electrochemical Syntheses under Deep Uncertainty" Processes 9, no. 4: 704. https://doi.org/10.3390/pr9040704
APA StyleFrancis-Xavier, F., Kubannek, F., & Schenkendorf, R. (2021). Hybrid Process Models in Electrochemical Syntheses under Deep Uncertainty. Processes, 9(4), 704. https://doi.org/10.3390/pr9040704






