Abstract
Forty years after the discovery of metallocene catalysts, there are still several aspects that remain unresolved, especially when the “conventional” alkylaluminum activators are not used. Herein, we systematically investigated the synthesis of polyethylene (PE) via three different zirconocene catalysts, with different alkyl substituents, activated via different organoboron compounds. The polymerization behavior, as well as the properties of the materials, were evaluated. The results demonstrate that the highest catalytic activity is shown by bis(cyclopentadienyl)dimethylzirconium activated by trityl tetra(pentafluorophenyl)borate. Additionally, it was found that toluene is the optimum solvent for these systems and at these reaction conditions. Moreover, to validate our experimental results, a comprehensive mathematical model was developed on the basis of thermodynamic and kinetic principles. The concentration of ethylene transferred to the solvent phase (toluene) in a liquid–vapor equilibrium (LVE) system was estimated based on Duhem’s theorem. Arrhenius expressions for the kinetic rate constants of a proposed kinetic mechanism were estimated by a kinetic model, in which the rate of polymerization was fitted by a least-square optimization procedure and the molecular weight averages by the method of moments. The simulations of the coordination polymerization suggest the presence of two types of active sites, principally at low temperatures, and the reactivation of the deactivated sites via a boron-based activator. However, the effect of the temperature on the reactivation step was not clear; a deeper understanding via designed experiments is required.
1. Introduction
Polyethylene (PE), one of the most used and commercialized thermoplastics in the world, is produced by the polymerization of ethylene which is catalyzed via two main different routes: using heterogeneous processes with Ziegler–Natta catalysts, or via metallocene catalytic systems. Since the discovery of the catalytic activity of the homogenous catalysts based on biscyclopentadienyl titanium or zirconium dialkyl systems in the ethylene polymerization in the 1980s by Kaminsky and Sinn [1,2,3,4], metallocene systems have revolutionized the polyolefins field, because they enable the production of PE with narrow molecular weight distributions, low content of extractables, good processability, and superior properties [5]. Moreover, metallocene catalysts, in comparison to Ziegler–Natta types, show a single type of active site, which enables predictions of the properties of the resulting polymers.
Several factors play an important role in the olefin’s polymerization via metallocene catalysis. For instance, the formation of weakly coordinating anions with a weak bonding to the metallocene active centers (acting as co-catalysts). The anions interact with the cationic metal species, in the reaction medium, creating active sites (ion-pairs), followed by the subsequent polymerization. Methylaluminoxane (MAO) is a popular activator due to its high efficiency; however, a large excess of MAO is usually required, and, despite extensive efforts, its detailed active-site structure has not yet been fully elucidated [6,7,8]. A prominent alternative to replace MAO is the use of other bulky coordinating anions such as organoboranes, e.g., tris(pentafluorophenyl)borane (B1) [9,10], and organoborates such as N,N-dimethylanilinium tetra(pentafluorophenyl)borate (B2) or trityl tetra(pentafluorophenyl)borate (B3) [11,12]. These types of activators can ionize the metallocene (pre-alkylated) catalyst, acting as Lewis acids, leading to excellent active cationic metallocene catalysts for the polymerization of olefins in quasi-equimolar amounts between the metallocene catalyst and the boron-based activator, and resulting in catalytic complexes with a definite chemical structure [13,14,15]. A breakthrough in this field was the introduction of the weakly coordinating tris(pentafluorophenyl)borate [B(C6F5)3] as a counterion, which can abstract a methyl group from the alkylated metallocene catalyst, to form ionic species such as [CP2ZrMe]+[MeB(C6F5)3]−, followed by the coordination of a monomer molecule and subsequent propagation [10]. Nevertheless, residual coordinative interactions between the activated metal center and the anion, via the abstracted methyl group, can slightly decrease the catalyst reactivity. Ionic organoboron activators, such as [C6H5NHMe2]+[B(C6F5)4]− and [(C6H5)3C]+[B(C6F5)4]−, on the other hand, avoid this form of ion–ion contact between the abstracted methyl group and the transition metal atom, while the cationic species takes the function of activating the metal active center (Figure 1).
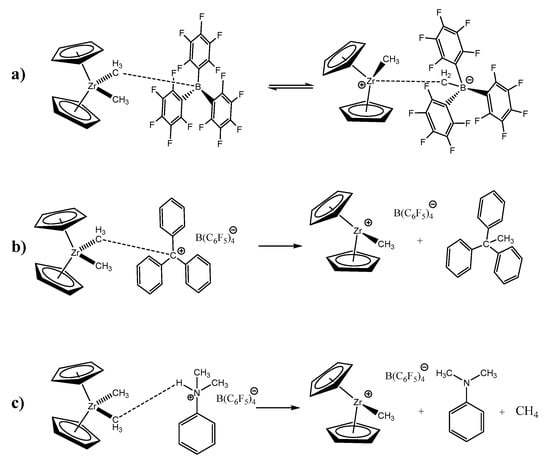
Figure 1.
Schematic representation of the activation of a zirconocene catalyst (CP2ZrCl2) by (a) [B(C6F5)3], (b) [(C6H5)3C]+[B(C6F5)4]− and (c) [C6H5NHMe2]+[B(C6F5)4]−.
There are a wide variety of metallocene catalysts with different symmetries and substitutions, because the configuration of the catalyst is another factor governing polymerization behavior. For instance, the steric and electronic environment of ligand substituents of the metal catalyst, as well as the ion–ion interactions between the electrophilic metal and the counterion, are critical factors that can dramatically alter the polymerization behavior due to steric hindrance and electronic factors.
Several works have previously studied this behavior. For instance, Ewen and Chien [13,16], studied the effect of different alkyl substituents in cyclopentadienyl (CP) groups for several zirconocene (Zr) catalysts, reporting the following behavior in terms of catalyst efficiency: (MeCP)2ZrCl2 > (EtCP)2ZrCl2 > CP2ZrCl2 > (Me5CP)CPZrCl2. Through this, they concluded that single alkyl substituents increase the catalytic activity due to electro donating effects, while the steric hindrance of bulky substituents has a detrimental effect instead. Zr-based catalysts have been also studied in heterogeneous systems for ethylene polymerizations; for example, Charles et al. reported ethylene polymerization using catalysts derived from the activation of Zr aluminohydride complexes, supported on silica, which was previously treated with MAO. The results were compared with those using the more traditional Zr dichloro complexes, finding higher activity in the former [17]. Zeolites (ZSM-5) [18], and solid polymethylaluminoxane [19] are among the supports reported for carrying out ethylene polymerizations catalyzed by Zr-based metallocenes, achieving high catalytic activities, high molecular weights, and narrow distributions. Although these works provide general features about the influence of the alkyl groups on the ligand substituents, and the influence of using solid supports during the polymerization, they were all carried out using MAO as the activator.
Few works have studied in-detail the ethylene polymerization behavior when the metallocene is activated by the bulky, weakly-coordinating organoboron anions (B). In this sense, our research group reported the use of tris(pentafluorophenyl)borane and N,N-dimethylanilinium tetrakis(pentafluorophenyl)borate (B1 and B2 in this work, respectively) to act in conjunction with MAO as activators on ethylene polymerization by using the catalyst CP2ZrCl2. The addition of these organoboron compounds of ionic and nonionic nature in a molar ratio B1(or B2)/Zr = 5 promoted a partial deactivation of the catalyst, causing a reduction in the catalytic activity; however, the crystallinity degree, as well as the macromolecular, thermal, and dynamic-mechanical properties of the obtained polyethylenes were improved, especially with B1 as co-activator in this evaluated catalytic system [14]. In the same context, González-Hernández et al. [19] reported the ethylene polymerization using catalysts derived from Zr aluminohydride complexes activated with tris(pentafluorophenyl)borane (B1), although with limited utility (catalytic activity) of these catalysts systems when compared with the corresponding use of MAO as the activator. Supported zirconocene catalysts activated by boron compounds for olefin polymerizations are not as widely reported in the literature, but there are some related works such as that reported by Charoenchidet et al. who treated silica with tris(pentafluorophenyl)borane (B1 in this work) to produce borane-functionalized support, which was then used as a support and co-catalyst for the CP2ZrCl2, CP2ZrCl2/Triisobutylaluminum (TIBA), CP2Zr(CH3)2 and CP2Zr(CH3)2/TIBA catalyst systems for ethylene polymerizations. The activations of the catalysts were carried out in two ways: pre-activation, and in situ activation. The pre-activated and in situ-activated metallocene systems produced PE with Mw between 96 and 154 Kg mol−1, and dispersity index (Ð) around 3. The bulk density of PE products was higher for the in situ-activated systems, but there was no significant difference between the products of both types of zirconocenes [20].
On the other hand, the kinetics of the catalyst coordination polymerization has been previously simulated, however a low number of reports can be found, compared to free-radical polymerization systems. Chien and Wang [13] reported the first kinetic model to study polymerization using zirconocene dichloride (CP2ZrCl2) and MAO as the catalyst and co-catalyst, respectively. The kinetic mechanism proposed the chain transfer to MAO, β-hydride chain transfer, multiple types of active sites, and deactivation step. Estrada and Hamielec [21] developed a model with two types of active sites, where the first one experienced a gradual transition (a state change) to the second type; this step was supported on the bimodal molecular weight distribution observed in the size exclusion chromatography (SEC) measurements. Both models did not provide an estimation of the ethylene concentration in the liquid phase. Moreover, Jiang et al. [22] carried out a comparative study between different models: in one of them, the reactivation of MAO was included as part of the kinetic mechanism, resulting in better agreement with the experimental polymerization rate profiles. A strategy of parameter estimation was reported by Ahmadi et al., in which a multivariable nonlinear optimization problem was solved using the Nelder–Mead simplex method [23]. The methodology combined the numerical solution of the kinetic model with the optimization algorithm, resulting in good agreement with the experimental data. Mehdiabadi and Soares [24] carried out a semi-batch reaction of a constrained geometry catalyst with MAO, and a kinetic model was proposed and then refined based on monomer uptake curves and polymer yield data. The deactivation of the catalyst/MAO system during ethylene polymerization was of the first order; the mechanism also included reversible activation and deactivation with MAO. The mechanism described the full kinetic picture. To the best knowledge of the authors, no study exists dealing with the modeling of zirconocene catalyst coordination polymerization using organoboron activators.
In this work, we aim to provide insights into the polymerization of ethylene catalyzed by Zr catalysts activated by organoboron compounds. Three Zr-based catalysts, with different ligand substituents, activated by three different organoboron compounds (B1, B2, and B3), were used for the PE synthesis. This work is focused on establishing the relationship between the catalytic system configuration with the polymerization behavior and with the final properties of the resultant polymers, in terms of molecular weight characteristics, crystallinity, and thermal behavior. Furthermore, the catalytic system leading to the highest catalytic activity was further analyzed, employing different solvents to elucidate the role over the features of the polymers. Moreover, a kinetic mechanism is proposed for the B3/Zr catalytic system, based on previous studies of MAO, and a mathematical model has been developed to estimate the kinetic rate coefficients of the two types of active species in the propagation, the chain transfer to monomer, polymer transition, spontaneous deactivation, and reactivation steps. With the knowledge of the kinetic parameters, the catalytic system is deeply studied, and some unexpected behaviors are analyzed.
2. Materials and Methods
2.1. Materials
All manipulations were carried out under an inert atmosphere using an MBraun glove box or via standard Schlenk techniques. Toluene, hexane, heptane, and isooctane were purchase from Sigma Aldrich (anhydrous grade) and were distilled twice from sodium and benzophenone before use. Bis(cyclopentadienyl)dimethyl zirconium (97%) (CP2Zr(CH3)2), dimethylbis(t-butylcyclopentadienyl)zirconium (97%) ((t-butyl-CP)2Zr(CH3)2) and dimethylbis(indenyl)zirconium (97%) ((ind)2Zr(CH3)2) were purchased from Sigma Aldrich and were used as received. Tris(pentafluorophenyl)borane (95%) (B(C6F5)3), N,N-dimethylanilinium tetra(pentafluorophenyl)borate (98%) ([C6H5N(CH3)2H]+[B(C6F5)4]−) and trityl tetrakis(pentafluorophenyl)borate (97%) ([(C6H5)3C]+[B(C6F5)4]−) were supplied by Strem Chemicals and were used as received. Polymer-grade ethylene was purchased from Praxair and was purified by passing it through 3–4 Å activated molecular sieves.
2.2. Polymerization Reactions
All polymerizations were performed in a 1 L stainless steel Parr reactor through the following procedure: three vacuum–argon cycles were first undertaken at 150 °C before the reaction to eliminate any traces of moisture. Then, the reactor was cooled down to room temperature and filled with 200 mL of solvent under an argon atmosphere. The reactor stirring system was set at 100 rpm and it was heated to 50 °C. The catalyst system was then fed into the reactor as follows: (i) boron compound solution (B) in 5 mL of toluene; (ii) metal catalyst solution in 5 mL of toluene. In all cases, 12.8 mmol of zirconium catalyst (Zr) was employed, and the B/Zr molar ratio was fixed to 2.5. The polymerizations were then initiated by introducing the ethylene monomer to the reactor at a continuous flow. All experiments were performed at an ethylene pressure of 1 bar and for 45 min. The reactions were terminated by the addition of acidified methanol. The resultant polymers were filtered off, washed with methanol, and vacuum dried.
2.3. Characterization
The molecular weight characteristics were determined by high-temperature size exclusion chromatography (SEC) with an Alliance chromatograph (GPC V-2000) equipped with two on-line detectors: a differential viscometer and refractometer, using three linear columns, PLgel 10 µm MIXED-B. The calibration was conducted under polystyrene standards using 1,2,4-trichlorobencene as eluent, and the measurements were carried out at a flow rate of 1 mL/min at 140 °C. The molar mass number and weight averages of the different polymers relative to polystyrene standards were corrected using the well-known principle of universal calibration employing the unique parameters for the Mark–Houwink–Sakurada equation for polyethylene: K = 0.000323 dL/g and a = 0.735. The melting temperature and crystallinity degree of the polymers was measured by differential scanning calorimetry (DSC), where the different thermograms were obtained through a TA instrument DSC 2920 at a heating rate of 10 °C/min under an inert atmosphere. Each sample was heated twice to eliminate the thermal history.
3. Mathematical Modeling
3.1. Kinetic Scheme
As the first approach to understand the mechanism, the following kinetic scheme is proposed in the ethylene polymerization in the work of Estrada and Hamielec [21] and Jiang [22].
To maintain the simplicity of the mechanism, here we considered that the complete catalyst has been instantaneously activated, producing the total concentration of the active sites (CAct); other works have used the named Instantaneous Initiation Hypothesis [25]. As shown in Figure 2, the monomer addition to active sites results in polymeric chains, which are denoted as the active polymer of type 1, (Pr,1, where r is the degree of polymerization of the active polymer of type 1). In the propagation step, these active species add monomers in the chains, increasing the degree of polymerization. Estrada and Hamielec [21] firstly assumed the gradual transition of the active polymer of type 1 (Pr,1) to the active polymer of type 2 (Pr,2) in the catalyst coordination systems. The transition reaction is supported in ethylene polymerization via zirconocene/organoboron catalysts by the two polymeric populations found in the deconvolution of the SEC signal, as will be discussed later. Additionally, species Pr,2 increases their chain length by propagation. Both active polymer types can undergo a chain transfer to monomer reaction by the abstraction of a proton H from a monomer molecule to the active polymer of type 1 or 2, obtaining a dead polymer (Dr,i, where i denotes the polymer type) and an active polymer type either 1 or 2 with one monomeric unit in the chain. The deactivation of Pr,1 is negligible, and therefore only Pr,2 is spontaneously deactivated, which can present a reactivation by catalyst and monomer, similarly to MAO cocatalyst polymerization.
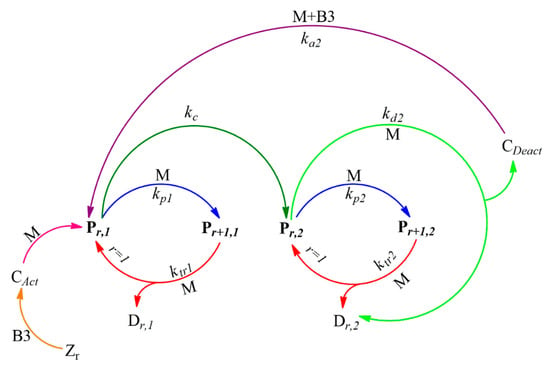
Figure 2.
Proposed kinetic mechanism for the ethylene polymerization by zirconocene catalysts and organoboron activators. Kinetic parameters: kpi denotes the propagation rate constant for active polymer type i; ktri denotes the transfer chain to monomer rate constant for active polymer type i; kc is the transition rate constant form Pr,1 to Pr,2; kd2 is the spontaneous deactivation rate constant of active polymer type 2; and ka2 is the re-activation of CDeact species, via the reaction with M and B3. The description of each species appears in the text.
3.2. Population Balance Equations
The population mass balances for each species are derived from the kinetic scheme previously described: active sites (CAct), deactivated sites (CDeact), active polymer type 1 or 2 (Pr,1, and Pr,2, respectively) and dead polymer type 1 or 2 (Dr,1 and Dr,2, respectively) have been considered in this work, in Equations (S1)–(S8) shown in the Supplementary Materials.
Polymerization rate Rp, Equation (1), is principally based on the monomer consumed by the propagation, and the long chain hypothesis (LCH) is assumed; therefore, the monomer consumption in the initiation and reactivation steps is negligible. The contribution of the chain transfer to the monomer is also discarded, because , as has been estimated in other coordination polymerization systems.
The monomer is fed on demand to keep constant pressure; therefore, the ethylene concentration is almost constant with time (dM/dt = 0), and as a result, the course of the polymerization rate throughout the reaction can be directly tracked in the flowmeter measurements.
A polymerization rate model of the kinetic mechanism presented in this study, Figure 2, was reported by Jiang et al. [22] (Equation (2)), named herein as Model 1.
where = kp1[M]l, = kp2[M]l, and = ka[B][M]l
If the reactivation step of the deactivated sites is negligible, Equation (2) is transformed into Equation (3), as reported by Vela-Estrada et al. [21] and named as Model 2.
3.3. Liquid–Vapor Equilibrium (LVE)
The concentration of ethylene transferred to the liquid phase ([M]l) in a liquid–vapor equilibrium (LVE) system is estimated based on Duhem’s theorem, in which a T, P-flash calculation was developed. We assumed that toluene at a pressure (P) equal or lower than its bubble-point pressure (PBubl), Equation (S9), was partially evaporated because the pressure was reduced so an LVE was established between the toluene/ethylene phases, but it should have been greater than the drew-point pressure (PDew)
Vapor pressure of a pure species (Pisat, where i = ethylene or toluene) is obtained by Equation (4), using the Antoine equation, and whose parameters are shown in Table 1.

Table 1.
Parameters used in the Antoine equation for toluene and ethylene.
The calculations of equation for PBubl or PDew involve {xi} = {zi} and {yi} = {zi}, respectively, with zi being the overall composition in the components.
First, P must lie in the range of the following constraint, Equation (5):
The K-value correlations are estimated by Equation (6):
The moles in the vapor phase () are calculated via a nonlinear algebraic equation, Equation (7), which is solved by the Newton method. The total molar mass in the liquid is obtained by the difference with respect to the total molar amount.
The factions yi and xi are calculated by Equations (8) and (9), respectively
The total moles in the liquid phase nL, Equation (10), is obtained from the mass balances of toluene, and ethylene, in both the phases, where net0 and nTol0 are the initial total moles of ethylene and toluene, respectively.
and
Finally, the ratio between the moles of ethylene and the solvent volume (the volume of the ethylene is very low, so it is negligible) produces the concentration of ethylene.
3.4. Optimization of the Parameter Estimation
The parameters , , kc, kd2, and in Equations (2) or (3) were found by an optimization tool in Matlab 2015a, and the minimization function, named fmincon [30], in which the objective function was defined as Equation (13):
Here, denotes the predicted polymerization rate at the time i, and is the measured polymerization rate at the time i. Additionally, the coefficient of determination denoted R2 was calculated (Equation (14)):
where
The standard deviation (S) is defined in Equation (17)
In a nonlinear model the covariance-variance of the kinetic parameter p () is estimated by Equation (18) [31]:
where J is the matrix of derivatives of the non-linear model with respect to the parameters (similar to the Jacobian matrix of the system) and is equal to pth diagonal term of the matix . Each element of J is
where F is the non-linear model and the are the experimental points.
3.5. Method of Moments
In this section, the mathematical model was developed by using the method of moments, in which an overall kinetic behavior is obtained. After writing out the mass balances of two polymer populations (Equations (S1)–(S8)), the three first moments were derived (Equations (20)–(31)), considering the moment definitions shown in Table 2.

Table 2.
Definition of moments.
Zeroth moments
First Moments
Second Moment
where = ktr1[M]l and = ktr2[M]l
Number (Mn) and weight (Mw) average molecular weights were calculated by Equations (32) and (33), respectively.
4. Results and Discussion
4.1. Polymerizations
With the aim to provide insights regarding the ethylene polymerization conceived by zirconocenes and organoboron activators, we carried out a series of experiments using three different zirconocene catalysts, with different ligand substituents, activated via three different organoboron compounds. The polymerization behavior, as well as the final properties, were evaluated. Moreover, we validated our experimental results via a kinetic modeling study, which is presented in the next section of the article. The general properties of the result polymers are shown in Table 3.

Table 3.
General features of the synthesized polyethylene (PE) using different catalytic systems.
The ethylene polymerization was greatly influenced by the type of organoboron compound used as the activator. Considering the catalytic activity, shown in Table 3, trityl tetrakis(pentafluorophenyl)borate (B3) was the one promoting the ethylene polymerization to the greatest extent, irrespectively of the zirconocene precursors, which presumably was due to the possible remaining interaction between the abstracted methyl group and the metal cation in the case of B1. While in B2, one of the by-products was a trisubstituted amine that might be able to trap the coordinatively unsaturated cation formed in this reaction, as has been previously reported for other systems [32]: both phenomena could potentially decrease the catalytic activity.
On the other hand, it was found that the non-substituted CP ring (Zr1) led to the highest catalytic activity, suggesting that by employing these organoboron compounds as activators, the bulkiness of the t-butyl substituent groups on the CP ring (Zr2), shows dominance towards the electro-donating effect, decreasing the polymerization activity due to steric hindrance. On the other hand, Zr1 also led to higher catalytic activity than Zr3, which has an indenyl substituent group. There is a discrepancy in the literature regarding the difference in the electronic environment in indenyl groups compared to CP. The general understanding has been that indenyl is more electron-rich than CP [33,34]. However, some authors have also suggested that indenyl is a poorer donor based on reduction potentials. Moreover, Nguyen et al. suggest that indenyl is electron-richer than CP, but an anodic shift of the reduction potential presumably occurs because an η5 to η3 haptotropic shift accompanies reduction, thus stabilizing the product [35]. Further understanding of this complex phenomenon is required, and at this point, any explanation appears to be merely speculative.
Concerning the molecular weight characteristics (shown in Table 3), the lowest molecular weight was exhibited by employing B2 as the activator, accompanied by an increase in dispersity index (Ð), suggesting chain transfer reactions during the polymerization, which was also reflected in the multimodal behavior of the molecular weight distributions (MWDs), shown in Figure 3. The MWD was further deconvoluted by statistical procedures to provide an approximate notion of the number of active sites carrying out the polymerization, considering that each active site possesses different probabilities of chain transfer and termination, therefore producing polymers with individual molar mass distributions, with the observed MWD being a superposition of all products.
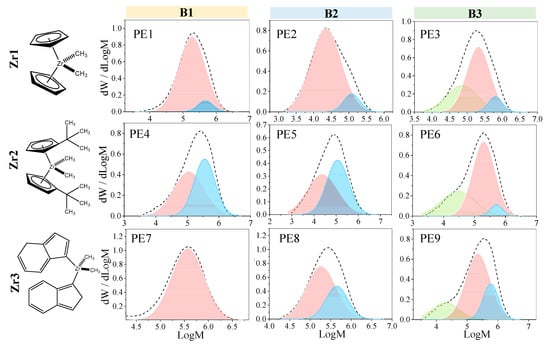
Figure 3.
Deconvoluted molecular weight distributions of the synthesized PE using the different catalytic systems.
A strong influence of the activator over the MWD was observed, while a narrow bimodal molecular weight distribution was observed by using B1 as a co-catalyst; at least three kinds of active sites were observed in the case of B3. Concerning B2 as the activator, a broad bimodal MWD was exhibited, presenting the Zr2 + B2 system as the highest polydispersity (Ð = 7.5) with the lowest catalytic activity due to the poor compatibility between (t-butyl-CP)2Zr(CH3) and [C6H5N(CH3)2H]+[B(C6F5)4] as the catalyst system for ethylene polymerization. The crystallinity degree was determined through DSC (values are shown in Table 3). A relatively high crystallinity degree of around 60–75% was observed in all cases, as expected for high density polyethylene (HDPE). However, a slightly higher degree of crystallinity was observed with B2 (around 72%) as the activator, attributed to the relatively lower molecular weight. Nevertheless, this activator also led to the broadest MWD, suggesting the presence of chain transfer reactions during the polymerization; however, it could be assumed that β-hydride was not predominant, because branching would take place thus decreasing the crystallinity. Concerning the melting temperature, no significant differences were exhibited among the samples, remaining above 134 °C as expected.
To elucidate the influence of different solvents over the polymerization behavior and polymer properties, isooctane, heptane, and hexane were tested for the catalytic system CP2Zr(CH3)2 + [(C6H5)3C]+[B(C6F5)4]− (Zr1 + B3), which led to the highest catalytic activity. The results were compared with those of the sample PE3, in which toluene was used. The results are shown in Table 4. As can be observed, a significant difference in the catalytic activity and molecular weight characteristics was exhibited by varying the solvent. The highest catalytic activity was found when using toluene as solvent, followed by isooctane, heptane and finally hexane; which results correlate to the solubility parameter of the solvents, implying that they play a fundamental role in the polymerization behavior. This behavior is presumably related to the higher miscibility of the catalyst system (solubility parameter not calculated in this work); however, additionally, the solubility parameter is related to the solvency behavior of a specific solvent, and could therefore influence the nature of the equilibrium of the complexation reaction together with the solvation effect. Further investigations are required to understand this behavior. Concerning the molecular weight characteristics, the highest molecular weight was obtained by using hexane, which is attributed to the reduced concentration of active sites, implied by the low catalytic activity. On the other hand, by using heptane, the lowest molecular weight was obtained, which suggests the increase in termination reactions, and which is supported by the higher polydispersity value reported in Table 4. Similar results were observed by using toluene and isooctane as solvents.

Table 4.
Influence of solvents over the ethylene polymerization using CP2Zr(CH3)2 (Zr1) as the catalyst, activated by [CPh3][B(C6F5)4] (B3).
4.2. Kinetic Parameter Estimations
The catalytic system (B + Zr) that showed the highest catalytic activity was B3/Zr1 (in toluene); therefore, in the following mathematical modeling sections, a polymerization series using the aforementioned system was synthesized. The resulting experimental data were analyzed in Table 5. The ratio B3/Zr1 was varied in two levels (1 and 2.5) and the operating temperature was changed in three levels (40, 50, and 60 °C). Additionally, the operating pressure was increased to 1.5 bar to increase the catalytic activity.

Table 5.
Reaction parameters and general features of the synthesized PEs using CP2Zr(CH3)2 (Zr1)/[CPh3][B(C6F5)4] (B3), used for kinetic modeling.
The thermodynamic state of the liquid and vapor phases was considered under VLE because the operational pressure (P = 150 bar, T = 40, 50, and 60 °C) lay between the bounds of PBubl and PDew under all the studied conditions (Equation (5)). Therefore, a T, P-flash calculation protocol was carried out, resulting in [M]l = 0.17, 0.14, and 0.11 mol L−1, as shown in Table 6. As the temperature increased, a higher amount of mass of both components (ethanol and toluene) was transferred to the vapor phase, resulting in a lower concentration of ethylene in the liquid phase. According to Lee et al. [36], the solubility of the ethylene in toluene is inversely proportional to a temperature increase; the results of our predictions are in agreement with these experimental findings. Figure 4 shows the dependency of [M]l with respect to the operating temperature and pressure.

Table 6.
Operating conditions, [M]l, estimated kinetic rate constants, coefficients of determination (R2), standard deviation (S), and operating pressure P = 150 bar.
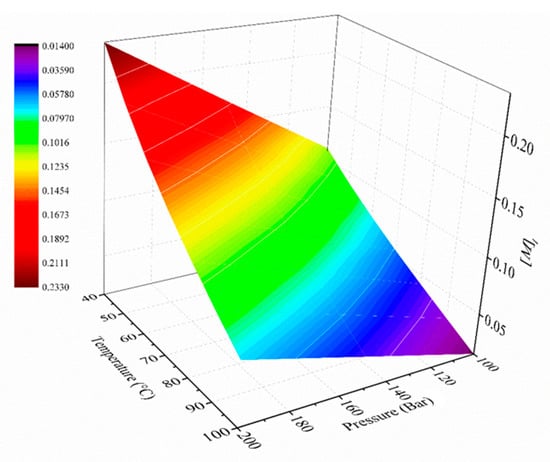
Figure 4.
Mapping of the influence of the temperature (°C) and pressure (bar) on the monomer concentration in the liquid phase (toluene).
The next step was to obtain the optimal values of the kinetic rate constants kp1, kp2, kd2, kc, and ka2 by fitting the experimental polymerization rate profiles to Model 1 (Equation (2)) and Model 2 (Equation (3)), by using Matlab tools. It must be noted that the lower bound of each parameter was limited to the value previously found at a lower temperature for experiments in the same series, i.e., PE14, PE16, and PE17. It is clear that these constraints are based on the expected physical behavior, described by the Arrhenius expression.
Comparisons between the optimization results of Model 1 (dashed lines), Model 2 (dotted lines), and the experimental profiles (continuous lines) for the five selected experiments are illustrated in Figure 5, and the kinetic parameter values and the coefficients of determination, R2, are presented in Table 6. The best fit with the experimental curves corresponds to predictions by Model 1 with the reactivation step of the deactivated catalytic system, with closer values of R2 to the unity than those obtained by Model 2 (Table 6). Therefore, it is assumed that the reactivation has high importance in the adequate prediction of the polymerization rate profile.
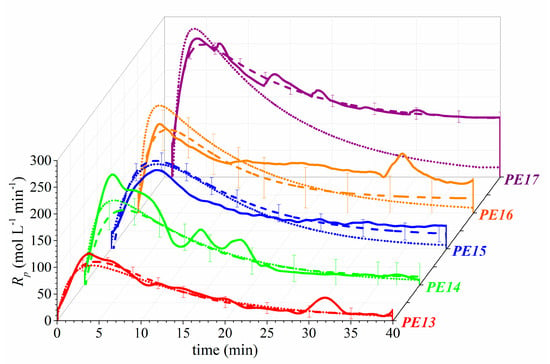
Figure 5.
Polymerization rate profiles using Zr1/B3 as a catalytic system, varying the temperature and the [B]0 for experimental data (continues lines): Model 1 (dashed lines), and Model 2 (dotted lines). The operating conditions are shown in Table 6. Bars denote the standard deviations (S) for Model 1.
To estimate the transfer chain kinetic rate constants (ktr1 and ktr2), the system of ordinary differential equations (ODEs) was solved by a routine called ode23s in Matlab. The previously estimated parameters for Model 1, shown in Table 6, were used, and the Mn and Mw values, computed by Equations (41) and (42), were fitted to the corresponding experimental values. The values of ktr1 and ktr2 were assigned until they reached a good agreement with the experimental data, but the low bound in the estimation was constrained to the fitted value at a lower temperature, analogous to the procedure previously described. As presented in Table 7, the fitted Mn and Mw values showed an excellent agreement with the experimental data with low values of the relative changes, and the proper values for ktr1 and ktr2 are summarized in Table 6.

Table 7.
Fitted (Model 1) and experimental molecular weights (gr mol−1) of polyethylene, and the relative change (R.C.). P = 150 bar.
All the kinetic rate constants of the series PE14, PE16, and PE17, where the temperature was increased at 40, 50, and 60 °C, respectively, with constant molar ratio B3/Zr1 = 2.5, were used in the estimation of the activation energy (EA) and steric factor (A0). Figure 6 depicts an Arrhenius plot (ln (kj) versus T−1) and the fitted equations for all the ks values. An excellent fit was achieved for all the kinetic rate constants (R2 > 0.92), with the exception of kc, giving R2 = 0.04, attributed to the almost-null increase in the constant with respect to the temperature, as shown in Table 6. In fact, when an optimization procedure without a constrained low bound on kc was run, a negative effect of the temperature on this rate constant was computed. This was probably due to a reversible transition reaction taking place, in which the difference between the EA(kc) and EA(k−c) predominately led to the formation of the active polymer of type 2 at low temperatures, but at high temperatures, the formation of active chains of type 1 could be favored, as reported for the ethylene polymerization using MAO and CP2ZrCl2 [22,23]. Hence, as a first approximation of the transition reaction in this system, in the next section a value of kc = 0.11 min−1 will be used for all the simulations.
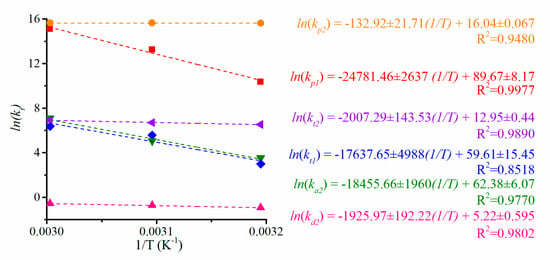
Figure 6.
Arrhenius plot for a set of ki values for the ethylene coordination polymerization using a ratio B/Zr = 2.5 and their linear regressions.
On the other hand, contrary to the findings reported by Jiang et al. [23], in which the reactivation reaction only was important at low temperatures (at 50 °C ka2 = 19 L2 mol−2 min−1, at 60 and 70 °C ka2 = 0), in this work the effect of the temperature on the reactivation of catalytic systems (CDeact) has been well described, obtaining R2 = 0.9880 in the linear regression, as shown in Figure 6: Ea (ka2) = 153.44 ± 16.29 kJ mol−1 and A0 (ka2) = 1.23 × 1027(exp(±6.07)) L2 mol−2 min−1. The values estimated for the spontaneous deactivation are EA (kd2) = 16.01 ± 1.60 kJ mol−1 and A0 (kd2) = 184.96(exp(±0.59)) L mol−1 min−1.
Additionally, high differences in the EA and A0 values between kp1 and kp2 were obtained (Figure 6), attributable to more reactive active polymers of type 2 than those initially generated of type 1. While the values of EA (kp2) = 1.09 ± 0.18 kJ mol−1 and A0 (kp2) = 9.16 × 1027(exp(±0.07)) L2 mol−2 min−1 were estimated for the former type, the following values of EA (kp1) = 206.03 ± 21.92 kJ mol−1 and A0 (kp1) = 8.77 × 1038 (exp(±8.17)) L mol−1 min−1 were estimated for the propagation step of the latter. As expected, the estimated behavior for the monomer rate constants for each type was related to the kp values with EA (ktr1) = 146.63 ± 41.47 kJ mol−1 and A0 (ktr1) = 7.73 × 1025(exp(±15.46))L mol−1 min−1; and EA (ktr2) = 16.68 ± 1.19 kJ mol−1 and A0 (ktr2) = 4.21 × 105(exp(±0.44)) L mol−1 min−1. Given such high values of EA (kp1), EA (ktr1), and EA (ka2), at high temperature (i.e., 70 °C) one would expect the active polymer of type 1 to present lower molecular weights than type 2, as well as a competitive step between the transition to type 2 and the chain transfer to monomer.
It is important to note a strong effect of the boron-based activator on the kinetic parameters, because a concentration change induces different values during the fitting procedure, as shown in Table 6. If the values of EA and A0 are estimated with the available experimental data at 40 and 50 °C with [B3] = 5.53 × 10−4 mol L−1, the values in Table 8 are obtained. A considerable decrease in the frequency factor and the activation energy of kp1 is observed in comparison to those estimated values at a high concentration of B3 (Table 6). Additionally, the energetic barrier is increased for kp2 with respect to a high concentration of B, but its frequency factor is greatly decreased, ascribable to an important steric hindrance of the active site with the monomer.

Table 8.
Parameter estimation results of the PE polymerization using B3 = 5.53 × 10−4 mol L−1.
4.3. Kinetic Simulations
The estimated kinetic rate constants were used as inputs in the mathematical model, and the results are shown in Figure 7. First, the effect of the temperature was studied in the series PE10, PE12, and PE14, corresponding to polymerizations at 40, 50, and 60 °C, respectively (Figure 7a,c,e). As expected, a higher temperature leads to an increase in the polymerization rate (Figure 7a versus Figure 7e). The Rp curves show an increase in the first five minutes of the reaction, which is attributed to the gradual generation of active polymer of type 2 (Y0,2), with a higher propagation rate than type 1 (Y0,2). Then, the profiles reach a maximum when the highest concentration of (Y0,2) is generated, as confirmed in Figure 7b,d,f. At longer reaction times, the deactivation of both active polymer chains is greater than their generation, resulting in a decrease in ethylene consumption.
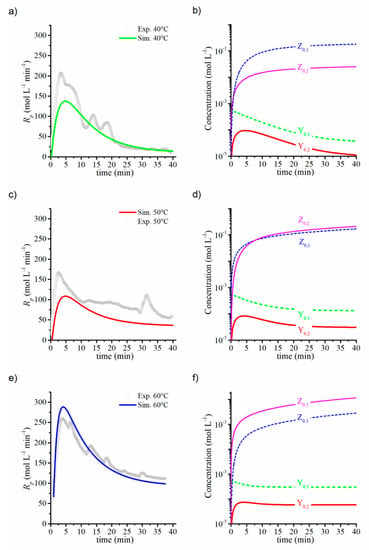
Figure 7.
Effect of the temperature variation at 40 °C (a,b), 50 °C (c,d), and 60 °C (e,f) on: Rp profiles (a,c,e) with the experimental data (gray symbols) and the simulation (continues lines), and total concentration of polymer species (zeroth moment) (b,d,f). The ratio of [B]0/[Zr]0 = 2.5 and P = 150 bar. Other operating conditions are shown in Table 6.
The concentration curves at 40 °C are shown in Figure 7b, in which Y0,1 constantly decreases, but Y0,2 reaches a maximum before 5 min of reaction have elapsed. A higher production of dead polymer of type 2 (Z0,2) than that for type 1 (Z0,1) was predicted by the model. Additionally, Mn for Z0,2 was five-fold higher than that for Z0,1 (Figure 8a), which reached a plateau after 5 min. As illustrated, the value of Mn for the final polymer product is very similar to that obtained to that predicted for Z0,2. Notably, the experimental values for Mn and Mw for the final product (symbols) show an excellent agreement with the predicted values (lines) with dispersity of 2.03. Such difference in the values of Mn between Z0,1 and Z0,2 resulted in two populations, which are observed in the MWD of the final product measured by SEC (Figure 8b), being the long tail of the distribution attributable to Z0,1. The two polymer populations have been obtained by statistical deconvolution of the SEC experimental data, and they should be taken with wariness. More advanced deconvolution procedures can be found in the literature [37], and these will be explored in further works.
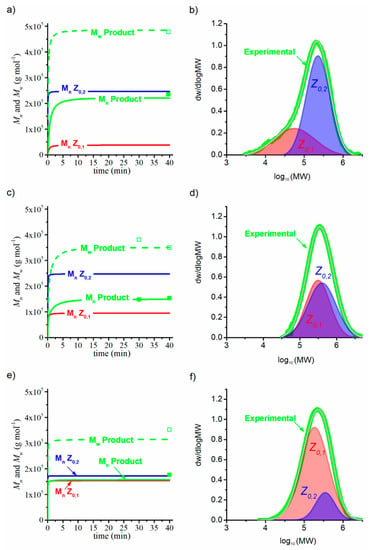
Figure 8.
Effect of the temperature variation at 40 °C (a,b), 50 °C (c,d), and 60 °C (e,f) on Mn and Mw for the final product and both types of polymer species (a,c,e) with the experimental data (green symbols) and the simulations (lines), and molecular weight distributions (b,d,f) for SEC data (green line) and partial populations (blue and red lines). The ratio of [B]0/[Zr]0 = 2.5 and P = 150 bar. Other operating conditions are shown in Table 6.
At 50 °C, the Rp profile was more sustained (Figure 7a); however, its maximum value was lower than that predicted at 40 °C, which was probably due to a fast transfer chain to polymer rate. This produces similar concentrations for Z0,1 and Z0,2 species throughout the polymerization, as shown in Figure 7b. At this temperature, the gap of Mn values between the Z0,1 and Z0,2 species was smaller than at lower temperatures (Figure 8a), and the populations of both species similarly contributed to the MWD (Figure 8a) with a dispersity of 2.65.
At 60 °C, the model accurately predicted the Rp experimental profile, presenting a maximum point at approximately 5 min: after that time, the curve suddenly falls until 100 mol L−1 min−1 at 40 min of reaction (Figure 7e). The concentration of Y0,2 reached a maximum at 5 min, followed by a plateau where the concentration remained almost constant throughout the whole reaction (Figure 7f). Here, the concentration of Z0,1 was higher than Z0,2, but both species presented very similar Mn—such values overlap with the experimental values of Mn (Figure 8e). Additionally, Figure 8f presents the MWD and its deconvolution in two populations, corresponding to Z0,1 and Z0,2, with a higher concentration of Z1,0, as determined previously. The dispersity value was 2.00; therefore, so it is possible to assume that a single population, such as Z0,2, is only generated in the system, and Y0,1 fulfills the role of intermediary species or transition state of Y0,2.
5. Conclusions
A systematic study about the influence of different parameters over the catalytic activity and polymer final properties was performed, using organoboron compounds as activators of zirconocenes with different ligand substituents. Carbocation organoboron compounds ([(C6H5)3C]+[B(C6F5)4]−) promoted the ethylene polymerization to the greatest extent, while zirconocenes with cyclopentadienyl rings having non-substituted-ligands were found to yield the highest activity, suggesting that, in this catalytic system, the steric hindrance from the substituents plays a greater role than their electron-releasing effect over the polymerization. Toluene was found to be the best solvent among those compared for this kind of system.
A comprehensive kinetic model for ethylene polymerization using a CP2Zr(CH3)2/[CPh3][B(C6F5)4] catalyst system and toluene as solvent was developed, based on a proposed reaction mechanism considering two active sites. A parameter estimation, involving the fit of the polymerization rate profiles using a nonlinear least square optimization, was carried out. A comparison between the two models revealed that the reactivation of the deactivated sites of type 2 is a very important step, obtaining coefficients of determination around the unit. Additionally, the chain transfer rate constants were fitted by using the method of moments, resulting in an excellent agreement with the molecular weight experimental data. Moreover, EA and A0 parameters were estimated in two series of experiments at ratios of B3/Zr1 of 1 and 2.5, and they presented high energetic barriers for rate constants corresponding to the active site 2 with the higher ratio. The model and the kinetic parameters were validated with the experimental data, confirming that a multiple (two) active site consideration is a possible explanation for the multimodal MWD, observed in SEC measurements. The predictions of the total concentrations expose a higher generation of the dead polymer of type 1 than type 2 when the temperature is higher.
Supplementary Materials
The following are available online at https://www.mdpi.com/2227-9717/9/1/162/s1.
Author Contributions
Conceptualization, R.D.d.L. and I.Z.-G.; methodology, J.D.-E. and F.E.-M.; software, I.Z.-G. and E.S.-G.; validation, I.Z.-G. and P.Q.-Á.; formal analysis, R.D.d.L. and I.Z.-G.; investigation, L.V. and R.L.-G.; resources, R.D.d.L.; data curation, I.Z.-G.; writing—original draft preparation, L.V., F.E.-M. and I.Z.-G.; writing—review and editing, L.V., R.D.d.L. and I.Z.-G.; visualization, L.V., P.Q.-Á. and I.Z.-G.; supervision, R.L.-G. and E.S.-G.; project administration, R.D.d.L. and I.Z.-G.; funding acquisition, R.D.d.L. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge the financial support of the Mexican National Council of Science and Technology (CONACyT) through the Basic Science project 258278.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available on request.
Acknowledgments
The authors thank Ricardo Mendoza for their technical support. I.Z.-G. thanks the financial support of CONACyT, though Cátedras CONACYT, project 707.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Sauter, D.W.; Taoufik, M.; Boisson, C. Polyolefins, a success story. Polymers 2017, 9, 185. [Google Scholar] [CrossRef]
- Kaminsky, W. The discovery and evolution of metallocene-based olefin polymerization catalysts. Rend. Lincei 2017, 28, 87–95. [Google Scholar] [CrossRef]
- Linnolahti, M.; Collins, S. Formation, Structure, and Composition of Methylaluminoxane. ChemPhysChem 2017, 18, 3369–3374. [Google Scholar] [CrossRef]
- Kaminsky, W. Discovery of methylaluminoxane as cocatalyst for olefin polymerization. Macromolecules 2012, 45, 3289–3297. [Google Scholar] [CrossRef]
- Velthoen, M.E.Z.; Muñoz-Murillo, A.; Bouhmadi, A.; Cecius, M.; Diefenbach, S.; Weckhuysen, B.M. The Multifaceted Role of Methylaluminoxane in Metallocene-Based Olefin Polymerization Catalysis. Macromolecules 2018, 51, 343–355. [Google Scholar] [CrossRef]
- Yang, X.; Stern, C.L.; Marks, T.J. “Cation-like” Homogeneous Olefin Polymerization Catalysts Based upon Zirconocene Alkyls and Tris(pentafluorophenyl)borane. J. Am. Chem. Soc. 1991, 113, 3623–3625. [Google Scholar] [CrossRef]
- Yang, X.; Stern, C.L.; Marks, T.J. Cationic Zirconocene Olefin Polymerization Catalysts Based on the Organo-Lewis Acid Tris(pentafluorophenyl)borane. A Synthetic, Structural, Solution Dynamic, and Polymerization Catalytic Study. J. Am. Chem. Soc. 1994, 116, 10015–10031. [Google Scholar] [CrossRef]
- Piers, W.E.; Chivers, T. ChemInform Abstract: Pentafluorophenylboranes: From Obscurity to Applications. Chem. Soc. Rev. 1997, 26, 345–354. [Google Scholar] [CrossRef]
- Chen, E.Y.X.; Marks, T.J. Cocatalysts for metal-catalyzed olefin polymerization: Activators, activation processes, and structure-activity relationships. Chem. Rev. 2000, 100, 1391–1434. [Google Scholar] [CrossRef]
- Mehdiabadi, S.; Soares, J.B.P.; Bilbao, D.; Brinen, J.L. A Polymerization Kinetics Comparison between a Metallocene Catalyst Activated by Tetrakis(pentafluorophenyl) Borate and MAO for the Polymerization of Ethylene in a Semi-batch Solution Reactor. Macromol. React. Eng. 2011, 5, 418–430. [Google Scholar] [CrossRef]
- Yang, X.; Stern, C.L.; Marks, T.J. Models for Organometallic Molecule-Support Complexes. Very Large Counterion Modulation of Cationic Actinide Alkyl Reactivity. Organometallics 1991, 10, 840–842. [Google Scholar] [CrossRef]
- Chien, J.C.W.; Tsai, W.M.; Rausch, M.D.; Rausch, M.D. Isospecific Polymerization of Propylene Catalyzed by rac-Ethylenebis(indenyl)methylzirconium “Cation”. J. Am. Chem. Soc. 1991, 113, 8570–8571. [Google Scholar] [CrossRef]
- Chien, J.C.W.; Wang, B.-P. Metallocene-methylaluminoxane catalysts for olefin polymerization. V. Comparison of Cp2ZrCl2 and CpZrCl3. J. Polym. Sci. Part A Polym. Chem. 1990, 28, 15–38. [Google Scholar] [CrossRef]
- Valencia López, L.A.; Enríquez-Medrano, F.J.; Mendoza Carrizales, R.; Soriano Corral, F.; Castañeda Facio, A.; Diaz De Leon Gomez, R.E. Influence of organoboron compounds on ethylene polymerization using cp2zrcl2/mao as catalyst system. Int. J. Polym. Sci. 2014, 2014. [Google Scholar] [CrossRef]
- Correa, S.A.; Daniliuc, C.G.; Stark, H.S.; Rojas, R.S. Nickel Catalysts Activated by rGO Modified with a Boron Lewis Acid to Produce rGO-Hyperbranched PE Nanocomposites. Organometallics 2019, 28, 3327–3337. [Google Scholar] [CrossRef]
- Ewen, A.J.A. Catalytic Polymerization of Olefins; Keii, T., Soga, K., Eds.; Elsevier: Tokyo, Japan, 1986; p. 271. [Google Scholar]
- Charles, R.; González-Hernández, R.; Morales, E.; Revilla, J.; Elizalde, L.E.; Cadenas, G.; Pérez-Camacho, O.; Collins, S. Novel supported catalysts for ethylene polymerization based on aluminohydride-zirconocene complexes. J. Mol. Catal. A Chem. 2009, 307, 98–104. [Google Scholar] [CrossRef]
- Favero, C.; Mignoni, M.L.; De Souza, R.F.; Bernardo-Gusmão, K. Polymerization of ethylene with zirconocene heterogenized on spherical ZSM-5. J. Braz. Chem. Soc. 2015, 26, 1405–1410. [Google Scholar] [CrossRef]
- González-Hernández, R.; Chai, J.; Charles, R.; Pérez-Camacho, O.; Kniajanski, S.; Collins, S. Catalytic system fot homogeneous ethylene polymerization based on aluminohydride-zirconocene complexes. Organometallics 2006, 25, 5366–5373. [Google Scholar] [CrossRef]
- Charoenchaidet, S.; Chavadej, S.; Gulari, E. Borane-functionalized silica supports. J. Mol. Catal. A Chem. 2002, 185, 167–177. [Google Scholar] [CrossRef]
- Estrada, J.M.V.; Hamielec, A.E. Modelling of ethylene polymerization with Cp2ZrCl2 MAO catalyst. Polymer (Guildf) 1994, 35, 808–818. [Google Scholar] [CrossRef]
- Jiang, S.; Wang, L.; Zhang, P.; Feng, L. New kinetic model of ethene polymerization with Cp2ZrCl2/MAO catalyst. Macromol. Theory Simul. 2002, 11, 77–83. [Google Scholar] [CrossRef]
- Ahmadi, M.; Nekoomanesh, M.; Jamjah, R.; Zohuri, G.; Arabi, H. Modeling of slurry polymerization of ethylene using a soluble Cp2ZrCl2/MAO catalytic system. Macromol. Theory Simul. 2007, 16, 557–565. [Google Scholar] [CrossRef]
- Mehdiabadi, S.; Soares, J.B.P. Ethylene homopolymerization kinetics with a constrained geometry catalyst in a solution reactor. Macromolecules 2012, 45, 1777–1791. [Google Scholar] [CrossRef]
- Soares, J.B.P.; McKenna, T.F.L.; Cheng, C.P. Coordination Polymerization. In Polymer Reaction Engineering; Asua, J., Ed.; Blackwell Publishing Ltd.: Kuala Lumpur, Malaysia, 2007; pp. 29–117. ISBN 978-1-4051-4442-1. [Google Scholar]
- Gaw, W.J.; Swinton, F.L. Thermodynamic Properties of Binary Systems containing. Trans. Faraday Soc. 1967, 64, 637–647. [Google Scholar] [CrossRef]
- National Institute of Standars and Technology. Toluene. Available online: https://webbook.nist.gov/cgi/cbook.cgi?ID=C108883&Mask=4&Type=ANTOINE&Plot=on (accessed on 11 November 2020).
- Michels, A.; Wassenaar, T. The vapour pressure of ethylene. Physica 1950, 16, 221–224. [Google Scholar] [CrossRef]
- National Institute of Standars and Technology. Ethylene. Available online: https://webbook.nist.gov/cgi/cbook.cgi?ID=C74851&Mask=4&Type=ANTOINE&Plot=on (accessed on 11 November 2020).
- MathWorks®. Fmincon. Available online: https://la.mathworks.com/help/optim/ug/fmincon.html?lang=en (accessed on 11 November 2020).
- Bates, D.M.; Watts, D.G. Nonlinear Regression Analysis and Its Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1998. [Google Scholar]
- Bochmann, M.; Lancaster, S.J. Cationic group IV metal alkyl complexes and their role as olefin polymerization catalysts: The formation of ethyl-bridged dinuclear and heterodinuclear zirconium and hafnium complexes. J. Organomet. Chem. 1995, 497, 55–59. [Google Scholar] [CrossRef]
- Crossley, N.S.; Green, J.C.; Nagy, A.; Stringer, G. Electronic structure of transition-metal indenyl compounds: A He I and He II photoelectron spectroscopic study of [Mn(η5-C9H7)(CO)3], [Fe(η5-C9H7)2], [Ru(η5-C9H7)2], and [Ru(η5-C9H7)η-C5Me5)]. J. Chem. Soc. Dalton Trans. 1989, 11, 2139–2147. [Google Scholar] [CrossRef]
- Frankcom, T.M.; Green, J.C.; Nagy, A.; Kakkar, A.K.; Marder, T.B. Electronic structure and photoelectron spectroscopy of d8 rhodium indenyl complexes. Organometallics 1993, 12, 3688–3697. [Google Scholar] [CrossRef]
- Nguyen, K.T.; Lane, E.E.; McMillen, C.D.; Pienkos, J.A.; Wagenknecht, P.S. Is Indenyl a Stronger or Weaker Electron Donor Ligand than Cyclopentadienyl? Opposing Effects of Indenyl Electron Density and Ring Slipping on Electrochemical Potentials. Organometallics 2020, 39, 670–678. [Google Scholar] [CrossRef]
- Lee, L.S.; Ou, H.J.; Hsu, H.L. The experiments and correlations of the solubility of ethylene in toluene solvent. Fluid Phase Equilib. 2005, 231, 221–230. [Google Scholar] [CrossRef]
- Soares, J.B.P.; McKenna, T.F.L. Polyolefin Reaction Engineering; Wiley-VCH: Weinheim, Germany, 2012; pp. 187–269. ISBN 9783527317103. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).