Extreme Learning Machine-Based Model for Solubility Estimation of Hydrocarbon Gases in Electrolyte Solutions
Abstract
1. Introduction
2. Methodology
2.1. Experimental Dataset Collection
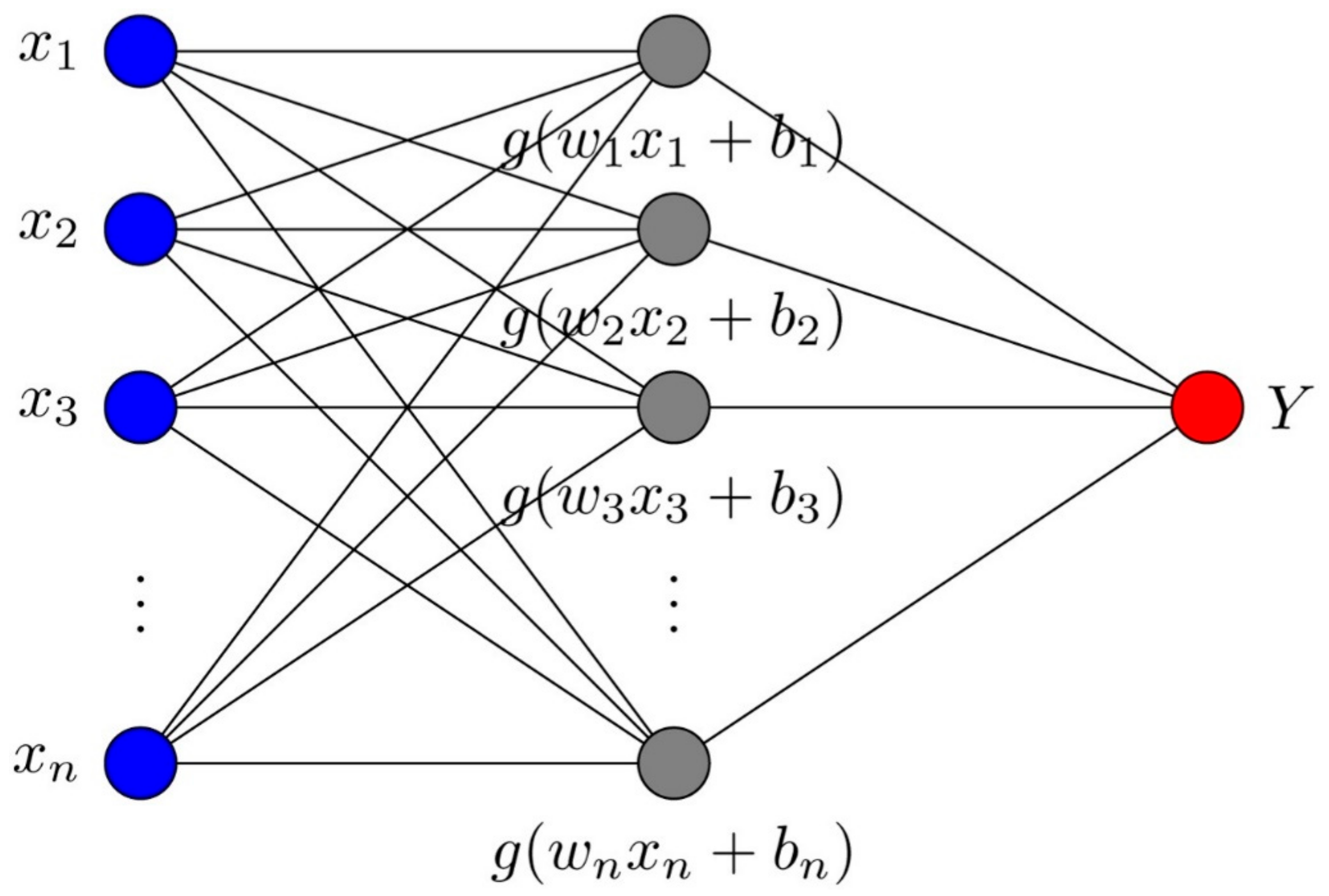
2.2. Extreme Learning Machine
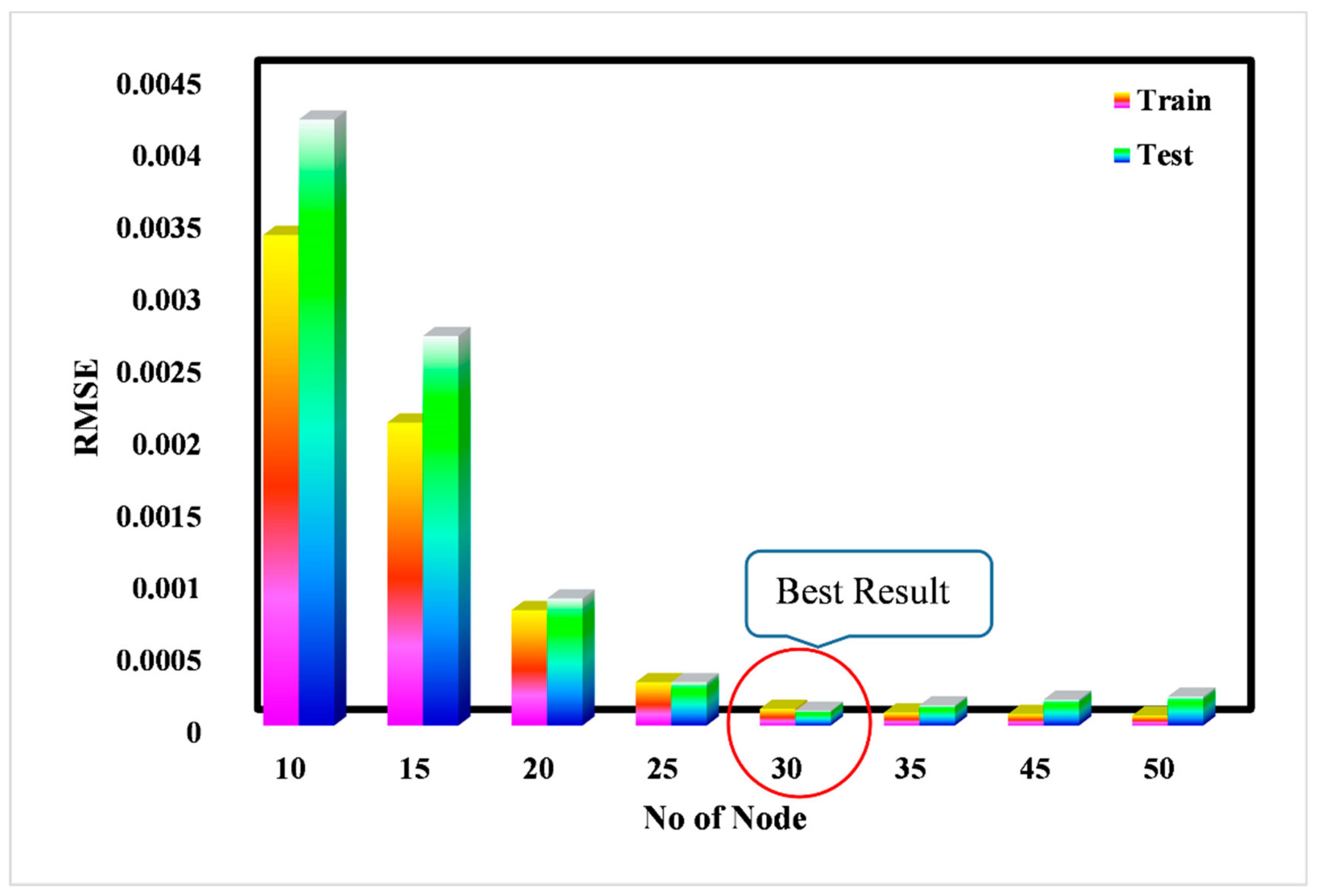
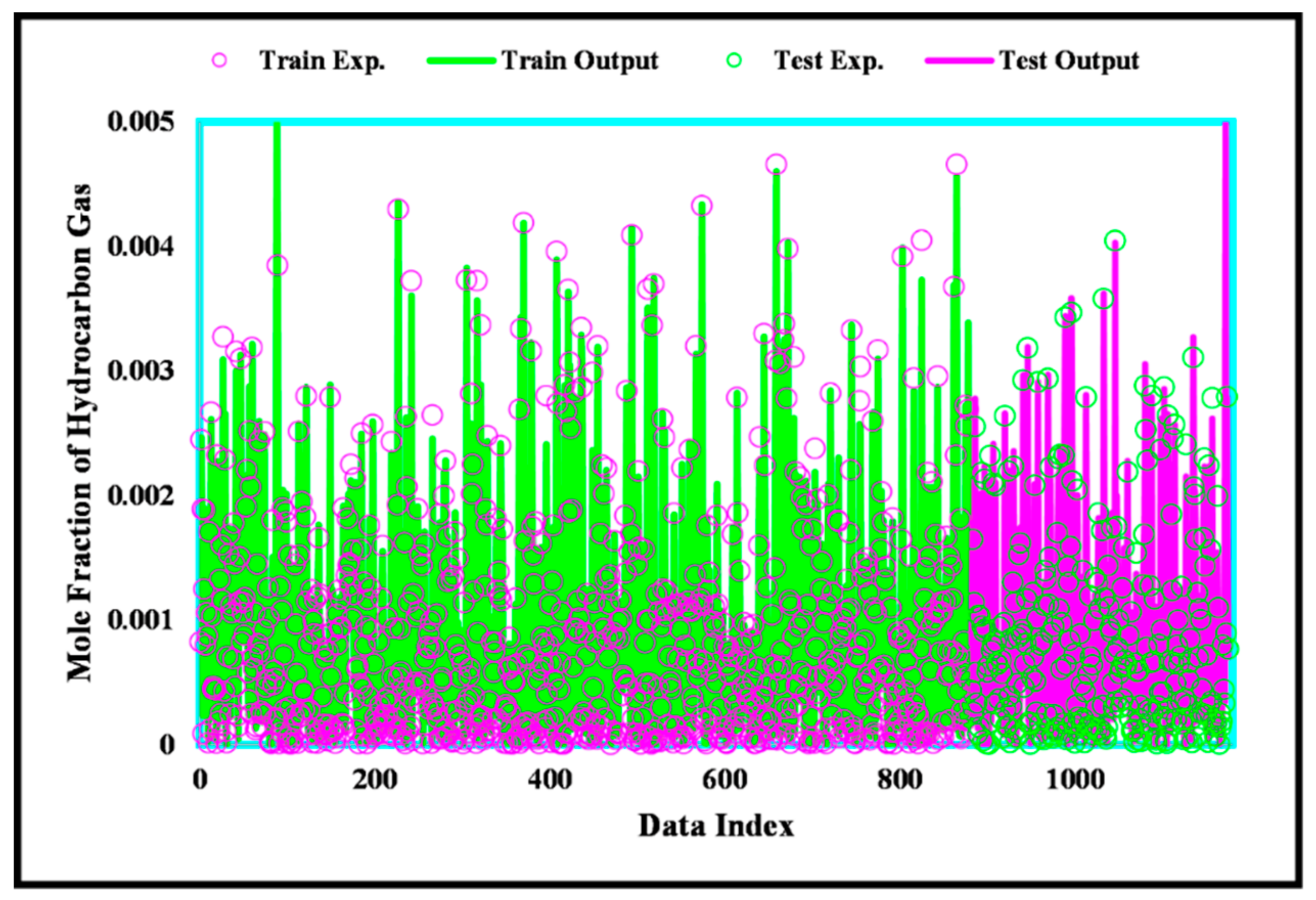
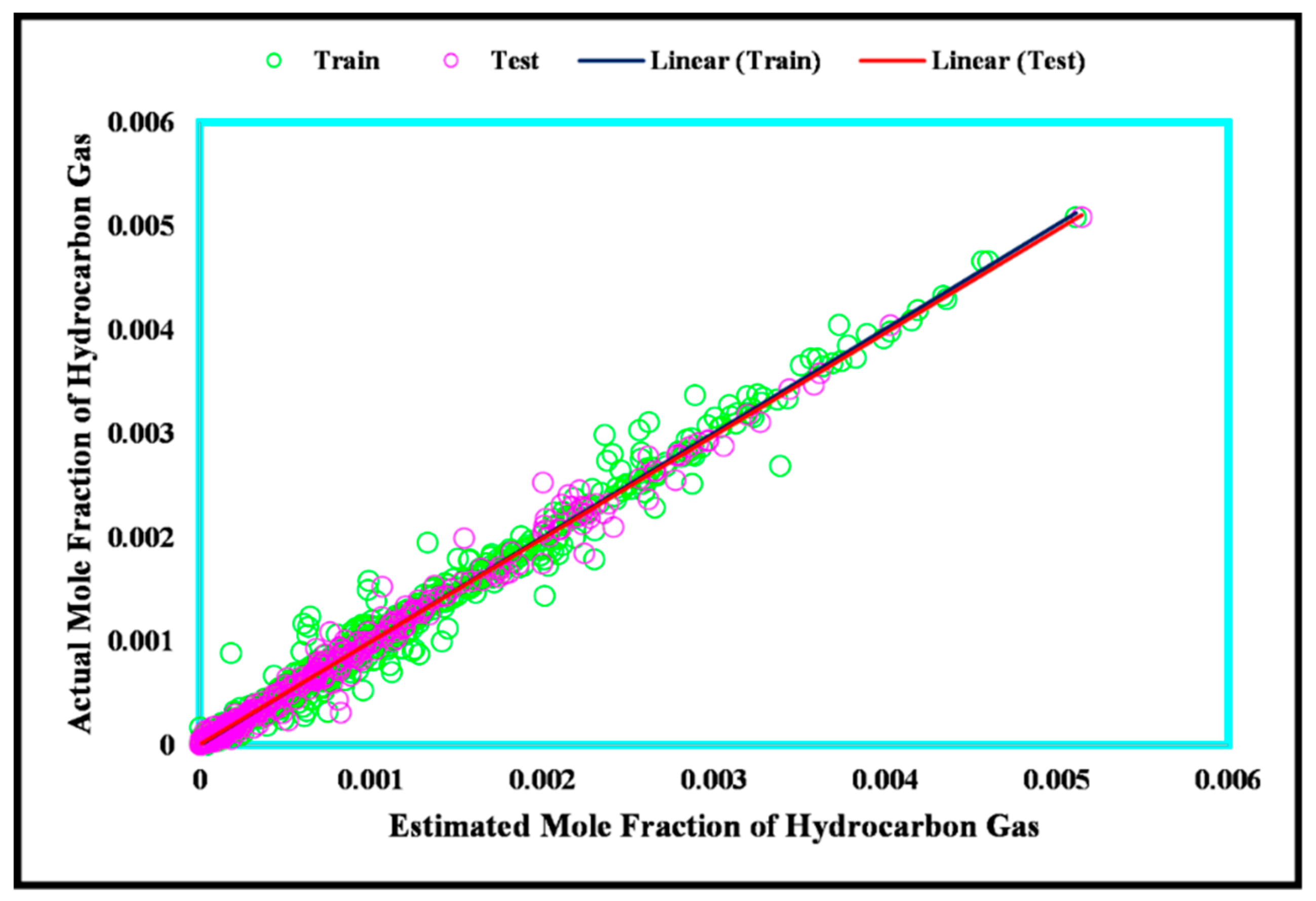
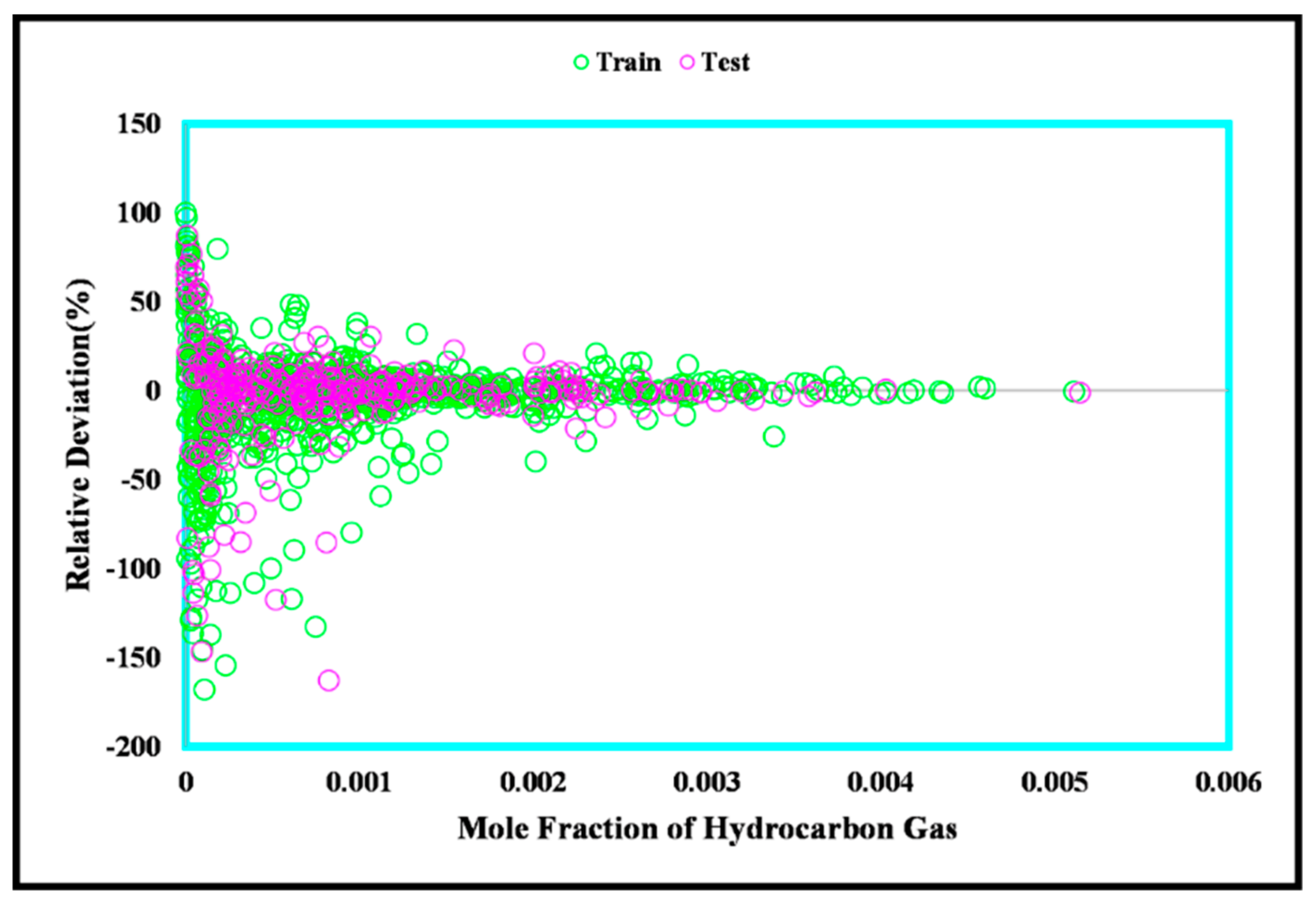
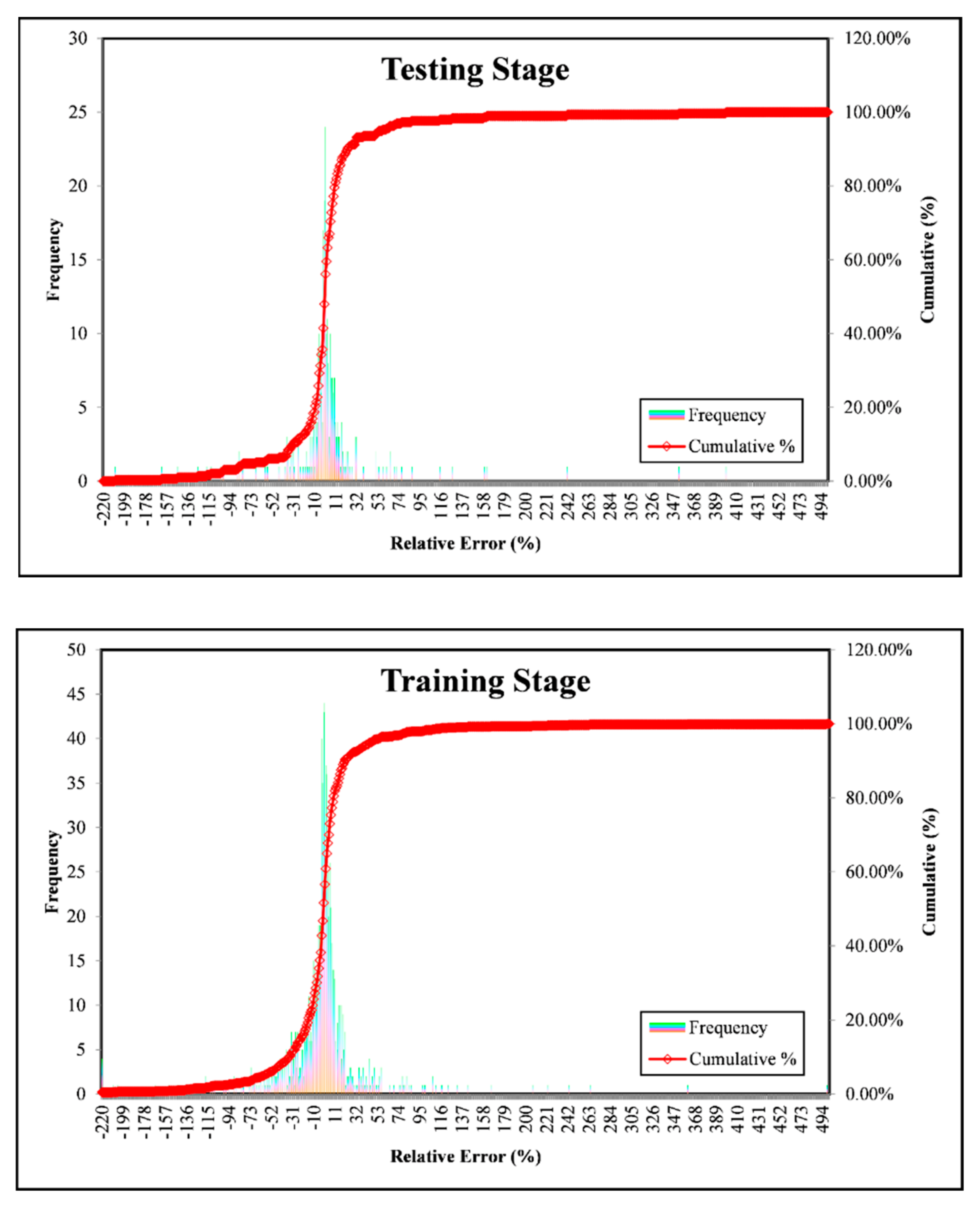
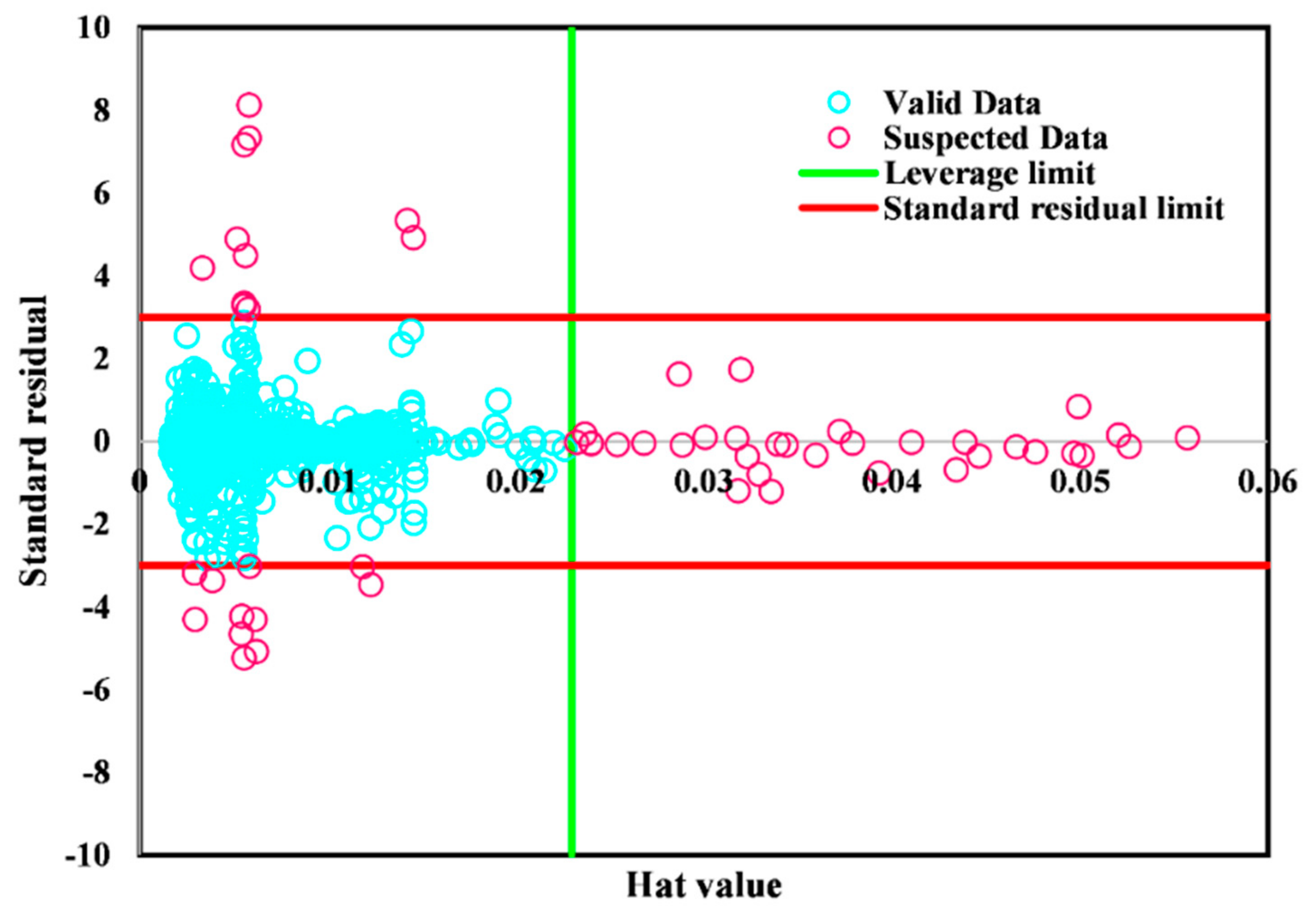
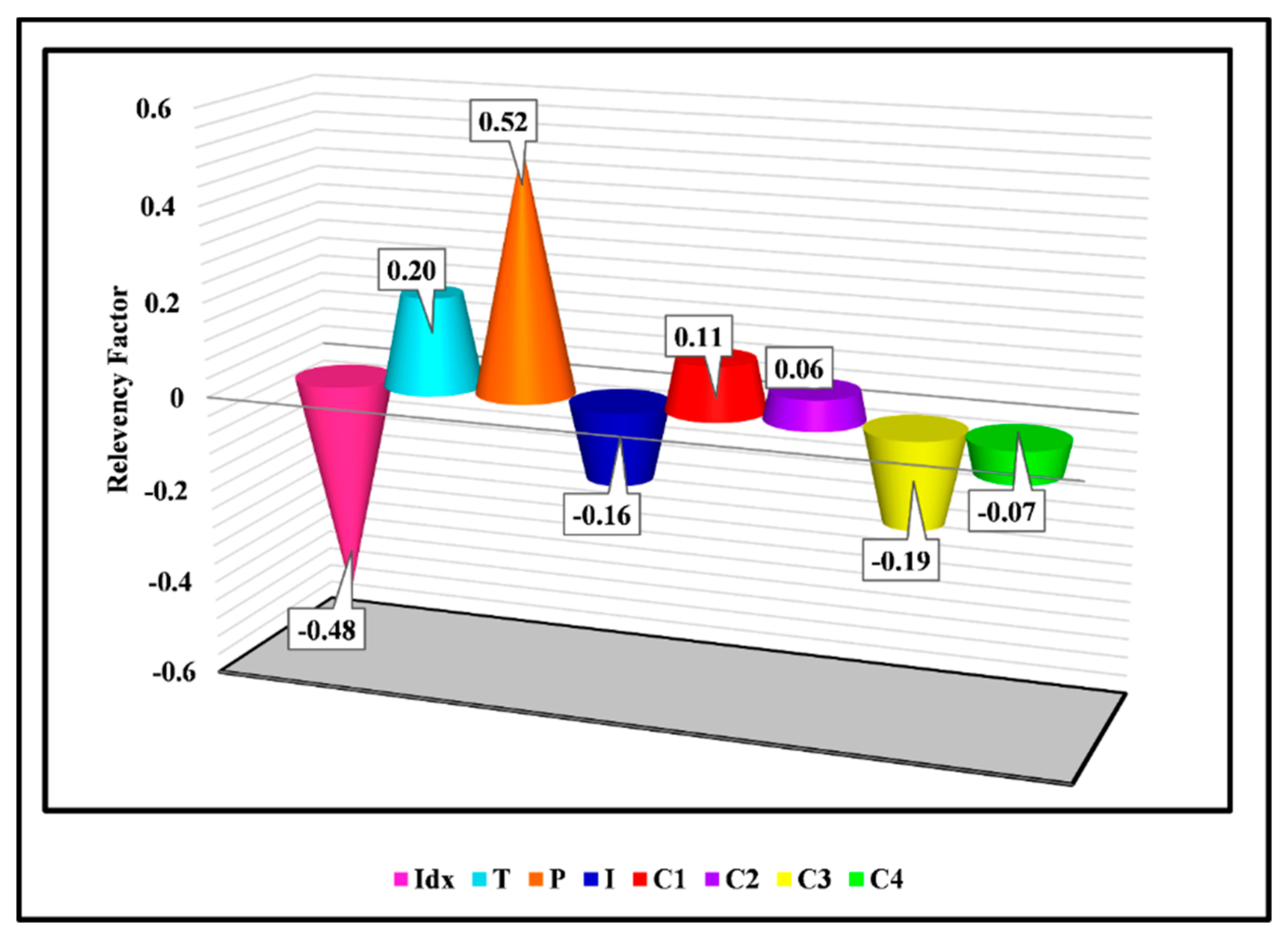
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mohammadi, A.H.; Chapoy, A.; Tohidi, B.; Richon, D. Gas solubility: A key to estimating the water content of natural gases. Ind. Eng. Chem. Res. 2006, 45, 4825–4829. [Google Scholar] [CrossRef]
- Chapoy, A.; Haghighi, H.; Tohidi, B. Development of a Henry’s constant correlation and solubility measurements of n-pentane, i-pentane, cyclopentane, n-hexane, and toluene in water. J. Chem. Thermodyn. 2008, 40, 1030–1037. [Google Scholar] [CrossRef]
- Chapoy, A.; Mokraoui, S.; Valtz, A.; Richon, D.; Mohammadi, A.H.; Tohidi, B. Solubility measurement and modeling for the system propane–water from 277.62 to 368.16 K. Fluid Phase Equilibria 2004, 226, 213–220. [Google Scholar] [CrossRef]
- Chapoy, A.; Mohammadi, A.H.; Richon, D.; Tohidi, B. Gas solubility measurement and modeling for methane–water and methane–ethane–n-butane–water systems at low temperature conditions. Fluid Phase Equilibria 2004, 220, 111–119. [Google Scholar] [CrossRef]
- Dhima, A.; de Hemptinne, J.-C.; Moracchini, G. Solubility of light hydrocarbons and their mixtures in pure water under high pressure. Fluid Phase Equilibria 1998, 145, 129–150. [Google Scholar] [CrossRef]
- Kiepe, J.; Horstmann, S.; Fischer, K.; Gmehling, J. Experimental determination and prediction of gas solubility data for methane+ water solutions containing different monovalent electrolytes. Ind. Eng. Chem. Res. 2003, 42, 5392–5398. [Google Scholar] [CrossRef]
- Bamberger, A.; Sieder, G.; Maurer, G. High-pressure (vapor+ liquid) equilibrium in binary mixtures of (carbon dioxide+ water or acetic acid) at temperatures from 313 to 353 K. J. Supercrit. Fluids 2000, 17, 97–110. [Google Scholar] [CrossRef]
- Mohammadi, A.H.; Chapoy, A.; Tohidi, B.; Richon, D. Water content measurement and modeling in the nitrogen+ water system. J. Chem. Eng. Data 2005, 50, 541–545. [Google Scholar] [CrossRef]
- Marinakis, D.; Varotsis, N. Solubility measurements of (methane+ ethane+ propane) mixtures in the aqueous phase with gas hydrates under vapour unsaturated conditions. J. Chem. Thermodyn. 2013, 65, 100–105. [Google Scholar] [CrossRef]
- Kondori, J.; Zendehboudi, S.; Hossain, M.E. A review on simulation of methane production from gas hydrate reservoirs: Molecular dynamics prospective. J. Pet. Sci. Eng. 2017, 159, 754–772. [Google Scholar] [CrossRef]
- Kondori, J.; Zendehboudi, S.; James, L. Evaluation of gas hydrate formation temperature for gas/water/salt/alcohol systems: Utilization of extended UNIQUAC model and PC-SAFT equation of state. Ind. Eng. Chem. Res. 2018, 57, 13833–13855. [Google Scholar] [CrossRef]
- Tong, D.; Trusler, J.M.; Vega-Maza, D. Solubility of CO2 in aqueous solutions of CaCl2 or MgCl2 and in a synthetic formation brine at temperatures up to 423 K and pressures up to 40 MPa. J. Chem. Eng. Data 2013, 58, 2116–2124. [Google Scholar] [CrossRef]
- Teng, H.; Yamasaki, A. Solubility of liquid CO2 in synthetic sea water at temperatures from 278 K to 293 K and pressures from 6.44 MPa to 29.49 MPa, and densities of the corresponding aqueous solutions. J. Chem. Eng. Data 1998, 43, 2–5. [Google Scholar] [CrossRef]
- Lucile, F.; Cézac, P.; Contamine, F.; Serin, J.-P.; Houssin, D.; Arpentinier, P. Solubility of carbon dioxide in water and aqueous solution containing sodium hydroxide at temperatures from (293.15 to 393.15) K and pressure up to 5 MPa: Experimental measurements. J. Chem. Eng. Data 2012, 57, 784–789. [Google Scholar] [CrossRef]
- Nighswander, J.A.; Kalogerakis, N.; Mehrotra, A.K. Solubilities of carbon dioxide in water and 1 wt.% sodium chloride solution at pressures up to 10 MPa and temperatures from 80 to 200.°C. J. Chem. Eng. Data 1989, 34, 355–360. [Google Scholar] [CrossRef]
- Dhima, A.; de Hemptinne, J.-C.; Jose, J. Solubility of hydrocarbons and CO2 mixtures in water under high pressure. Ind. Eng. Chem. Res. 1999, 38, 3144–3161. [Google Scholar] [CrossRef]
- Michels, A.; Gerver, J.; Bijl, A. The influence of pressure on the solubility of gases. Physica 1936, 3, 797–808. [Google Scholar] [CrossRef]
- O’Sullivan, T.D.; Smith, N.O. Solubility and partial molar volume of nitrogen and methane in water and in aqueous sodium chloride from 50 to 125.deg. and 100 to 600 atm. J. Phys. Chem. 1970, 74, 1460–1466. [Google Scholar]
- Vul’fson, A.; Borodin, O. A thermodynamic analysis of the solubility of gases in water at high pressures and supercritical temperatures. Russ. J. Phys. Chem. A 2007, 81, 510–514. [Google Scholar] [CrossRef]
- Wang, L.-K.; Chen, G.-J.; Han, G.-H.; Guo, X.-Q.; Guo, T.-M. Experimental study on the solubility of natural gas components in water with or without hydrate inhibitor. Fluid Phase Equilibria 2003, 207, 143–154. [Google Scholar] [CrossRef]
- Chapoy, A.; Mohammadi, A.H.; Tohidi, B.; Richon, D. Gas solubility measurement and modeling for the nitrogen+ water system from 274.18 K to 363.02 K. J. Chem. Eng. Data 2004, 49, 1110–1115. [Google Scholar] [CrossRef]
- Prutton, C.; Savage, R. The solubility of carbon dioxide in calcium chloride-water solutions at 75, 100, 120 and high pressures1. J. Am. Chem. Soc. 1945, 67, 1550–1554. [Google Scholar] [CrossRef]
- Bando, S.; Takemura, F.; Nishio, M.; Hihara, E.; Akai, M. Solubility of CO2 in aqueous solutions of NaCl at (30 to 60) C and (10 to 20) MPa. J. Chem. Eng. Data 2003, 48, 576–579. [Google Scholar] [CrossRef]
- Smith, N.O.; Kelemen, S.; Nagy, B. Solubility of natural gases in aqueous salt solutions—II: Nitrogen in aqueous NaCl, CaCl2, Na2SO4 and MgSO4 at room temperatures and at pressures below 1000 psia. Geochim. Cosmochim. Acta 1962, 26, 921–926. [Google Scholar] [CrossRef]
- Crovetto, R.; Fernández-Prini, R.; Japas, M.L. Solubilities of inert gases and methane in H2O and in D2O in the temperature range of 300 to 600 K. J. Chem. Phys. 1982, 76, 1077–1086. [Google Scholar] [CrossRef]
- Battino, R.; Clever, H.L. The solubility of gases in liquids. Chem. Rev. 1966, 66, 395–463. [Google Scholar] [CrossRef]
- Kang, X.; Liu, C.; Zeng, S.; Zhao, Z.; Qian, J.; Zhao, Y. Prediction of Henry’s law constant of CO2 in ionic liquids based on SEP and Sσ-profile molecular descriptors. J. Mol. Liq. 2018, 262, 139–147. [Google Scholar] [CrossRef]
- Kang, X.; Qian, J.; Deng, J.; Latif, U.; Zhao, Y. Novel molecular descriptors for prediction of H2S solubility in ionic liquids. J. Mol. Liq. 2018, 265, 756–764. [Google Scholar] [CrossRef]
- Kang, X.; Zhao, Y.; Li, J. Predicting refractive index of ionic liquids based on the extreme learning machine (ELM) intelligence algorithm. J. Mol. Liq. 2018, 250, 44–49. [Google Scholar] [CrossRef]
- Qiao, W.; Huang, K.; Azimi, M.; Han, S. A Novel Hybrid Prediction Model for Hourly Gas Consumption in Supply Side Based on Improved Machine Learning Algorithms. IEEE Access 2019, 7, 88218–88230. [Google Scholar] [CrossRef]
- Qiao, W.; Lu, H.; Zhou, G.; Azimi, M.; Yang, Q.; Tian, W. A hybrid algorithm for carbon dioxide emissions forecasting based on improved lion swarm optimizer. J. Clean. Prod. 2020, 244, 118612. [Google Scholar] [CrossRef]
- Hemmati-Sarapardeh, A.; Hajirezaie, S.; Soltanian, M.R.; Mosavi, A.; Nabipour, N.; Shamshirband, S.; Chau, K.W. Modeling natural gas compressibility factor using a hybrid group method of data handling. Eng. Appl. Comput. Fluid Mech. 2020, 14, 27–37. [Google Scholar] [CrossRef]
- Qiao, W.; Yang, Z.; Kang, Z.; Pan, Z. Short-term natural gas consumption prediction based on Volterra adaptive filter and improved whale optimization algorithm. Eng. Appl. Artif. Intell. 2020, 87, 103323. [Google Scholar] [CrossRef]
- Choubin, B.; Abdolshahnejad, M.; Moradi, E.; Querol, X.; Mosavi, A.; Shamshirband, S.; Ghamisi, P. Spatial hazard assessment of the PM10 using machine learning models in Barcelona, Spain. Sci. Total Environ. 2020, 701, 134474. [Google Scholar] [CrossRef]
- Zhao, Y.; Gao, J.; Huang, Y.; Afzal, R.M.; Zhang, X.; Zhang, S. Predicting H 2 S solubility in ionic liquids by the quantitative structure–property relationship method using S σ-profile molecular descriptors. RSC Adv. 2016, 6, 70405–70413. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: A new learning scheme of feedforward neural networks. Neural Netw. 2004, 2, 985–990. [Google Scholar]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Bengio, Y. Learning deep architectures for AI. Found. Trends® Mach. Learn. 2009, 2, 1–127. [Google Scholar] [CrossRef]
- Liu, Q.; Yin, J.; Leung, V.C.; Zhai, J.-H.; Cai, Z.; Lin, J. Applying a new localized generalization error model to design neural networks trained with extreme learning machine. Neural Comput. Appl. 2016, 27, 59–66. [Google Scholar] [CrossRef]
- Rao, C.R.; Mitra, S.K. Further contributions to the theory of generalized inverse of matrices and its applications. Sankhyā Indian J. Stat. Ser. A 1971, 33, 289–300. [Google Scholar]
- Bemani, A.; Baghban, A.; Mohammadi, A.H. An insight into the modeling of sulfur solubility of sour gases in supercritical region. J. Pet. Sci. Eng. 2019, 184, 106459. [Google Scholar] [CrossRef]
- Razavi, R.; Bemani, A.; Baghban, A.; Mohammadi, A.H.; Habibzadeh, S. An insight into the estimation of fatty acid methyl ester based biodiesel properties using a LSSVM model. Fuel 2019, 243, 133–141. [Google Scholar] [CrossRef]
- Mesbah, M.; Soroush, E.; Azari, V.; Lee, M.; Bahadori, A.; Habibnia, S. Vapor liquid equilibrium prediction of carbon dioxide and hydrocarbon systems using LSSVM algorithm. J. Supercrit. Fluids 2015, 97, 256–267. [Google Scholar] [CrossRef]
- Rousseeuw, P.J.; Leroy, A.M. Robust Regression and Outlier Detection; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Razavi, R.; Sabaghmoghadam, A.; Bemani, A.; Baghban, A.; Chau, K.-W.; Salwana, E. Application of ANFIS and LSSVM strategies for estimating thermal conductivity enhancement of metal and metal oxide based nanofluids. Eng. Appl. Comput. Fluid Mech. 2019, 13, 560–578. [Google Scholar] [CrossRef]
- Baghban, A.; Kahani, M.; Nazari, M.A.; Ahmadi, M.H.; Yan, W.-M. Sensitivity analysis and application of machine learning methods to predict the heat transfer performance of CNT/water nanofluid flows through coils. Int. J. Heat Mass Transf. 2019, 128, 825–835. [Google Scholar] [CrossRef]
- Baghban, A.; Kardani, M.N.; Mohammadi, A.H. Improved estimation of Cetane number of fatty acid methyl esters (FAMEs) based biodiesels using TLBO-NN and PSO-NN models. Fuel 2018, 232, 620–631. [Google Scholar] [CrossRef]
- Baghban, A.; Adelizadeh, M. On the determination of cetane number of hydrocarbons and oxygenates using Adaptive Neuro Fuzzy Inference System optimized with evolutionary algorithms. Fuel 2018, 230, 344–354. [Google Scholar] [CrossRef]
- Zarei, F.; Rahimi, M.R.; Razavi, R.; Baghban, A. Insight into the experimental and modeling study of process intensification for post-combustion CO2 capture by rotating packed bed. J. Clean. Prod. 2019, 211, 953–961. [Google Scholar] [CrossRef]
- Baghban, A.; Pourfayaz, F.; Ahmadi, M.H.; Kasaeian, A.; Pourkiaei, S.M.; Lorenzini, G. Connectionist intelligent model estimates of convective heat transfer coefficient of nanofluids in circular cross-sectional channels. J. Therm. Anal. Calorim. 2018, 132, 1213–1239. [Google Scholar] [CrossRef]
- Bemani, A.; Baghban, A.; Shamshirband, S.; Mosavi, A.; Csiba, P.; Varkonyi-Koczy, A.R. Applying ANN, ANFIS, and LSSVM Models for Estimation of Acid Solvent Solubility in Supercritical CO2. Preprints 2019. [CrossRef]
- Shamshirband, S.; Hadipoor, M.; Baghban, A.; Mosavi, A.; Bukor, J.; Várkonyi-Kóczy, A.R. Developing an ANFIS-PSO Model to Predict Mercury Emissions in Combustion Flue Gases. Mathematics 2019, 7, 965. [Google Scholar] [CrossRef]
- Shabani, S.; Samadianfard, S.; Sattari, M.T.; Mosavi, A.; Shamshirband, S.; Kmet, T.; Várkonyi-Kóczy, A.R. Modeling Pan Evaporation Using Gaussian Process Regression K-Nearest Neighbors Random Forest and Support Vector Machines; Comparative Analysis. Atmosphere 2020, 11, 66. [Google Scholar] [CrossRef]
- Ouaer, H.; Hosseini, A.H.; Nait Amar, M.; El Amine Ben Seghier, M.; Ghriga, M.A.; Nabipour, N.; Andersen, P.Ø.; Mosavi, A.; Shamshirband, S. Rigorous Connectionist Models to Predict Carbon Dioxide Solubility in Various Ionic Liquids. Appl. Sci. 2020, 10, 304. [Google Scholar] [CrossRef]
| Author | P (Mpa) | T (°C) | Composition | Mole Fraction of the Components in the Gaseous Phase |
|---|---|---|---|---|
| Culberson et al. | 0.8–69.61 | 37.78–171.11 | Pure water | C1: 0.0000698–0.0033 |
| Kiepe et al. | 0.304–10.23 | 40–100.14 | Pure water, LiBr, KBr, LiCl, KCl | C1: 0.00003–0.00154 |
| Chapoy et al. | 0.357–18 | 1.98–95.01 | Pure water | C1: 0.000204–0.002459 |
| C2: 0.0000147–0.0000674 | ||||
| C3: 0.0000321–0.0002694 | ||||
| C4: 0.00000387–0.00001121 | ||||
| Marinakis et al. | 6.22–20.1 | 1.4–25.98 | Pure water, NaCl | C1: 0.00099–0.00282 |
| C2: 0.000038–0.000249 | ||||
| C3: 0.000006–0.000042 | ||||
| Crovetto et al. | 1.327–6.451 | 24.35–245.15 | Pure water | C1: 0.0002124–0.0010337 |
| Wang et al. | 1–40.03 | 2.5–30.05 | Pure water | C1: 0.000563–0.004049 |
| C2: 0.0000986–0.000864 | ||||
| Amirjafari | 4.66–56.16 | 54.44–104.44 | Pure water | C1: 0.00045–0.0037 |
| C2: 0.000119–0.001768 | ||||
| C3: 1.9 × 10−5–0.001863 | ||||
| O’Sullivan et al. | 10.2–62 | 51.5–125 | Pure water, NaCl | C1: 0.000805–0.0043 |
| C2: 0.000825–0.001438 | ||||
| Michels et al. | 4.09–45.89 | 25–150 | Pure water, NaCl, LiCl, NaBr, NaI, CaCl2 | C1: 0.000173–0.00269 |
| Mohammadi et al. | 1.14–31.1 | 4.65–24.75 | Pure water | C1: 0.000313–0.00311 |
| Vul’fson et al. | 2.53–60.8 | 19.95–79.95 | Pure water | C1: 0.000361–0.004328 |
| Dhima | 2.5–100 | 71 | Pure water | C1: 0.000127–0.005085 |
| C2: 0.000821–0.001398 | ||||
| C4: 0.000021–0.000103 |
| Dataset | R2 | MRE (%) | MSE | RMSE |
|---|---|---|---|---|
| Training | 0.985 | 22.049 | 1.33285 × 10−8 | 0.0001 |
| Testing | 0.987 | 22.054 | 1.05351 × 10−8 | 0.0001 |
| Overall | 0.985 | 22.050 | 1.26295 × 10−8 | 0.0001 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nabipour, N.; Mosavi, A.; Baghban, A.; Shamshirband, S.; Felde, I. Extreme Learning Machine-Based Model for Solubility Estimation of Hydrocarbon Gases in Electrolyte Solutions. Processes 2020, 8, 92. https://doi.org/10.3390/pr8010092
Nabipour N, Mosavi A, Baghban A, Shamshirband S, Felde I. Extreme Learning Machine-Based Model for Solubility Estimation of Hydrocarbon Gases in Electrolyte Solutions. Processes. 2020; 8(1):92. https://doi.org/10.3390/pr8010092
Chicago/Turabian StyleNabipour, Narjes, Amir Mosavi, Alireza Baghban, Shahaboddin Shamshirband, and Imre Felde. 2020. "Extreme Learning Machine-Based Model for Solubility Estimation of Hydrocarbon Gases in Electrolyte Solutions" Processes 8, no. 1: 92. https://doi.org/10.3390/pr8010092
APA StyleNabipour, N., Mosavi, A., Baghban, A., Shamshirband, S., & Felde, I. (2020). Extreme Learning Machine-Based Model for Solubility Estimation of Hydrocarbon Gases in Electrolyte Solutions. Processes, 8(1), 92. https://doi.org/10.3390/pr8010092







