Ascertainment of Surfactin Concentration in Bubbles and Foam Column Operated in Semi-Batch
Abstract
1. Introduction
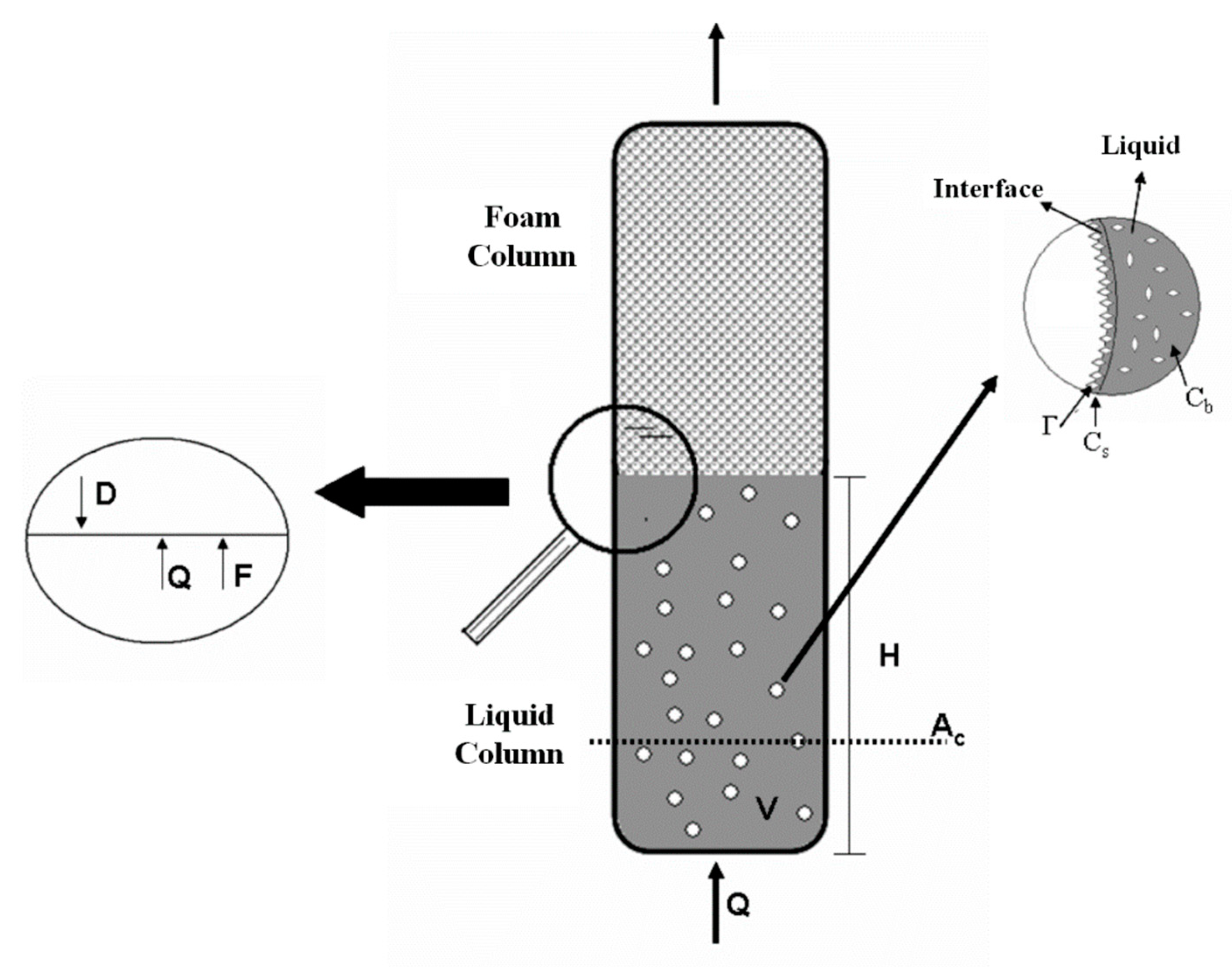
1.1. Mathematical Modeling
1.2. Overall Mass Balance in the Liquid Column
1.3. Liquid Column Surfactant Mass Balance
1.4. Mass Balance for the Surfactant on the Bubble Surface
2. Materials and Methods
2.1. Surfactin
2.2. Bubbles and Foam Column
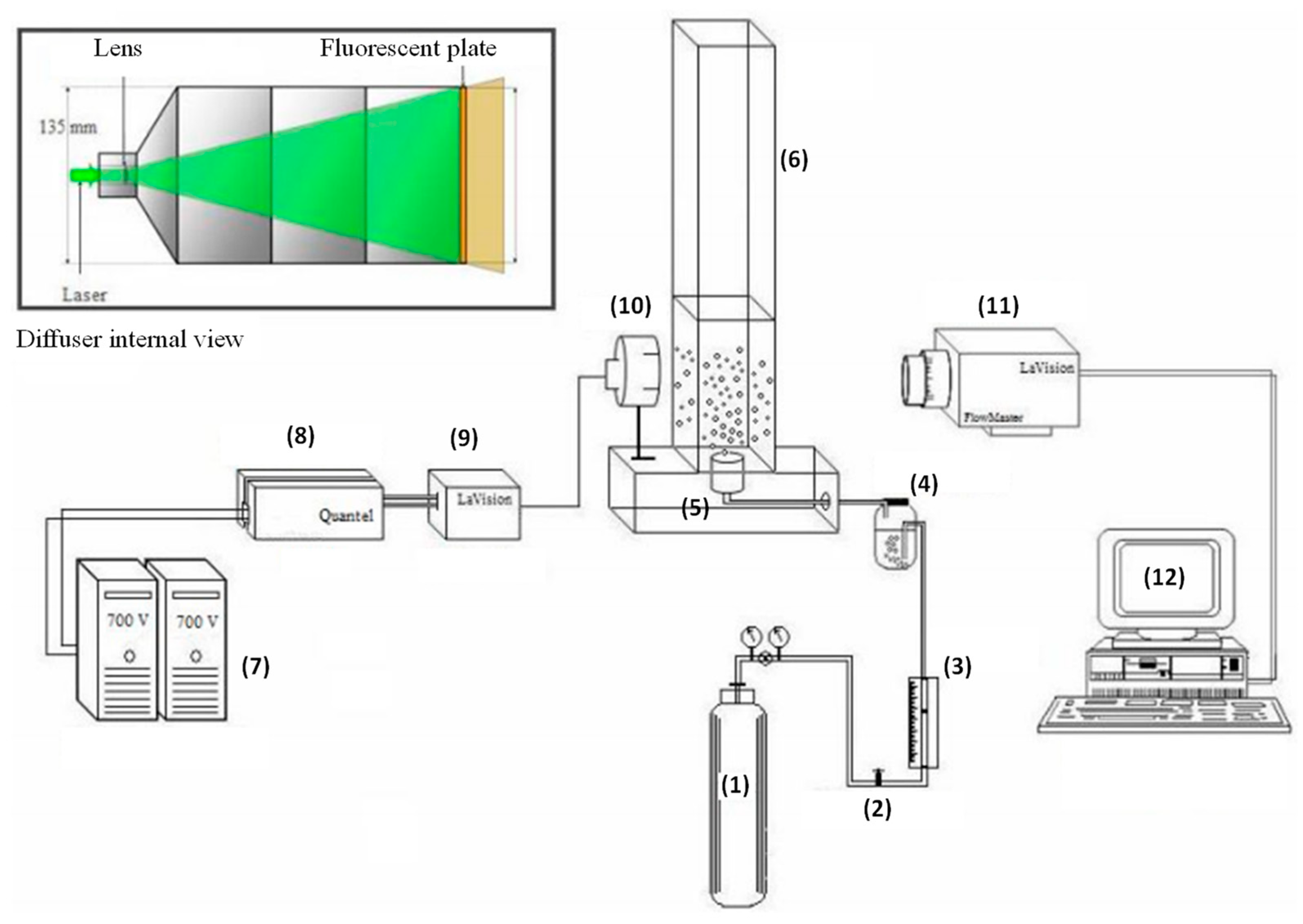
2.2.1. Experimental Apparatus
2.2.2. Column Operation
2.3. Ascertainment of the Biosurfactant Concentration
2.4. Resolution of the Mass Balance Equations: Process Simulation
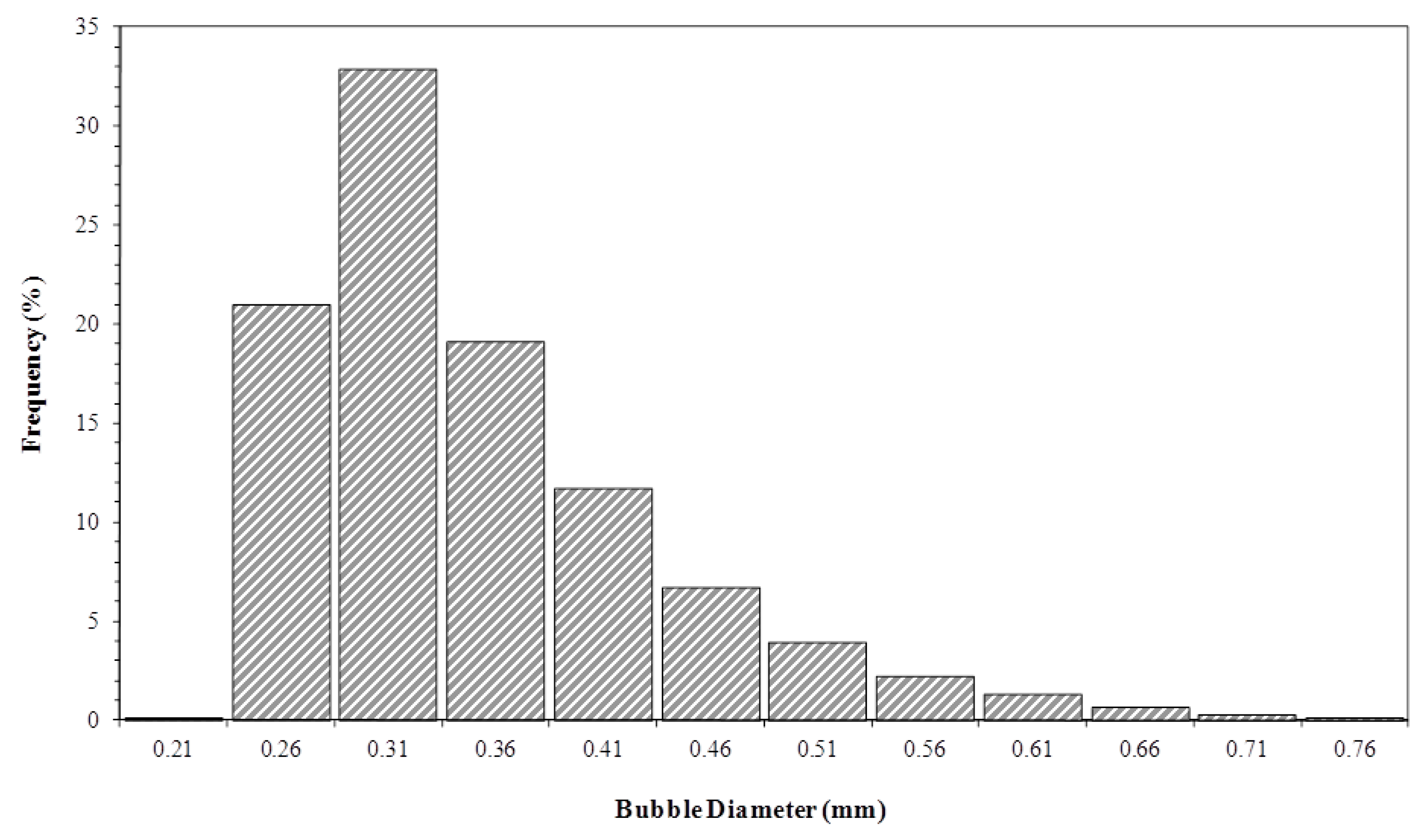
2.5. Bubble Size Distribution in the Liquid Column
2.5.1. Experimental Apparatus
2.5.2. Experimental Procedure
2.6. Obtaining the Isotherms
3. Results and Discussion
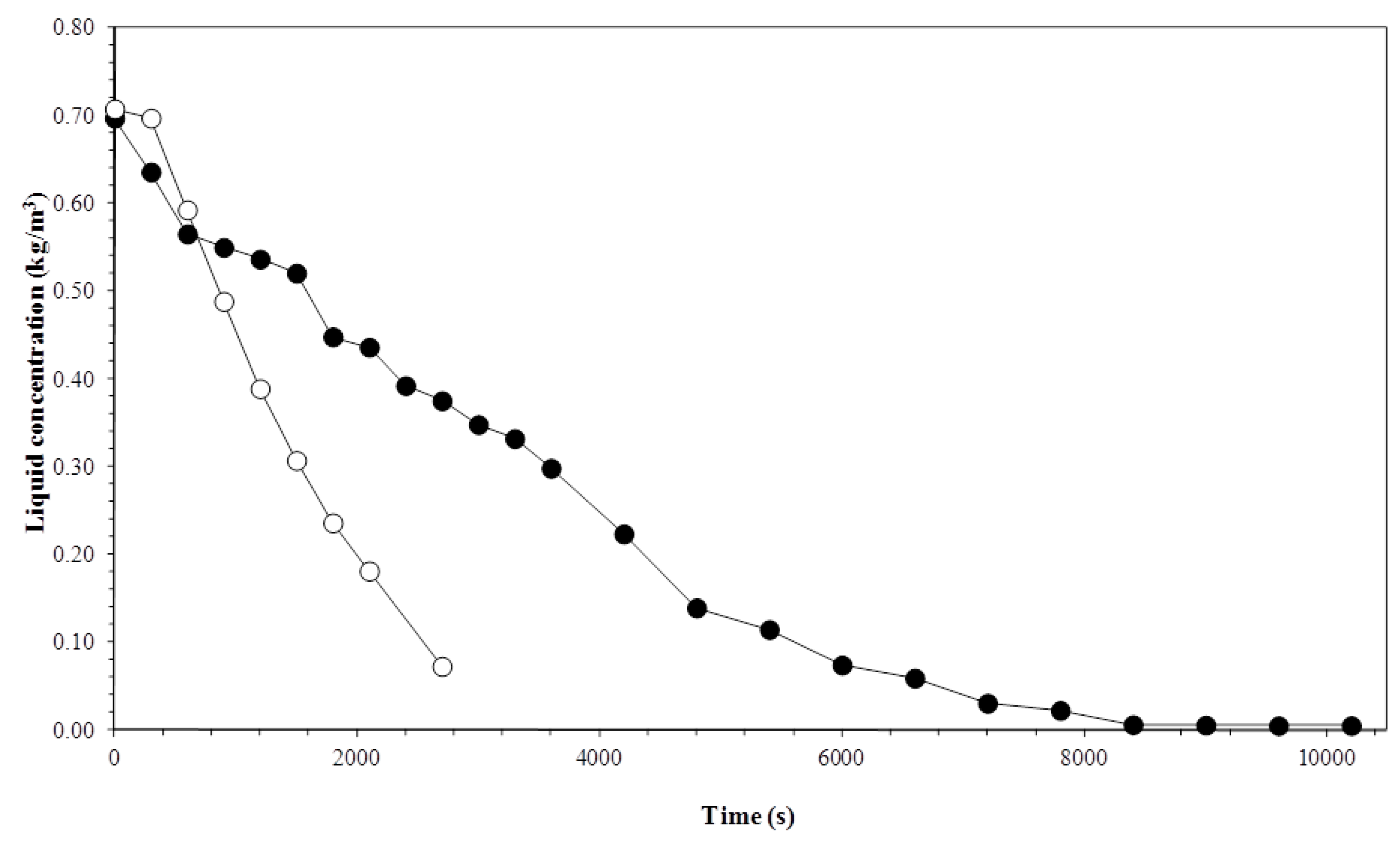
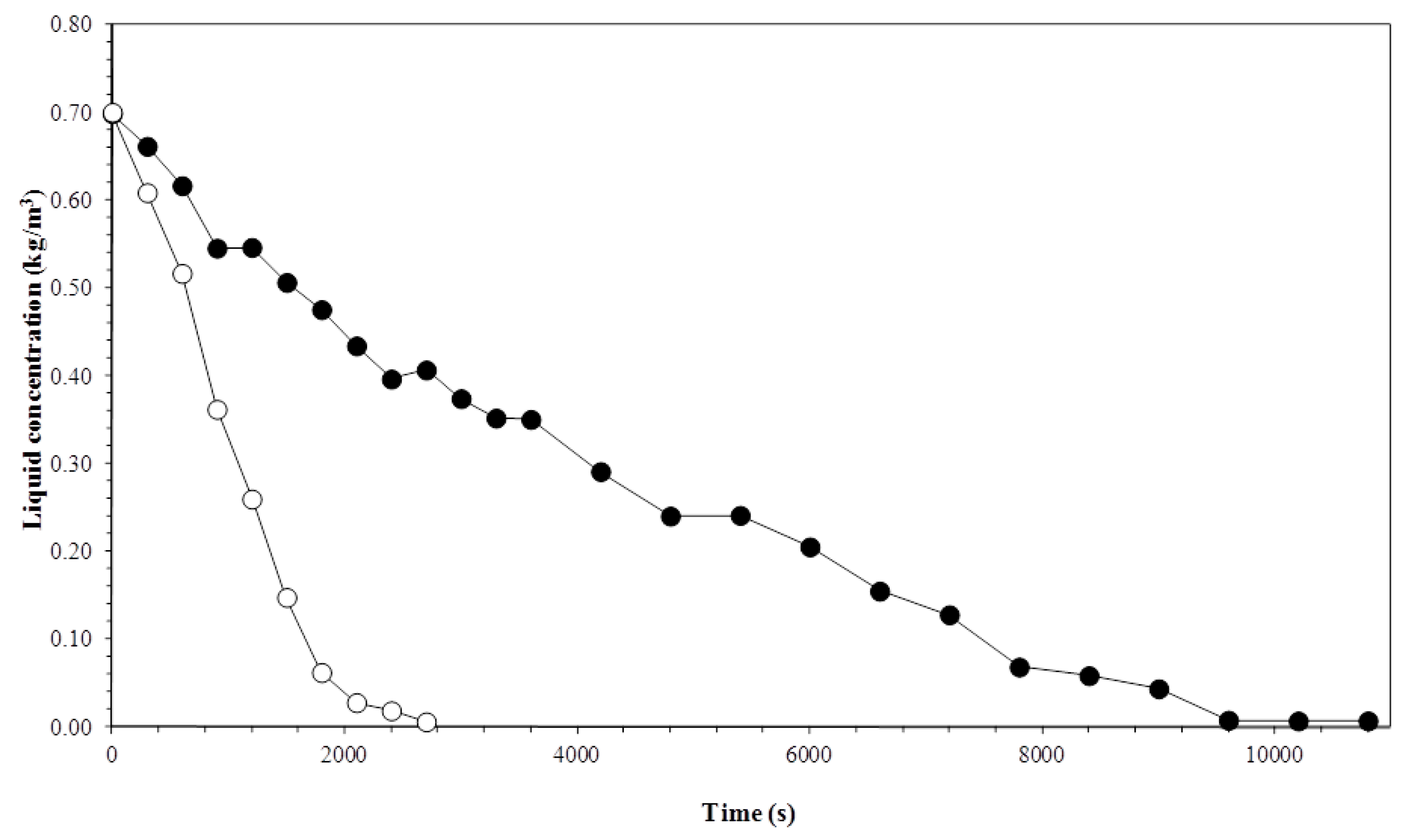
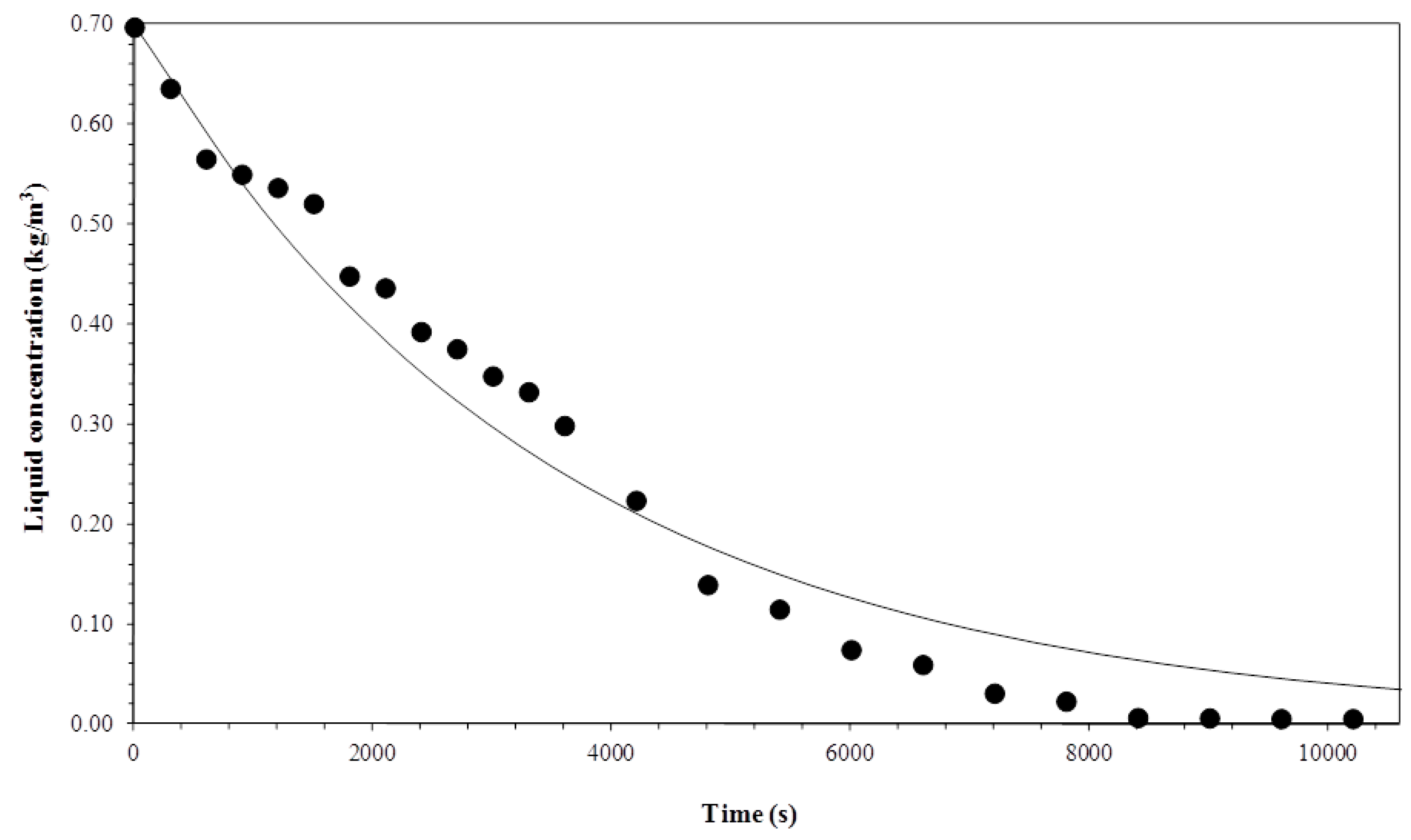
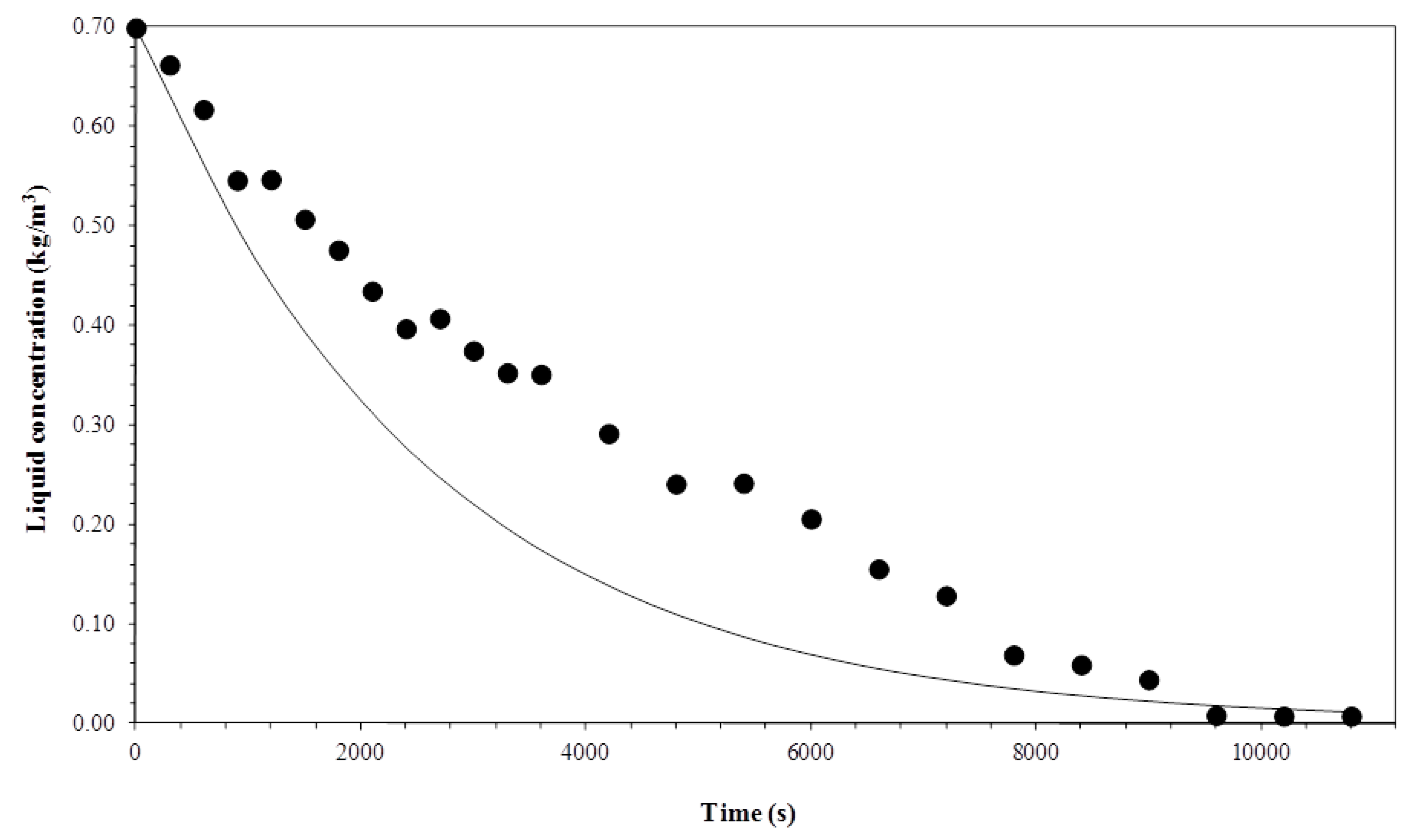
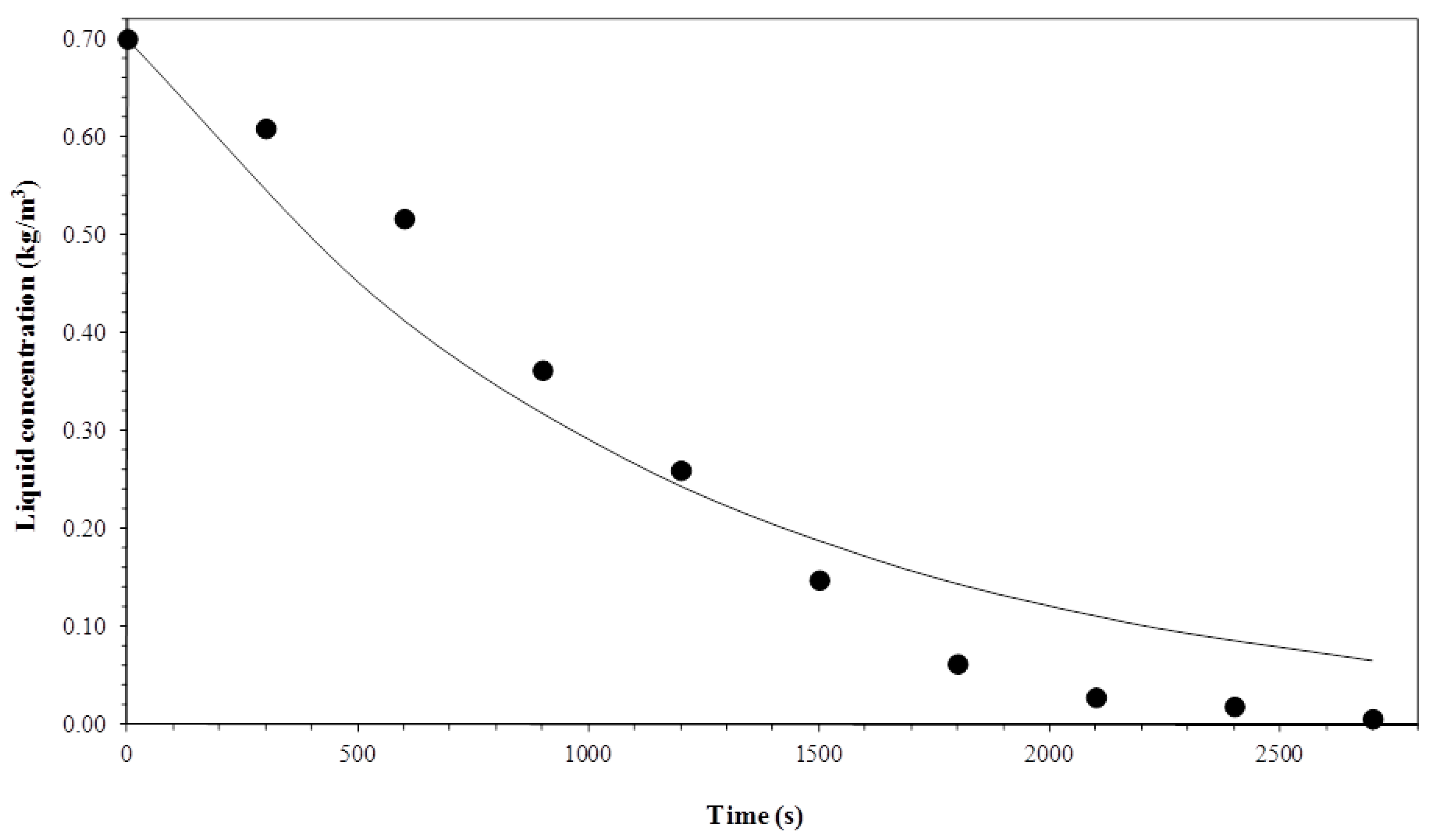
3.1. Biosurfactant Concentration in the Liquid Column
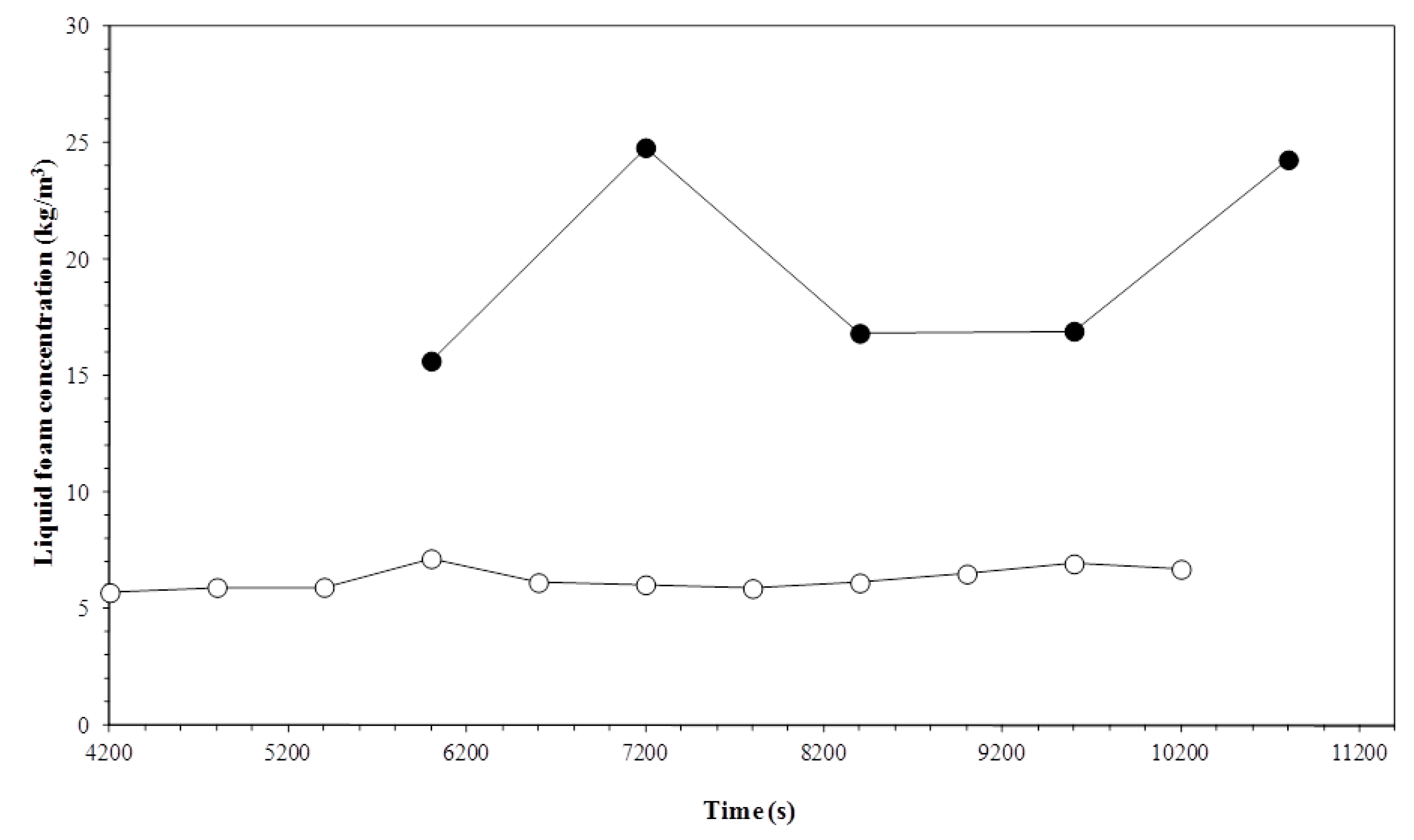
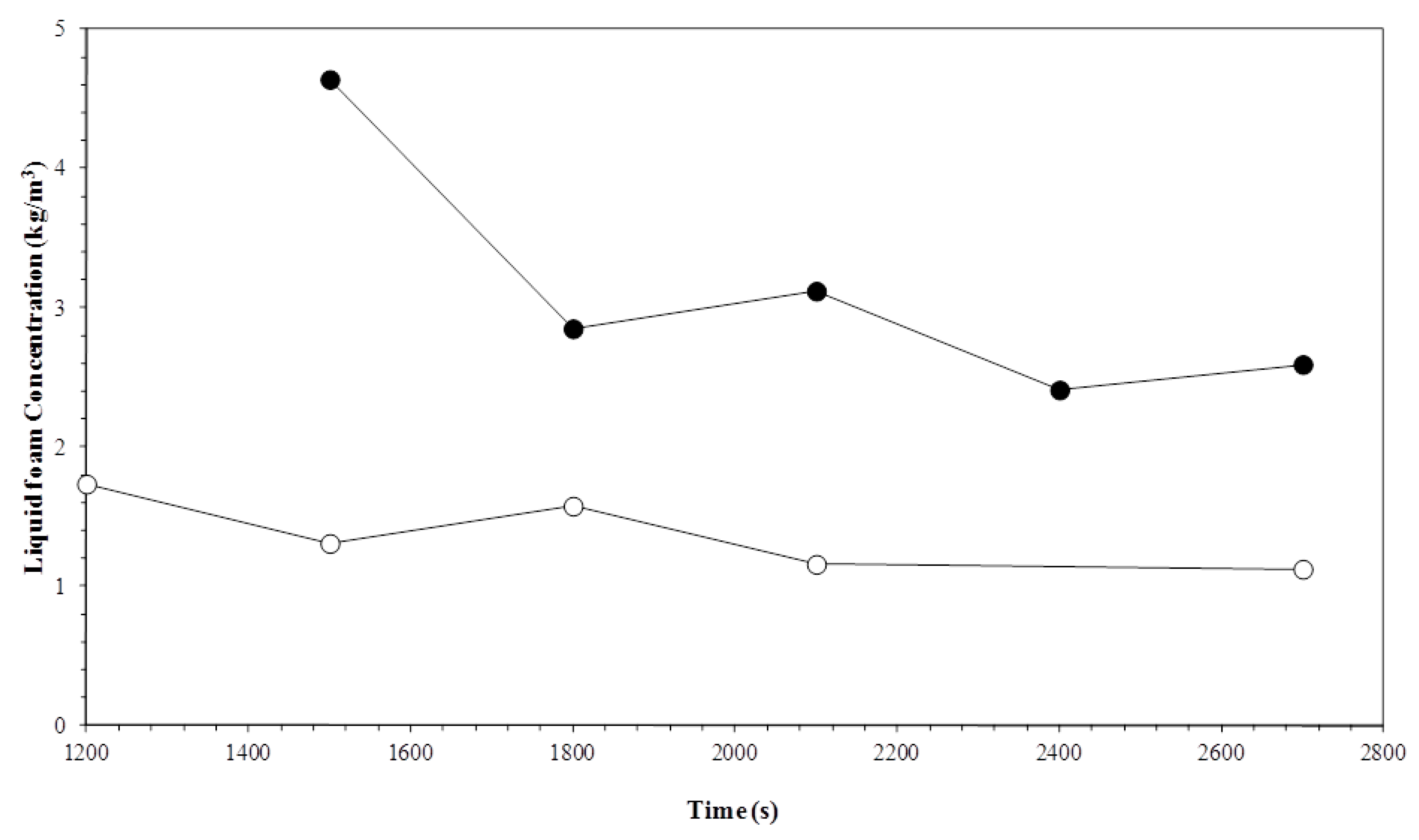
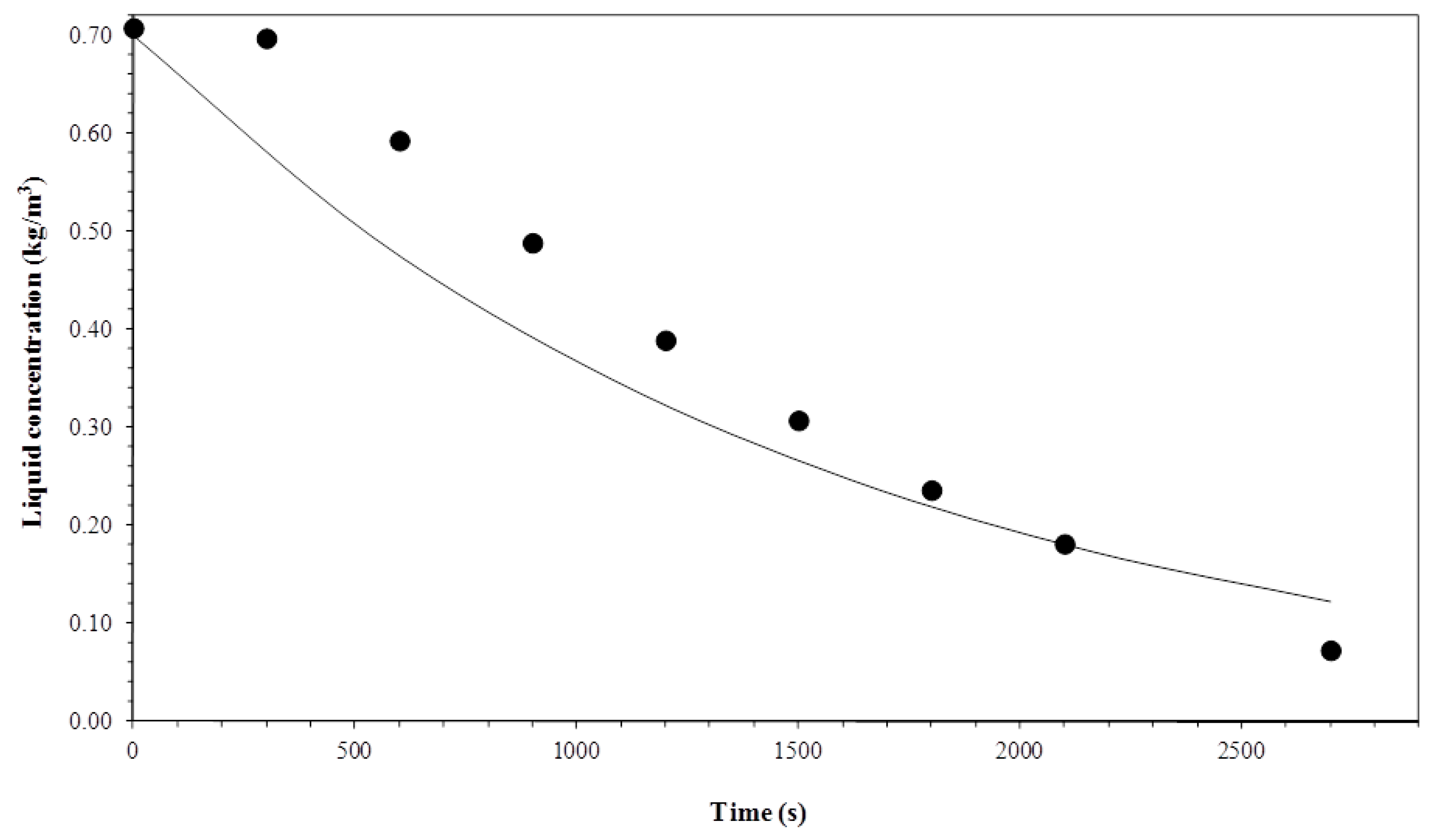
3.2. Liquid Foam Concentration
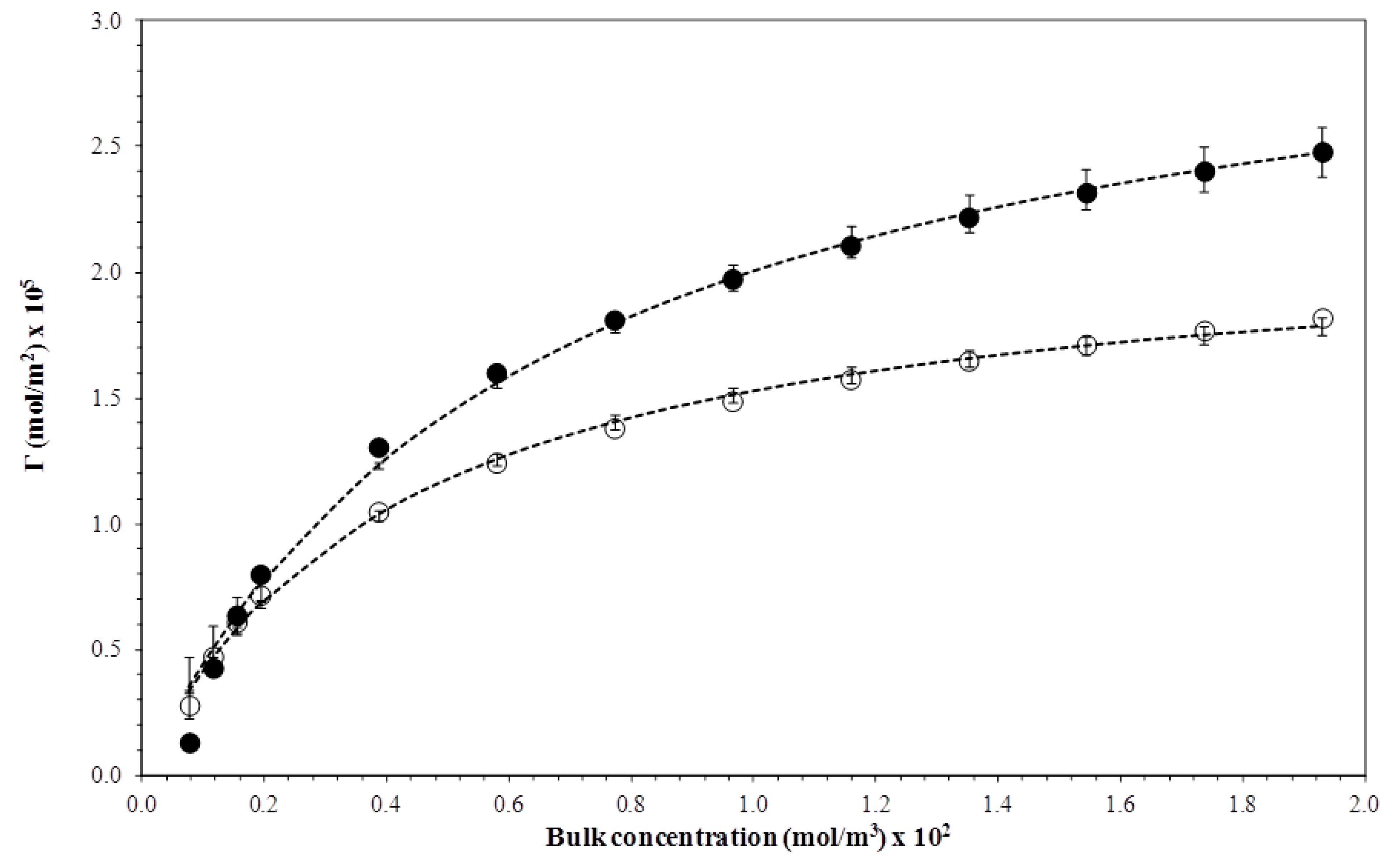
3.3. Adsorption Isotherm
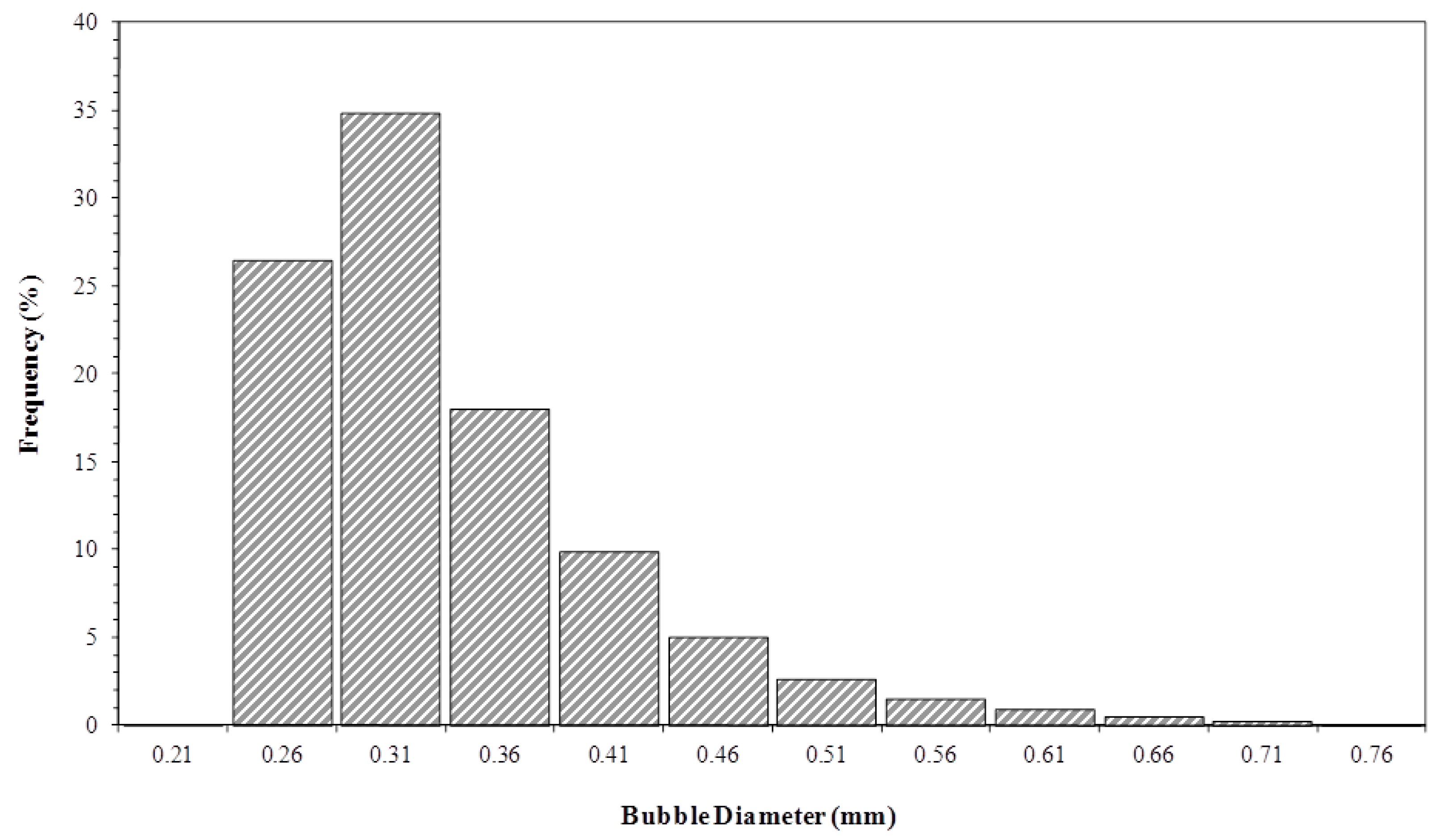
3.4. Bubble Size Distribution in the Liquid Column
3.5. Comparison between Experimental and Simulated Data
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Â | monolayer area/molecule (m2 kg−1) |
| Ab | gas bubble area (m2) |
| Ac | cross-sectional area (m2) |
| Cb | surfactant bulk concentration (kg m−3) |
| Cd | drainage liquid surfactant concentration (kg m−3) |
| CF | surfactant concentration in the interstitial liquid foam (kg m−3) |
| Cs | surfactant concentration in the layer around the bubbles (kg m−3) |
| D | foam column drainage fluid volumetric flow (m3 s−1) |
| db | diameter of bubbles (m) |
| Di | diffusion coefficient (m2 s−1) |
| F | liquid column dragged fluid volumetric flow (m3 s−1) |
| g | gravity acceleration (m s−2) |
| H | liquid column height (m) |
| K | equilibrium constant (m3 kg−1) |
| Kd | equilibrium constant (mol m−3) |
| kLa | volumetric mass transfer coefficient (s−1) |
| Mi | solute molar mass (kg mol−1) |
| ni | number of bubbles (-) |
| Q | gas flow rate (m3 s−1) |
| R | gas constant (J K−1 mol−1) |
| T | temperature (K) |
| V | liquid column volume (m3) |
| Vb | gas bubble volume (m3) |
| Vg | gas surface velocity (m s−1) |
| Greek Letters | |
| µl | liquid viscosity (Pa s) |
| Γ | surface concentration (mol m−2) |
| Γ | surface tension (mN m−1) |
| Γexit | surface concentration at the liquid column exit (mol m−2) |
| Γm | average surface concentration in the liquid column (mol m−2) |
| Γmax | maximum concentration in the adsorbed liquid gas interface (mol m−2) |
| εg | liquid column gas fraction (-) |
| ρg | gas density (kg m−3) |
| ρl | liquid density (kg m−3) |
| τ | bubble ascent time (s) |
| υ | bubbles ascent velocity (m s−1) |
References
- Atlaa, S.B.; Chen, C.Y.; Yang, J.; Chen, C.C.; Sun, A.C.; Lin, K.H.; Maity, J.P.; Pan, W.; Cheng, K.C. Foam fractionation of crystal growth for nanotechnology. Chem. Eng. J. 2012, 184, 333–341. [Google Scholar] [CrossRef]
- Brown, A.K.; Kaul, A.; Varley, J. Continuous foaming for protein recovery: Part II. Selective recovery of proteins from binary mixtures. Biotechnol. Bioeng. 1999, 62, 291–300. [Google Scholar] [CrossRef]
- Brown, L.; Narsimhan, G.; Wankat, P.C. Foam fractionation of globular proteins. Biotechnol. Bioeng. 1990, 036, 947–959. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Liu, W.; Wu, Z.; Zhao, Y.; Yin, H.; Ding, L.; Hu, N.; Li, H.; Zheng, H. The separation of catechol and phenol with each other by two-stage batch foam fractionation. Chem. Eng. J. 2017, 308, 683. [Google Scholar] [CrossRef]
- Kamalanathan, I.D.; Martin, P.J. Competitive adsorption of surfactant–protein mixtures in a continuous stripping mode foam fractionation column. Chem. Eng. Sci. 2016, 146, 291–301. [Google Scholar] [CrossRef]
- Lu, K.; Li, R.; Wu, Z.; Hou, K.; Du, X.; Zhao, Y. Wall effect on rising foam drainage and its application to foam separation. Sep. Purif. Technol. 2013, 118, 710. [Google Scholar] [CrossRef]
- Lucena, S.L. Efeito do Refluxo Externo no Fracionamento de Soluções Diluídas de Proteínas em Colunas de Bolhas e Espuma. Master’s Thesis, University of Campinas, Campinas, Brazil, 1995. [Google Scholar]
- Santana, C.C. Separação cromatográfica. Braz. J. Chem. Eng. 1994, 5, 1. [Google Scholar]
- Silva, M.T.S.; Soares, C.M.F.; Lima, A.S.; Santana, C.C. Integral production and concentration of surfactin from Bacillus sp. ITP-001 by semi-batch foam fractionation. Biochem. Eng. J. 2015, 104, 91–97. [Google Scholar] [CrossRef]
- Rosa, P.T.V.; Santana, C.C.; Carbonell, R.G. Determination of the liquid pool surfactant and protein concentration for semi-batch foam fractionation columns. Braz. J. Chem. Eng. 2007, 24, 1. [Google Scholar] [CrossRef]
- Tobin, S.T.; Weaire, D.; Hutzler, S. Theoretical analysis of the performance of a foam fractionation column. Proc. R. Soc. A 2014, 470, 470. [Google Scholar] [CrossRef]
- Huang, D.; Liu, W.; Wu, Z.; Liu, G.; Yin, H.; Chen, Y.; Hu, N.; Jia, L. Removal of pyridine from its wastewater by using a novel foam fractionation column. Chem. Eng. J. 2017, 321, 151. [Google Scholar] [CrossRef]
- Lucena, S.L.; Santana, C.C. Separation of bovine serum albumin and cytochrome c using gas-liquid interface adsorption. Hungar. J. Ind. Chem. 2000, 28, 81–84. [Google Scholar]
- Perna, R.F. Fractionation of Surfactin on a Bubble and Foam Column. Master’s Thesis, University of Campinas, Campinas, Brazil, 2010. [Google Scholar]
- Grieves, R.B. Treatise on Analytical Chemistry, 2nd ed.; Wiley: New York, NY, USA, 1982; Volume 5, p. 371. [Google Scholar]
- Lemlich, R. Adsorptive Bubble Separation Techniques; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Thomas, A.; Winkler, A. Topics in Enzyme and Fermentation Biotechnology; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 1977. [Google Scholar]
- Chen, C.; Baker, S.C.; Darton, R.C. Batch production of biosurfactant with foam fractionation. J. Chem. Tech. Biotechnol. 2006, 81, 1923. [Google Scholar] [CrossRef]
- Davis, D.A.; Lynch, H.C.; Varley, J. The application of foaming for the recovery of Surfactin from B. subtilis ATCC 21332 cultures. Enzyme Microb. Technol. 2001, 28, 346–354. [Google Scholar] [CrossRef]
- Guo, S.; Wu, Z.; Liu, W.; Huang, D.; Li, H.; Hu, N.J. Enrichment and isolation of phenol from its aqueous solution using foam fractionation. Ind. Eng. Chem. 2016, 36, 180. [Google Scholar] [CrossRef]
- Huang, D.; Wu, Z.L.; Liu, W.; Hu, N.; Li, H.Z. A novel process intensification approach of recovering creatine from its wastewater by batch foam fractionation. Chem. Eng. Process. 2016, 104, 13–21. [Google Scholar] [CrossRef]
- Kang, S.; Li, R.; Wu, Z.; Guo, S.; Gao, Y. Effective improvement of defoaming efficiency using foam breaker with synthetic sponge cylinders in foam fractionation. Chem. Eng. Process. 2016, 106, 26. [Google Scholar] [CrossRef]
- Krishna, R.; Van Baten, J.M. Mass Transfer in Bubble Column. Catal. Today 2003, 67, 79–80. [Google Scholar] [CrossRef]
- Li, R.; Zhang, Y.; Chang, Y.; Wu, Z.; Wang, Y.; Chen, X.; Wang, T. Role of foam drainage in producing protein aggregates in foam fractionation. Colloids Surf. B 2017, 158, 562. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, M.; Lv, Y.; Tian, S.; Li, N.; Wu, Z.J. Foam fractionation for recovering whey soy protein from whey wastewater: Strengthening foam drainage using a novel internal component with superhydrophobic surface. Taiwan Inst. Chem. Eng. 2017, 78, 39. [Google Scholar] [CrossRef]
- Mouza, A.A.; Dalakoglou, G.K.; Paras, S.V. Effect of liquid properties on the performance of bubble column reactors with fine pore spargers. Chem. Eng. Sci. 2005, 60, 1465–1475. [Google Scholar] [CrossRef]
- Pohorecki, R.; Moniuk, W.; Bielski, P.; Sobieszuk, P.; Dabrowiecki, G. Bubble diameter correlation via numerical experiment. Chem. Eng. J. 2005, 113, 35–39. [Google Scholar] [CrossRef]
- Tian, S.; Wu, Z.; Liu, W.; Zhang, M.; Lv, Y.; Xu, Y.; Liu, G.; Zhao, Y.J. Effective recovery of casein from its highly diluted solution by using a technology of foam fractionation coupled with isoelectric precipitation. Food Eng. 2018, 216, 72. [Google Scholar] [CrossRef]
- Vandu, C.O.; Krishna, R. Influence of scale on the volumetric mass transfer coefficients in bubble columns. Chem. Eng. Process. 2004, 43, 575–579. [Google Scholar] [CrossRef]
- Veera, U.P.; Kataria, K.L.; Joshi, J.B. Effect of superficial gas velocity on gas hold-up profiles in foaming liquids in bubble column reactors. Chem. Eng. J. 2004, 99, 53–58. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, Z.; Liu, G.J. Interfacial adsorption of methyl orange in liquid phase of foam fractionation using dodecyl dimethyl betaine as the collector. Ind. Eng. Chem. 2015, 28, 184. [Google Scholar] [CrossRef]
- Rosa, P.T.V. Fracionamento de Proteínas e Outros Tensoativos em Colunas de Bolhas e Espumas. Ph.D. Thesis, University of Campinas, Campinas, Brazil, 1996. [Google Scholar]
- Lugon, J., Jr.; Silva Neto, A.; Santana, C.C. A hybrid approach with artificial neural networks, levenberg-marquardt and simulated annealing methods for the solution of gas-liquid adsorption inverse problems. Inverse Probl. Sci Eng. 2009, 17, 85–96. [Google Scholar] [CrossRef]
- Alhseinat, E.; Amr, M.; Jumah, R.; Banat, F. Removal of MDEA foam creators using foam fractionation: Parametric study coupled with foam characterization. J. Nat. Gas Sci. Eng. 2015, 26, 502–509. [Google Scholar] [CrossRef]
- Li, R.; Chen, X.; Chang, Y.; Zhang, L.; Zhang, Y.; Zhu, Y.; Wang, T. Increase of bubble size playing a critical role in foam-induced protein aggregation: Aggregation of BSA in foam fractionation. Chem. Eng. Sci. 2017, 174, 387. [Google Scholar] [CrossRef]
- Li, R.; Ding, L.; Wu, Z.; Wang, Y.; Liu, W.; Wang, Y. β-cyclodextrin assisted two-stage foam fractionation of bromelain from the crude extract of pineapple peels. Ind. Crops Prod. 2016, 94, 233. [Google Scholar] [CrossRef]
- Liu, W.; Wu, Z.; Wang, Y.; Li, R.; Huang, D. Isolation of soy whey proteins from isoflavones in the concentrated solution using foam fractionation. Sep. Purif. Technol. 2015, 149, 31. [Google Scholar] [CrossRef]
- Rienzo, M.A.D.; Kamalanathan, I.D.; Martin, P.J. Comparative study of the production of rhamnolipid biosurfactants by B. thailandensis E264 and P. aeruginosa ATCC 9027 using foam fractionation. Process Biochem. 2016, 51, 820. [Google Scholar] [CrossRef]
- Arima, K.; Kakinuma, A.; Tamura, G. Surfactin, a crystalline peptidelipid surfactant produced by Bacillus subtilis: Isolation, characterization and its inhibition of fibrin clot formation. Biochem. Biophys. Res. Commun. 1968, 31, 488. [Google Scholar] [CrossRef]
- Mulligan, C. Environmental applications for biosurfactants. Environ. Pollut. 2005, 133, 183. [Google Scholar] [CrossRef]
- Peypoux, F.; Bonmatin, J.M.; Wallach, J. Recent trends in the biochemistry of surfactin. J. Appl. Microbiol. Biotechnol. 1999, 51, 553. [Google Scholar] [CrossRef]
- Ward, A.F.H.; Tordai, L.J. Time-Dependence of Boundary Tensions of Solutions I. The Role of Diffusion in Time-Effects. Chem. Phys. 1946, 14, 453. [Google Scholar]
- Deckwer, W.D.; Schumpe, A. Improved tools for bubble column reactor design and scale-up. Chem. Eng. Sci. 1993, 48, 889. [Google Scholar] [CrossRef]
- Ozturk, S.S.; Schumpe, A.; Deckwer, W.D. Organic liquids in a bubble column: Holdups and mass transfer coefficients. AIChe J. 1987, 33, 1473. [Google Scholar] [CrossRef]
- Du Nouy, P.L. A new apparatus for measuring surface tension. J. Gen. Physiol. 1919, 5, 521. [Google Scholar] [CrossRef]
- Geankoplis, C.J. Transport Processes and Unit Operations; Prentice-Hall International: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Hamilton, M. Competitive Adsorption of Ethoxylated Alcohol Surfactants to Air-Water Interfaces. Master’s Thesis, North Carolina State University, Raleigh, NV, USA, 1989. [Google Scholar]
- Florence, A.T.; Attwood, D. Physicochemical Principles of Pharmacy; Royal Pharmaceutical Society of Great Britain, Pharmaceutical Press: London, UK, 2006. [Google Scholar]

| Temperature (°C) | Parameters of Adsorption Isotherm | |||
|---|---|---|---|---|
| Γmax (mol m−2) | Kd (mol m−3) | â (m2 kg−1) | K (m3 kg−1) | |
| 15 | 3.32 × 10−5 | 6.55 × 10−3 | 29,000 | 145 |
| 35 | 2.18 × 10−5 | 4.27 × 10−3 | 44,000 | 224 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Firmani Perna, R.; Pereira Gonçalves, M.C.; Costapinto Santana, C. Ascertainment of Surfactin Concentration in Bubbles and Foam Column Operated in Semi-Batch. Processes 2019, 7, 154. https://doi.org/10.3390/pr7030154
Firmani Perna R, Pereira Gonçalves MC, Costapinto Santana C. Ascertainment of Surfactin Concentration in Bubbles and Foam Column Operated in Semi-Batch. Processes. 2019; 7(3):154. https://doi.org/10.3390/pr7030154
Chicago/Turabian StyleFirmani Perna, Rafael, Maria Carolina Pereira Gonçalves, and Cesar Costapinto Santana. 2019. "Ascertainment of Surfactin Concentration in Bubbles and Foam Column Operated in Semi-Batch" Processes 7, no. 3: 154. https://doi.org/10.3390/pr7030154
APA StyleFirmani Perna, R., Pereira Gonçalves, M. C., & Costapinto Santana, C. (2019). Ascertainment of Surfactin Concentration in Bubbles and Foam Column Operated in Semi-Batch. Processes, 7(3), 154. https://doi.org/10.3390/pr7030154






