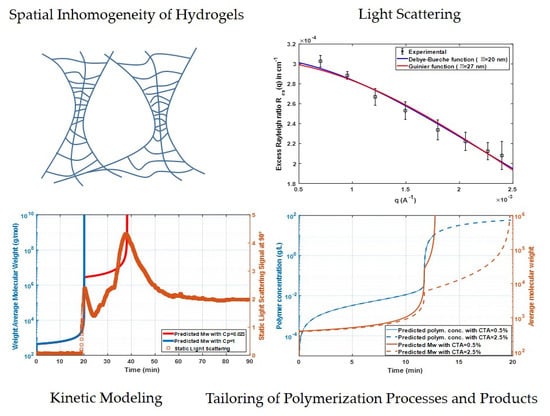
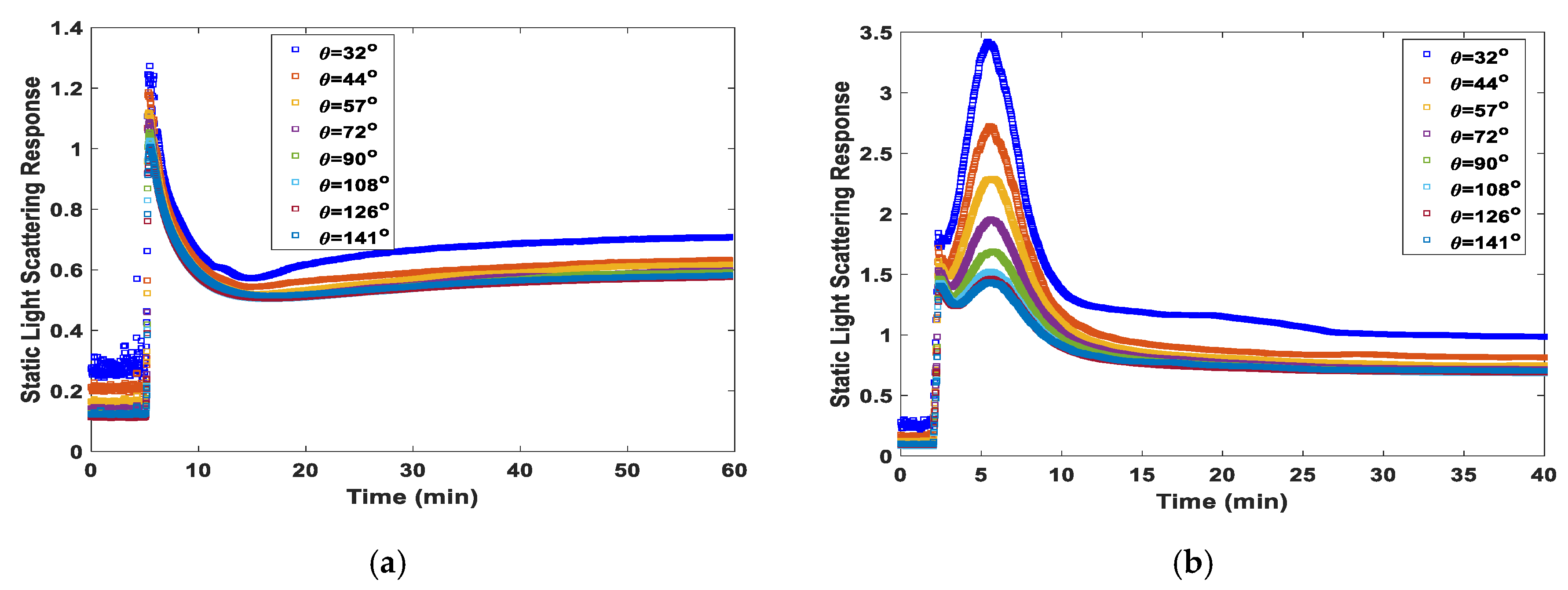
Static Light Scattering Monitoring and Kinetic Modeling of Polyacrylamide Hydrogel Synthesis
Abstract
1. Introduction
2. Materials and Methods
2.1. Reagents
2.2. Static Light Scattering (SLS) Instrument
2.3. Polymerization with Ammonium Persulfate/Tetramethylethylenediamine (APS/TEMED) and In-Line SLS Monitoring
2.4. Polymerization with VA-044 at T = 40 °C
2.5. Polymerization Conditions Used in the Experimental Runs
3. Theoretical Background
3.1. Kinetic Modeling of Hydrogel Synthesis through Population Balances of Generating Functions
3.2. Analysis of Gels and Gel Formation Processes by SLS
3.2.1. SLS with Diluted Polymer Solutions
3.2.2. SLS with Semi-Diluted Polymer Solutions and Gels
3.2.3. In-Line SLS Monitoring of Polymers and Polymer Gel Formation
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Penlidis, A. Special Issue: Water Soluble Polymers. Processes 2017, 5, 31. [Google Scholar] [CrossRef]
- Preusser, C.; Chovancová, A.; Lacík, I.; Hutchinson, R.A. Modeling the Radical Batch Homopolymerization of Acrylamide in Aqueous Solution. Macromol. React. Eng. 2016, 10, 490–501. [Google Scholar] [CrossRef]
- Asúa, J.M. Polymer Reaction Engineering; Blackwell Publishing: Oxford, UK, 2007; ISBN 978-1-4051-4442-1. [Google Scholar]
- Okay, O. General Properties of Hydrogels. Hydrogel Sensors and Actuators; Gerlach, G., Arndt, K.-F., Eds.; Springer Series on Chemical Sensors and Biosensors 6; Springer: Berlin, Germany, 2009. [Google Scholar] [CrossRef]
- Costa, M.R.; Dias, R.C. A general kinetic analysis of non-linear irreversible copolymerisations. Chem. Eng. Sci. 1994, 49, 491–516. [Google Scholar] [CrossRef][Green Version]
- Costa, M.R.; Dias, R.C. An improved general kinetic analysis of non-linear irreversible polymerisations. Chem. Eng. Sci. 2005, 60, 423–446. [Google Scholar] [CrossRef][Green Version]
- Costa, M.R.; Dias, R.C. Prediction of sol fraction and average molecular weights after gelation for non-linear free radical polymerizations using a kinetic approach. Macromol. Theory Simul. 2003, 12, 560–572. [Google Scholar] [CrossRef]
- Dias, R.C.; Costa, M.R. A New Look at Kinetic Modeling of Nonlinear Free Radical Polymerizations with Terminal Branching and Chain Transfer to Polymer. Macromolecules 2003, 36, 8853–8863. [Google Scholar] [CrossRef][Green Version]
- Dias, R.C.; Costa, M.R. Transient Behavior and Gelation of Free Radical Polymerizations in Continuous Stirred Tank Reactors. Macromol. Theory Simul. 2005, 14, 243–255. [Google Scholar] [CrossRef]
- Dias, R.C.; Costa, M.R. Semi-batch operation and primary cyclization effects in homogeneous free-radical crosslinking copolymerizations. Polymer 2005, 46, 6163–6173. [Google Scholar] [CrossRef][Green Version]
- Dias, R.C.; Costa, M.R. A General Kinetic Method to Predict Sequence Length Distributions for Non-Linear Irreversible Multicomponent Polymerizations. Polymer 2006, 47, 6895–6913. [Google Scholar] [CrossRef]
- Costa, M.R.; Dias, R.C. Prediction of Mean Square Radius of Gyration of Tree-Like Polymers by a General Kinetic Approach. Polymer 2007, 48, 1785–1801. [Google Scholar] [CrossRef]
- Dias, R.C.; Costa, M.R. Branching and crosslinking in coordination terpolymerizations. Macromol. React Eng. 2007, 1, 440–467. [Google Scholar] [CrossRef]
- Lazzari, S.; Hamzehlou, S.; Reyes, Y.; Leiza, J.R.; Costa, M.R.; Dias, R.C.; Storti, G. Bulk Crosslinking Copolymerization: Comparison of Different Modeling Approaches. Macromol. React. Eng. 2014, 8, 678–695. [Google Scholar] [CrossRef]
- Gonçalves, M.A.D.; Costa, M.R.; Dias, R.C. Modeling Studies on the Synthesis of Superabsorbent Hydrogels Using Population Balance Equations. Macromol. Symp. 2011, 306–307, 107–125. [Google Scholar] [CrossRef]
- Gonçalves, M.A.D.; Pinto, V.D.; Costa, M.R.; Dias, R.C. Polymer Reaction Engineering Studies on Smart Hydrogels Formation. J. Nanostruct. Polym. Nanocompos. 2013, 9, 40–45. [Google Scholar]
- Gomes, C.P.; Costa, M.R.; Dias, R.C. Polymer Reaction Engineering Tools to Tailor Smart and Superabsorbent Hydrogels. In Cellulose-Based Superabsorbent Hydrogels. Polymers and Polymeric Composites: A Reference Series; Mondal, M., Ed.; Springer: Cham, Switzerland, 2019; pp. 513–574. [Google Scholar] [CrossRef]
- Lacík, I.; Chovancová, A.; Uhelská, L.; Preusser, C.; Hutchinson, R.A.; Buback, M. PLP-SEC Studies into the Propagation Rate Coefficient of Acrylamide Radical Polymerization in Aqueous Solution. Macromolecules 2016, 49, 3244–3253. [Google Scholar] [CrossRef]
- Gonçalves, M.A.D.; Pinto, V.D.; Costa, M.R.; Dias, R.C. FTIR-ATR Monitoring and SEC/RI/MALLS Characterization of ATRP Synthesized Hyperbranched Polyacrylates. Macromol. Symp. 2010, 296, 210–228. [Google Scholar] [CrossRef]
- Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953; Chapter VII; ISBN 0-8014-0134-8. [Google Scholar]
- Patterson, G. Physical Chemistry of Macromolecules; CRC Press: Boca Raton, FL, USA, 2007; ISBN 0-8247-9467-2. [Google Scholar]
- Hiemenz, P.C.; Lodge, T.P. Polymer Chemistry, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2007; Chapter 8; ISBN 1-57444-779-3. [Google Scholar]
- Zimm, B.H. Apparatus and Methods for Measurement and Interpretation of the Angular Variation of Light Scattering; Preliminary Results on Polystyrene Solutions. J. Chem. Phys. 1948, 16, 1099–1116. [Google Scholar] [CrossRef]
- Shibayama, M.; Norisuye, T. Gel Formation Analyses by Dynamic Light Scattering. Bull. Chem. Soc. Jpn. 2002, 75, 641–659. [Google Scholar] [CrossRef]
- de Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979; ISBN 0-08-044286-2. [Google Scholar]
- Shibayama, M. Spatial inhomogeneity and dynamic fluctuations of polymer gels. Macromol. Chem. Phys. 1998, 199, 1–30. [Google Scholar] [CrossRef]
- Shibayama, M. Exploration of Ideal Polymer Networks. Macromol. Symp. 2017, 372, 7–13. [Google Scholar] [CrossRef]
- Shibayama, M.; Okamoto, M. Dynamic light scattering study on gelatin aqueous solutions and gels. J. Chem. Phys. 2001, 4285–4291. [Google Scholar] [CrossRef]
- Shibayama, M.; Ozeki, S.; Norisuye, T. Real-time dynamic light scattering on gelation and vitrification. Polymer 2005, 97, 2381–2388. [Google Scholar] [CrossRef]
- Debye, P.; Bueche, A.M. Light Scattering by an Inhomogeneous Solid. J. Appl. Phys. 1949, 20, 518–525. [Google Scholar] [CrossRef]
- Debye, P.; Anderson, H.R.; Brumberger, H. Scattering by an Inhomogeneous Solid. II. The Correlation Function and Its Application. J. Appl. Phys. 1957, 28, 679–683. [Google Scholar] [CrossRef]
- Bueche, F. Light Scattering from Swollen Gels. J. Colloid Interface Sci. 1970, 33, 61–66. [Google Scholar] [CrossRef]
- Soni, V.K.; Stein, R.S. Light Scattering Studies of Poly(dimethylsi1oxane) Solutions and Swollen Networks. Macromolecules 1990, 23, 5257–5265. [Google Scholar] [CrossRef]
- Mehravar, E.; Agirre, A.; Ballard, N.; van Es, S.; Arbe, A.; Leiza, J.R.; Asua, J.M. Insights into the Network Structure of Cross-Linked Polymers Synthesized via Miniemulsion Nitroxide-Mediated Radical Polymerization. Macromolecules 2018, 51, 9740–9748. [Google Scholar] [CrossRef]
- Wu, W.-L.; Shibayama, M.; Roy, S.; Kurokawa, H.; Coyne, L.D.; Nomura, S.; Stein, R.S. Physical Gels of Aqueous Poly(vinyl alcohol) Solutions: A Small-Angle Neutron-Scattering Study. Macromolecules 1990, 23, 2245–2251. [Google Scholar] [CrossRef]
- Shibayama, M.; Tanaka, T. Small angle neutron scattering study on poly(N isopropyl acrylamide) gels near their volume-phase transition temperature. J. Chem. Phys. 1992, 97, 6829–6841. [Google Scholar] [CrossRef]
- Horkay, F.; Hecht, A.-M.; Geissler, E. Small Angle Neutron Scattering in Poly(viny1 alcohol) Hydrogels. Macromolecules 1994, 27, 1795–1798. [Google Scholar] [CrossRef]
- Pérez-Salinas, P.; Jaramillo-Soto, G.; Rosas-Aburto, A.; Vázquez-Torres, H.; Bernad-Bernad, M.J.; Licea-Claverie, Á.; Vivaldo-Lima, E. Comparison of Polymer Networks Synthesized by Conventional Free Radical and RAFT Copolymerization Processes in Supercritical Carbon Dioxide. Processes 2017, 5, 26. [Google Scholar] [CrossRef]
- Norisuye, T.; Shibayama, M.; Nomura, S. Time-resolved light scattering study on the gelation process of poly(N-isopropylacrylamide). Polymer 1998, 39, 2769–2775. [Google Scholar] [CrossRef]
- Norisuye, T.; Takeda, M.; Shibayama, M. Cluster-Size Distribution of Cross-Linked Polymer Chains across the Gelation Threshold. Macromolecules 1998, 31, 5316–5322. [Google Scholar] [CrossRef]
- Francis, R.S.; Patterson, G.D.; Kim, S.H. Liquid-like structure of polymer solutions near the overlap concentration. J. Polym. Sci. Part B Polym. Phys. 2006, 44, 703–710. [Google Scholar] [CrossRef]
- Giz, A.; Çatalgil-Giz, H.; Alb, A.; Brousseau, J.-L.; Reed, W.F. Kinetics and Mechanisms of Acrylamide Polymerization from Absolute, Online Monitoring of Polymerization Reaction. Macromolecules 2001, 34, 1180–1191. [Google Scholar] [CrossRef]
- Alb, A.M.; Mignard, E.; Drenski, M.F.; Reed, W.F. In Situ Time-Dependent Signatures of Light Scattered from Solutions undergoing Polymerization Reactions. Macromolecules 2004, 37, 2578–2587. [Google Scholar] [CrossRef]
- Drenski, M.F.; Mignard, E.; Alb, A.M.; Reed, W.F. Simultaneous in-Situ Monitoring of Parallel Polymerization Reactions Using Light Scattering; A New Tool for High-Throughput Screening. J. Comb. Chem. 2004, 6, 710–716. [Google Scholar] [CrossRef]
- Orakdogen, N.; Kizilay, M.Y.; Okay, O. Suppression of inhomogeneities in hydrogels formed by free-radical crosslinking copolymerization. Polymer 2005, 46, 11407–11415. [Google Scholar] [CrossRef]
- Wako-Chemicals. Available online: https://www.wako-chemicals.de/en/product/va-044 (accessed on 30 January 2019).
- Moad, G.; Solomon, D.H. The Chemistry of Radical Polymerization, 2nd ed.; Elsevier: Amsterdan, The Netherlands, 2006; ISBN 0-08-044286-2. [Google Scholar]
- Kuru, E.A.; Orakdogen, N.; Okay, O. Preparation of homogeneous polyacrylamide hydrogels by free-radical crosslinking copolymerization. Eur. Polym. J. 2007, 43, 2913–2921. [Google Scholar] [CrossRef]
- Orakdogen, N.; Okay, O. Influence of the Initiator System on the Spatial Inhomogeneity in Acrylamide-Based Hydrogels. J. Appl. Polym. Sci. 2007, 103, 3228–3237. [Google Scholar] [CrossRef]
- Abdurrahmanoglu, S.; Okay, O. Preparation of Homogeneous Hydrogels by Controlling the Crosslinker Reactivity and Availability. J. Macromol. Sci. Part A Pure Appl. Chem. 2008, 45, 769–775. [Google Scholar] [CrossRef]
- Yazici, I.; Okay, O. Spatial inhomogeneity in poly(acrylic acid) hydrogels. Polymer 2005, 46, 2595–2602. [Google Scholar] [CrossRef]
- Boyko, V.; Richter, S. Monitoring of the Gelation Process on a Radical Chain Cross-Linking Reaction Based on N-Vinylcaprolactam by Using Dynamic Light Scattering. Macromol. Chem. Phys. 2004, 205, 724–730. [Google Scholar] [CrossRef]
- Lesturgeon, V.; Nicolai, T.; Durand, D. Dynamic and static light scattering study of the formation of cross-linked PMMA gels. Eur. Phys. J. 1999, B9, 71–82. [Google Scholar] [CrossRef]














| Product | Monomers | Initiator | T (°C) | CTA | ||||
|---|---|---|---|---|---|---|---|---|
| L1 | AAm | APS/TEMED | 26 | - | 9 | 0.1 | - | - |
| L2 | AAm | APS/TEMED | 26 | - | 9 | 0.2 | - | - |
| L3 | AAm | APS/TEMED | 26 | - | 5 | 0.2 | - | - |
| L4 | AAm | APS/TEMED | 26 | - | 13 | 0.1 | - | - |
| H1 | AAm/MBAm | APS/TEMED | 26 | - | 9 | 0.1 | 0.5 | - |
| H2 | AAm/MBAm | APS/TEMED | 26 | - | 9 | 0.1 | 1.0 | - |
| H3 | AAm/MBAm | APS/TEMED | 26 | - | 9 | 0.1 | 2.0 | - |
| H4 | AAm/MBAm | APS/TEMED | 26 | - | 9 | 0.2 | 1.0 | - |
| H5 | AAm/MBAm | APS/TEMED | 26 | - | 13 | 0.1 | 0.1 | |
| H6 | AAm/MBAm | APS/TEMED | 26 | - | 13 | 0.1 | 0.5 | - |
| L5 | AAm | VA-044 | 40 | - | 9 | 0.2 | - | - |
| L6 | AAm | VA-044 | 40 | - | 5 | 0.2 | - | - |
| H7 | AAm/MBAm | VA-044 | 40 | - | 9 | 0.2 | 0.5 | - |
| H8 | AAm/MBAm | VA-044 | 40 | - | 5 | 0.2 | 1.0 | - |
| H9 | AAm/MBAm | VA-044 | 40 | - | 9 | 0.2 | 1.0 | - |
| L7 | AAm | APS/TEMED | 26 | TA | 9 | 0.2 | - | 0.5 |
| H10 | AAm/MBAm | APS/TEMED | 26 | TA | 9 | 0.2 | 1.0 | 0.5 |
| Group Alias | Group Description | ||
|---|---|---|---|
| A1 | Secondary propagation polymer radical (SPR) | 1 | 1 |
| A2 | Pendant double bond | 1 | 1 |
| A3 | Mid-chain tertiary polymer radical (MCR) | 1 | 1 |
| A4 | Polymerized Acrylamide unit | 1 | 0 |
| A5 | Polymerized methylene bisacrylamide unit | 1 | 0 |
| A6 | Branching point due to backbiting | 1 | 0 |
| A7 | Acrylamide monomer | 0 | 1 |
| A8 | Methylene bisacrylamide monomer | 0 | 1 |
| A9 | Primary radical | 0 | 1 |
| A10 | Initiator | 0 | 1 |
| A11 | Chain transfer agent | 0 | 1 |
| A12 | Inhibitor/retarder | 0 | 1 |
| Chemical Reaction | Chemical Equation |
|---|---|
| Initiator decomposition | |
| Acrylamide initiation | |
| Methylene bisacrylamide initiation | |
| Pendant double bond initiation | |
| Acrylamide propagation with SPR | |
| Methylene bisacrylamide propagation with SPR | |
| Pendant double bond propagation with SPR | |
| Backbiting | |
| Acrylamide propagation with MCR | |
| Methylene bisacrylamide propagation with MCR | |
| Pendant double bond propagation with MCR | |
| Transfer to monomer | |
| Transfer to chain transfer agent | |
| Inhibition of primary radicals | |
| Inhibition of SPR radicals | |
| Inhibition of MRC radicals | |
| Termination by combination SPR/SPR | |
| Termination by disproportionation SPR/SPR | |
| Termination by combination SPR/MCR | |
| Termination by disproportionation of SPR/MCR | |
| Termination by combination MCR/MCR | |
| Termination by disproportionation of MCR/MCR |
| Kinetic Step | Rate Parameters | Reference |
|---|---|---|
| Initiator decomposition | With VA0-44 | [46] |
| With K2S2O8 in 0.1 M NaOH solution | [47] | |
| A multiplication factor of 2000 on the value for K2S2O8 was estimated in this work with APS/TEMED | This work | |
| Chain propagation | [2,18] | |
| Transfer to monomer | [2,18] | |
| Termination SPR-SPR | [2,18] | |
| Backbiting | [2,18] | |
| Addition to MCR | [2,18] | |
| Cross termination SPR-MCR | [2,18] | |
| Termination MCR-MCR | [2,18] | |
| Inhibition | This work | |
| Chain transfer to agent | This work |
| Product | H1 | H2 | H3 | H4 | H5 | H6 | H7 | H8 | H9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| DB | 24 | 27 | - | 20 | - | 36 | 64 | 48 | 24 | |
| GU | 31 | 35 | - | 27 | - | 42 | 65 | 54 | 31 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomes, C.; Dias, R.C.S.; Costa, M.R.P.F.N. Static Light Scattering Monitoring and Kinetic Modeling of Polyacrylamide Hydrogel Synthesis. Processes 2019, 7, 237. https://doi.org/10.3390/pr7040237
Gomes C, Dias RCS, Costa MRPFN. Static Light Scattering Monitoring and Kinetic Modeling of Polyacrylamide Hydrogel Synthesis. Processes. 2019; 7(4):237. https://doi.org/10.3390/pr7040237
Chicago/Turabian StyleGomes, Catarina, Rolando C.S. Dias, and Mário Rui P.F.N. Costa. 2019. "Static Light Scattering Monitoring and Kinetic Modeling of Polyacrylamide Hydrogel Synthesis" Processes 7, no. 4: 237. https://doi.org/10.3390/pr7040237
APA StyleGomes, C., Dias, R. C. S., & Costa, M. R. P. F. N. (2019). Static Light Scattering Monitoring and Kinetic Modeling of Polyacrylamide Hydrogel Synthesis. Processes, 7(4), 237. https://doi.org/10.3390/pr7040237