Control and Design of a Quasi-Y-Source Inverter for Vehicle-to-Grid Applications in Virtual Power Plants

Abstract

This paper proposes a design and control methodology for a Quasi-Y-Source impedance source inverter (QS-YSI) as a power electronics interface for Vehicle-to-Grid (V2G) and Grid-to-Vehicle (G2V) applications in the context of virtual power plants (VPPs). The work presents an analysis of bidirectional power transfer using Electric Vehicles (EVs) to supply power to the utility grid, businesses, and homes, thereby acting as distributed energy resources. The proposed QS-YSI topology supports both V2G and G2V operation while providing reactive power compensation and enabling the decoupled tracking of active power (P) and reactive power (Q), demonstrating the capability of EVs to return energy to the grid and to provide ancillary services such as power factor correction. The key contributions are a detailed control design methodology that includes pulsating DC-link voltage regulation, inverter output current reference tracking in the synchronous $dq$ reference frame considering DC-link voltage dynamics, and a modified Pulse Width Modulation (PWM) technique for effective decoupling of DC link and inverter output current control. Finally, the feasibility and validity of the proposed approach are demonstrated through simulations of the complete system under nominal conditions and experiments conducted considering a small-scale prototype.

1. Introduction

The growing and recent electrification of the vehicle fleet has placed Electric Vehicles (EVs) as strategic components within the modern energy infrastructure [1]. However, the adoption of EVs faces challenges in infrastructure, cost, energy technology, and market dynamics. Addressing these needs requires fiscal incentives, international cooperation, and regulatory frameworks to attract consumers [2]. In addition, the increased integration of EVs with the grid brings benefits, but also risks, meaning it requires standardized communication and cybersecurity protocols considering the limitations of the EV and the grid [3], while practical integration must follow standards such as IEEE and comply with appropriate normatives, such as IBC (International Building Code) and NEC (National Electrical Code) guidelines (for example, with strategic data analysis for charger placement and demand management [4]). Considering all these aspects and the complexity of this subject, this work focuses on the design and control of a Quasi-Y inverter power electronics interface of an EV charging station.

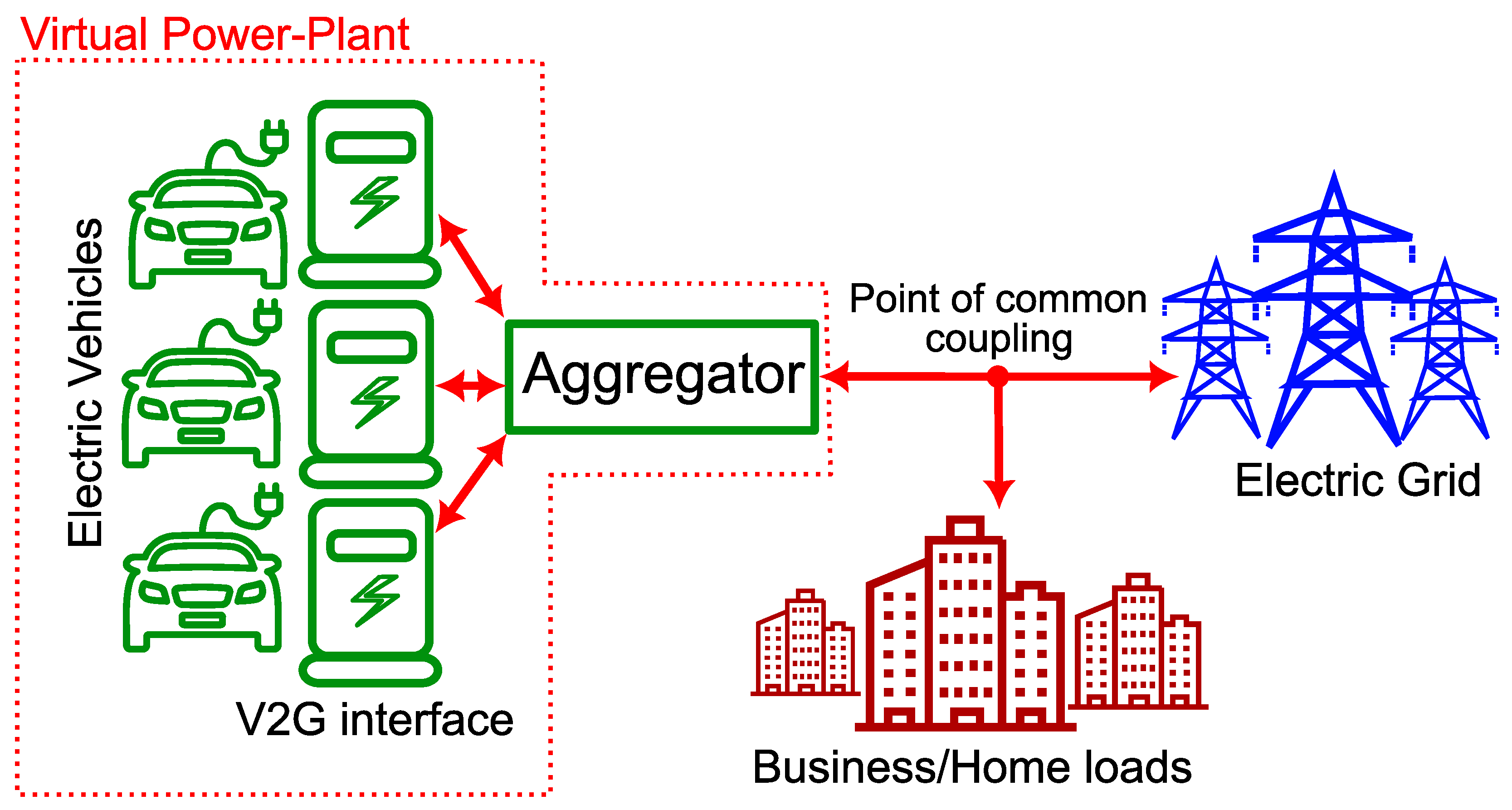
Besides the Grid-to-Vehicle (G2V) operational mode, EV charging stations can enable Vehicle-to-Grid (V2G) operations, allowing EVs to supply energy back to the grid [5]. The V2G functionality is crucial for EVs to provide grid services such as active power during peak demand and reactive power for voltage regulation [6]. In this context, virtual power plants (VPPs) facilitate coordinated participation in EVs by aggregating distributed energy resources into a virtual generation plant for grid services and participation in the energy market [7,8]. Figure 1 illustrates a VPP infrastructure using EVs in V2G mode. This allows EVs to bidirectionally transfer power to the grid or to loads via a V2G/G2V interface, serving as a distributed energy resource. The function of aggregators is to manage the operations between the grid and EVs, including regulations of the electricity market related to consumption and production [9]. In this sense, efficient and flexible bidirectional V2G/G2V interfaces are essential for the implementation of VPPs, which require flexible and bidirectional power electronics interfaces.

In this context, multiple power converter topologies can be used to connect EV batteries to the grid [10]. Among these, impedance source inverters (ISIs) stand out as single-stage converters and have been investigated in multiple recent works in the literature [11]. ISIs present interesting features for EV charging stations, with flexible energy conversion, modular scalability, and better fault tolerance [12]. Their operational mode extends the capacity of the inverter to synthesize AC voltage, allowing voltage buck and boosting to occur in one stage, tackling the limits of traditional inverters [13]. Derived topologies such as Quasi-Z-Source and Y-Source networks further enhance energy transfer, allowing continuous input current and increased voltage boost, which are desirable characteristics for charging of EV batteries, reducing stress and extending system life [14]. Moreover, the single-stage ISI design reduces the power conversion stages, which helps to improve reliability [15]. In particular, Y-Source and Quasi-Y-Source inverters stand out in high-voltage gain and operational flexibility scenarios, due to the presence of coupled inductors [16], which also help to obtain low shoot-through duty cycle ratios, minimizing switching losses and improving energy efficiency [17].

Recent research has emphasized the role of ISIs in enabling the integration of EVs into VPPs through advanced converter topologies. Existing studies have demonstrated their advantages in improving reliability and performance in multisource EV systems [18], as well as their ability to handle variable voltage inputs and support efficient battery interfacing in hybrid energy scenarios [19]. Other contributions have proposed modulation techniques and alternative designs to improve efficiency, voltage gain, and system stability in EV applications [20,21]. Although these works confirm the versatility of ISIs, they mainly focus on specific converter variants or application-oriented improvements. In contrast, there is still a lack of detailed design methodologies and integrated control strategies tailored for Quasi-Y-Source inverters (QS-YSIs) in VPP-oriented EV applications, which is the gap addressed in this paper. This paper addresses this issue by demonstrating how to apply the QS-YSI topology designed for G2V and V2G operation in VPP contexts. Therefore, the main contributions of this work are as follows:

• Proposition of a DC-link voltage controller and inverter output current controller in $dq$ frame, taking into account the dynamic characteristics of the pulsating DC link voltage of the QS-YSI.
• A seamless and decoupled integration methodology of DC-link and inverter output current controllers in G2V and V2G operations, considering the provision of reactive power compensation.
• Design of a QS-YSI including the impedance source network components and inverter output LCL filter, considering a typical V2G/G2V application.

This paper is structured as follows. Section 2 introduces the Quasi-Y-Source inverter (QS-YSI) system, detailing its converter topology, impedance network configuration, equivalent circuit models in different operating states and a comparative qualitative analysis with other conventional power electronics converter topologies used in such applications. Section 3 presents the component design methodology, including analytical derivations for the Quasi-Y impedance network, design equations for the LCL filter, and practical design of components such as inductors and capacitors. Section 4 describes the system parameters’ definition, covering the EV battery modeling, calculation of QS-YSI components including the LCL filter and the connected grid load that models business/home loads. Section 5 discusses the proposed control strategy, covering the design of the DC-link voltage PI controller, the control of the inverter output current in the synchronous reference frame $dq$, and the implementation of a modified PWM technique that decouples the control of the DC-link and the inverter output current. Section 6 outlines the simulation setup and validates the system performance under two operational scenarios: bidirectional power exchange and reactive power compensation. Section 7 presents experimental results using a small-scale prototype operational under nominal voltage conditions. Section 8 provides a discussion of the obtained simulation and experimental results and design trade-offs, and Section 9 concludes the paper, summarizing the main contributions and suggesting future research directions.

2. Converter Topology and Operating Principle

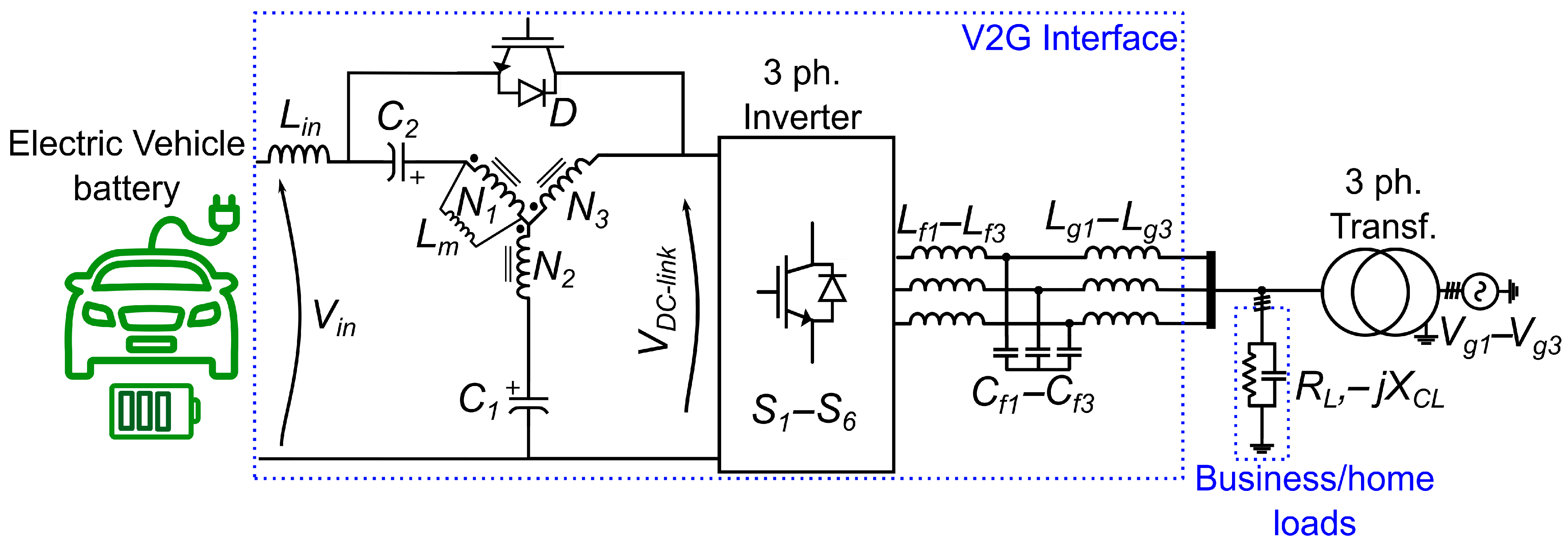
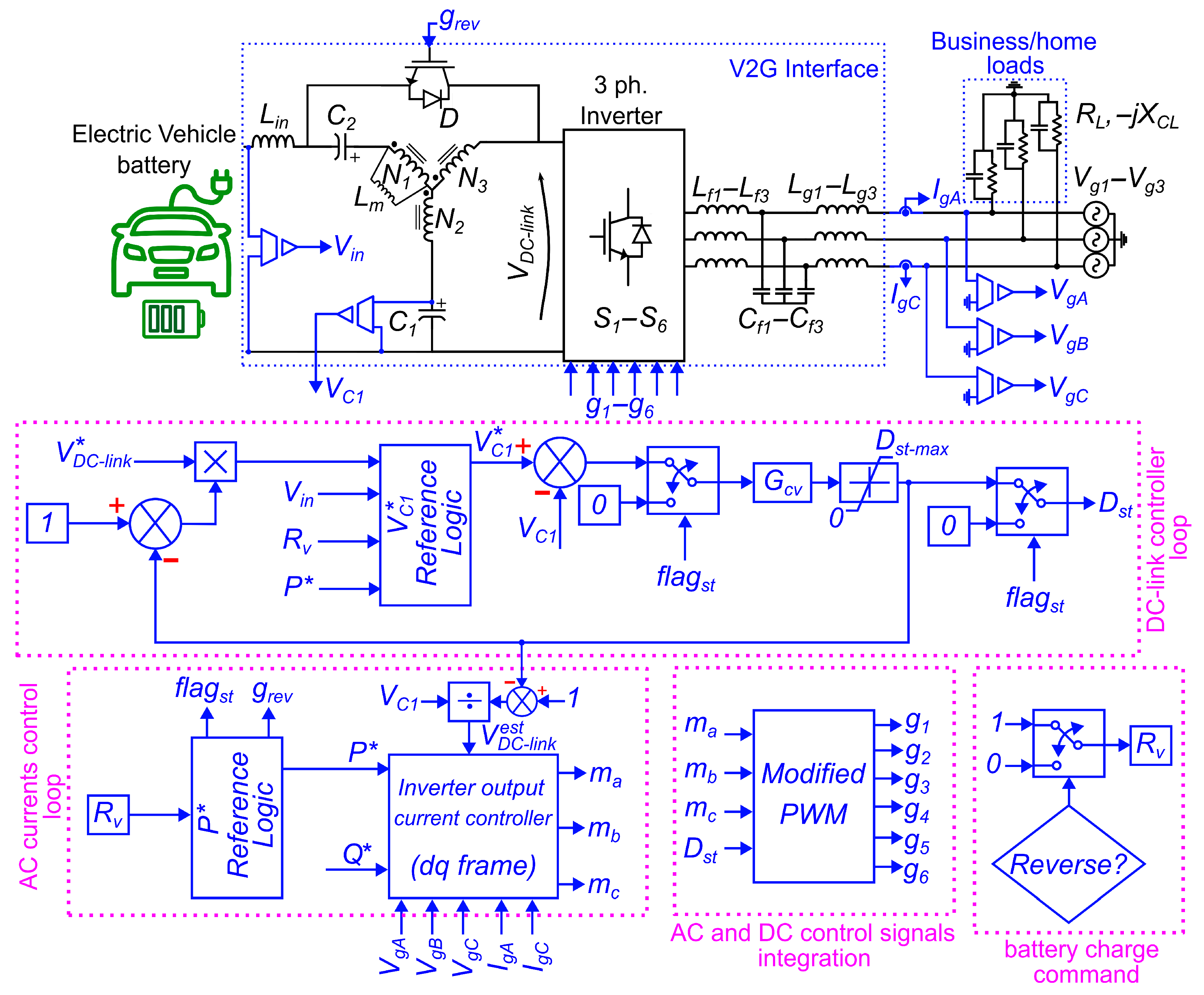
Figure 2 illustrates the bidirectional QS-YSI topology for EV V2G/G2V applications, configured for the connection of a three-phase grid using a galvanic isolation transformer connected to the grid, with phase voltages $V_{g1}$–$V_{g3}$. To model business and home loads, a three-phase load connected in wye and composed of a resistive impedance ($R_L$) and capacitive impedance ($j{X}_{CL}$) is connected at the point of the common coupling. The inverter stage employs a three-phase full bridge arrangement with six transistors $S_1$–$S_6$ to generate the inverter output current output, filtered by an LCL network of inverter side inductors ($L_{f1}$, $L_{f2}$, $L_{f3}$), intermediate capacitors ($C_{f1}$, $C_{f2}$, $C_{f3}$), and grid-side inductors ($L_{g1}$, $L_{g2}$, $L_{g3}$) to reduce high-frequency switching harmonics before grid connection. On the DC side of the inverter bridge, there is the impedance network, which is the key part of the energy conversion stage, whose components are described in the following. The input inductor $L_{in}$ allows for continuous current at the input stage, and the diode D prevents short circuits between the input stage and the inverter bridge transistors during the shoot-through operation mode. To allow bidirectional energy flow, there is an antiparallel transistor with diode D, which is turned on when the EV battery needs to be charged (G2V mode). The impedance network also contains three coupled inductors with the turns ratio given by $N_1$:$N_2$:$N_3$ and magnetizing inductance $L_m$, along with capacitors ($C_1$, $C_2$).

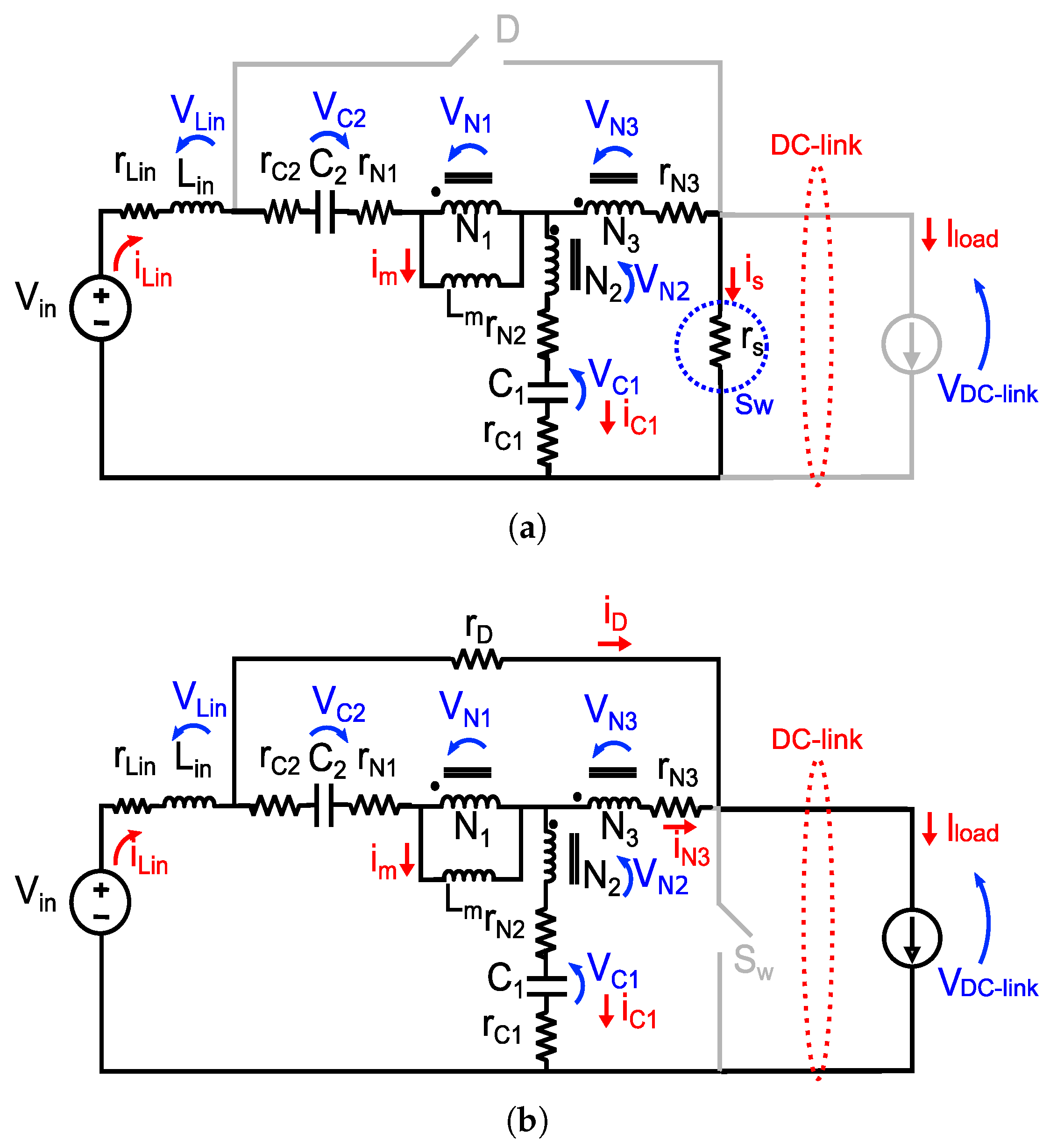
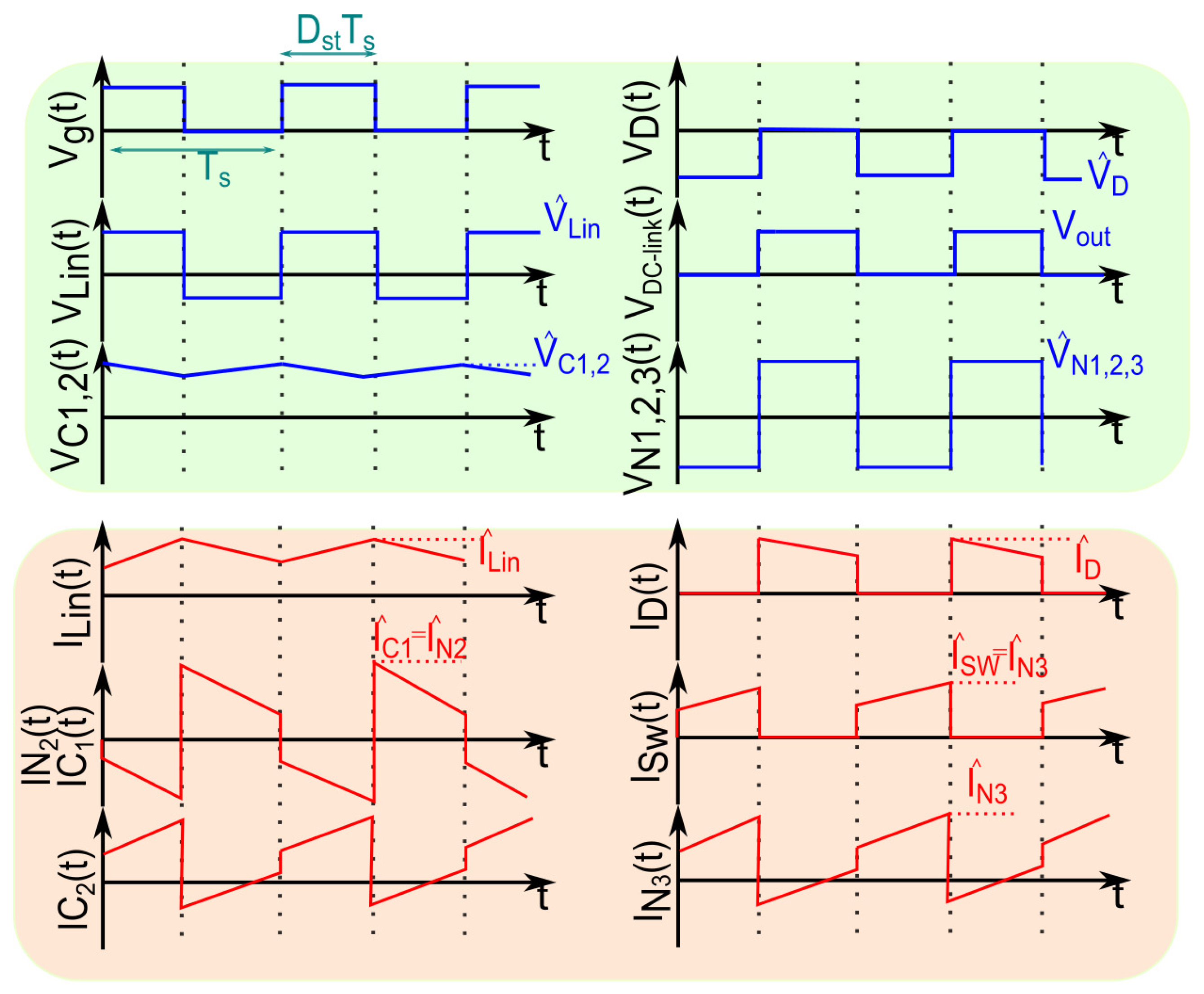
When operating in continuous conduction mode (CCM) with reduced leakage inductance values, the QS-YSI operating stages can be defined by shoot-through and active stages, whose equivalent circuits for both operating stages are presented in Figure 3. The shoot-through stage is the one defined when the transistors of the same inverter bridge leg are turned on simultaneously, creating a short-circuit condition, whereas the active stage is the conventional inverter operation. Therefore, in Figure 3, the switch $S_w$ represents the shoot-through conduction mode of the three-phase inverter bridge. The load dynamics is modeled as a current source $I_{load}$, and the corresponding voltage and current waveforms are illustrated in Figure 4, where $D_{st}$ denotes the shoot-through duty cycle, $T_s$ the switching period, and $V_g$ the gate signal for $S_w$, which remains high during the shoot-through interval and low during the active state. As can be seen in Figure 3a, in the shoot-through state, with $S_w$ conducting and diode D blocked, the input energy is transferred to the coupled inductors, while the capacitor $C_1$ discharges, rendering the load current independent of the input. Now, during the active state, as described in Figure 3b when D is turned on and $S_w$ is turned off, the capacitor $C_1$ is charged and the input voltage $V_{in}$ energy is delivered to the load through D, supplemented by the energy previously stored in the coupled inductors via the DC link. As indicated in the literature [22], the ideal voltage gain of the QS-YSI converter is expressed as $B={\displaystyle \frac{V_{DC-link}}{V_{in}}}={\displaystyle \frac{1}{(1-\delta D_{st})}}$, where the coupled-inductor factor is defined as $\delta ={\displaystyle \frac{N_1+N_2}{N_2-N_3}}$.

Comparison with Other Conventional Topologies for V2G/G2V Applications

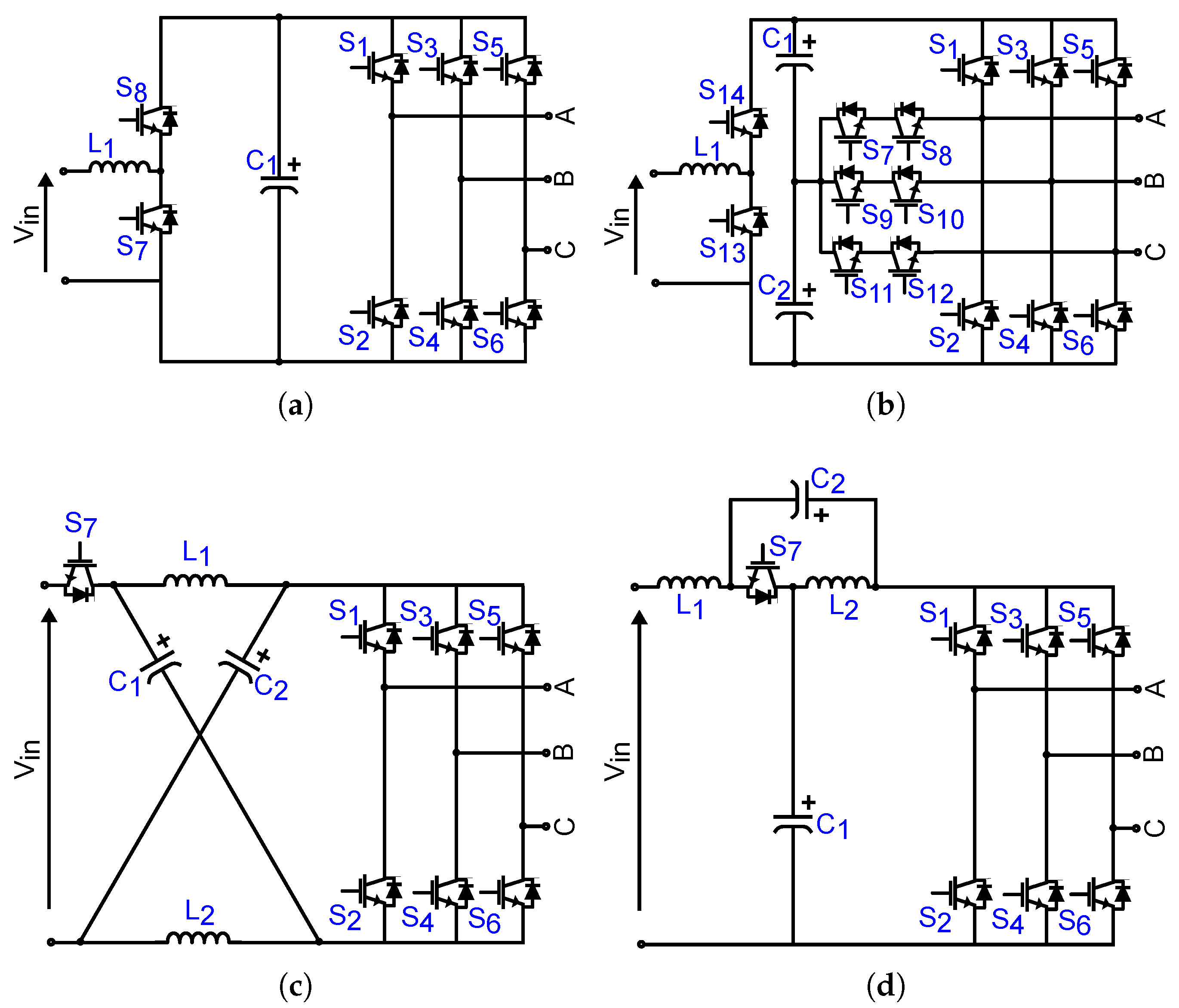
Figure 5 shows conventional bidirectional power electronics topologies used in EV applications, representing the two-stage full-bridge three-phase inverter, or Boost VSI (Figure 5a); the T-type inverter (Boost T-type) (Figure 5b); the Z-Source impedance inverter (Figure 5c); and the Quasi-Z-Source inverter (Figure 5d).

Table 1. Qualitative comparative table of different bidirectional converter topologies for EV applications.

Feature	Boost VSI	Boost T-Type	Z-Source	Quasi-Z-Source	Quasi-Y-Source
No. of stages	2	2	1	1	1
Voltage gain	requires boost stage	requires boost stage	embedded	embedded	embedded
Input current	CCM	CCM	DCM	CCM	CCM
Shoot-through tolerance	no	no	yes	yes	yes
No. of transistors/diodes	8	14	7	7	7
No. of capacitors	1	2	2	2	2
No. of inductors	1	1	2	2	4
Voltage boost gain	${\displaystyle \frac{1}{1-D_{cycle}}}$	${\displaystyle \frac{1}{1-D_{cycle}}}$	${\displaystyle \frac{1}{1-2D_{st}}}$	${\displaystyle \frac{1}{1-2D_{st}}}$	${\displaystyle \frac{1}{1-\delta D_{st}}}$

shows a qualitative comparison among these topologies compared to the proposed QS-YSI presented in this work.

As indicated in Table 1, conventional two-stage solutions such as a DC/DC boost stage followed by a VSI or T-type inverter require a dedicated boost converter to achieve voltage step-up, which depends on the duty cycle $D_{cycle}$ adopted, which increases the complexity of the overall system. In contrast, impedance source families (Z-Source, Quasi-Z-Source, and Quasi-Y-Source) inherently provide buck-boost capability through their impedance networks, enabling single-stage power conversion.

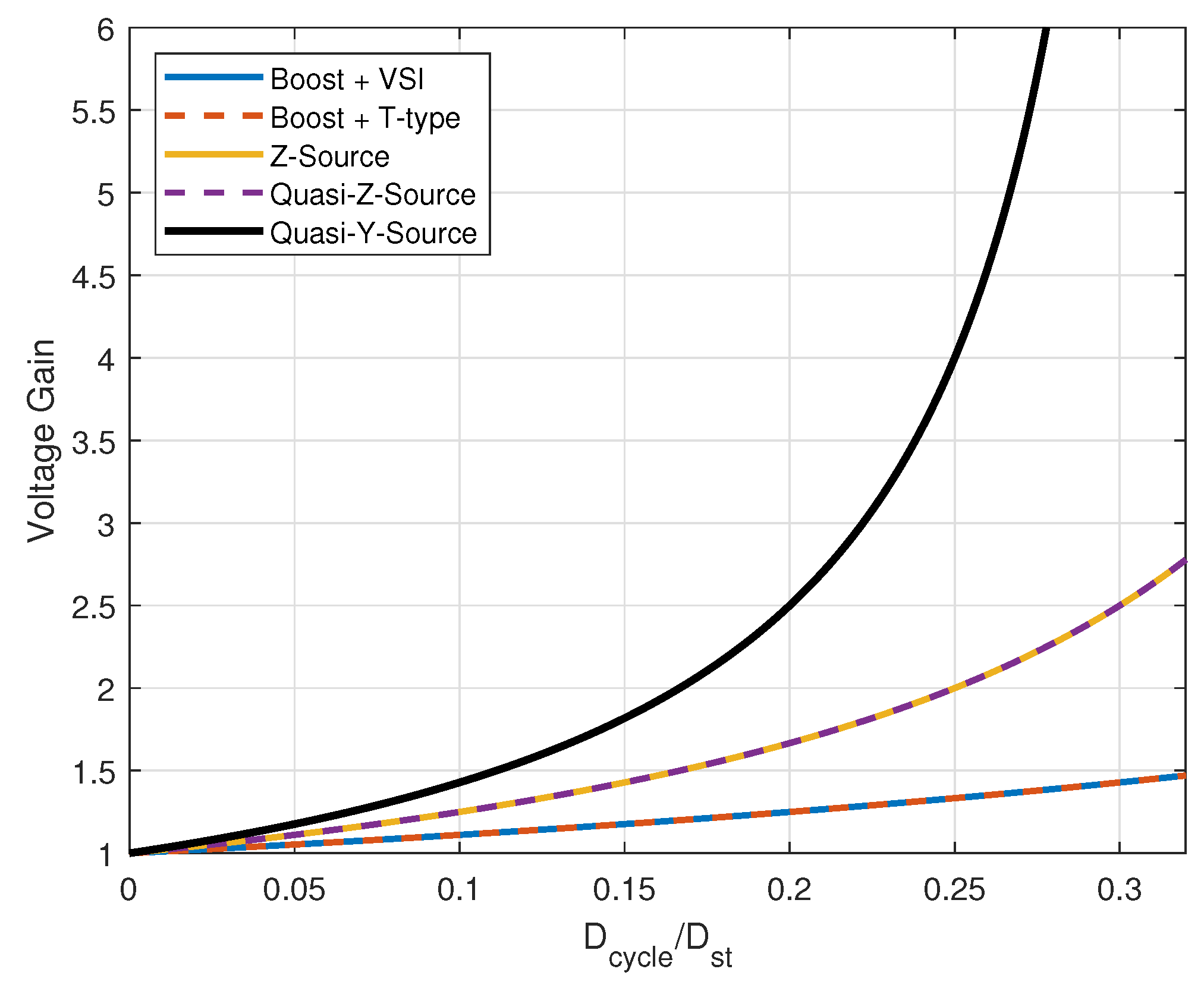
Moreover, the classical Z-Source inverter achieves voltage gain through shoot-through states but typically operates with a discontinuous input current (DCM), which increases the stress in the EV battery. Alternatively, the Quasi-Z-Source topology improves this by ensuring CCM, thus reducing stress and improving compatibility with EV batteries. However, both structures have limited boost capability at moderate shoot-through duty cycles $D_{st}$, when compared to QS-YSI, as can be seen in Figure 6, which depicts the ideal voltage gain.

The proposed QS-YSI inherits the advantages of the Quasi-Z-Source—namely, CCM, shoot-through tolerance and single-stage conversion—while providing higher voltage gain due to the use of coupled inductors and its winding proportion ratio factor given by $\delta$. This feature allows the same boost level to be achieved with a lower $D_{st}$, which reduces switching stress and improves efficiency. Moreover, the QS-YSI has superior voltage gain characteristics and operational flexibility, making it especially attractive for EV V2G/G2V applications where high step-up capability and reliable bidirectional operation are required.

3. Impedance Network and LCL Filter Components Design

This section presents the design of the QS-YSI power stage, including the impedance network and the LCL filter components. The Quasi-Y network is dimensioned under steady-state assumptions, with ideal switching and assuming CCM, using expressions based on voltage/current balance, ripple factors, and switching frequency. Moreover, impedance network non-idealities are addressed via equivalent series resistances (ESRs) and design factors. However, the LCL filter is designed to suppress switching harmonics, with component values based on ripple, power factor variation, and attenuation requirements.

3.1. Quasi-Y Impedance Network Component Design

For the steady-state evaluation, the assumptions made include the following: (a) the leakage inductances of the coupled inductors are negligible; (b) the power switches $S_w$ and D switch instantly; (c) the converter operates in CCM mode; and (d) all passive elements are linear, time-invariant, and frequency independent. Based on the waveforms shown in Figure 4 and considering the balance of inductor voltages and capacitor charges during the steady state, expressions for the QS-YSI network components can be deduced. Since the focus of this work relies on the demonstration of QS-YSI in V2G/G2V applications, the detailed derivation is not included here, as it was explored by the authors in [23]. Therefore,

Table 2. Expressions for QS-YSI components.

Component	Expression
$L_{in}$	${\displaystyle \frac{V_{in}^2(1-B{\delta }^{\prime })D_{st}}{2f_{tri}{P}_o{k}_{l1}}}$ [H]
$L_m$	${\displaystyle \frac{N_1^2{\mu }_0{\mu }_r{A}_C}{l}}$ [H]
$C_1$	${\displaystyle \frac{-{\delta }^{\prime }{D}_{st}}{2V_{out}{D}_{st}^{\prime }{f}_{tri}{k}_{C1}}}{\displaystyle \frac{P_o}{V_{in}}}$ [F]
$C_2$	${\displaystyle \frac{1}{2V_o\delta f_{tri}{k}_{C2}}}{\displaystyle \frac{P_o}{V_{in}}}$ [F]

lists the derived expressions, where ${\delta }^{\prime }=1-\delta$, $D_{st}^{\prime }=1-D_{st}$, and $f_{tri}$ is the inverter output current synthesis switching frequency.

In Table 2, the factors $k_{l1}$, $k_{C1}$, and $k_{C2}$ represent the ripple factors for the voltages $L_{in}$ and $C_1$ and $C_2$, respectively, while the total processed power is given as $P_o$. Additionally, it is considered that the coupled-inductor core can be treated as a uniform magnetic circuit, that is, the air gap reluctance is incorporated in the core body and l is the mean length of the magnetic circuit; ${\mu }_o$ is the air magnetic permeability; ${\mu }_r$ is the relative magnetic material permeability; and $A_C$ is the cross section area of the core.

3.2. LCL Filter Design

The LCL filter is a third-order low-pass filter that reduces the high-frequency harmonic content in the output current of the inverter. The methodology used for the design of the LCL filter is based on the research work conducted by [24]. Therefore, inductances on the inverter side, denoted $L_{f1-3}$, are given by the expression (1), where $\Delta I_1$ indicates the desired current ripple and $I_{max}$ is the maximum current flowing through the inductor. The maximum inductor current $I_{max}$ is described by (2), with $P_o$ being the rated power of the inverter and $V_{ph}$ being the root mean square of the phase voltage. The equivalent series resistances of $L_{f1-3}$, given by $r_{f1-3}$, are defined as a percentage $F_{ESR}$ of the inductance values of $L_{f1-3}$ at the fundamental frequency of the grid $f_g$, according to (3).

$$\begin{array}{c}{L}_{f1-3}={\displaystyle \frac{V_{DC-link}}{6f_{sw}\Delta I_1{I}_{max}}}\left[\mathrm{H}\right]\end{array}$$

(1)

$$\begin{array}{c}{I}_{max}={\displaystyle \frac{P_o\sqrt{2}}{3V_{ph}}}\left[\mathrm{A}\right]\end{array}$$

(2)

$$\begin{array}{c}{r}_{f1-3}=F_{ESR}\left(2\pi f_g{L}_{f1-3}\right)[\Omega ]\end{array}$$

(3)

The capacitor value $C_{f1-3}$ is determined by (4), where $x_{PF}$ represents the maximum variation of the power factor observed by the grid, and $C_b$ is the base capacitance, which depends on the base impedance $Z_b$, according to (5) to (6), respectively.

$$\begin{array}{c}{C}_{f1-3}={\displaystyle \frac{x_{PF}{C}_b}{3}}\left[\mathrm{F}\right]\end{array}$$

(4)

$$\begin{array}{c}{C}_b={\displaystyle \frac{1}{2\pi f_g{Z}_b}}\left[\mathrm{F}\right]\end{array}$$

(5)

$$\begin{array}{c}{Z}_b={\displaystyle \frac{3V_{ph}^2}{P_o}}[\Omega ]\end{array}$$

(6)

Grid-side inductors $L_{g1-3}$ are calculated using (7), where $k_a$ is the attenuation factor, which indicates the filter’s ability to reduce harmonic content. The equivalent series resistances of $L_{g1-3}$, given by $r_{g1-3}$, are defined in the same way as $r_{f1-3}$, as shown by (8).

$$\begin{array}{c}{L}_{g1-3}={\displaystyle \frac{x_{PF}\left(\sqrt{\frac{1}{k_a^2}}+1\right)}{\Delta I_1·C_b·f_{\mathrm{sw}}^2}}\left[\mathrm{H}\right]\end{array}$$

(7)

$$\begin{array}{c}{r}_{g1-3}=F_{ESR}\left(2\pi f_g{L}_{g1-3}\right)[\Omega ]\end{array}$$

(8)

The resonance frequency $f_{res}$ is given by (9), and it is crucial during the design phase to ensure that $f_{res}$ is higher than ten times the grid frequency $f_g$ and lower than one-fifth of $f_{tri}$, to prevent amplification of unwanted harmonic frequencies during inverter operation. To mitigate the resonance frequency components, the values of $r_{f1-3}$ are calculated using (10).

$$\begin{array}{c}{f}_{res}={\displaystyle \frac{1}{2\pi }}\sqrt{{\displaystyle \frac{L_{f1-3}+L_{g1-3}}{L_{f1-3}{L}_{g1-3}{C}_{f1-3}}}}\left[\mathrm{Hz}\right]\end{array}$$

(9)

$$\begin{array}{c}{r}_{f1-3}={\displaystyle \frac{1}{2\pi f_{res}{C}_{f1-3}}}[\Omega ]\end{array}$$

(10)

4. System Parameters

This section presents the adopted methodology for designing overall system parameters, which will be helpful in demonstrating the control strategy proposed in Section 5.

4.1. EV Battery

Table 3. Examples of a commercial EVs’ battery characteristics (adapted from [26]).

Manufacturer	BMW	Mercedes-Benz	Nissan	Porsche	Renault	Tesla	Toyota	VW
Model	i3	EQC	Leaf e+	Taycan 4S	Zoe	Model S	Rav4	ID.3
Power (kW)	137	304	162	395	101	593	228	152
Type	BEV	BEV	BEV	BEV	BEV	BEV	PHEV	BEV
Battery (kWh)	42.2	80	62	93.4	52	100	18	82
Voltage (V)	360	405	384	800	346	350	386	323

shows examples of commercial EV models and their Li-ion battery characteristics, considering both battery Electric Vehicles (BEVs) and plug-in hybrid EVs (PHEVs). In this work, the Tesla Model S vehicle is chosen to configure the battery parameters. As can be seen in Table 3, the Model S battery is a Li-ion battery with 593 kW of power, 100 kWh of energy, and 350 V of terminal voltage. Additionally, with this data, the current capacity of this battery is calculated as 100 kWh/350 V = 286 Ah. In addition, the Panasonic NCR18650B cell is used in the Model S battery [25], with its main characteristics described in

Table 4. NCR 18650B cell parameters (source: [27]).

Parameter	Value
Nominal voltage	3.60 V
Nominal capacity	3.35 Ah
Rated capacity	3.20 Ah
Full charge voltage	4.20 V
Charge current	1.625 A
Cut-off voltage	2.50 V

.

As will be discussed in Section 6, PSIM software is used to perform computer simulations, and the points ($Q_{full},E_{full}$), ($Q_{top},E_{top}$), ($Q_{nom},E_{nom}$) and ($Q_{max},E_{cut}$) indicated in Figure 7 together with the cell data available in Table 4 are used to configure the PSIM Li-ion battery block, whose final parameters are listed in

Table 5. EV Li-ion battery parameters used in the PSIM Li-ion battery block.

Parameter	Value
No. of Cells in Series	98
No. of Cells in Parallel	90
Voltage Derating Factor	1
Capacity Derating Factor	1
Rated Voltage	3.60 V
Discharge Cut-off Voltage	2.50 V
Rated Capacity	3.20 Ah
Internal Resistance	$50\times {10}^{-3}$$\Omega$
Discharge Current	3.35 A (1C)
Capacity Factor	1.225
Full Voltage	4.00 V
Exponential Point Voltage	3.90 V
Nominal Voltage	3.06 V
Maximum Capacity	$3.264/3600$ Ah
Exponential Point Capacity	$0.0759/3600$ Ah
Nominal Capacity	$2.7974/3600$ Ah
Initial State of Charge	1.00

. It is important to note that the parameters labeled “Maximum Capacity”, “Exponential Point Capacity”, and “Nominal Capacity” in Table 5 were subjected to a derating process by a multiplication factor of 1/3600. This adjustment was necessary to represent the behavior of 1 h in 1 s. Furthermore, as can be seen in Table 5, to achieve the desired terminal voltage rated close to 350 V, 98 cells are placed in series, and to obtain the 286 Ah-rated capacity ($R_Q$), 90 cells are placed in parallel.

Moreover, seeking to obtain a simplified model in which the voltage at the battery terminal depends solely on its state of charge (SOC), a look-up table (LUT) model was derived, as can be seen in Figure 8a. In this model, the battery terminal voltage is available through a voltage-controlled voltage source, which is fed by an LUT that stores data points related to the relationship between the battery terminal voltage and the SOC, as can be seen in Figure 8b, obtained with the Li-ion PSIM block using the parameters listed in Table 5. To update the terminal voltage, the actual battery SOC, given as $SO{C}_a$, is calculated as (11), based on the battery current $I_{Bat}$ and the initial battery SOC value given by $SO{C}_0$.

$$\begin{array}{c}SO{C}_a=SO{C}_0-\int {\displaystyle \frac{I_{Bat}}{R_Q}}dt\end{array}$$

(11)

4.2. Quasi-Y Impedance Network Components and LCL Filter

The Quasi-Y network was designed with the objective of providing a value of $V_{DC-link}$ of 600 V. As can be seen in Figure 8b, the voltage of the battery terminal can vary from approximately 409 V (fully charged) to 229 V (low SOC), considering that SOC = 0% refers to the stage where the battery terminal voltage has its minimum allowed value (cutoff voltage). Therefore, the impedance network is designed for the worst-case scenario, that is, $V_{inv}$ = 229 V, which implies a maximum voltage boost factor of $B_{max}$ = 2.62 and a minimum of $B_{min}$ = 1.47 when the battery is fully charged. Furthermore, a coupled winding factor of $\delta =3$, with winding proportions $N_1$:$N_2$:$N_3$ = 3:3:1, and a switching frequency of $f_{tri}$ = 24 kHz were adopted. The total power processing capacity of 100 kW was considered for this application, based on the energy rating of Model S and in the work developed by [10], with a current ripple factor $k_{l1}$ = 2% and voltage ripples $C_1$ and $C_2$ of $k_{C1}$ = 0. 1% and $k_{C2}$ = 5%, respectively. Therefore, using the formulae presented in Table 2, the calculated values of the impedance network were $L_{in}$ = 703 μH, with an ESR of 150 mΩ; $C_1$ = 7.9 mF and $C_2$ = 152 μF, with ESRs of 10 mΩ, respectively; and an adopted value of $L_m$ = 250 μH.

For the design of the LCL filter, a phase voltage $V_{ph}$ of 127 V RMS at $f_g$ of 60 Hz with a nominal power $P_o$ of 100 kW and an expected DC voltage value $V_{DC-link}$ of 600 V was considered. The maximum variation of the power factor seen by the grid was established at $x_{PF}$ = 0.05, and an attenuation factor $k_a$ = 0.3 was adopted. The rippled current $\Delta I_1$ was adopted as 1%, and the ESR factor used was $F_{ESR}$ of 15%. Then, the values of $L_{f1-3}$ were calculated as 1.12 mH, $r_{L1-3}$ of 63 mΩ, $L_{g1-3}$ of 7 μH, and an $r_{Lg1-3}$ of 0.4 mΩ, using the formulae shown in Section 3.2. In addition, the value of $C_f$ was calculated as 92 μF with a damping resistance of $r_{fC1-3}$ = 158 mΩ.

4.3. Grid-Connected Loads (Business/Home Loads)

In this study, the load connected at the common coupling point of the electrical grid is modeled to represent one office building. This scenario is inspired by the case study provided by [28] and uses data from their work to construct a hypothetical setting. Each office building exhibits an average energy consumption of 145 kWh per hour. The cumulative base load of the buildings is substantial, consistently maintaining about $P_{load}$ = 113 kW of active power and $Q_{load}$ = 55 kVA of reactive power. Despite the presence of non-linear loads and due to the capacitor banks already present in the load described by [28], for simplicity and to focus the analysis on the EV power electronics interface, the load is modeled as a parallel RC branch. Therefore, the load resistances $R_L$ and capacitance $X_{CL}$ are calculated as (12) and (13), respectively, considering that each phase processes one third of the total load power at 60 Hz.

$$\begin{array}{c}{R}_L=3{\displaystyle \frac{V_{g-rms}^2}{P_{load}}}=3{\displaystyle \frac{{127}^2}{113·{10}^3}}=0.428\Omega \end{array}$$

(12)

$$\begin{array}{c}{X}_{CL}={\displaystyle \frac{1}{2\pi f_g{C}_{CL}}}=3{\displaystyle \frac{V_{g-rms}^2}{Q_{load}}}=3{\displaystyle \frac{{127}^2}{55·{10}^3}}=0.880\Omega \end{array}$$

(13)

5. Proposed Control Strategy

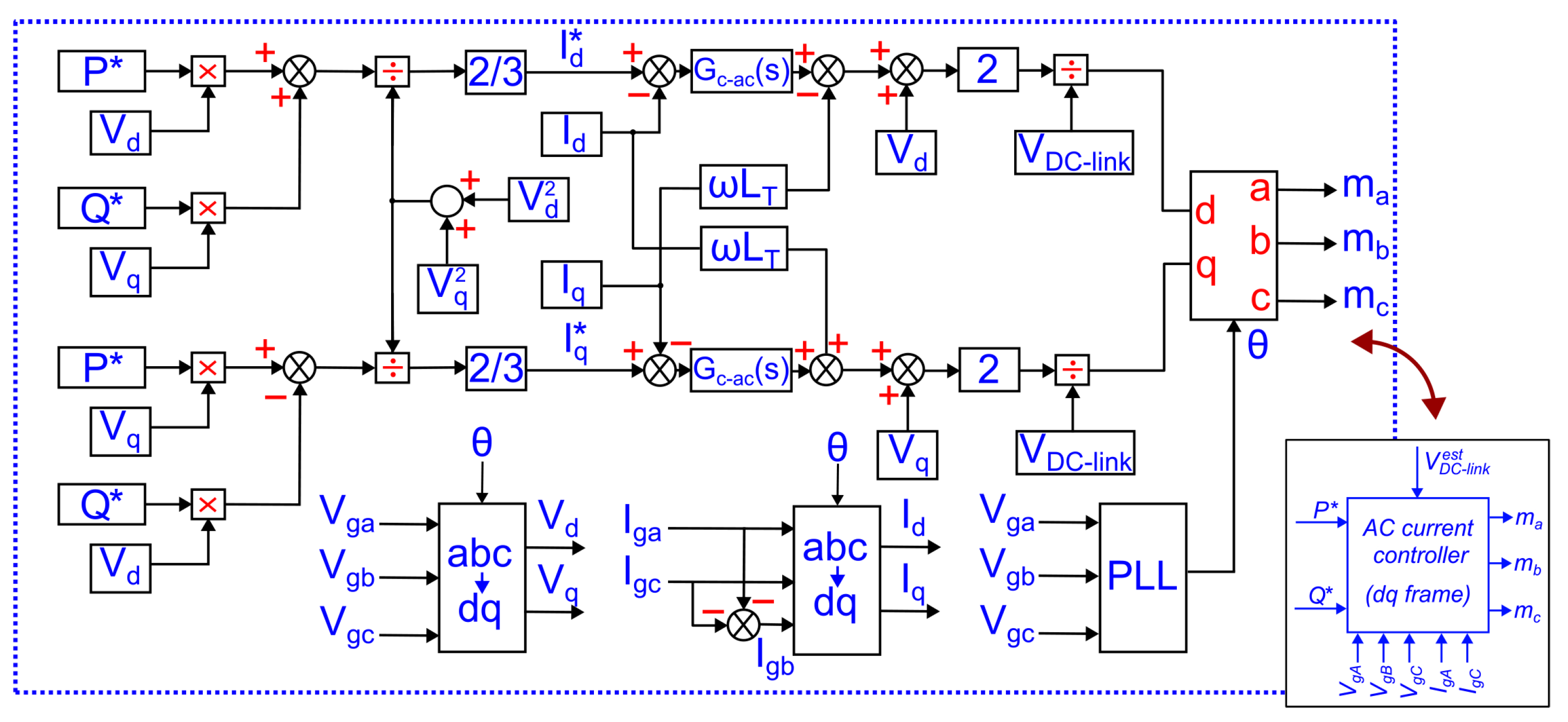
In this section, the proposed control strategy is presented, using a multi-loop architecture to regulate both the DC link voltage and the inverter output currents injected into the grid in a QS-YSI, as shown in Figure 9. The controller $G_{cv}$ is designed for the DC-link voltage based on the frequency domain method, with control parameters tuned to ensure greater system stability margins due to the converter’s non-minimum phase behavior. On the AC side, the control operates in the synchronous $dq$ reference frame, enabling the decoupled regulation of active $P^{\ast }$ and reactive $Q^{\ast }$ power references through independent PI controllers. The inverter output current controller relies on readings of the grid voltages $V_{ga}$-$V_{gc}$ and the inverter injected currents $I_{ga}$ and $I_{gc}$, where $I_{gb}$ is obtained mathematically. The reference currents for the d and q axes are calculated using the reference power commands $P^{\ast }$ and $Q^{\ast }$ and the components of the voltage and current of the grid in the $dq$ frame. To allow integration between the DC and AC control signals in the conventional SPWM technique, a modified PWM method is described that uses two distinct triangular carriers, one dedicated to the DC-link voltage control and another to inverter output current control, achieving a decoupled and simplified controller design. The complete system is synchronized with the grid through a phase-locked loop (PLL), which supports precise and stable bidirectional power exchange for V2G applications. In Figure 9, the PLL and Park transforms are inside the inverter output current controller block.

As can be seen in the “$V_{C1}^{\ast }$ reference logic” and “$P^{\ast }$ reference logic” in Figure 9, the way that $V_{C1}^{\ast }$ and $P^{\ast }$ behave changes if the active power flow changes from the battery to the grid (V2G) or from the grid to the battery (G2V). If the control system is required to operate in the V2G mode, then the voltage reference of the capacitor $C_1$ is calculated in terms of the desired DC link voltage, according to (14). In contrast, the DC link voltage is dynamically estimated in terms of the actual $C_1$ voltage, according to (15).

$$\begin{array}{c}{V}_{C1}^{\ast }=V_{DC-link}^{\ast }(1-D_{st})\end{array}$$

(14)

$$\begin{array}{c}{V}_{DC-link}^{est}={\displaystyle \frac{V_{C1}}{1-D_{st}}}\end{array}$$

(15)

If the control system is required to work in G2V mode, then the $R_v$ flag is turned to 1; otherwise, it is 0. If $R_v$ is 1, then the DC link controller loop is’stopped’ by means of the control flag $fla{g}_{st}$ and the control signal for the anti-parallel transistor in the impedance network $g_{rev}$ is turned to one, allowing the G2V operation. Furthermore, to avoid excessive current transients at $I_{Lin}$ due to stored energy in the impedance network components, $V_{DC-link}^{\ast }$ gradually decreases to $V_{in}$, and if the system was previously working in V2G mode, $P^{\ast }$ gradually decreases to a negative value, depending on the amount of power that should be injected into the battery. Finally, to avoid unwanted excessive values for $D_{st}$, a saturation bounds the excursion of $D_{st}$ from 0 to $D_{st-max}$. In the next sections, a detailed design methodology for the components of the proposed control system is given.

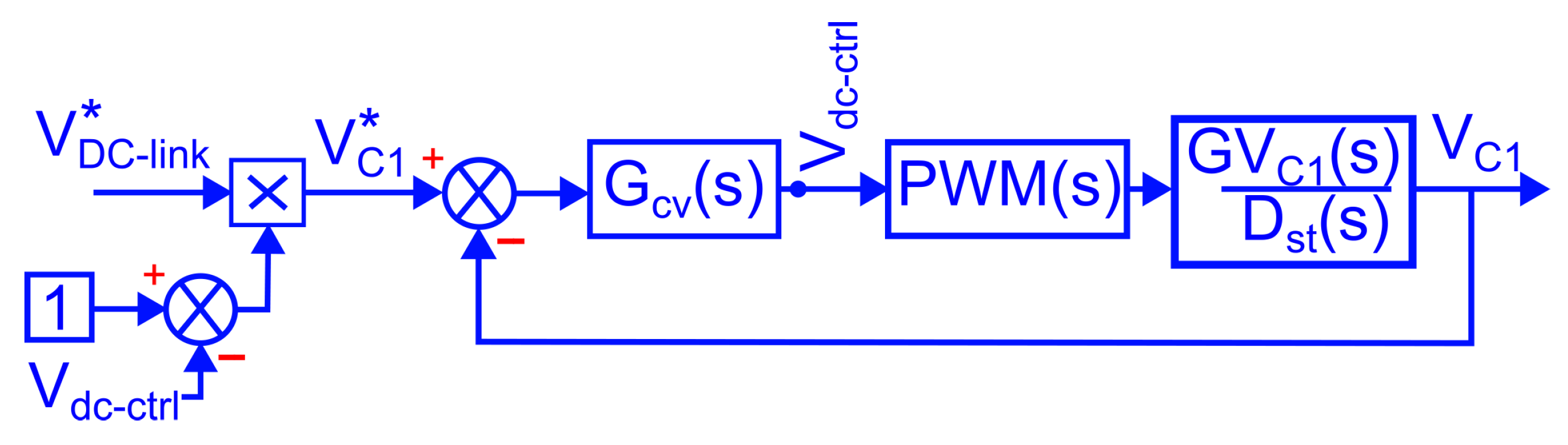
5.1. DC-Link Voltage Controller Design

Figure 10 shows the block diagram of the DC link voltage control of the QS-YSI. Taking into account the impedance network specifications outlined in

Table 6. Proposed V2G system with Quasi-Y impedance source inverter parameters.

Parameter	Value	Parameter	Value
$f_{tri},f_{2tri}$	24 kHz, 48 kHz	$f_g$	60 Hz
$V_{\mathrm{in}}$	229–409 V	$V_{\mathrm{DC}-\mathrm{link}}$	600 V
$V_{ga-c}$ (peak)	180 V	$\delta$	3
$L_{\mathrm{in}}$	703 μH	$L_m$	250 μH
$L_{f1-3}$	1.12 mH	$L_{g1-3}$	7 μH
$C_1$	7.9 mF	$C_2$	152 μF
$C_{f1-3}$	152 μF	$r_{fC1-3}$	158 mΩ
$N_1$:$N_2$:$N_3$	3:3:1	$r_{Lin}$	150 mΩ
$r_{N1-3}$	25 mΩ	$r_{C1,2}$	55 mΩ
$r_D$	10 mΩ	$r_S$	10 mΩ
$r_{Lg1-3}$	0.4 mΩ	$r_{Lf1-3}$	63 mΩ
$R_L$	0.428 $\Omega$	$C_{CL}$	3 mF

, the uncompensated open-loop transfer function, represented as $T_{nc}\left(s\right)$ in the continuous domain, is defined by (16), where the PWM dynamics $PWM\left(s\right)$ is modeled as a delay of one sample, with a transfer function given by (17). The transfer function for the voltage $V_{C1}$ to the control signal $D_{st}$ is specified by (18), already considering the parameters of Table 6. The ${\displaystyle \frac{V_{C1}\left(s\right)}{D_{st}\left(s\right)}}$ transfer function is derived from a state-space average small-signal model, which was derived by the authors in [23].

$$\begin{array}{c}{T}_{nc}\left(s\right)=PWM\left(s\right)G{\displaystyle \frac{V_{C1}\left(s\right)}{D_{st}\left(s\right)}}\end{array}$$

(16)

$$\begin{array}{c}PWM\left(s\right)={\displaystyle \frac{1-s\frac{20.83·{10}^{-6}}{2}}{1+s\frac{20.83·{10}^{-6}}{2}}}\end{array}$$

(17)

$$\begin{array}{c}G{\displaystyle \frac{V_{C1}\left(s\right)}{D_{st}\left(s\right)}}={\displaystyle \frac{-8.853·{10}^4·s^4-2.412·{10}^8·s^3-1.186·{10}^{12}·s^2-2.335·{10}^{15}·s+2.427·{10}^{17}}{s^5+2632·s^4+1.193·{10}^7·s^3+2.47·{10}^{10}·s^2+9.732·{10}^{12}·s+1.239·{10}^{15}}}\end{array}$$

(18)

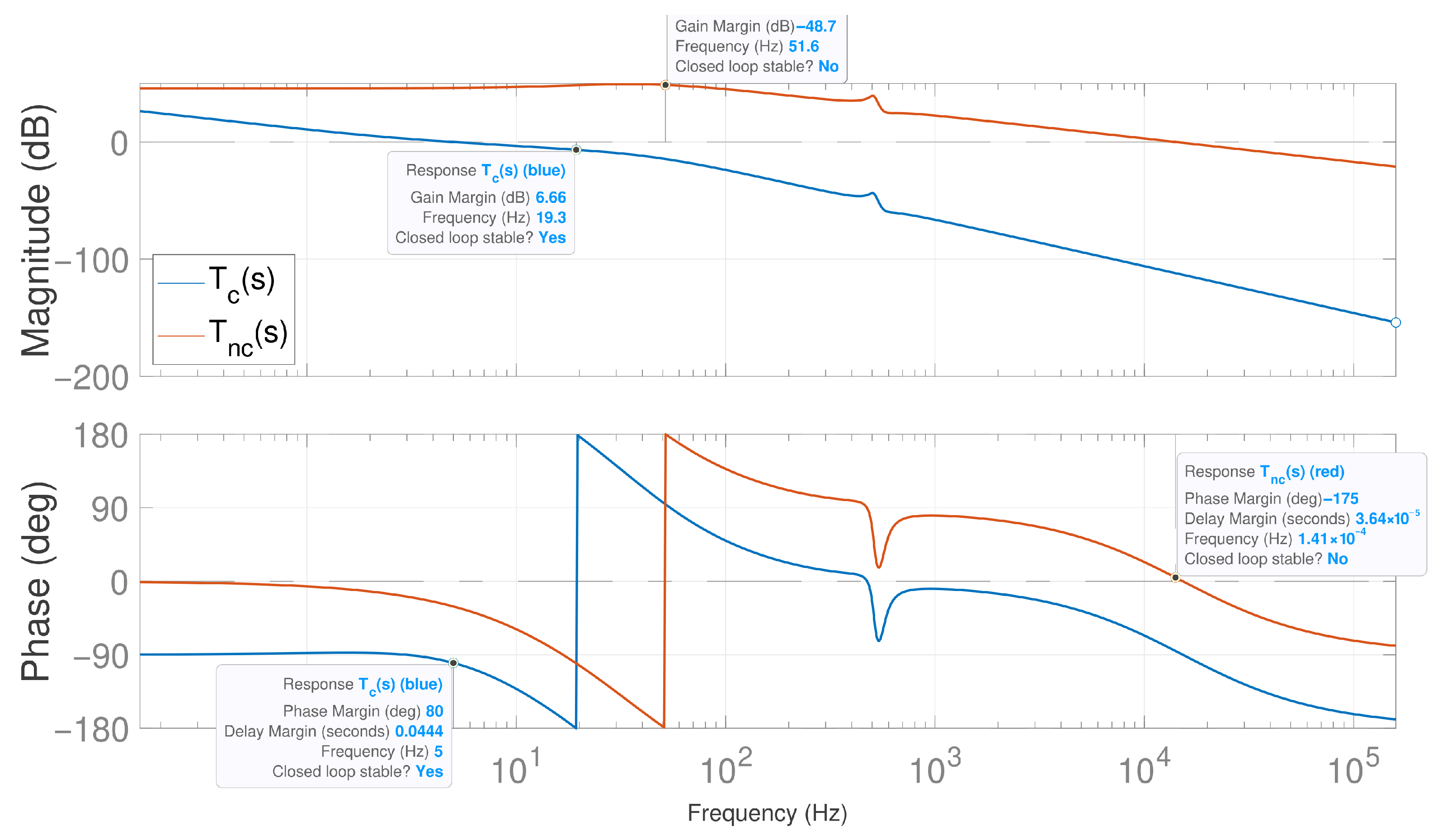
Figure 11 presents the Bode plots for the compensated open-loop function $T_c\left(s\right)$ and $T_{nc}\left(s\right)$. Before controller design ($G_{cv}\left(s\right)=1$), the Bode plot of $T_{nc}\left(s\right)$, shown in Figure 11, reveals that it exhibits a negative gain margin (−48.7 dB) and a negative phase margin (−175°) at 14.1 kHz, indicating closed-loop instability and requiring proper controller design. Moreover, the existence of a non-minimum phase complicates controller design as it demands extensive phase inclusion at high frequencies to broaden the controller bandwidth. To modify these characteristics, a voltage controller $G_{cv}$ is designed to track the reference voltage. However, for non-minimum phase systems, such as the QS-YSI analyzed here, achieving a higher bandwidth frequency $f_{bw}$ without causing closed-loop instability is not always feasible. Therefore, a value of $f_{bw}$ = 5 Hz is chosen, which gives a satisfactory dynamic response and robustness to changes in operational conditions. A higher phase margin $PM$ results in a more damped response with an extended settling time, whereas lower values lead to a faster settling with potential overshoot and oscillations. Thus, a $PM$ of 80° is selected for this design, prioritizing damping over response speed. Following the method outlined in [29], a type–II PI controller was designed for $G_{cv}\left(s\right)$ in the continuous-time domain, considering the design requirements described before. The controller $G_{cv}\left(s\right)$ transfer function is given in (19). After the inclusion of $G_{cv}\left(s\right)$, as can be seen in Figure 11, the compensated open-loop gain $T_c\left(s\right)$ presents a phase-margin of 80° at 5 Hz and a gain margin of 6.66 dB, achieving closed-loop stability and meeting the design requirements.

$$G_{cv}\left(s\right)={\displaystyle \frac{0.22432(s+21.64)}{s(s+45.61)}}$$

(19)

5.2. Inverter Output Current Control in dq Frame

The $abc/dq$ or Park transformation expresses three-phase quantities, such as the injected currents of the grid $I_{ga-c}$ and the grid voltages $V_{ga-c}$, in a rotating reference frame, simplifying the analysis in the phasor domain. This transformation is expressed by (20), where x can be a current or voltage variable. In the $dq$ domain, the complex power is defined as (21), with ∗ denoting the complex conjugate and the vectors of complex voltage $\overrightarrow{V_g}$ and current $\overrightarrow{I_g}$ defined by (22) and (23), respectively.

$$\left[\begin{array}{c}{x}_d\\ x_q\\ x_0\end{array}\right]={\displaystyle \frac{2}{3}}\left[\begin{array}{ccc}cos\theta & cos\left(\theta -{\displaystyle \frac{2\pi }{3}}\right)& cos\left(\theta +{\displaystyle \frac{2\pi }{3}}\right)\\ -sin\theta & -sin\left(\theta -{\displaystyle \frac{2\pi }{3}}\right)& -sin\left(\theta +{\displaystyle \frac{2\pi }{3}}\right)\\ {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}\end{array}\right]\left[\begin{array}{c}{x}_a\\ x_b\\ x_c\end{array}\right]$$

(20)

$$\begin{array}{c}S={\displaystyle \frac{3}{2}}·\overrightarrow{V_g}·{\overrightarrow{I_g}}^{\ast }\end{array}$$

(21)

$$\begin{array}{c}\overrightarrow{V_g}=V_{gd}+j{V}_{gq}\end{array}$$

(22)

$$\begin{array}{c}\overrightarrow{I_g}=I_{gd}+j{I}_{gq}\end{array}$$

(23)

Substituting (22) and (23) into (21), the complex power of the grid $S_g$ can be formulated as (24). From (24), the active $P^{\ast }$ and reactive $Q^{\ast }$ powers can be isolated as (25) and (26), respectively.

$$\begin{array}{c}{S}_g={\displaystyle \frac{3}{2}}(V_{gd}+j{V}_{gq})(I_{gd}-j{I}_{gq})\end{array}$$

(24)

$$\begin{array}{c}{P}_g={\displaystyle \frac{3}{2}}(V_{gd}{I}_{gd}+V_{gq}{I}_{gq})\end{array}$$

(25)

$$\begin{array}{c}{Q}_g={\displaystyle \frac{3}{2}}(V_{gq}{I}_{gd}-V_{gd}{I}_{gq})\end{array}$$

(26)

Solving (25) and (26) for $I_{gd}$ and $I_{gq}$, the direct and quadrature current references $I_{gd}^{\ast }$ and $I_{gq}^{\ast }$ can be calculated as (27) and (28), respectively. Therefore, given $V_{gd}$, $V_{gq}$, $P^{\ast }$, and $Q^{\ast }$, it is possible to compute the reference values for $I_{gd}^{\ast }$ and $I_{gq}^{\ast }$, respectively.

$$\begin{array}{c}{I}_{gd}^{\ast }={\displaystyle \frac{2}{3}}·{\displaystyle \frac{P^{\ast }{V}_{gd}+Q^{\ast }{V}_{gq}}{V_{gd}^2+V_{gq}^2}}\end{array}$$

(27)

$$\begin{array}{c}{I}_{gq}^{\ast }={\displaystyle \frac{2}{3}}·{\displaystyle \frac{P^{\ast }{V}_{gq}-Q^{\ast }{V}_{gd}}{V_{gd}^2+V_{gq}^2}}\end{array}$$

(28)

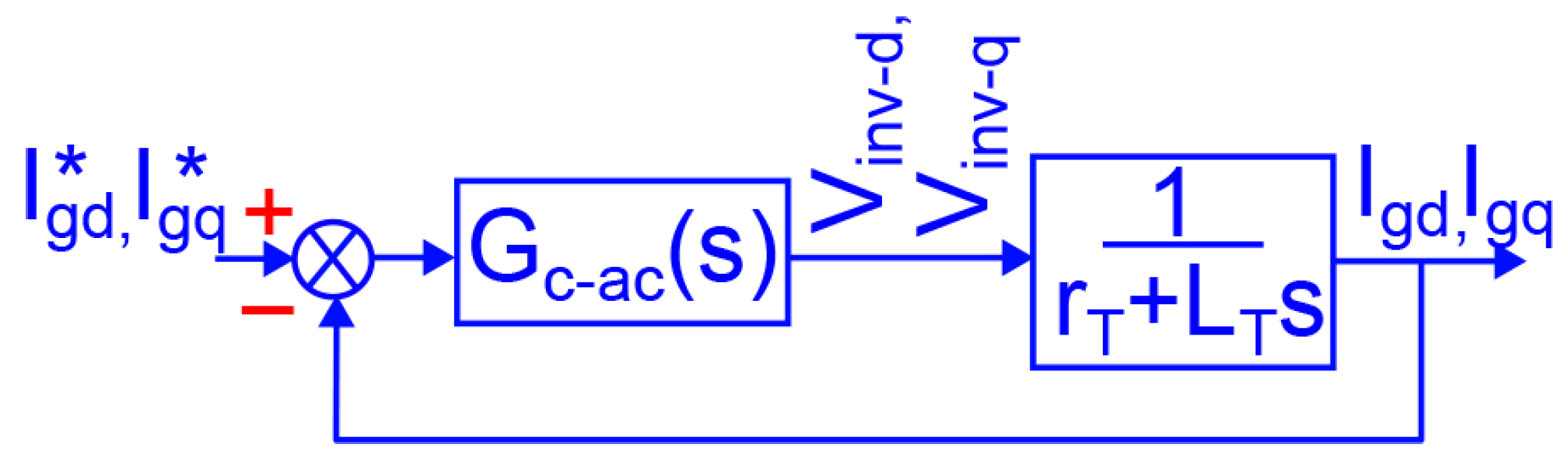
Taking into account that the impedance branch composed of $C_{f1-3}$ has a high impedance at the fundamental frequency, $dq$ control of the three-phase inverter with the LCL filter can be adapted from the conventional LC or L filter schemes, that is, it is assumed that the total inductance is the sum of the inverter and the grid inductance, $L_T=L_f+L_g$. In the same way, the equivalent total series resistance $r_T=r_{Lf}+r_{Lg}$. Therefore, inverter synthesized voltages can be written as (29)–(31).

$$\begin{array}{c}{V}_{inv-a}=r_T{I}_{ga}+L_T{\displaystyle \frac{d{I}_{ga}}{dt}}+V_{ga}\end{array}$$

(29)

$$\begin{array}{c}{V}_{inv-b}=r_T{I}_{gb}+L_T{\displaystyle \frac{d{I}_{gb}}{dt}}+V_{gb}\end{array}$$

(30)

$$\begin{array}{c}{V}_{inv-c}=r_T{I}_{gc}+L_T{\displaystyle \frac{d{I}_{gc}}{dt}}+V_{gc}\end{array}$$

(31)

Applying the Park transform in Equations (29)–(31), one can obtain (32) and (33), which describe the synthesized inverter voltage in the $dq$ reference frame. Taking the Laplace transform of (32) and (33), one can obtain (34) and (35), which describe the dynamics of $I_{gd}\left(s\right)$ and $I_{gq}\left(s\right)$, respectively, in the complex frequency domain. However, it can be seen from (34) and (35) that by adding the feed-forward gains $-I_{gq}\left(s\right)\omega L_T$ and $V_{gd}\left(s\right)$ to (34) and $I_{gd}\left(s\right)\omega L_T$ and $V_{gq}\left(s\right)$ to (35), the system is decoupled, and the variables $I_{gd}\left(s\right)$ and $I_{gq}\left(s\right)$ are only controlled by $V_{inv-d}\left(s\right)$ and $V_{inv-q}\left(s\right)$, respectively, as shown by the block diagram in Figure 12 (which is the same for the design of the PI controller for $I_{gd}\left(s\right)$ and $I_{gq}\left(s\right)$). Since the system shown in Figure 12 is a type 0 system and $I_{gd}^{\ast }$ and $I_{gq}^{\ast }$ are usually given as constant values, a null steady-state error in a closed-loop system can be achieved with a simple PI controller.

$$\begin{array}{c}{V}_{inv-d}=r_T{i}_{gd}+L_T\left({\displaystyle \frac{d{i}_{gd}}{dt}}-\omega i_{gq}\right)+V_{gd}\end{array}$$

(32)

$$\begin{array}{c}{V}_{inv-q}=r_T{i}_{gq}+L_T\left({\displaystyle \frac{d{i}_{gq}}{dt}}+\omega i_{gd}\right)+V_{gq}\end{array}$$

(33)

$$\begin{array}{c}{I}_{gd}\left(s\right)={\displaystyle \frac{V_{inv-d}\left(s\right)-V_{gd}\left(s\right)+L_T\omega I_{gq}\left(s\right)}{r_T+L_{T}s}}\end{array}$$

(34)

$$\begin{array}{c}{I}_{gq}\left(s\right)={\displaystyle \frac{V_{inv-q}\left(s\right)-V_{gq}\left(s\right)-L_T\omega I_{gd}\left(s\right)}{r_T+L_{T}s}}\end{array}$$

(35)

Therefore, the following design requirements are defined to obtain the PI controllers for the inverter current control loop in the $dq$ frame: a bandwidth frequency $f_{bw-ac}$ = 240 Hz which is set three decades below $f_{tri}$ and a phase margin $P{M}_{ac}$ set at 60°. The designed $G_{c-ac}\left(s\right)$ transfer function is given by (36) and was obtained using traditional design rules for the frequency domain response [30]. 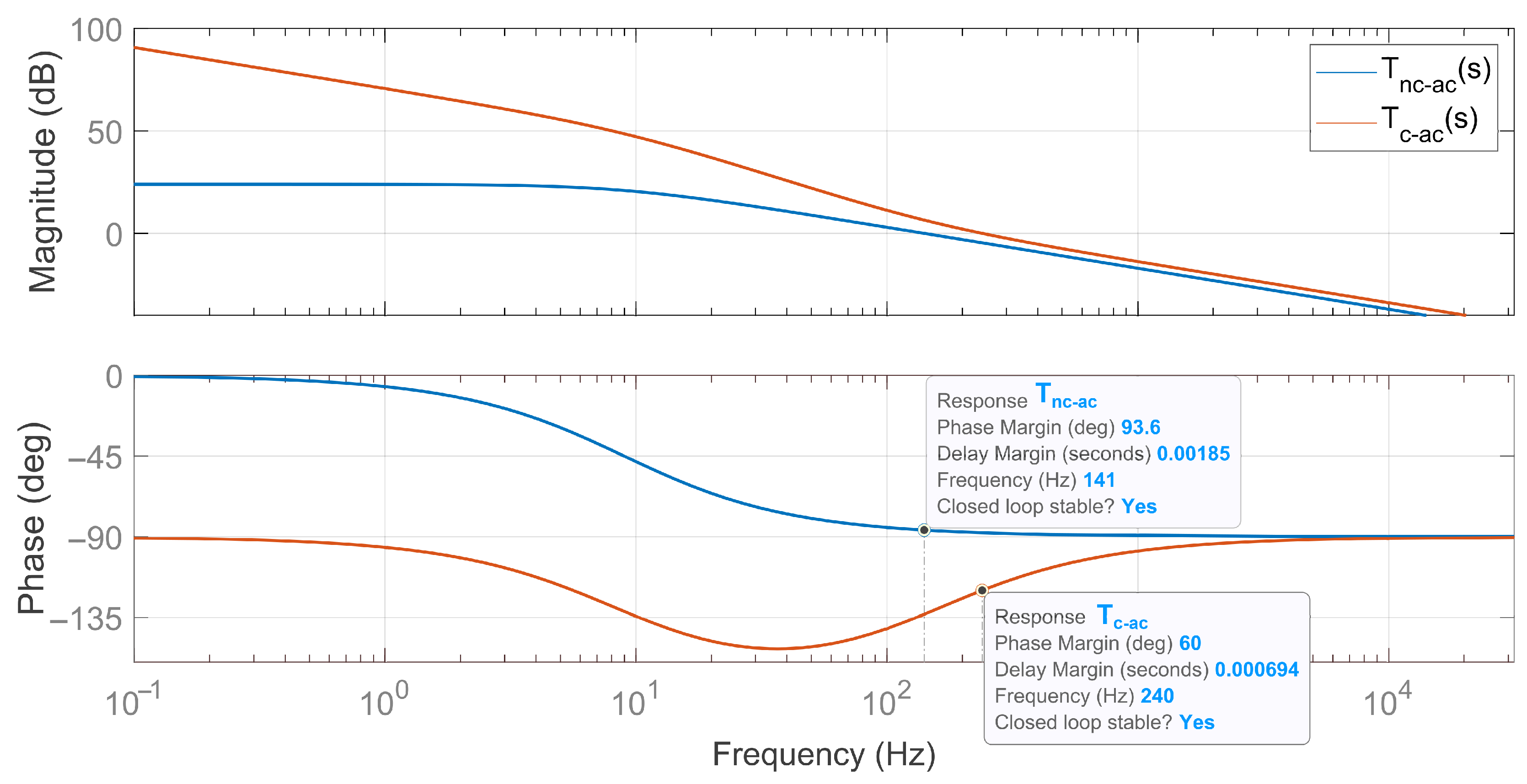Figure 13 shows the Bode plots of the uncompensated open-loop gain $T_{nc-ac}\left(s\right)$ and the compensated open-loop gain $T_{c-ac}\left(s\right)$, considering the block diagram shown in Figure 12. It can be seen in Figure 13 that both $T_{nc-ac}\left(s\right)$ and $T_{c-ac}\left(s\right)$ have infinite gain margins and are closed-loop stable, but the uncompensated loop $T_{nc-ac}\left(s\right)$ has a value of $P{M}_{ac}$ of 93.6°, while $T_{c-ac}\left(s\right)$ has 60° of $P{M}_{ac}$ at 240 Hz, thus indicating the successful design of $G_{c-ac}\left(s\right)$.

$$G_{c-ac}\left(s\right)=1.44{\displaystyle \frac{(s+947.3)}{s}}$$

(36)

The control architecture shown in Figure 14 shows the complete block diagram of the inverter output current controller in the $dq$ frame, indicating the content of the block “inverter output current controller” shown in Figure 9. The PLL processes the three-phase voltage inputs $V_{ga}$, $V_{gb}$, and $V_{gc}$ to estimate the instantaneous grid angle $\theta$, which is then used to transform the measured grid voltages into the frame components $dq$, $V_{gd}$, and $V_{gq}$. The same is true for the grid currents $I_{ga}$ and $I_{gc}$, where $I_{gb}$ is obtained mathematically from $I_{ga}$ and $I_{gc}$. The control objective is defined by the active and reactive power references $P^{\ast }$ and $Q^{\ast }$. These references are used in combination with the measured voltage components to compute the reference currents $I_d^{\ast }$ and $I_q^{\ast }$, using (27) and (28). The $G_{c-ac}\left(s\right)$ controllers designed before regulate the output currents of the converter by minimizing the error between the reference currents $I_d^{\ast }$ and $I_q^{\ast }$ and the actual currents $I_d$ and $I_q$, respectively. The controller outputs are subsequently transformed back into the three-phase $abc$ frame through inverse Park and Clarke transformations, using the angle $\theta$ provided by the PLL. The resulting modulation signals $m_a$, $m_b$, and $m_c$ are used to generate SPWM gating signals $g_1$–$g_6$.

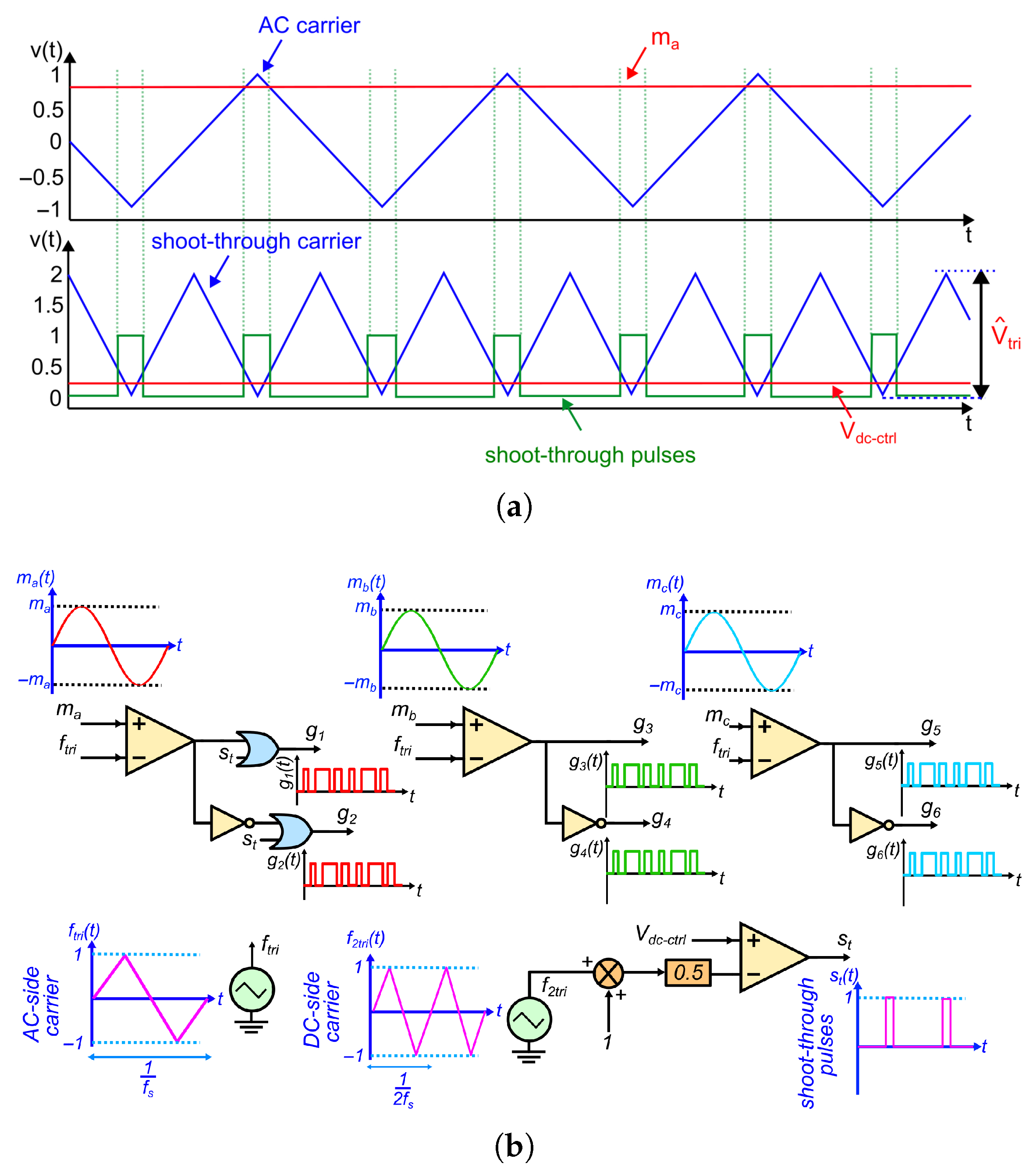
5.3. Modified PWM for Shoot-Through Integration

Table 7. Modified SPWM technique expressions for $D_{st}$ in terms of $V_{dc-ctrl}$.

SPWM Technique	Expression
Simple Boost Control (SBC)	$D_{st}=1-V_{dc-ctrl}$
Maximum Boost Control (MBC)	$D_{st}={\displaystyle \frac{2\pi -3\sqrt{3}{V}_{dc-ctrl}}{2\pi }}$
Maximum Constant Boost Control (MCBC)	$D_{st}={\displaystyle \frac{1-\sqrt{3}{V}_{dc-ctrl}}{2}}$

presents expressions for determining $D_{st}$ for various carrier-based modified SPWM techniques commonly found in the literature for ISIs [31]. For these techniques, the control variable $V_{dc-ctrl}$ not only establishes the control of the DC bus by determining the shoot-through duty cycle but also limits the linear modulation index M used to synthesize the sinusoidal modulating wave and consequently control the magnitude of the fundamental component of the voltage generated by the QS-YSI, as will be discussed later. As can be seen from the expressions presented in Table 7, the transfer function $D_{st}\left(s\right)/V_{dc-ctrl}\left(s\right)$ cannot be obtained directly, which indicates that there is no decoupling between the control information related to the DC-side and the AC-side control of the converter, thus complicating the controller design.

In this sense, ref. [32] proposes a modified SPWM technique that allows a direct expression of $D_{st}\left(s\right)/V_{dc-ctrl}\left(s\right)$ and provides decoupling between the control of the DC side and the AC side of the inverter. Figure 15a presents the waveforms for the modified SPWM strategy proposed by [32], and Figure 15b presents the block diagram that implements this strategy. It can be seen that two distinct triangular carriers are now used, unlike the SBC, MBC, and MCBC techniques, which use only one. In this case, there is a triangular carrier $f_{tri}\left(t\right)$ for the AC-side control, which interacts only with the linear modulation index M and $f_{2tri}\left(t\right)$ for the DC-side control, which interacts only with the control signal for the regulation of the DC bus, $V_{dc-ctrl}$. In this way, there is decoupling between the control signals of the DC-link loop ($D_{st}$) and the AC sides (signals $m_a$, $m_b$ and $m_c$), which allows for a direct relationship between $V_{dc-ctrl}$ and $D_{st}$ given by (37), which facilitates the design of the controller for the regulation of the DC bus. The triangular carrier $f_{2tri}\left(t\right)$ has twice the carrier frequency on the AC side to ensure that shoot-through conduction will occur only for zero-voltage switching configurations of the inverter. Furthermore, keeping the magnitude of this carrier ${\widehat{V}}_{tri}$ equal to 2, the controller output command $V_{dc-ctrl}$ becomes numerically equal to $D_{st}$, as can be observed from (37). The proposed modified SPWM scheme is developed based on the simple boost control strategy, and the maximum values of the control variables $m_a,m_b,m_c$ and the maximum allowed shoot-through duty cycle $D_{st-max}$ are related by Equation (38).

$$\begin{array}{c}{\displaystyle \frac{D_{st}}{V_{dc-ctrl}}}={\displaystyle \frac{2}{{\widehat{V}}_{tri}}}\end{array}$$

(37)

$$\begin{array}{c}{M}_{max}=1-D_{st-max}\end{array}$$

(38)

6. Simulation Results

To demonstrate the operation of the proposed electrical system, simulations were performed considering the architecture depicted in Figure 9. The simulations were carried out using PSIM version 2021b.1.7, with the solver parameters set as follows: a time step of 4.16667 × 10⁻⁷ s, ‘R_switch_on’ = 1 × 10⁻⁵ Ω, ‘R_switch_off’ = 1 × 10⁷ Ω, and a fixed-step solver type. In addition, the simulation environment was designed to reflect realistic operating conditions, incorporating grid constraints, dynamic power references, and DC-link voltage control and inverter output current control integration. Therefore, this section presents simulation results for two different scenarios. In scenario 1, or in scenario V2G-G2V-V2G, the V2G operation is activated, where the EV supplies active power to the grid, followed by the G2V mode as the grid recharges the EV. The EV subsequently resumes injecting active power into the grid. In scenario 2, the EV initially injects active power, and then it is required to exchange reactive power due to the resistive–capacitive nature of business/home loads. This scenario demonstrates the EV’s capability to not only return energy to the grid but also to provide ancillary services, including power factor correction.

6.1. Scenario 1—V2G-G2V-V2G

The active power injected by the QS-YSI, as can be seen in Figure 16a, successfully tracked the desired reference value of 50 kW both in the injection of active power into the point of common coupling and in the injection of reactive power close to zero; in its behavior as a load (between 0.80 s and 1.0 s), it consumes the same reference power previously injected.During the transitions between the V2G and G2V modes, the converter successfully followed the reference.

The impact of the operating mode of the QS-YSI from V2G to G2V can be seen in the behavior of the DC-link voltage, as shown in Figure 16b. When in V2G mode, the DC bus voltage $V_{DC-link}$ exhibited a pulsating behavior due to the presence of shoot-through conduction, reaching a maximum value of 615 V. The input current $I_{Lin}$, as shown in Figure 16c, presented CCM mode throughout the period and had a low current ripple, with 2.95 A in V2G mode and 2.51 A in G2V mode, with average currents of 168.5 A and −113 A, respectively.

In the curve shown in Figure 16d, the excursion of the state of charge has an initial discharge of 82% at 0.4 s, reaching a minimum value of 69% at 0.7 s, and then a regeneration of 10% of its state of charge at 1.1 s. Furthermore, the waveform of the grid current supplied by the QS-YSI shown in Figure 17a–c exhibits good behavior in both operating modes, having an RMS value of 131 A in the V2G and G2V modes, with a maximum $TH{D}_i$ of 0.23% and 0.32%, respectively, calculated using the PSIM SimView application.

6.2. Scenario 2—Active Power Injection and Reactive Power Compensation

In the mode of active power injection and reactive power compensation illustrated in Figure 18, the QS-YSI succeeded in following the constant reference value of 50 kW for active power and in following the reference profile of reactive power from 0 Var to 52.5 kVar. The converter was able to achieve the required reactive power compensation for the load, stabilizing the power factor seen by the grid close to 1.

Just like in scenario 1, when EV was acting as V2G, the DC link voltage of the converter, shown in Figure 19a,b, had a pulsed behavior with the maximum value reached being 623 V when injecting only active power and zero reactive power, maintaining the electrical grid with a power factor of 0.875. In reactive compensation, the bus voltage showed a greater peak voltage oscillation, ranging from 578 V to 618 V. The waveforms of the DC bus in both modes can be seen in Figure 19c,d.

7. Experimental Results

In this section, preliminary experimental results are shown for the proposed system, considering a small-scale prototype operating with nominal voltage levels, with programmable sources acting as the grid and storage systems, respectively.

Table 8. QS-YSI circuit parameters—laboratory prototype.

Component	Value	Component	Value
$L_{in}$	4.24 mH	$r_{Lin}$	0.85 $\Omega$
$C_2$	15 μF	$r_{C2}$	29.33 mΩ
$C_1$	2040 μF	$r_{C1}$	142.68 mΩ
$r_D$	25 mΩ	$r_S$	25 mΩ
$L_m$	0.222 mH	$N_1$:$N_2$:$N_3$	37:186:112
$R_o$	149.27 $\Omega$	$L_o$	10 mH
$V_{in}$	250 V	$f_{st}$	18 kHz
$\delta$	3.0135	$D_{st}$	155.328689 × ${10}^{-3}$

shows the prototype parameters, which are different from Table 6 due to the power scale capability of the prototype and the limitations of the components. The parameters shown in Table 8 were used in the computer simulation using PSIM, with F28379D blocks for the configuration of ADC and PWM peripherals and the SimCoder package for automatic code generation. The PSIM code generator tool was used to create the controller C code, while Code Composer Studio was used to upload the code to DSC F28379D. The coupled inductors were built on a sendust toroidal core (${\mu }_r$ = 60 H/m) with a winding turn ratio of 37:112:186 and 2 × 22 AWG and 3 × 20 AWG Litz wires. The capacitors $C_1$ and $C_2$ were implemented with the A511EJ68M450F and the C4AQLLU5150A19K model of 15 μF, 500 V film capacitor. The IRG4PF50WD IGBT and GC2X5MPS12 26 A and 1200 V SiC Schottky diode were used as $S_{1-6}$ and D. During grid-connected tests, the inverter output passive filter comprised three inductors with 10 mH, being a first-order low-pass filter. 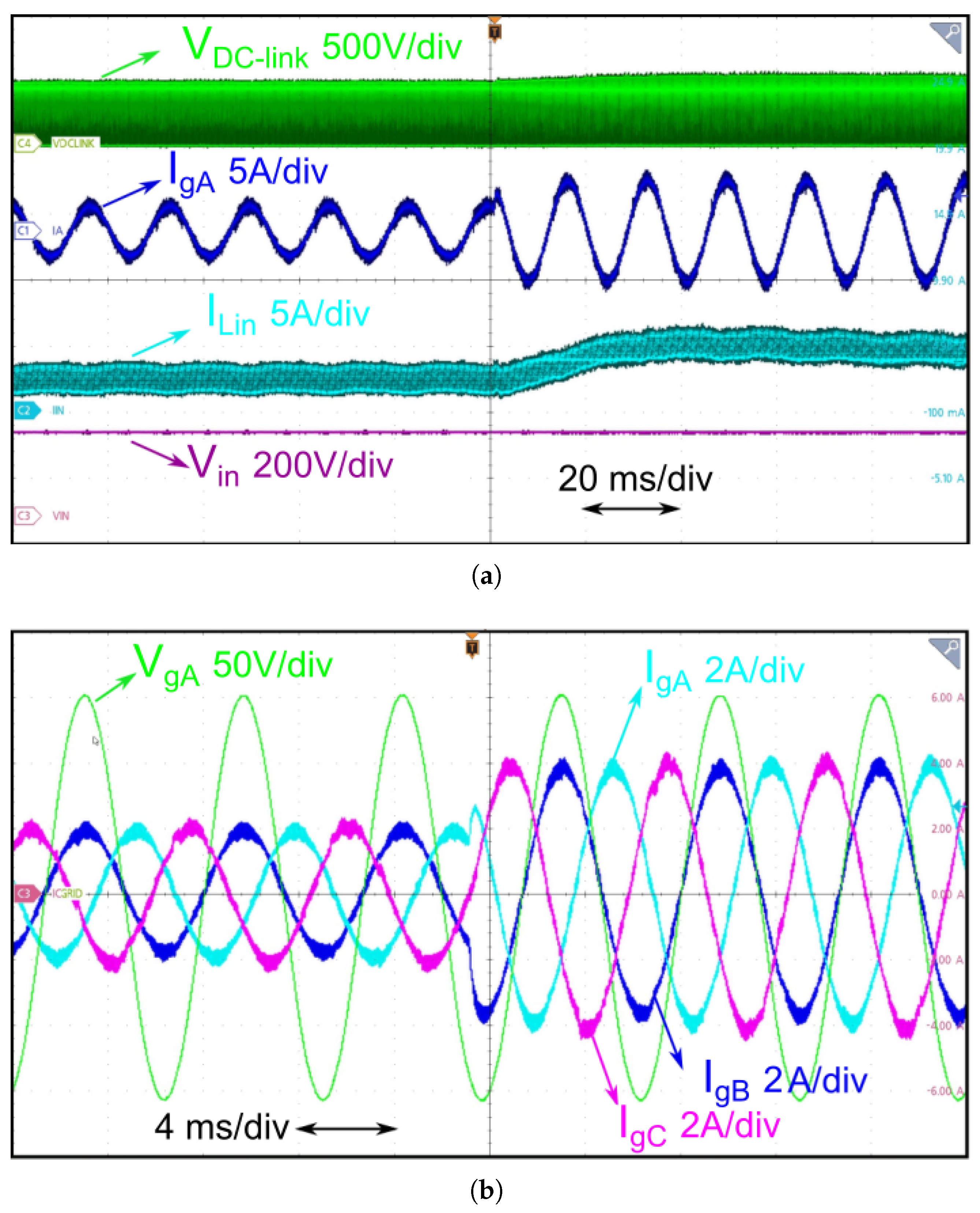Figure 20a shows the waveforms obtained for $V_{DC-link}$, $I_{gA}$, $I_{Lin}$, and $V_{in}$, while Figure 20b shows the inverter-injected currents and phase voltage for V2G operation and a step reference change in the injected current.

8. Discussion

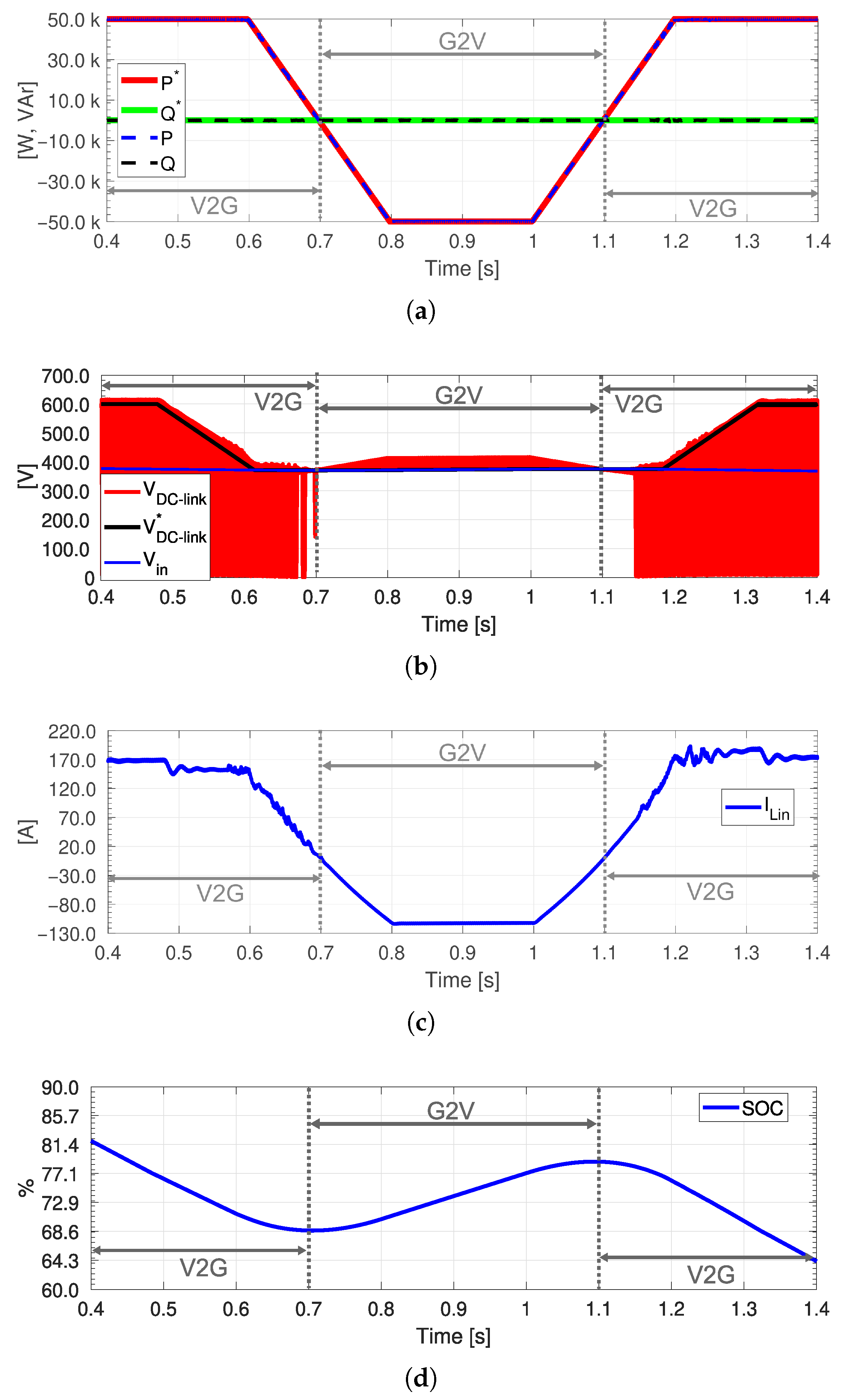
The results obtained for Scenario 1, shown in Figure 16 and Figure 17, clearly illustrate the effectiveness of the V2G and G2V operations of the proposed system. In Scenario 1, the QS-YSI successfully followed the active power reference $P^{\ast }$ and $Q^{\ast }$, resulting in only active power injection without reactive power exchange. Moreover, during power injection and charging, the EV managed 50 kW of active power transfer. The transition from V2G to G2V is smooth, using a reduction in the ramp for the power reference between 0.6 and 0.8 s and a ramp increase from 1.00 to 1.20 s, as shown in Figure 16a. Furthermore, the $V_{DC-link}^{\ast }$ reference signal decreases in a ramp from 0.5 to 0.6 s and increases from 1.2 s to 1.3 s. This approach prevents excessive $I_{Lin}$ current spikes during the V2G to G2V transitions, by ensuring that any energy stored in the impedance network during V2G is removed before entering G2V. The reason for this is that during V2G, the QS-YSI operates in boost mode, amplifying the DC link voltage to approximately 600 V using the shoot-through state, as shown in Figure 16b. However, the V2G to G2V transition involves a gradual adjustment of $V_{DC-link}^{\ast }$ to $V_{in}$, which reduces the values of $V_{dc-ctrl}$, thus decreasing the stored energy. This, along with active power reference ramping, ensures a seamless mode transition, which diminishes the spikes at $I_{Lin}$ during the transients. Figure 16c shows the waveforms $I_{Lin}\left(t\right)$, highlighting nearly continuous operation with reduced ripple and oscillations during the change of the V2G-G2V modes. As can be seen, the input inductor $L_{in}$ allows a continuous current flow, demonstrating the inherent benefit of QS-YSI to this type of application, which involves battery charging.

Concerning the battery dynamics, Figure 16d illustrates the evolution of the state of charge (SOC) during transitions between the operational modes of V2G and G2V. As the system shifts from the V2G to the G2V mode, the SOC variation rate over time decreases progressively, highlighting a gradual reduction in the injection of energy into the grid by the EV, since the power reference is decreased, as discussed before. Between 0.70 s and 1.10 s, which corresponds to the G2V mode, the battery SOC increases from approximately 69% to 79%, indicating that the EV battery is being charged. After 1.10 s, the V2G mode is again enabled and the SOC decreases, since the battery energy is sent to the grid. This aspect confirms that the system operates as intended with regard to the transitions of both modes. 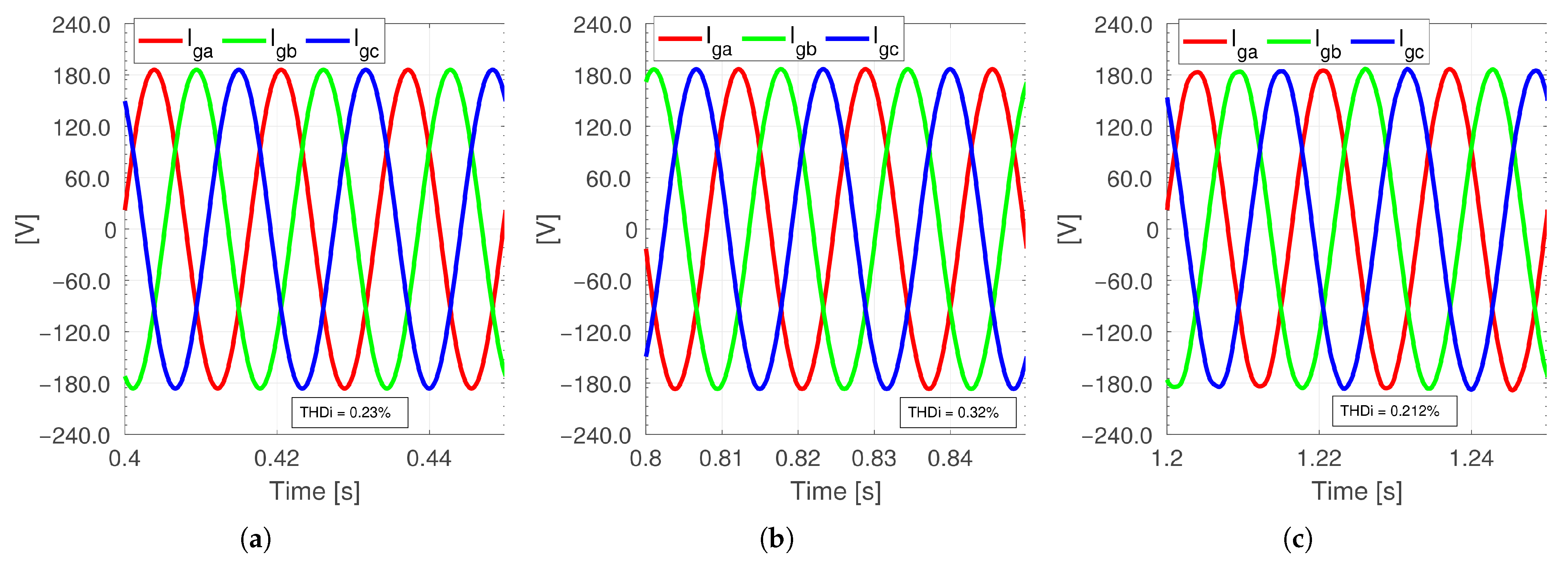As can be seen in Figure 17a,c $TH{D}_i$ remains between 0.21% and 0.23% in the V2G mode, while it reaches 0.32% during the G2V mode, as can be seen from Figure 17b. This indicates that the implemented QS-YSI system successfully maintains a $TH{D}_i$ profile under 5%, adhering to the harmonic standards [33].

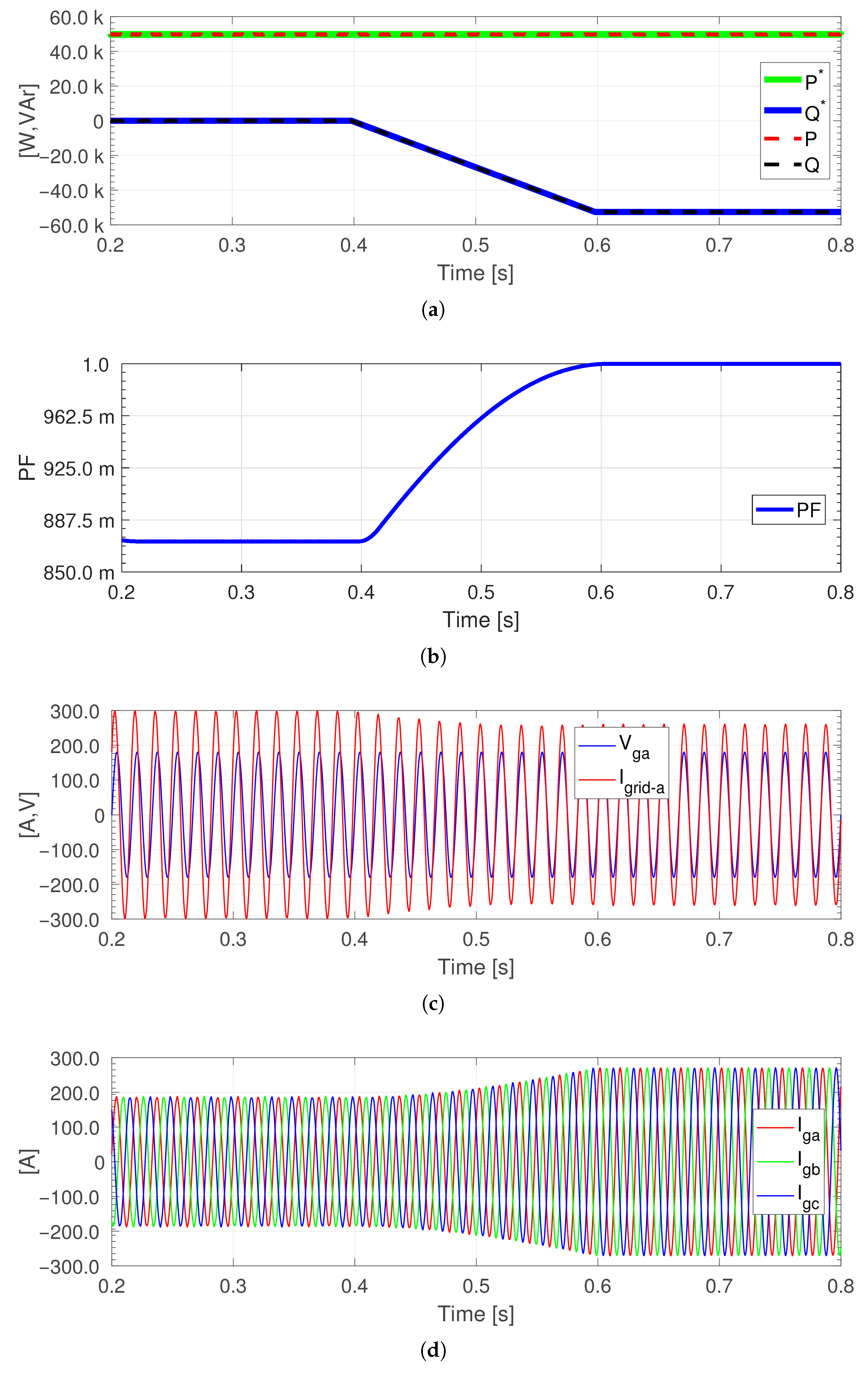
For scenario 2, Figure 18a demonstrates the effective achievement of the reference signals of EV $P^{\ast }$ and $Q^{\ast }$. Initially, before 0.4 s, the EV injected only active power into the grid. Between 0.4 s and 0.6 s, the reactive power reference $Q^{\ast }$ gradually decreased, stabilizing after 0.6 s alongside $P^{\ast }$. This indicates efficient active power injection and ancillary service, improving the grid power factor from approximately 0.875 to 1, as shown in Figure 18b. As can be seen in Figure 18c,d, the grid currents decrease as the injected current of the inverter increases, and it can be seen from Figure 18c that the phase current gradually becomes in phase with the phase voltage. 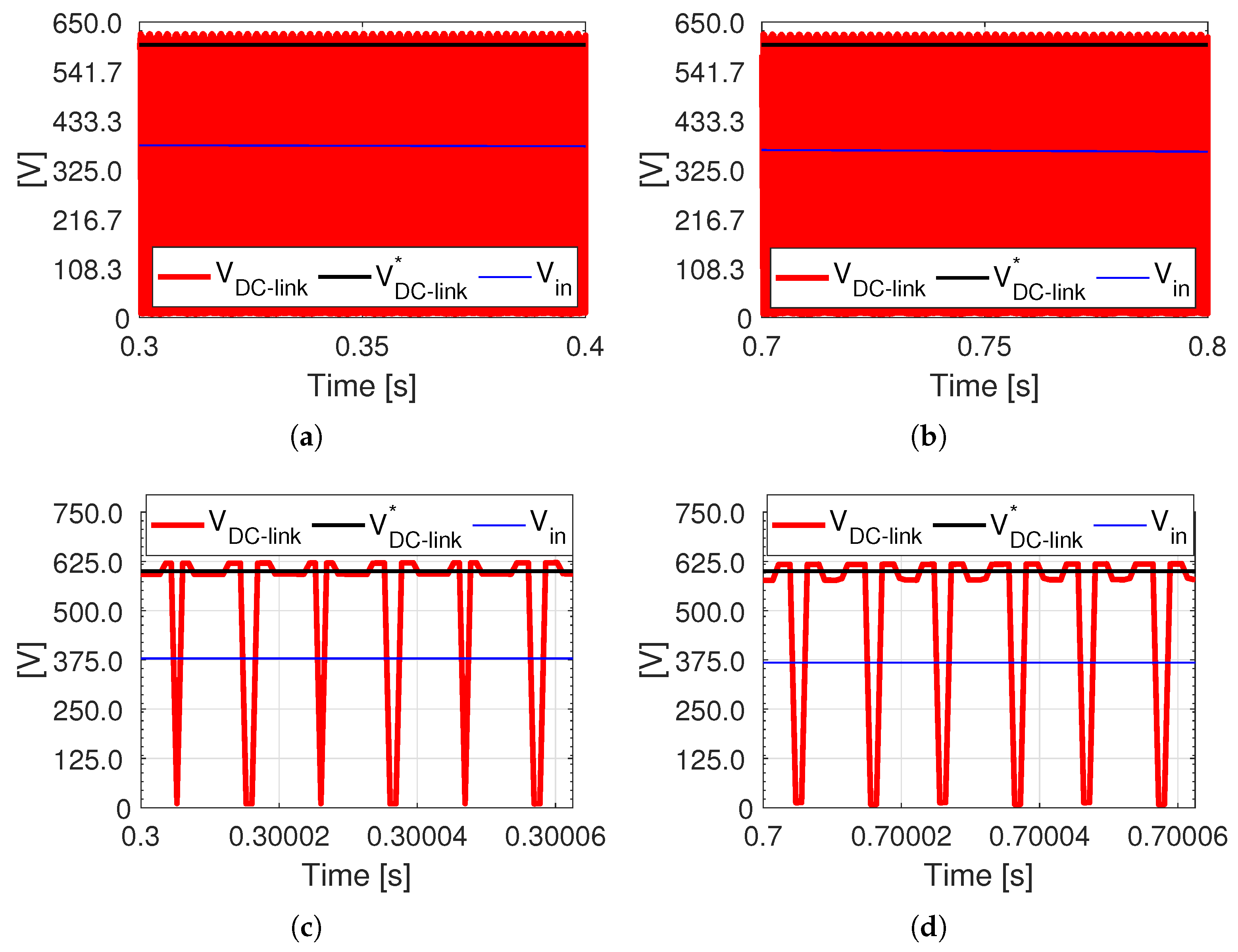Figure 19a,b confirm that $V_{DC-link}$ accurately followed reference $V_{DC-link}^{\ast }$; detailed waveforms of $V_{DC-link}$ before and after reactive power exchange are shown in Figure 19c,d, revealing the effects of the active and shoot-through states.

From the experimental results, Figure 20a shows the capability of QS-YSI to inject power into the grid, and it can be seen that the voltage $V_{DC-link}$ remains regulated at 470 V, reaching a peak value of 560 V after the reference change in $I_{gA}$ from 2 A to 4 A RMS. It is also possible to observe the reference tracking capability due to the inverter output current controller in Figure 20b. Furthermore, the QS-YSI input current $I_{Lin}$ remains in CCM mode throughout all operations, with a mean value that varies from approximately 2.5 to 4.5 A, while the input voltage $V_{in}$ remains at 250 V. Regarding the inverter currents injected into the grid, Figure 20b show the three inverter output currents, $I_{gA}$–$I_{gC}$ waveforms, including the grid voltage $V_{gA}$. It is clear from the comparison of the angular displacement of $I_{gA}$ with $V_{gA}$ that the inverter currents are injected with a power factor (PF) close to unity, which is mandatory for a grid-connected inverter. This was confirmed by the measured PF value of 0.997, obtained after the current reference change.

9. Conclusions

This paper introduced a Quasi-Y impedance source inverter (QS-YSI) specifically designed to operate as a Vehicle-to-Grid (V2G) and Grid-to-Vehicle (G2V) power electronics interface for EVs in the context of a virtual power plant (VPP). Based on the studies conducted, the main conclusions are as follows.

• The proposed QS-YSI facilitates both V2G and G2V operational modes, enabling bidirectional energy transfer between EVs and the grid. This allows EVs to either supply power back to the grid or draw energy for charging, while also providing reactive power support.
• Simulation scenarios and experimental validation demonstrate the capability of the inverter to exchange power with the grid and assist in the regulation of the power factor.
• A detailed design methodology was presented for the impedance network elements, including operational principles and control system development. This considers pulsating DC link voltage regulation and inverter output current control in the $dq$ frame, both integrated into a modified PWM scheme for decoupled operation.
• The main contribution of this research lies in demonstrating how to design and control QS-YSI in V2G/G2V applications with reactive power compensation, leveraging its single-stage buck–boost capability, bidirectional operation, and continuous input conduction, all of which are advantageous for EV batteries.

However, this study did not address challenges commonly encountered with the implementation of impedance source inverters, such as leakage inductance effects, DC-link voltage spikes, the need for auxiliary snubber circuits, complexities in coupled inductor design, and EMI considerations. Although these issues can be mitigated with appropriate methodologies, a detailed treatment is beyond the scope of this work. Future research will address systematic benchmarking against alternative converter topologies, refined grid modeling, and extended experimental validation.