Optimal Operation of Combined Cooling, Heating, and Power Systems with High-Penetration Renewables: A State-of-the-Art Review

Abstract

Under the global decarbonization trend, combined cooling, heating, and power (CCHP) systems are critical for improving regional energy efficiency. However, the integration of high-penetration variable renewable energy (RE) sources introduces significant volatility and multi-dimensional uncertainties, challenging conventional operation strategies designed for stable energy inputs. This review systematically examines recent advances in CCHP optimization under high-RE scenarios, with a focus on flexibility-enabled operation mechanisms and uncertainty-aware optimization strategies. It first analyzes the evolving architecture of variable RE-driven CCHP systems and core challenges arising from RE intermittency, demand volatility, and multi-energy coupling. Subsequently, it categorizes key flexibility resources and clarifies their roles in mitigating uncertainties. The review further elaborates on optimization methodologies tailored to high-RE contexts, along with their comparative analysis and selection criteria. Additionally, it details the formulation of optimization models, model formulation, and solution techniques. Key findings include the following: Generalized energy storage, which integrates physical and virtual storage, increases renewable energy utilization by 12–18% and reduces costs by 45%. Hybrid optimization strategies that combine robust optimization and deep reinforcement learning lower operational costs by 15–20% while strengthening system robustness against renewable energy volatility by 30–40%. Multi-energy synergy and exergy-efficient flexibility resources collectively improve system efficiency by 8–15% and reduce carbon emissions by 12–18%. Overall, this work provides a comprehensive technical pathway for enhancing the efficiency, stability, and low-carbon performance of CCHP systems in high-RE environments, supporting their scalable contribution to global decarbonization efforts.

1. Introduction

The rapid deployment of renewable energy (RE) is reshaping global power systems. By 2024, worldwide distributed energy capacity had exceeded 1.5 billion kW, a 230% increase since 2015, with cooling–heating–electricity coupling intensity rising by 47% [1]. In China, RE penetration in regional energy systems exceeds 30%, yet operational challenges persist. Air conditioning loads constitute 42% of peak summer grid demand, while industrial heating demand fluctuates by over 60% in winter [2,3]. Traditional segregated energy supply systems achieve only 38–45% utilization efficiency, failing to address spatiotemporal mismatches between supply and demand.

This efficiency gap is particularly critical given the accelerating global energy transition. Major economies now target 40–70% renewable penetration by 2035, with CCHP systems positioned as key multi-energy hubs for integrating variable renewables. However, unlike conventional fossil-based CCHP, high-penetration variable renewable energy systems face compounded uncertainties: renewable forecast errors (15–30% RMSE for solar/wind), demand volatility amplified by electrified heating/cooling, and price fluctuations in liberalized energy markets. These challenges fundamentally undermine traditional operation paradigms like the Following Thermal Load strategy or Following Electrical Load strategy, which assume predictable energy inputs. Consequently, industrial implementations exhibit persistent performance shortfalls, up to 15% efficiency losses, and 30% cost penalties in scenarios of high variable renewable penetration, highlighting an urgent need for uncertainty-resilient optimization frameworks.

CCHP systems derive their name from the integration of energy demand types, enabling simultaneous provision of dual thermal energy forms and electricity through an inherently efficient architecture. The first review of CCHP systems, published by Wu and Wang in 2006 [4], established foundational insights by first articulating the intrinsic advantages of integrated systems over segregated counterparts. The study systematically characterized prime mover (PM) technologies and thermally activated cooling subsystems, subsequently categorizing diverse technical configurations based on capacity scales, application boundaries, energy conversion efficiencies, and environmental performance metrics. CCHP systems, leveraging energy cascade utilization and multi-energy complementarity, can elevate primary energy efficiency to 75–85%. However, high-RE integration intensifies system volatility. Empirical studies indicate an 8–15% efficiency gap between designed and actual performance in industrial CCHP projects, attributed to dynamic components modeling, system planning frameworks and system operation strategy under multi-uncertainties [5].

The evolution of CCHP optimization methodologies reflects three generations of responses to these challenges. Initially, in Phase 1 (2000–2010), thermodynamics-focused approaches prioritized component efficiency but lacked adaptability to variability. Phase 2 (2010–2020) introduced multi-objective optimization, enabling cost-emission tradeoffs yet remaining computationally intractable for high-dimensional uncertainties. Currently, in Phase 3 (2021–present), strategies embrace uncertainty-aware coordination—leveraging AI for real-time adaptation and cross-sectoral flexibility. This paradigm shift responds to field observations: systems using Phase 2 methods still exhibit 8–12% efficiency gaps when VRE penetration exceeds 30%, while early Phase 3 implementations show 15–20% performance recovery through generalized storage and multi-energy synergy. Nevertheless, critical knowledge gaps persist in scalable uncertainty quantification and heterogeneous resource coordination, motivating this comprehensive review.

1.1. Evolution of CCHP Operation Optimization Paradigms

The operation optimization of CCHP systems has undergone significant paradigm shifts over the past two decades, driven by technological advancements and the integration of renewable energy sources. This evolution can be categorized into three distinct phases, each addressing the limitations of its predecessor while adapting to emerging energy challenges.

(1)

Phase 1: Thermodynamics-Driven Strategies (2000–2010)

Early research was characterized by thermodynamics-driven strategies and foundational component innovations, with seminal work by Wu and Wang [4] establishing the core operational paradigms of Following Thermal Load (FTL), Following Electrical Load (FEL), and Following Hybrid Load (FHL), each presenting distinct efficiency tradeoffs in stable-load environments. Concurrent component research by Al Moussawi [6] systematically categorized prime movers by capacity and thermal characteristics, while Mago’s analysis [7] of small-scale systems revealed promising 40–50% primary energy efficiencies that were nonetheless constrained by prohibitively high capital costs. During this period, substantial progress was made in thermal recovery technologies. Notably, Kalina cycles enhanced low-grade heat recovery efficiency by 15–20%, while absorption chillers achieved coefficients of performance ranging from 0.7 to 1.2 [8]. However, these static operational strategies gradually revealed their inadequacies, as they inherently relied on the assumption of predictable load profiles. Specifically, FEL strategies resulted in 20–35% thermal energy waste in commercial buildings, and FTL approaches necessitated up to 40% grid electricity supplementation in heating-dominated facilities [9,10]. These limitations ultimately propelled the field toward the development of more adaptive optimization approaches in the following years.

(2)

Phase 2: Single/Multi-Objective Optimization (2010–2020)

With optimization objectives expanding to encompass the 4E criteria (energy efficiency, exergy utilization, environmental performance, and economic performance), divergent operational strategies emerged, driving this phase to focus predominantly on single- and multi-objective optimization methodologies as a departure from earlier rigid thermodynamic frameworks [11,12,13]. Research shifted toward mathematical frameworks tailored to CCHP systems’ inherent complexity, characterized by binary variables and nonlinear/linear constraints that form mixed-integer nonlinear programming (MINLP) or mixed-integer linear programming (MILP) problems. Optimization methodologies evolved from single-objective to multi-objective paradigms. Classical approaches included weight methods, which simplify objectives via weighting factors and are aided by TOPSIS [14] or AHP [15] for weight selection, and $\epsilon$ constraint methods [16], which generate superior Pareto solutions despite higher computational complexity. Commercial solvers like CPLEX, Gurobi, and COPT offered efficient solutions for MILP/MINLP problems, while metaheuristic algorithms provided robust, scalable approaches for single- and multi-objective optimization for CCHP systems. This phase enhanced adaptability to load variability but faced challenges in computational efficiency for high-dimensional scenarios.

(3)

Phase 3: Uncertainty-Resilient Coordination (2021–Present)

This phase focuses on enhancing the greenness, stability, and reliability of CCHP systems by leveraging diverse flexible resources, including electric vehicles, air conditioners, multi-type energy storage, and flexible loads, through coordinated scheduling to buffer renewable intermittency [17]. It also addresses multi-stakeholder dynamics involving conflicting objectives among end-users, operators, and grid entities, where aggregators play a pivotal role in optimizing CCHP dispatch by aligning incentives to balance competing priorities. Additionally, CCHP systems are increasingly integrated to complement renewable generation with dispatchable thermal–electric output, enabling participation in broader energy markets and services. These advancements are underpinned by the widespread application of reinforcement learning (RL) and deep learning (DL), which enhance real-time dispatch optimization and forecasting capabilities, thereby enabling reliable operation amid renewable fluctuations. However, key challenges remain, including equitable benefit distribution among stakeholders, privacy-preserving coordination across multi-CCHP systems, and improving the generalization of AI techniques, which is critical for scaling as renewable penetration targets higher levels.

The operation optimization of CCHP systems has undergone significant paradigm shifts.

Table 1. Evolution of CCHP optimization paradigms: key characteristics and limitations.

Phase and Timeframe	Core Paradigm	Key Developments	Critical Limitations
Phase 1: 2000–2010 Thermodynamics-Driven	Component-centric efficiency	FTL/FEL/FHL strategies Prime mover classification Thermal recovery	20–35% thermal waste (FEL) 40% grid dependence (FTL) Static load assumptions
Phase 2: 2010–2020 Single/Multi-Objective Optimization	4E tradeoffs	4E criteria adoption MILP/MINLP formulations Metaheuristics (GA, PSO)	Computational intractability Forecast dependency Neglected flexibility resources
Phase 3: 2021–Present Uncertainty-Resilient Coordination	AI-enabled adaptive control	Generalized storage (PES/VES) Multi-energy synergy DRL/RO hybrid optimization VPP participation	Stakeholder equity challenges Privacy in multi-CCHP coordination AI generalization gaps

synthesizes the core characteristics, technological milestones, and limitations of these evolutionary phases.

1.2. Scope and Novelty of This Review

The existing reviews address CCHP optimization comprehensively, covering capacity planning [4], techno-economic analysis of gas-fired systems [7], hybrid configurations [11], component-level prime mover efficiency [6], and classical load-following strategies [4,9]. However, they exhibit critical limitations in high-renewable penetration scenarios. Prior works focus predominantly on fossil-fueled systems with stable inputs, emphasizing deterministic multi-objective tradeoffs [12,13] or single-energy vector optimization [7,11]. They rarely integrate the multi-dimensional uncertainty modeling or cross-vector flexibility essential for variable renewable energy integration, nor do they provide frameworks for selecting uncertainty-aware algorithms tailored to high-RE dynamics. These gaps underscore the need for a focused review addressing the unique challenges of CCHP systems under high renewable penetration.

To bridge these gaps, this review makes four groundbreaking contributions:

(1)

It establishes a multi-dimensional uncertainty analysis framework tailored to high-penetration renewable CCHP systems, systematically quantifying the interactions between renewable intermittency, demand volatility, and market dynamics. Unlike fragmented uncertainty discussions in prior studies, this framework maps uncertainty propagation across energy vectors and identifies critical coupling points where volatility amplifies, providing a holistic basis for targeted mitigation;

(2)

It summarizes the advantages of generalized energy storage (GES) in CCHP optimal operation, particularly in high-penetration renewable scenarios. By systematically integrating physical energy storage (PES) and virtual energy storage (VES) into a cohesive flexibility portfolio, GES demonstrates remarkable performance in addressing the core challenges of high renewable penetration;

(3)

It synthesizes modern uncertainty-aware optimization strategies into a structured decision matrix, enabling algorithm selection based on uncertainty characteristics, time scales, and risk preferences;

(4)

It develops a real-world application pathway for optimization algorithms, linking theoretical strategies to operational scenarios.

Overall, this work aims to provide a comprehensive technical pathway for enhancing CCHP systems’ efficiency, stability, and low-carbon performance in high-RE environments, thereby supporting their scalable role in global decarbonization efforts.

2. CCHP Systems with High-Penetration Renewables: Framework and Challenges

The integration of high-penetration renewable energy into CCHP systems has fundamentally transformed their operational paradigms. While traditional CCHP systems were primarily designed around stable fossil fuel inputs, the intermittent nature of renewable sources such as wind and solar demands a more flexible and adaptive architecture. This section examines the evolving system framework and the resulting technical challenges, beginning with an analysis of modern CCHP configurations optimized for RE variability.

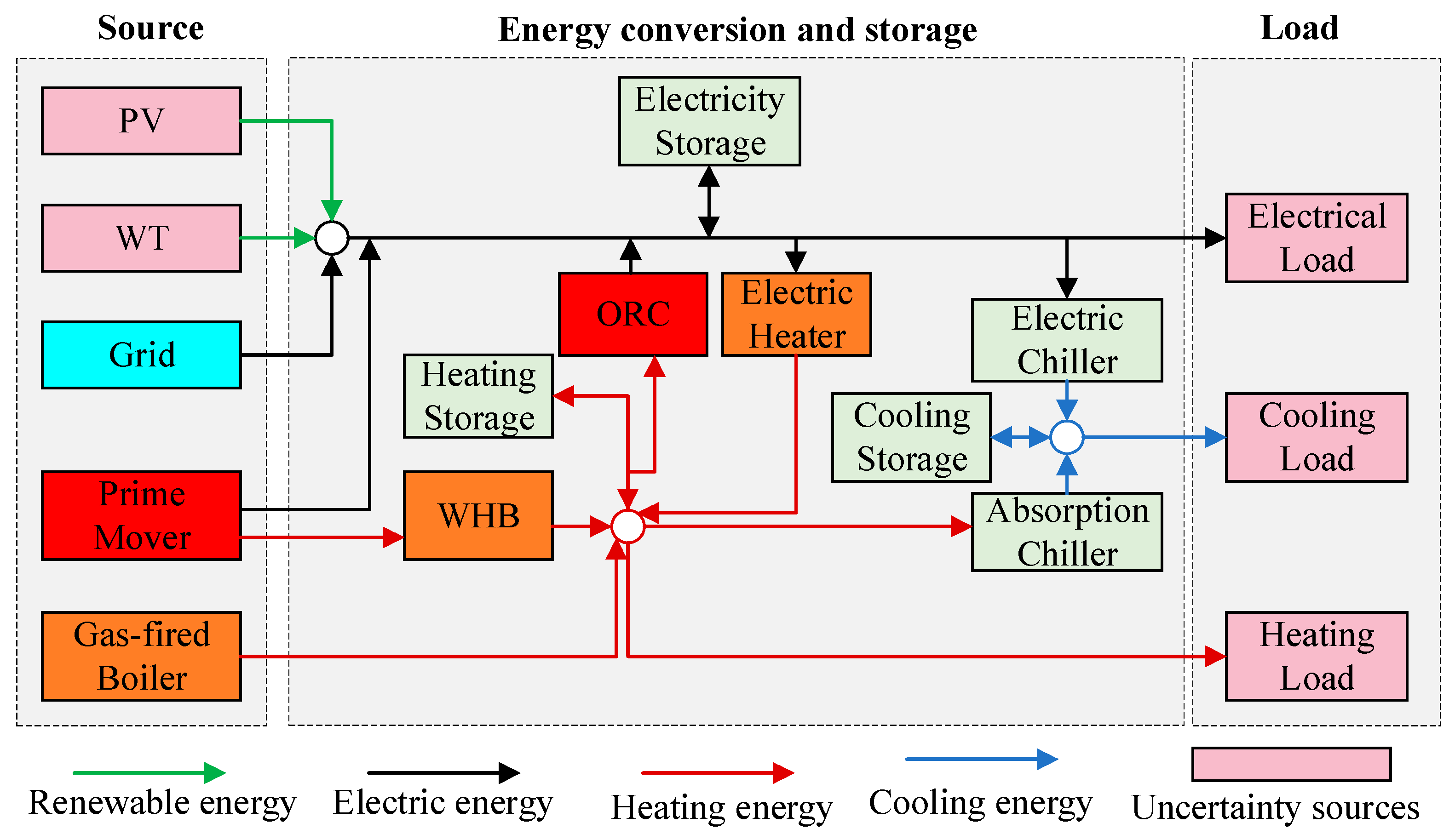
2.1. System Architecture

“High-penetration renewables” in this work specifically refers to variable renewable energy (VRE) sources, primarily wind and solar photovoltaics. While geothermal and biomass are renewable resources, their inherently stable and dispatchable nature fundamentally differs from the intermittency of wind/solar. Thus, these non-VRE renewables fall outside the scope of this study, which focuses on addressing volatility-induced challenges in CCHP systems. The representative architecture of a VRE-driven CCHP system is depicted in Figure 1.

In the operation of CCHP systems, the prime mover (PM) serves as the core component, with types including internal combustion engines, fuel cells, Stirling engines, steam and gas turbines, and micro turbines. The PM converts this primary energy into electricity, which directly serves end-user electrical demands. A portion of the electricity may also be allocated to auxiliary components like electric chillers or electric heater when additional cooling/heating is required. During electricity generation, the PM inherently produces waste heat, which can be captured via a waste heat recovery system and directed to thermally activated subsystems: organic Rankine cycle (ORC) units for secondary electricity generation, absorption chiller units for cooling production, and absorption heating units for space heating or hot water supply. Moreover, the electricity, cooling, and heating storage units play critical roles in enhancing the flexibility and efficiency of CCHP systems, particularly amid high-penetration renewable energy and variable loads.

2.2. The Core Challenge: Uncertainty and Variability

High-penetration variable renewable energy introduces intrinsic stochasticity that critically disrupts load matching in CCHP systems. The classical CCHP operation paradigms such as FTL, FEL, and FHL are fundamentally inadequate for maintaining effective load matching [18,19,20,21]. These traditional strategies, designed for stable fossil-fueled systems, fail catastrophically when confronted with the dual unpredictability of variable renewable supply and shifting demand patterns.

At the core of this failure lies renewable energy intermittency: solar and wind generation, the primary variable renewable sources, exhibit extreme spatiotemporal volatility. For instance, solar output can plummet by 40% during cloud transients, while wind power surges unpredictably due to atmospheric fluctuations—phenomena that render FTL strategies obsolete when thermal demand remains stable, forcing emergency grid imports that spike costs by 25–30% [22,23]. Compounding this is the inherent limitation of forecasting: solar irradiance predictions often exceed 20% RMSE, and wind power forecasts struggle to capture sudden gusts, leaving traditional load-following strategies blind to rapid supply shifts.

This renewable-driven uncertainty is further exacerbated by demand-side volatility. Cooling and heating loads are inherently weather-dependent and behavior-sensitive: cooling demand can surge by 30% during heat waves, while industrial heating requirements fluctuate by over 60% due to production schedules [24]. FEL approaches usually collapse when wind power surges coincide with low thermal demand, wasting 35–40% of recoverable heat energy, as the system cannot rebalance electricity oversupply against stagnant heating needs [25]. Even hybrid FHL strategies, which dynamically switch modes, fail to account for such multi-scale demand fluctuations—their preset thresholds become obsolete within minutes, triggering mode oscillations that shorten equipment lifetime by 15–20% [26].

Adding complexity is the non-linearity of multi-energy coupling. CCHP systems integrate electricity, heat, and cooling via interdependent conversion technologies: prime mover efficiency depends on ambient temperature, which in turn affects waste heat availability for absorption chillers. When renewable supply fluctuates, these couplings propagate mismatches across energy vectors: an unexpected solar drop not only reduces electricity output but also diminishes the thermal energy needed for cooling, creating cascading imbalances that erode the system’s 75–85% efficiency potential to a mere 55–60% in practice [27].

Beyond technical dynamics, market and policy uncertainties amplify operational risks. Energy price volatility may distort the economic trade-offs that traditional strategies rely on. For example, FEL’s grid supplementation costs can swing by 25% within a day due to real-time electricity market prices, while shifting subsidy policies for renewable integration further destabilize long-term operational planning. These external factors render static load-following logics unviable, as their cost assumptions become outdated almost as quickly as supply–demand conditions [28].

The root cause of these failures is the deterministic foundation of classical paradigms, which assume perfect foresight of supply, demand, and market conditions, a reality that is impossible in high-RE scenarios. Without real-time adaptive control that accounts for multi-dimensional uncertainties, CCHP systems cannot leverage their inherent efficiency advantages. This demands a paradigm shift from reactive load following to predictive, uncertainty-aware optimization that explicitly models renewable intermittency, demand volatility, multi-energy coupling, and market dynamics.

Beyond technical dynamics, evolving market structures and climate policies introduce additional operational uncertainties. Three key regional examples demonstrate these challenges:

(1)

China’s Electricity Market Reform: In Guangdong’s spot market pilot, intraday price volatility reached 25% [29], forcing CCHP operators to develop more dynamic bidding strategies to maintain profitability;

(2)

EU Carbon Pricing Mechanisms: The EU Carbon Border Adjustment Mechanism, fully effective in 2026, aligns with EU ETS prices (projected at EUR 85/ton CO₂ in 2025) [30]. While not directly regulating CCHP systems, it significantly impacts the economics of gas-fired generation supporting covered industrial exports;

(3)

California Renewable Integration Challenges: The state’s “duck curve” phenomenon, driven by high solar penetration, creates late-afternoon net load ramps with historical price spikes reaching USD 200/MWh [31]. This requires CCHP systems to optimize storage dispatch and generation schedules around these predictable volatility patterns.

3. Flexibility-Enabled Operation for High-RE CCHP Systems

The integration of high-penetration renewable energy introduces multi-dimensional uncertainties, including RE intermittency, demand volatility, and nonlinear multi-energy coupling, posing unprecedented challenges to traditional CCHP operation. To address these issues, leveraging flexibility resources has become the core strategy, as they can dynamically buffer fluctuations, decouple supply–demand time scales, and rebalance multi-energy flows.

Table 2. Flexibility Resources in CCHP Systems: Categories and Functions.

Flexibility Resource	Subcategories	Primary Function	Typical Performance Metrics
Storage-Driven Buffering	Physical Energy Storage, Virtual Storage	Decouples energy supply–demand across timescales	Response time (seconds–days), capacity (kWh/m3), efficiency (%)
Demand-Side Adjustment	Electrical, Gas/Thermal, Sector-Specific	Alters consumption patterns to match RE availability	Load shift potential (MW), adjustable duration (h)
Multi-Energy Synergy	Gas–Electricity, Heat–Electricity, Hydrogen	Leverages coupling between energy vectors for dynamic rebalancing	RE utilization increase (%), cost reduction (%)

categorizes the key flexibility resources and their roles in mitigating multi-dimensional uncertainties [32]. The following sections will elaborate on the operational mechanisms, performance characteristics, and practical applications of each type of flexibility resource, providing a detailed framework for enhancing CCHP system resilience to RE volatility.

3.1. Storage-Driven Uncertainty Buffering

The inherent intermittency and variability of high-penetration renewable energy sources introduce significant supply-side uncertainties into CCHP systems. To effectively decouple energy supply and demand across time scales, diverse storage technologies act as temporal “shock absorbers”, buffering fluctuations through energy shifting and conversion. These technologies are categorized into physical energy storage (PES), virtual energy storage (VES), and generalized energy storage (GES). GES emerges as a comprehensive framework that systematically integrates both PES and VES, combining their complementary strengths to create a unified flexibility solution.

To clarify the unique yet complementary operational characteristics of physical and virtual energy storage,

Table 3. Comparative Analysis of Physical and Virtual Energy Storage Characteristics for High-RE CCHP Systems.

Feature	Physical Energy Storage	Virtual Energy Storage
Charge/Discharge Power	Rated power of storage device	Adjustable load deviation from baseline
Capacity Definition	Energy capacity	Equivalent energy-adjustment range
Power Dynamics	Fixed charge/discharge power limits	Time-dependent adjustable power deviation
State of Charge (SOC)	Remaining energy/rated capacity	VSOC: Normalized flexibility potential
Response Time	Seconds (batteries) to hours (TES)	Ultra-fast (seconds for TCLs/EVs)
Scalability	Limited by capital expenditures and space	Highly scalable through aggregation
Primary Role in CCHP	Bulk energy shifting (hours–days)	Real-time imbalance correction

systematically compares their technical metrics and functional features [33,34,35].

From the comparison in Table 2, it is evident that physical energy storage and virtual energy storage form a complementary relationship in addressing the uncertainties of high-penetration renewable energy. Physical energy storage, with its stable capacity and deterministic energy buffering, is suitable for handling long-term energy mismatch problems, such as the difference between renewable energy generation and load demand over days or even seasons. Virtual energy storage, relying on the adjustability of loads and processes, excels in real-time response to short-term fluctuations, which is crucial for stabilizing the system during sudden changes in renewable energy output. This functional differentiation lays the foundation for their coordinated application in CCHP systems, enabling the system to cope with multi-time-scale and multi-dimensional uncertainties more comprehensively.

3.1.1. Physical Energy Storage (PES)

Physical storage technologies provide deterministic capacity for electricity, thermal, and chemical energy buffering.

Table 4. Physical energy storage technologies in high-RE CCHP systems.

Storage Type	Medium	Function	Performance Metrics	Limitations
Thermal	Water/ice/PCMs/molten salt	Decouples thermal/cooling production from demand	Capacity: 50–500 kWh/m3 Response: 5–30 min Efficiency: 70–85% Cost: USD 5–20/kWh Lifespan: 20+ years	Reduces peak cooling load 15–25% Provides 4–8 h heat inertia
Electrochemical (Batteries)	Li-ion/flow batteries	Buffers short-term RE fluctuations	Capacity utilization: 80–95% Response: <1 s Round-trip eff.: 85–95% Cost: USD 150–300/kWh Lifespan: 4k–6k cycles	Boosts RE self-use 25%
Shared Storage	Aggregated batteries/thermal tanks	Pools distributed resources for cost efficiency	CAPEX reduction: 40–45% Utilization: 70–80% Payback: 5–8 years Access: Pay-per-use model	Community microgrids reduce user CAPEX 45% Increases asset utilization to 80%
Mobile Storage	EVs/mobile H2 tanks/thermal carriers	Enables cross-regional energy transfer	Deployment: <30 min Capacity: 50–500 kWh/unit Grid support: 50 MW/km2 Cost saving: 18–25%	EV swarms provide 50 MW/km2 V2G capacity Mobile H2 trucks resolve 85% supply emergencies
Chemical (Power-to-Gas/H2)	Hydrogen/methane via electrolysis	Converts surplus RE to storable fuels	Density: 1000–5000 kWh/m3 Response: 2–6 h Elec → H2 eff.: 45–60% Storage cost: USD 10–30/kWh	Seasonal storage boosts RE utilization 12–18%

compares their functional characteristics in mitigating renewable uncertainties and enabling demand–supply decoupling across operational time horizons.

Physical energy storage provides deterministic buffering capacity through tangible energy carriers. In electricity domains, electrochemical batteries, such as lithium iron phosphate batteries and flow batteries, can absorb sub-hourly renewable fluctuations with 85–95% round-trip efficiency, enhancing photovoltaic self-consumption by 25% in campus-scale CCHP microgrids [36,37]. Thermal storage, which utilizes water, phase-change materials, or molten salt, decouples heating/cooling production from demand cycles. Industrial implementations demonstrate 4–8 h of thermal inertia, reducing peak cooling loads by 15–25% through off-peak chilling [38,39]. For seasonal balancing, power-to-gas technologies convert surplus renewables into hydrogen or synthetic methane [40,41]. With chemical storage densities reaching 1000–5000 kWh/m³, these technologies enable an annual increase in renewable energy utilization of 12–18%. Despite these advantages, physical energy storage has inherent limitations: high capital expenditure, spatial constraints for large-scale deployment, and fixed charge/discharge rates; these factors restrict operational flexibility during multi-hour renewable energy deficits.

Shared storage and shared hydrogen storage, as emerging forms of physical energy storage, further unlock the value of distributed resources in CCHP systems by leveraging resource aggregation and on-demand allocation. Their applications in CCHP optimization are particularly critical for balancing cost efficiency, renewable energy absorption, and system stability. By eliminating redundant storage investments, shared storage significantly lowers the financial burden on individual users. A study [42] on community-scale CCHP systems showed that compared to independent storage, shared storage reduced the daily operating costs of user groups by 18–25%, with capital expenditure per user decreasing by 45% due to economies of scale. For industrial parks with fluctuating thermal loads, shared thermal storage further cut peak-shaving costs by 30% by centralizing heat dispatch [43]. Aggregated storage resources are dynamically allocated to match real-time demand across users. For example, in a CCHP microgrid with high PV penetration, shared batteries absorb midday solar surpluses from residential users and redirect stored energy to industrial loads during evening peaks, increasing overall storage utilization from 40% to 70–80% [44]. Shared hydrogen storage extends the shared storage concept to chemical energy, pooling hydrogen produced by distributed electrolyzers or imported from centralized plants, and distributing it to CCHP users on demand [45].

3.1.2. Virtual Energy Storage (VES)

Virtual energy storage represents a paradigm shift in flexibility provision, exploiting the inherent adjustability of controllable loads and processes without physical energy media. As shown in

Table 5. Virtual energy storage technologies in high-RE CCHP systems.

VES Type	Regulation Mechanism	Efficiency	Performance in CCHP
Temperature-Control Loads	Thermal inertia	70–80% (heat loss over 2–4 h)	Reduces chiller startup frequency by 30–40%
Electric Vehicles (V2G)	Smart charging/discharging	80–90% (round-trip efficiency)	Shifts 30% of charging load to solar peaks
Heating Network	Pipeline thermal storage	85–95% (heat retention over 8 h)	Decouples heat-power ratio by 4–8 h

, VES metrics are derived by analogy to physical storage parameters, enabling standardized evaluation of flexibility potential.

Temperature-controlled loads, such as building HVAC (heating, ventilation, and air conditioning) systems, emulate storage functions through thermal inertia, offering equivalent capacities of 0.5–2 kWh/m² while maintaining comfort within ±2 °C bounds. Electric vehicles operate as distributed “batteries on wheels”, with smart charging clusters providing 50 MW/km² grid-balancing capacity, which can shift 30% of the charging load to solar-rich periods, boosting RE self-consumption by 20% in residential CCHP networks [46]. Electrolyzers further extend VES functionality by converting curtailed renewables into hydrogen, acting as 30–50 kWh/kg virtual storage [47]. The agility of VES is unparalleled: thermostatically controlled loads respond within seconds, while EV charging adjustments execute in under 30 min [48]. Over longer time scales (2–4 h), when RE generation is predicted to be insufficient, these VES resources can pre-cool or pre-heat spaces during RE surpluses, storing “thermal potential” to offset peak-period thermal loads and lowering the operational burden on the prime movers. This synergy has been shown to reduce the daily startup frequency of chillers by 30–40% in campus CCHP projects while maintaining thermal comfort [49]. Moreover, VES enhances the economic efficiency of CCHP optimization by reducing reliance on physical storage investments. By aggregating flexible loads, a community-scale CCHP system can achieve the same peak-shaving effect as a 500 kWh battery storage system at 60–70% of the cost while avoiding the lifecycle limitations of physical batteries [50].

However, VES capacity remains constrained by behavioral uncertainties and comfort thresholds, with flexibility typically limited to 2–4 h. Reliance on communication infrastructure also introduces cybersecurity vulnerabilities, and the absence of standardized compensation frameworks complicates multi-user coordination.

3.1.3. Synergistic Integration: Generalized Energy Storage

The coordinated operation of physical and virtual energy storage resources is formally conceptualized as generalized energy storage (GES), a unified flexibility framework essential for high-renewable CCHP systems. GES transcends conventional storage boundaries by synergizing two complementary domains: (i) physical energy storage with deterministic, large-capacity buffering capabilities for diurnal imbalances and (ii) virtual energy storage providing agile, distributed adjustment for real-time fluctuations. This integration addresses three critical gaps in traditional approaches: the spatial and economic constraints of PES, the behavioral uncertainties of VES, and the disjointed management of multi-energy vectors.

Generalized energy storage expands flexibility resource boundaries in CCHP systems. Reference [51] treated flexible electricity/heat loads and electrical/thermal storage as generalized energy storage resources. By participating in economic dispatch, it analyzed regulatory characteristics of different types, fully exploiting multi-energy load and storage flexibility. Reference [52] regarded integrated demand response and pipeline storage as virtual storage. This broadened flexibility resource ranges and, by introducing a Wasserstein-metric-based distributionally robust optimization method, effectively quantified system uncertainties. Through such methods, the flexibility potential of generalized energy storage in supporting demand response can be accurately measured, providing a reliable basis for stable CCHP operation under high renewable penetration. Reference [53] quantified generalized energy storage resource flexibility. Based on this, distributed energy-storage coordinated planning optimizes new energy absorption in the power grid, breaking single-energy dispatching limitations and enabling electricity–heat–cooling complementary operation. Reference [54] proposed a generalized energy storage model integrating user-side adjustable resources and a multi-source (electricity–heat–cooling) energy storage system. Its optimized dispatching model realizes multi-energy optimal allocation in CCHP systems, improving overall energy utilization efficiency. Moreover, references [55,56] took EVs and air conditioning clusters as generalized energy storage resources. Through multi-time-scale dispatching and synergistic optimization, they boosted system energy supply stability, ensuring reliable CCHP operation during high renewable volatility.

In summary, synergistic generalized energy storage integration combines physical storage, virtual storage from diverse loads, and multi-energy coordination. It provides a comprehensive solution for CCHP systems to cope with high renewable penetration. It optimizes economic efficiency via flexible resource dispatch and enhances operational resilience by addressing multi-time-scale, multi-energy-form uncertainties and laying a solid foundation for CCHP sustainable development in modern energy landscapes.

Table 6. Comparative summary of PES, VES, and GES in High-RE CCHP Systems.

Feature	PES	VES	GES	Integration Pathways
Primary Role	Deterministic energy buffering via tangible media	Flexibility provision through load/process adjustment	Unified framework synergizing PES and VES	Systemic coordination of multi-energy vectors
Key Benefits	High capacity Predictable performance Long-duration shifting	Low CAPEX Ultra-fast response Spatial scalability	Holistic uncertainty mitigation Cost reduction Multi-timescale coordination	Cross-domain flexibility transfer via multi-energy coupling
Major Limitations	High capital cost Spatial constraints Fixed charge/discharge rates	Behavioral uncertainties Limited duration Cyber vulnerabilities	Coordination complexity Requires advanced control algorithms	Dependent on communication infrastructure and market mechanism
CCHP Integration	Centralized/decentralized hardware deployment	Demand response programs and aggregator coordination	AI-driven dynamic resource allocation	Hierarchical control: Device-level → Cluster-level → System-level optimization

provides the advantages, limitations, and collaborative mechanisms of PES, VES, and GES in high-RE CCHP systems.

While storage resources provide critical temporal buffering for renewable volatility, demand-side flexibility enables spatial and behavioral adaptation through active load participation. This paradigm shift exploits the inherent controllability of distributed electrical, thermal, and sector-specific loads. As detailed next, these resources transform end-users into dynamic grid assets that complement storage-based strategies through interruptible operations, shiftable consumption, and cross-vector substitution.

3.2. Demand-Side Flexibility Activation

Demand-side flexibility represents a critical paradigm shift from the traditional supply-follows-load operation to source-load coordination in high-renewable CCHP systems. By leveraging flexible electrical loads and distributed resources, demand-side adjustments provide essential grid-balancing services that complement storage-based buffering strategies. Beyond electrical, gas, and thermal loads, specific sectors, such as data centers, industrial parks, commercial buildings, and residential complexes, exhibit unique flexibility characteristics through delayable, transferable, or interruptible operations, further enhancing CCHP adaptability to renewable volatility.

3.2.1. Electrical Flexible Loads: Interruptible and Shiftable Resources

Electrical loads form the foundational layer of demand-side flexibility in high-RE CCHP systems, with two primary categories enabling real-time adjustments: interruptible loads and shiftable loads. Interruptible loads, such as non-critical industrial motors, commercial lighting systems, and auxiliary equipment in manufacturing, can temporarily cease operation without impacting core processes, providing rapid power reduction during renewable energy deficits. In reference [57], aggregating 10 MW of such loads in a CCHP-integrated industrial zone reduced peak grid imports by 15% during wind lulls. Shiftable loads, including residential appliances such as dishwashers and laundry machines and electric vehicle charging, adjusted their operating time to align with RE surpluses. Reference [58] showed that shifting 30% of EV charging from evening peaks to midday solar-rich periods increased RE self-consumption by 20% in residential CCHP clusters. Beyond these real-time adjustment mechanisms, price-driven demand response further enhances the flexibility of electrical loads in CCHP systems. Reference [59] developed an optimal operation model for CCHP micro-energy grids with solar thermal power plants, incorporating price-based demand response. The results indicate that the participation of elastic electrical and thermal loads in demand response can reduce electricity and heat demand during peak periods, thereby lowering overall system operating costs. Similarly, reference [60] established a day-ahead scheduling optimization model for multi-energy microgrids in commercial parks, accounting for time-of-use electricity prices and integrated demand response across gas, cooling, heating, and electricity sectors under supply–demand uncertainty.

These findings reveal that the implementation of flexible load management not only improves the economic efficiency and reliability of system operation but also reduces the required reserve capacity, underscoring the multi-dimensional value of electrical flexible loads in high-RE CCHP environments.

3.2.2. Gas and Thermal Flexible Loads: Convertible and Transferable Resources

Gas and thermal loads in CCHP systems extend demand-side flexibility beyond electricity, leveraging convertibility and temporal transfer to balance multi-energy fluctuations. Industrial gas/thermal loads, such as chemical process heating, metallurgical furnaces, and food processing boilers, adjust production schedules to shift energy consumption to RE-rich periods. A 50 MW industrial cluster with flexible heating schedules, for example, reduces reliance on gas turbines by 25% during wind surpluses by delaying non-urgent heating stages [61]. Residential convertible loads, including switchable electric/gas stoves and hybrid heat pump/gas boiler systems, toggle between energy vectors based on real-time RE availability; during high solar output, a residential complex using electric heat pumps instead of gas boilers absorbs 10% more surplus electricity, reducing gas consumption [62]. The integration of gas and thermal flexible loads with storage technologies further enhances their role in optimizing CCHP system performance under high RE penetration. Reference [63] demonstrated that the deployment of heat pumps, thermal energy storage, electrical energy storage, and transferable loads can significantly improve photovoltaic penetration and self-consumption rates in user energy systems. By incorporating market electricity prices into the optimization framework, this approach achieved an annual electricity cost savings of 13–25% while reducing grid electricity purchases by 18–38%. In building-level applications, the coordination of gas/thermal flexibility with user comfort constraints has proven effective in RE absorption. Reference [64] developed an electricity–heat coordinated dispatch method for rural buildings, accounting for user comfort bounds through flexible temperature ranges. The proposed strategy, which integrates thermal storage and flexible loads into electricity–heat coordination, not only enhances photovoltaic consumption but also improves system economics by aligning energy use with RE generation patterns.

The inherent substitutability of gas, heat, and electricity in these loads reduces reliance on single-energy flexibility, enabling the CCHP system to leverage the most abundant energy vector at any given time, mitigating the impact of RE intermittency across energy domains, and supporting the efficient and low-carbon operation of high-RE CCHP systems.

3.2.3. Sector-Specific Flexible Loads: Data Centers, Industrial Parks, and Buildings

Sector-specific loads such as data centers, industrial parks, commercial buildings, and residential complexes amplify demand-side flexibility through tailored mechanisms, including delayable processing, spatial transfer, temporal translation, and adjustable operations. Data centers leverage delayable non-real-time tasks such as data backups and AI training to shift workloads to RE surpluses, with a 10 MW facility reducing grid imports by 25% by deferring 40–60% of such tasks to midday solar peaks; multi-location clusters further enable spatial load transfer, redirecting tasks from RE-scarce regions to those with surplus wind, cutting transmission losses by 15% [65,66]. Industrial parks utilize temporal translation of energy-intensive processes such as chemical distillation and metal annealing, with a 500 MW cluster reducing peak demand by 40 MW through synchronized scheduling, lowering wind curtailment from 20% to 5% [67]. Commercial buildings balance comfort and flexibility via transferable thermal loads, for example, through pre-cooling offices during RE surpluses to reduce afternoon peaks by 10–15% and through short-term interruptible services such as pausing decorative lighting to offset solar drops by 5 MW [68]. Residential complexes aggregate transferable appliances, for example, by shifting 40% of washing machine use to solar peaks, and interruptible devices, for example, briefly turning off standby electronics, with 5000 homes reducing peak demand by 10 MW during RE deficits [69]. Together, these sector-specific loads transform diverse end-users into coordinated flexibility providers, enhancing CCHP systems’ ability to absorb high-penetration RE.

3.2.4. Hydrogen-Integrated Flexible Resources

Hydrogen, as a cross-sectoral energy carrier, extends demand-side flexibility across power, buildings, industry, and transportation in CCHP systems. Hydrogen-producing loads, such as electrolyzers, consume surplus RE to generate hydrogen, acting as “virtual batteries” with 30–50 kWh/kg energy density, and a 1 MW electrolyzer in a CCHP microgrid can absorb 40% of midday solar curtailment [70,71]. Hydrogen-fueled flexible loads, including fuel cell vehicles and industrial furnaces, adjust hydrogen consumption to align with RE availability [72]. In reference [73], a hydrogen-integrated manufacturing plant shifted 30% of its heating demand to periods with low RE curtailment, reducing reliance on natural gas. By connecting traditionally siloed sectors, hydrogen turns end-use consumption into a system-wide flexibility resource, further enabling CCHP systems to navigate the volatility of high-penetration renewables.

Building on demand-side adjustments, multi-energy conversion synergy transcends load-centric flexibility by exploiting inherent coupling dynamics between electricity, heat, gas, and hydrogen vectors. Whereas demand-side resources alter consumption patterns, synergy mechanisms actively reconfigure energy flows across conversion technologies, leveraging gas turbine ramping, thermal inertia, and power-to-fuel pathways. This enables real-time rebalancing of multi-dimensional mismatches, as analyzed next through gas–electricity, heat–electricity, and electricity–transportation interdependencies.

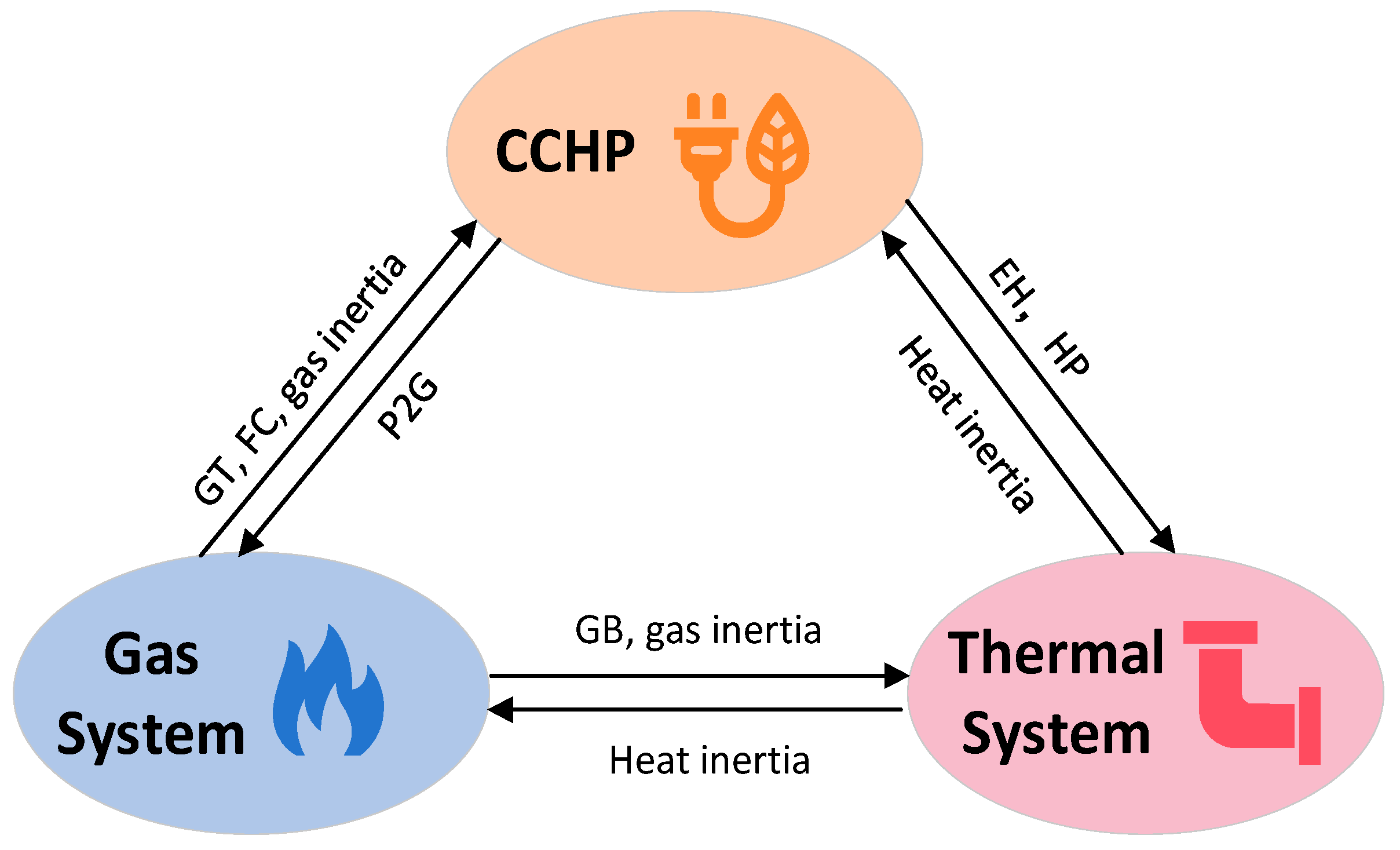
3.3. Multi-Energy Conversion Synergy

Multi-energy conversion synergy leverages the coupling and flexible dispatch of diverse energy vectors to mitigate fluctuations in renewable energy output, ensuring stable operation of CCHP systems during RE shortages or surpluses. This section elaborates on the core mechanisms and empirical validations of such synergy across key energy coupling pathways. The schematic of multi-energy coupling and flexibility interaction within a CCHP system, featuring three interconnected subsystems (the CCHP unit, natural gas system, and thermal system), is shown in Figure 2. The bidirectional arrows depict the coupling mechanisms:

(1)

CCHP–Gas System Interaction: The CCHP unit connects to the gas system via gas turbines, fuel cells, and power-to-gas technology. GTs and FCs leverage gas inertia to enable dynamic response, while P2G converts surplus electricity into gas for storage, creating a bidirectional energy flow;

(2)

CCHP–Thermal System Interaction: Heat pumps, electric heaters, and thermal inertia support bidirectional heat-power adjustment. This allows the CCHP unit to reallocate its output priority between heat and electricity based on real-time renewable energy availability;

(3)

Gas–Thermal System Interaction: Gas boilers utilize gas inertia to supply heat, while heat inertia buffers temperature fluctuations. This cross-system coupling further enhances the system’s ability to balance supply and demand.

Figure 2 depicts the intricate multi-energy coupling and flexibility interaction framework in high-RE CCHP systems, focusing on how flexible resources are shared across subsystems and how flexibility requirements are dynamically transferred between energy vectors. The diagram consists of three interconnected subsystems, with bidirectional arrows explicitly representing the flow of energy and flexibility coordination:

(1)

Interaction between the CCHP unit and natural gas system

The CCHP unit is tightly coupled to the natural gas system through two key pathways: gas-to-electricity/heat and electricity-to-gas. In the CCHP unit, gas turbines and fuel cells consume natural gas to generate electricity, while their waste heat is recovered for heating or cooling, and P2G technology converts surplus renewable electricity into hydrogen or synthetic natural gas for storage in the gas grid, enabling bidirectional energy flow that allows “gas buffering” to mitigate RE volatility—storing excess electricity as gas during surpluses and utilizing stored gas to ramp up power generation during deficits.

(2)

Interaction between the CCHP unit and thermal system

The thermal system collaborates with the CCHP unit to decouple heat and electricity production, enhancing flexibility. When RE generation is high, the CCHP unit prioritizes electricity output, with excess waste heat stored in thermal tanks. When RE is scarce, stored heat is released to meet thermal demand, allowing the CCHP unit to reduce thermal output and focus on electricity generation. Heat pumps further optimize this interaction by switching between electricity-driven and heat-driven modes based on real-time RE availability, balancing energy supply and demand across vectors.

(3)

Interaction between the thermal system and natural gas system

The natural gas system and thermal system form a complementary buffer. Gas boilers can quickly increase heat supply using stored gas during thermal demand surges, reducing reliance on CCHP waste heat. Pipeline thermal inertia delays temperature fluctuations, providing a temporal buffer for other flexible resources to respond.

3.3.1. Gas–Electricity Synergy

Gas–electricity coupling plays a pivotal role in balancing RE volatility, utilizing the flexibility of gas-fired power generation, power-to-gas (P2G) technology, and natural gas system storage capacities to enhance RE integration. During periods of insufficient RE output, natural gas networks can release stored gas to enable gas turbines to ramp up electricity generation, while dynamic pipeline storage provides short-term buffering. Conversely, during RE surpluses, P2G technology converts excess electricity into hydrogen or synthetic natural gas, which is stored in the gas grid for later use, effectively addressing RE curtailment.

The gas–electricity synergy utilizes the flexibility of gas-fired generation, P2G technology, and the inherent storage capacity of natural gas networks. Gas flow in pipelines exhibits inertial behavior, providing short-term buffering. Mass flow continuity and momentum equations govern transient flow:

$$\{\begin{array}{l}{\displaystyle \frac{\mathsf{\partial }\rho }{\mathsf{\partial }t}}+{\displaystyle \frac{\mathsf{\partial }(\rho v)}{\mathsf{\partial }x}}=0\\ {\displaystyle \frac{\mathsf{\partial }(\rho v)}{\mathsf{\partial }t}}+{\displaystyle \frac{\mathsf{\partial }(\rho v^2)}{\mathsf{\partial }x}}+{\displaystyle \frac{\mathsf{\partial }p}{\mathsf{\partial }x}}+{\displaystyle \frac{f\rho v\left|v\right|}{2D}}+\rho g\sin \theta =0\end{array}$$

(1)

Here, $\rho$ is gas density, $v$ is gas velocity, $p$ is gas pressure, $f$ is friction factor, $D$ is pipe diameter, and $\theta$ is pipe inclination.

In P2G conversion, the electrolyzers convert surplus electricity to hydrogen/methane:

$$\{\begin{array}{l}{P}_{\mathrm{P}2\mathrm{G},t}={\eta }_{\mathrm{P}2\mathrm{G}}\cdot P_{\mathrm{elec},\mathrm{in},t}\\ {\dot{m}}_{{\mathrm{H}}_2,t}={\displaystyle \frac{P_{\mathrm{P}2\mathrm{G},t}}{LH{V}_{{\mathrm{H}}_2}}}\end{array}$$

(2)

Here, $P_{\mathrm{P}2\mathrm{G},t}$ is gas output power equivalent, ${\eta }_{\mathrm{P}2\mathrm{G}}$ is conversion efficiency, $LH{V}_{{\mathrm{H}}_2}$ is the lower heating value of hydrogen, and ${\dot{m}}_{{\mathrm{H}}_2,t}$ is hydrogen mass.

Reference [74] employed dynamic scenarios to characterize the stochasticity of RE output and demonstrated, through co-optimization of integrated electricity–gas systems, that gas grids, with their higher flexibility, effectively mitigate the intermittency of renewable sources. Reference [75] proposed a coordinated dispatch model for integrated energy systems incorporating P2G, quantifying its economic benefits for wind power integration. Reference [76] developed an optimal dispatch model for electricity–gas interconnected systems considering dynamic pipeline storage and wind power absorption, verifying that dynamic pipeline storage characteristics alleviate the uncertainty of wind power output. Reference [77] quantitatively evaluated the positive impacts of P2G–gas turbine coordination on wind power integration, carbon emissions reduction, and economic efficiency. Reference [78] analyzed the economics of converting RE to hydrogen or synthetic natural gas via P2G for storage in gas networks, quantifying the flexibility value of seasonal gas storage.

3.3.2. Heat–Electricity Synergy

Heat–electricity synergy enhances RE absorption by leveraging the flexibility of CHP units, electric boilers, heat pumps, and thermal storage in heating networks. These components collectively adjust heat–electricity output ratios to align with RE fluctuations. The use of multi-energy flow synergy to maintain real-time balance of electric power, with new energy output shortages as an example, is shown in Figure 3. The natural gas pipeline releases gas storage to support the gas turbine unit to increase power generation; meanwhile, the heat pipeline releases heat storage to ensure the CHP unit reduces heat output and increases electricity output.

Figure 3 exemplifies multi-energy coordination during a renewable energy shortage through two simultaneous flexibility actions: gas storage releasing and thermal storage deployment. When there are abrupt reductions in solar or wind output, the natural gas pipeline network releases stored gas to fuel gas turbine units, allowing gas turbines to rapidly increase electricity generation within their ramp limits so as to compensate for the RE deficit. Simultaneously, the thermal pipeline network releases stored heat from thermal energy storage tanks. This stored heat offsets the reduced waste heat output from the CCHP unit, enabling the unit to shift its operational priority from co-generating heat and electricity to focusing solely on electricity production.

This synergy leverages the flexibility of CHP units, electric boilers/heat pumps, thermal storage, and heat network inertia. Specifically, pipelines and buildings exhibit thermal inertia, delaying temperature changes:

$${\rho }_w{c}_p{\displaystyle \frac{\mathsf{\partial }T}{\mathsf{\partial }t}}+{\rho }_w{c}_{p}v{\displaystyle \frac{\mathsf{\partial }T}{\mathsf{\partial }x}}+{\displaystyle \frac{U}{A}}(T-T_{amb})=0$$

(3)

Here, $\tau$ is time constant, $T$ is supply temperature, ${\rho }_w$ is water density, $c_p$ is specific heat, $U$ is heat loss coefficient, $A$ is pipe cross-section, and $T_{amb}$ is ambient temperature.

Natural gas pipelines inherently provide storage capability through linepack—the mass of gas stored within the network due to pressure variation. The linepack storage capacity can be modeled as

$$M_{linepack}={\displaystyle \frac{V_{pipe}}{Z_{\mathrm{gas}}{R}_{\mathrm{gas}}{T}_{\mathrm{gas}}}}\left(\overline{p}-p_{min}\right)$$

(4)

Here, $M_{linepack}$ is the available gas mass stored in pipelines, $V_{pipe}$ is total pipeline volume, $Z_{\mathrm{gas}}$ is gas compressibility factor, $R_{\mathrm{gas}}$ is specific gas constant, $T_{\mathrm{gas}}$ is average gas temperature, $\overline{p}$ is area-weighted average pressure in the network, and $p_{min}$ is minimum operating pressure.

Reference [79] quantitatively analyzed the effect of large-capacity thermal storage on improving system flexibility and wind power absorption capacity. Reference [80] demonstrated that coordinated heating by CHP units with thermal storage and electric boilers optimizes wind power integration, with electric boilers showing superior economics in absorbing curtailed wind power. References [81,82] developed an optimal dispatch model for electricity–heat interconnected systems targeting wind power absorption, incorporating heat network delay characteristics and thermal load comfort elasticity, further refining the practical application of heat–electricity synergy.

3.3.3. Electricity–Transportation and Electricity–Hydrogen Synergy

Electricity–transportation and electricity–hydrogen synergy harness the flexibility of power-to-hydrogen (P2H) technology, electric vehicles (EVs), and hydrogen fuel cell vehicles to buffer RE fluctuations, expanding RE absorption pathways beyond traditional grids. Electric vehicles, through smart charging/discharging (V2G), adjust their electricity consumption to align with RE peaks, while hydrogen fuel cell vehicles utilize hydrogen produced from surplus RE via P2H, creating a closed-loop energy cycle.

Relevant research highlights this potential: Reference [83] outlined an electricity–hydrogen energy system framework for high-penetration RE absorption, envisioning electricity and hydrogen as core energy carriers. Reference [84] showed that navigating fast-charging vehicles to leverage their mobility enhances flexibility, simultaneously alleviating grid congestion and traffic bottlenecks. Reference [85] developed an energy optimization method for integrated new energy vehicle charging stations incorporating wind, solar, EVs, and hydrogen fuel cell vehicles, demonstrating multi-vector coordination. Reference [86] studied coordinated dispatch of power and transportation systems considering RE and hydrogen fuel cell vehicles, emphasizing the critical role of hydrogen storage in improving system flexibility.

4. Optimization Strategies for Uncertain Scenarios

The flexibility mechanisms detailed in Section 3, including storage buffering, demand-side adjustments, and multi-energy synergy, provide a technical foundation for mitigating renewable energy volatility in CCHP systems. However, effective coordination of these diverse resources requires rigorous uncertainty-aware optimization frameworks, which must explicitly account for the multi-dimensional uncertainties inherent to high-RE and demand-side scenarios.

Uncertainty-aware optimization strategies for high-RE CCHP systems encompass diverse methodological frameworks, each tailored to address specific types of uncertainty and decision-making contexts, including emerging data-driven and robustness-focused approaches.

Table 7. Summary of optimization methods for CCHP systems under uncertainty.

Methods	Characteristics	Uncertainty Handling Mechanism
Robust optimization	Uncertain parameter sets are known	Worst-case immunization within uncertainty set
Stochastic programming	Probability distributions of uncertain parameters are known	Expected value optimization via scenario trees
Distributionally robust optimization	Unknown true distribution but belongs to ambiguity set	Min-max expected cost over ambiguity set
Information gap decision theory	Severe uncertainty about uncertainty bounds	Dual objective: robustness and opportunity
Deep reinforcement learning	Model-free learning from environment interactions	Q-learning/policy gradients with function approximation
Chance-constrained programming	Constraint violation probabilities specified	Probabilistic feasibility guarantees
Adaptive robust optimization (ARO)	Multi-stage decisions with recourse actions	Here-and-now + wait-and-see adaptive decisions

summarizes the key characteristics of these methods.

4.1. Robust Optimization (RO) Paradigms

Robust optimization paradigms enhance CCHP system resilience by immunizing operational decisions against worst-case uncertainty realizations within predefined bounds, prioritizing feasibility and stability over cost efficiency in high-RE scenarios. Three dominant RO methodologies, namely classic RO, distributionally robust optimization (DRO), and adaptive RO, have been widely applied to CCHP operation optimization, each addressing distinct uncertainty characteristics.

4.1.1. Classic RO

Classic RO operates on the premise that uncertain parameters fluctuate within known bounded sets. It formulates optimization problems to minimize the maximum operational cost or inefficiency, ensuring feasibility for all possible parameter realizations within the set $\mathit{x}$. For CCHP systems, its general formulation is

$$\{\begin{array}{l}\underset{x}{\min } \underset{\xi \in \mathcal{U}}{\max } c^{\mathrm{T}}\mathit{x}+q(\mathit{\xi },\mathit{x})\\ \mathrm{s}.\mathrm{t}.Ax+B(\mathsf{\xi })\le b,\forall \mathit{\xi }\in \mathcal{U}\end{array}$$

(5)

Here, $\mathit{x}$ represents first-stage decision variables; $\mathsf{\xi }$ denotes uncertain parameters; $\mathcal{U}$ is the bounded uncertainty set; $c^{\mathrm{T}}\mathit{x}$ is the total cost; $q(\mathsf{\xi },\mathit{x})$ denotes the uncertainty-dependent costs.

Classic RO’s min-max structure is typically solved via duality transformation, which converts the inner max problem into a set of constraints, reducing the formulation to a single-level optimization. For linear uncertainty sets, the dualization leverages strong duality theorem, transforming the problem into a mixed-integer linear program or linear program that can be efficiently solved with commercial solvers such as Gurobi, CPLEX, and COPT, among others.

4.1.2. Distributionally RO

Distributionally robust optimization relaxes the strict boundedness of classic RO by optimizing against the worst-case probability distribution within a predefined “distribution family”. It balances robustness and optimality, leveraging partial statistical information of uncertainties. For CCHP systems, the formulation is

$$\{\begin{array}{l}\underset{x}{\min } \underset{\mathbf{P}\in \mathcal{P}}{\sup } {\mathbf{E}}_{\mathbf{P}}\left[c^{\mathrm{T}}\mathit{x}+q(\mathsf{\xi },x)\right]\\ \mathrm{s}.\mathrm{t}.Ax+{\mathbf{E}}_{\mathbf{P}}[B(\mathsf{\xi })]\le b,\forall \mathbf{P}\in \mathcal{P}\end{array}$$

(6)

Here, $\mathbf{P}$ is a probability distribution of uncertain parameters $\xi$; $\mathcal{P}$ is the distribution family.

DRO’s solution hinges on reformulating the worst-case expectation over the distribution family $\mathcal{P}$ into tractable constraints. For Wasserstein-distance-based DRO, the problem can be transformed into a conic program by leveraging properties of the Wasserstein metric. This transformation converts the sup over $\mathbf{P}\in \mathcal{P}$ into linear or conic constraints involving auxiliary variables, enabling efficient solving with commercial solvers.

4.1.3. Adaptive RO

Adaptive robust optimization introduces multi-stage decision-making, where wait-and-see decisions adapt to observed uncertainty realizations to reduce conservatism compared with static classic RO. For CCHP systems, ARO separates decisions into first-stage decisions called here-and-now decisions, such as day-ahead scheduling, and second-stage decisions called wait-and-see decisions, such as real-time dispatch:

$$\{\begin{array}{l}\underset{x}{\min } \underset{\xi \in \mathcal{U}}{\max }[{\mathit{c}}^{\mathrm{T}}\mathit{x}+\underset{y(\xi )}{\min } {\mathit{d}}^{\mathrm{T}}\mathit{y}(\xi )]\\ \mathrm{s}.\mathrm{t}.\mathit{A}\mathit{x}\le {\mathit{b}}_1 ,\forall \xi \in \mathcal{U}\\ \mathit{B}\mathit{x}+\mathit{C}\mathit{y}(\xi )\le {\mathit{b}}_2 +\mathit{D}\xi ,\forall \xi \in \mathcal{U}\end{array}$$

(7)

Here, $\mathit{x}$ represents first-stage decision variables; $\mathit{y}(\xi )$ denotes the second-stage adaptive variable.

ARO’s multi-stage structure, consisting of first-stage “here-and-now” decisions and second-stage “wait-and-see” adaptations, is solved using two key techniques chosen based on the scale of adaptive decisions in CCHP systems:

(1)

Benders decomposition [87]

Benders decomposition splits ARO into a master problem and subproblems for each uncertainty realization. The master problem focuses on optimizing first-stage decisions such as day-ahead CCHP unit scheduling. As the algorithm iterates, it incorporates feasibility and optimality constraints termed cuts derived from the subproblems. The subproblems for given first-stage decisions assess the worst-case cost of second-stage adaptive actions like real-time various storage units’ dispatch and demand response programs. When a subproblem is infeasible, a feasibility cut is generated to rule out invalid first-stage solutions. If the subproblem is feasible, an optimality cut is produced to bound the worst-case cost. This iterative refinement balances robustness and computational feasibility, making it well-suited for moderate-scale CCHP systems such as campus microgrids with 4–8-h dispatch time horizons.

(2)

Cut-and-column generation (C&CG) [88]

Cut-and-column generation is designed to handle high-dimensional adaptive decisions in ARO by simultaneously adding new decision variables termed columns and constraints known as cuts. Initially, the master problem optimizes a subset of second-stage decisions. Cutting planes enforce robustness against worst-case uncertainties. Unlike Benders decomposition, C&CG expands the solution space iteratively by adding new variables and constraints. This characteristic accelerates convergence in complex CCHP scenarios such as the coordination of residential EV charging. In contexts involving high-frequency flexibility, C&CG can reduce computation time by 40–60% compared to Benders decomposition, allowing for efficient management of time-varying renewable energy and load dynamics.

4.2. Stochastic Optimization (SO) Paradigms

The SO paradigms address uncertainty by leveraging known probability distributions of uncertain parameters such as renewable energy output and load demand. Unlike robust optimization, which focuses on worst-case scenarios, SO minimizes the expected operational cost across all possible uncertainty realizations, balancing optimality and statistical feasibility. For CCHP systems, SO decomposes decision making into scenarios that reflect different realizations of uncertainties each weighted by its probability.

For CCHP systems, SO decomposes decision making into two stages to accommodate the temporal nature of uncertainties:

(1)

First-stage (here-and-now) decisions: These are made before uncertainties are observed, including day-ahead commitments that form the foundational operational framework. The core formulation is as follows:

$$\{\begin{array}{l}\underset{x}{\min } c^{\mathrm{T}}\mathit{x}+{\mathbf{E}}_{\mathbf{P}}\left[\underset{{\mathit{y}}_s}{\min }{\displaystyle \sum _{s=1}^S{\pi }_s}q({\mathsf{\xi }}_s,\mathit{x},{\mathit{y}}_s)\right]\\ \mathrm{s}.\mathrm{t}.\hspace{1em}\mathit{A}\mathit{x}\le b_1\end{array}$$

(8)

Here, $\mathit{x}$ represents first-stage decision variables; $c^{\mathrm{T}}\mathit{x}$ denotes the fixed cost of first-stage decisions. ${\mathbf{E}}_{\mathbf{P}}[\cdot ]$ represents expectation over probability distribution $\mathbf{P}$ of uncertainties; $s$ and $S$ denote the scenario index and total number of scenarios; ${\pi }_s$ denotes probability of scenario s; ${\xi }_s$ denotes the uncertain parameters in scenario s; ${\mathit{y}}_s$ denotes second-stage recourse variables for scenario s; $\mathit{q}(\cdot )$ denotes cost function of second-stage actions; $A\mathit{x}\le b_1$ denotes first-stage feasibility constraints.

(2)

Second-stage (wait-and-see) recourse actions: These are adjusted after observing specific uncertainty realizations, such as modifying battery discharge rates or grid import/export volumes to maintain balance. The core formulation is as follows:

$$\{\begin{array}{l}\underset{y_s}{\min } q({\mathit{\xi }}_s,\mathit{x},{\mathit{y}}_s)\\ \mathrm{s}.\mathrm{t}.\mathit{B}\mathit{x}+\mathit{C}{\mathit{y}}_s\le {\mathit{b}}_2 +\mathit{D}{\mathit{\xi }}_s\end{array}$$

(9)

Here, $\mathit{B}\mathit{x}+\mathit{C}{\mathit{y}}_s\le {\mathit{b}}_2 +\mathit{D}{\mathit{\xi }}_s$ represents scenario-specific constraints in the second stage.

The solution method for SO relies on scenario generation and decomposition. Scenarios are generated from the known probability distribution using methods like Monte Carlo sampling or Latin hypercube sampling to capture the uncertainty spectrum, ensuring that various realizations of uncertain parameters. Decomposition techniques such as the L-shaped method then split the problem into a master problem for the first-stage decisions and subproblems for the scenario-specific recourse actions. This approach is particularly effective for CCHP systems with well-characterized renewable energy distributions.

4.3. Information Gap Decision Theory

Information gap decision theory (IGDT) focuses on optimizing system robustness against unknown uncertainty ranges rather than relying on probability distributions. Its core is to define an “information gap” that quantifies the deviation between forecasted and actual values of uncertain parameters such as renewable energy output or energy prices. IGDT aims to maximize the system’s performance guarantee within the largest possible uncertainty range ensuring stability even under extreme deviations.

For CCHP systems, the formulation of information gap decision theory typically takes the following form:

$$\{\begin{array}{l}\underset{\alpha }{\min }\underset{\mathit{\xi }\in \mathcal{U}\left(\alpha \right)}{\max }\hspace{1em}{c}^{\mathrm{T}}\mathit{x}+q(\mathit{\xi },\mathit{x})\\ \mathrm{s}.\mathrm{t}.\hspace{1em}\mathit{A}\mathit{x}+\mathit{B}(\mathit{\xi })\le b,\hspace{1em}\forall \mathit{\xi }\in \mathcal{U}\\ \hspace{1em}\hspace{1em} \mathcal{U}(\alpha )=\left\{\mathit{\xi }|\Vert \mathit{\xi }-\widehat{\mathit{\xi }}\Vert \le \alpha \rho \right\}\end{array}$$

(10)

Here, $\alpha$ represents the uncertainty radius quantifying the maximum deviation; $\widehat{\mathit{\xi }}$ and $\rho$ represent the forecasted value and the scaling parameter, respectively; $\mathcal{U}(\alpha )$ represents the uncertainty set expanding with $\alpha$.

The solution method involves converting the bi-level problem into a single-objective optimization by maximizing $\alpha$ while ensuring the system meets performance thresholds such as minimum efficiency or maximum cost. This makes information gap decision theory well-suited for CCHP systems with limited historical data where probability distributions are unknown.

4.4. Deep Reinforcement Learning

In the framework of deep reinforcement learning, the operational optimization of CCHP systems can be modeled as a Markov decision process (MDP), with the following core mathematical formulations:

(1)

Definition of Markov Decision Process

The interaction between the intelligent agent and the dynamic energy environment of CCHP systems is abstracted as a quadruple:

$$ℳ=(\mathcal{S},\mathcal{A},P,r)$$

(11)

Here, $\mathcal{S}$ is the state vector, and $\mathcal{S}=[P_{\mathrm{GT}},Q_{\mathrm{HB}},SO{C}_{\mathrm{ES}},SO{C}_{\mathrm{TS}},L_{\mathrm{el}},L_{\mathrm{th}},P_{\mathrm{PV}},P_{\mathrm{WT}},\dots ]$; $\mathcal{A}$ is the action space, including executable operations by the agent, such as the gas turbine power adjustment, electrical storage charge/discharge power, and grid power exchange adjustment, among others; $P(s^{\prime }|s,a)$ is state transition probability, describing the probability of transitioning from state $s$ to $s^{\prime }$; $r\left(s,a\right)$ is the reward function which quantifies the single-step performance.

(2)

Policies and value functions

Deep reinforcement learning approximates policies or value functions using deep neural networks. For example, deep Q-networks employ a parameterized network $Q(s,a;\theta )$ to estimate action values:

$$Q^{*}(s,a)=\mathbf{E}\left[{\displaystyle \sum _{t=0}^{\infty }{\gamma }^t}r(s_t,a_t)|s_0=s,a_0=a\right]$$

(12)

Here, $\gamma \in [0,1)$ is the discount factor, balancing immediate and long-term rewards.

The loss function is typically the mean squared error between the target value and the value predicted value the network:

$$L(\theta )={\mathbf{E}}_{s,a,r,s^{\prime }}\left[{\left(y-Q(s,a;\theta )\right)}^2\right]$$

(13)

Here, $y=r+\gamma {\max }_{a^{\prime }}Q(s^{\prime },a^{\prime };{\theta }^{-})$ is the target value, and ${\theta }^{-}$ is the parameter of the target network.

Recent applications demonstrate DRL’s transformative impact on high-RE CCHP operations through real-time adaptive control. For example, in a hospital CCHP microgrid with 40% solar penetration [89], a DRL agent reduced operational costs by 18% by dynamically coordinating fuel cells, thermal storage, and grid imports while maintaining thermal comfort constraints (±0.5 °C). The agent learned to pre-cool buildings during solar surpluses and shift electrical loads to avoid peak tariffs, cutting energy costs by 22% compared to model-predictive control. Similarly, a hybrid RO-DRL framework [90] applied to an industrial CCHP park mitigated wind forecast errors (RMSE: 28%), where RO generated day-ahead risk-averse schedules, and DRL fine-tuned real-time responses to forecast deviations, reducing wind curtailment by 35% and gas turbine wear by 20%. Complementary deep learning advances, such as CNN-LSTM forecasting models [91], improved solar prediction accuracy by 22% for campus CCHP systems, enabling proactive adjustment of absorption chillers and battery scheduling.

4.5. Chance-Constrained Programming

Chance-constrained programming (CCP) provides a rigorous mathematical framework for optimizing CCHP systems under uncertainty by allowing controlled constraint violations within probabilistic safety margins. The general CCP formulation for CCHP systems is expressed as

$$\{\begin{array}{l}\min \mathbf{E}\left(C_{\mathrm{total}}\right)\\ Pr\{g_k (\mathit{x},\mathit{\xi })\le 0\}\ge 1-{ϵ}_k ,\forall k\in K\end{array}$$

(14)

Here, $g_k (\cdot )$ denotes the constraint function defining a physical/operational limit, and the subscript k denotes the k-th constraint, such as power balance, equipment capacity, and so on. ${ϵ}_k$ denotes the allowable violation probability.

Solution methodologies for chance-constrained optimization of high-renewable CCHP systems primarily encompass four established approaches: analytical reformulation, scenario-based approximation, conservative convex surrogates, and adaptive cutting-plane algorithms.

4.6. Algorithm Comparison and Selection

4.6.1. Algorithm Comparison

For CCHP systems operating under high renewable penetration, selecting the appropriate optimization method requires careful consideration of uncertainty characteristics, computational requirements, and operational constraints. To systematically evaluate optimization methods for high-renewable CCHP systems,

Table 8. Comparative analysis of optimization methods for CCHP systems under uncertainty.

Criterion	SO	RO	DRO	Adaptive RO	DRL	CCP
Uncertainty type	Probabilistic	Bounded	Ambiguous set	Multi-stage bounded	Model-free	Probabilistic
Time scale	Hours–days	Days	Hours	Hours–days	Seconds–minutes	Minutes–hours
Risk handling	Expected value	Absolute	Distributional	Recourse-adjusted	Learned	Explicit probabilistic
Computation	High (O(Sn))	Medium (O(2m))	High (O(N1.5))	Very H = high (O(T·2m))	Low (online)	Medium (O(n3.5))
Key feature	Scenario-based	Worst-case	Data-driven	Dynamic adjustment	AI-driven	Safety margins
CCHP fit	Day-ahead	Extreme events	Market volatility	Multi-time dispatch	Real-time control	Critical constraints

presents a comprehensive decision matrix that compares key algorithmic characteristics against critical operational requirements.

4.6.2. Algorithm Selection

Building on the comparative analysis of optimization algorithms in Table 6, which encompasses their handling of uncertainty, time-scale adaptation, risk management, and computational profiles, a structured selection framework is essential to guide practical decision making for high-renewable CCHP systems.

To operationalize the theoretical comparisons into actionable engineering decisions, we propose a three-tiered selection protocol that transforms methodological characteristics into implementable guidelines:

(1)

Select by Uncertainty Information

• If uncertainty has clear bounds, choose RO;
• If probability distribution is known, choose SO;
• If distribution is unknown, but historical data exist, choose DRO;
• If probabilistic constraints need to be satisfied, choose CCP;
• If uncertainty bounds are unknown, and both robustness and opportuneness matter, choose IGDT;
• If the system is complex, and online learning is needed, choose DRL.

(2)

Select by Time Scale

• For long-term planning, choose IGDT or SO;
• For day-ahead scheduling, choose RO, DRO, or SO;
• For intraday scheduling, choose SO or CCP;
• For multi-time scale dispatch (hours–days), choose adaptive RO;
• For real-time control, choose DRL or CCP.

(3)

Select by Risk Preference

• If risk-averse (avoid worst-case scenarios), choose RO;
• If risk-neutral (optimize expected value), choose SO;
• For probabilistic risk control (allow small-probability violations), choose CCP;
• If there is distributionally robust risk, choose DRO;
• If risk handling requires recourse adjustment across stages, choose adaptive RO.

To address the multifaceted challenges of high-renewable CCHP systems, where single algorithms may struggle to balance conflicting demands like efficiency, robustness, and real-time adaptability, hybrid strategies that integrate complementary methods offer enhanced performance. The following hybrid strategy recommendations combine algorithmic strengths to tackle complex operational scenarios:

• SO + CCP: Embed chance constraints in stochastic optimization to balance economy and safety;
• RO + DRL: Use RO to generate initial strategies, with DRL for online fine-tuning, as this is suitable for high-volatility scenarios;
• DRO + CCP: Add probabilistic constraints to the distributionally robust framework to address safety requirements under ambiguous distributions.

To quantitatively demonstrate the advantages of hybrid optimization strategies in high-RE CCHP systems,

Table 9. Performance of hybrid optimization strategies in high-RE CCHP scenarios.

Hybrid Strategy	Best-Suited Scenario	Key Advantages	Simulation Results
RO + DRL [57]	Forecast uncertainty	Balances robustness and online adaptation	Cost ↓ 18–22%, robustness ↑ 30–40%
SO + CCP [61]	Gaussian-distributed	Cost-optimal with safety guarantees	Expected cost ↓ 15%, violation probability < 5%
DRO + CCP [59]	Ambiguous distributions + safety	Handles distributional ambiguity + risk	Worst-case cost ↓ 12%, CVaR ↓ 25%

↓ means decrease; ↑ means increase.

compares their performance across key operational scenarios, highlighting scenario-specific benefits in cost reduction, robustness, and constraint satisfaction

4.7. Constraint Handling in Uncertainty-Aware Optimization

Uncertainty-aware optimization methods play a critical role in ensuring the feasibility and stability of CCHP systems under high renewable penetration by explicitly addressing operational constraints. ARO enforces multi-stage constraints, such as energy balance, ramp-rate limits, and storage state-of-charge bounds, through recourse adjustments that adapt to worst-case uncertainty realizations. In [42], ARO dynamically adjusts gas turbine output and thermal storage dispatch to comply with equipment ramp-rate limits while maintaining indoor temperature within comfort thresholds, as demonstrated in district-scale CCHP implementations. This approach ensures robust feasibility across all possible uncertainty scenarios without excessive conservatism.

DRO provides a probabilistic safeguard against constraint violations when uncertainty distributions are ambiguous but partially characterized. By leveraging Wasserstein-metric ambiguity sets, DRO guarantees high-confidence satisfaction of electrical-thermal balance and flexibility limits even with limited historical data. Reference [60] showed that DRO outperforms stochastic optimization in preserving user comfort under forecast errors, achieving 95% reliability in constraint adherence. This makes DRO particularly suitable for systems where uncertainty distributions are poorly defined but where safety margins must be rigorously maintained.

DRL uses real-time state-action feedback to enforce constraints. DRL policies dynamically optimize energy storage cycling, multi-energy coupling, and thermal comfort by penalizing deviations from SOC limits or temperature bounds. For example, DRL-based strategies in EV-integrated CCHP systems [58] reduce chiller startup frequency by 30% while strictly enforcing indoor comfort constraints, demonstrating its ability to learn adaptive policies that balance cost efficiency with operational feasibility. Unlike traditional methods, DRL excels in high-dimensional, nonlinear environments where explicit constraint modeling is computationally intractable, offering a data-driven alternative for complex, dynamic CCHP operations.

ARO adapts constraints via multi-stage recourse, DRO robustifies them across ambiguous distributions, and DRL learns constraint-compliant policies through feedback. Together, they ensure CCHP systems operate within feasible bounds under high RE volatility, enabling the model formulations and solution techniques explored in the next section.

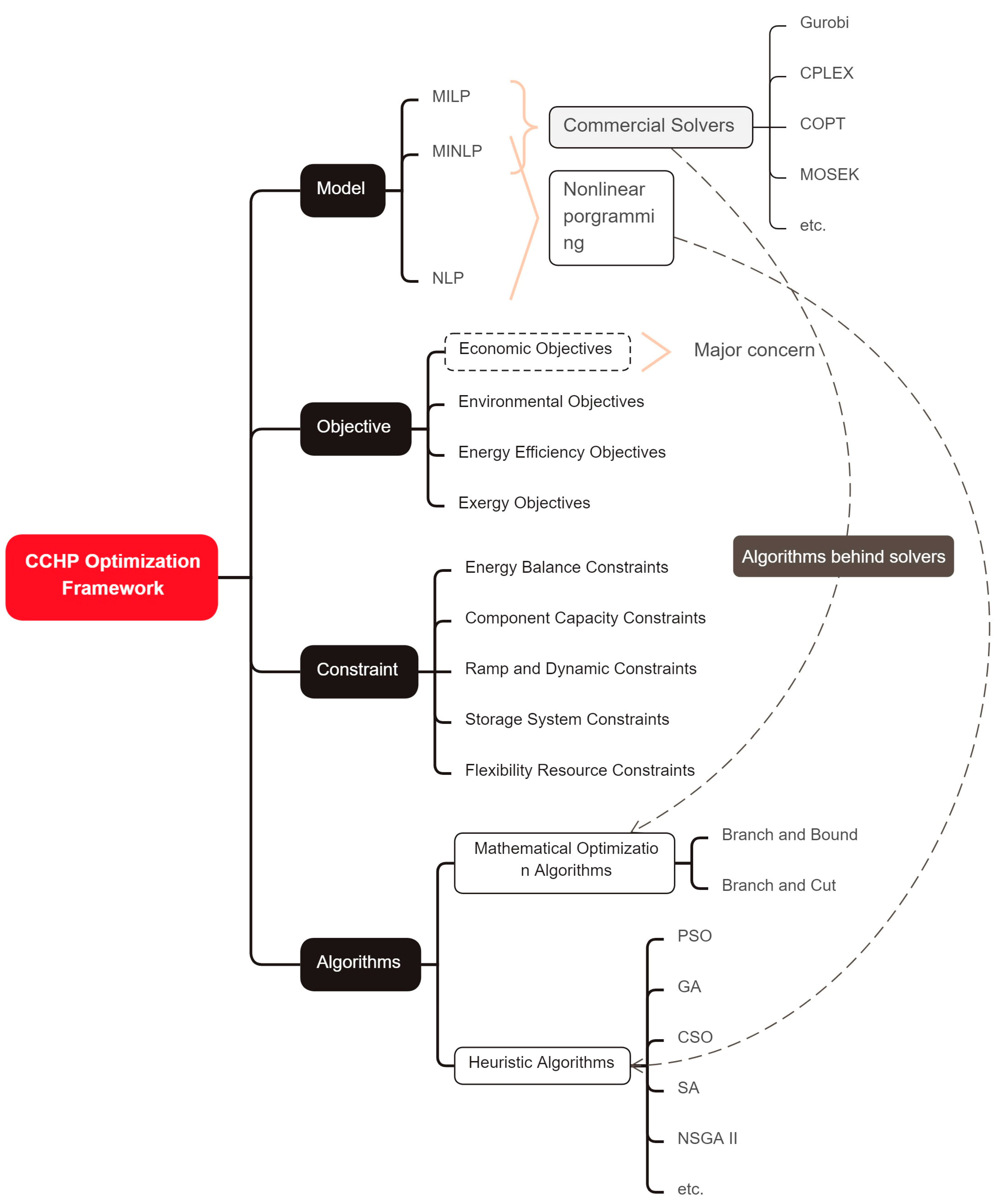
5. Modeling and Solution Techniques

The optimization of high-RE CCHP systems requires rigorous modeling of objectives, constraints, and solution algorithms tailored to multi-energy coupling and uncertainty. Figure 4 presents an overview of the operation optimization framework for the CCHP system.

5.1. Optimization Model Formulation

Optimization models for CCHP systems under high renewable penetration are defined by their objective functions guiding performance goals and key constraints ensuring operational feasibility.

5.1.1. Objective Functions

Objective functions in CCHP optimization balance multiple performance criteria, often categorized under the “4E” framework, which includes energy, exergy, environment, economy, with adaptions for high-RE integration.

(1)

Economic Objectives

The goal is to minimize total operational costs, including fuel consumption, grid import/export expenses, maintenance costs, and flexibility-related costs. The typical formulation is

$$\mathrm{Cost}={\displaystyle \sum \left(c_{\mathrm{fuel}}\cdot P_{\mathrm{PM}}+c_{\mathrm{grid}}\cdot P_{\mathrm{import}}-c_{\mathrm{export}}\cdot P_{\mathrm{export}}+c_{\mathrm{DR}}\cdot \Delta L\right)}$$

(15)

Here, $c_{\mathrm{fuel}}$ denotes the cost per unit energy from prime mover fuel consumption; $c_{\mathrm{grid}}$ and $c_{\mathrm{export}}$ denote the cost coefficient for grid-imported electricity and revenue coefficient for grid-exported electricity, respectively; $P_{\mathrm{PM}}$ is the electrical power output of the prime mover; $P_{\mathrm{import}}$ and $P_{\mathrm{export}}$ denote the power imported from the external grid and exported to the external grid, respectively; $c_{\mathrm{DR}}$ is the incentive/disincentive coefficient for demand response adjustments; $\Delta L$ is the load adjustment from demand response.

(2)

Environmental Objectives

In addition to economic performance, minimizing environmental impact, particularly reducing carbon emissions from energy conversion and consumption, forms a core focus of CCHP optimization:

$$\mathrm{Emission}={\displaystyle \sum \left({\mu }_{\mathrm{CHP}}\cdot P_{\mathrm{PM}}+{\mu }_{\mathrm{grid}}\cdot P_{\mathrm{import}}\right)}$$

(16)

Here, ${\mu }_{\mathrm{CHP}}$ and ${\mu }_{\mathrm{grid}}$ denote the carbon emission factor of the prime mover unit and of grid-purchased electricity, respectively.

(3)

Energy Efficiency Objectives

Building on economic and environmental goals, optimizing energy efficiency is critical for maximizing the utilization of primary energy resources and minimizing waste in CCHP systems. The following formula quantifies the energy efficiency objective:

$${\eta }_{\mathrm{energy}}={\displaystyle \frac{P_{\mathrm{elec}}+Q_{\mathrm{heat}}+Q_{\mathrm{cool}}}{E_{\mathrm{fuel}}+E_{\mathrm{RE}}}}$$

(17)

Here, ${\eta }_{\mathrm{energy}}$ denotes the energy efficiency ratio; $P_{\mathrm{elec}}$, $Q_{\mathrm{heat}}$, and $Q_{\mathrm{cool}}$ denote the useful electrical energy output, heating energy output, and cooling energy output, respectively; $E_{\mathrm{fuel}}$ and $E_{\mathrm{RE}}$ denote the primary energy input from fossil fuels and from renewable sources, respectively.

(4)

Exergy Objectives

Exergy analysis quantifies energy quality by measuring usable work potential. For CCHP systems, exergy efficiency is defined as the ratio of useful exergy output to total exergy input:

$${\eta }_{\mathrm{exergy}}={\displaystyle \frac{E_x^{\mathrm{elec}}+E_x^{\mathrm{heat}}+E_x^{\mathrm{cool}}}{E_x^{\mathrm{fuel}}+E_x^{\mathrm{RE}}}}$$

(18)

Here, $E_x^{\mathrm{fuel}}$ and $E_x^{\mathrm{RE}}$ are the fuel exergy and the renewable exergy, respectively; $E_x^{\mathrm{elec}}$, $E_x^{\mathrm{heat}}$, and $E_x^{\mathrm{cool}}$ denote the useful electrical exergy, heating exergy, and cooling exergy, respectively.

Exergy efficiency varies by application: in commercial buildings with moderate waste heat recovery, CCHP systems typically achieve 40–50% exergy efficiency; industrial facilities leverage high-temperature process heat and efficient waste heat recovery. For systems integrating high-penetration renewable, exergy efficiency can reach 50–60% when optimized for multi-energy synergy.

(5)

Multi-Objective Trade-offs

Conflicting goals such as cost vs. emissions and efficiency vs. flexibility can be balanced via the weighted sum method to achieve the Pareto optimality. Combine the “4E” objectives into a single scalar using weights:

$$\min \left({\omega }_1\cdot \mathrm{Cost}+{\omega }_2\cdot \mathrm{Emission}-{\omega }_3\cdot {\eta }_{\mathrm{exergy}}-{\omega }_4\cdot {\eta }_{\mathrm{energy}}\right)$$

(19)

Here, ${\omega }_{i }$ is the weight for each objective, and $\sum {\omega }_{i }=1$.

5.1.2. Key Constraints

To ensure operational feasibility, safety, and adherence to the physical limits of CCHP components, key constraints are formalized through the following mathematical expressions.

(1)

Energy Balance Constraints

As shown in Figure 1, the energy balance in the CCHP system is divided into electrical power balance, cooling power balance, and thermal power balance, with their expressions as follows:

$$\{\begin{array}{l}{P}_{\mathrm{PV}}+P_{\mathrm{WT}}+P_{\mathrm{PM}}+P_{\mathrm{import}}+P_{\mathrm{ES},\mathrm{dis}}=P_{\mathrm{export}}+P_{\mathrm{EL}}+P_{\mathrm{EC}}+P_{\mathrm{EH}}+P_{\mathrm{ES},\mathrm{cha}}\\ Q_{\mathrm{PM},\mathrm{waste}}+Q_{\mathrm{boiler}}+Q_{\mathrm{TS},\mathrm{dis}}+Q_{\mathrm{EH}}=Q_{\mathrm{HL}}+Q_{\mathrm{TS},\mathrm{cha}}\\ Q_{\mathrm{AC}}+Q_{\mathrm{EC}}+Q_{\mathrm{CS},\mathrm{dis}}=Q_{\mathrm{CL}}+Q_{\mathrm{CS},\mathrm{cha}}\end{array}$$

(20)

Here, $P_{\mathrm{PV}}$ and $P_{\mathrm{WT}}$ are the photovoltaic power output and wind turbine power output, respectively; $P_{\mathrm{ES},\mathrm{dis}}$ and $P_{\mathrm{ES},\mathrm{cha}}$ are the discharge power and charge power of electrical energy storage, respectively; $P_{\mathrm{CS},\mathrm{dis}}$ and $P_{\mathrm{CS},\mathrm{cha}}$ are the discharge power and charge power of cooling energy storage, respectively; $P_{\mathrm{HS},\mathrm{dis}}$ and $P_{\mathrm{HS},\mathrm{cha}}$ are the discharge power and charge power of heating energy storage, respectively; $P_{\mathrm{EL}}$, $P_{\mathrm{CL}}$, and $P_{\mathrm{HL}}$ are electrical load, cooling load, and heating load, respectively; $P_{\mathrm{HS},\mathrm{dis}}$ and $P_{\mathrm{HS},\mathrm{cha}}$ are the discharge power and heat output of the auxiliary boiler, respectively; $Q_{\mathrm{AC}}$ and $Q_{\mathrm{EC}}$ are the cooling output of absorption chillers and cooling output of electrical chillers, respectively.

(2)

Component Capacity Constraints

To ensure safe operation within physical limits, the output of generation and conversion devices is bounded by capacity constraints. The following takes the CCHP unit and electrical chiller units as an example:

$$\{\begin{array}{l}{P}_{\mathrm{PM},\min }\le P_{\mathrm{PM}}\le P_{\mathrm{PM},\max }\\ P_{\mathrm{EC},\min }\le P_{\mathrm{EC}}\le P_{\mathrm{EC},\max }\end{array}$$

(21)

Here, $P_{\mathrm{PM},\max }$ and $P_{\mathrm{PM},\min }$ are the maximum electrical power output and minimum output of CHP unit, respectively. $P_{\mathrm{EC},\max }$ and $P_{\mathrm{EC},\min }$ are the maximum operating power and minimum operating power of electrical chiller unit, respectively.

(3)

Ramp and Dynamic Constraints

To mitigate mechanical stress and stabilize operation amid renewable energy volatility, the rate of power change for generation or conversion devices is constrained by ramp limits. The following takes the CHP unit as an example:

$$\left|P_{\mathrm{PM},t}-P_{\mathrm{PM},t-1}\right|\le r_{\mathrm{PM},\max }$$

(22)

Here, $r_{\mathrm{PM},\max }$ represents the maximum ramping rate of the CHP unit.

(4)

Storage System Constraints

To enable energy shifting and stabilize operation amid renewable variability, energy storage systems (electrical, heating, or cooling) are bound by SOC limits and dynamic energy balance constraints. The following takes an electrical energy storage as an example:

$$\{\begin{array}{l}{\mathrm{SOC}}_{\mathrm{ES},t}={\mathrm{SOC}}_{\mathrm{ES},t-1}+{\eta }_{\mathrm{ES},\mathrm{cha}}\cdot P_{\mathrm{ES},\mathrm{cha}}-P_{\mathrm{ES},\mathrm{dis}}/{\eta }_{\mathrm{ES},\mathrm{dis}}\\ {\mathrm{SOC}}_{\mathrm{ES},\min }\le {\mathrm{SOC}}_{\mathrm{ES},t}\le {\mathrm{SOC}}_{\mathrm{ES},\max }\end{array}$$

(23)

Here, ${\mathrm{SOC}}_{\mathrm{ES},t}$ and ${\mathrm{SOC}}_{\mathrm{ES},t-1}$ represent the state of charge of ES at time t and at time t − 1, respectively. ${\eta }_{\mathrm{ES},\mathrm{cha}}$ and $r_{\mathrm{PM},\max }$ represent the charging efficiency and discharging efficiency of ES, respectively. ${\mathrm{SOC}}_{\mathrm{ES},\max }$ and ${\mathrm{SOC}}_{\mathrm{ES},\min }$ are the maximum and minimum SOC of ES, respectively.

(5)

Flexibility Resource Constraints

To leverage flexibility resources, such as adjustable loads and EVs, for balancing renewable volatility while ensuring user comfort or process integrity, operational constraints govern their adjustment range and timing.

The EV charging window constraints and EV energy requirement constraints are

$$\{\begin{array}{l}{t}_{\mathrm{start}}\le t_{\mathrm{charge}}\le t_{\mathrm{deadline}}\\ E_{\mathrm{EV}}={\displaystyle \int P_{\mathrm{EV},t}}dt\end{array}$$

(24)

Here, $t_{\mathrm{start}}$ and $t_{\mathrm{deadline}}$ represent the earliest allowable start time and latest allowable end time for EV charging operation; $P_{\mathrm{EV},t}$ represents the EV charging power at time t; $E_{\mathrm{EV}}$ represents the total energy required by EV state-of-charge target.

To preserve user comfort amid flexible adjustments, operational limits are defined under comfort constraints:

$$T_{\min }\le T_{\mathrm{building}}\le T_{\max }$$

(25)

Here, $T_{\mathrm{building}}$ represents the Indoor temperature of the building; $T_{\max }$ and $T_{\min }$ represent the maximum and minimum allowable temperature for comfort integrity.

5.2. Solution Algorithms

The CCHP optimization models can be formulated as a large-scale, nonlinear, and multi-constrained model, which requires tailored algorithms to balance accuracy and computational efficiency, especially under high-RE uncertainty.

5.2.1. Mathematical Programming

Mathematical programming methods solve structured optimization problems with linear or convex formulations, leveraging rigorous theory for optimal solutions.

(1)

Linear/Quadratic Programming (LP/QP)

This can be applied to linearized models, e.g., MILP approximations of CCHP/CHP operation. LP is used for day-ahead scheduling of electricity–heat balance with linearized storage losses, solved efficiently by solvers like Gurobi. However, this model usually fails to capture equipment start–stop costs.

(2)

Mixed-Integer Linear/Nonlinear Programming (MILP/MINLP)

This handles discrete decisions, such as the on/off status of CHP units, and nonlinearities, such as the dependence of heat pump COP on temperature. MINLP is critical for modeling P2G and hydrogen storage, where chemical conversion efficiencies are nonlinear. Commercial solvers like CPLEX and COPT enable solutions for medium-scale systems.

(3)

Decomposition Methods

These break large problems into subproblems. Benders decomposition and C&CG (introduced in Section 4.1.3) can split multi-stage problems into master and subproblem.

5.2.2. Heuristic and Metaheuristic Algorithms

These methods approximate optimal solutions for complex, nonconvex, or large-scale problems where mathematical programming is intractable. In CCHP optimization, prevalent metaheuristic algorithms include genetic algorithms (GA), particle swarm optimization (PSO), simulated annealing (SA), cross search optimization (CSO), ant colony optimization (ACO), bat algorithm (BA), and grey wolf optimizer (GWO), among others.

Due to inherent limitations in standalone algorithms, such as pronounced premature convergence and lower parameter sensitivity, hybrid approaches integrate the strengths of standalone algorithms to overcome their inherent limitations in CCHP optimization. Key hybrid approaches include PSO-GA, GWO-PSO, and quantum-inspired GA, among others.

5.3. Real-World Implementation Framework

Translating theoretical optimization models and flexibility mechanisms into practical CCHP operations requires addressing field-specific constraints such as stakeholder dynamics, infrastructure limitations, and regulatory boundaries. This section establishes a systematic pathway to bridge this gap, with validation protocols tailored to real-world complexity.

5.3.1. From Theoretical Innovations to Deployable Solutions

Building upon the flexibility mechanisms (Section 3) and optimization strategies (Section 4), this section establishes a translational pathway for deploying the proposed methodologies. The implementation follows a cascading three-phase framework, progressing from controlled pilots to city-scale systems, with each phase resolving specific barriers identified in Section 6.2.

5.3.2. Phase-Driven Deployment Roadmap

The deployment roadmap balances technical validation, stakeholder engagement, and scalability to ensure theoretical advancements align with real-world operational demands.

(1)

Phase 1: Technology Validation in Campus Microgrids

This phase focuses on validating core technologies in low-complexity, controlled environments such as university campuses or small research parks. Systems in this stage typically range from 50 to 200 kW, with renewable energy penetration limited to 10–20% (primarily solar PV and small wind turbines). Key components include a simplified generalized energy storage framework integrating physical storage and virtual storage. Optimization strategies are streamlined to test basic coordination: robust optimization for day-ahead scheduling to handle bounded forecast errors and model predictive control for real-time adjustments to short-term renewable fluctuations. Success metrics include renewable energy utilization rates exceeding 85%, operational cost reductions of at least 10% compared to conventional operation, and stable performance within predefined comfort and equipment constraints. This phase resolves initial technical uncertainties, such as compatibility between storage types and optimization algorithms, laying a foundation for larger-scale deployment.

(2)

Phase 2: Industrial Scaling with Hybrid Optimization

Scaling to industrial parks and medium-sized communities (500 kW to 2 MW), this phase increases renewable penetration to 20–40% and introduces multi-stakeholder coordination. The GES framework expands to include shared storage resources and diversified virtual storage (e.g., adjustable industrial processes, EV charging clusters, etc.). Hybrid optimization strategies are fully implemented: distributionally robust optimization handles day-ahead scheduling to address ambiguous renewable distributions, while deep reinforcement learning manages real-time dispatch to adapt to 20–30% forecast deviations. Local energy aggregators facilitate stakeholder collaboration, with transparent benefit-sharing mechanisms to incentivize participation from industrial users, residents, and grid operators. Integration with regional energy markets enhances economic viability, while performance targets include maintaining renewable penetration above 30% without compromising reliability and achieving a payback period of 5–6 years for storage investments. This phase addresses challenges in multi-energy coupling and market-aligned optimization, validating scalability beyond isolated microgrids.

(3)

Phase 3: Urban Energy Hub Integration

The final phase achieves large-scale integration across urban districts, with systems ranging from 5 to 20 MW and renewable penetration reaching 40–60%. Multiple CCHP clusters are interconnected via district heating and cooling networks, incorporating long-duration energy storage (e.g., hydrogen storage, molten salt tanks, etc.) to manage seasonal mismatches between renewable generation and demand. Decentralized optimization, supported by federated learning, enables cross-cluster coordination while preserving data privacy for industrial and residential stakeholders. Algorithms are adapted to align with regional decarbonization policies and grid codes, with participation in ancillary service markets via fast-response virtual storage. Key outcomes include system-wide renewable utilization exceeding 80%, carbon emissions reductions of 30–40% compared to grid-dependent baselines, and robust performance across diverse urban sub-systems (commercial, residential, and light industrial). This phase demonstrates the scalability of the proposed framework, establishing its role in high-renewable urban energy systems.

6. Conclusions

This review comprehensively explores the optimal operation of CCHP systems under high-penetration renewable energy integration, addressing the fundamental shifts in operational paradigms driven by RE volatility. The key implications are summarized as follows:

6.1. Decisive Findings

(1)

Decision-Making Taxonomy for Uncertain Environments

We establish a methodological selection matrix that matches optimization algorithms (RO/SO/DRO/DRL) to uncertainty characteristics. Hybrid strategies, such as distributionally robust chance-constrained programming, are identified as superior solutions for scenarios demanding both probabilistic safety and ambiguity resistance. Empirically, hybrid RO-DRL optimization achieves 92–97% constraint satisfaction under forecast uncertainties (RMSE > 20%), bridging theoretical methodologies with practical operational requirements.

(2)

Cross-Sectoral Flexibility Mechanisms

A multi-dimensional flexibility resource system is constructed to mitigate RE volatility, integrating storage-driven buffering, demand-side adjustment, and multi-energy synergy. These mechanisms collectively enhance adaptability to uncertainties, with multi-energy synergy boosting RE utilization by 25–41% while reducing carbon emissions by 30–60%.

(3)

Systemic Integration of Generalized Energy Storage

Generalized energy storage, formed by synergistic integration of PES and VES, breaks through the limitations of single-type storage, resolving the limitations of standalone storage solutions by integrating PES and VES into a cohesive flexibility portfolio. This integration reduces operational costs by 18–25% and narrows design-actual efficiency gaps from 8–15% to 3–5%, laying a technical foundation for efficient, stable, and low-carbon CCHP operation in high-RE environments.

6.2. Persistent Challenges

Despite these advances, challenges remain:

(1)

Improving computational efficiency for high-dimensional uncertainty in multi-stakeholder coordination;

(2)

Refining uncertainty modeling to capture extreme weather or market dynamics;

(3)

Addressing equitable benefit distribution in VPP-integrated CCHP clusters;

(4)

Enhancing AI techniques’ generalization for scalable real-world applications.

6.3. Future Research Trajectories

Three critical research trajectories demand prioritized investigation to advance high-renewable CCHP systems:

(1)

Hybrid Physics–AI Uncertainty Quantification

Integrating numerical weather prediction with deep ensemble architectures through residual learning frameworks can reduce renewable forecast RMSE below 10% for 72 h horizons. This requires resolving the fundamental tension between physical constraints and data-driven feature representation during joint training. Successful implementation will enable >15% improvement in storage scheduling accuracy.

(2)

Privacy-Preserving Multi-CCHP Coordination

Developing federated optimization with cryptographic privacy guarantees is essential for scalable stakeholder coordination. Key challenges include maintaining >90% centralized optimality while ensuring <5% information leakage in large-scale systems. Breakthroughs in convergence criteria for distributed algorithms will unlock equitable cost–benefit distribution across participant tiers.

(3)

Long-Duration Energy Storage for Seasonal Balancing

Long-duration energy storage technologies can address seasonal mismatches between high renewable energy generation and peak demand. Research should focus on improving round-trip efficiency, reducing lifecycle costs through material innovation, and optimizing integration with multi-energy conversion systems, such as hydrogen-fueled CHP units paired with seasonal storage, to ensure scalability for high-RE grids.