Intelligent Optimization of Single-Stand Control in Directional Drilling with Single-Bent-Housing Motors
Abstract
1. Introduction
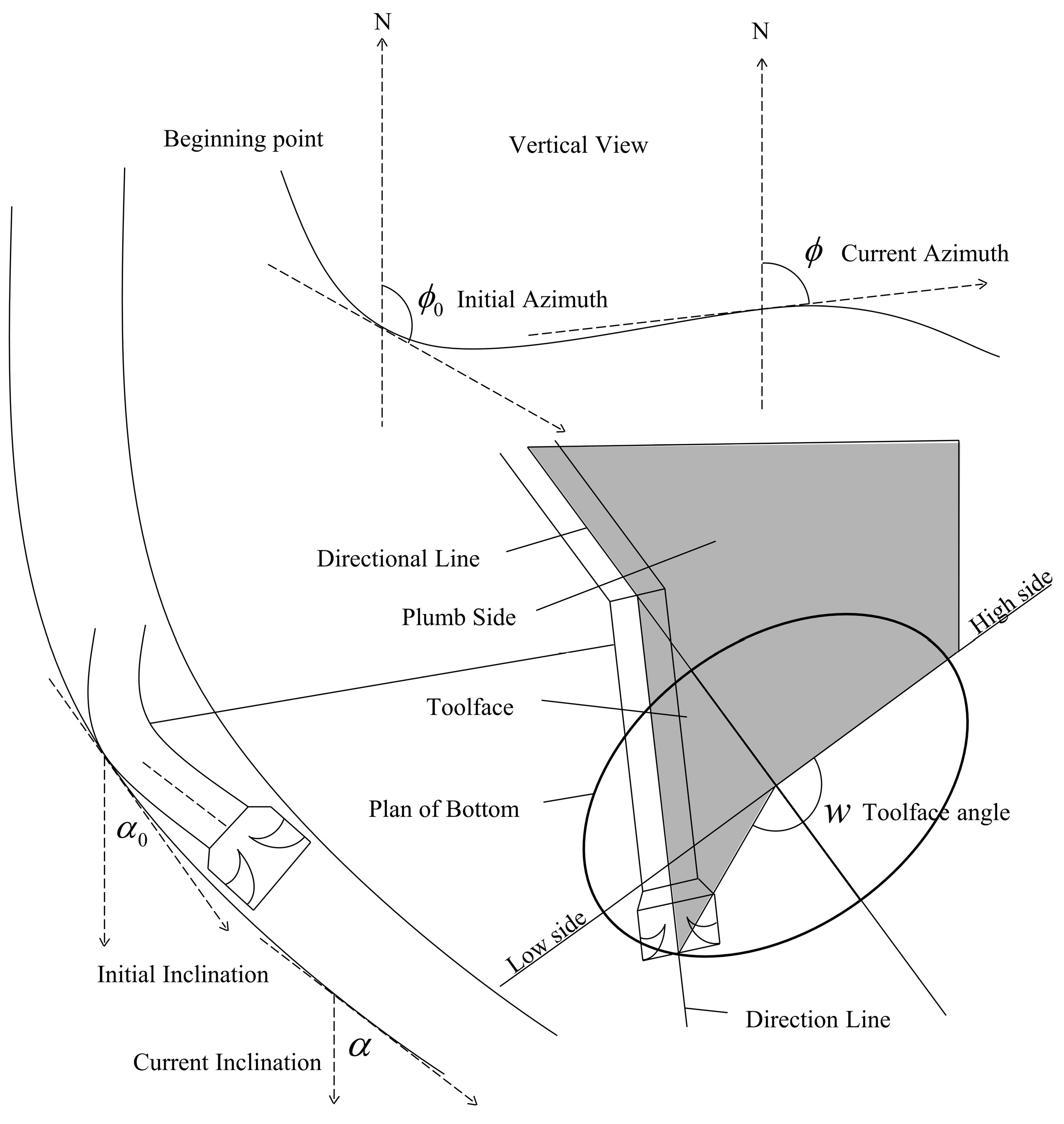
2. Physical Model—Constant-Toolface Model
- (1)
- When , there is no solution.
- (2)
- When and ,
3. Single-Stand Control Design Program
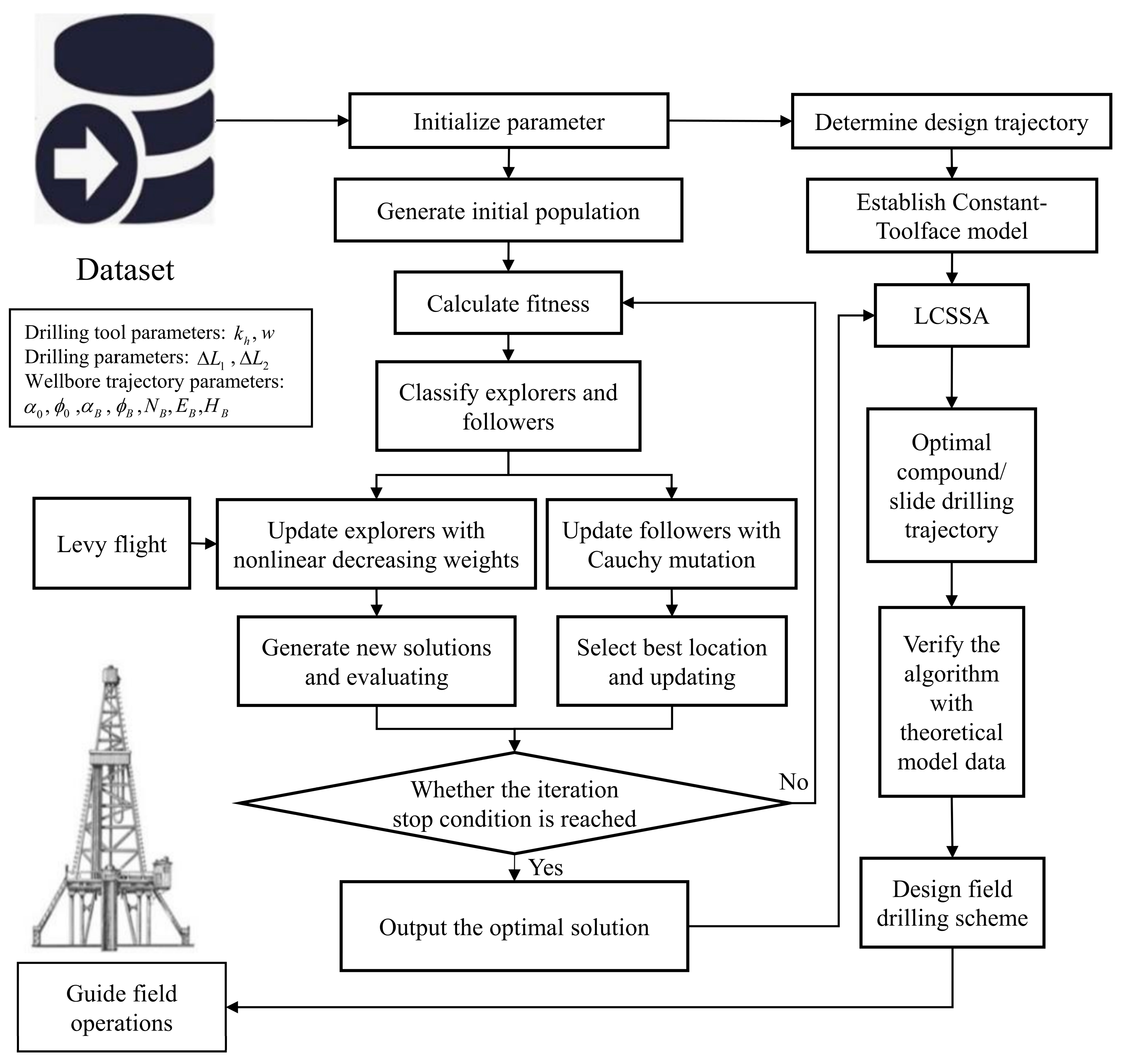
4. Model-Based Intelligent Algorithm
4.1. Algorithm I—Full Search
4.2. Algorithm II—Particle Swarm Optimization
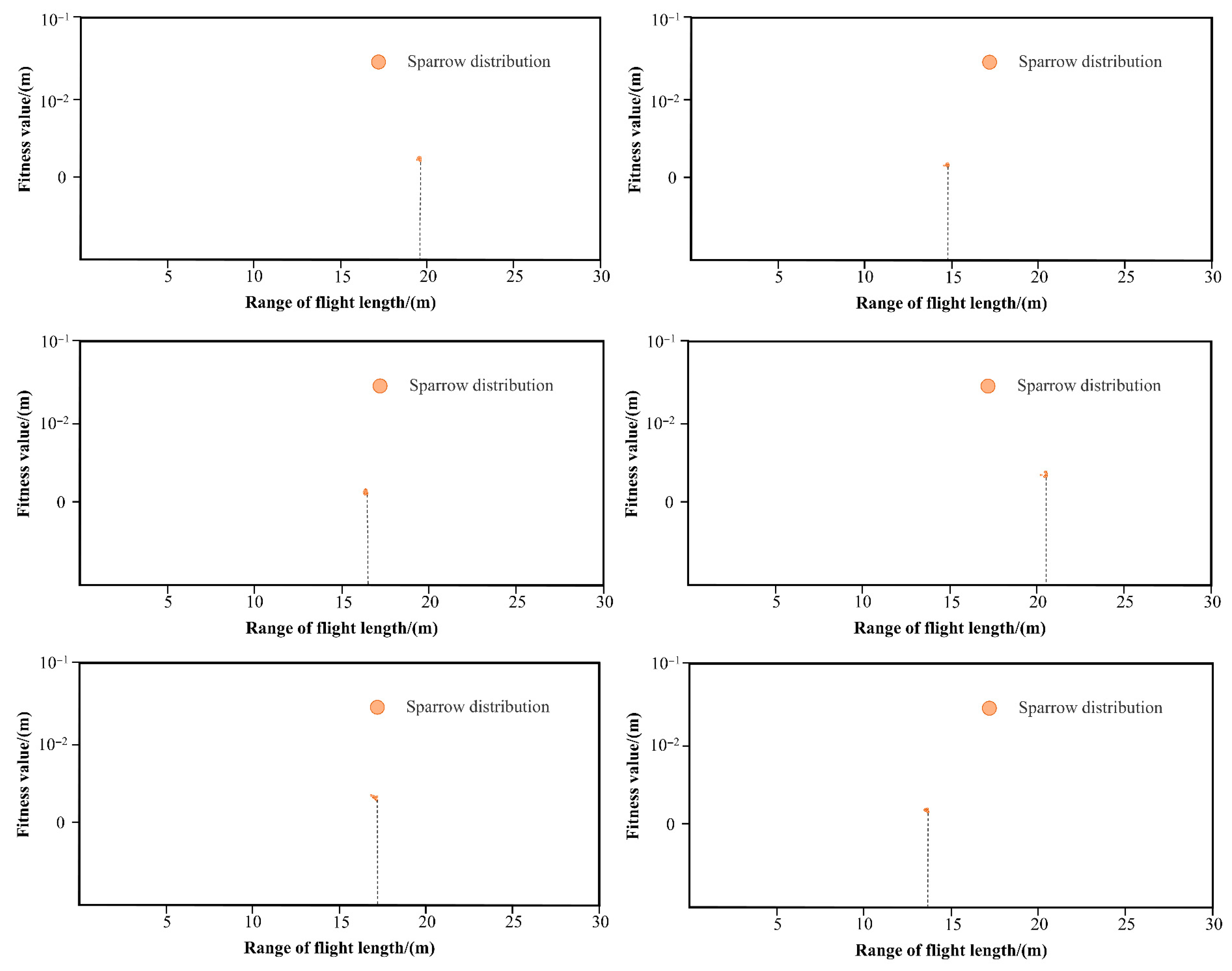
4.3. Algorithm III—Sparrow Search Algorithm
4.4. Algorithm IV—Improved Sparrow Search Algorithm
4.4.1. Updating Explorers’ Location with Nonlinear Decreasing Weights
4.4.2. Levy Flight Strategy
4.4.3. Updating Followers’ Location with the Cauchy Mutation Strategy
5. Computational Case
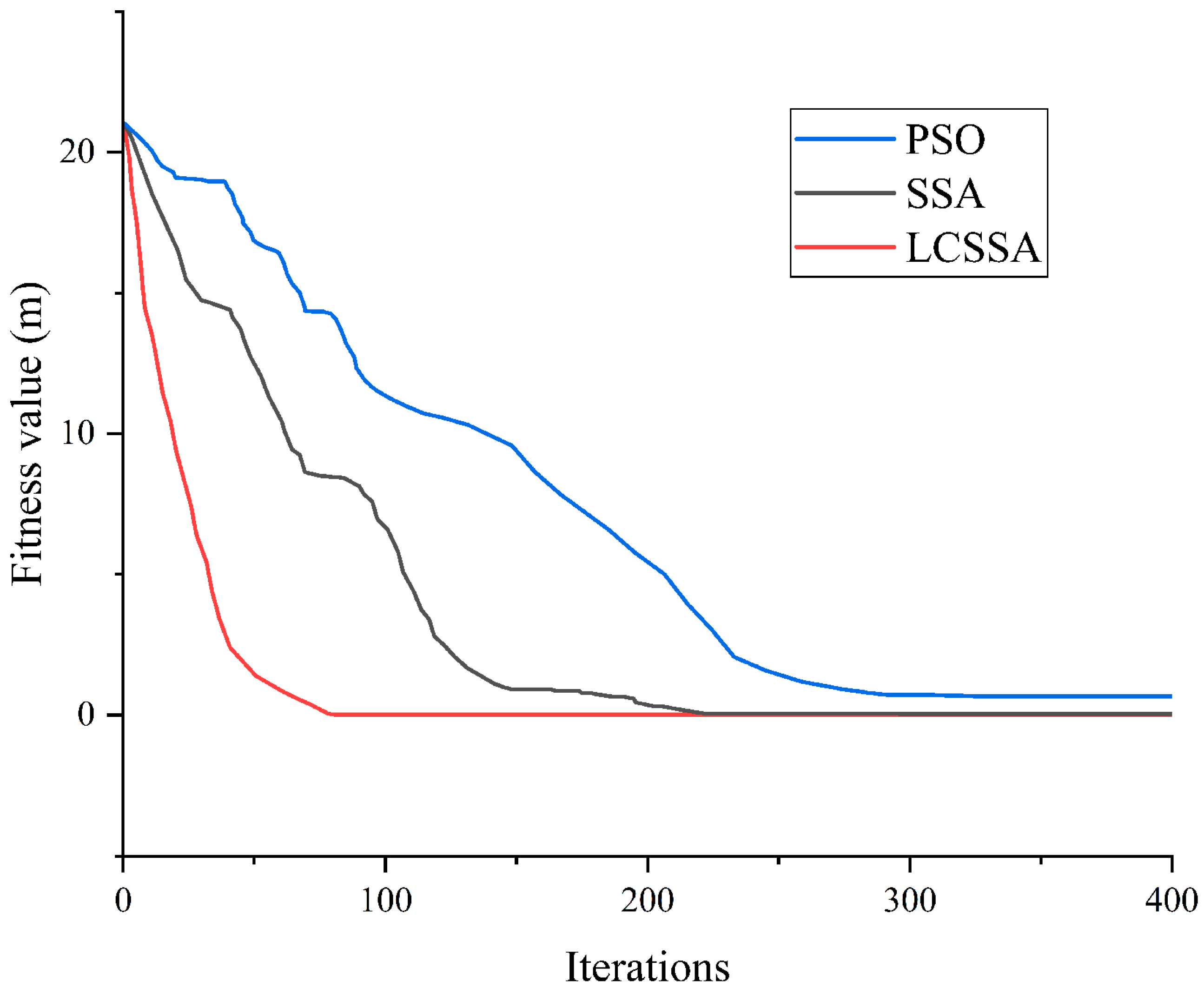
5.1. Case 1
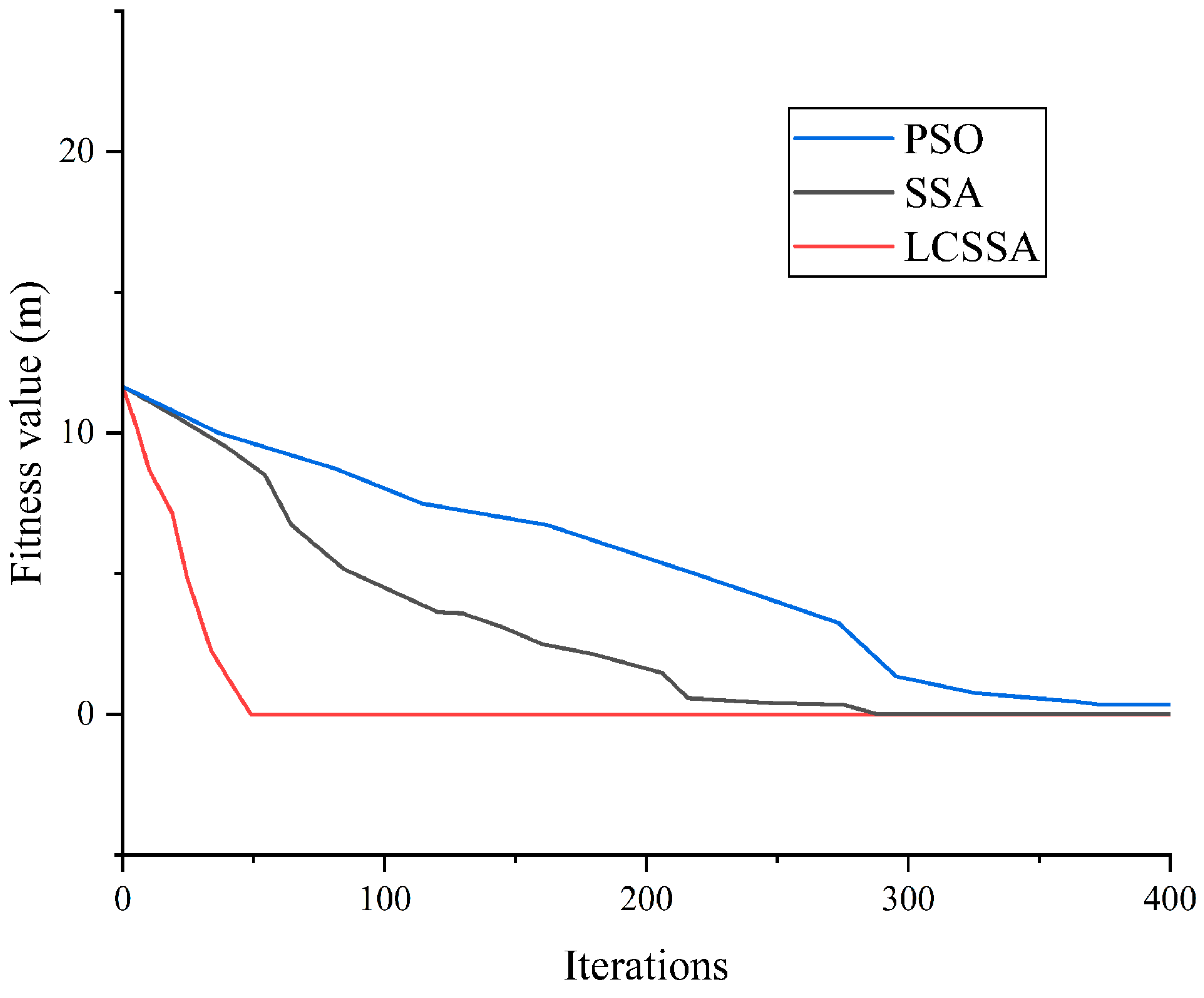
5.2. Case 2
5.3. Analysis of the Case
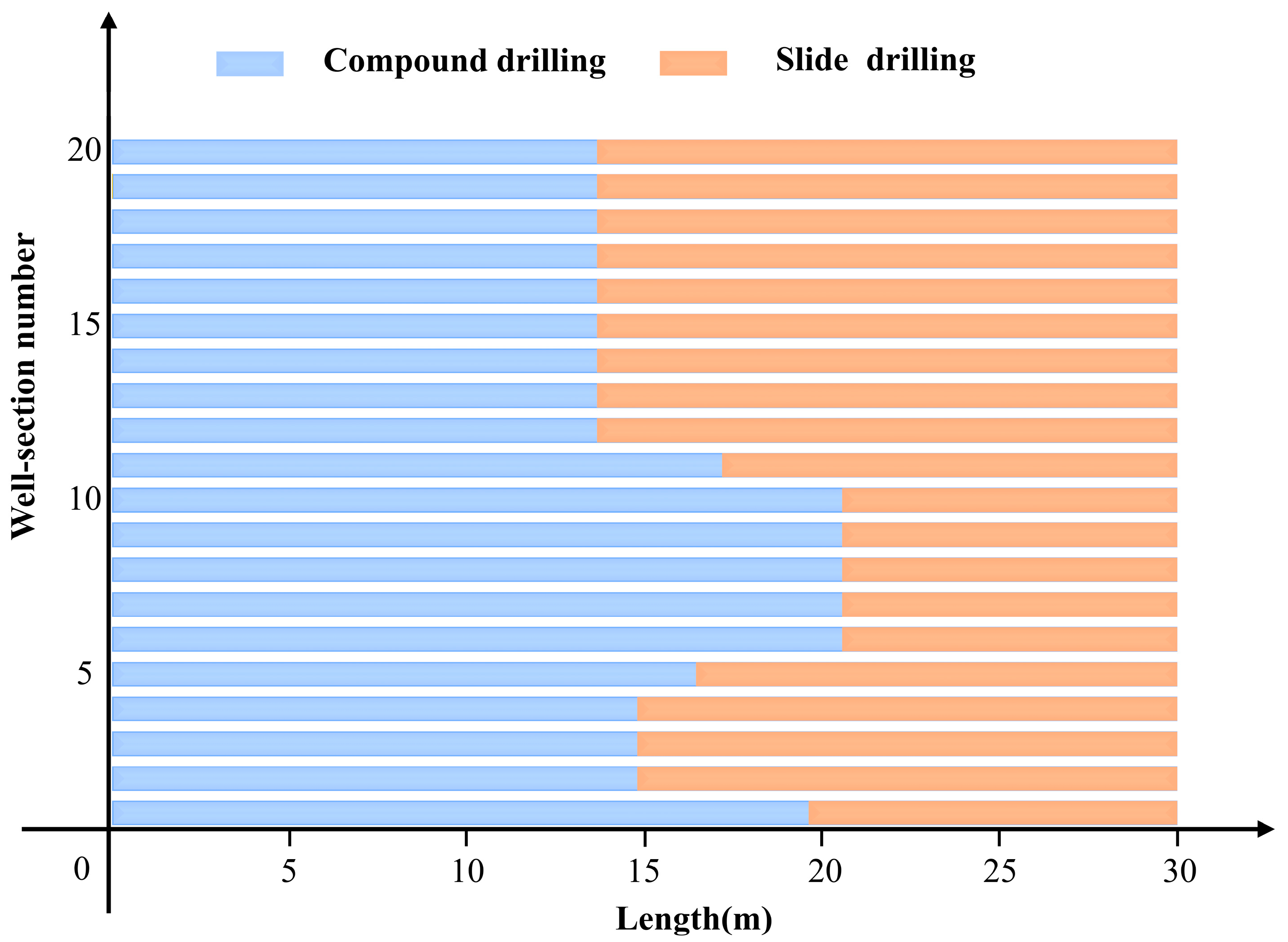
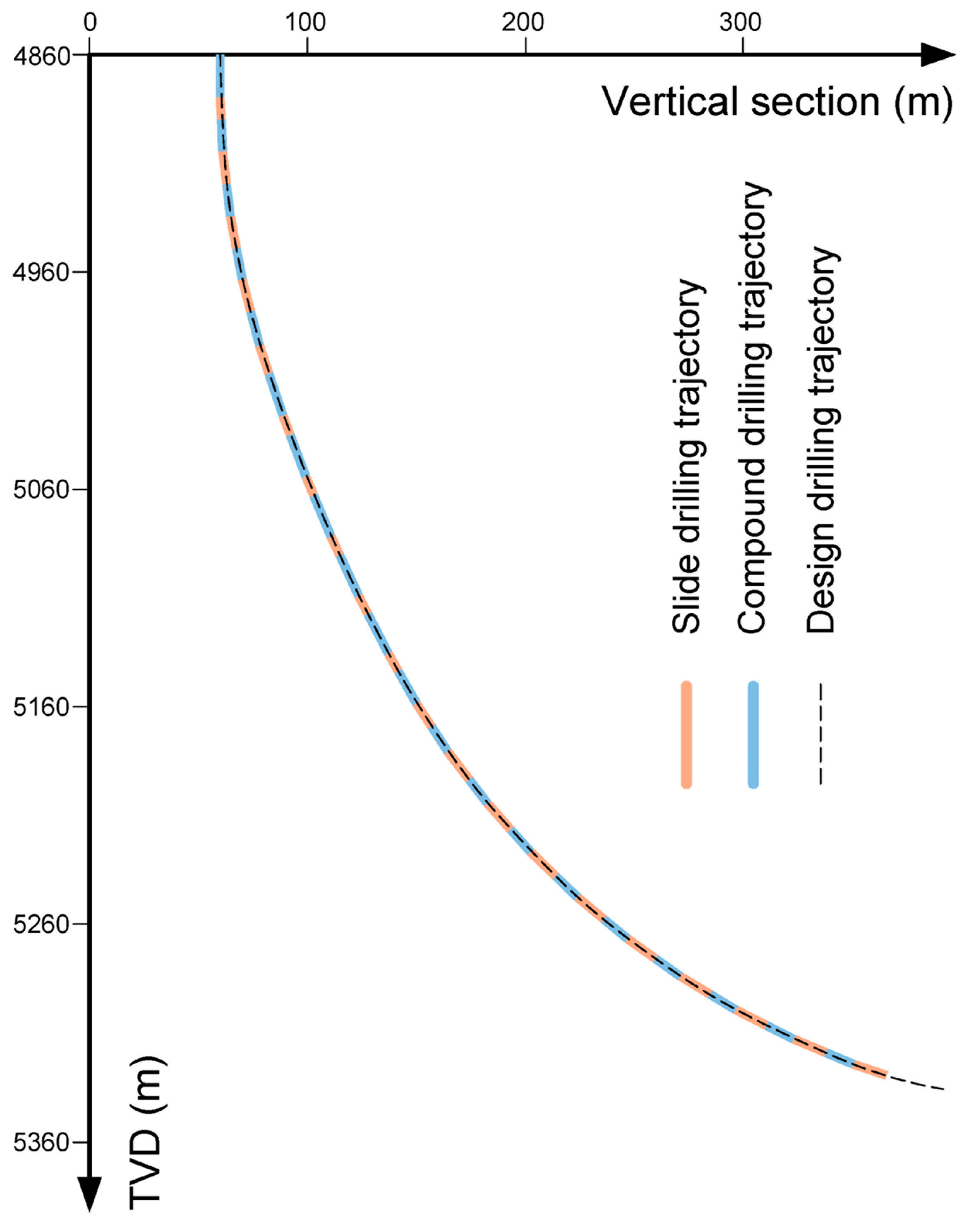
6. Field Application
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
References
- Han, Z.Y. Design and Calculation of Directional Drilling; China Petroleum University Press: Dongying, China, 2007. [Google Scholar]
- Liu, X.S. Geometry of Wellbore Trajectory; Petroleum Industry Press: Beijing, China, 2006. [Google Scholar]
- Coffey, S.; Groover, A. Achieving Automated Directional Drilling Across Us Onshore Basins. In Proceedings of the IADC/SPE International Drilling Conference and Exhibition, Galveston, TX, USA, 3–4 March 2020. [Google Scholar]
- Coffey, S.; Groover, A. Improvements in Slide Quality and Execution Speed Through Automation. In Proceedings of the 2019 AADE National Technical Conference and Exhibition, Denver, CO, USA, 9–10 April 2019. [Google Scholar]
- Pollock, J.; Stoecker-Sylvia, Z.; Veedu, V.; Panchal, N.; Elshahawi, H. Machine Learning for Improved Directional Drilling. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 2018. [Google Scholar]
- Zhao, Y.; Zalluhoglu, U.; Marck, J.; Demirer, N.; Morari, M. Model Predictive Control for Mud Motor Operation in Directional Drilling. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019. [Google Scholar]
- Zalluhoglu, U.; Gharib, H.; Marck, J.; Demirer, N.; Darbe, R. Steering Advisory System for Mud Motors. In Proceedings of the SPE/IADC International Drilling Conference and Exhibition, Hague, The Netherlands, 5–7 March 2019. [Google Scholar]
- Pehlivantürk, C.; D’angelo, J.; Cao, D.; Chen, D.; Ashok, P.; Van Oort, E. Slide Drilling Guidance System for Directional Drilling Path Optimization. In Proceedings of the SPE/IADC International Drilling Conference and Exhibition, Hague, The Netherlands, 5–7 March 2019. [Google Scholar]
- Pehlivantürk, C.; Chen, D.; Ashok, P.; van Oort, E. Path Advisory for Slide Drilling Using a Nonlinear Wellbore Propagation Model and Genetic Algorithm. J. Pet. Sci. Eng. 2019, 179, 734–741. [Google Scholar] [CrossRef]
- Angelo, J.D.; Khaled, M.S.; Ashok, P.; van Oort, E. Pareto Optimal Directional Drilling Advisory for Improved Real-Time Decision Making. J. Pet. Sci. Eng. 2022, 210, 110031. [Google Scholar] [CrossRef]
- Hausher, A.; Kern, S.; Chmela, W.; Cantwell, J.; Mims, K. Automated Sliding: Efficiencies Achieved in the Next Stage of Drilling Automation. In Proceedings of the IADC/SPE International Drilling Conference and Exhibition, Galveston, TX, USA, 3–4 March 2020. [Google Scholar]
- Yu, Y.; Chen, W.; Liu, Q.; Chau, M. Training an Automated Directional Drilling Agent with Deep Reinforcement Learning in a Simulated Environment. In Proceedings of the SPE/IADC International Drilling Conference and Exhibition, Stavanger, Norway, 8–12 March 2021. [Google Scholar]
- Braga, D.C.; Kamyab, M.; Joshi, D.; Harclerode, B.; Cheatham, C. Using Particle Swarm Optimization to Compute Hundreds of Possible Directional Paths to Get Back/Stay in the Drilling Window. In Proceedings of the 2021 SPE Annual Technical Conference and Exhibition, Dubai, United Arab Emirates, 21–23 September 2021. [Google Scholar]
- Joshi, D.R.; Kamyab, M.; Braga, D.C.; Cheatham, C.A. Real-Time Directional Guidance Through Cloud-Based Well Path Optimization. In Proceedings of the SPE/IADC International Drilling Conference and Exhibition, Stavanger, Norway, 7–9 March 2023. [Google Scholar]
- Wang, N.; Cheng, Z.; Lu, Y.; He, B.; Ren, G. Automated Slide Drilling System and Multi-Body Dynamics Aided Slide Drilling Simulation. In Proceedings of the SPE Digital Energy Conference and Exhibition, Woodlands, TX, USA, 3–5 March 2015. Society of Petroleum Engineers. [Google Scholar]
- Cheng, Z.B.; Ren, G.X.; Li, B.H.; He, B. Directional Drilling Dynamics and Control Theory Research and Application; China Petrochemical Press: Beijing, China, 2021. [Google Scholar]
- Lu, G.; Zhong, X.M.; Li, S.Z.; Lai, J.Q. A New Calculation Method of The Well Trajectory of Joint Control. Oil Drill. Prod. Technol. 2021, 43, 146–150, 159. [Google Scholar]
- Xue, J.; Shen, B. A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Li, J.; Wu, Y. Improved Sparrow Search Algorithm with the Extreme Learning Machine and Its Application for Prediction. Neural Process. Lett. 2022, 54, 4189–4209. [Google Scholar] [CrossRef]
- Li, J.Y.; Chen, J.; Shi, J. Evaluation of New Sparrow Search Algorithms with Sequential Fusion of Improvement Strategies. Comput. Ind. Eng. 2023, 182, 109425. [Google Scholar] [CrossRef]
- Le, M.H.; Li, J. Improved Sparrow Search Algorithm with Multi Strategy Fusion and Application in AGV Path Planning. Foreign Electron. Meas. Technol. 2024, 43, 129–139. [Google Scholar] [CrossRef]
- Ke, Y.T.; Wang, Z.; Wang, W.S. Path Planning Based on Integrated Composite Chaotic Adaptive Sparrow Search Algorithm. Modul. Mach. Tool Autom. Manuf. Tech. 2025, 6, 36–42, 48. [Google Scholar]
- Han, Z.Y. The New Techniques of Well Trajectory Design and Well Path Control Fit For 3d-Direction Wells. Pet. Drill. Tech. 2003, 31, 5. [Google Scholar]
- Fang, M.; Lu, G. Semi-Analytic Computing of Constant-Tool-Face-Angle Curves. J. Tongji Univ. (Nat. Sci.) 2008, 36, 844–848. [Google Scholar]
- Tang, X.; Hong, D.F.; Sheng, L.M.; Dou, X.R.; Wang, J. Planning Models and Solving Methods for a Well Path with Constant Tool Face Angle. Acta Pet. Sin. 2018, 39, 1193–1198. [Google Scholar]
- Lee, S.; Stephen, K.D. Field Application Study on Automatic History Matching Using Particle Swarm Optimization. In Proceedings of the SPE Reservoir Characterization and Simulation Conference and Exhibition, Abu Dhabi, United Arab Emirates, 17–19 September 2019. [Google Scholar] [CrossRef]
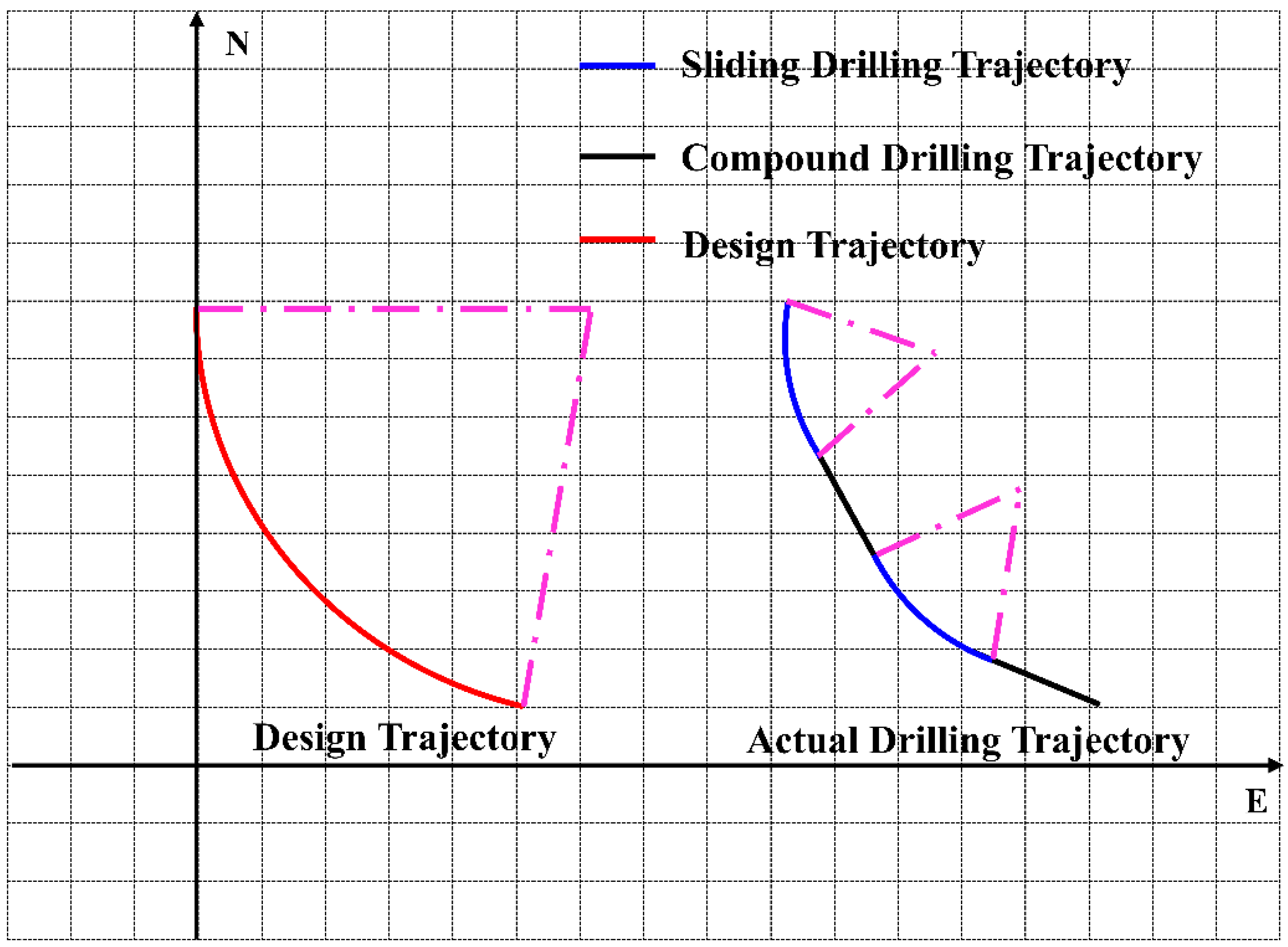



| Key Point | MD (m) | Inclination (°) | Azimuth (°) | North Increments (m) | East Increments (m) | TVD (m) |
|---|---|---|---|---|---|---|
| Beginning point | 0 | 30.0000 | 120.0000 | 0 | 0 | 0 |
| Endpoint | 30.0000 | 32.8049 | 128.9568 | −7.7384 | 12.8717 | 25.6080 |
| The Type of Algorithm | of the Objective Function (m) | Where the Minimum Value Occurs (m) |
|---|---|---|
| Algorithm 1—Full Search | 0.003560 | 21.060000 |
| Algorithm 2—PSO | 0.674400 | 22.171602 |
| Algorithm 3—SSA | 0.046675 | 21.098032 |
| Algorithm 4—LCSSA | 0.003558 | 21.059736 |
| Key Point | MD (m) | Inclination (°) | Azimuth (°) | North Increments (m) | East Increments (m) | TVD (m) | Borehole Curvature (°/30 m) |
|---|---|---|---|---|---|---|---|
| Beginning point | 2520.0000 | 29.5800 | 135.0000 | 0 | 0 | 0 | 6.9957 |
| Endpoint | 2550.0000 | 34.1900 | 124.3400 | −10.0985 | 12.1767 | 25.4664 |
| The Type of Algorithm | of the Objective Function (m) | Where the Minimum Value Occurs (m) |
|---|---|---|
| Algorithm 1—Full Search | 0.000879 | 18.180000 |
| Algorithm—2-PSO | 0.338750 | 16.673415 |
| Algorithm 3—SSA | 0.013856 | 18.517832 |
| Algorithm 4—LCSSA | 0.000882 | 18.179995 |
| Well Section Number | MD (m) | Inclination (°) | Azimuth (°) | TVD (m) | North Coordinate (m) | East Coordinate (m) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 4860 | 0 | 233.42 | 4860.00 | 0 | 0 |
| 2 | 4890 | 2.67 | 233.42 | 4889.99 | −0.28 | −0.37 |
| 3 | 4920 | 6.67 | 233.42 | 4919.89 | −1.73 | −2.33 |
| 4 | 4950 | 10.67 | 233.42 | 4949.54 | −4.43 | −5.96 |
| 5 | 4980 | 14.67 | 233.42 | 4978.80 | −8.34 | −11.24 |
| 6 | 5010 | 18.37 | 233.42 | 5007.54 | −13.46 | −18.14 |
| 7 | 5040 | 20.57 | 233.42 | 5035.82 | −19.42 | −26.17 |
| 8 | 5070 | 22.77 | 233.42 | 5063.70 | −26.02 | −35.06 |
| 9 | 5100 | 24.97 | 233.42 | 5091.14 | −33.26 | −44.81 |
| 10 | 5130 | 27.17 | 233.42 | 5118.08 | −41.11 | −55.40 |
| 11 | 5160 | 29.37 | 233.42 | 5144.50 | −49.58 | −66.80 |
| 12 | 5190 | 33.05 | 233.42 | 5170.21 | −58.78 | −79.21 |
| 13 | 5220 | 37.33 | 233.42 | 5194.73 | −69.08 | −93.09 |
| 14 | 5250 | 41.62 | 233.42 | 5217.88 | −80.45 | −108.40 |
| 15 | 5280 | 45.90 | 233.42 | 5239.54 | −92.81 | −125.06 |
| 16 | 5310 | 50.18 | 233.42 | 5259.60 | −106.10 | −142.97 |
| 17 | 5340 | 54.46 | 233.42 | 5277.93 | −120.25 | −162.03 |
| 18 | 5370 | 58.75 | 233.42 | 5294.44 | −135.17 | −182.14 |
| 19 | 5400 | 63.03 | 233.42 | 5309.03 | −150.79 | −203.18 |
| 20 | 5430 | 67.31 | 233.42 | 5321.62 | −167.01 | −225.04 |
| 21 | 5460 | 71.60 | 233.42 | 5332.15 | −183.74 | −247.59 |
| Section Number of the Well | Percent of Slide Drilling (%) | Sliding Drilling Length (m) | Deviation (m) |
|---|---|---|---|
| 1 | 34.59 | 10.38 | 0.000801 |
| 2 | 50.67 | 15.20 | 0.003759 |
| 3 | 50.67 | 15.20 | 0.003759 |
| 4 | 50.67 | 15.20 | 0.003759 |
| 5 | 45.18 | 13.55 | 0.001943 |
| 6 | 31.45 | 9.44 | 0.000502 |
| 7 | 31.45 | 9.44 | 0.000502 |
| 8 | 31.45 | 9.44 | 0.000502 |
| 9 | 31.45 | 9.44 | 0.000502 |
| 10 | 31.45 | 9.44 | 0.000502 |
| 11 | 42.73 | 12.82 | 0.000242 |
| 12 | 54.49 | 16.35 | 0.000946 |
| 13 | 54.49 | 16.35 | 0.000946 |
| 14 | 54.49 | 16.35 | 0.000946 |
| 15 | 54.49 | 16.35 | 0.000946 |
| 16 | 54.49 | 16.35 | 0.000946 |
| 17 | 54.49 | 16.35 | 0.000946 |
| 18 | 54.49 | 16.35 | 0.000946 |
| 19 | 54.49 | 16.35 | 0.000946 |
| 20 | 54.49 | 16.35 | 0.000946 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, H.; Long, Y.; Li, Q.; Zhao, T.; Wu, X. Intelligent Optimization of Single-Stand Control in Directional Drilling with Single-Bent-Housing Motors. Processes 2025, 13, 2593. https://doi.org/10.3390/pr13082593
Yin H, Long Y, Li Q, Zhao T, Wu X. Intelligent Optimization of Single-Stand Control in Directional Drilling with Single-Bent-Housing Motors. Processes. 2025; 13(8):2593. https://doi.org/10.3390/pr13082593
Chicago/Turabian StyleYin, Hu, Yihao Long, Qian Li, Tong Zhao, and Xianzhu Wu. 2025. "Intelligent Optimization of Single-Stand Control in Directional Drilling with Single-Bent-Housing Motors" Processes 13, no. 8: 2593. https://doi.org/10.3390/pr13082593
APA StyleYin, H., Long, Y., Li, Q., Zhao, T., & Wu, X. (2025). Intelligent Optimization of Single-Stand Control in Directional Drilling with Single-Bent-Housing Motors. Processes, 13(8), 2593. https://doi.org/10.3390/pr13082593






