Data-Driven Multi-Mode Adaptive Control for Distribution Networks with Multi-Region Coordination
Abstract
1. Introduction
- (1)
- A data-driven, multi-region coordinated control framework is proposed to rapidly respond to DG fluctuations. By fully leveraging multi-source measurement data, the proposed framework effectively addresses the issue of incomplete or unavailable line parameters. Moreover, through information exchange between adjacent regions and the construction of equivalent control variables, multi-region coordinated control is achieved, thereby reducing computational and communication burdens.
- (2)
- To address the heterogeneous operational requirements of distribution networks, a regional multi-mode adaptive control model is proposed. Based on voltage and current measurement data and using dynamic linearization, data models for four control modes are established: voltage control, load balancing, economic operation, and mixed control. Regions can adaptively switch between these control modes according to actual operating conditions, thereby meeting diverse control needs under different scenarios and significantly enhancing flexible operation performance of distribution network.
2. Methodology
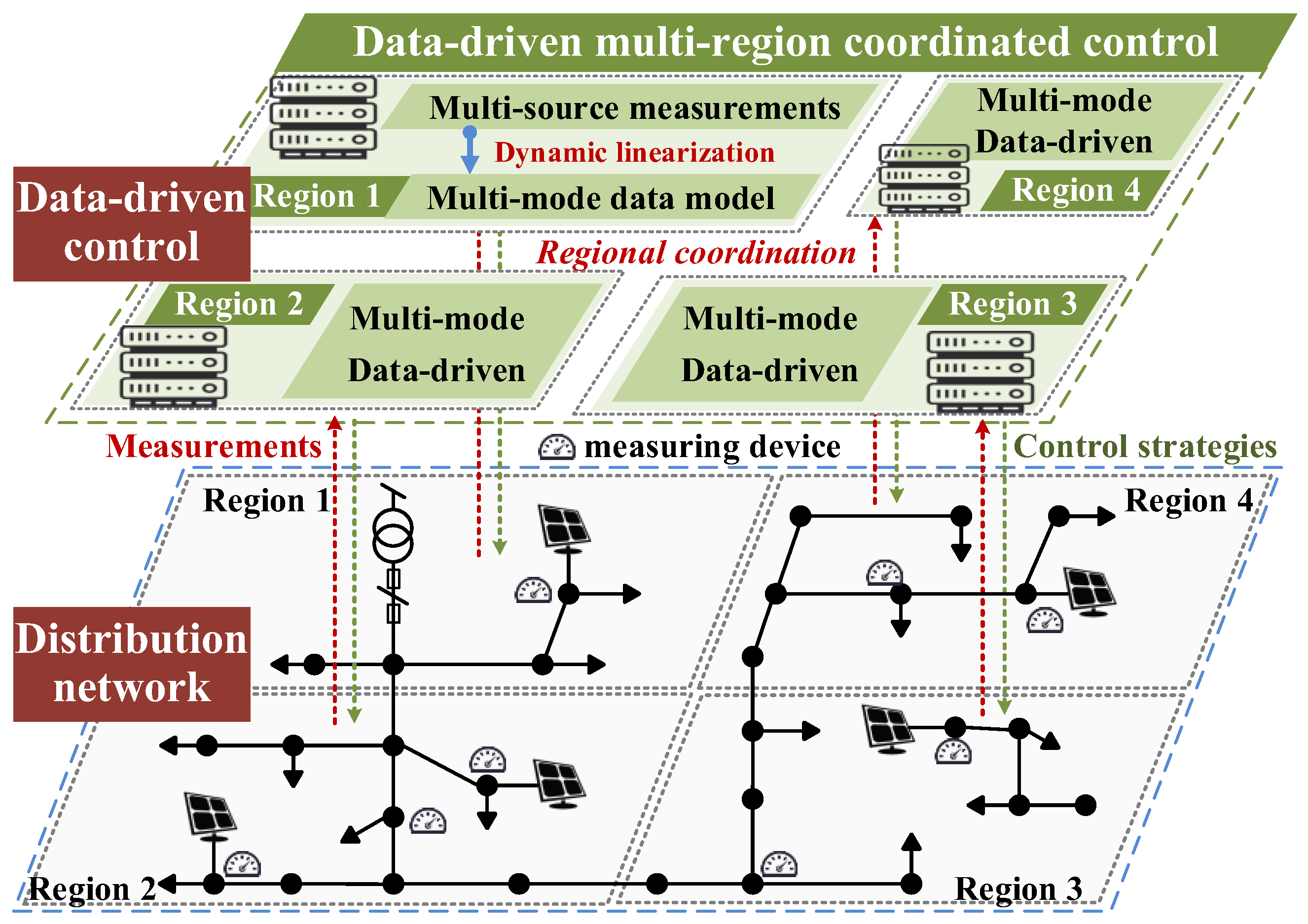
2.1. Framework of Data-Driven Multi-Region Coordinated Control
- (1)
- Each region of the distribution network acquires measurements of nodes and lines, including current, voltage, and power. Subsequently, regions exchange this measurement information with adjacent regions and construct a control mapping matrix using dynamic linearization to approximate the linear relationship between regional inputs and outputs.
- (2)
- Each region establishes a multi-mode adaptive control model to reduce deviation from the operating states of adjacent regions and DG output variation. The objective function is solved in parallel via gradient descent to obtain reactive power control strategies for the DGs, thereby effectively reducing computational and communication burdens.
- (3)
- Based on the actual operational requirements of different regions, four control modes are defined: voltage control, load balancing, economic operation, and mixed control. Each region adaptively selects the appropriate mode according to its operating conditions with the shared measurement data, thereby enhancing the overall operational flexibility of the distribution network.
2.2. Models of Multi-Mode Adaptive Control
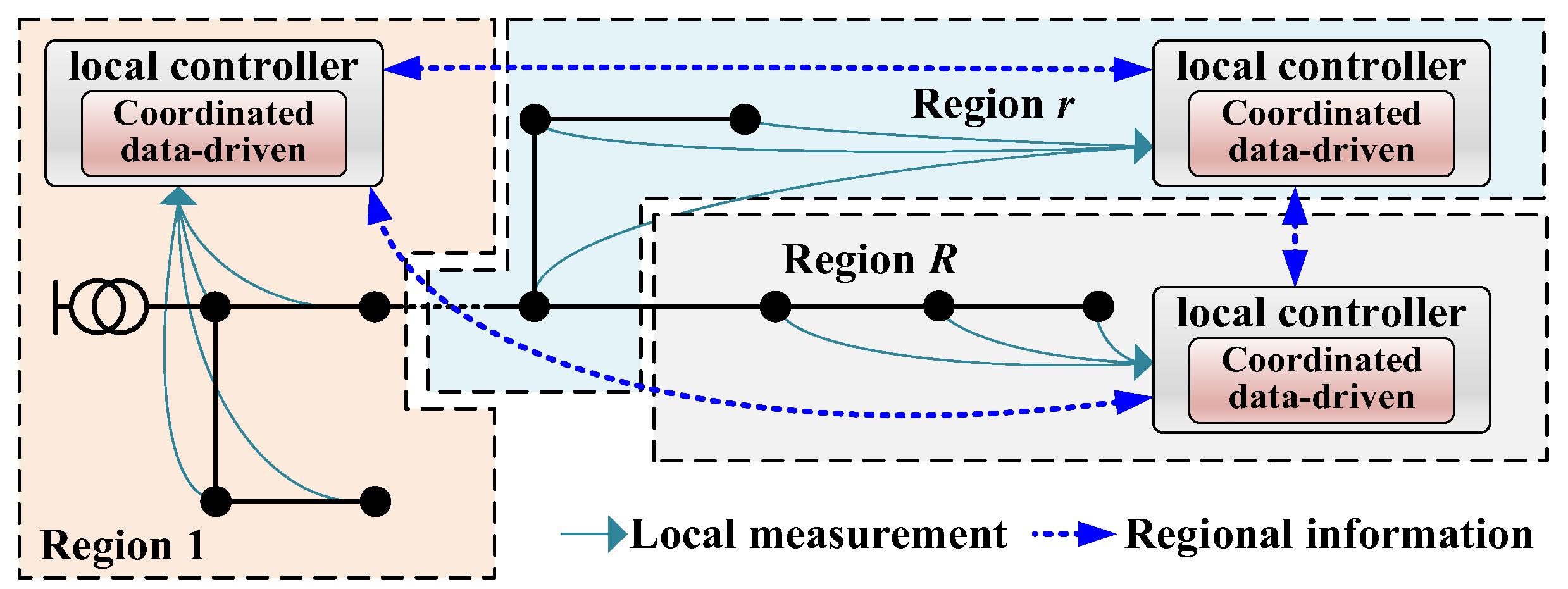
2.2.1. Principles of Regional Partitioning
- (1)
- Regions should be delineated according to the actual topological structure or geographical location, with the number of nodes in each region kept as balanced as possible. This approach helps equalize the computation time across regions and thereby reduces the overall computational duration.
- (2)
- Each region must include at least one local controller responsible for aggregating measurement data, performing local computation, and supporting decision-making. The placement of measurement terminals must guarantee the observability of the network within each region.
- (3)
- Adjacent regions should be connected by lines without overlapping nodes. Each pair of adjacent regions shares the measurement information of the boundary lines.
2.2.2. Regional Dynamic Linearization
2.2.3. Multi-Mode Data Model
- (1)
- Mode I: Voltage Control Mode
- (2)
- Mode II: Load Balancing Mode
- (3)
- Mode III: Economic Operation Mode
- (4)
- Mode IV: Mixed Control Mode
- (5)
- Objective function in multi-mode
2.3. Solution for Data-Driven Control Strategy
2.3.1. Mode Mapping Matrix Update
2.3.2. Distributed Solution of Control Strategies
2.3.3. Implementation of Control Strategies
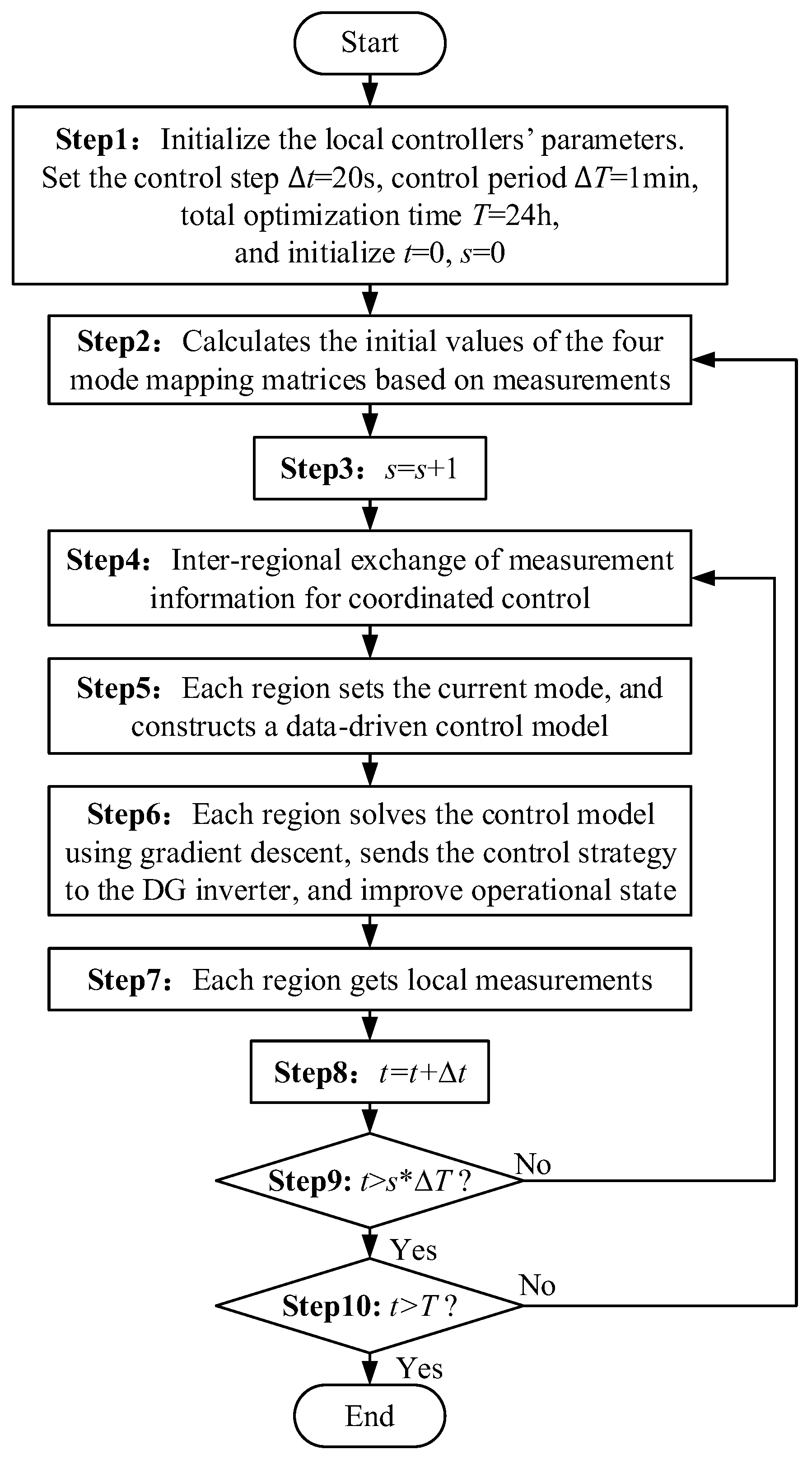
- (1)
- The control device in each region initializes the parameters, as shown in Step1.
- (2)
- The regional measurement devices collect voltage and current data and use them to calculate the initial values of the four mode mapping matrices, as shown in Step2.
- (3)
- Each region exchanges information with its adjacent regions to establish a data-driven model. These models are solved in a distributed manner, and the resulting reactive power control strategies for DGs are sent to their corresponding inverters, thereby improving the operational state, as shown from Step3 to Step6.
- (4)
- Each region acquires new voltage and current measurements, as shown in Step7.
- (5)
- Each region initiates a new control cycle based on the updated measurement data, as shown in Step8, returning to Step2. This iterative process continues until the system operational control t reaches the preset total time T, as shown in Step10 until End.
3. Case Studies and Analysis
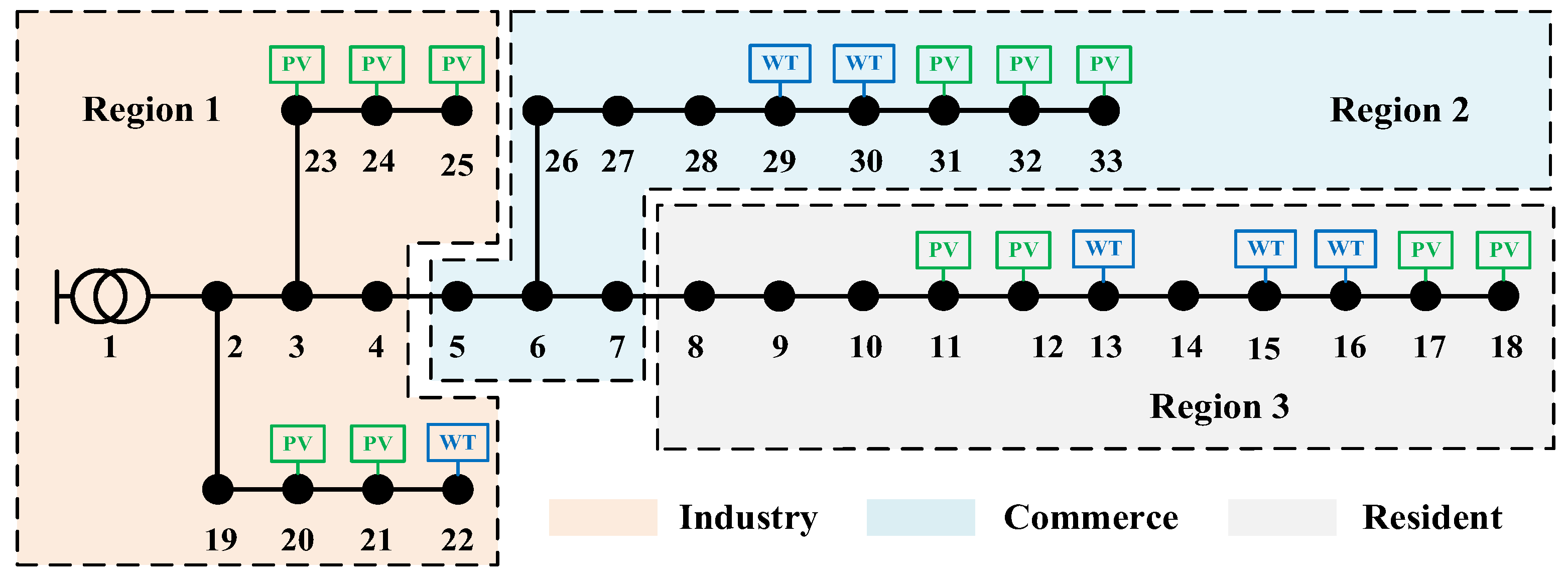
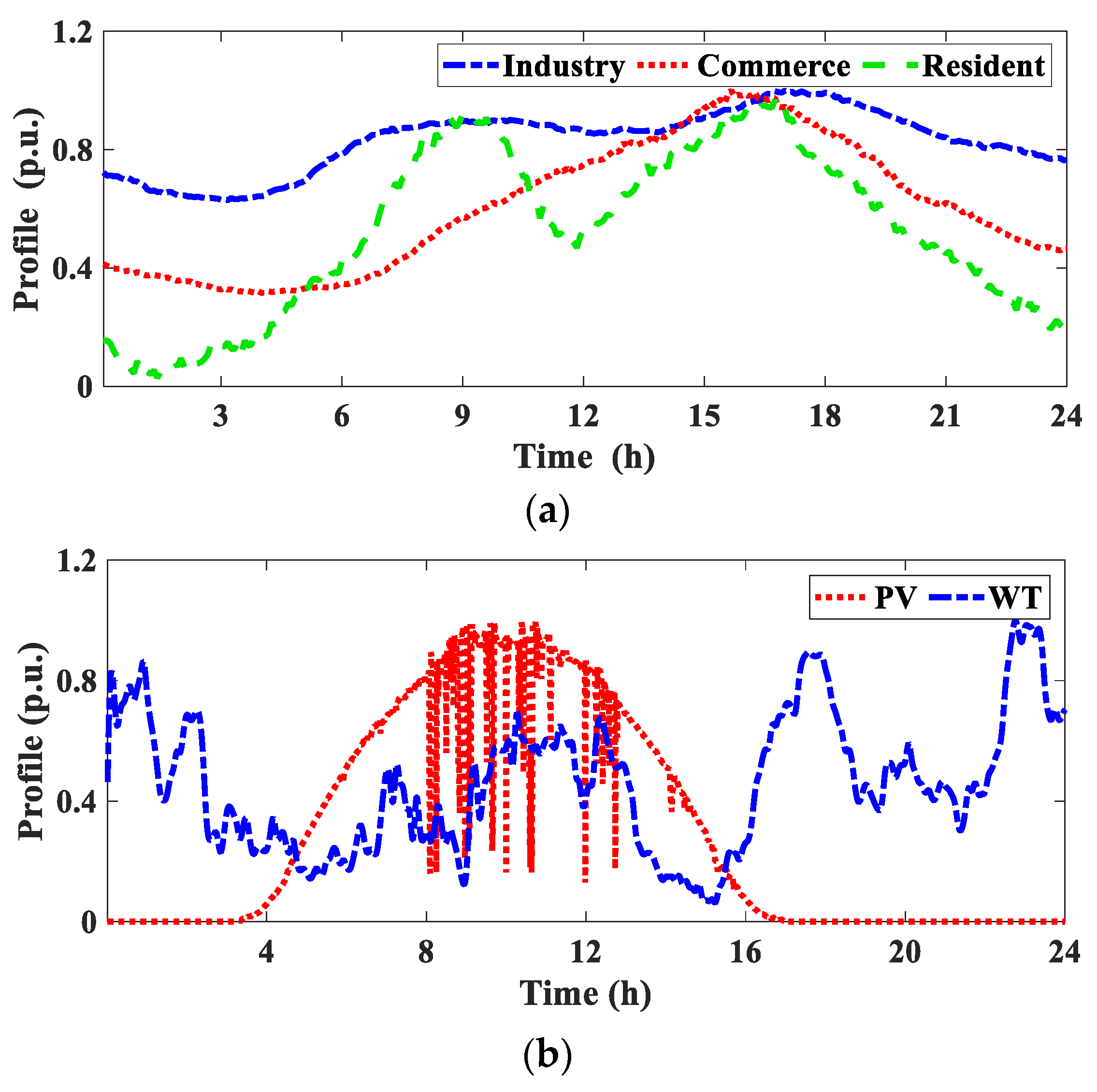
3.1. Modified IEEE 33-Node Distribution Network
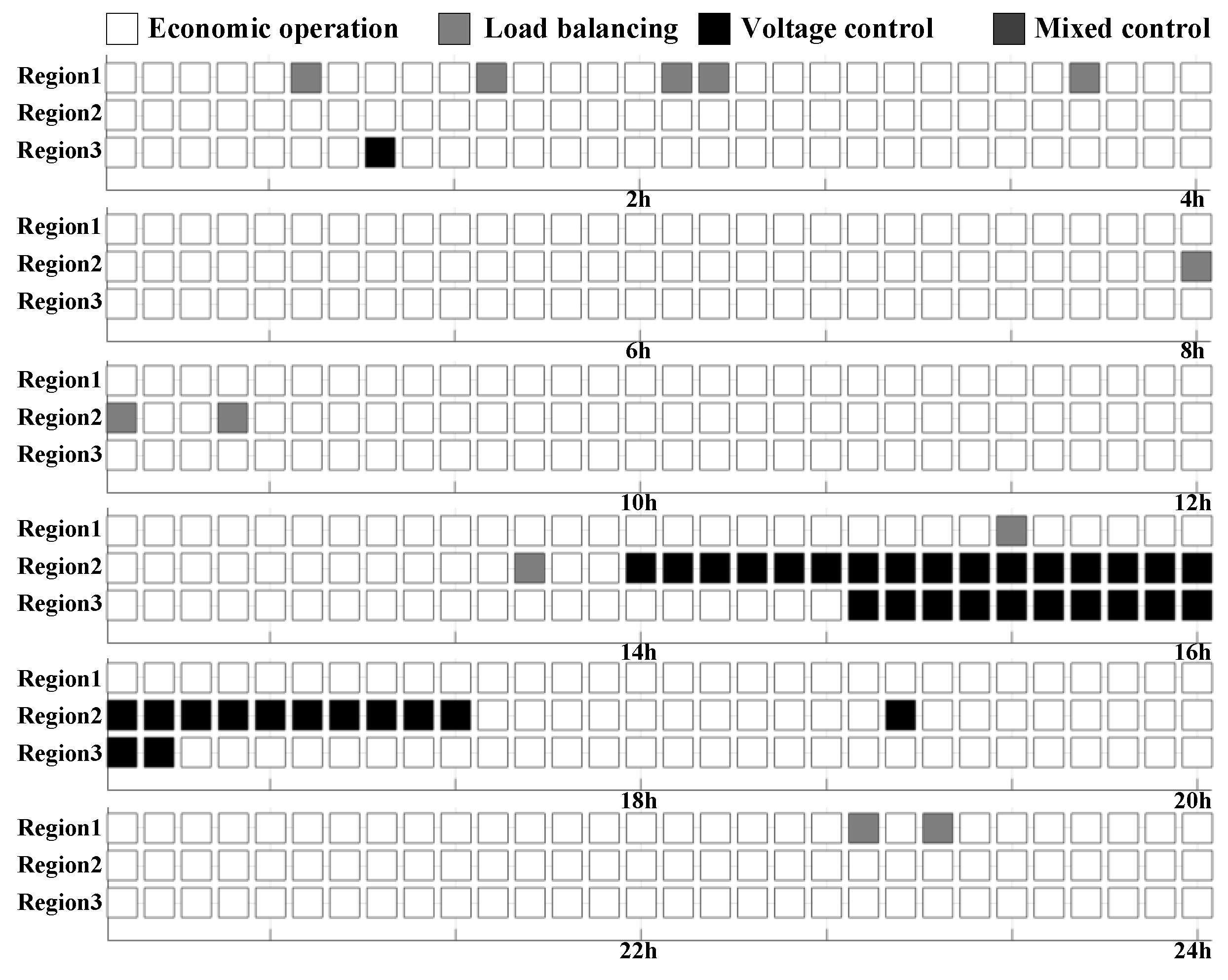
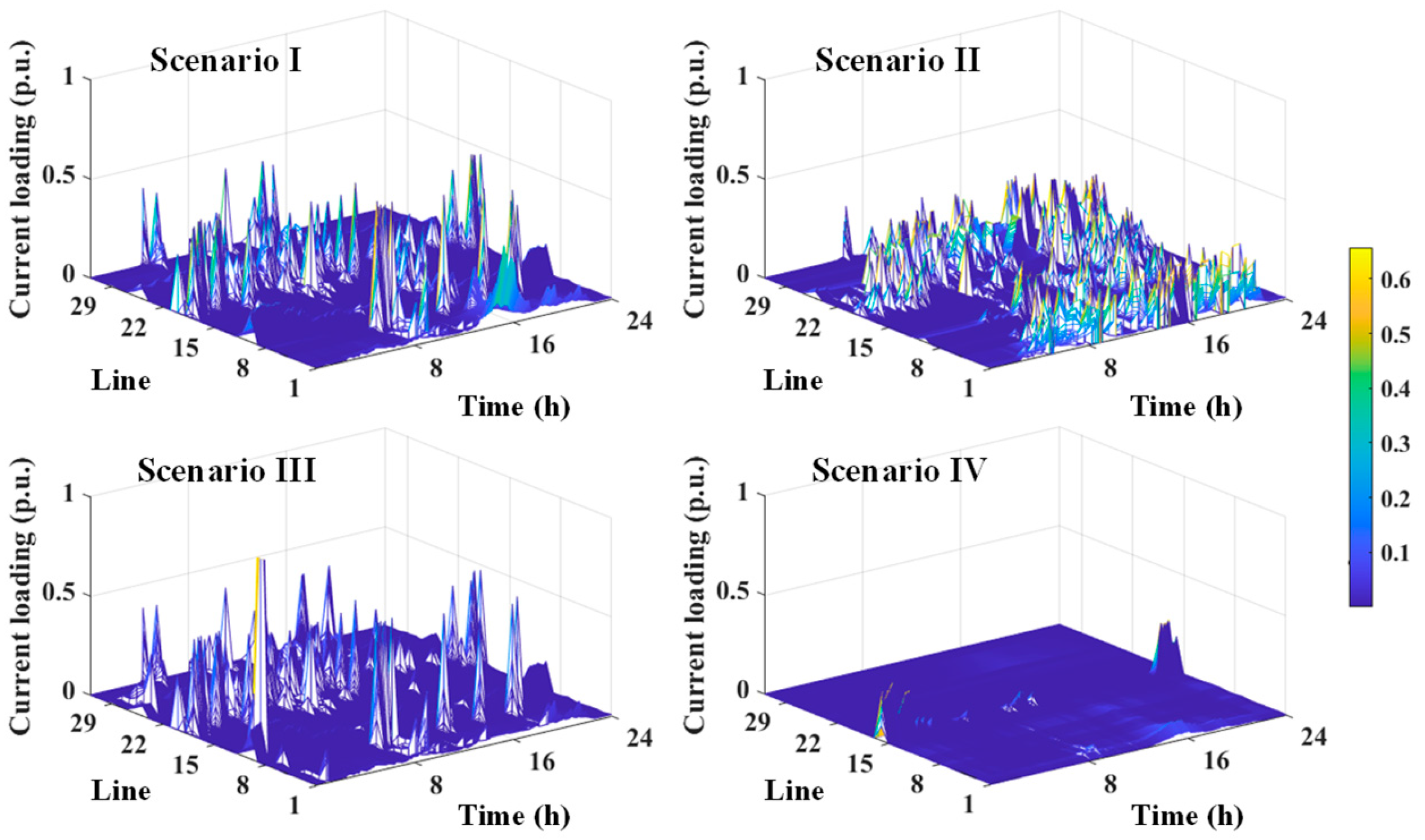
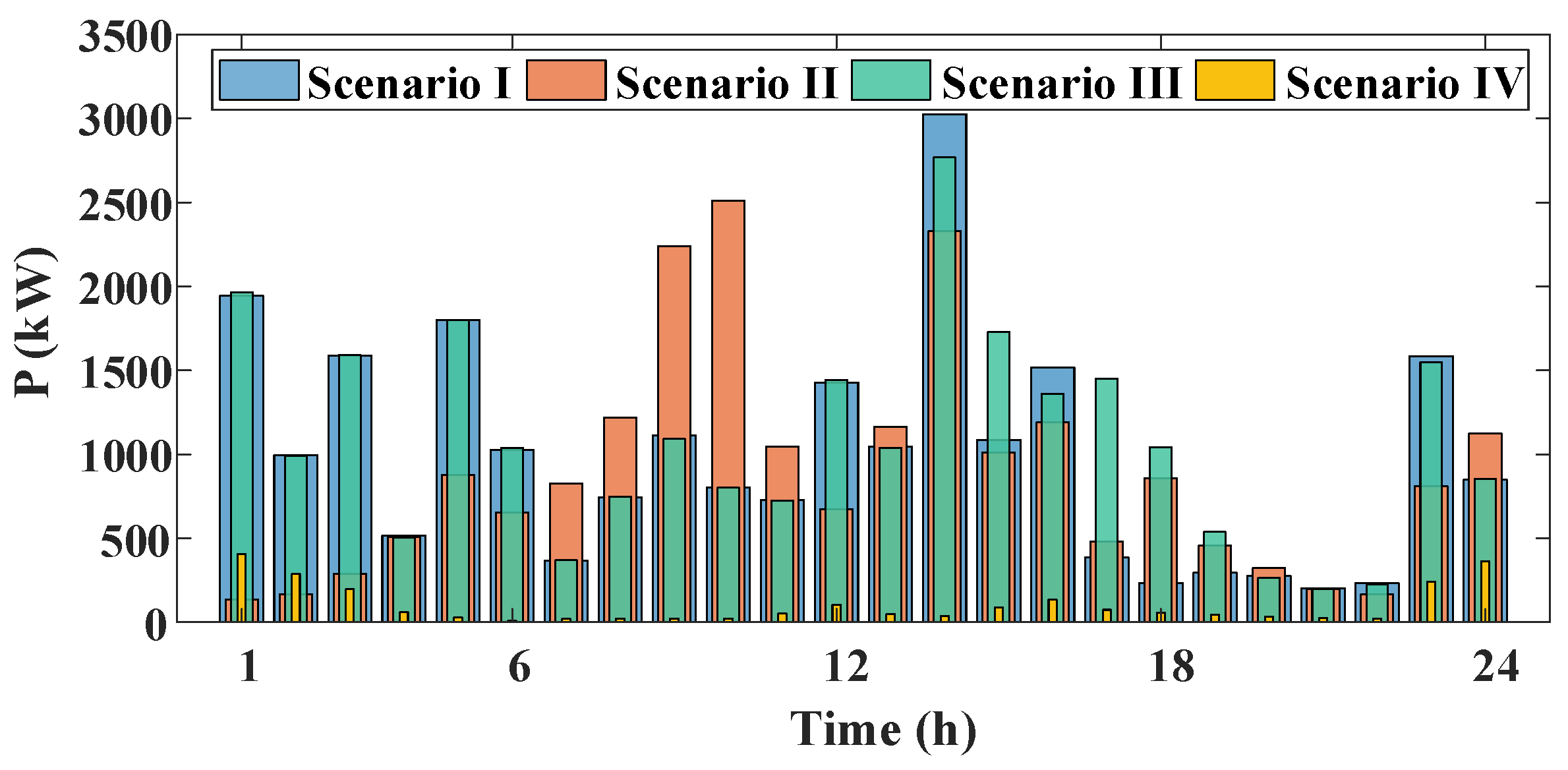
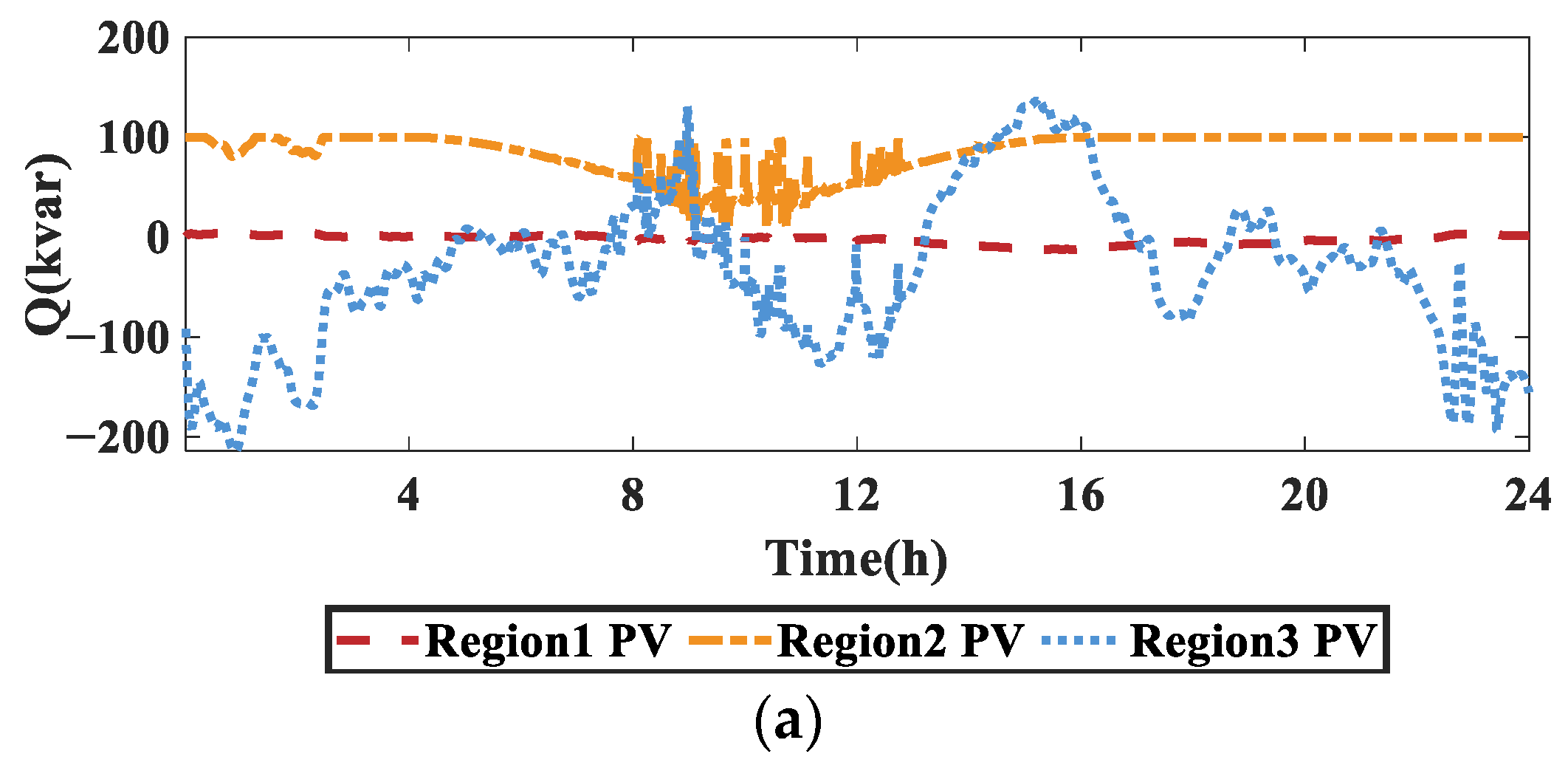
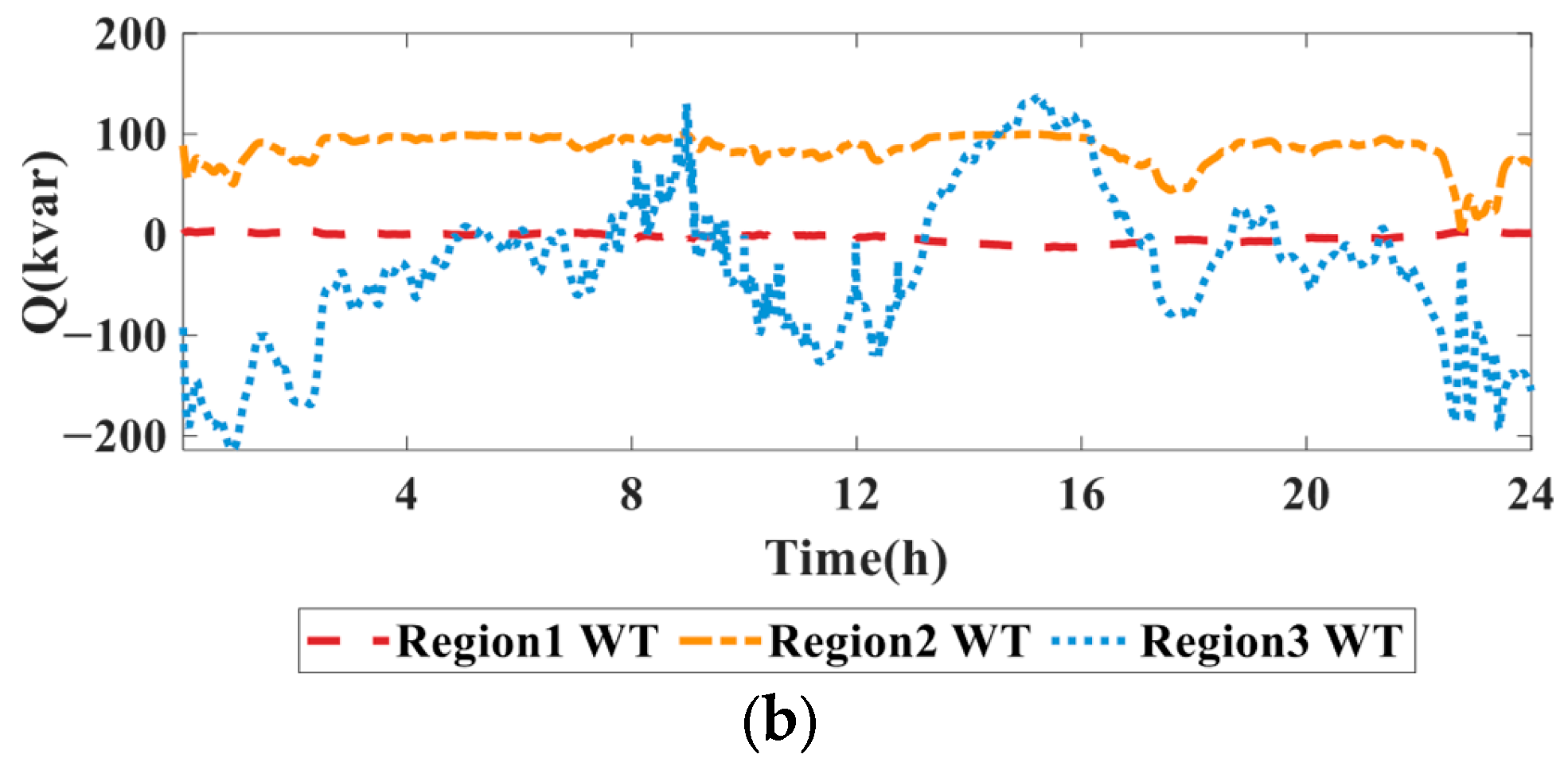
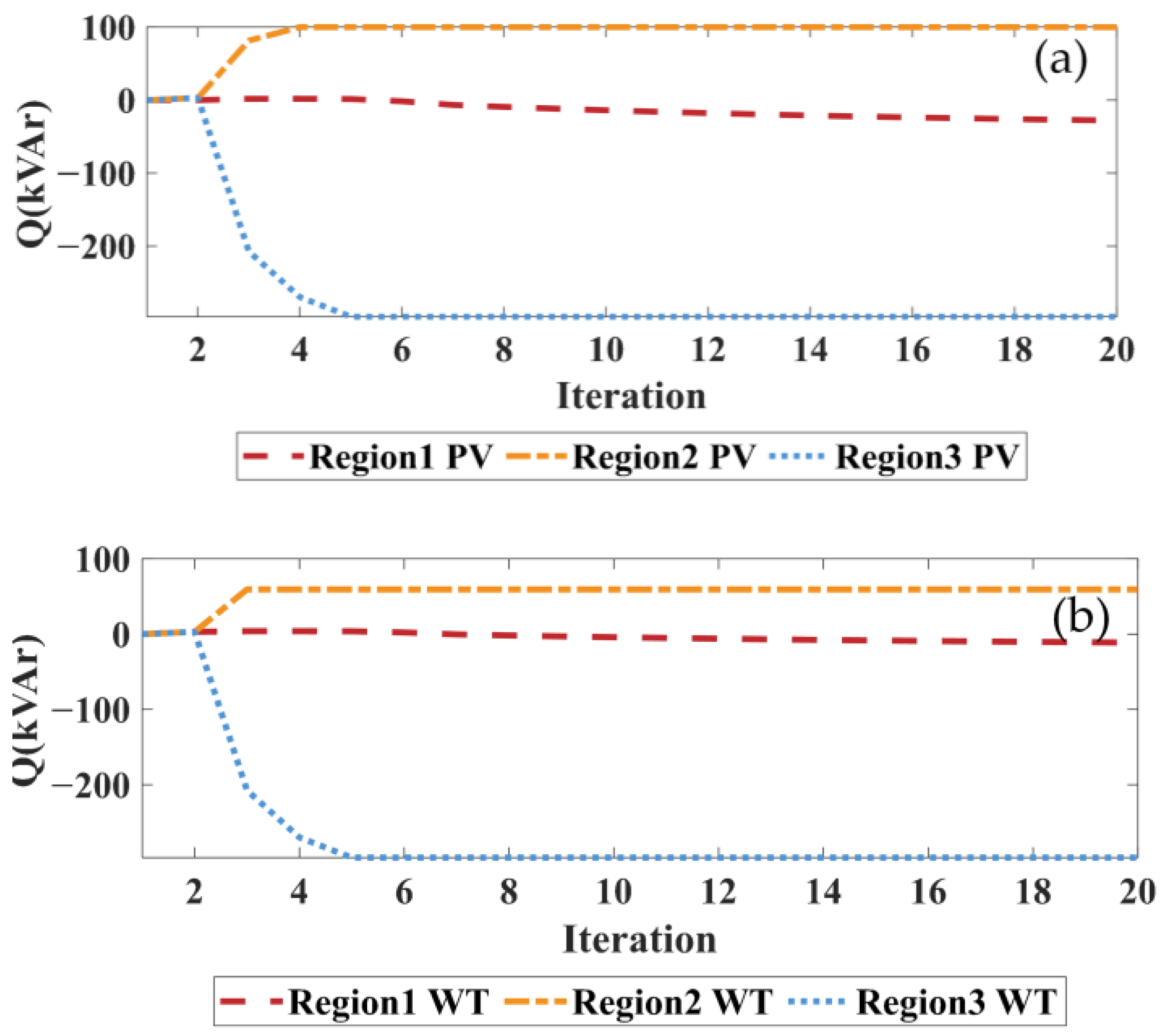
3.2. Multi-Mode Control Effect Analysis
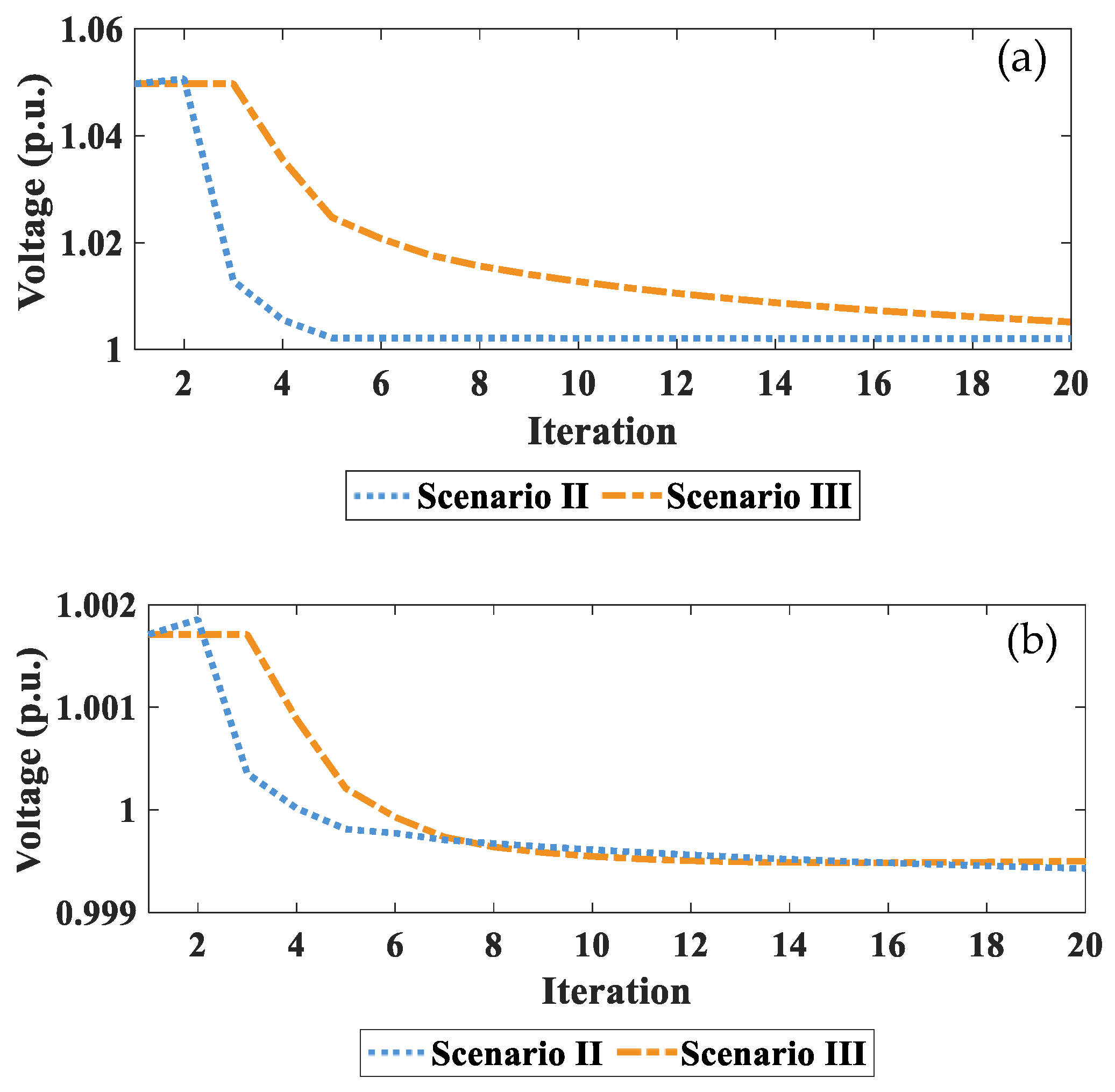
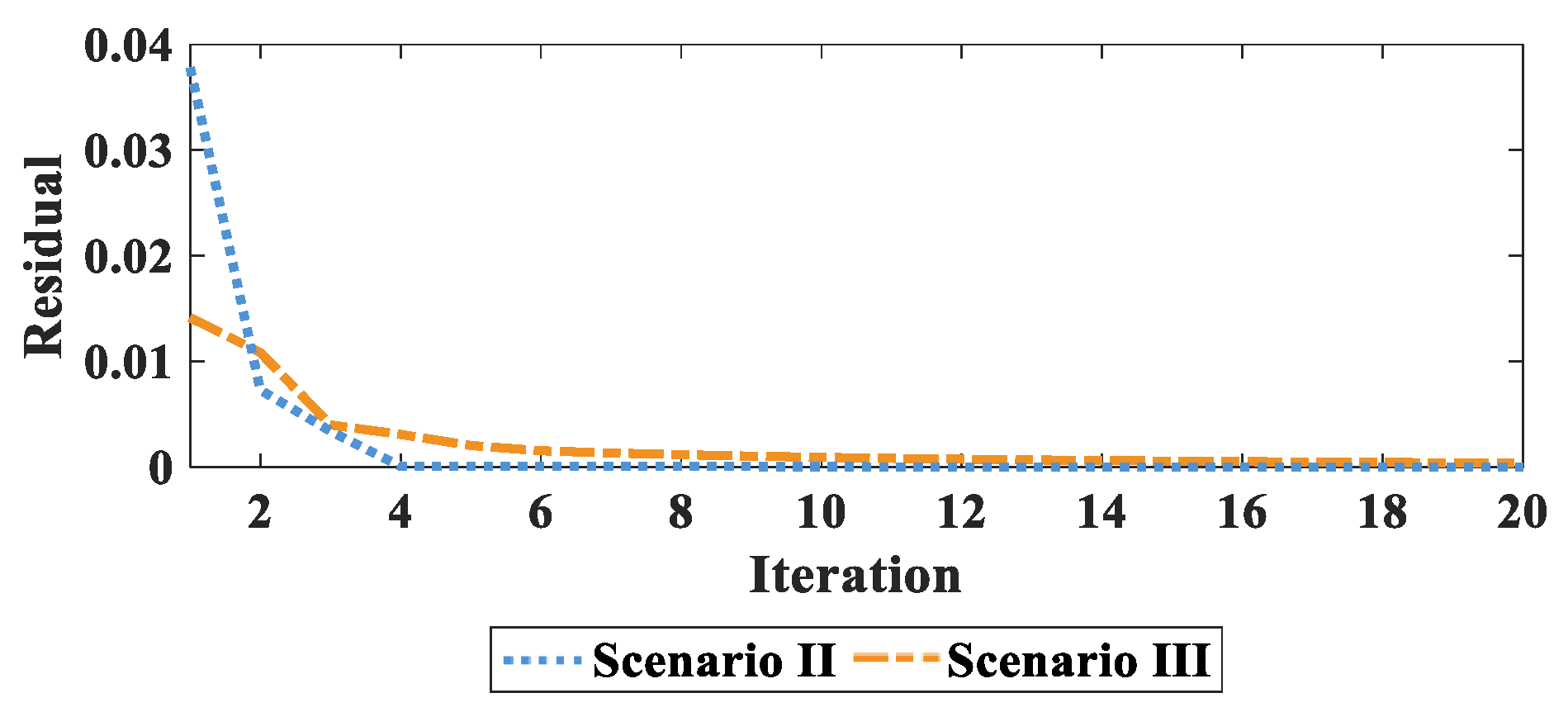
3.3. Computational Efficiency Analysis
3.4. Robustness Analysis
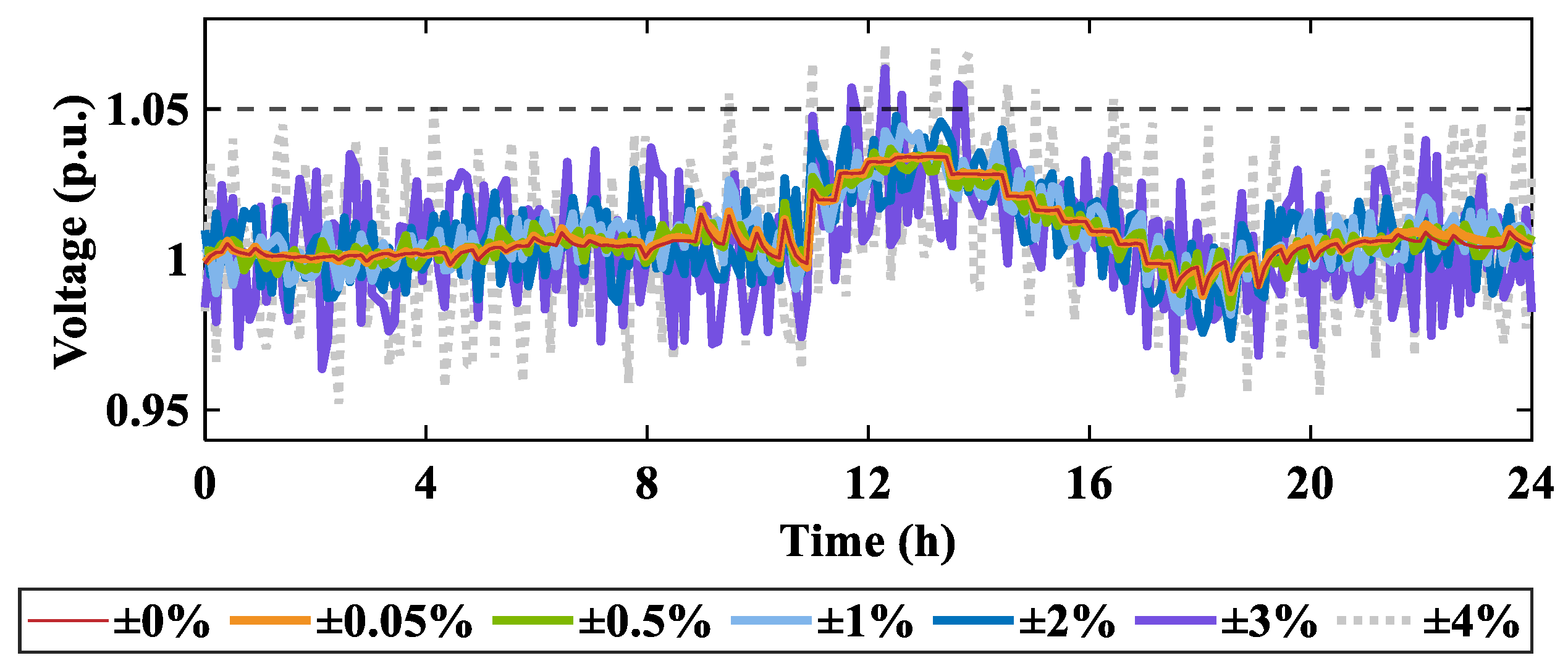
3.4.1. Robustness to Measurement Errors
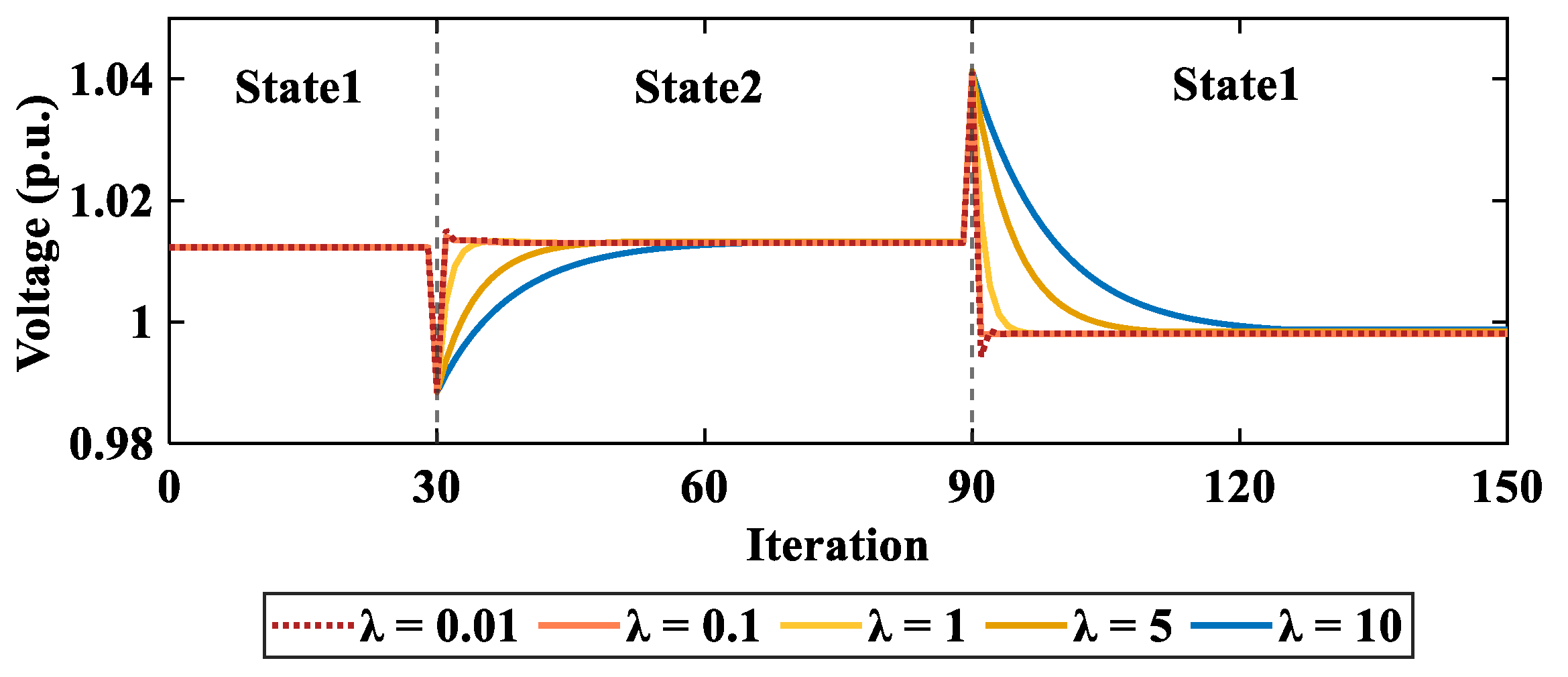
3.4.2. Adaptability to Voltage Sudden Changes
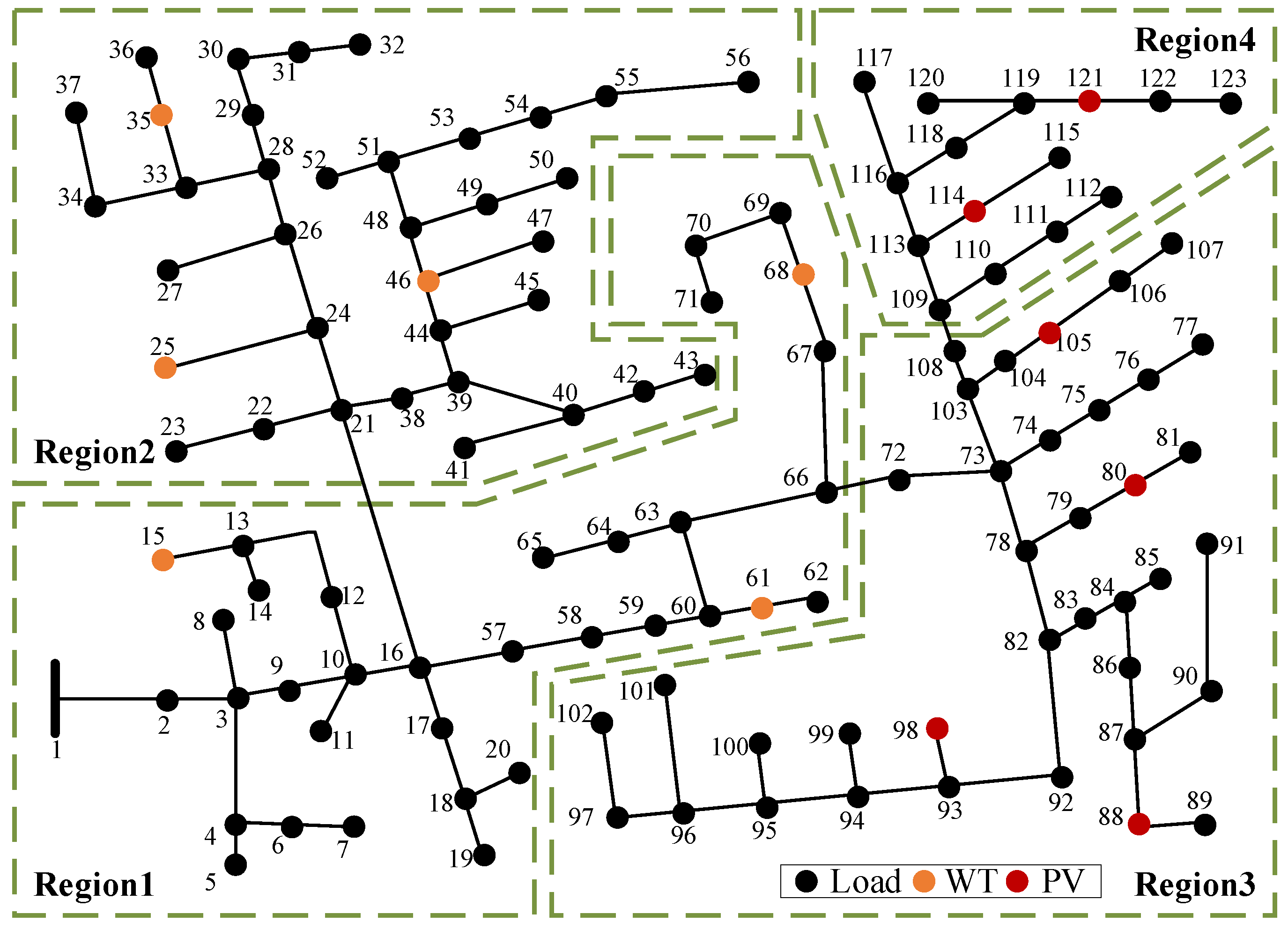
3.5. Scalability Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Luo, Y.; Tian, P.; Yan, X.; Xiao, X.; Ci, S.; Zhou, Q.; Yang, Y. Energy Storage Dynamic Configuration of Active Distribution Networks-Joint Planning of Grid Structures. Processes 2024, 12, 79. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, L.; Cai, Y.; Peng, Z.; Shi, L.; Li, X. Analysis of Line Loss Change Trend of Large-scale New Energy Access Distribution Network Under New Power System. Power Syst. Big Data 2024, 27, 11–22. (In Chinese) [Google Scholar] [CrossRef]
- Haider, R.; Annaswamy, A.M. A Hybrid Architecture for Volt-Var Control in Active Distribution Grids. Appl. Energy 2022, 312, 118735. [Google Scholar] [CrossRef]
- Yao, Q.; Li, X. Active-reactive Power Coordinated Optimization Control Method of Rural Power Distribution System with High Proportion of Distributed Resources. Power Syst. Big Data 2024, 27, 19–30. [Google Scholar] [CrossRef]
- Yuan, W.; Yuan, X.; Xu, L.; Zhang, C.; Ma, X. Harmonic Loss Analysis of Low-Voltage Distribution Network Integrated with Distributed Photovoltaic. Sustainability 2023, 15, 4334. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, P.; Ji, H.; Yu, H.; Zhao, J.; Xi, W.; Wu, J. Adaptive Voltage Control of Inverter-Based DG in Active Distribution Networks with Measurement-Strategy Mapping Matrix. IEEE Trans. Sustain. Energy 2025, 16, 1238–1252. [Google Scholar] [CrossRef]
- Zhou, H.; Liang, J.; Du, X.; Wu, M. Multi-Timescale Reactive Power Optimization and Regulation Method for Distribution Networks Under a Multi-Source Interaction Environment. Processes 2024, 12, 2254. [Google Scholar] [CrossRef]
- Aboshady, F.M.; Pisica, I.; Zobaa, A.F.; Taylor, G.A.; Ceylan, O.; Ozdemir, A. Reactive Power Control of PV Inverters in Active Distribution Grids with High PV Penetration. IEEE Access 2023, 11, 81477–81496. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, Y.; Dong, Z.; Ravishankar, J. Three-Stage Robust Inverter-Based Voltage/Var Control for Distribution Networks with High-Level PV. IEEE Trans. Smart Grid 2019, 10, 782–793. [Google Scholar] [CrossRef]
- Xu, R.; Zhang, C.; Xu, Y.; Dong, Z.; Zhang, R. Multi-Objective Hierarchically-Coordinated Volt/Var Control for Active Distribution Networks with Droop-Controlled PV Inverters. IEEE Trans. Smart Grid 2022, 13, 998–1011. [Google Scholar] [CrossRef]
- Jiao, W.; Chen, J.; Wu, Q.; Li, C.; Zhou, B.; Huang, S. Distributed Coordinated Voltage Control for Distribution Networks with DG and OLTC Based on MPC and Gradient Projection. IEEE Trans. Power Syst. 2022, 37, 680–690. [Google Scholar] [CrossRef]
- Li, P.; Ji, H.; Wang, C.; Zhao, J.; Song, G.; Ding, F.; Wu, J. Coordinated Control Method of Voltage and Reactive Power for Active Distribution Networks Based on Soft Open Point. IEEE Trans. Sustain. Energy 2017, 8, 1430–1442. [Google Scholar] [CrossRef]
- Bu, X.; Hou, Z.; Zhang, H. Data-Driven Multiagent Systems Consensus Tracking Using Model Free Adaptive Control. IEEE Trans. Neural Netw. Learn Syst. 2018, 29, 1514–1524. [Google Scholar] [CrossRef]
- Babu, R.; Raj, S.; Bhattacharyya, B. Weak Bus-Constrained PMU Placement for Complete Observability of a Connected Power Network Considering Voltage Stability Indices. Prot. Control Mod. Power Syst. 2020, 5, 28. [Google Scholar] [CrossRef]
- Cheng, G.; Lin, Y.; Abur, A.; Gómez-Expósito, A.; Wu, W. A Survey of Power System State Estimation Using Multiple Data Sources: PMUs, SCADA, AMI, and Beyond. IEEE Trans. Smart Grid 2024, 15, 1129–1151. [Google Scholar] [CrossRef]
- Liang, X.; Fang, R.; Gan, Q.; Shi, L.; He, L.; Guan, C. Big Data Integration Technology and Application in Novel Power Distribution Network. Power Syst. Big Data 2022, 25, 53–61. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, X.; Wu, Z.; Sun, Q.; Gu, W.; Zheng, S.; Zhao, J. Application and Progress of Artificial Intelligence Technology in the Field of Distribution Network Voltage Control: A Review. Renew. Sustain. Energy Rev. 2024, 192, 114282. [Google Scholar] [CrossRef]
- Huo, Y.; Li, P.; Ji, H.; Yu, H.; Yan, J.; Wu, J.; Wang, C. Data-Driven Coordinated Voltage Control Method of Distribution Networks with High DG Penetration. IEEE Trans. Power Syst. 2023, 38, 1543–1557. [Google Scholar] [CrossRef]
- Yuan, Z.; Cavraro, G.; Singh, M.K.; Cortés, J. Learning Provably Stable Local Volt/Var Controllers for Efficient Network Operation. IEEE Trans. Power Syst. 2024, 39, 2066–2079. [Google Scholar] [CrossRef]
- Sun, X.; Qiu, J.; Zhao, J. Optimal Local Volt/Var Control for Photovoltaic Inverters in Active Distribution Networks. IEEE Trans. Power Syst. 2021, 36, 5756–5766. [Google Scholar] [CrossRef]
- Liang, X.; Zhou, N.; Fang, R.; Gan, Q.; Jiang, Y.; Guan, C.; Shi, L. Bi-level Optimization for Integrated Energy System Considering Cloud-Edge Collaboration. Power Syst. Big Data 2023, 26, 9–17. (In Chinese) [Google Scholar] [CrossRef]
- Hossain, R.R.; Kumar, R. A Distributed-MPC Framework for Voltage Control Under Discrete Time-Wise Variable Generation/Load. IEEE Trans. Power Syst. 2024, 39, 809–820. [Google Scholar] [CrossRef]
- Wang, S.; Duan, J.; Shi, D.; Xu, C.; Li, H.; Diao, R.; Wang, Z. A Data-Driven Multi-Agent Autonomous Voltage Control Framework Using Deep Reinforcement Learning. IEEE Trans. Power Syst. 2020, 35, 4644–4654. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Duan, J.; Shi, D.; Benidris, M. A Deep Reinforcement Learning-Based Multi-Agent Framework to Enhance Power System Resilience Using Shunt Resources. IEEE Trans. Power Syst. 2021, 36, 5525–5536. [Google Scholar] [CrossRef]
- Wang, Y.; Vittal, V. Data Driven Real-Time Dynamic Voltage Control Using Decentralized Execution Multi-Agent Deep Reinforcement Learning. IEEE Open Access J. Power Energy 2024, 11, 508–519. [Google Scholar] [CrossRef]
- Zhang, M.; Guo, G.; Magnússon, S.; Pilawa-Podgurski, R.C.N.; Xu, Q. Data Driven Decentralized Control of Inverter Based Renewable Energy Sources Using Safe Guaranteed Multi-Agent Deep Reinforcement Learning. IEEE Trans. Sustain. Energy 2024, 15, 1288–1299. [Google Scholar] [CrossRef]
- Mi, B.; Huo, X.; Ma, K.; Jin, S. Dynamic Linearization Residual-Assisted Model-Free Adaptive Control with Modified Criterion Function Based on Extended FFDL Data Model. IEEE Trans. Ind. Electron. 2025, 75, 10585–10594. [Google Scholar] [CrossRef]
- Coutinho, P.H.S.; Bessa, I.; Peixoto, M.L.C.; Palhares, R.M. A co-design condition for dynamic event-triggered feedback linearization control. Syst. Control Lett. 2024, 183, 105678. [Google Scholar] [CrossRef]
- Bozza, A.; Martin, T.; Cavone, G.; Carli, R.; Dotoli, M.; Allgöwer, F. Online Data-Driven Control of Nonlinear Systems Using Semidefinite Programming. IEEE Control Syst. Lett. 2024, 8, 3189–3194. [Google Scholar] [CrossRef]
- Clelland, J.N.; Klotz, T.J.; Vassiliou, P.J. Dynamic Feedback Linearization of Control Systems with Symmetry. SIGMA 2024, 20, 058. [Google Scholar] [CrossRef]
- Da Cunha, S.B. On the robustness of feedback linearization. Int. J. Dyn. Control 2024, 12, 3318–3331. [Google Scholar] [CrossRef]
- Hou, Z.; Xiong, S. On Model-Free Adaptive Control and Its Stability Analysis. IEEE Trans. Autom. Control 2019, 64, 4555–4569. [Google Scholar] [CrossRef]
- Guo, Y.; Hou, Z.; Liu, S.; Jin, S. Data-Driven Model-Free Adaptive Predictive Control for a Class of MIMO Nonlinear Discrete-Time Systems with Stability Analysis. IEEE Access 2019, 7, 102852–102866. [Google Scholar] [CrossRef]
- Wu, X.; Wang, M.; Shahidehpour, M.; Feng, S.; Chen, X. Model-Free Adaptive Control of STATCOM for SSO Mitigation in DFIG-Based Wind Farm. IEEE Trans. Power Syst. 2021, 36, 5282–5293. [Google Scholar] [CrossRef]
- Gao, S.; Li, P.; Ji, H.; Zhao, J.; Yu, H.; Wu, J.; Wang, C. Data-driven Multi-mode Adaptive Operation of Soft Open Point with Measuring Bad Data. IEEE Trans. Power Syst. 2024, 39, 6482–6495. [Google Scholar] [CrossRef]
- Song, G.; Yu, C.; Ji, H.; Zhao, J.; Xu, J.; Li, P. Data-Driven Voltage Control of Energy Storage Integrated Soft Open Point Considering Quality of Measurement Data. Autom. Electr. Power Syst. 2023, 47, 90–100. (In Chinese) [Google Scholar]
- Sun, J.; Chen, Q.; Xia, M. Data-Driven Detection and Identification of Line Parameters with PMU and Unsynchronized SCADA Measurements in Distribution Grids. CSEE J. Power Energy Syst. 2024, 10, 261–271. [Google Scholar] [CrossRef]
- Chai, Y.; Guo, L.; Wang, C.; Zhao, Z.; Du, X.; Pan, J. Network Partition and Voltage Coordination Control for Distribution Networks with High Penetration of Distributed PV Units. IEEE Trans. Power Syst. 2018, 33, 3396–3407. [Google Scholar] [CrossRef]


| Reference | Method Mechanism | Without Relying on Accurate Network Parameters | Without Training Process | Inter-Area Coordination | Fully Distributed Online |
|---|---|---|---|---|---|
| [8,9,10,11,12] | Model-based | - | √ | - | - |
| [18,19,20] | Data-driven | √ | - | - | - |
| [23,24,25,26] | Data-driven | √ | - | √ | - |
| This paper | Data-driven | √ | √ | √ | √ |
| Region | Location | Type | Capacity (kVA) | Region | Location | Type | Capacity (kVA) |
|---|---|---|---|---|---|---|---|
| 1 | 20 | PV | 100 | 2 | 32 | PV | 100 |
| 1 | 21 | PV | 100 | 2 | 33 | PV | 100 |
| 1 | 22 | WT | 100 | 3 | 11 | PV | 100 |
| 1 | 23 | PV | 100 | 3 | 12 | PV | 100 |
| 1 | 24 | PV | 100 | 3 | 13 | WT | 500 |
| 1 | 25 | PV | 100 | 3 | 15 | WT | 500 |
| 2 | 29 | WT | 100 | 3 | 16 | WT | 500 |
| 2 | 30 | WT | 100 | 3 | 17 | PV | 100 |
| 2 | 31 | PV | 100 | 3 | 18 | PV | 100 |
| Scenario | Total Controlled Nodes | Total Controlled DGs | Total Controllers | Average Controlled Nodes Per Controller | Average Communication Link Per Controller |
|---|---|---|---|---|---|
| I | 0 | 0 | 0 | - | - |
| II | 33 | 18 | 3 | 11 | 31 |
| III | 33 | 18 | 1 | 33 | 51 |
| IV | 33 | 18 | 1 | 33 | 51 |
| Scenario | Minimum Voltage (p.u.) | Maximum Voltage (p.u.) | VDI (p.u.) | LBI (p.u.) | Network Loss (kW) |
|---|---|---|---|---|---|
| I | 0.9288 | 1.0516 | 0.0144 | 25.5692 | 991.0612 |
| II | 0.9505 | 1.0364 | 0.0099 | 20.6668 | 786.1201 |
| III | 0.9305 | 1.0452 | 0.0115 | 19.6443 | 1082.1521 |
| IV | 0.9572 | 1.0191 | 0.0067 | 10.0748 | 600.2836 |
| Scenario | Convergence Step | Average Computational Time Per Step (s) | Total Computational Time (s) | Total Data Exchanged Per Controller (KB) |
|---|---|---|---|---|
| II | 6 | 0.0642 | 0.3847 | 2.1 |
| III | 15 | 0.1569 | 2.3539 | 7.7 |
| IV | - | - | 2.9887 | - |
| Scenario | Minimum Voltage (p.u.) | Maximum Voltage (p.u.) | VDI (p.u.) | Scenario | Minimum Voltage (p.u.) | Maximum Voltage (p.u.) | VDI (p.u.) |
|---|---|---|---|---|---|---|---|
| I | 0.9288 | 1.0516 | 0.0144 | ±1% | 0.9424 | 1.0385 | 0.0112 |
| ±0% | 0.9505 | 1.0364 | 0.0099 | ±2% | 0.9301 | 1.0463 | 0.0127 |
| ±0.05% | 0.9501 | 1.0367 | 0.0103 | ±3% | 0.9203 | 1.0577 | 0.0186 |
| ±0.5% | 0.9467 | 1.0372 | 1.0109 | ±4% | 0.9061 | 1.0714 | 0.0253 |
| DG Location | DG Type | DG Capacity (MVA) |
|---|---|---|
| 25, 35, 46 | WT | 0.6 |
| 15, 61, 68 | WT | 0.8 |
| 80, 88, 98, 105 | PV | 1.0 |
| 114, 121 | PV | 1.2 |
| Scenario | Minimum Voltage (p.u.) | Maximum Voltage (p.u.) | VDI (p.u.) | LBI (p.u.) | Network Loss (kW) |
|---|---|---|---|---|---|
| I | 0.9024 | 1.0578 | 0.0416 | 31.2580 | 878.2314 |
| II | 0.9317 | 1.0322 | 0.0266 | 15.3813 | 428.8927 |
| Test Case | Average Calculation Time in Each Iteration (Second) | Average Data Exchanged in Each Iteration Per Controller (KB) |
|---|---|---|
| Modified IEEE 33-node distribution network | 0.0624 | 0.35 |
| Modified IEEE 123-node distribution network | 0.1358 | 0.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Zhang, H.; Long, Z.; Gao, S.; Yang, Q.; Ji, H. Data-Driven Multi-Mode Adaptive Control for Distribution Networks with Multi-Region Coordination. Processes 2025, 13, 3046. https://doi.org/10.3390/pr13103046
Zheng Y, Zhang H, Long Z, Gao S, Yang Q, Ji H. Data-Driven Multi-Mode Adaptive Control for Distribution Networks with Multi-Region Coordination. Processes. 2025; 13(10):3046. https://doi.org/10.3390/pr13103046
Chicago/Turabian StyleZheng, Youzhuo, Hengrong Zhang, Zhi Long, Shiyuan Gao, Qihang Yang, and Haoran Ji. 2025. "Data-Driven Multi-Mode Adaptive Control for Distribution Networks with Multi-Region Coordination" Processes 13, no. 10: 3046. https://doi.org/10.3390/pr13103046
APA StyleZheng, Y., Zhang, H., Long, Z., Gao, S., Yang, Q., & Ji, H. (2025). Data-Driven Multi-Mode Adaptive Control for Distribution Networks with Multi-Region Coordination. Processes, 13(10), 3046. https://doi.org/10.3390/pr13103046








