Steel-Based Gravity Energy Storage: A Two-Stage Planning Approach for Industrial Parks with Renewable Energy Integration
Abstract
1. Introduction
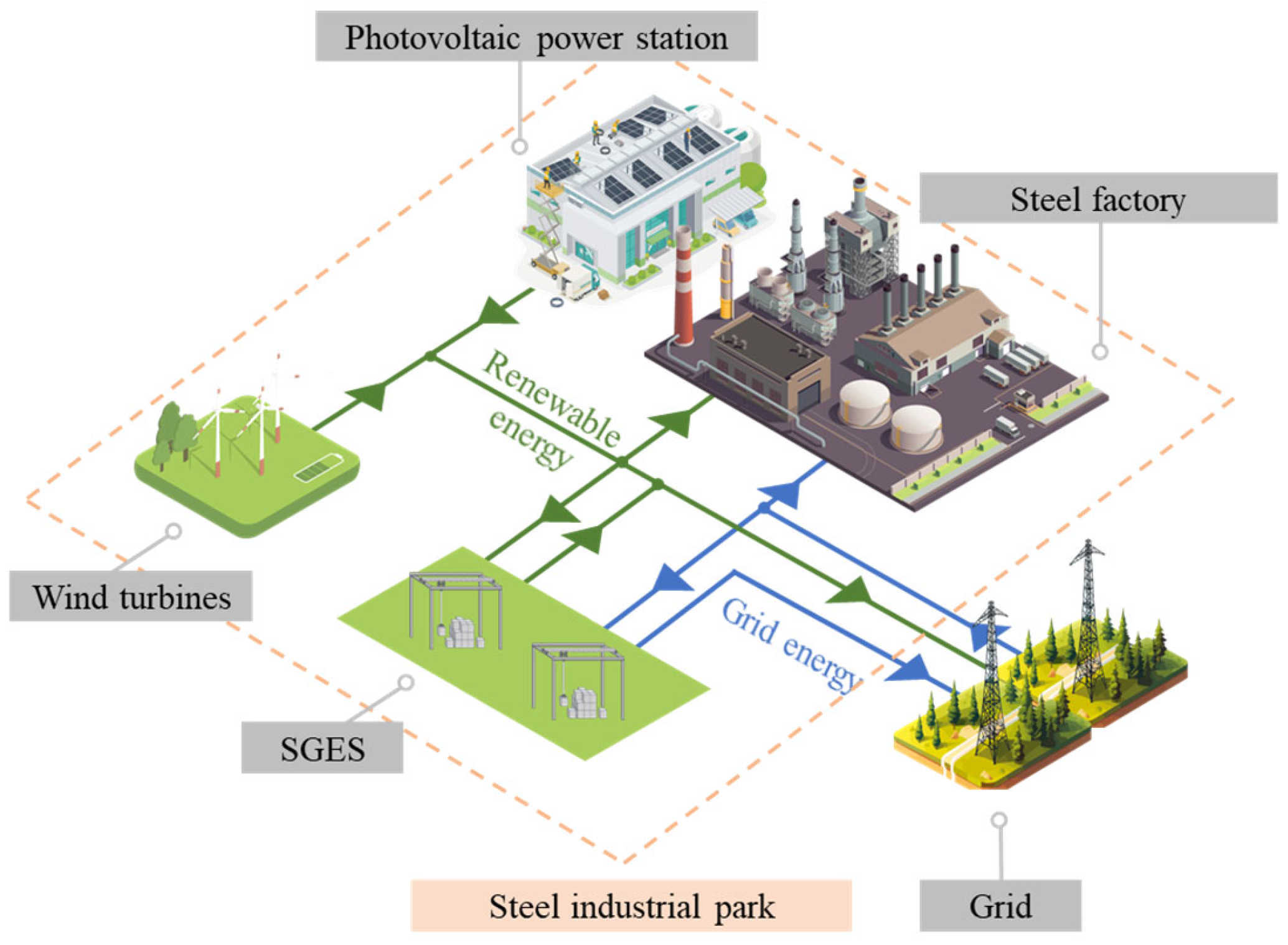
2. System Description
2.1. System Structure Analysis
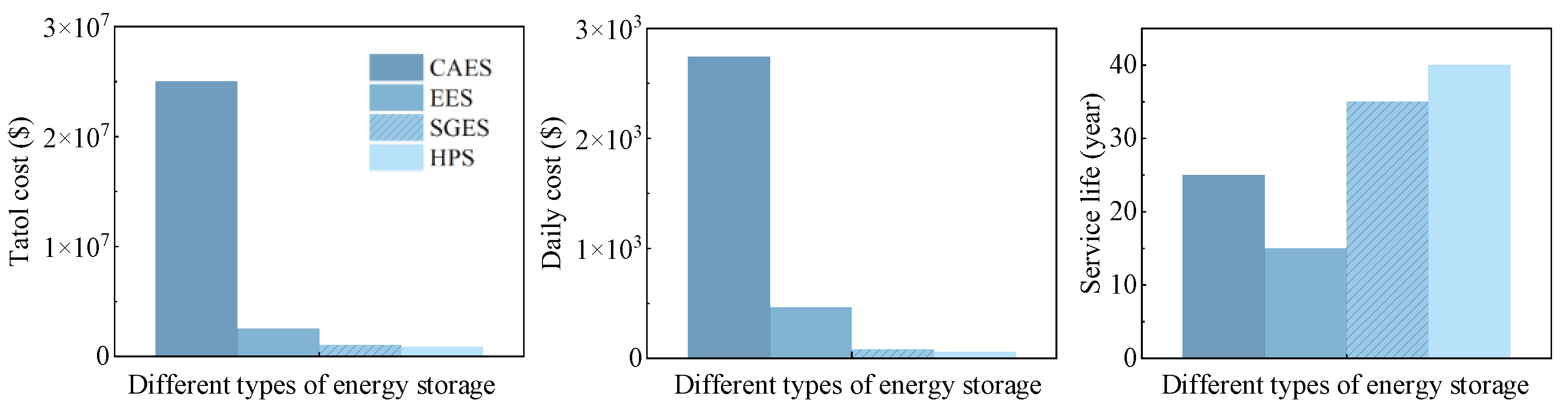
2.2. Comparison of Typical Energy Storage Types
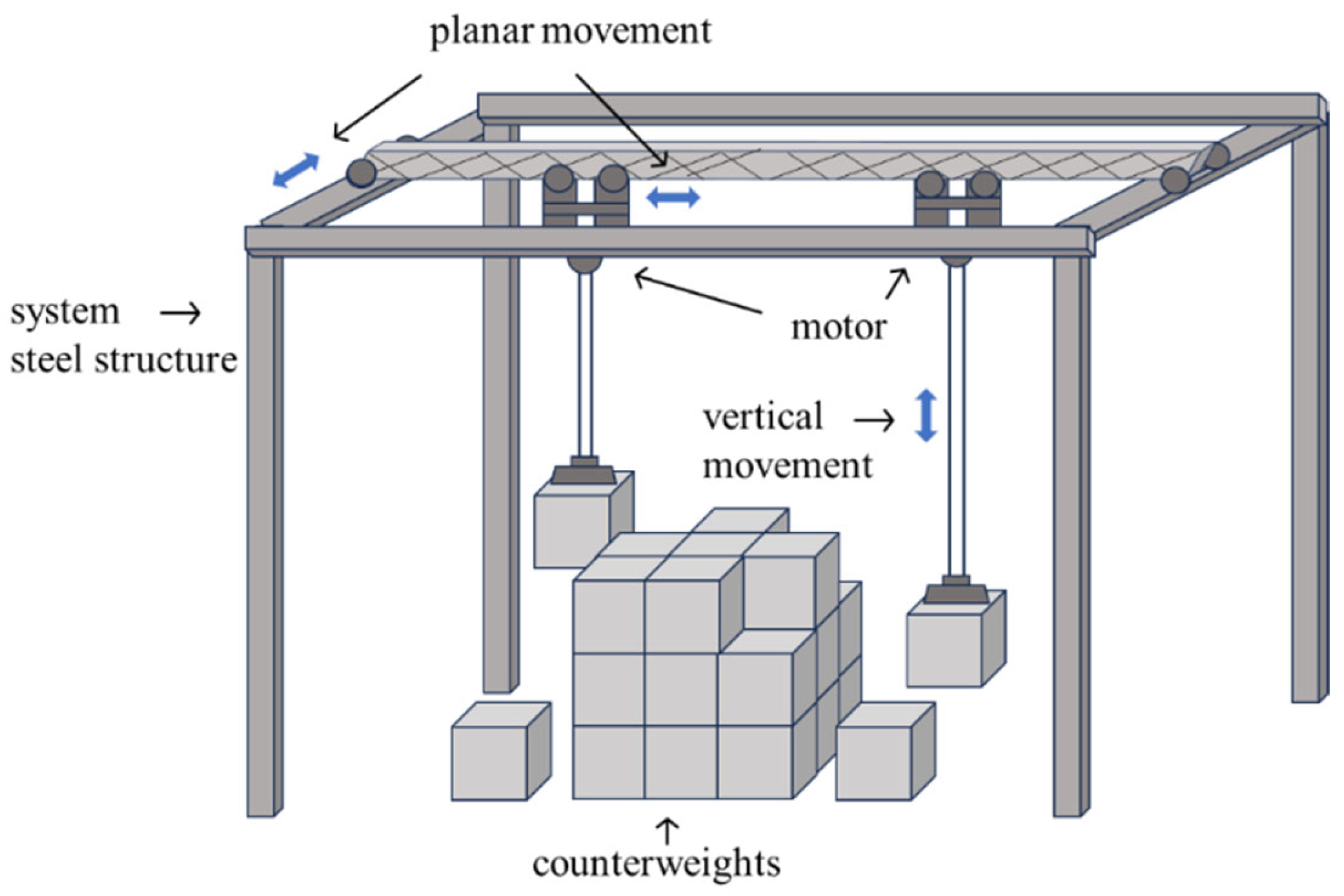
2.3. Model of SGES
2.4. Mechanical Restraints
3. Methodology
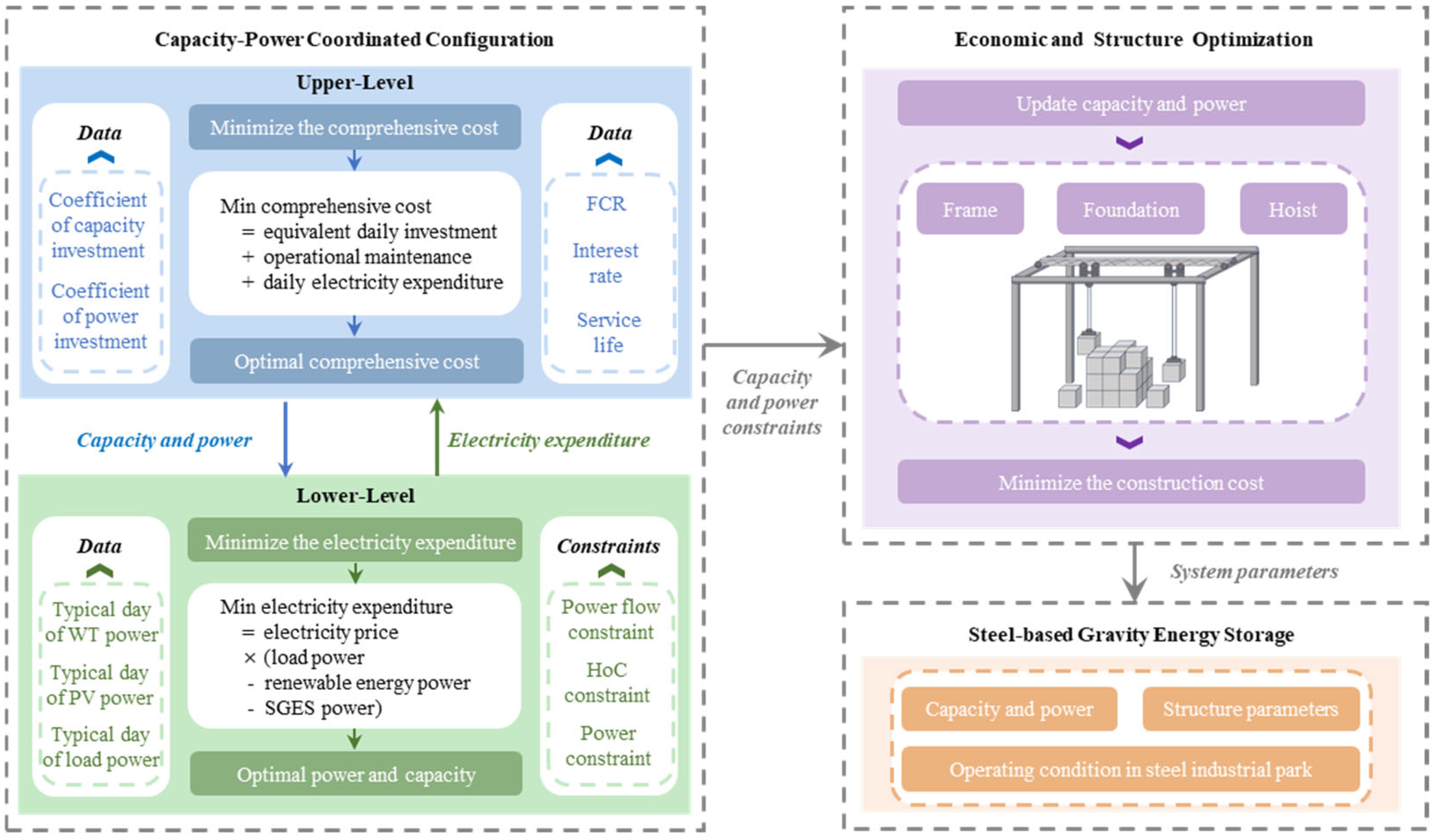
3.1. Two-Stage Planning Model
3.1.1. Overall Framework
3.1.2. Stage I
- 1.
- Upper level
- 2.
- Lower level
3.1.3. Stage II
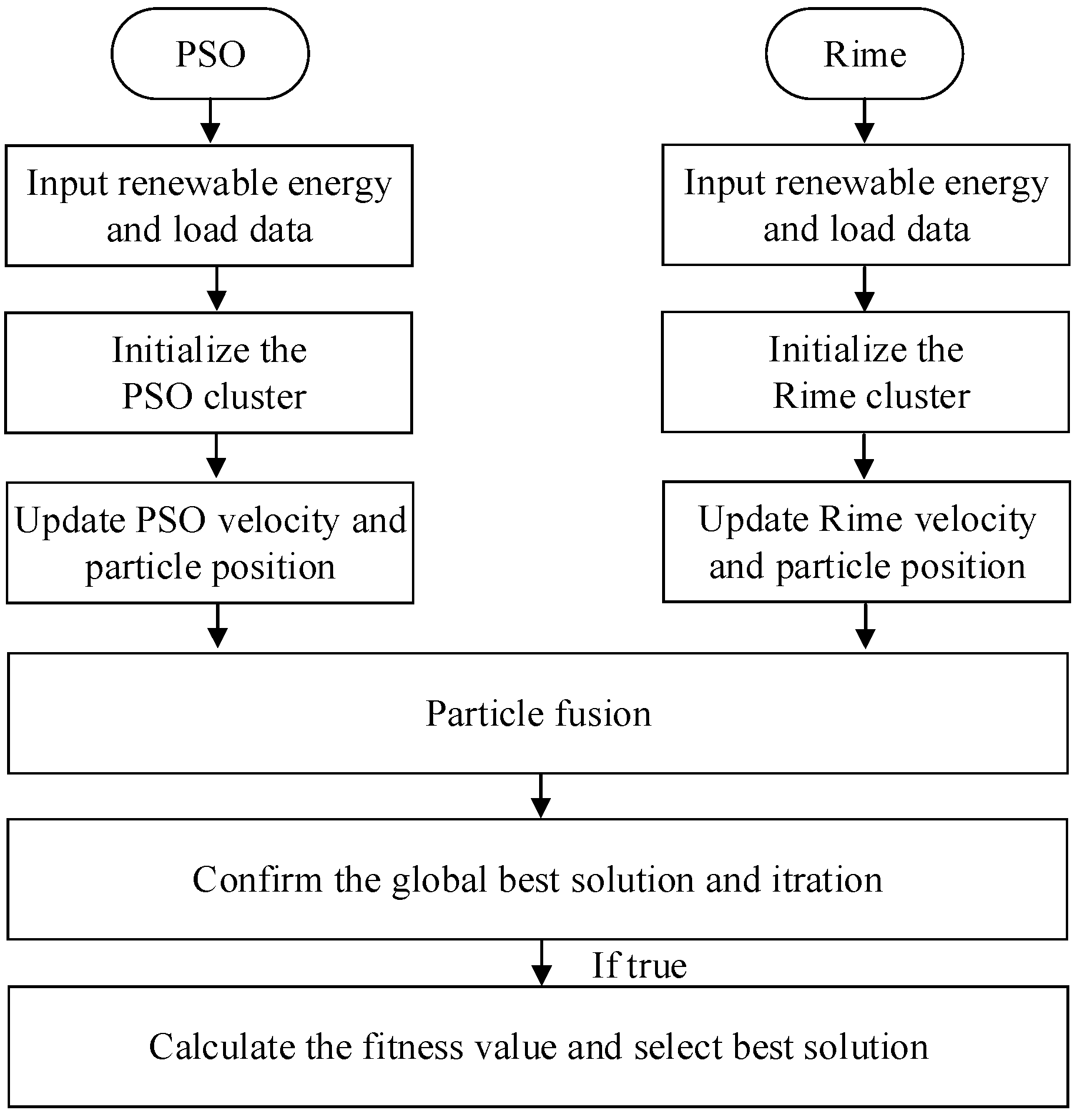
3.2. Solution Approach
3.2.1. Rime Algorithm
3.2.2. RI-PSO Algorithm
4. Case Study
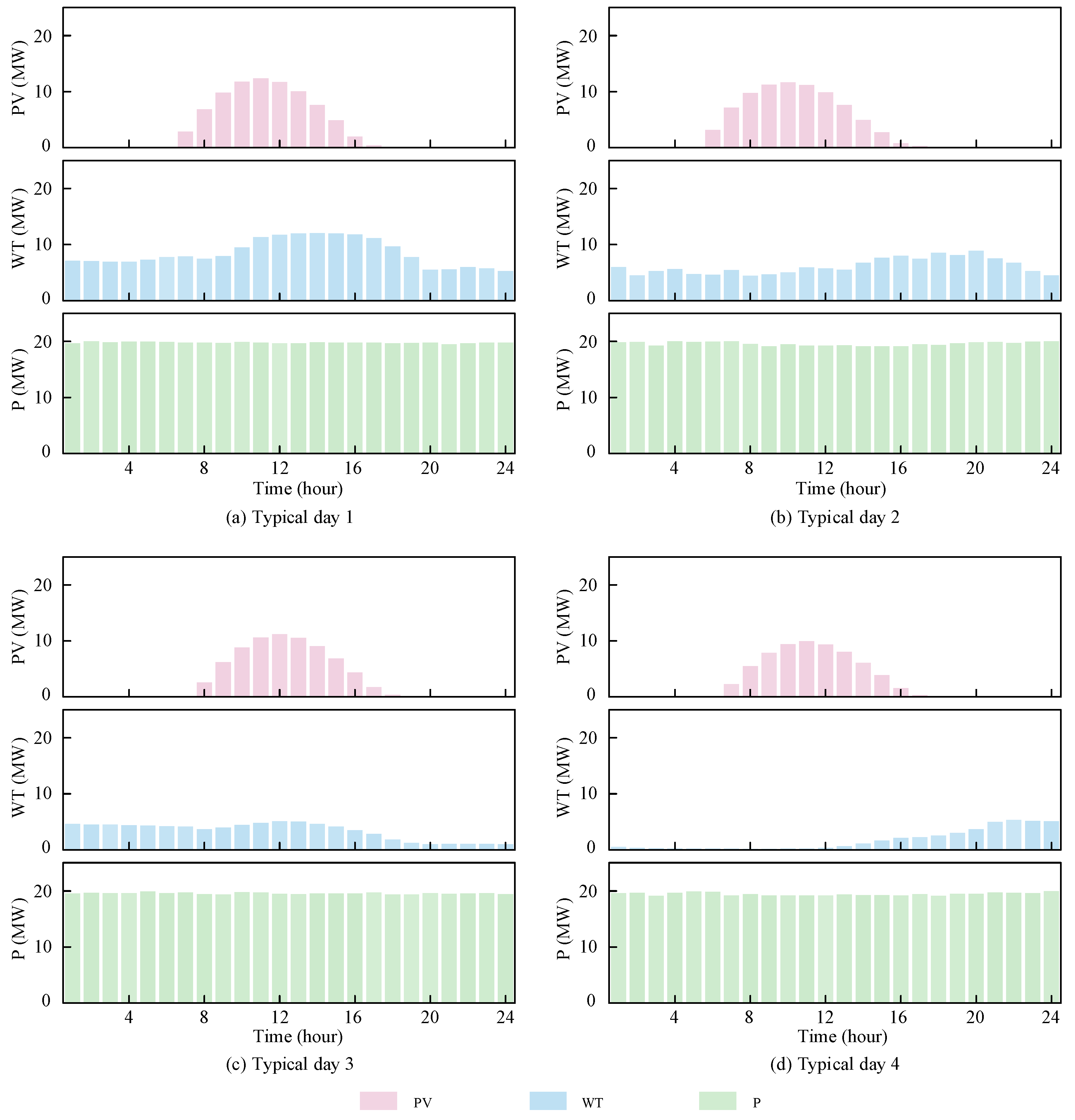
4.1. Simulation Settings
4.1.1. Environmental Settings
4.1.2. Parameter Settings
4.1.3. Mechanical Restraint Settings
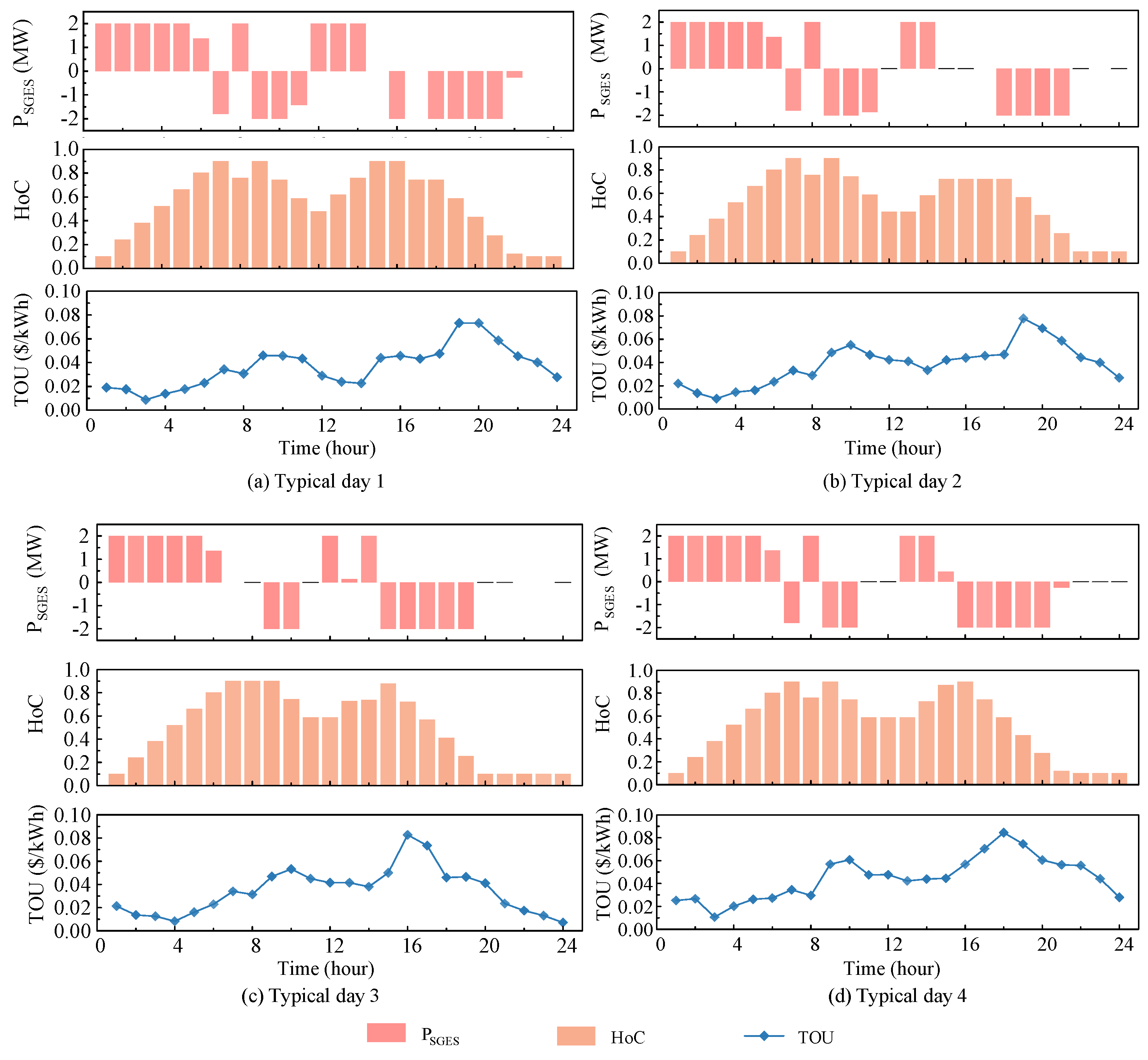
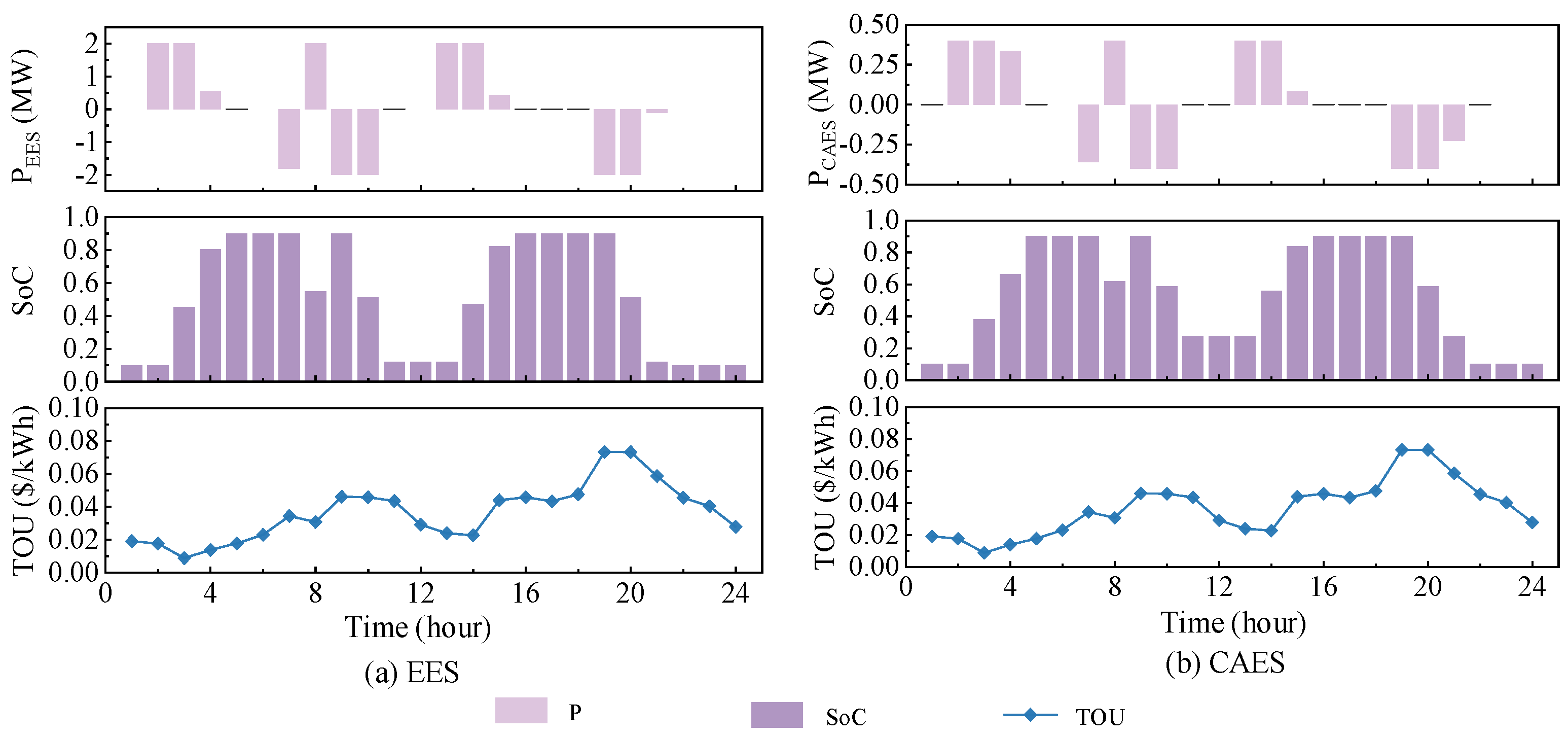
4.2. Result Analysis
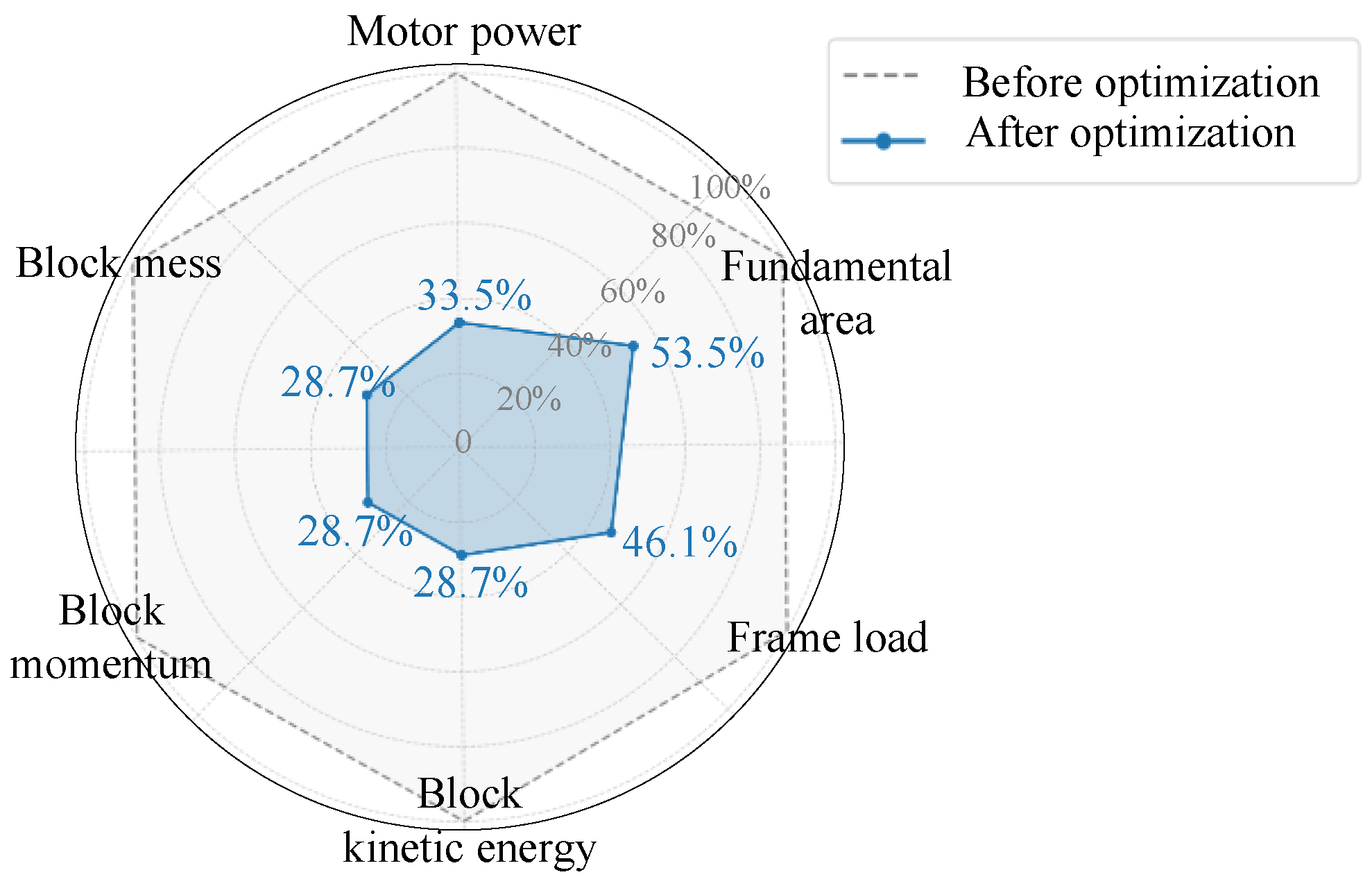
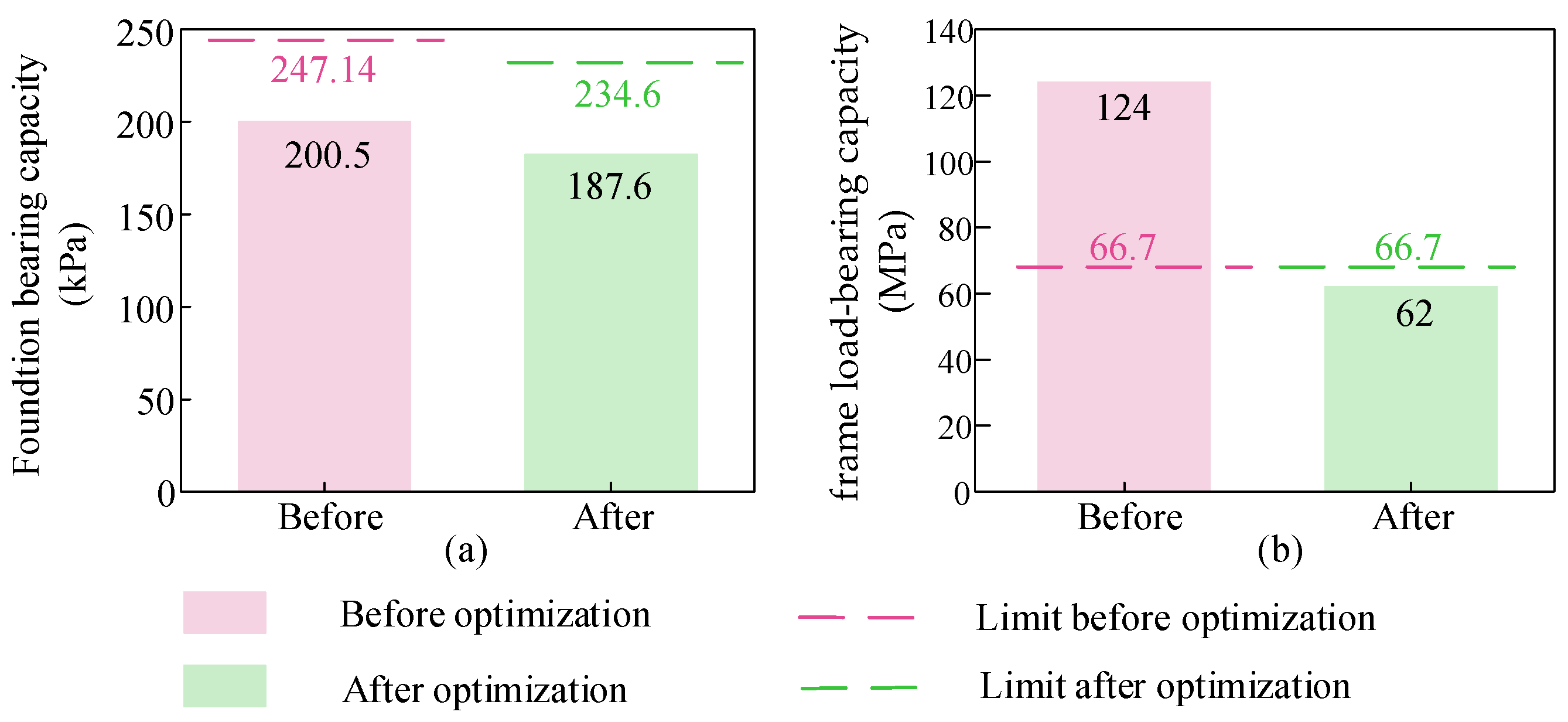
4.2.1. Mechanical Analysis of the Proposed SGES
4.2.2. Economic Analysis of the Proposed SGES
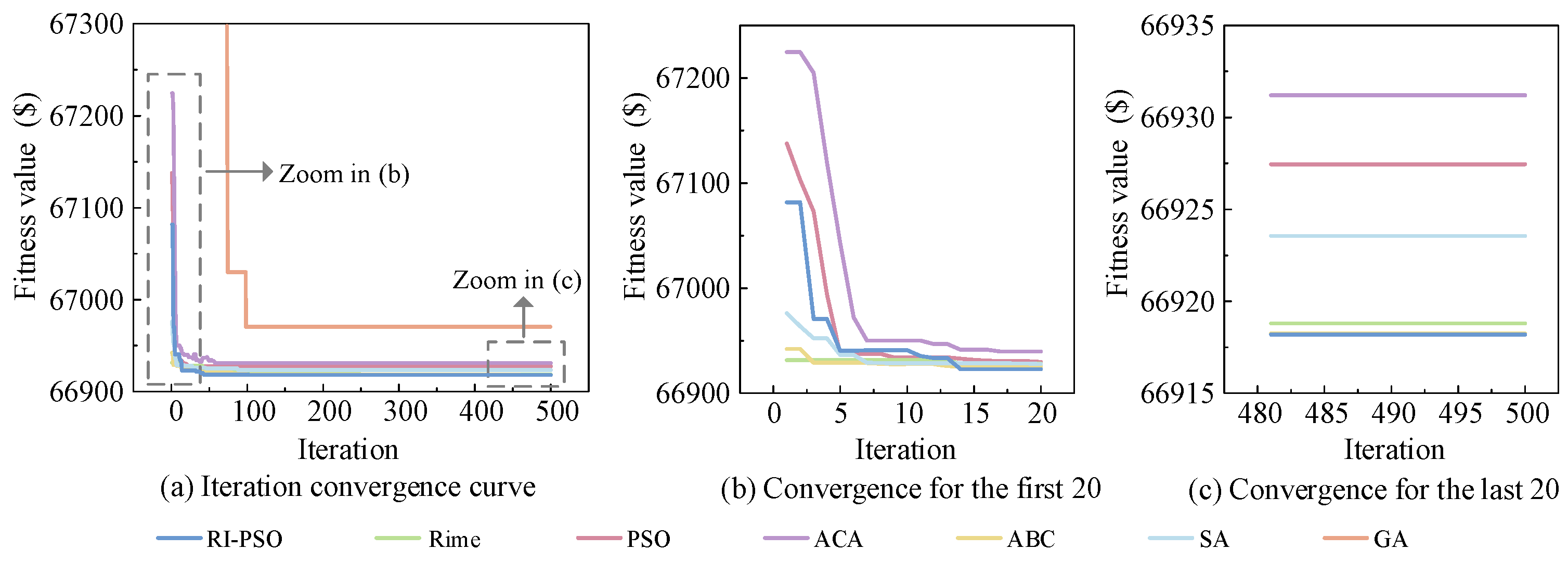
4.2.3. Superiority Analysis of the Proposed RI-PSO Algorithm
4.2.4. Sensitivity Analysis of the Proposed Planning Model
4.3. Environmental Safety and Regulatory Considerations
5. Conclusions
6. Patents
- Guo Y.; Sun Q.; Yu j. “A Method for Gravity Energy Storage Capacity Configuration Considering Renewable Energy Accommodation and Carbon Emission.” CN202411685619.0, 23 November 2024.
- Yu J.; Guo Y.; Sun Q. “A Friendly Control Strategy for Steel Park Grid Considering Gravity Energy Storage of Steel Blocks.” CN202410627474.2, 21 May 2024.
- Guo Y.; Xu W.; Yu J.; Wang Y.; Sun Q. “Grid Day-Ahead Scheduling Method, Device, Medium, and Product Based on Gravity Energy Storage.” CN202410442715.6, 12 April 2024.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GES | Gravity energy storage |
| SGES | Steel-based gravity energy storage |
| RI-PSO | A fusion of Rime and particle swarm optimization |
| PSO | Particle swarm optimization |
| ECMWF | Linear dichroism |
| CAES | Compressed air energy storage |
| EES | Electrochemical energy storage |
| HPS | Hydroelectric pumped storage |
References
- Katerina, K.; Oreane, Y.; Wina, C.; Bas, J.; Detlef, P.; Ernst, W. Improving material projections in Integrated Assessment Models: The use of a stock-based versus a flow-based approach for the iron and steel industry. Energy 2022, 239, 122434. [Google Scholar]
- Wei, L.; Zhang, S.; Lu, C. Research on the driving factors and carbon emission reduction pathways of China’s iron and steel industry under the vision of carbon neutrality. J. Clean. Prod. 2022, 361, 132237. [Google Scholar]
- Zhu, T.; Liu, X.; Wang, X.; Bas, J.; Detlef, P.; Ernst, W. Technical Development and Prospect for Collaborative Reduction of Pollution and Carbon Emissions from Iron and Steel Industry in China. Engineering 2023, 31, 37–49. [Google Scholar] [CrossRef]
- Zhang, J.; Shen, J.; Xu, L.; Zhang, Q. The CO2 emission reduction path towards carbon neutrality in the Chinese steel industry: A review. Environ. Impact Assess. Rev. 2023, 99, 107017. [Google Scholar] [CrossRef]
- Xu, D.; Yuan, Z.; Bai, Z.; Zhang, Q. Optimal operation of geothermal-solar-wind renewables for community multi-energy supplies. Energy 2022, 249, 123672. [Google Scholar] [CrossRef]
- Aneke, M.; Wang, M. Energy storage technologies and real-life applications—A state of the art review. Appl. Energy 2016, 179, 350–377. [Google Scholar] [CrossRef]
- Wu, G.; Zeng, M.; Peng, L.; Liu, X.; Li, B.; Duan, J. China’s new energy development: Status, constraints and reforms. Renew. Sustain. Energy Rev. 2016, 53, 885–896. [Google Scholar]
- Wang, W.; Yuan, B.; Sun, Q.; Wennersten, R. Application of energy storage in integrated energy systems—A solution to fluctuation and uncertainty of renewable energy. J. Energy Storage 2022, 52, 104812. [Google Scholar] [CrossRef]
- Tan, K.; Babu, T.; Vigna, K. Empowering smart grid: A comprehensive review of energy storage technology and application with renewable energy integration. J. Energy Storage 2021, 39, 102591. [Google Scholar] [CrossRef]
- Carne, D.; Maroufi, S.; Beiranvand, H. The role of energy storage systems for a secure energy supply: A comprehensive review of system needs and technology solutions. Electr. Power Syst. Res. 2024, 236, 110963. [Google Scholar] [CrossRef]
- Zhao, L.; Li, Y.; Yu, M.; Peng, Y.; Ran, F. Electrolyte-Wettability Issues and Challenges of Electrode Materials in Electrochemical Energy Storage, Energy Conversion, and Beyond. Adv. Sci. 2023, 10, 2300283. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Zhang, Y.; Xing, G.; Chou, S.; Tang, Y. Electrochemical energy storage devices working in extreme conditions. Energy Environ. Sci. 2021, 14, 3323–3351. [Google Scholar] [CrossRef]
- Zhang, C.; Yan, B.; Wieberdink, J.; Li, P.; Vandeven, J.; Loth, E.; Simon, T. Thermal analysis of a compressor for application to compressed air energy storage. Appl. Therm. Eng. 2024, 73, 1402–1411. [Google Scholar] [CrossRef]
- Budt, M.; Wolf, D.; Span, R.; Yan, J. A review on compressed air energy storage: Basic principles, past milestones and recent developments. Appl. Energy 2016, 170, 250–268. [Google Scholar] [CrossRef]
- Koohi-Fayegh, S.; Rosen, M. A review of energy storage types, applications and recent developments. J. Energy Storage 2020, 27, 101047. [Google Scholar] [CrossRef]
- Hua, W.; Lv, X.; Zhang, X.; Zhe, J.; Zhu, J. Research progress of seasonal thermal energy storage technology based on supercooled phase change materials. J. Energy Storage 2023, 67, 107378. [Google Scholar] [CrossRef]
- Wei, X.; Liu, D.; Shu, Y.; Chen, F.; Weng, J. Optimal sizing of energy storage in generation expansion planning of new power system with high penetration of renewable energies. Energy Rep. 2023, 9, 1938–1947. [Google Scholar] [CrossRef]
- Djamila, R. Energy Storage Systems for Photovoltaic and Wind Systems: A Review. Energies 2023, 16, 3893. [Google Scholar] [CrossRef]
- Matos, C.; Carneiro, J.; Silva, P. Overview of Large-Scale Underground Energy Storage Technologies for Integration of Renewable Energies and Criteria for Reservoir Identification. J. Energy Storage 2019, 21, 241–258. [Google Scholar] [CrossRef]
- Mahon, H.; O’Connor, D.; Friedrich, D.; Hughes, H. A review of thermal energy storage technologies for seasonal loops. Energy 2021, 239, 122207. [Google Scholar] [CrossRef]
- Tong, W.; Lu, Z.; Chen, W.; Han, X.; Zhao, G.; Wang, X.; Deng, Z. Solid gravity energy storage: A review. J. Energy Storage 2022, 53, 105226. [Google Scholar] [CrossRef]
- Li, F.; Xie, J.; Fan, Y.; Qiu, J. Potential of different forms of gravity energy storage. Sustain. Energy Technol. Assess. 2024, 64, 103728. [Google Scholar] [CrossRef]
- Mostafa, E.; Saber, A.; Ahmed, A.; Abd Elrahman, M.A. Parametric optimization for the design of gravity energy storage system using Taguchi method. Sci. Rep. 2022, 12, 19648. [Google Scholar]
- Chen, Q.; Guo, Y.; Wang, T. Research Status and Development Trend of Gravity Energy Storage Technology. IEEE Access 2024, 1169, 474–481. [Google Scholar]
- Morstyn, T.; Chilcott, M.; McCulloch, M. Gravity energy storage with suspended weights for abandoned mineshafts. Appl. Energy 2019, 239, 201–206. [Google Scholar] [CrossRef]
- Li, X.; Zhu, C.; Liu, Y. Traction power supply system of China high-speed railway under low-carbon target: Form evolution and operation control. Electr. Power Syst. Res. 2023, 223, 109682. [Google Scholar] [CrossRef]
- Yuan, J.; Peng, L.; Zhou, h.; Gan, D.; Qu, K. Recent research progress and application of energy storage system in electrified railway. Electr. Power Syst. Res. 2024, 226, 109893. [Google Scholar] [CrossRef]
- Berrada, A.; Loudiyi, K.; Zorkani, I. System design and economic performance of gravity energy storage. J. Clean. Prod. 2017, 156, 317–326. [Google Scholar] [CrossRef]
- Wang, R.; Li, M.; Ming, M.; Wu, G.; Wang, L. An efficient multi-objective model and algorithm for sizing a stand-alone hybrid renewable energy system. Energy 2017, 141, 2288–2299. [Google Scholar] [CrossRef]
- He, X.; Ge, S.; Liu, H.; Xu, Z.; Yang, M.; Wang, C. Frequency regulation of multi-microgrid with shared energy storage based on deep reinforcement learning. Electr. Power Syst. Res. 2022, 214, 108962. [Google Scholar] [CrossRef]
- Li, K.; Zhang, T.; Wang, R. Deep reinforcement learning-based multi-objective optimization for electricity–gas–heat integrated energy systems. Expert Syst. Appl. 2025, 262, 125558. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, J.; Zhu, R.; Kong, D.; Guo, H. Double layers optimal scheduling of distribution networks and photovoltaic charging and storage station cluster based on leader follower game theory. Sci. Rep. 2025, 15, 612. [Google Scholar] [CrossRef] [PubMed]
- Dufo-López, R.; Bernal-Agustín, J.; Yusta-Loyo, J.; Domínguez-Navarro, J.; Ramírez-Rosado, R.; Lujano, J.; Aso, I. Multi-objective optimization minimizing cost and life cycle emissions of stand-alone PV–wind–diesel systems with batteries storage. Appl. Energy 2011, 88, 4033–4041. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, J.; Yang, J.; Liang, H.; Zhang, J. Multi-objective planning of multi-type distributed generation considering timing characteristics and environmental benefits. Energies 2014, 7, 6242–6257. [Google Scholar] [CrossRef]
- Jülch, V. Comparison of electricity storage options using levelized cost of storage (LCOS) method. Appl. Energy 2016, 183, 1594–1606. [Google Scholar] [CrossRef]
- Ilja, P. The Cost of Storage—How to Calculate the Levelized Cost of Stored Energy (LCOE) and Applications to Renewable Energy Generation. Energy Procedia 2014, 46, 68–77. [Google Scholar]
- Zhou, Z.; Ma, Z.; Mu, T. Hybrid energy storage capacity optimization based on VMD-SG and improved Firehawk optimization. Electr. Power Syst. Res. 2024, 139, 111218. [Google Scholar] [CrossRef]
- Hunt, J.; Zakeri, B.; Falchetta, G.; Nascimento, A.; Wada, Y.; Riahi, K. Mountain gravity energy storage: A new solution for closing the gap between existing short and long-term storage technologies. Energy 2019, 190, 116419. [Google Scholar] [CrossRef]
- Hou, H.; Xu, T.; Wu, X.; Wang, H.; Tang, A.; Chen, Y. Optimal capacity configuration of the wind-photovoltaic-storage hybrid power system based on gravity energy storage system. Appl. Energy 2020, 271, 115052. [Google Scholar] [CrossRef]
- Kim, J.; Benjamin, K.; Bazilian, M.; Wang, H.; Tang, A.; Chen, Y. Decarbonizing the iron and steel industry: A systematic review of sociotechnical systems, technological innovations, and policy options. Energy Res. Soc. Sci. 2022, 89, 102565. [Google Scholar] [CrossRef]
- Sun, W.; Wen, Q.; Zhou, Y. Material and energy flows of the iron and steel industry: Status quo, challenges and perspectives. Appl. Energy 2020, 268, 114946. [Google Scholar] [CrossRef]
- Inayat, A. Current progress of process integration for waste heat recovery in steel and iron industries. Fuel 2022, 338, 127237. [Google Scholar] [CrossRef]
- Liu, D.; Wang, P.; Sun, Y. Co-abatement of carbon and air pollutants emission in China’s iron and steel industry under carbon neutrality scenarios. Renew. Sustain. Energy Rev. 2024, 191, 114140. [Google Scholar] [CrossRef]
- Su, H.; Zhao, D.; Heidari, A.; Liu, L.; Zhang, X.; Mafarja, M.; Chen, H. RIME: A physical-based optimization. Neurocomputing 2023, 532, 183–214. [Google Scholar] [CrossRef]
- He, W.; King, M.; Luo, X.; Dooner, M.; Li, D.; Wang, J. Technologies and economics of electric energy storage in power systems: Review and perspective. Adv. Appl. Energy 2021, 4, 100060. [Google Scholar] [CrossRef]
- Zakeri, B.; Syri, S. Electrical energy storage systems: A comparative life cycle cost analysis. Renew. Sustain. Energy Rev. 2015, 42, 569–596. [Google Scholar] [CrossRef]
- 2023 Levelized Cost of Energy. Available online: https://www.lazard.com/research-insights/2023-levelized-cost-of-energyplus/ (accessed on 2 October 2023).
- Emrani, A.; Berrada, A.; Bakhouya, M. Optimal sizing and deployment of gravity energy storage system in hybrid PV-Wind power plant. Renew. Energy 2022, 183, 12–17. [Google Scholar] [CrossRef]
| Type of GES | Characteristics |
|---|---|
| Staking | Stacked heavy objects do not require additional storage platforms and can be deployed within a smaller space. |
| Suspension tower | Stores gravitational potential energy using lifting equipment and a platform. |
| Mine shaft | Utilizing existing mine shafts to provide a height difference for gravitational energy storage. |
| Piston | Using pistons with extremely high mechanical strength and sealing levels to store gravitational energy. |
| Cable car | In steep terrain, the gravitational potential energy is transferred using cable cars. |
| Mine car | In steep terrain, the gravitational potential energy is transferred using mine cars. |
| Investment Type | USD/kWh | USD/kWh | USD/kWh | USD/m2 | USD/m |
|---|---|---|---|---|---|
| Cost Fator | 583.3 | 166.7 | 166.7 | 138.9 | 83.3 |
| Power (MW) | 0.1 | 0.2 | 0.3 | 0.5 | 1 | 2 |
|---|---|---|---|---|---|---|
| Price (USD) | 472.2 | 986.1 | 1388.9 | 4569.4 | 8472.2 | 138,888.9 |
| Algorithms | Parameters | Value |
|---|---|---|
| PSO | 0.5 | |
| 0.5 | ||
| 100 | ||
| Rime | 20 | |
| RI-PSO | 0.5 | |
| 2.5 | ||
| 0.01 | ||
| 0.9 | ||
| 100 | ||
| 20 | ||
| 0.6 | ||
| 0.4 | ||
| Common parameters | Dimensions | 2 |
| Population size | 30 | |
| Max number of iterations | 500 |
| * | * | ||||||
| 980,700 N | 200 MPa | 110 mm | 220 mm | 3 | 1 m/s | 210 MPa | 1.5 |
| * | * | |||||
| 150 kPa | 0.3 | 1.5 | 19 kN/m2 | 18 kN/m2 | 3 m | 0.3 m |
| Type | * | , , | * | * | |||
|---|---|---|---|---|---|---|---|
| Before optimization | 1 | 8.4 m | 2.8 m | 8 | 1000 kW | 2 | USD 40,047 |
| After optimization | 2 | 6 m | 1.5 m | 54 | 350 kW | 6 | USD 30,541 |
| 3.77 | 9.85 | 13.50 | 17.21 | 20.00 | |
| 0.90 | 1.42 | 2.00 | 2.48 | 2.88 |
| 13.69 | 13.51 | 13.50 | 13.51 | 13.49 | |
| 2.03 | 1.99 | 2.00 | 1.99 | 1.99 |
| Type | Content |
|---|---|
| Environmental implications | Energy consumption: Electrified hoisting machinery may increase local grid load. Noise pollution: The operation of the crane will generate noise, and when deploying it, it is necessary to keep it away from residential areas. Land footprint: The foundation may disrupt the ecological balance of the soil. |
| Occupational safety and risk | Structural collapse and worker–machine collision: It is necessary to strengthen equipment supervision, comply with national standards, and consider deploying high-level automated equipment. |
| Regulation compliance | Safety-by-design integration: The idle steel blocks must comply with the national steel management requirements and must not contain contaminated materials. Policy advocacy: Land use must also conform to the regulations regarding the bearing capacity of dynamic loads as stipulated by the Chinese authorities. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Q.; Guo, Y.; Xu, W.; Zhang, B.; Du, Y.; Liu, Y. Steel-Based Gravity Energy Storage: A Two-Stage Planning Approach for Industrial Parks with Renewable Energy Integration. Processes 2025, 13, 1922. https://doi.org/10.3390/pr13061922
Sun Q, Guo Y, Xu W, Zhang B, Du Y, Liu Y. Steel-Based Gravity Energy Storage: A Two-Stage Planning Approach for Industrial Parks with Renewable Energy Integration. Processes. 2025; 13(6):1922. https://doi.org/10.3390/pr13061922
Chicago/Turabian StyleSun, Qingqi, Yufeng Guo, Wei Xu, Bixi Zhang, Yilin Du, and Yifei Liu. 2025. "Steel-Based Gravity Energy Storage: A Two-Stage Planning Approach for Industrial Parks with Renewable Energy Integration" Processes 13, no. 6: 1922. https://doi.org/10.3390/pr13061922
APA StyleSun, Q., Guo, Y., Xu, W., Zhang, B., Du, Y., & Liu, Y. (2025). Steel-Based Gravity Energy Storage: A Two-Stage Planning Approach for Industrial Parks with Renewable Energy Integration. Processes, 13(6), 1922. https://doi.org/10.3390/pr13061922






