Multimodal Switching Control Strategy for Wide Voltage Range Operation of Three-Phase Dual Active Bridge Converters
Abstract
1. Introduction
- Firstly, aiming at the problem that the traditional control of 3p-DAB is difficult to achieve soft switching and target optimization under wide voltage range and medium- to low-power conditions, the 3pSPCPS working mode is proposed to enable 3p-DAB to operate in a mode similar to 1p-DAB. In this mode, 3p-DAB adopts synchronous parallel operation, which can be equivalent to 1p-DAB, and then operates in a periodic cyclic rolling manner to ensure a consistent utilization rate of switching tubes. By invoking the TPS control scheme, ZVS and minimum current stress optimization are achieved, thereby improving the working efficiency in the medium–low power range.
- Then, facing the actual demand for wide voltage regulation of 3p-DAB, a standardized, unified, minimum current stress optimization scheme based on a virtual phase-shift ratio is proposed. This scheme introduces a virtual phase-shift ratio to eliminate power aliasing and establishes a unified control structure and optimization control table as a standard quantity, which can reduce the complexity of controller design and gain expression.
- Finally, through detailed theoretical modeling, simulation, and hardware-in-the-loop (HIL) experiment verification, improvement in efficiency and soft-switching performance is confirmed.
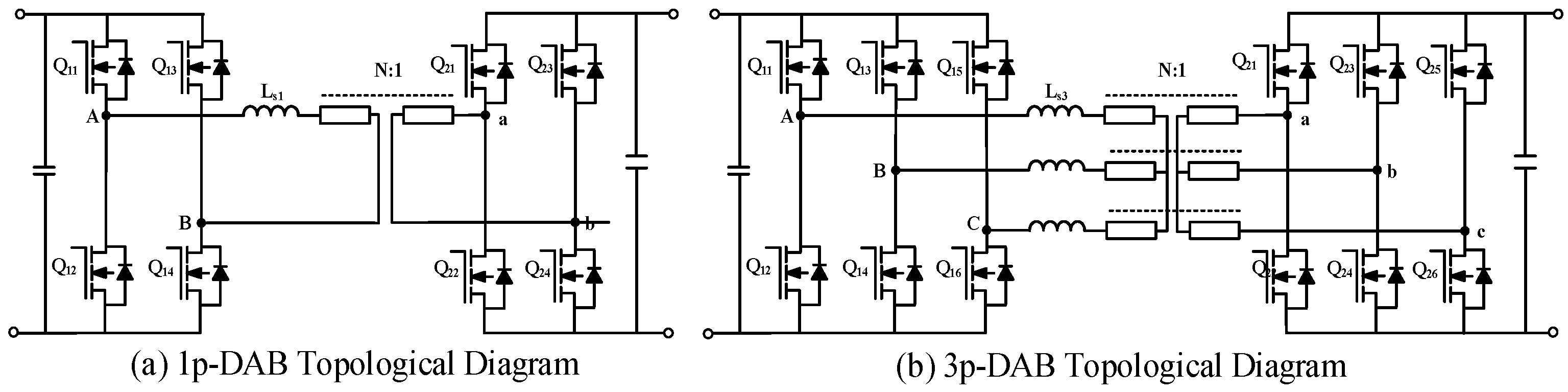
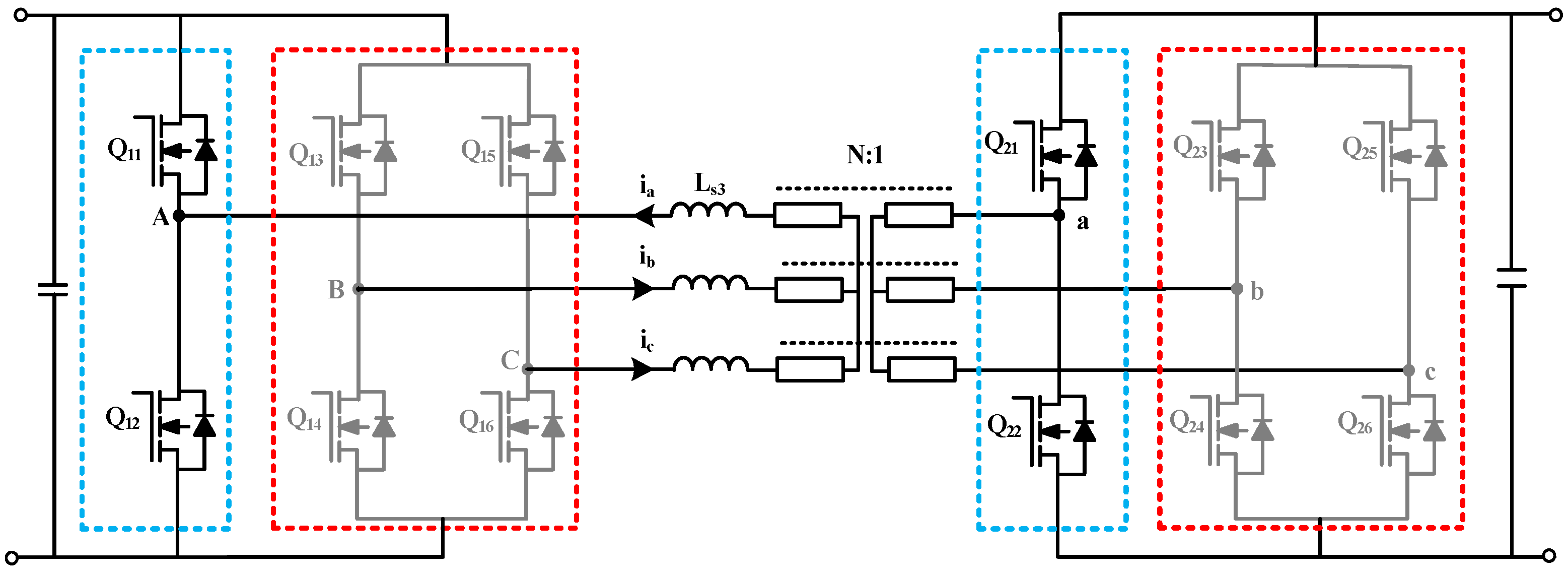
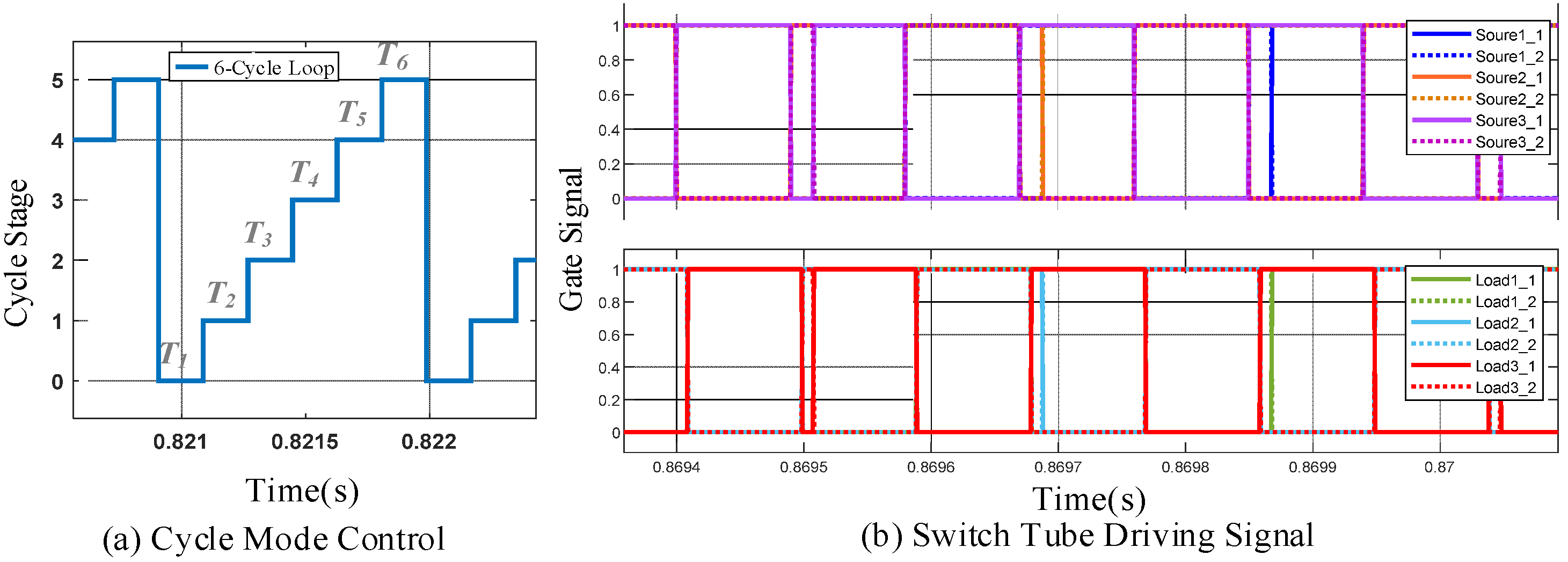
2. Three-Phase, Single-Cycle, Parallel-Cycling Phase-Shifting (3pSPCPS) Mode
2.1. Basic Working Principle of the 3pSPCPS Mode
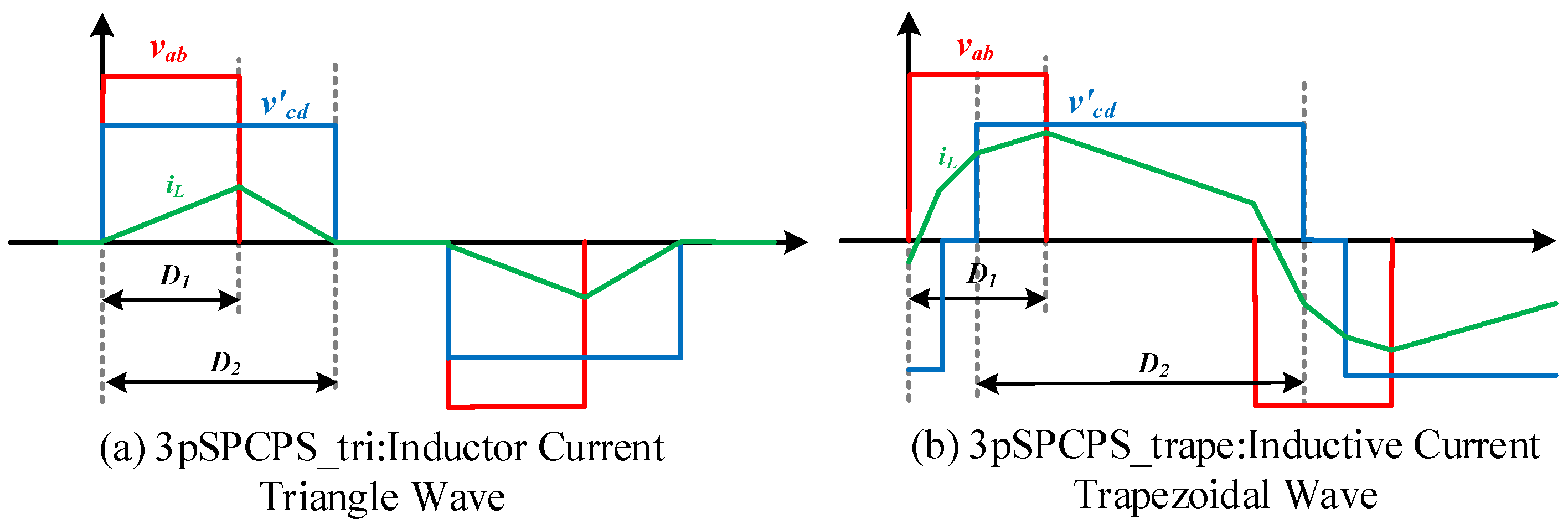
2.2. Detailed Analysis of 3pSPCPS Applied to DAB
- (1)
- The Concept of Switching
- (2)
- Switching State and Sequence
- (3)
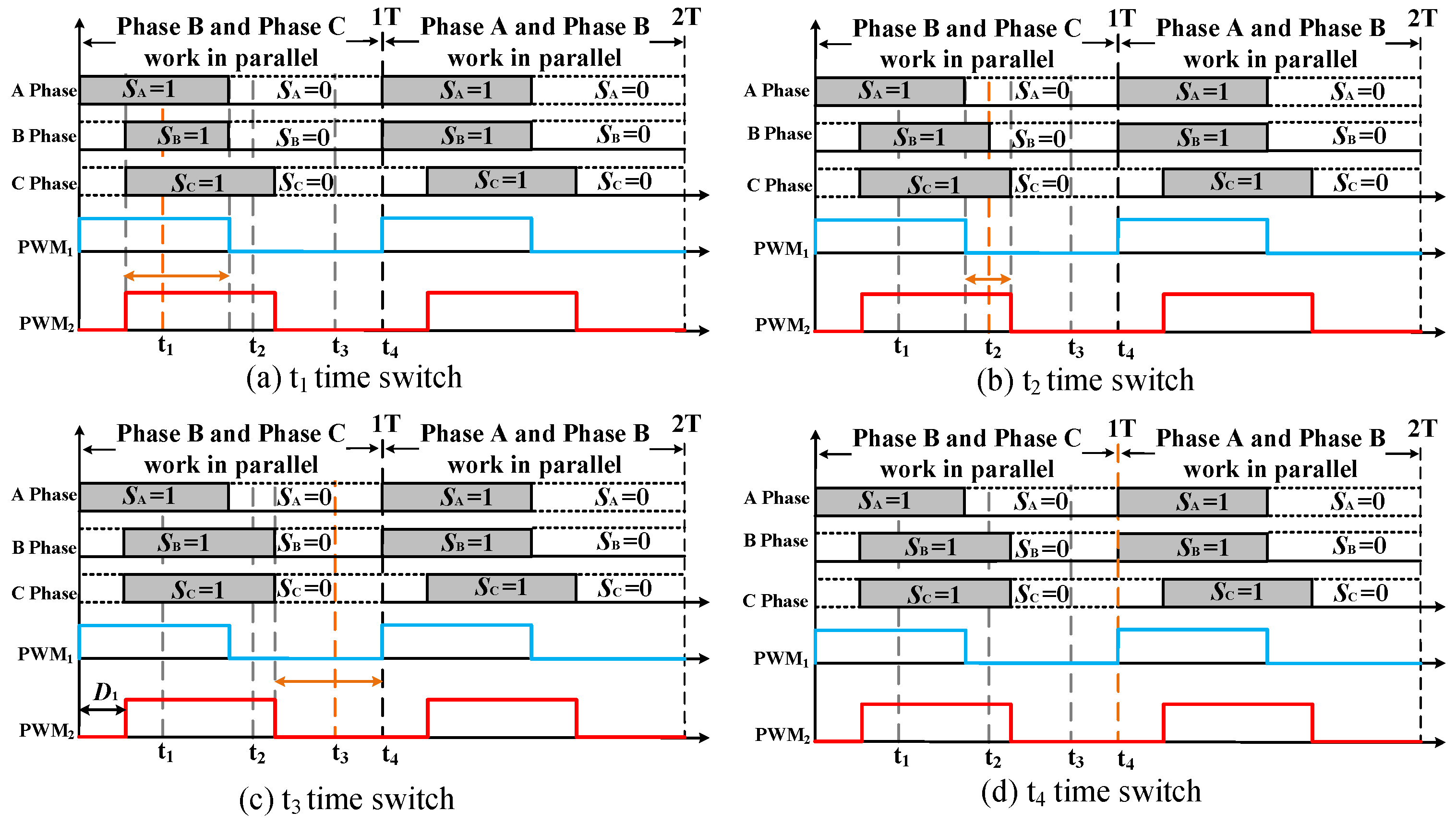
- Switching Time Points
- Choosing time node for switching from phase to for B, even though no switch tube operation occurs, the duty cycle of B within T is not 50%, leading to a DC bias issue at the switching moment.
- At time node , switching from 6 back to instantly changes B’s state from to , resulting in additional switching losses. Similarly, the duty cycle of B within T not being 50% introduces a DC bias issue.
- Selecting time node and switching from back to for B, B’s state instantly remains at , avoiding additional switching losses. Moreover, with B’s duty cycle within T remaining at 50%, DC bias issues are prevented.
- By choosing time node for switching from back to , both A and B’s states instantly change from to , causing extra switching losses. However, B’s duty cycle within T still being 50% prevents DC bias issues.
3. Standardized Global Unified Operation Strategy Under Wide Voltage Range
3.1. Wide Voltage Range Optimization Scheme at Low and Medium Power Levels
3.2. Control Scheme for Wide Voltage Range Under High-Power Conditions
3.3. Standardized Unification Based on Virtual Phase-Shift Ratio
- (1)
- Correction of Operating Range under Medium- and Low-Power Conditions
- (2)
- Expanding the Meaning of the External Phase-Shift Ratio
- Slow dynamic response, with ringing occurring under input and load disturbances.
- Mode switching under multiple conditions can oscillate due to the lagging effect of power.
- It may affect system stability, requiring higher stability margins for the control system.
- (3)
- Unification of Reference Quantities Across the Full Power Range
3.4. Global Operational Improvement Strategy to Suppress Switching Oscillations
- (1)
- Oscillations during switching between and as well as and are caused by changes in the mid-segment of the control optimization algorithm. Since is a continuous function during the switch, the impact of oscillations is minimal and can be largely ignored; thus, no further action is taken in this paper.
- (2)
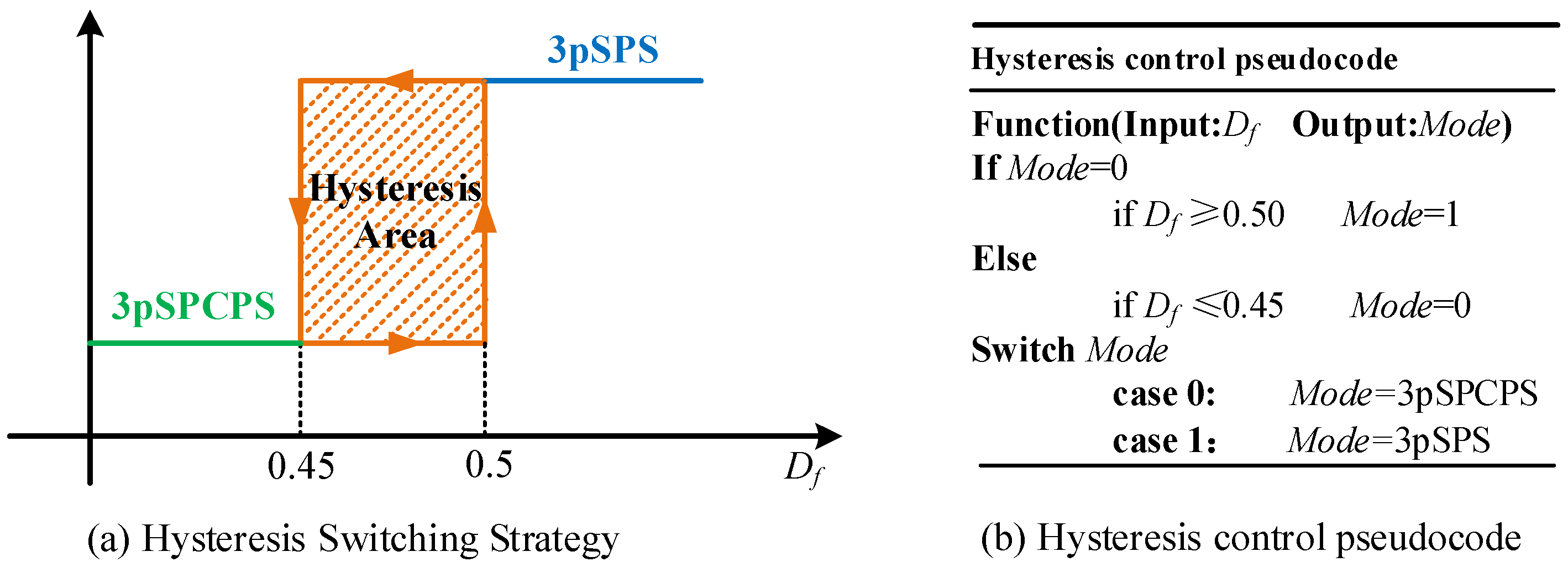
- Oscillations during the switch between medium and low power in and are caused by changes in the input of the control optimization algorithm. The switching of can result in discontinuous branch structures in the optimization algorithm, potentially leading to severe oscillations. At medium and low power, it has been found that soft switching can be achieved under any gain using SPS control when , and the system reliability is very high. Therefore, this paper designs a high-reliability buffer zone in the prone-to-oscillation area, with a specific scheme to operate under SPS control when .
- (3)
- Oscillations between and at medium to low power are caused, on the one hand, by the influence of Df, leading to discontinuous branch structures in the optimization algorithm, and, on the other hand, by the mode switch altering the circuit’s topology, thus causing severe oscillations. This paper employs hysteresis control to suppress such oscillations.
4. Analysis of DAB Operational Characteristics Under Multiple Working Modes
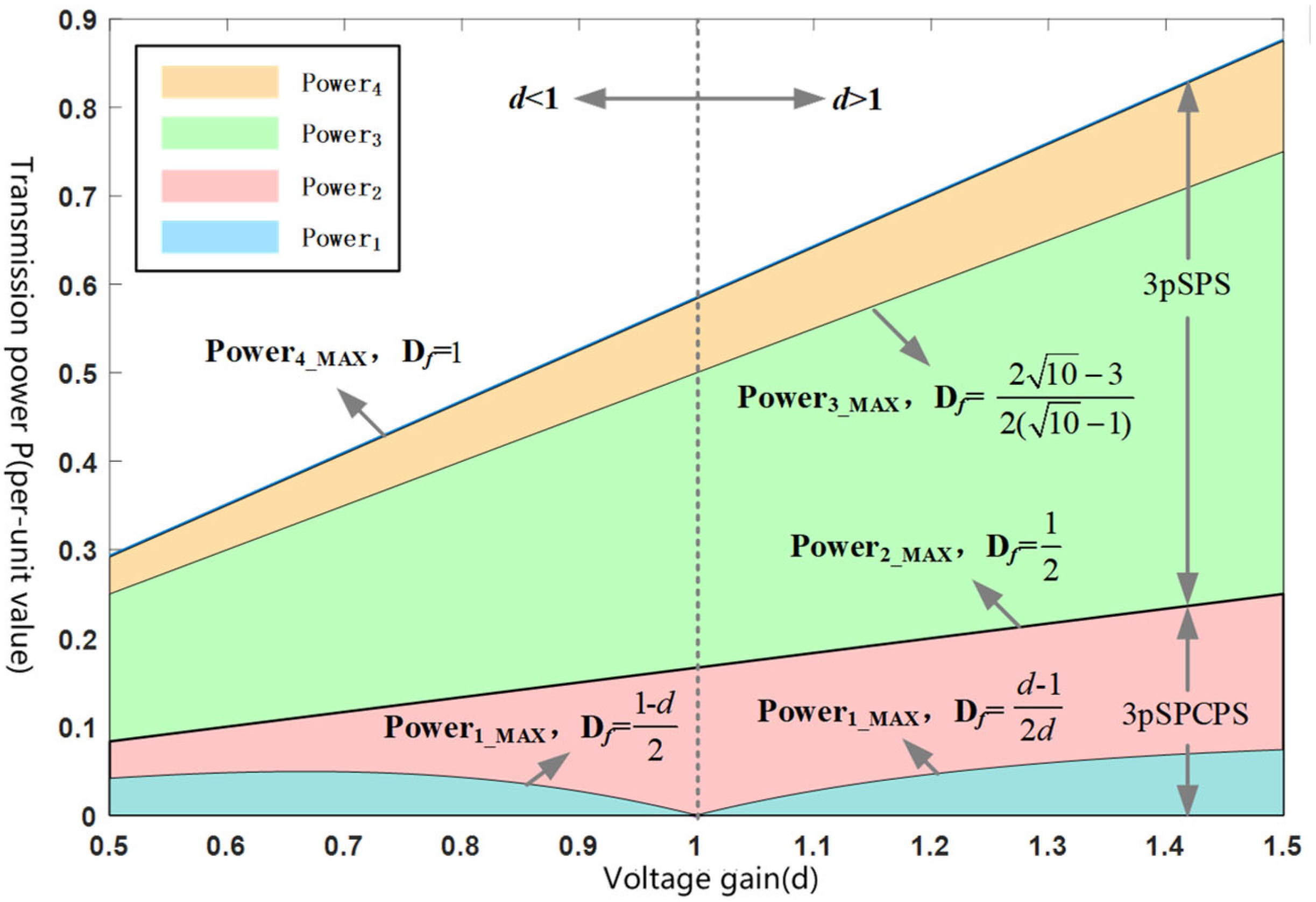
- (1)
- Power Characteristics Analysis
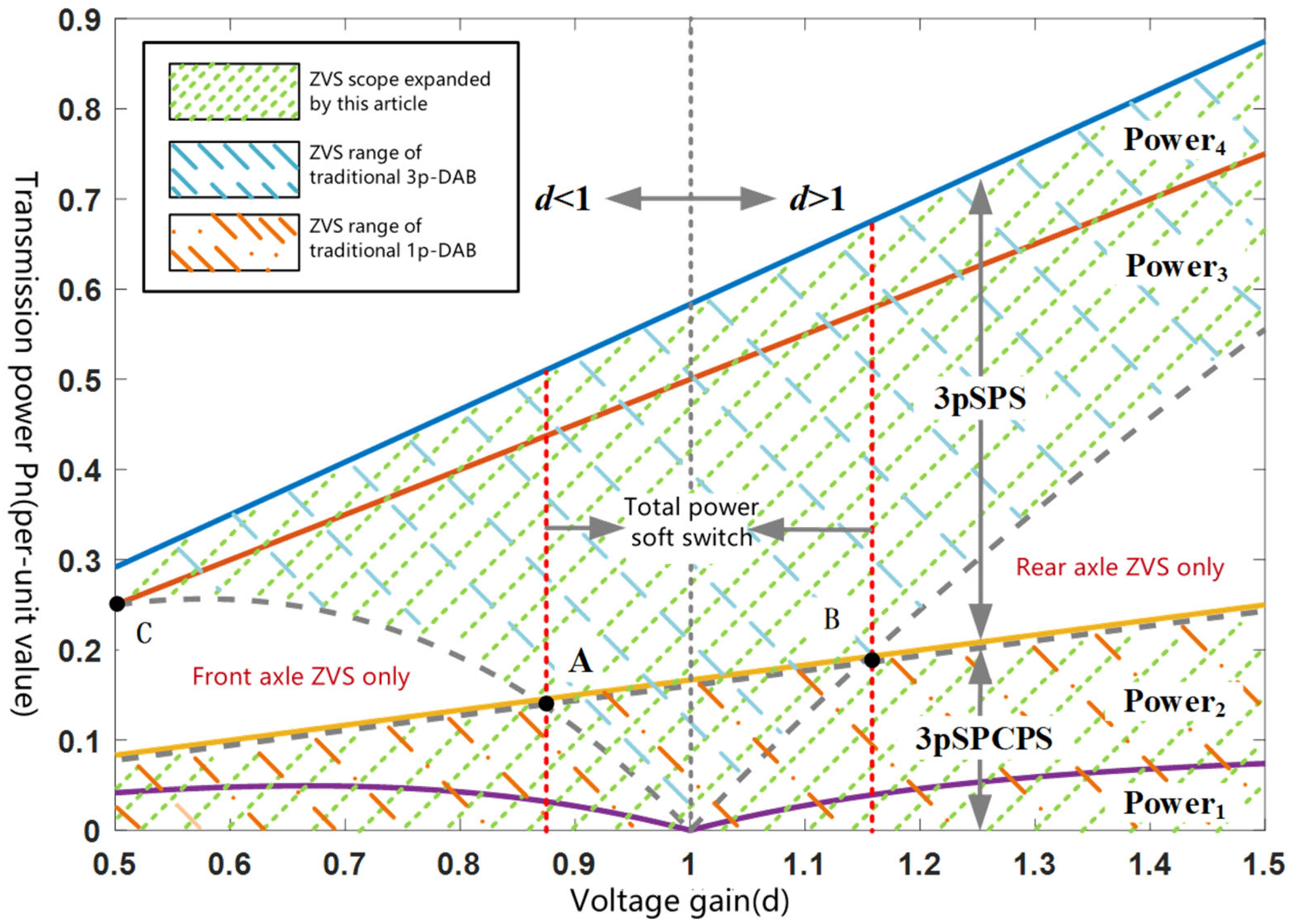
- (2)
- Soft-Switching Characteristics Analysis
- (3)
- Points C and D: As shown in the figure, points C and D are the intersections of the upper power limit of Y and the soft-switching boundary. When the duty ratio (d) is less than the gain corresponding to point C or greater than the gain corresponding to point D, all soft-switching characteristics are lost below Y, with an extremely narrow range of soft-switching across the full power range. Unless specifically required by the design, it is not recommended to set the voltage gain within this range. The expression for point C is as follows:
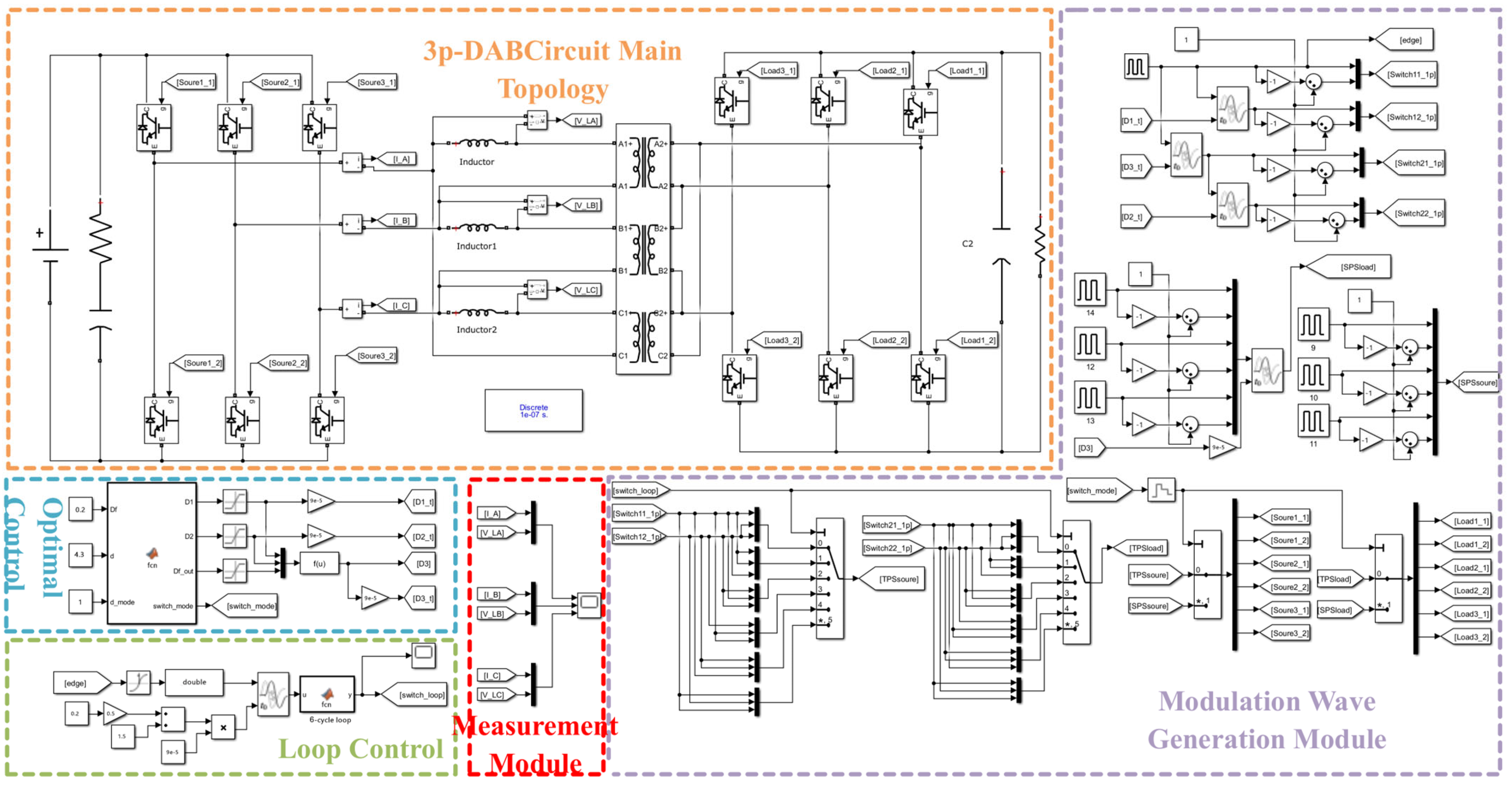
5. Simulation Verification
- (1)
- Simulation Verification of the Implementation Effectiveness and Feasibility of the 3pSPCPS
- (2)
- Simulation Verification of Multimodal Working Effects under Unified Global Operation
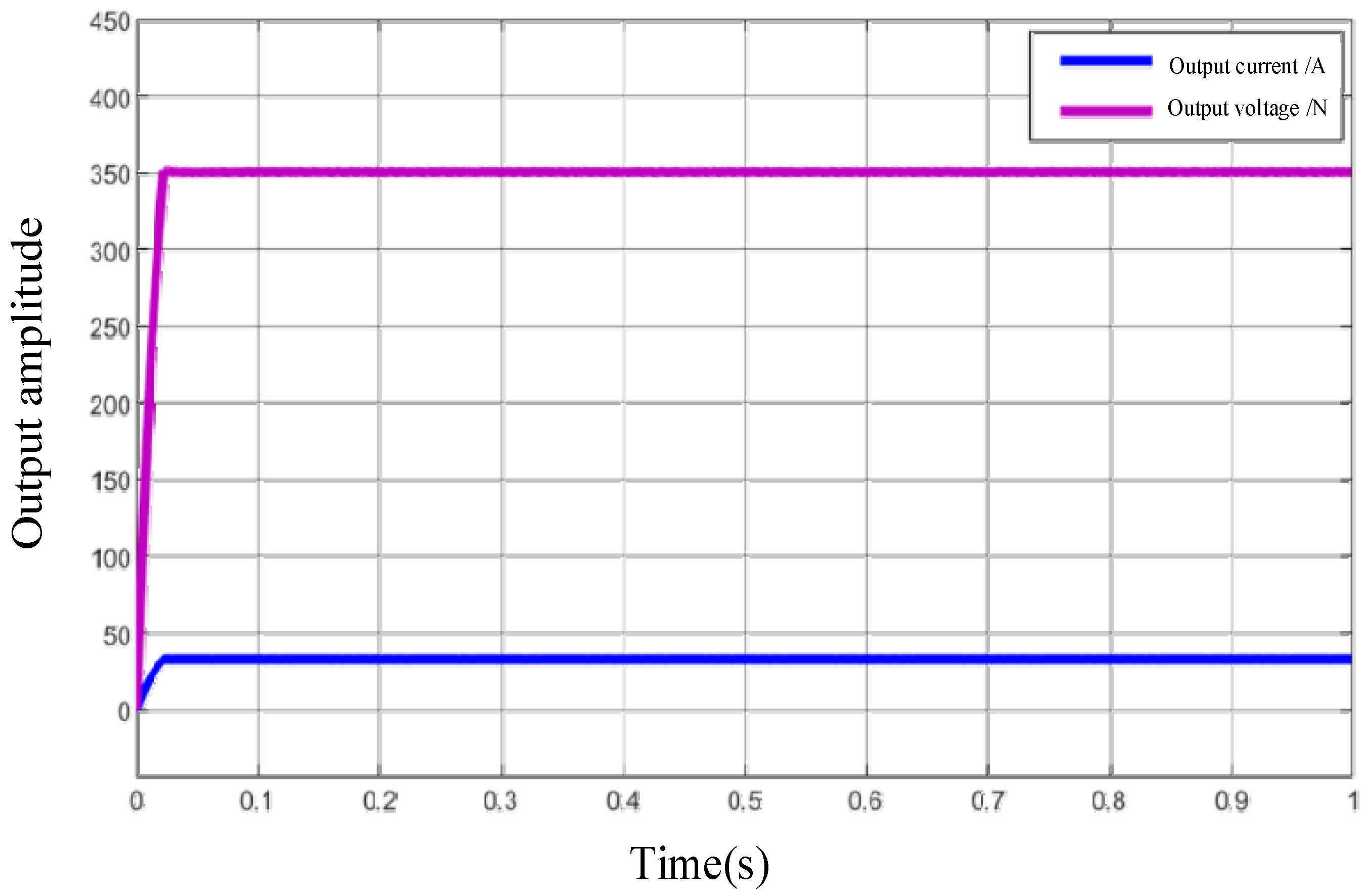
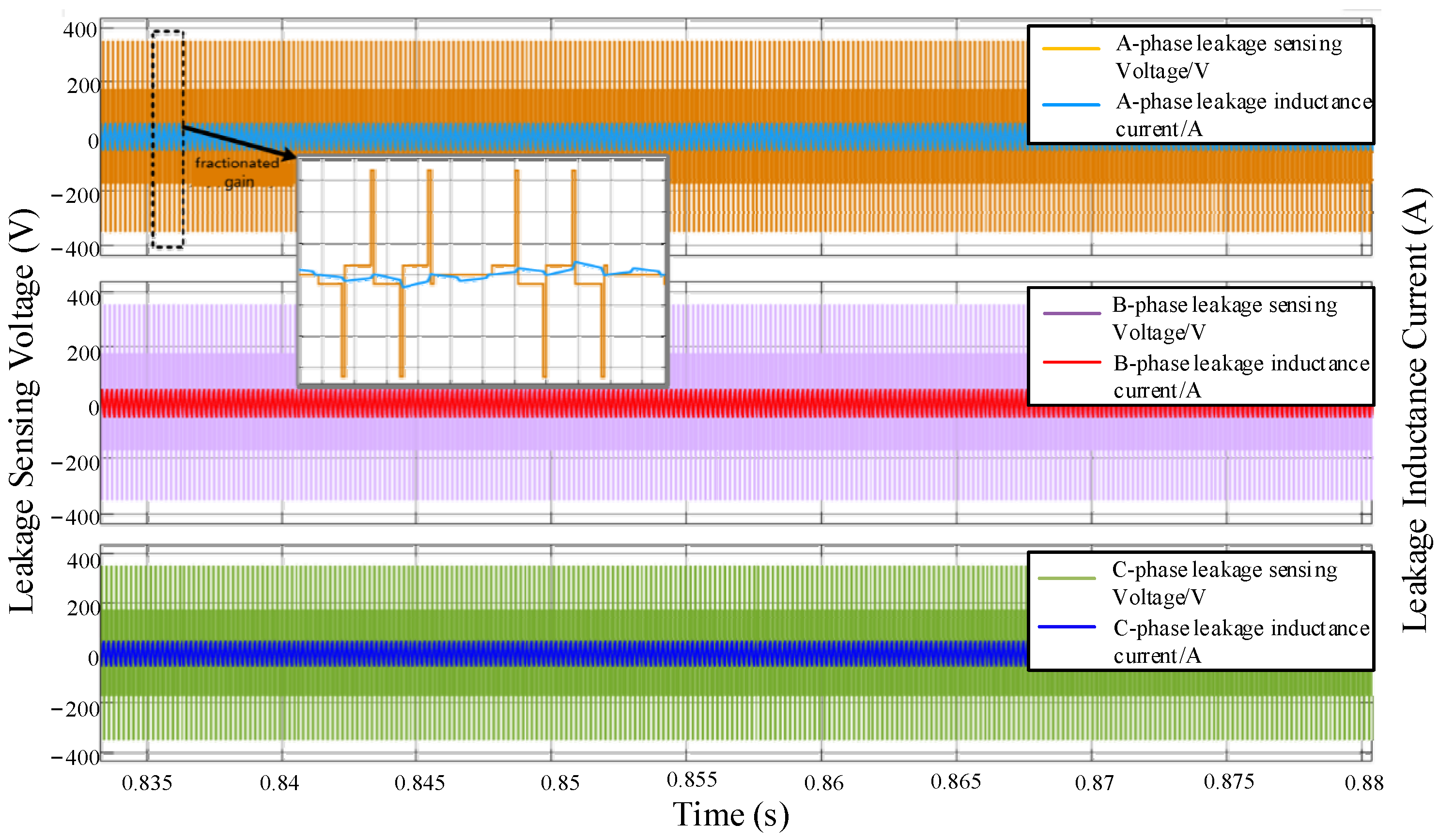
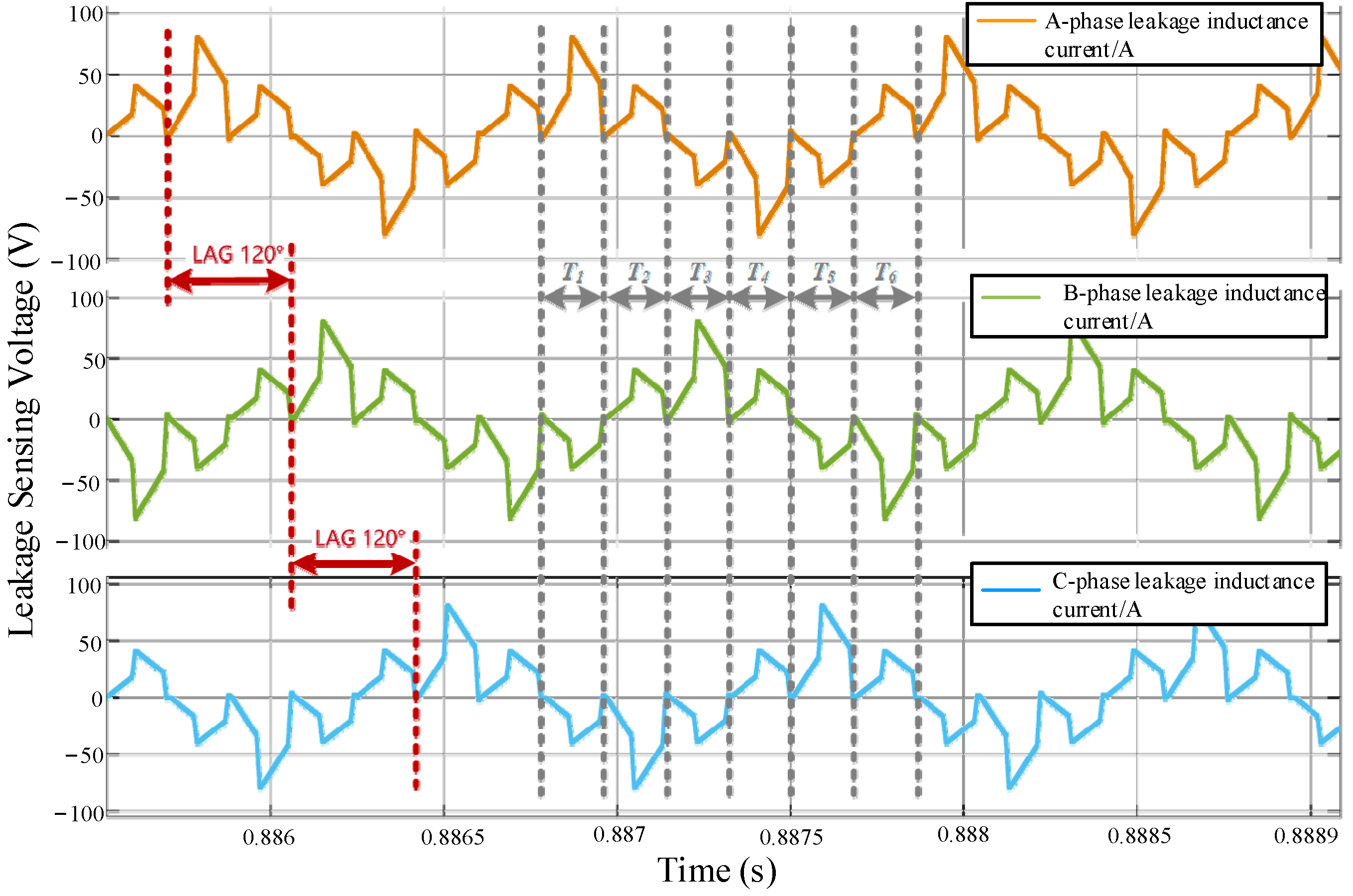
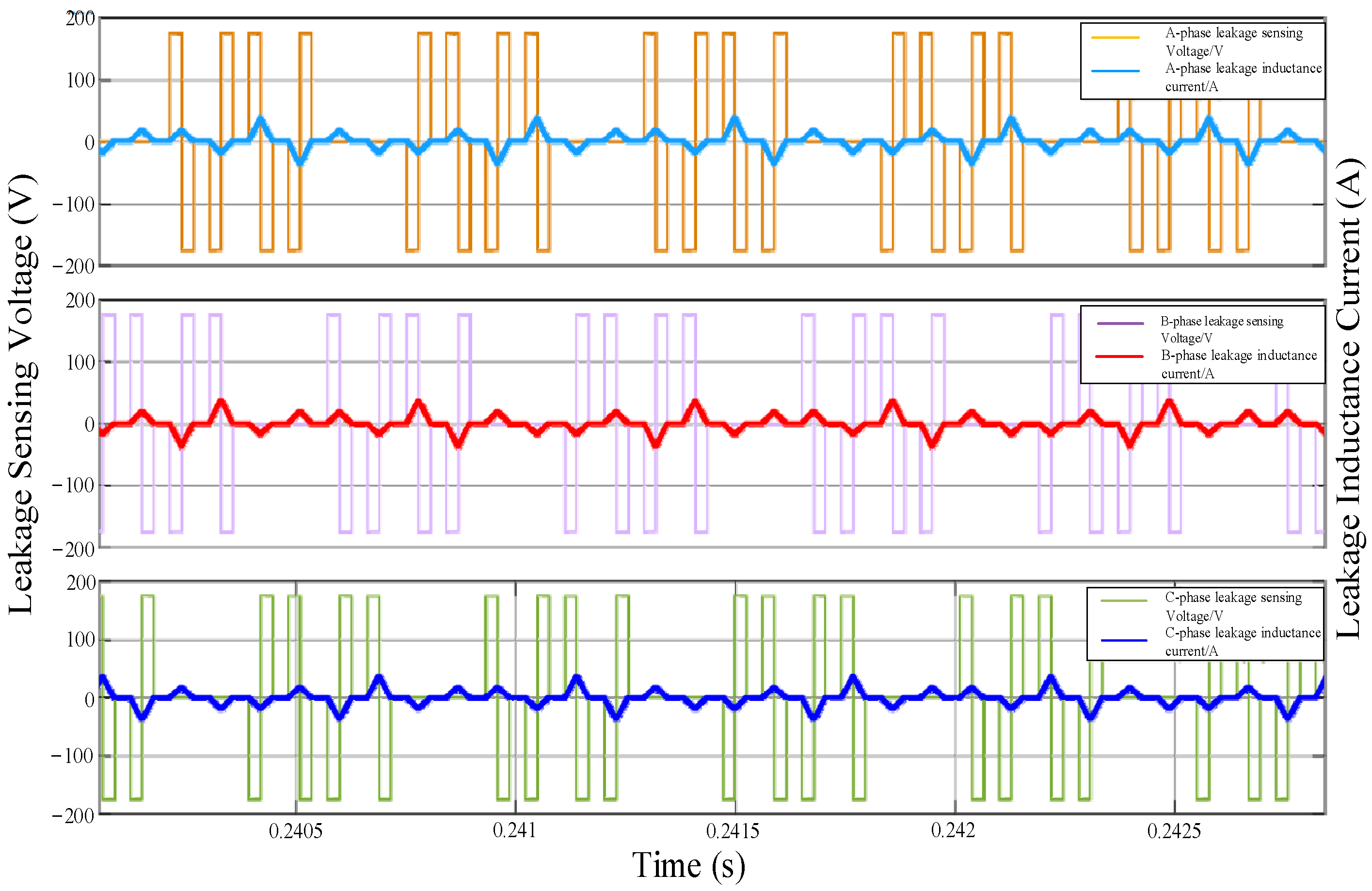
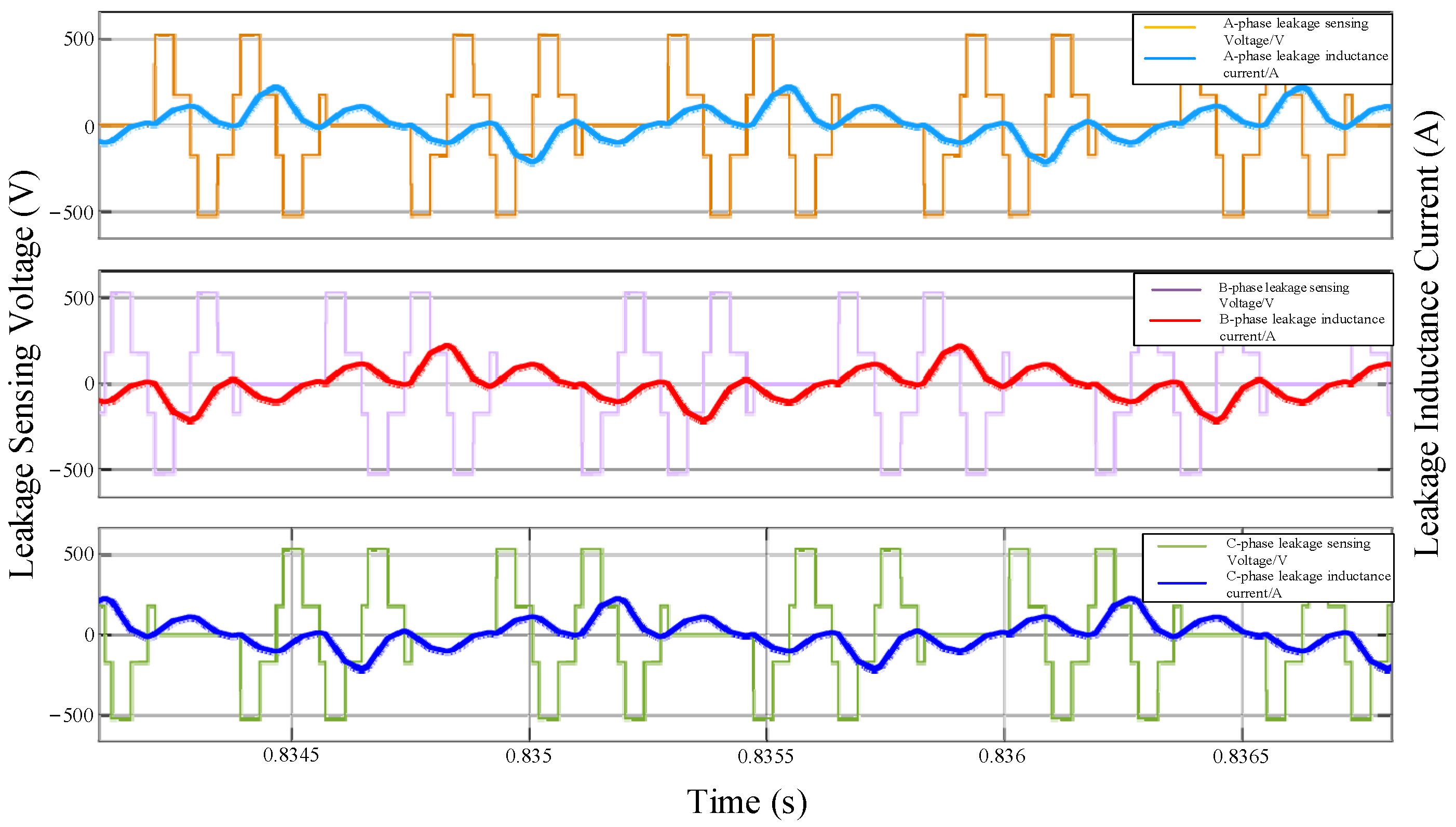
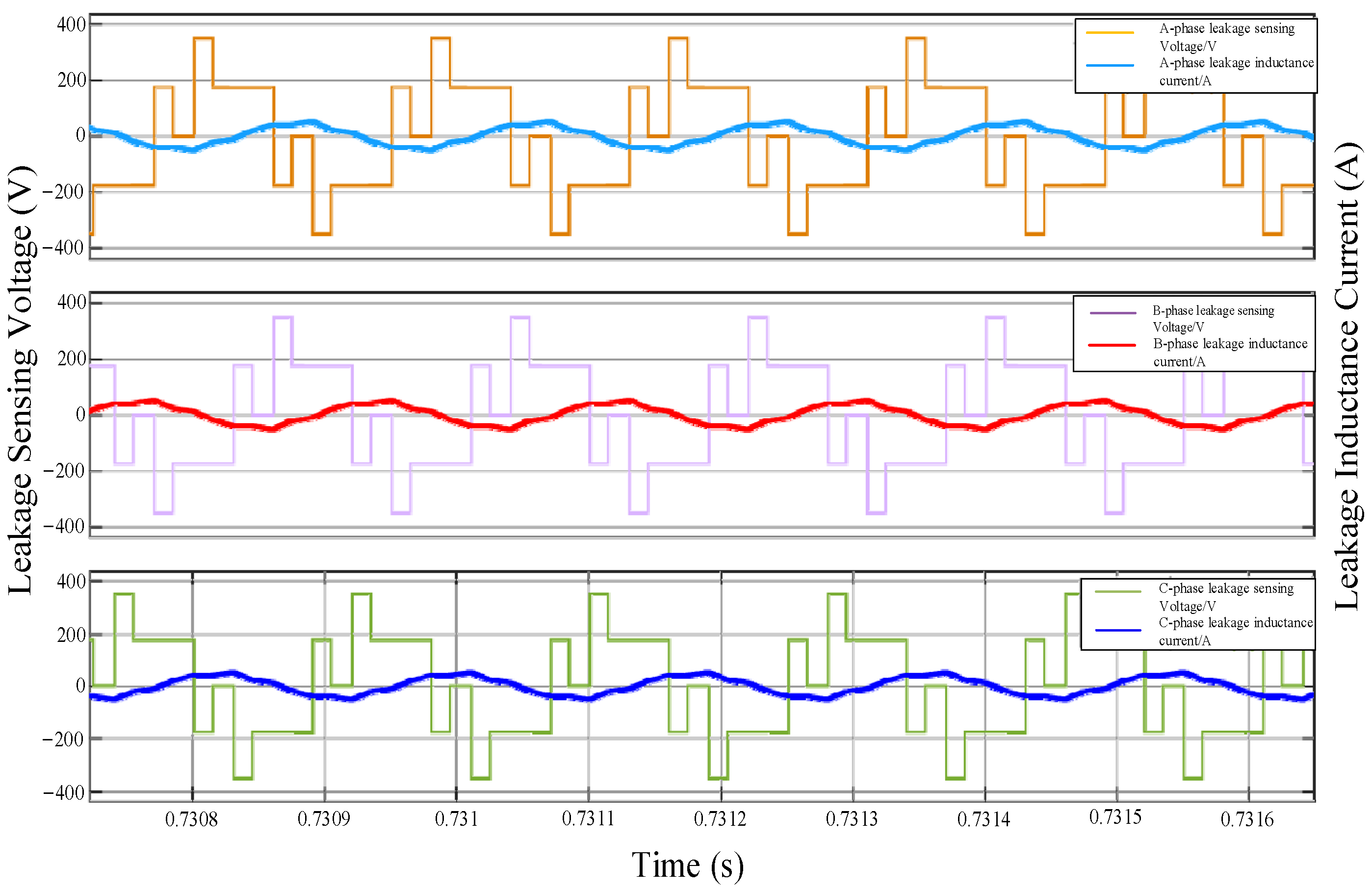
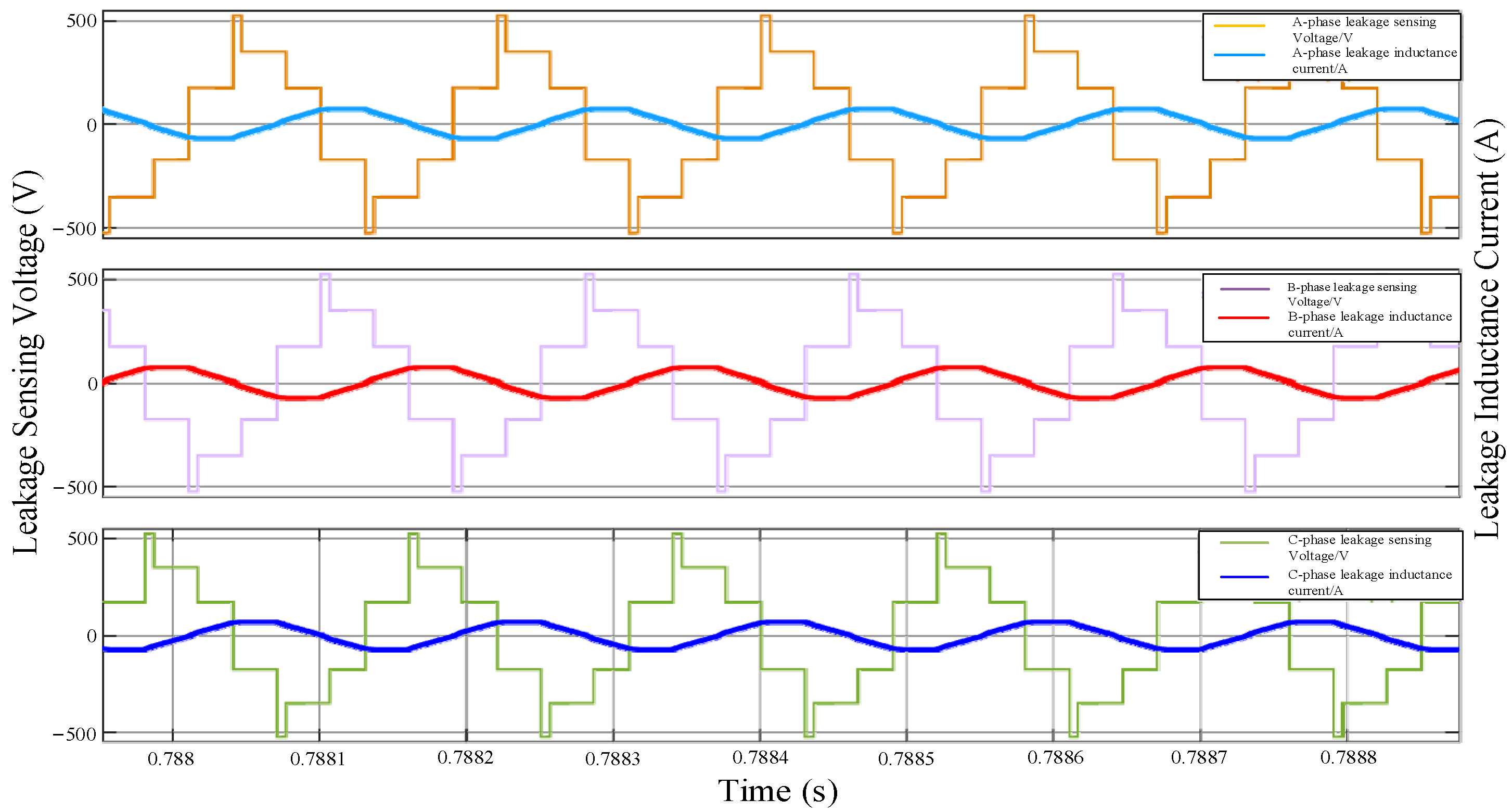
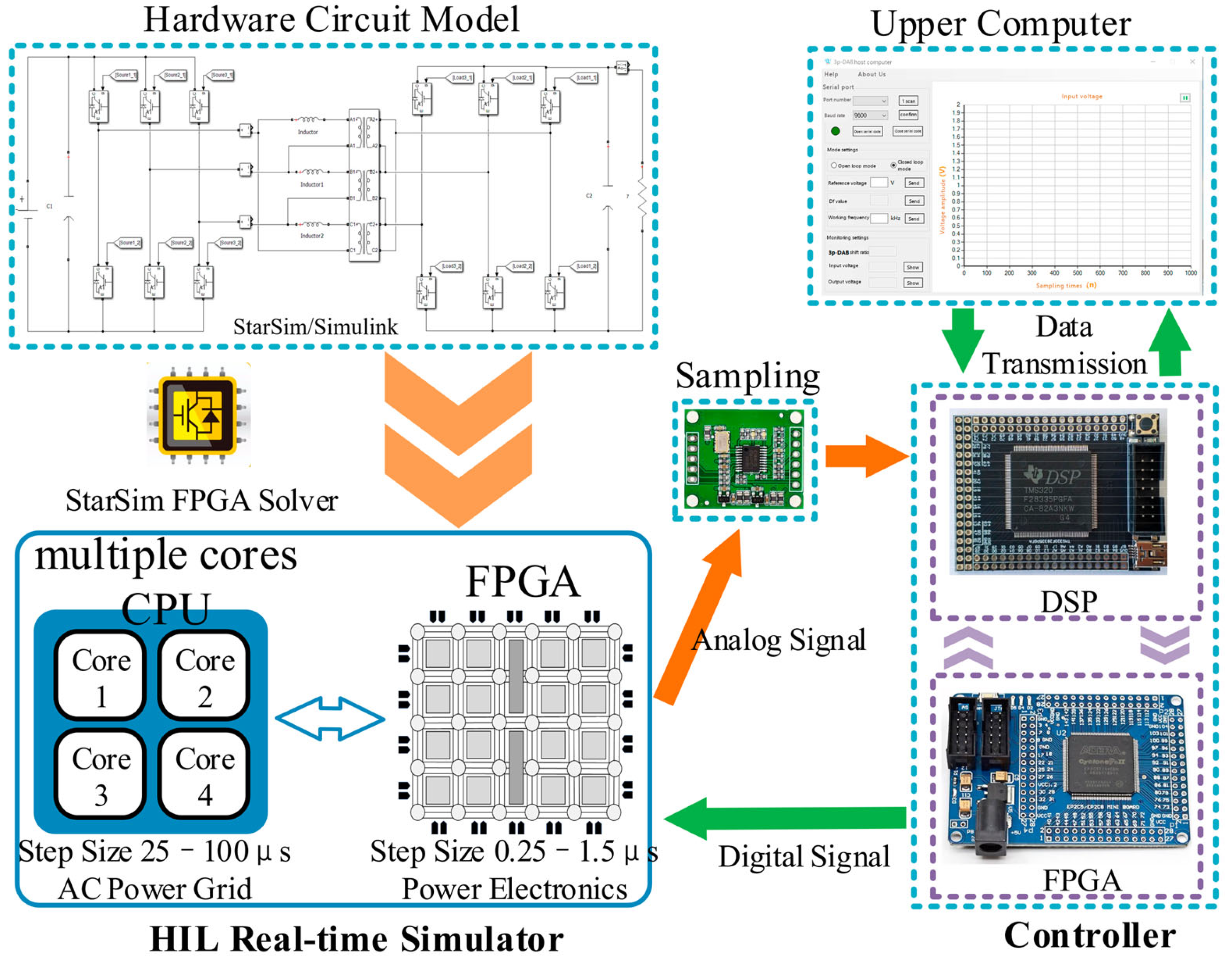
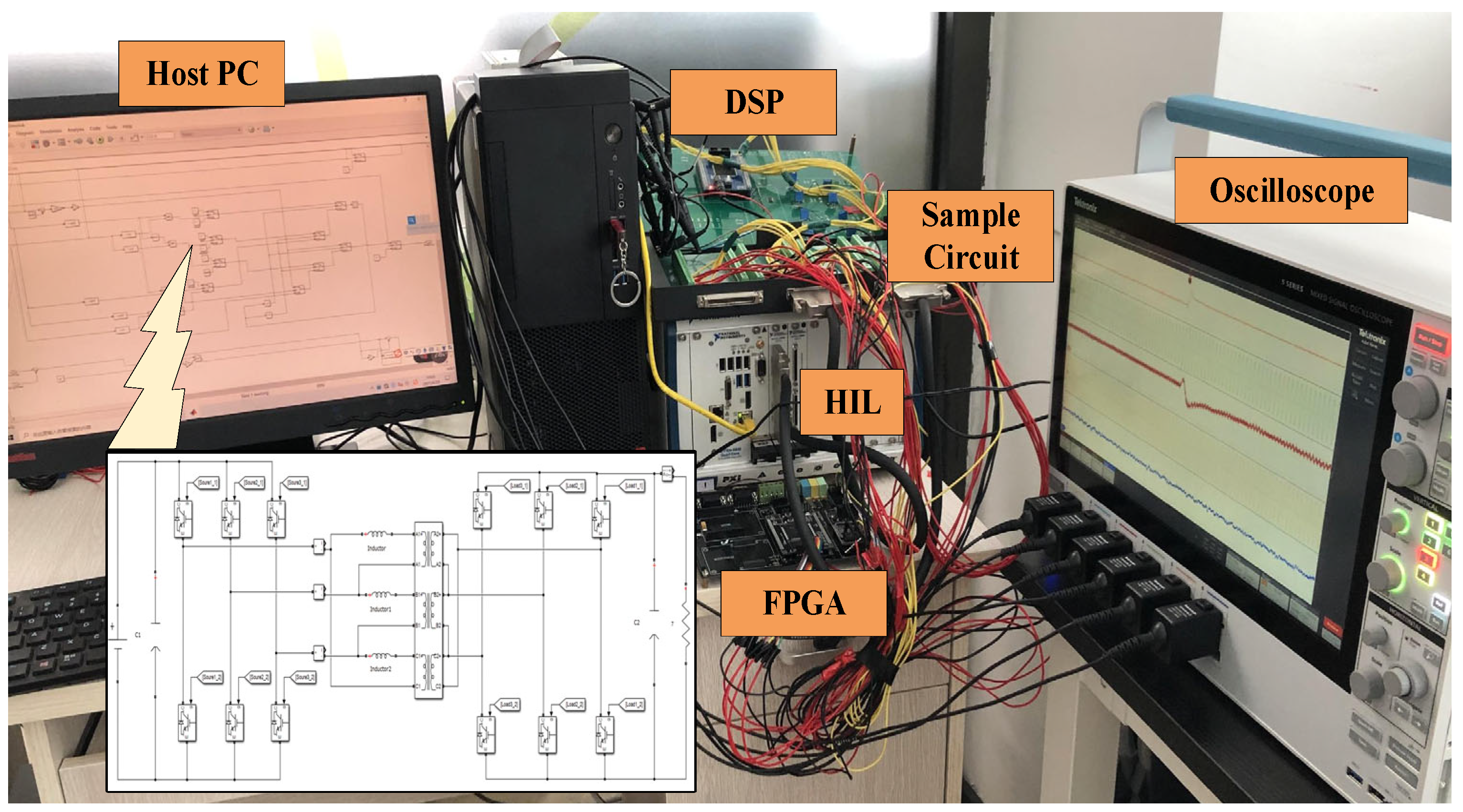
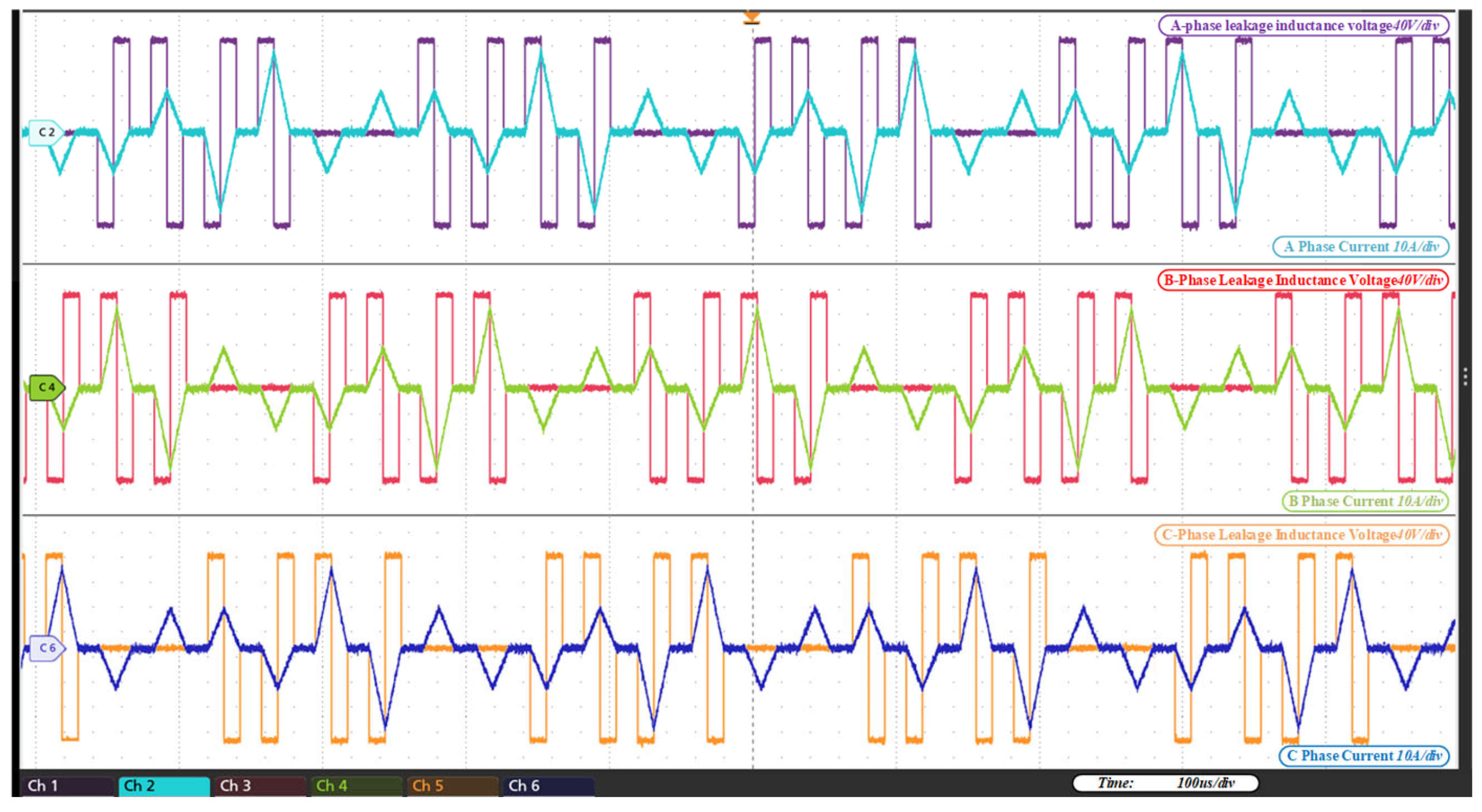
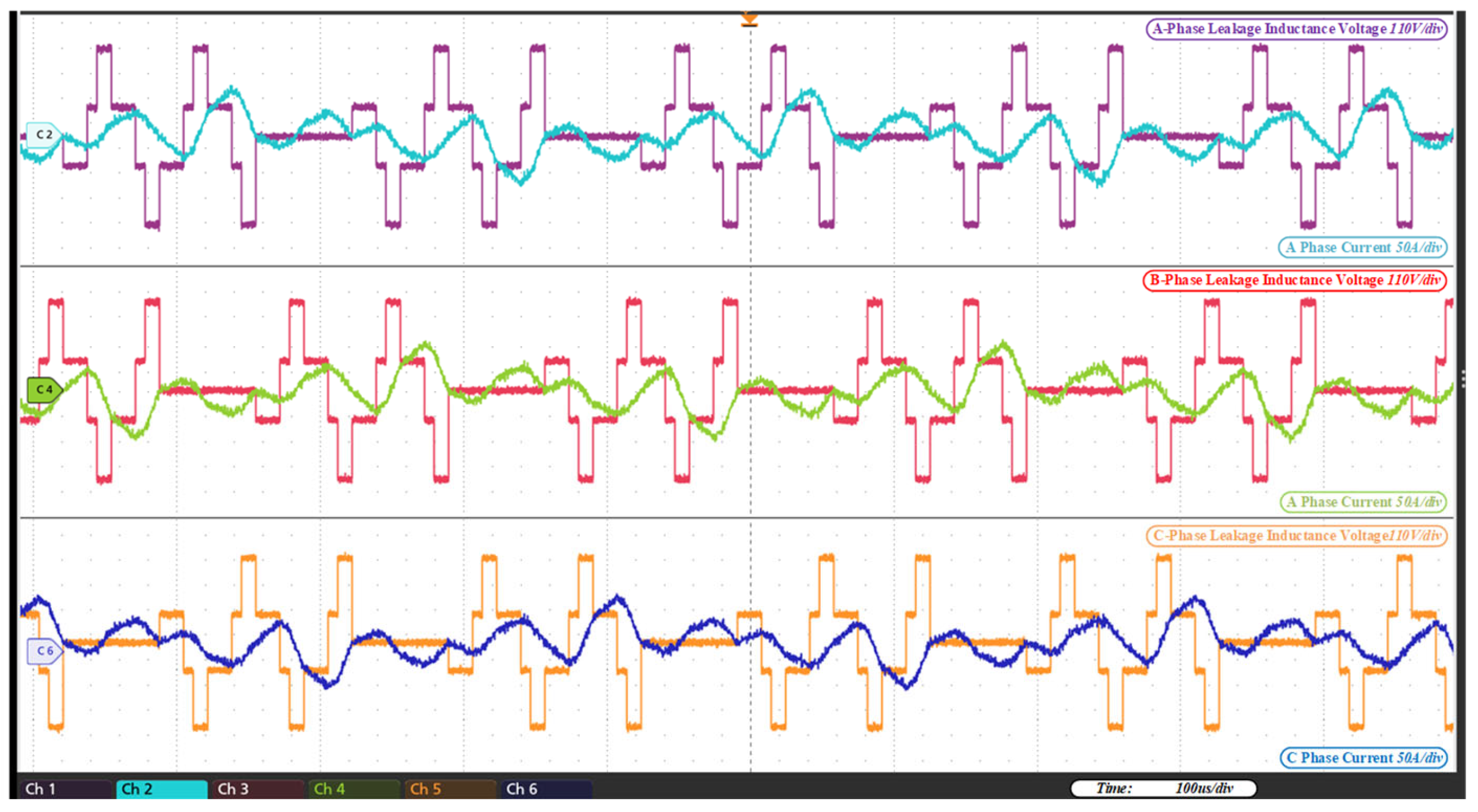
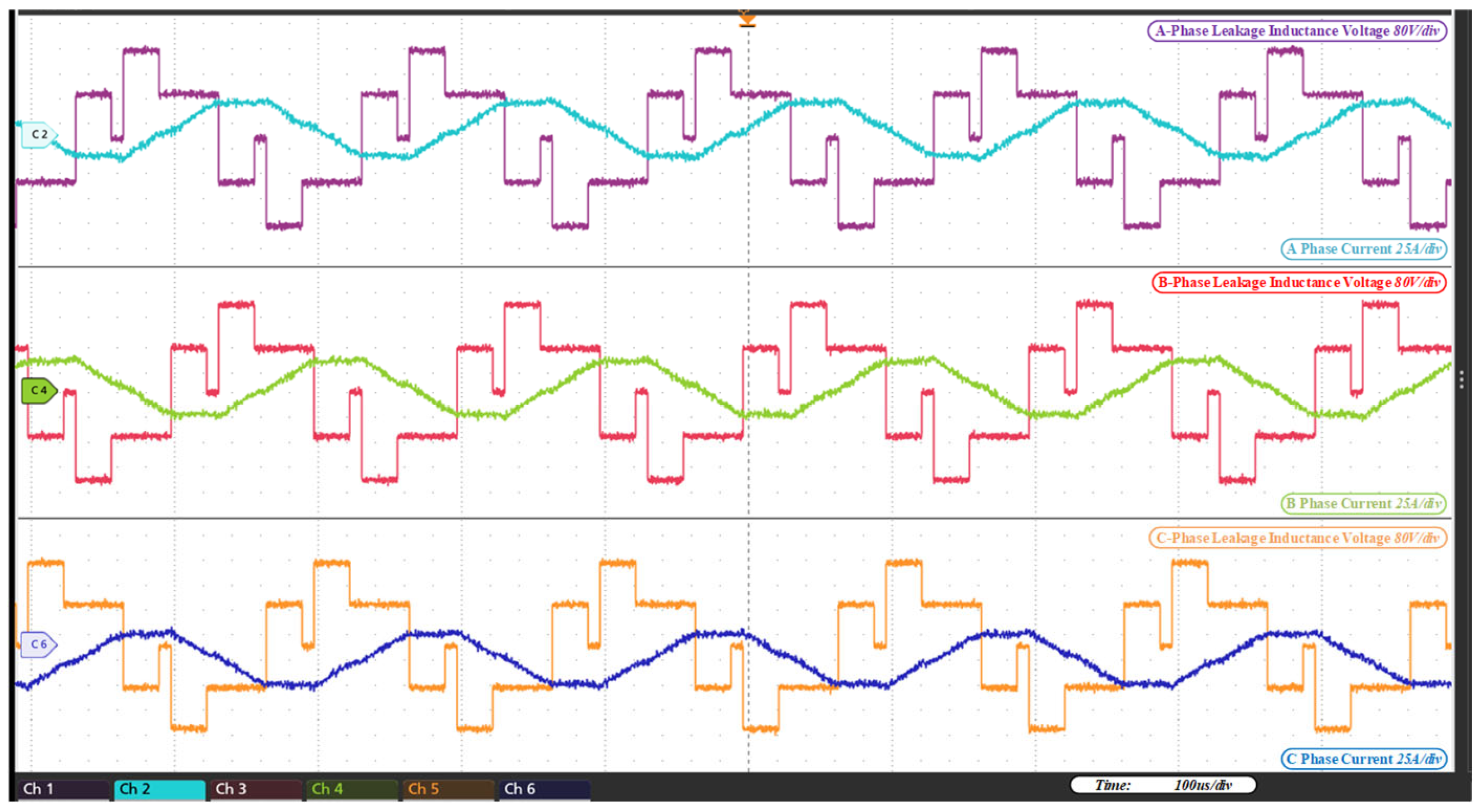
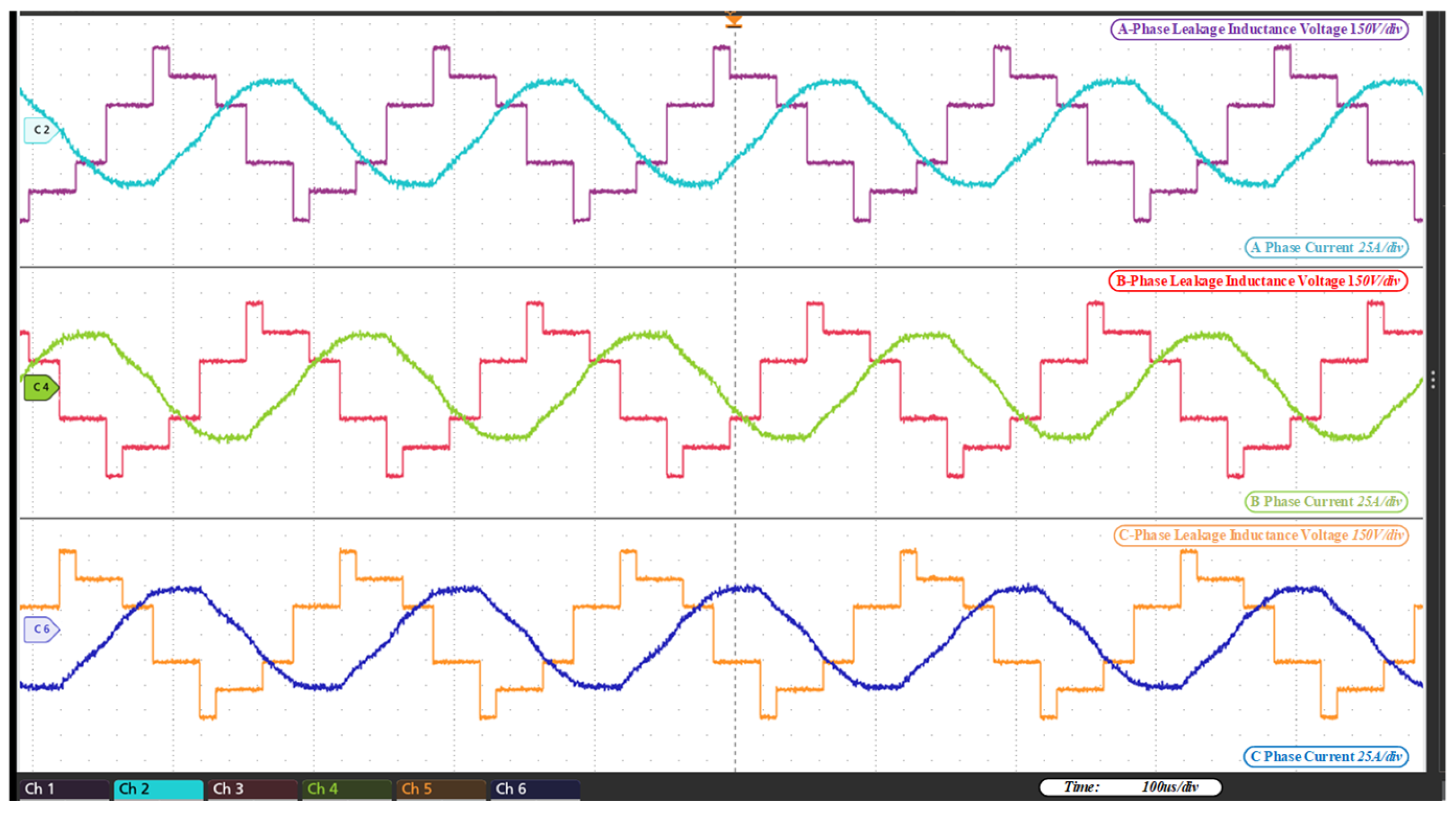
6. Experimental Verification
- (1)
- Operating performance of the mode under Power1 condition:
- (2)
- Operating performance of the mode under the Power2 condition:
- (3)
- Operating performance of the 3pSPCPS mode under condition:
- (4)
- Operating performance of the 3pSPCPS mode under condition:
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations Sets and Indices | Switching frequency | ||
| DAB | Dual Active Bridge | , | Reflected secondary-side voltage, Primary-side voltage between nodes a and b |
| 3p-DAB | Three-Phase Dual Active Bridge | , , | Duty ratios |
| 1p-DAB | Single-Phase Dual Active Bridge | Input voltage | |
| 3pSPCPS | Three-Phase Single-Cycle Parallel-Cycle Phase-Shifting | Series leakage inductance | |
| 3pSPS | Three-Phase Single-Phase-Shift | Operating mode selection variable | |
| TPS | Three-Phase-Shift | Power under 3-phase Single-Phase-Shift control | |
| SPS | Single-Phase-Shift | Phase-shift ratio in 3-phase SPS mode | |
| EPS | Extended Phase-Shift | A function of the normalized duty ratio | |
| APS | Asymmetric Phase-Shift | 3-phase Single-Phase-Shift control | |
| DCC | Duty Cycle Control | , , | Phase A, B, C current |
| RMS | Root Mean Square | Decision Variables | |
| ZVS | Zero Voltage Switching | Switching time instants within a clock cycle | |
| HIL | Hardware-in-the-Loop | On-state duty ratio of switch 1 | |
| DSP | Digital Signal Processor | On-state duty ratio of switch 2 | |
| FPGA | Field Programmable Gate Array | Optimized virtual phase-shift ratio | |
| Parameters and constants | The reciprocal of the voltage gain | ||
| Switching period | , | Primary voltage equals the reflected secondary voltage, Reflected secondary voltage equals the primary voltage | |
| , | Primary and secondary duty ratios | , , | Mapped duty ratios |
| Three-Phase Single-Cycle Parallel-Cycling Phase-Shift Control (Triangular Mode) | Base current for normalization, Base power for normalization | ||
| Three-Phase Single-Cycle Parallel-Cycling Phase-Shift Control (Trapezoidal Mode) | Virtual phase-shift ratio (used for mode switching and global unification) | ||
| Power delivered during switch-on interval | Maximum power of 1-phase DAB in mode M | ||
| Voltage gain | Boundary duty ratio for switching from 3pSPCPS to 3pSPS | ||
| Power1, Power2, Power3 and Power4 | Low-power region, Medium-power region, Quasi-high-power region, High-power region | Power at the boundary of high-power intermediate state | |
References
- Energy Crisis vs. Energy Revolution; World Knowledge Ltd.: Slough, UK, 2021; Volume 23, pp. 12–13.
- Liu, F. International Energy Agency: Global Electricity Demand Will Accelerate. Oil Gas New Energy 2023, 35, 31. [Google Scholar]
- Zhao, H. New Challenges in Energy Security During the International Energy Transition. Natl. Secur. Res. 2022, 6, 88–104. [Google Scholar]
- Jiang, R. The Global Economic Impact of the Energy Crisis. World Knowl. 2022, 21, 72–73. [Google Scholar]
- Saranyaa, J.S.; Peer, F.A. A Comprehensive Survey on the Current Trends in Improvising the Renewable Energy Incorporated Global Power System Market. IEEE Access 2023, 11, 24016–24038. [Google Scholar] [CrossRef]
- Wang, R.; Ma, D.; Li, M.-J.; Sun, Q.; Zhang, H.; Wang, P. Accurate Current Sharing and Voltage Regulation in Hybrid Wind/Solar Systems: An Adaptive Dynamic Programming Approach. IEEE Trans. Consum. Electron. 2022, 68, 261–272. [Google Scholar] [CrossRef]
- International Energy Agency. The Worst Global Energy Crisis May Still Be Ahead. China Foreign Energy 2022, 27, 103. [Google Scholar]
- Wang, R.; Hu, J.; Sun, Q.; Zhang, H.; Wang, P. Electric Vehicle-Research on Energy Reciprocity Control Strategy. Sci. China Technol. Sci. 2022, 52, 957–970. [Google Scholar]
- Wang, R.; Li, M.J.; Wang, Y.; Sun, Q.; Zhang, P. A Study of Novel Real-Time Power Balance Strategy with Virtual Asynchronous Machine Control for Regional Integrated Electric-Thermal Energy Systems. Sci. China Technol. Sci. 2024, 67, 2074–2089. [Google Scholar] [CrossRef]
- Zhai, S.; Zhang, Z.; Wang, W.; Li, X.; Chen, Y. Research on Energy Mutual Aid Control Strategy for Electric Vehicles. Integr. Smart Energy 2025, 2025, 1–9. [Google Scholar]
- Wang, R.; Yu, X.; Sun, Q.; Li, D.; Gui, Y.; Wang, P. The Integrated Reference Region Analysis for Parallel DFIGs’ Interfacing Inductors. IEEE Trans. Power Electron. 2024, 39, 7632–7642. [Google Scholar] [CrossRef]
- Wang, R.; Sun, Q.; Hu, W.; Li, Y.; Ma, D.; Wang, P. SoC-Based Droop Coefficients Stability Region Analysis of the Battery for Stand-Alone Supply Systems with Constant Power Loads. IEEE Trans. Power Electron. 2021, 36, 7866–7879. [Google Scholar] [CrossRef]
- Wang, R.; Sun, Q.; Zhang, P.; Gui, Y.; Qin, D.; Wang, P. Reduced-Order Transfer Function Model of the Droop-Controlled Inverter via Jordan Continued-Fraction Expansion. IEEE Trans. Energy Convers. 2020, 35, 1585–1595. [Google Scholar]
- Wang, Q.; Zhang, Z.; Liu, B.; Han, D.; Zhao, M.; Guo, J.; Li, S.; Guo, Y. Global Optimization Control of Minimum Reflux Power for Dual Active Bridge Converters Under Dual Phase Shift Control. Power Syst. Technol. 2024, 48, 3921–3930. [Google Scholar]
- Yang, X.; Wang, J.; Kong, L.; Du, Y.; Zhang, T. Efficiency Optimization Method for Dual Active Bridge Converters Under Voltage Mismatch Operating Conditions. Trans. China Electrotech. Soc. 2022, 37, 6239–6251. [Google Scholar]
- Zeng, J.; Zhang, C.; Cao, B.; Yu, X.; Lan, Z.; Zou, B.; Wang, T.; Cao, Y. Fundamental Circulating Current Optimization Control Strategy for Dual Active Bridge DC-DC Converter Based on Unified Phase-Shifting Control Model. Electr. Power Autom. Equip. 2024, 44, 74–81. [Google Scholar]
- Sun, J.; Qiu, L.; Liu, X.; Ma, J.; Rodriguez, J.; Fang, Y. Model-Free Moving-Discretized-Control-Set Predictive Control for Three-Phase Dual-Active-Bridge Converters. IEEE Trans. Power Electron. 2024, 39, 9160–9173. [Google Scholar] [CrossRef]
- Schulz, G.; Bauman, J. Time-Domain Analysis and Optimization of a Three-Phase Dual-Active-Bridge Converter with Variable Duty-Cycle Modulation. IEEE Trans. Power Electron. 2023, 38, 500–510. [Google Scholar] [CrossRef]
- Chen, H.; Ouyang, S.; Liu, J.; Li, X. An Asymmetrical Phase-Shift Scheme of Three-Phase Dual Active Bridge with Minimum Current Root-Mean-Square Value Control. IEEE Trans. Power Electron. 2022, 37, 6320–6333. [Google Scholar] [CrossRef]
- Van Hoek, H.; Neubert, M.; De Doncker, R.W. Enhanced Modulation Strategy for a Three-Phase Dual Active Bridge-Boosting Efficiency of an Electric Vehicle Converter. IEEE Trans. Power Electron. 2013, 28, 5499–5507. [Google Scholar] [CrossRef]
- Tu, C.; Guan, L.; Xiao, F.; Liu, B.; Ge, Q.; Lan, Z. Modal Analysis Method for Dual Active Bridge DC-DC Converters. Proc. CSEE 2019, 39, 5468–5479. [Google Scholar]
- Gong, L.; Li, W.; Xu, J.; Li, H.; Wang, Y. Hybrid Multi-Phase Shifting Control Strategy for High-Frequency DAB Converters Based on Multi-Objective Optimization. Proc. CSEE 2024, 44, 1517–1534. [Google Scholar]
- Sun, B.; Li, J.; Zhang, Q.; Yang, Z.; Deng, X. Dual Phase-Shifted Segmented Control of Minimum Reflux Power for Bidirectional Full-Bridge DC-DC Converter Based on ZVS. Acta Energiae Solaris Sin. 2023, 44, 39–48. [Google Scholar]
- Ren, Q.; Ai, S. DAB Three Degree of Freedom Optimization Control Strategy for the Entire Operating Range. Chin. J. Electr. Eng. 2020, 40, 2500–2510. [Google Scholar]
- Yu, H.; Hang, L.; Zhang, X.; He, Z.; He, Y.; Shen, L. Globally Unified ZVS and Quasi-Optimal Minimum Conduction Loss Modulation of DAB Converters. IEEE Trans. Transp. Electrif. 2022, 8, 3989–4000. [Google Scholar] [CrossRef]
- Wang, R.; Jiang, S.; Ma, D.; Sun, Q.; Zhang, H.; Wang, P. The Energy Management of Multiport Energy Router in Smart Home. IEEE Trans. Consum. Electron. 2022, 68, 344–353. [Google Scholar] [CrossRef]
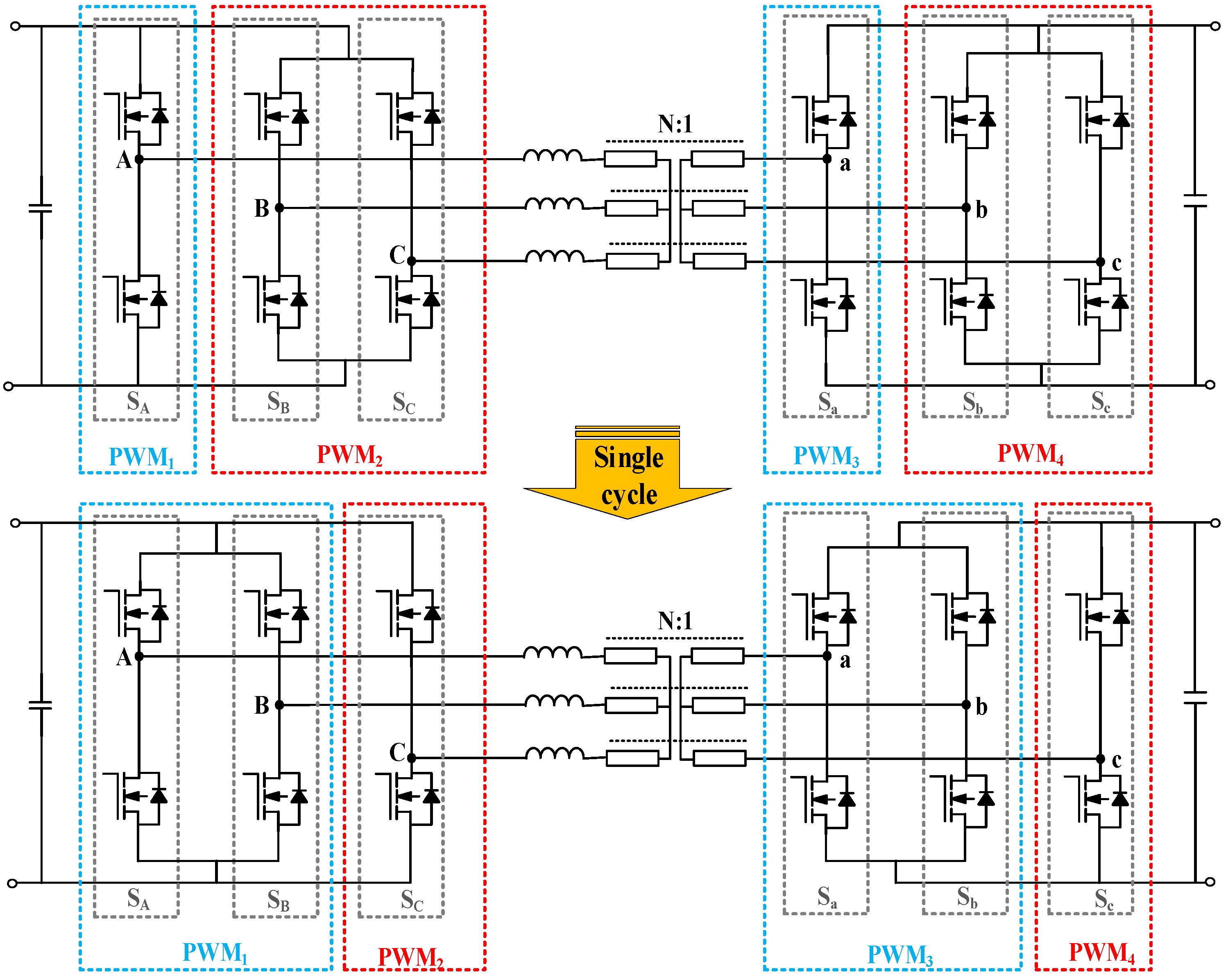
| Non-Cyclic | Fixed Cycle | Single Cycle | |
|---|---|---|---|
| Single phase | Advantages: Simple implementation, high reliability Disadvantages: Circuit redundancy | Advantages: Higher reliability Disadvantages: Inefficient circuit utilization | Advantages: Higher reliability Disadvantages: Inefficient circuit utilization |
| Parallel phase | Advantages: Efficient circuit utilization Disadvantages: Uneven heating, high requirements for parallel symmetry | Advantages: Efficient circuit utilization, uniform heating Disadvantages: Control requires additional costs, fluctuations in the cycling process, high requirements for parallel symmetry | Advantages: High circuit utilization, uniform heating, low thermal design difficulty Disadvantages: High requirements for parallel symmetry |
| T1 | T2 | T3 | T4 | T5 | T6 | T7 | |
|---|---|---|---|---|---|---|---|
| PWM1 | SA | SA, SB | SB | SB, SC | SC | SC, SA | SA |
| PWM2 | SB, SC | SC | SC, SA | SA | SA, SB | SB | SB, SC |
| Condition | Power Range | Operating Mode | Optimization |
|---|---|---|---|
| Condition | Power Range | Operating Mode | Optimization |
|---|---|---|---|
| Voltage Gain | Condition | Power Range | Operating Mode | Optimization |
|---|---|---|---|---|
| Power Range | Operating Mode | Optimization Strategy |
|---|---|---|
| Voltage Gain | ||
|---|---|---|
| Condition | (Low Power) | (Medium Power) | (Quasi-High Power) | (High Power) |
|---|---|---|---|---|
| range | ||||
| Operating mode | ||||
| Optimization | ||||
| Voltage Gain | Range | Condition | Control Mode | Operation Plan |
|---|---|---|---|---|
| hysteresis zone | ||||
| medium and low power level | ||||
| hysteresis zone | ||||
| hysteresis zone | ||||
| Parameters | Numerical Value |
|---|---|
| Input voltage U | 350 V |
| Input capacitor C1 | 2200 μF |
| Output capacitor C2 | 2200 μF |
| High-frequency transformer ration | 1.1 |
| 3p-DAB leakage inductance La/Lb/Lc | 0.25 mH |
| Switching frequency fs | 5.6 kHz |
| Technical Indicators | Parameters | Technical Indicators | Parameters |
|---|---|---|---|
| System Rated Power: | 5 kW | Switching Frequency: | 10 kHz |
| Maximum Transmission Power: | 10 kW | Input Voltage: | 300 V |
| Input Voltage Overshoot: | <10% | Output Voltage: | 150 V–400 V |
| Input Voltage Droop: | <10% | Output Voltage Ripple Ratio: | <5% |
| Electrical Parameters | Parameters |
|---|---|
| Switching frequency: | 10 kHz |
| Number of MOSFETs: | 12 |
| Input capacitor C1: | 1000 µF |
| Input capacitor C2: | 1500 µF |
| Leakage inductance L: | 140 µH |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Huang, C.; Jiang, S.; Wang, R. Multimodal Switching Control Strategy for Wide Voltage Range Operation of Three-Phase Dual Active Bridge Converters. Processes 2025, 13, 1921. https://doi.org/10.3390/pr13061921
Zhao C, Huang C, Jiang S, Wang R. Multimodal Switching Control Strategy for Wide Voltage Range Operation of Three-Phase Dual Active Bridge Converters. Processes. 2025; 13(6):1921. https://doi.org/10.3390/pr13061921
Chicago/Turabian StyleZhao, Chenhao, Chuang Huang, Shaoxu Jiang, and Rui Wang. 2025. "Multimodal Switching Control Strategy for Wide Voltage Range Operation of Three-Phase Dual Active Bridge Converters" Processes 13, no. 6: 1921. https://doi.org/10.3390/pr13061921
APA StyleZhao, C., Huang, C., Jiang, S., & Wang, R. (2025). Multimodal Switching Control Strategy for Wide Voltage Range Operation of Three-Phase Dual Active Bridge Converters. Processes, 13(6), 1921. https://doi.org/10.3390/pr13061921






