Power Supply Resilience Under Typhoon Disasters: A Recovery Strategy Considering the Coordinated Dispatchable Potential of Electric Vehicles and Mobile Energy Storage
Abstract
1. Introduction
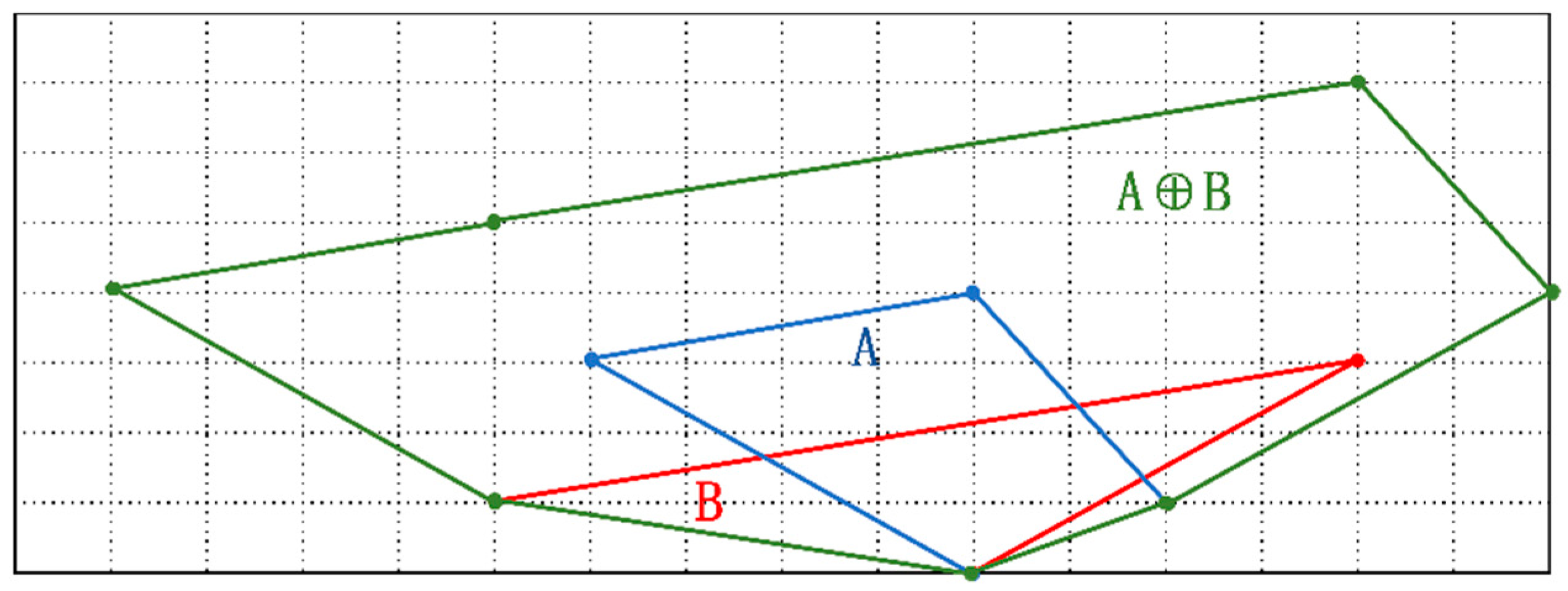
2. EV Dispatchable Potential Based on Minkowski Summation and Data-Driven Approaches
2.1. EV Individual Modeling
2.2. Generalized Energy Storage Models
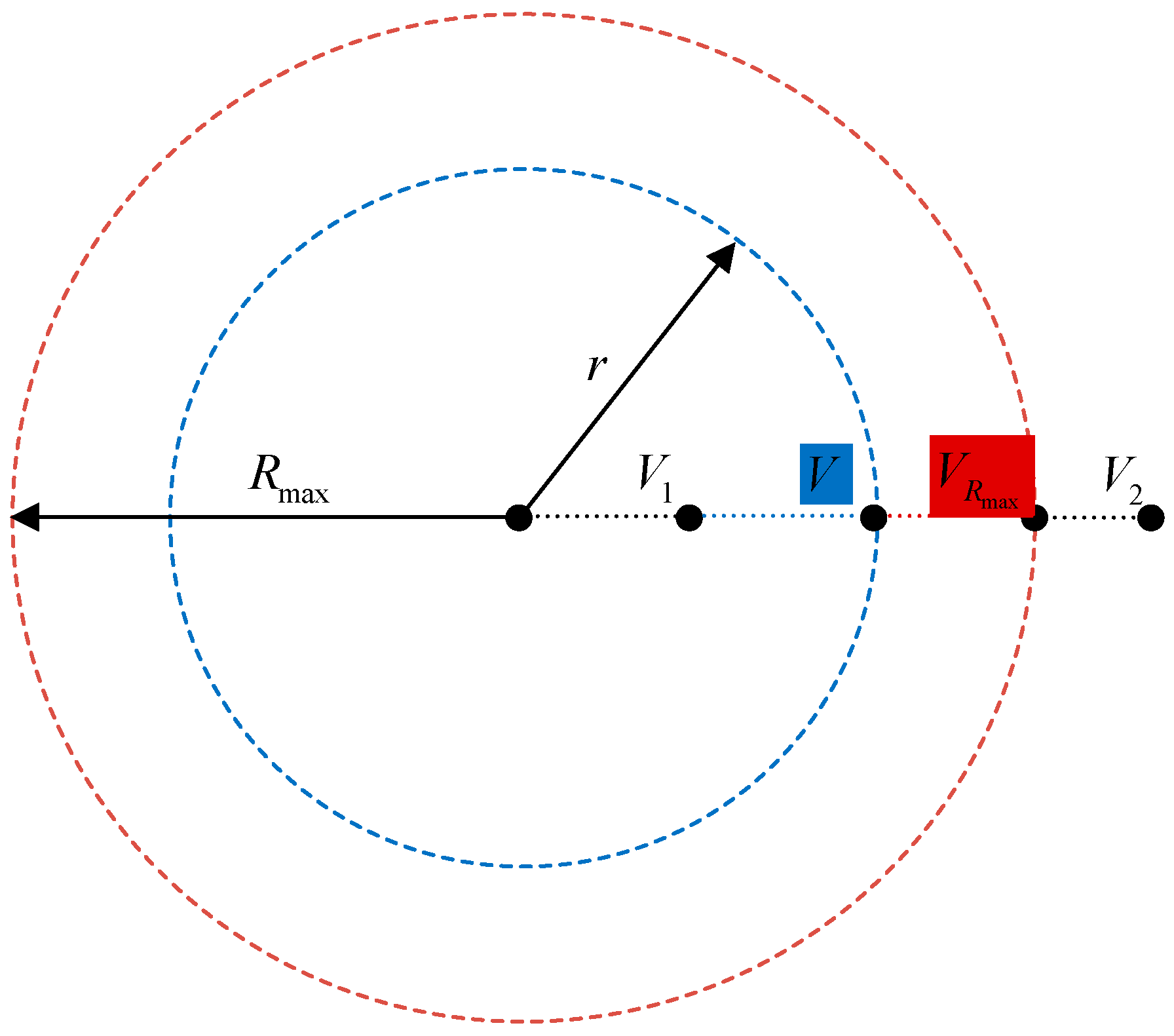
3. Overhead Line Fault Rate Model Based on Typhoon Disaster Process
3.1. Typhoon Impact Mechanisms
3.2. Generation of Fault Scenarios for Distribution Network Line Towers Under Typhoon Conditions
4. Strategies for Multi-Source Collaborative Restoration of Distribution Networks
4.1. Objective Function
4.2. Constraints
4.2.1. Constraints for Scheduling Mobile Energy Storage Systems
4.2.2. Radiality Constraints in Distribution Networks
4.2.3. Distribution Network Operational Constraints
5. Example Analyses
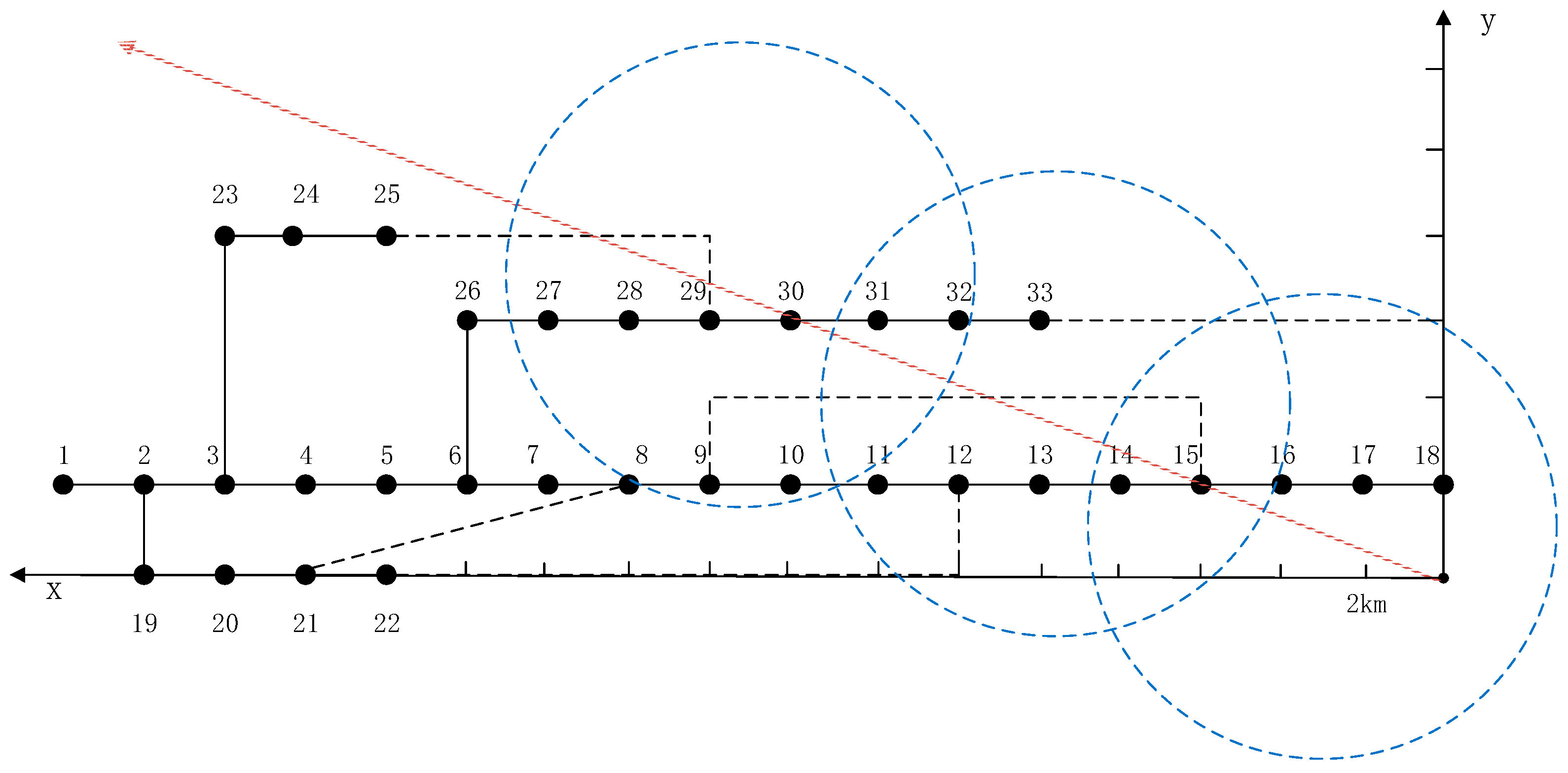
5.1. Arithmetic Examples and Their Parameterization
5.2. Considering the Time-Varying Failure Rate of Distribution Lines Under the Influence of Typhoons
5.3. Power Supply Restoration Strategy and Result Analysis
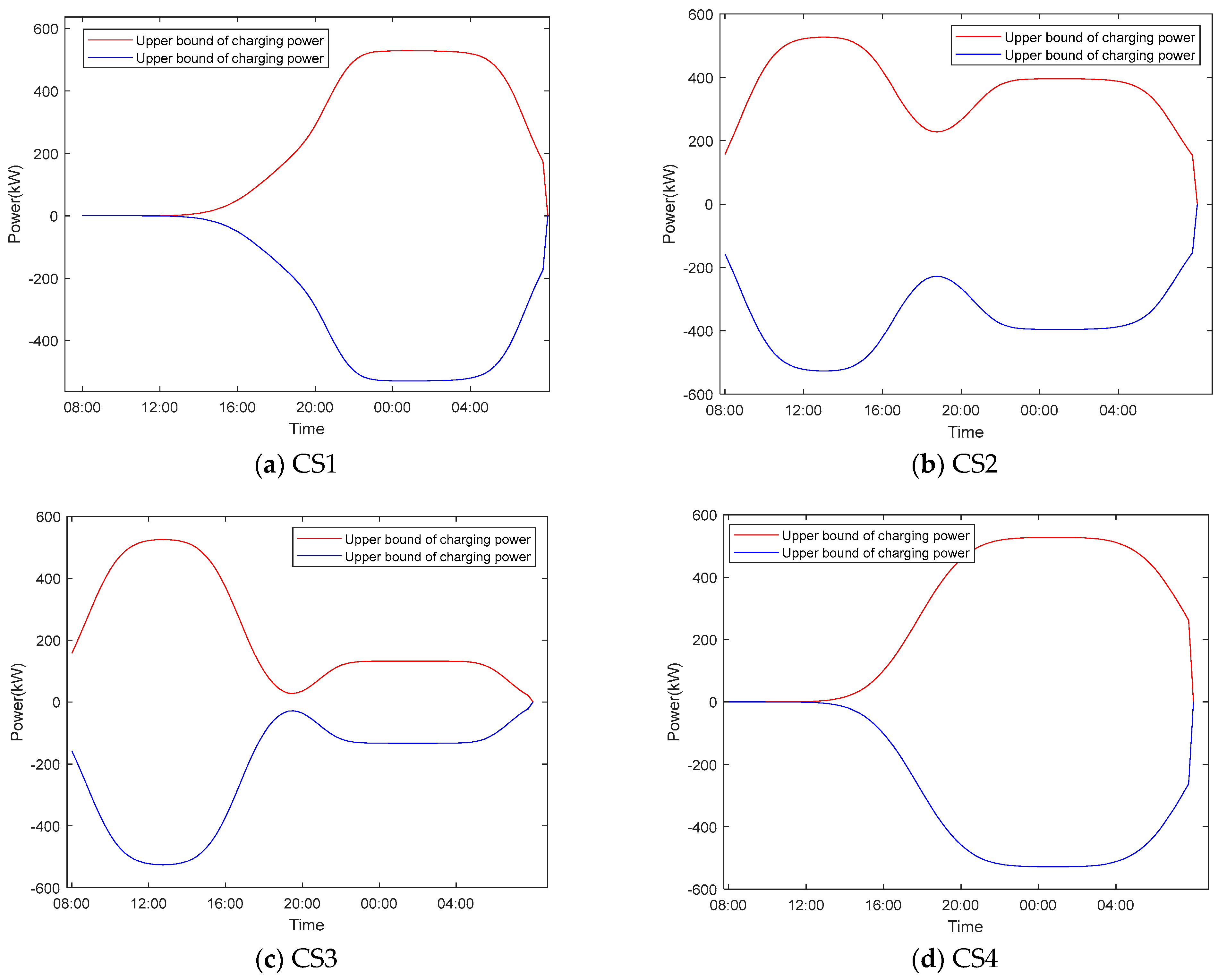
5.3.1. Analysis of Mobile Energy Storage Systems (MESS) and Dynamic Network Reconfiguration Strategy
5.3.2. Analysis of the Effectiveness and Necessity of Electric Vehicle (EV) Cluster Participation in Distribution Network Restoration for Discharge Response
6. Conclusions
- The proposed Minkowski summation-based approach successfully compresses EV clusters into generalized energy storage devices, enabling dimensionality reduction while preserving variable constraints. This method ensures the accuracy and reliability of charging station operations, facilitating effective load support during typhoon disasters.
- By integrating the Batts wind field model, this study quantifies typhoon-induced failures in distribution networks and traffic systems. The derived line failure rates and scenario analyses provide actionable insights for resilience planning.
- Introducing MESS into the post-disaster distribution network restoration strategy that uniformly considers the reconfiguration of the distribution network and the division of active islands can realize the spatial and temporal transfer of electric energy, equalize the electric energy resources between the regions of the distribution network, and effectively improve the level of load restoration.
- In the case of limited stationary energy sources, considering V2G participation in distribution network power supply restoration can play an auxiliary support role in the energy spatial and temporal transfer functions of MESS, and the proposed method reduces the economic loss of power outage by 29.78% compared with the traditional scheme by dispatching EV as a mobile power source, which can help to connect off-grid islands with the outside world, improve the resilience of the distribution network, reduce the amount of lost power, and increase the strategy’s economy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Liu, W.; Shi, Q.; Huang, Y.; Huang, S. Resilience assessment of multi-decision complex energy interconnection system. Int. J. Electr. Power Energy Syst. 2022, 137, 107809. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, T.; Yao, S.; Wang, P.; Goel, L.K. Power System Hurricane Resilience Assessment Considering Fuel Supply System. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- Fang, Y.-P.; Zio, E. An adaptive robust framework for the optimization of the resilience of interdependent infrastructures under natural hazards. Eur. J. Oper. Res. 2019, 276, 1119–1136. [Google Scholar] [CrossRef]
- Aldarajee, A.H.M.; Hosseinian, S.H.; Vahidi, B.; Dehghan, S. A coordinated planner-disaster-risk-averse-planner investment model for enhancing the resilience of integrated electric power and natural gas networks. Int. J. Electr. Power Energy Syst. 2020, 119, 105948. [Google Scholar] [CrossRef]
- Igder, M.A.; Liang, X.; Mitolo, M. Service Restoration Through Microgrid Formation in Distribution Networks: A Review. IEEE Access 2022, 10, 46618–46632. [Google Scholar] [CrossRef]
- Shi, Q.; Liu, W.; Zeng, B.; Hui, H.; Li, F. Enhancing distribution system resilience against extreme weather events: Concept review, algorithm summary, and future vision. Int. J. Electr. Power Energy Syst. 2022, 138, 107860. [Google Scholar] [CrossRef]
- Liu, W.; Ding, F. Hierarchical Distribution System Adaptive Restoration with Diverse Distributed Energy Resources. IEEE Trans. Sustain. Energy 2021, 12, 1347–1359. [Google Scholar] [CrossRef]
- Moreno, R.; Torres, A. Security of the power system based on the separation into islands. In Proceedings of the 2011 IEEE Pes Conference on Innovative Smart Grid Technologies Latin America (ISGT LA), Medellin, Colombia, 19–21 October 2011; pp. 1–5. [Google Scholar]
- Panteli, M.; Trakas, D.N.; Mancarella, P.; Hatziargyriou, N.D. Boosting the Power Grid Resilience to Extreme Weather Events Using Defensive Islanding. IEEE Trans. Smart Grid 2016, 7, 2913–2922. [Google Scholar] [CrossRef]
- Du, Y.; Wu, D. Deep Reinforcement Learning from Demonstrations to Assist Service Restoration in Islanded Microgrids. IEEE Trans. Sustain. Energy 2022, 13, 1062–1072. [Google Scholar] [CrossRef]
- Sun, S.; Cong, W.; Qiu, J.; Chen, M.; Wei, Z.; Zhang, Z. Power Restoration Method of Distribution Network with ESS and DG. In Proceedings of the 2021 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Chengdu, China, 18–21 July 2021; pp. 1075–1079. [Google Scholar]
- Kim, J.; Dvorkin, Y. Enhancing Distribution System Resilience with Mobile Energy Storage and Microgrids. IEEE Trans. Smart Grid 2019, 10, 4996–5006. [Google Scholar] [CrossRef]
- Nazemi, M.; Dehghanian, P.; Lu, X.; Chen, C. Uncertainty-Aware Deployment of Mobile Energy Storage Systems for Distribution Grid Resilience. IEEE Trans. Smart Grid 2021, 12, 3200–3214. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, S.; Zhang, B.; Li, G.; Wang, Z.; Tang, W. Coordinated Optimization of Emergency Power Vehicles and Distribution Network Reconfiguration Considering the Uncertain Restoration Capability of E-Taxis. IEEE Trans. Ind. Appl. 2022, 58, 2707–2717. [Google Scholar] [CrossRef]
- Alghamdi, A.; Jayaweera, D. Resilience of modern power distribution networks with active coordination of EVs and smart restoration. IET Gener. Transm. Distrib. 2023, 17, 4836–4857. [Google Scholar] [CrossRef]
- El-Hawary, M.E. The Smart Grid—State-of-the-art and future trends. In Proceedings of the 2016 Eighteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 27–29 December 2016; p. xvii. [Google Scholar] [CrossRef]
- Kang, Y.; Lu, G.; Chen, M.; Li, X.; Li, S. Fault recovery method of DC distribution network considering EV charging and discharging and SOP network reconfiguration. Electr. Power Syst. Res. 2025, 245, 111607. [Google Scholar] [CrossRef]
- Su, S.; Wei, C.; Li, Z.; Xia, M.; Chen, Q. Critical load restoration in coupled power distribution and traffic networks considering spatio-temporal scheduling of electric vehicles. Int. J. Electr. Power Energy Syst. 2022, 141, 108180. [Google Scholar] [CrossRef]
- Wu, C.; Cen, C.; Ma, Y.; Li, F.; Sui, Q. Enhancing resilient restoration of distribution systems utilizing electric vehicles and supporting incentive mechanism. Appl. Energy 2022, 9, 372–380. [Google Scholar] [CrossRef]
- Wang, L.; Chen, B.; Ye, Y.; Chongfuangprinya, P.; Yang, B.; Zhao, D.; Hong, T. Enhancing Distribution System Restoration with Coordination of Repair Crew, Electric Vehicle, and Renewable Energy. IEEE Trans. Smart Grid 2024, 15, 3694–3705. [Google Scholar] [CrossRef]
- Chao, L.; Yu, L.; Yihua, L.; Menghua, D.; Yanjun, C.; Ruochen, D. An evaluation method for integrating EVs in distribution networks with clustering algorithms. Front. Energy Res. 2024, 12, 1403430. [Google Scholar] [CrossRef]
- Huang, L.; Li, H.; Lai, C.S.; Zobaa, A.F.; Zhong, B.; Zhao, Z.; Lai, L.L. Electric Vehicle Cluster Scheduling Model for Distribution Systems Considering Reactive-Power Compensation of Charging Piles. Energies 2024, 17, 2541. [Google Scholar] [CrossRef]
- Bourrières, J.-P. The Minkowski sum of simplices in 3-dimensional space: An analytical description. Comput. Geom. 2014, 47, 856–867. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Z. A novel preventive islanding scheme of power system under extreme typhoon events. Int. J. Electr. Power Energy Syst. 2023, 147, 108857. [Google Scholar] [CrossRef]
- Li, Q.S.; Li, X.; He, Y.; Yi, J. Observation of wind fields over different terrains and wind effects on a super-tall building during a severe typhoon and verification of wind tunnel predictions. J. Wind. Eng. Ind. Aerodyn. 2017, 162, 73–84. [Google Scholar] [CrossRef]
- Wu, F.; Huang, G.; Zhou, X. Enhanced Circular Subregion Method in Typhoon Hazard Analysis. J. Struct. Eng. 2021, 147, 06021003. [Google Scholar] [CrossRef]
- Wu, F.; Huang, G. Refined empirical model of typhoon wind field and its application in China. J. Struct. Eng. 2019, 145, 04019122. [Google Scholar] [CrossRef]


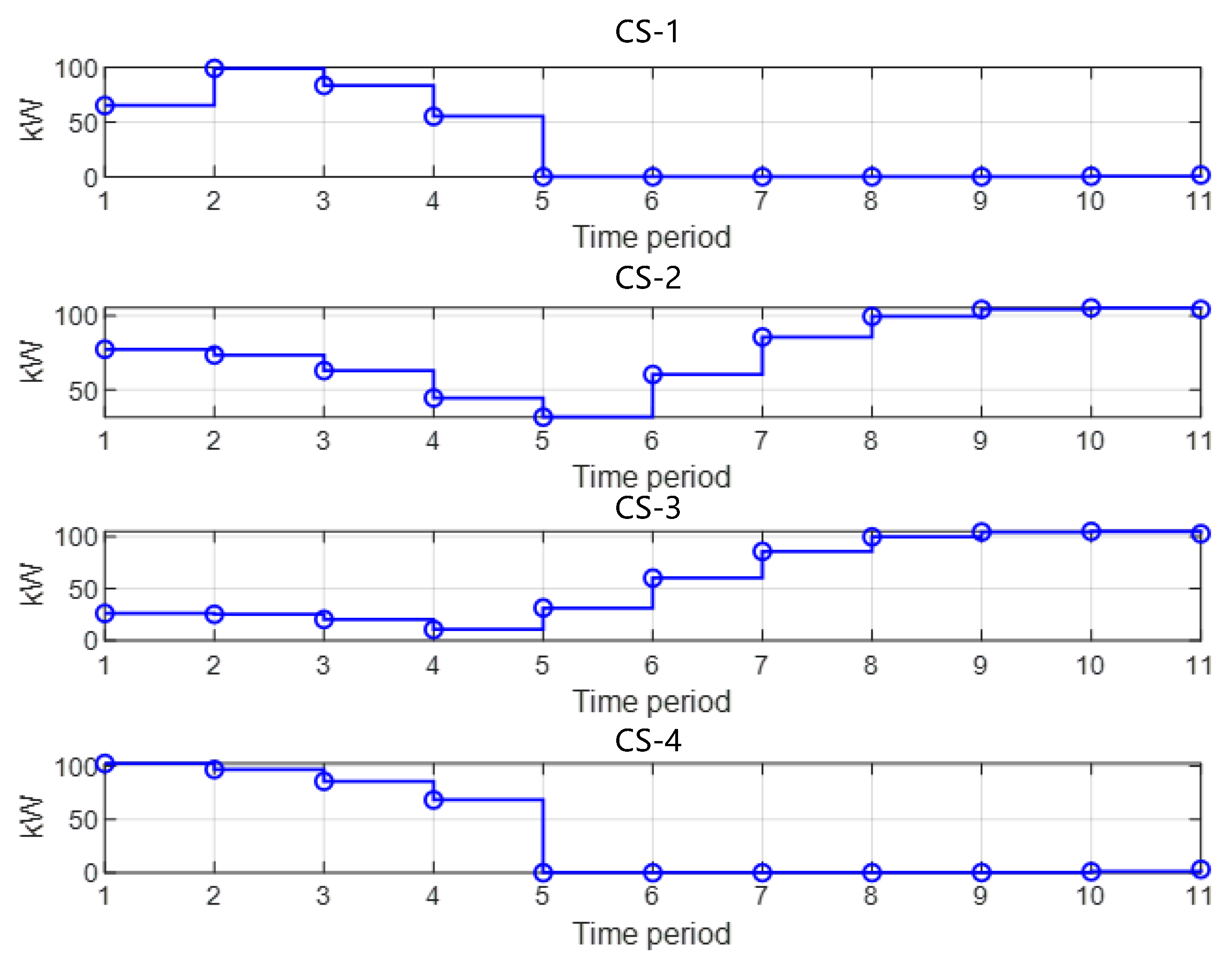
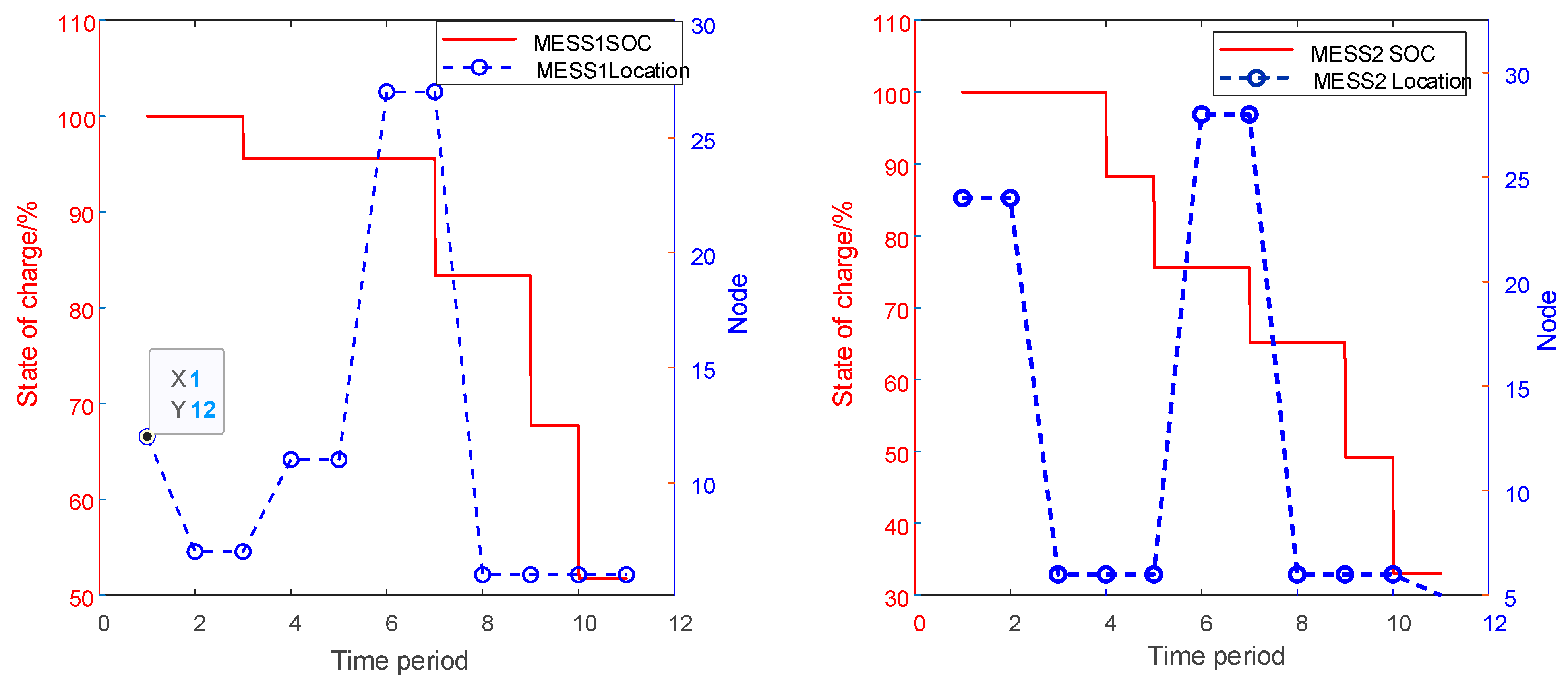
| Load Classification | Node |
|---|---|
| Critical loads | 3, 4, 6, 10, 11, 15, 17, 19, 24, 26, 28, 33 |
| Non-critical loads | Nodes other than critical loads |
| EV Parameter Distribution | |||
|---|---|---|---|
| Type A | N (18, 4) | N (8, 4) | U (0.4, 0.6) |
| Type B | N (21, 1) | N (7, 1) | U (0.2, 0.4) |
| Type C | N (9, 2) | N (17, 4) | U (0.4, 0.6) |
| Number of EVs | Type A | Type B | Type C |
|---|---|---|---|
| CS1 | U (36, 44) | U (38, 42) | - |
| CS2 | U (36, 44) | U (16, 24) | U (76, 84) |
| CS3 | - | U (18, 22) | U (76, 84) |
| CS4 | U (76, 84) | - | - |
| Pmax/kW | Qmax/kW | η | E/kWh | |
|---|---|---|---|---|
| DSG1\DSG2\DSG3 | 120 | 100 | - | - |
| DSG4\DSG5 | 80 | 60 | - | - |
| MESS | 200 | 170 | 0.98 | 600 |
| Number | First Node | Last Node | Failure Rate (Times/h) | Number | First Node | Last Node | Failure Rate (Times/h) |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 0.053792 | 17 | 14 | 15 | 0.3487650 |
| 2 | 2 | 3 | 0.287630 | 18 | 15 | 16 | 0.435412 |
| 3 | 2 | 19 | 0.213535 | 19 | 16 | 17 | 0.592039 |
| 4 | 3 | 4 | 0.222344 | 20 | 17 | 18 | 0.428976 |
| 5 | 3 | 23 | 0.477828 | 21 | 19 | 20 | 0.584876 |
| 6 | 4 | 5 | 0.109218 | 22 | 20 | 21 | 0.217654 |
| 7 | 5 | 6 | 0.425051 | 23 | 21 | 22 | 0.390875 |
| 8 | 6 | 7 | 0.490932 | 24 | 23 | 24 | 0.523919 |
| 9 | 6 | 26 | 0.469099 | 25 | 24 | 25 | 0.526275 |
| 10 | 7 | 8 | 0.184703 | 26 | 26 | 27 | 0.155811 |
| 11 | 8 | 9 | 0.217646 | 27 | 27 | 28 | 0.567851 |
| 12 | 9 | 10 | 0.399854 | 28 | 28 | 29 | 0.439865 |
| 13 | 10 | 11 | 0.318765 | 29 | 29 | 30 | 0.276050 |
| 14 | 11 | 12 | 0.348765 | 30 | 30 | 31 | 0.517894 |
| 15 | 12 | 13 | 0.439076 | 31 | 31 | 32 | 0.186548 |
| 16 | 13 | 14 | 0.327865 | 32 | 32 | 33 | 0.390675 |
| Loss of Power/MW | Percentage Reduction in Power Loss/% | |
|---|---|---|
| Scheme 1 | 2.3415 | - |
| Scheme 2 | 1.8912 | 19.23 |
| Scheme 3 | 1.6554 | 29.78 |
| Economic Losses/USD | Percentage Reduction in Cost/% | |
|---|---|---|
| Scheme 1 | 45,187.67 | - |
| Scheme 2 | 54,892.98 | −21.48 |
| Scheme 3 | 33,384.76 | 26.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, X.; Xiong, X.; Yang, D.; Wang, S.; Zhu, Y. Power Supply Resilience Under Typhoon Disasters: A Recovery Strategy Considering the Coordinated Dispatchable Potential of Electric Vehicles and Mobile Energy Storage. Processes 2025, 13, 1638. https://doi.org/10.3390/pr13061638
Dong X, Xiong X, Yang D, Wang S, Zhu Y. Power Supply Resilience Under Typhoon Disasters: A Recovery Strategy Considering the Coordinated Dispatchable Potential of Electric Vehicles and Mobile Energy Storage. Processes. 2025; 13(6):1638. https://doi.org/10.3390/pr13061638
Chicago/Turabian StyleDong, Xinyi, Xiaofu Xiong, Di Yang, Song Wang, and Yanghaoran Zhu. 2025. "Power Supply Resilience Under Typhoon Disasters: A Recovery Strategy Considering the Coordinated Dispatchable Potential of Electric Vehicles and Mobile Energy Storage" Processes 13, no. 6: 1638. https://doi.org/10.3390/pr13061638
APA StyleDong, X., Xiong, X., Yang, D., Wang, S., & Zhu, Y. (2025). Power Supply Resilience Under Typhoon Disasters: A Recovery Strategy Considering the Coordinated Dispatchable Potential of Electric Vehicles and Mobile Energy Storage. Processes, 13(6), 1638. https://doi.org/10.3390/pr13061638





