Accurate and Efficient Process Modeling and Inverse Optimization for Trench Metal Oxide Semiconductor Field Effect Transistors: A Machine Learning Proxy Approach
Abstract
1. Introduction
2. Process Simulation
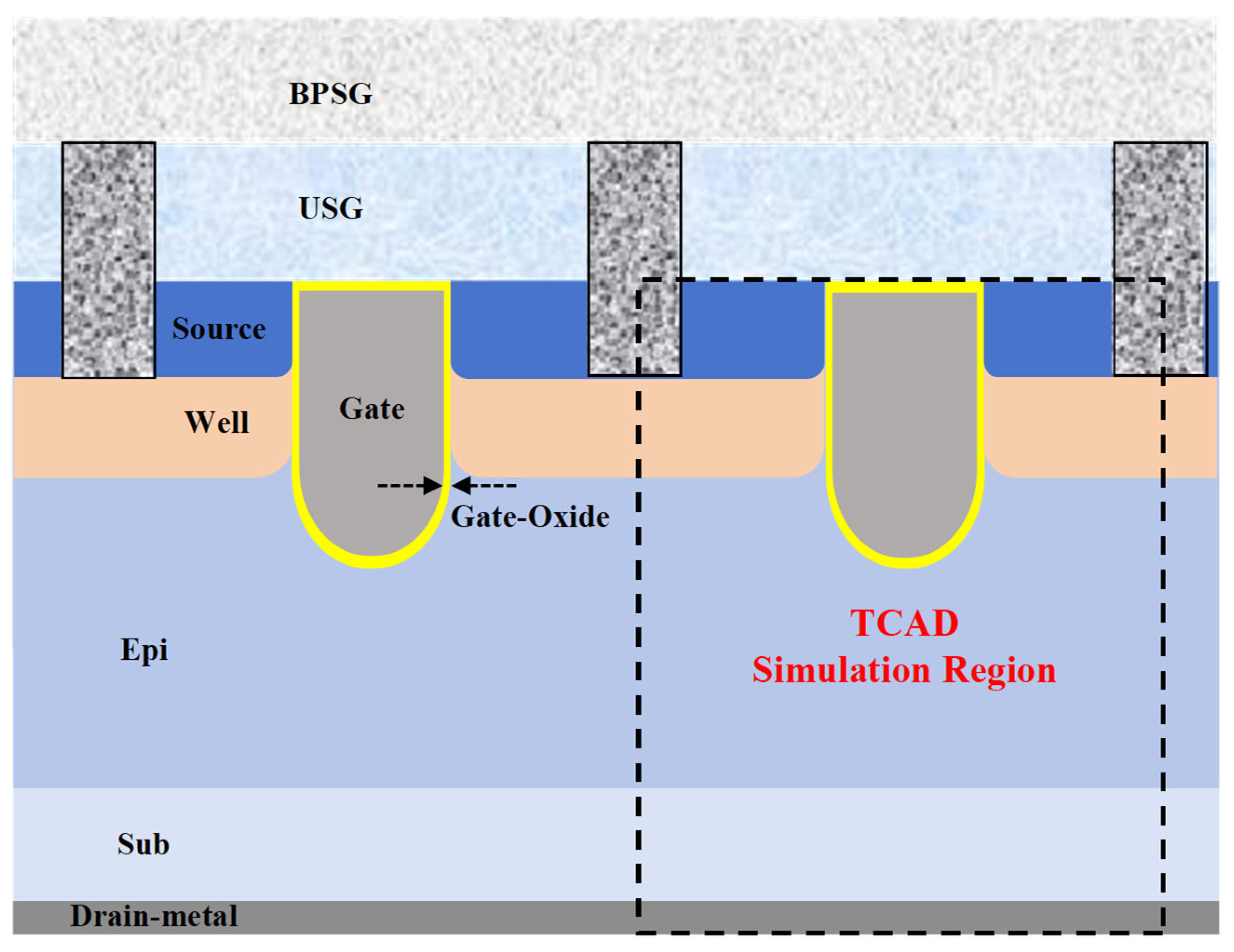
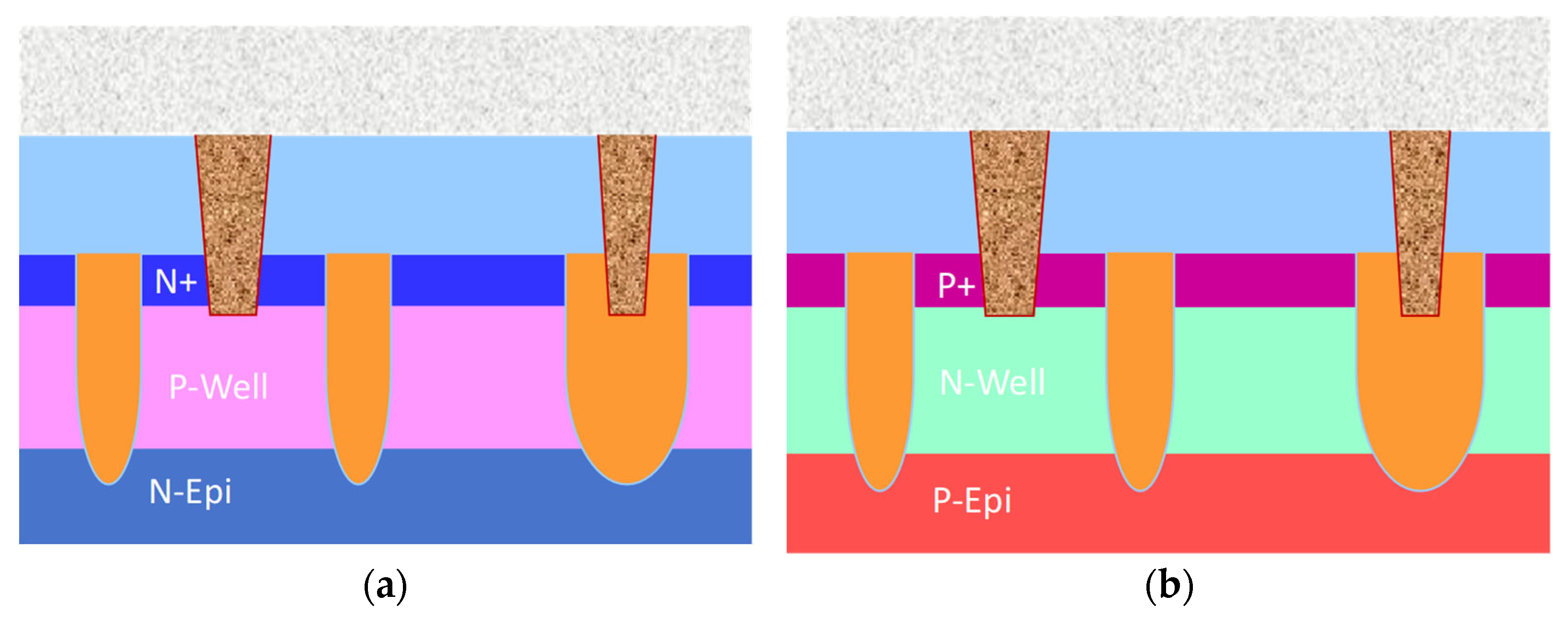
2.1. Trench MOSFET
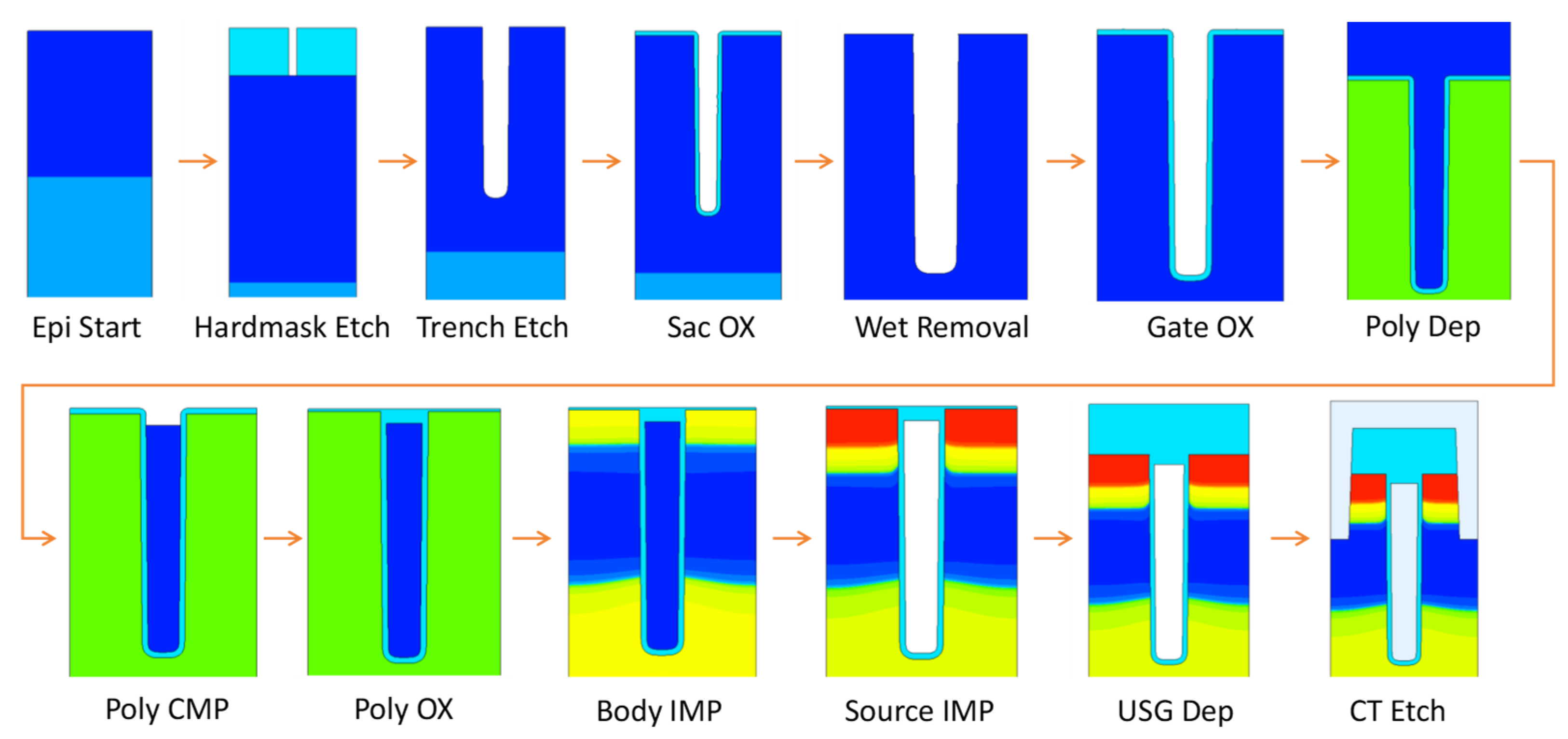
2.2. Device Process Flow
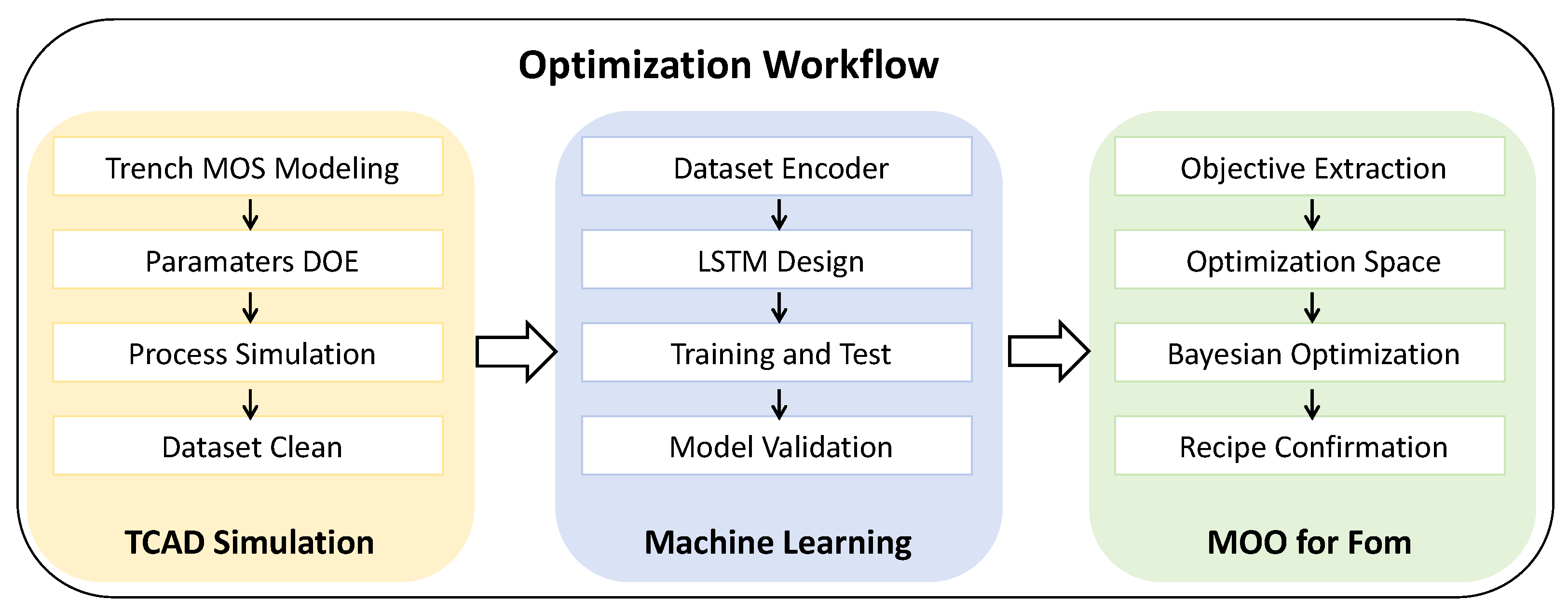
3. Methodology
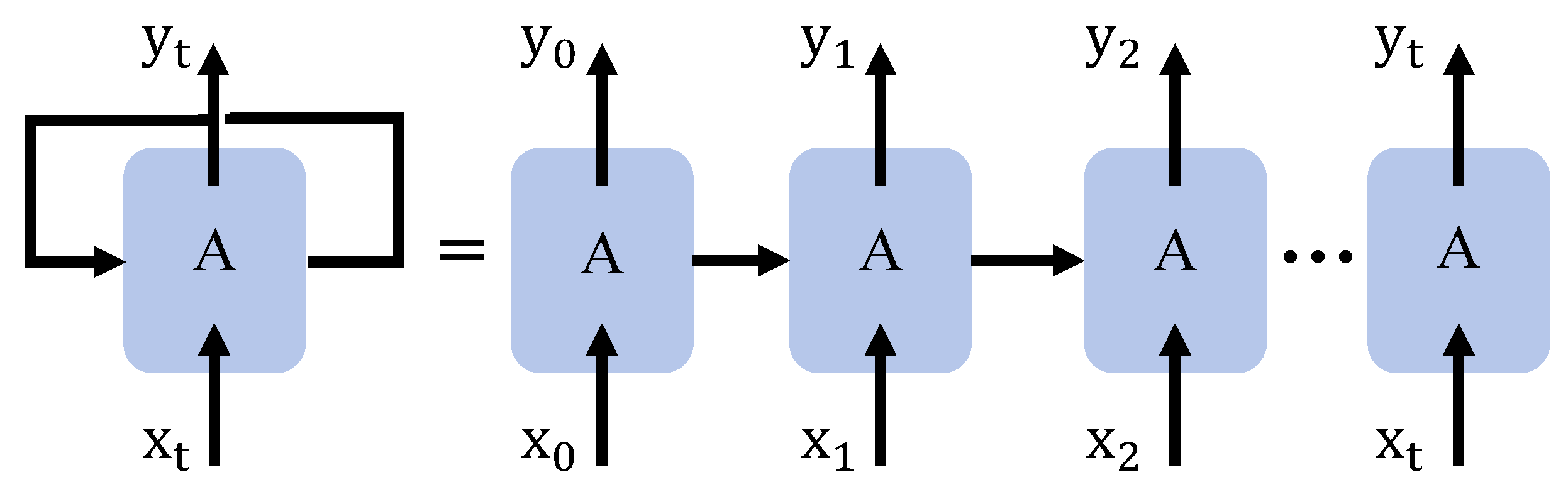
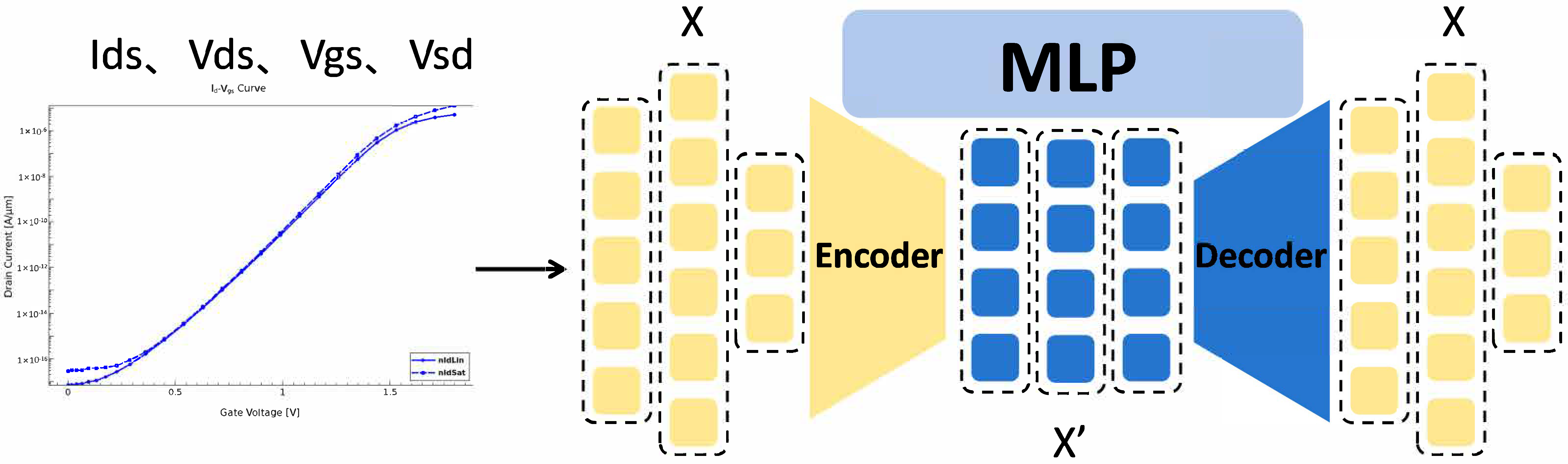
3.1. Machine Learning Methodology
- 1.
- Input gate ( and candidate state (): Control the integration of new information into with the following:
- 2.
- Forget gate : Regulates the retention of the persistent memory state using the following:
- 3.
- Output gate (): Modulates the exposure of to the transient state through the following:
- 4.
- The persistent memory state is updated via a weighted combination of historical and novel inputs, which can be depicted as follows:
- 5.
- Where denotes element-wise multiplication. The transient state , which serves as the network’s output, is computed as follows:
- Gradient stability: The additive nature of mitigates gradient dissipation/explosion, enabling stable training over long sequences.
- Contextual selectivity: Gating mechanisms allow the network to prioritize relevant temporal features while suppressing noise.
- Black-box modeling: LSTMs eliminate the need for explicit physical equations, making them ideal for modeling complex nonlinear systems like GaN HEMTs.
LSTM Technique-Based Process Model
3.2. Multi-Objective Optimization
4. Results and Discussion
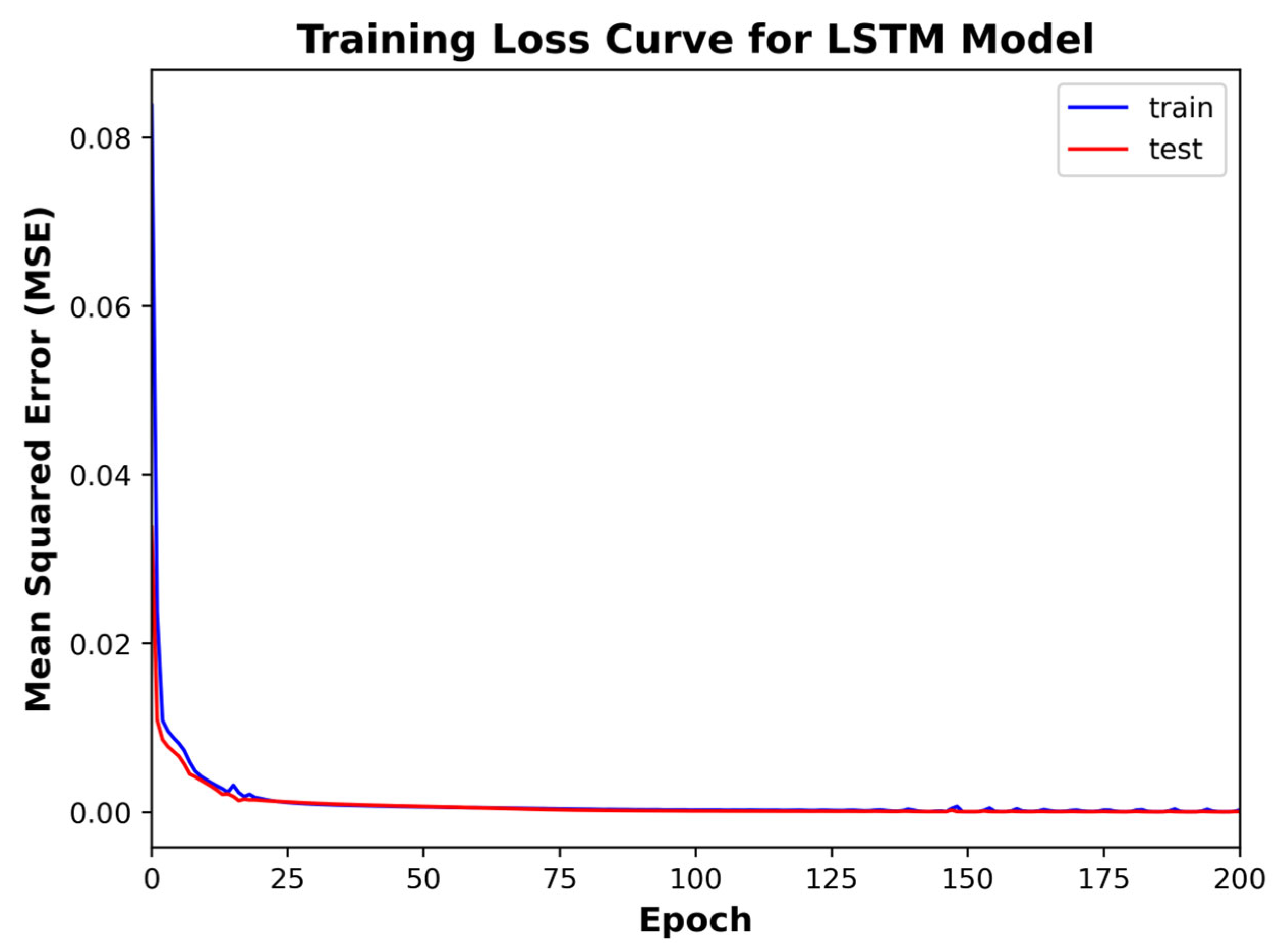
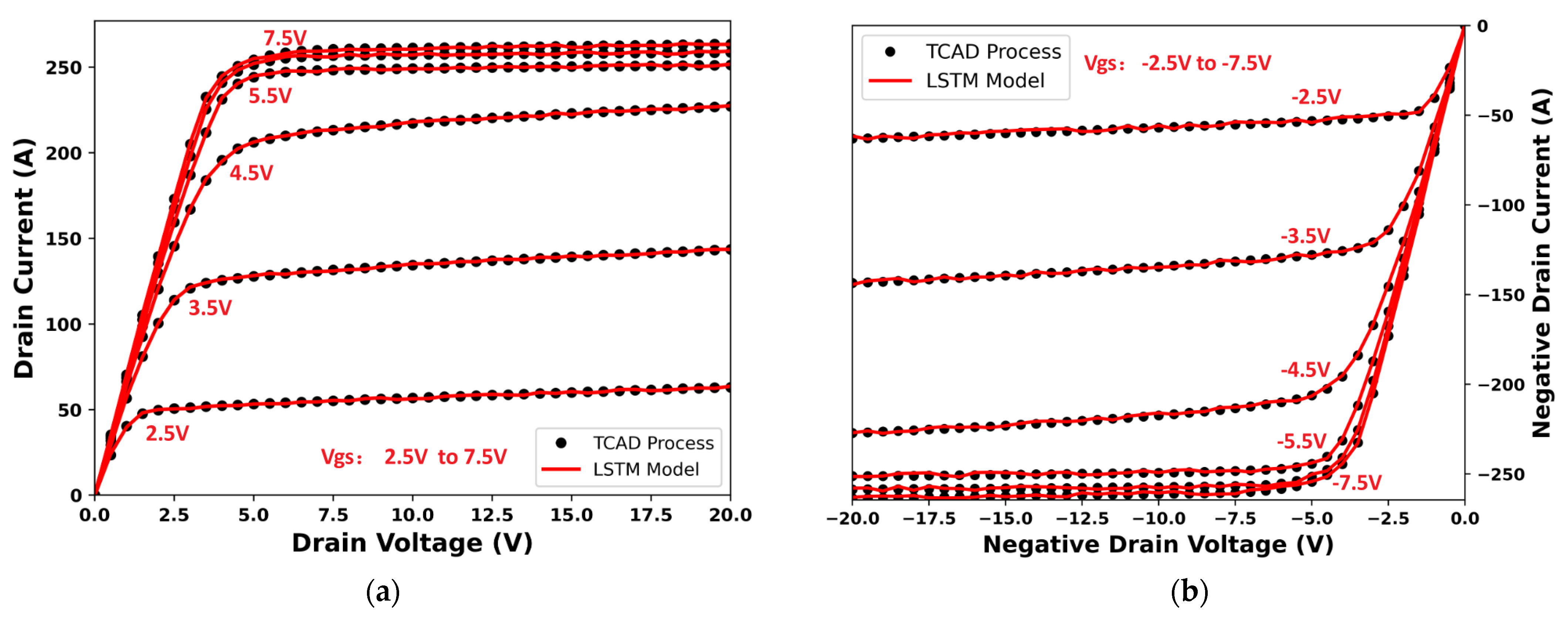
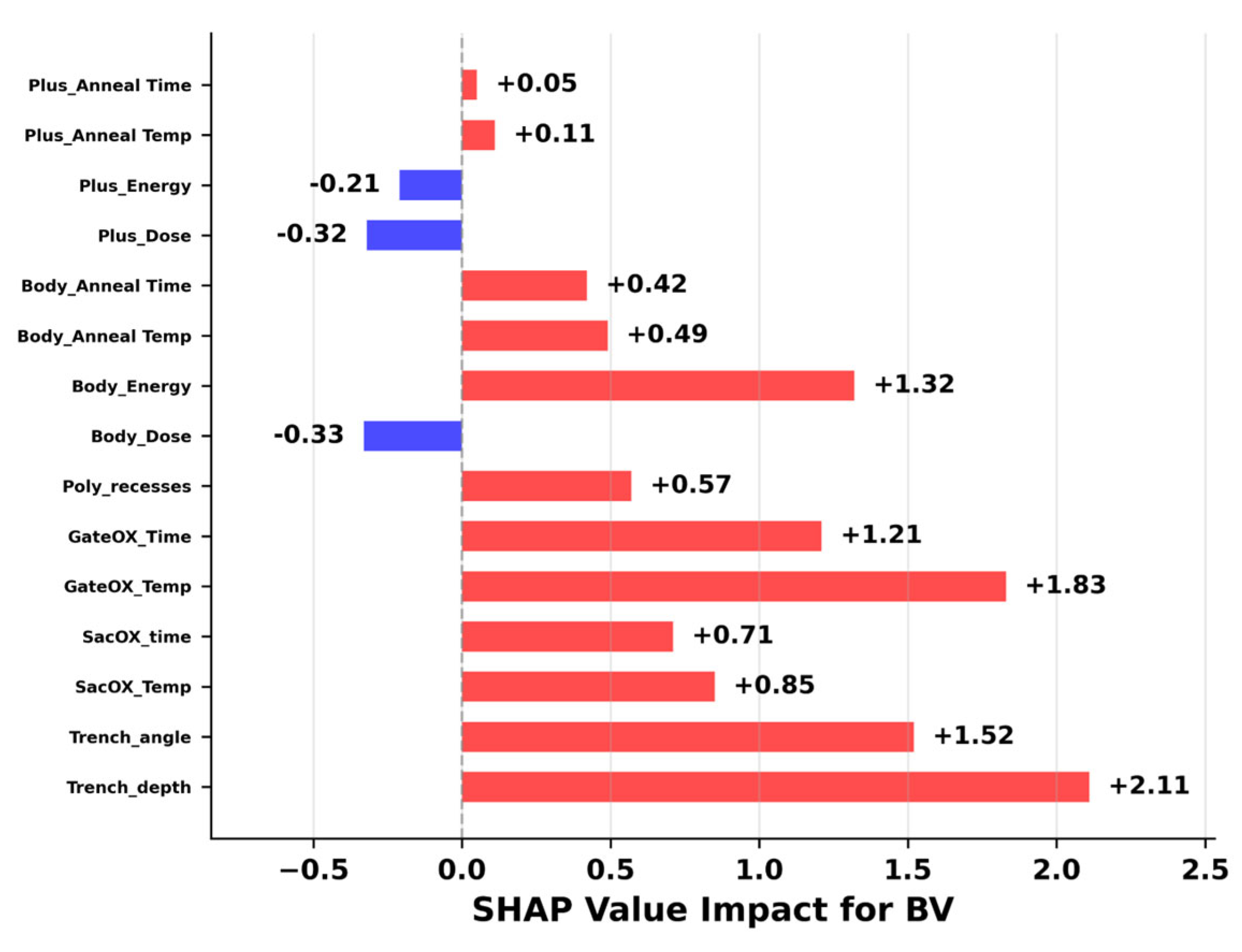
4.1. Model Validation
4.2. Inverse Optimization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RNN | Recurrent Neural Network |
| LSTM | Long Short-Term Memory |
| GRU | Gated Recurrent Unit |
| MOO | Multi-Objective Optimization |
| TCAD | Technology Computer-Aided Design |
| SBD | Schottky barrier diode |
References
- Williams, R.K.; Darwish, M.N.; Blanchard, R.A.; Siemieniec, R.; Rutter, P.; Kawaguchi, Y. The Trench Power MOSFET: Part I—History, Technology, and Prospects. IEEE Trans. Electron. Devices 2017, 64, 674–691. [Google Scholar] [CrossRef]
- Williams, R.K.; Darwish, M.N.; Blanchard, R.A.; Siemieniec, R.; Rutter, P.; Kawaguchi, Y. The Trench Power MOSFET—Part II: Application Specific VDMOS, LDMOS, Packaging, and Reliability. IEEE Trans. Electron. Devices 2017, 64, 692–712. [Google Scholar] [CrossRef]
- Chuang, C.S.P.; Chen, K.Y.G.; Hung, Y.R.R.; Kuo, T.C.; Huang, C.C.T. Forward-voltage-tunable schottky-integrated trench MOSFETs. In Proceedings of the 2014 IEEE 26th International Symposium on Power Semiconductor Devices & IC’s (ISPSD), Waikoloa, HI, USA, 15–19 June 2014; pp. 159–162. [Google Scholar]
- Dolny; Sapp; Elbanhaway; Wheatley. The influence of body effect and threshold voltage reduction on trench MOSFET body diode characteristics. In Proceedings of the 16th International Symposium on Power Semiconductor Devices and ICs, Kitakyushu, Japan, 24–27 May 2004; pp. 217–220. [Google Scholar]
- Prado, E.O.; Bolsi, P.C.; Sartori, H.C.; Pinheiro, J.R. An Overview about Si, Superjunction, SiC and GaN Power MOSFET Technologies in Power Electronics Applications. Energies 2022, 15, 5244. [Google Scholar] [CrossRef]
- Mirchandani; Thapar; Boden; Sodhi; Kinzer. A novel n-channel MOSFET featuring an integrated Schottky and no internal p-n junction. In Proceedings of the 16th International Symposium on Power Semiconductor Devices and ICs, Kitakyushu, Japan, 24–27 May 2004; pp. 405–408. [Google Scholar]
- Hirao, T.; Hashimoto, T. Low Reverse Recovery Charge 30 V Power MOSFET With Double Epi Structure for DC–DC Converters. IEEE Trans. Electron. Devices 2016, 63, 1154–1160. [Google Scholar] [CrossRef]
- Hirao, T.; Hashimoto, T.; Shirai, N.; Arai, H.; Matsuura, N.; Matsuura, H. Low reverse recovery charge 30-V power MOSFETs for DC-DC converters. In Proceedings of the 2013 25th International Symposium on Power Semiconductor Devices & IC’s (ISPSD), Kanazawa, Japan, 26–30 May 2013; pp. 221–224. [Google Scholar]
- Xiao, C.; Yang, W.; Liu, Y.; Zhou, X.; Feng, H.; Sin, J.K.O. A Trench-Field-Plate High-Voltage Power MOSFET. IEEE Trans. Electron. Devices 2020, 67, 2482–2488. [Google Scholar] [CrossRef]
- Xu, H.; Gan, W.; Cao, L.; Yang, C.; Wu, J.; Zhou, M.; Qu, H.; Zhang, S.; Yin, H.; Wu, Z. A Machine Learning Approach for Optimization of Channel Geometry and Source/Drain Doping Profile of Stacked Nanosheet Transistors. IEEE Trans. Electron. Devices 2022, 69, 3568–3574. [Google Scholar] [CrossRef]
- Kim, Y.; Myung, S.; Ryu, J.; Jeong, C.; Kim, D.S. Physics-augmented Neural Compact Model for Emerging Device Technologies. In Proceedings of the 2020 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Kobe, Japan, 23 September–6 October 2020; pp. 257–260. [Google Scholar]
- Liu, C.C.; Li, Y.; Yang, Y.S.; Chen, C.Y.; Chuang, M.H. Automatic Device Model Parameter Extractions via Hybrid Intelligent Methodology. In Proceedings of the 2020 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Kobe, Japan, 23 September–6 October 2020; pp. 355–358. [Google Scholar]
- Yang, Q.; Qi, G.; Gan, W.; Wu, Z.; Yin, H.; Chen, T.; Hu, G.; Wan, J.; Yu, S.; Lu, Y. Transistor Compact Model Based on Multigradient Neural Network and Its Application in SPICE Circuit Simulations for Gate-All-Around Si Cold Source FETs. IEEE Trans. Electron. Devices 2021, 68, 4181–4188. [Google Scholar] [CrossRef]
- Colinge, J.-P.; Lee, C.-W.; Afzalian, A.; Akhavan, N.D.; Yan, R.; Ferain, I.; Razavi, P.; O’Neill, B.; Blake, A.; White, M.; et al. Nanowire transistors without junctions. Nat. Nanotechnol. 2010, 5, 225–229. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Guo, J. Multiobjective Design of 2-D-Material-Based Field-Effect Transistors with Machine Learning Methods. IEEE Trans. Electron. Devices 2021, 68, 5476–5482. [Google Scholar] [CrossRef]
- Crose, M.; Kwon, J.S.-I.; Tran, A.; Christofides, P.D. Multiscale modeling and run-to-run control of PECVD of thin film solar cells. Renew. Energy 2017, 100, 129–140. [Google Scholar] [CrossRef]
- Dhillon, H.; Mehta, K.; Xiao, M.; Wang, B.; Zhang, Y.; Wong, H.Y. TCAD-Augmented Machine Learning with and Without Domain Expertise. IEEE Trans. Electron. Devices 2021, 68, 5498–5503. [Google Scholar] [CrossRef]
- Han, S.C.; Choi, J.; Hong, S.M. Acceleration of Semiconductor Device Simulation with Approximate Solutions Predicted by Trained Neural Networks. IEEE Trans. Electron. Devices 2021, 68, 5483–5489. [Google Scholar] [CrossRef]
- Xiao, T.; Ni, D. Multiscale Modeling and Recurrent Neural Network Based Optimization of a Plasma Etch Process. Processes 2021, 9, 151. [Google Scholar] [CrossRef]
- Myung, S.; Kim, J.; Jeon, Y.; Jang, W.; Huh, I.; Kim, J.; Han, S.; Baek, K.h.; Ryu, J.; Kim, Y.S.; et al. Real-Time TCAD: A new paradigm for TCAD in the artificial intelligence era. In Proceedings of the 2020 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Kobe, Japan, 23 September–6 October 2020; pp. 347–350. [Google Scholar]
- Liu, P.; Wu, Q.; Ren, X.; Wang, Y.; Ni, D. A deep-learning-based surrogate modeling method with application to plasma processing. Chem. Eng. Res. Des. 2024, 211, 299–317. [Google Scholar] [CrossRef]
- Graves, A.; Mohamed, A.r.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6645–6649. [Google Scholar]
- Geng, M.; Crupi, G.; Cai, J. Accurate and Effective Nonlinear Behavioral Modeling of a 10-W GaN HEMT Based on LSTM Neural Networks. IEEE Access 2023, 11, 27267–27279. [Google Scholar] [CrossRef]
- Guo, J.; Geng, M.; Ren, K.; Ni, D.; Gao, D. Optimizing Plasma Etching: Integrating Precise Three-Dimensional Etching Simulation and Machine Learning for Multi-Objective Optimization. IEEE Access 2024, 12, 127065–127073. [Google Scholar] [CrossRef]
- Geng, M.; Zhu, Z.; Cai, J. Small-Signal Behavioral Model for GaN HEMTs based on Long-Short Term Memory Networks. In Proceedings of the 2021 IEEE MTT-S International Wireless Symposium (IWS), Nanjing, China, 23–26 May 2021; pp. 1–3. [Google Scholar]
- Olajire, T.O. Accelerating Manufacturing Decisions Using Bayesian Optimization: An Optimization and Prediction Perspective. Master’s Thesis, West Virginia University, Morgantown, WV, USA, 2023. [Google Scholar]
- Shrivastava, A.; Kalaswad, M.; Custer, J.O.; Adams, D.P.; Najm, H.N. Bayesian optimization for stable properties amid processing fluctuations in sputter deposition. J. Vac. Sci. Technol. A 2024, 42, 033408. [Google Scholar] [CrossRef]
- Zhang, H.P.; Sun, C.L.L.; Jiang, C.L.F.; Xu, L.Y.; Lin, M. Process simulation of trench gate and plate and trench drain SOI nLDMOS with TCAD tools. In Proceedings of the 2008 IEEE International Conference on Semiconductor Electronics, Johor Bahru, Malaysia, 25–27 November 2008; pp. 92–95. [Google Scholar]
- Ono, S.; Yamaguchi, Y.; Matsuda, N.; Takano, A.; Akiyama, M.; Kawaguchi, Y.; Nakagawa, A. High density MOSBD (UMOS with built-in Trench Schottky Barrier Diode) for Synchronous Buck Converters. In Proceedings of the 2006 IEEE International Symposium on Power Semiconductor Devices and IC’s, Naples, Italy, 4–8 June 2006; pp. 1–4. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Graczyk, K.; Witkowski, K. Bayesian Reasoning for Physics Informed Neural Networks. arXiv 2023, arXiv:2308.13222. [Google Scholar]




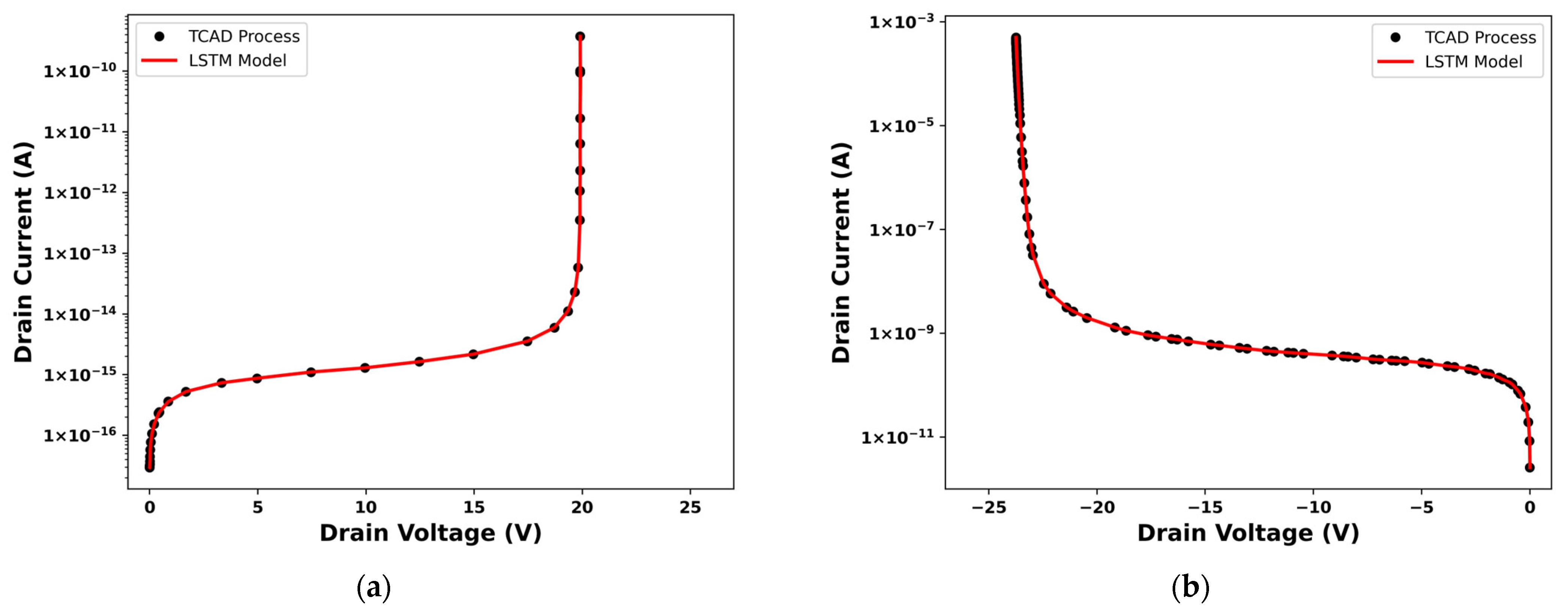
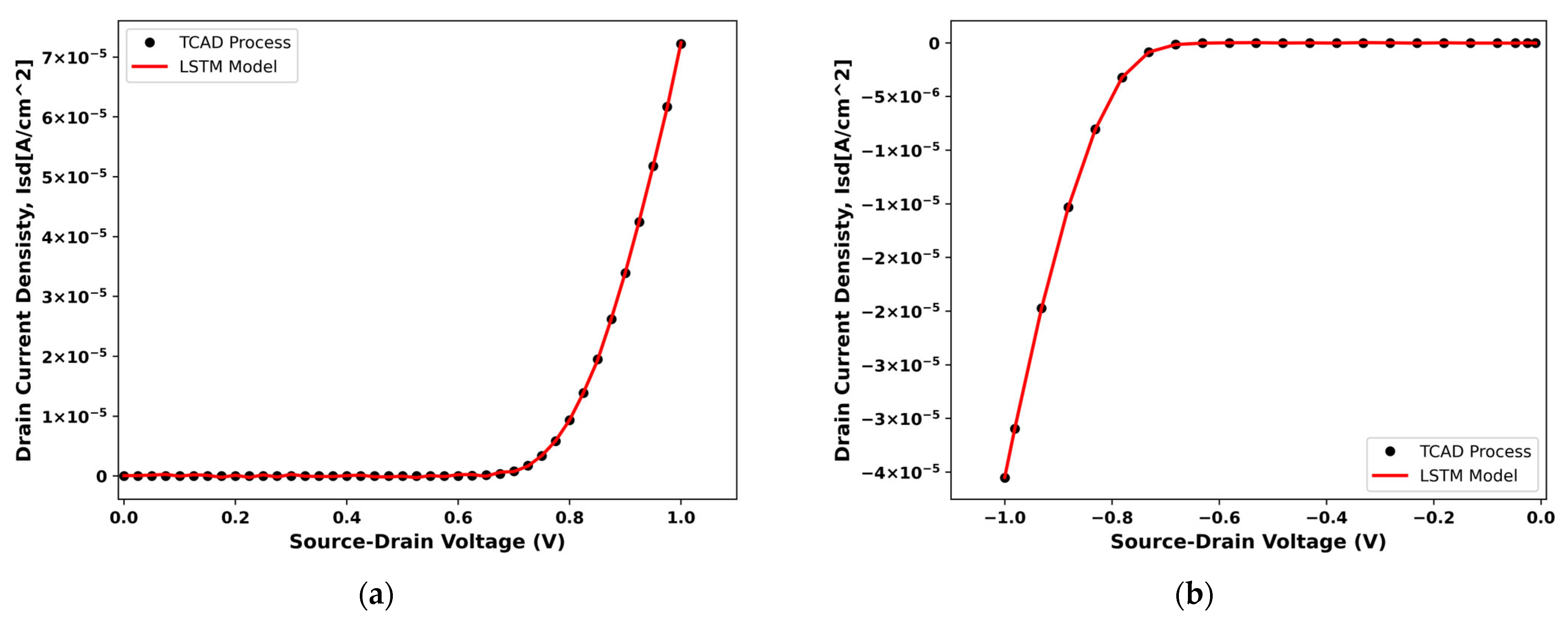
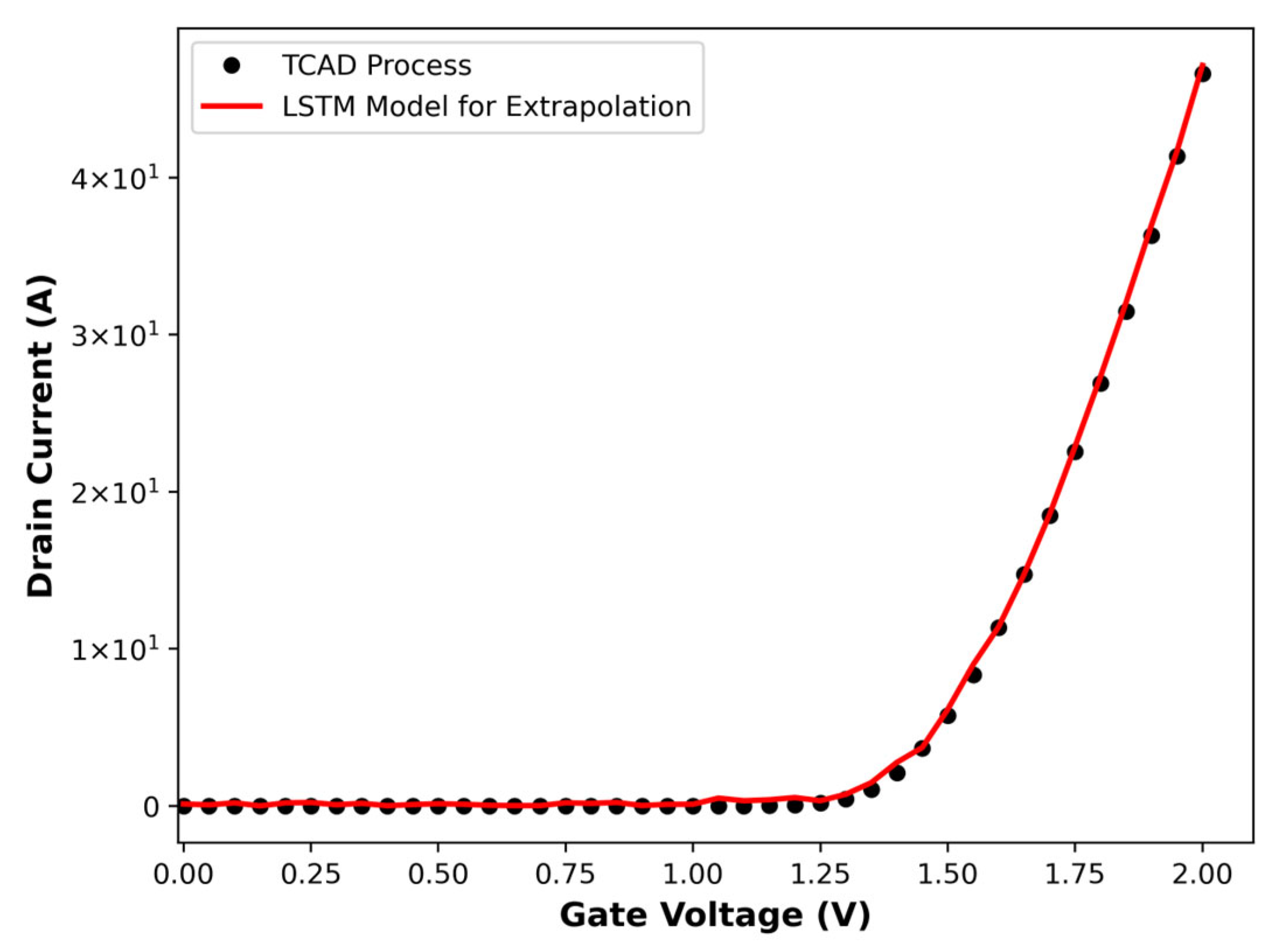
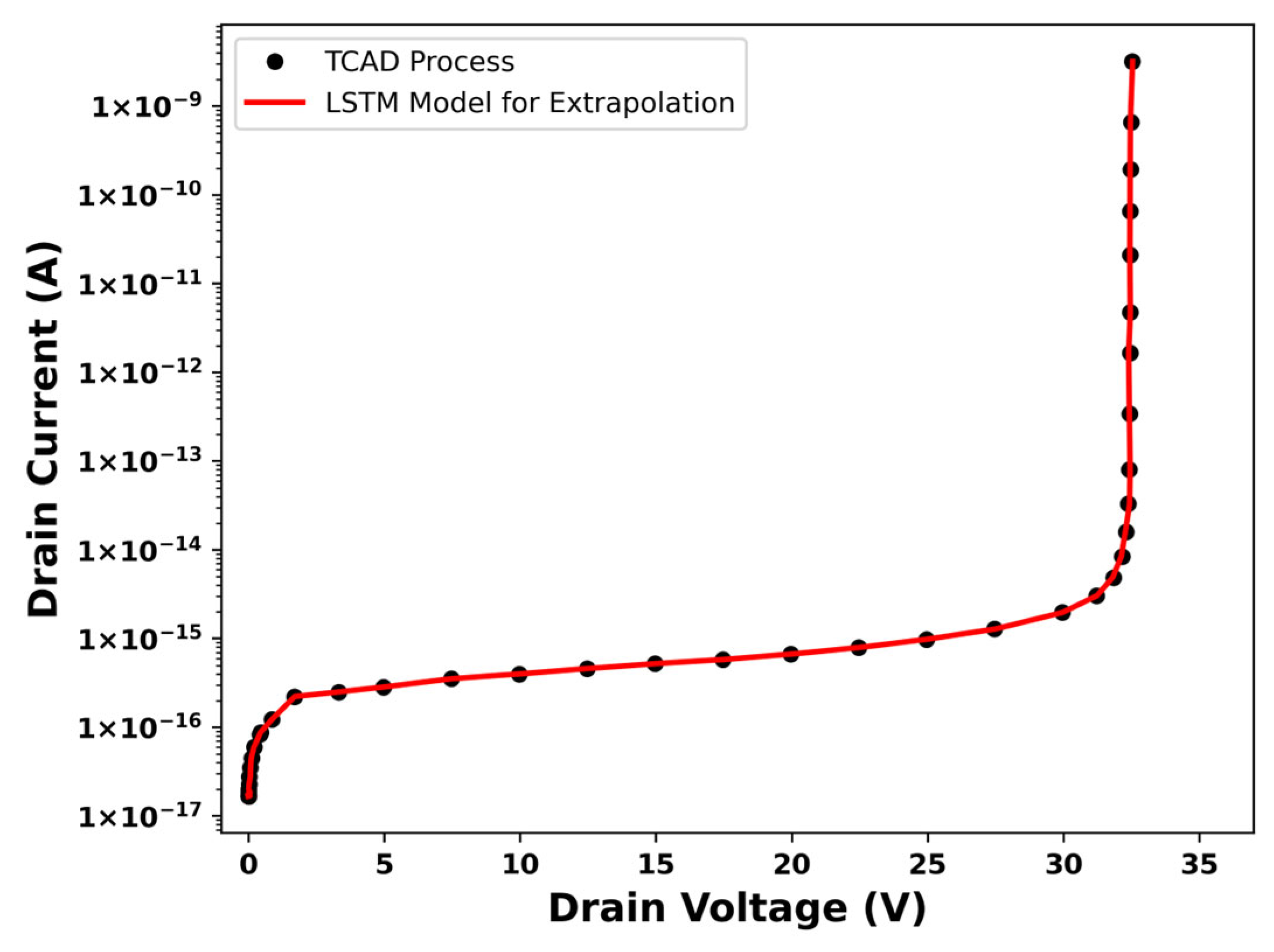



| Model | Total Layers (Equivalent Parameters) | Gating Complexity | Parameters per Layer | Long-Term Dependency Capture | Extraction Time (s) | Average Relative Error (%) |
|---|---|---|---|---|---|---|
| RNN | 16 | None | Lowest | Weak | 57.67 | 2.870 |
| GRU | 13 | Moderate (2 gates) | Lower | Moderate | 68.92 | 1.323 |
| LSTM | 11 | High (3 gates) | Higher | Strong | 78.26 | 1.092 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, M.; Guo, J.; Sun, Y.; Gao, D.; Ni, D. Accurate and Efficient Process Modeling and Inverse Optimization for Trench Metal Oxide Semiconductor Field Effect Transistors: A Machine Learning Proxy Approach. Processes 2025, 13, 1544. https://doi.org/10.3390/pr13051544
Geng M, Guo J, Sun Y, Gao D, Ni D. Accurate and Efficient Process Modeling and Inverse Optimization for Trench Metal Oxide Semiconductor Field Effect Transistors: A Machine Learning Proxy Approach. Processes. 2025; 13(5):1544. https://doi.org/10.3390/pr13051544
Chicago/Turabian StyleGeng, Mingqiang, Jianming Guo, Yuting Sun, Dawei Gao, and Dong Ni. 2025. "Accurate and Efficient Process Modeling and Inverse Optimization for Trench Metal Oxide Semiconductor Field Effect Transistors: A Machine Learning Proxy Approach" Processes 13, no. 5: 1544. https://doi.org/10.3390/pr13051544
APA StyleGeng, M., Guo, J., Sun, Y., Gao, D., & Ni, D. (2025). Accurate and Efficient Process Modeling and Inverse Optimization for Trench Metal Oxide Semiconductor Field Effect Transistors: A Machine Learning Proxy Approach. Processes, 13(5), 1544. https://doi.org/10.3390/pr13051544







