Bayesian Deep Reinforcement Learning for Operational Optimization of a Fluid Catalytic Cracking Unit
Abstract
1. Introduction
- We propose a BRL method for the operation problem of the FCC unit. Unlike traditional RL methods that employ deterministic networks, we utilize Bayesian neural networks (BNNs) to represent the RL agent, effectively capturing the uncertainties in FCC.
- We adopt a primal-dual method to handle the process constraints, ensuring the optimality of the control policy while satisfying safety, which is new in the framework of BRL.
- Extensive simulations are conducted to investigate the dynamic responses of FCC under different operating conditions. Compared with traditional deterministic gradient methods, the proposed approach achieved improved economic profits and more stable control performance.
2. Constrained Markov Decision Process
3. Bayesian Primal-Dual Deep Deterministic Policy Gradient
3.1. Bayesian Neural Network
3.2. Variational Inference in BNN with -Divergences
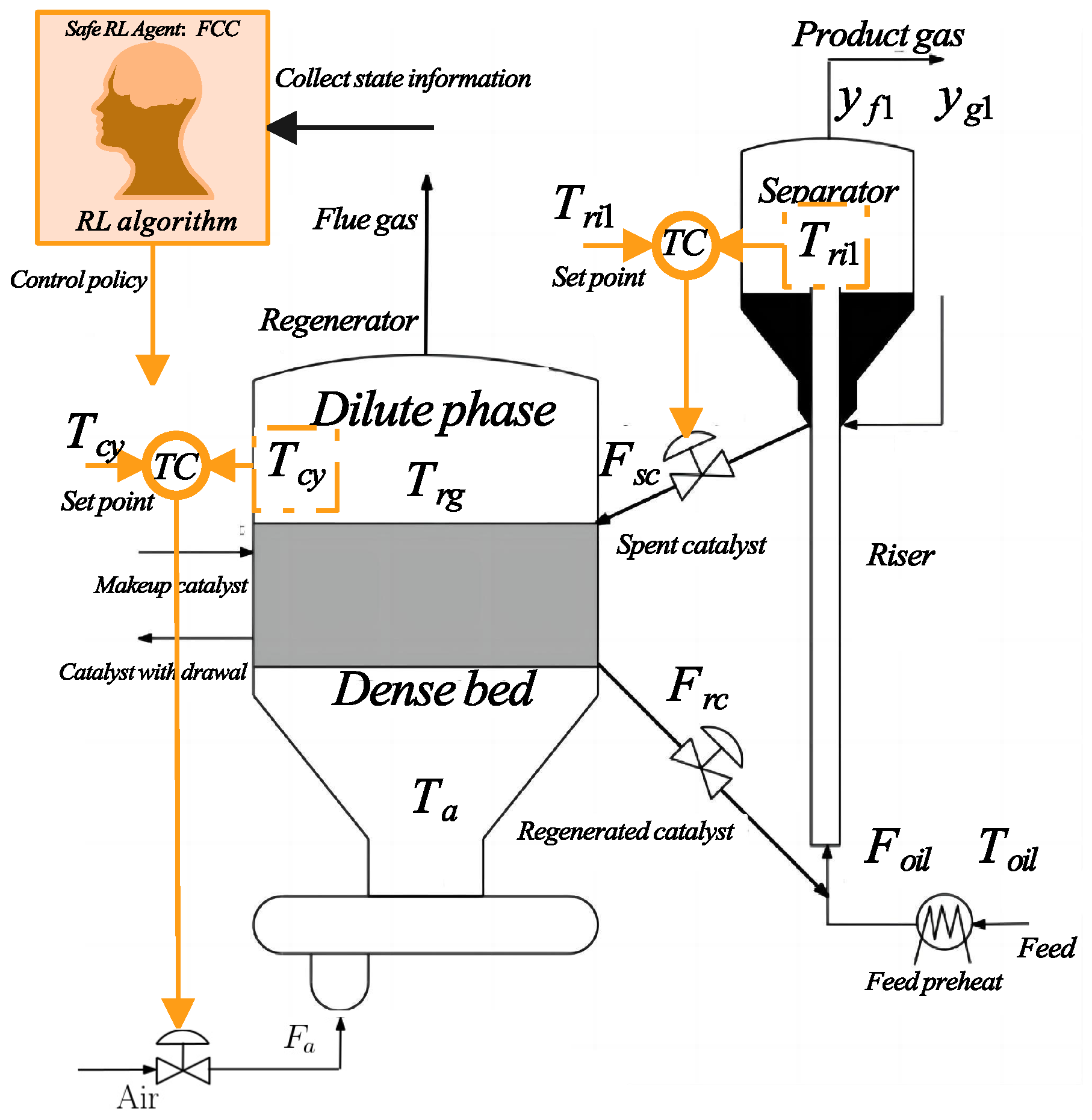
4. The Fluid Catalytic Cracking Process
4.1. Process Descriptions
4.2. Formulating as a SRL Problem
5. Simulation Results
5.1. Training Algorithms
| Algorithm 1 BPD3PG |
Input: Initial netowrk Input: Target parameters: Input: Initial replay buffer and Lagrangian multiplier 1: for each episode do 2: for each time step do 3: 4: 5: 6: end for 7: for each gradient step do 8: Sample experience from replay buffer 9: Update the reward and cost critic network by minimizing the loss function (14). 10: Update the Lagrangian multiplier using (30). 11: Update the actor network using (29). 12: Update the target network soft update [33] 13: end for 14: end for Output: |
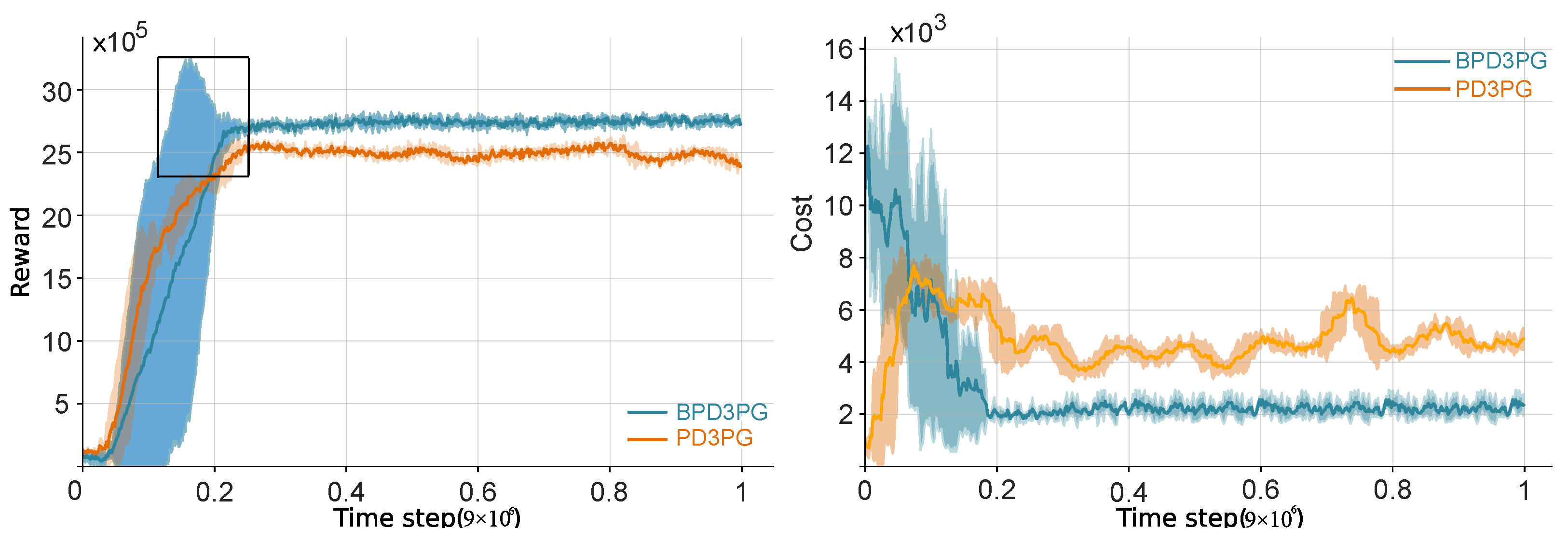
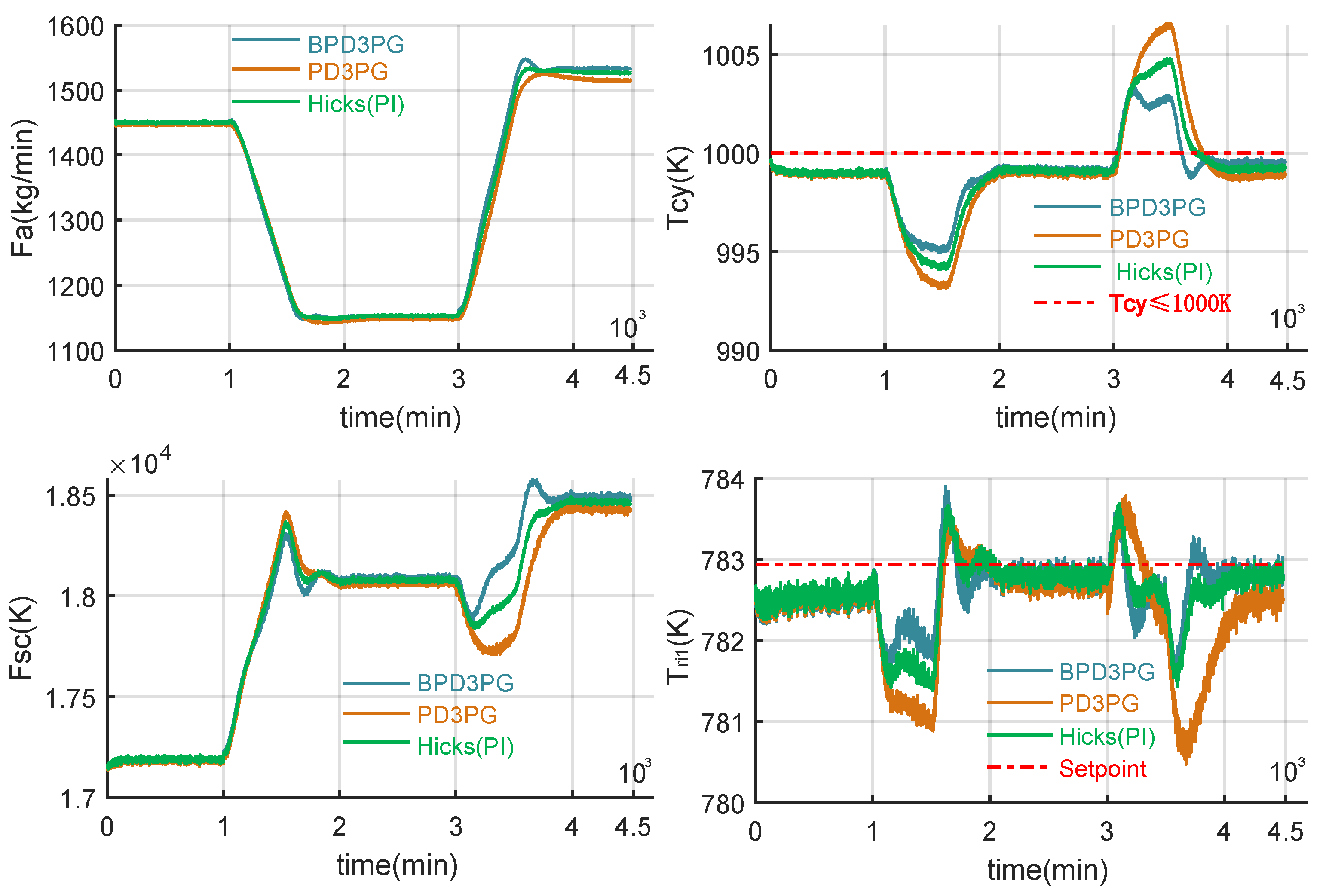
5.2. Experimental Results
- Undisturbed condition: The system operates in an ideal control environment. The manipulated variables and are precisely regulated by the controller, while the key parameters change according to disturbance scenarios and , but no random disturbances or measurement noises are introduced.
- Disturbed condition: In addition to the key parameter changes following disturbance scenarios and , the system is also subject to random disturbances. Specifically, the manipulated variables become and , and the measured variables become and , where and the noise power .
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bloor, M.; Ahmed, A.; Kotecha, N.; Mercangöz, M.; Tsay, C.; Chanona, E.A.D.R. Control-Informed Reinforcement Learning for Chemical Processes. Ind. Eng. Chem. Res. 2025, 64, 4966–4978. [Google Scholar] [CrossRef] [PubMed]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed Machine Learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Byun, H.E.; Kim, B.; Lee, J.H. Embedding Active Learning in Batch-to-batch Optimization Using Reinforcement Learning. Automatica 2023, 157, 111260. [Google Scholar] [CrossRef]
- Oh, T.H.; Park, H.M.; Kim, J.W.; Lee, J.M. Integration of reinforcement learning and model predictive control to optimize semi-batch bioreactor. AIChE J. 2022, 68, e17658. [Google Scholar] [CrossRef]
- Syauqi, A.; Kim, H.; Lim, H. Optimizing Olefin Purification: An Artificial Intelligence-Based Process-Conscious PI Controller Tuning for Double Dividing Wall Column Distillation. Chem. Eng. J. 2024, 500, 156645. [Google Scholar] [CrossRef]
- Petukhov, A.N.; Shablykin, D.N.; Trubyanov, M.M.; Atlaskin, A.A.; Zarubin, D.M.; Vorotyntsev, A.V.; Stepanova, E.A.; Smorodin, K.A.; Kazarina, O.V.; Petukhova, A.N.; et al. A hybrid batch distillation/membrane process for high purification part 2: Removing of heavy impurities from xenon extracted from natural gas. Sep. Purif. Technol. 2022, 294, 121230. [Google Scholar] [CrossRef]
- Singh, V.; Kodamana, H. Reinforcement Learning Based Control of Batch Polymerisation Processes. IFAC-PapersOnLine 2020, 53, 667–672. [Google Scholar] [CrossRef]
- Hartlieb, M. Photo-iniferter RAFT polymerization. Macromol. Rapid Commun. 2022, 43, 2100514. [Google Scholar] [CrossRef]
- Chen, J.; Wang, F. Cost Reduction of CO2 Capture Processes Using Reinforcement Learning Based Iterative Design: A Pilot-Scale Absorption–stripping System. Sep. Purif. Technol. 2013, 122, 149–158. [Google Scholar] [CrossRef]
- Perera, A.T.D.; Wickramasinghe, P.U.; Nik, V.M.; Scartezzini, J.L. Introducing Reinforcement Learning to the Energy System Design Process. Appl. Energy 2020, 262, 114580. [Google Scholar] [CrossRef]
- Sachio, S.; Mowbray, M.; Papathanasiou, M.M.; del Rio-Chanona, E.A.; Petsagkourakis, P. Integrating Process Design and Control Using Reinforcement Learning. Chem. Eng. Res. Des. 2021, 183, 160–169. [Google Scholar] [CrossRef]
- Kim, S.; Jang, M.G.; Kim, J.K. Process Design and Optimization of Single Mixed-Refrigerant Processes with the Application of Deep Reinforcement Learning. Appl. Therm. Eng. 2023, 223, 120038. [Google Scholar] [CrossRef]
- Hicks, R.; Worrell, G.; Durney, R. Atlantic seeks improved control; studies analog-digital models. Oil Gas J. 1966, 24, 97. [Google Scholar]
- Boum, A.T.; Latifi, A.; Corriou, J.P. Model predictive control of a fluid catalytic cracking unit. In Proceedings of the 2013 International Conference on Process Control (PC), Strbske Pleso, Slovakia, 18–21 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 335–340. [Google Scholar]
- Skogestad, S. Plantwide control: The search for the self-optimizing control structure. J. Process Control 2000, 10, 487–507. [Google Scholar] [CrossRef]
- Ye, L.; Cao, Y.; Yuan, X. Global approximation of self-optimizing controlled variables with average loss minimization. Ind. Eng. Chem. Res. 2015, 54, 12040–12053. [Google Scholar] [CrossRef]
- Altman, E. Constrained Markov Decision Processes; Chapman and Hall/CRC: Boca Raton, FL, USA, 1999. [Google Scholar]
- Ji, J.; Zhou, J.; Zhang, B.; Dai, J.; Pan, X.; Sun, R.; Huang, W.; Geng, Y.; Liu, M.; Yang, Y. OmniSafe: An Infrastructure for Accelerating Safe Reinforcement Learning Research. J. Mach. Learn. Res. 2024, 25, 1–6. [Google Scholar]
- Yoo, H.; Kim, B.; Kim, J.W.; Lee, J.H. Reinforcement Learning Based Optimal Control of Batch Processes Using Monte-Carlo Deep Deterministic Policy Gradient with Phase Segmentation. Comput. Chem. Eng. 2021, 144, 107133. [Google Scholar] [CrossRef]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef]
- Neal, R.M. Bayesian Learning for Neural Networks; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 118. [Google Scholar]
- Graves, A. Practical variational inference for neural networks. Adv. Neural Inf. Process. Syst. 2011, 24, 2348–2356. [Google Scholar]
- Minka, T.P. Expectation propagation for approximate Bayesian inference. arXiv 2013, arXiv:1301.2294. [Google Scholar]
- Gal, Y.; McAllister, R.; Rasmussen, C.E. Improving PILCO with Bayesian neural network dynamics models. In Proceedings of the Data-Efficient Machine Learning Workshop, ICML, New York, NY, USA, 24 June 2016; Volume 4, p. 25. [Google Scholar]
- Henderson, P.; Doan, T.; Islam, R.; Meger, D. Bayesian Policy Gradients via Alpha Divergence Dropout Inference. In Proceedings of the NIPS Bayesian Deep Learning Workshop, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Li, Y.; Gal, Y. Dropout Inference in Bayesian Neural Networks with Alpha-divergences. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 2052–2061. [Google Scholar]
- Hernandez-Lobato, J.; Li, Y.; Rowland, M.; Bui, T.; Hernández-Lobato, D.; Turner, R. Black-box alpha divergence minimization. In Proceedings of the International Conference on Machine Learning, PMLR, New York, NY, USA, 19–24 June 2016; pp. 1511–1520. [Google Scholar]
- LeCun, Y.; Chopra, S.; Hadsell, R.; Ranzato, M.; Huang, F. A tutorial on energy-based learning. In Predicting Structured Data; MIT Press: Cambridge, MA, USA, 2006; Volume 1. [Google Scholar]
- Liu, X.; Sun, S. Alpha-divergence Minimization with Mixed Variational Posterior for Bayesian Neural Networks and Its Robustness Against Adversarial Examples. Neurocomputing 2020, 423, 427–434. [Google Scholar] [CrossRef]
- Guan, H.; Ye, L.; Shen, F.; Song, Z. Economic Operation of a Fluid Catalytic Cracking Process Using Self-Optimizing Control and Reconfiguration. J. Taiwan Inst. Chem. Eng. 2019, 96, 104–113. [Google Scholar] [CrossRef]
- Loeblein, C.; Perkins, J. Structural design for on-line process optimization: II. Application to a simulated FCC. AIChE J. 1999, 45, 1030–1040. [Google Scholar] [CrossRef]
- Hovd, M.; Skogestad, S. Procedure for regulatory control structure selection with application to the FCC process. AIChE J. 1993, 39, 1938–1953. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In Proceedings of the International Conference on Machine Learning, PMLR, Beijing, China, 22–24 June 2014; pp. 387–395. [Google Scholar]




| Variable | Description | Value and Unit |
|---|---|---|
| Activation energy for coke burning reaction | 158.6 kJ/mol | |
| Mass flow rate of gas oil feed | 2438.0 kg/min | |
| Gasoline yield factor of catalyst | 1.0 kg/min | |
| Rate constant for catalytic coke formation | 0.01897 | |
| Rate constant for coke burning | 29.338 | |
| Rate constant for gas oil cracking | 962,000 | |
| Temperature of air to regenerator | 320.0 K | |
| Temperature of gas oil feed | 420.0 K | |
| CO2/CO dependence on the temperature | 0.006244 | |
| , | Parameters for approximating | 521,150.0, 245.0 |
| Variable | Description | Unit |
|---|---|---|
| Mass flow rate of air to regenerator | kg/min | |
| Mass flow rate of spent catalyst | kg/min | |
| Temperature of catalyst in regenerator dense bed | K | |
| Temperature of cyclone | K | |
| Temperature of catalyst and gas oil mixture at riser inlet | K | |
| Temperature of catalyst and gas oil mixture at riser outlet | K | |
| Weight fraction of gas oil in product | - | |
| Weight fraction of gasoline in product | - |
| Price | Component | Value |
|---|---|---|
| gasoline | 0.14 USD/kg | |
| light gases | 0.132 USD/kg | |
| unconverted gas oil | 0.088 USD/kg |
| Parameter | Value |
|---|---|
| Hidden layer | 64-128-64 |
| Batch size | 64 |
| Time step | 9 × 106 |
| Episode | 2000 |
| MC sample (Only for BPD3PG) | 50 |
| Dropout rate (Only for BPD3PG) | 0.995 |
| Actor-learning rate | 0.0001 |
| Reward/Cost-learning rate | 0.0001 |
| Discount factor | 0.99 |
| -divergence (Only for BPD3PG) | 0.95 |
| KeepProp (Only for BPD3PG) | 0.95 |
| (Only for BPD3PG) | 0.92 |
| Parameter | Version |
|---|---|
| Computer | Windows10 |
| CPU | i5-12400F 2.50 GHz |
| RAM | 32.0 GB |
| GPU | NVIDIA GeForce RTX4060Ti |
| Tensorflow | 2.2.0 |
| Python | 3.8 |
| Comparison | Condition | J (USD/min) | Improvement (%) |
|---|---|---|---|
| BPD3PG vs. Hicks | Undisturbed | 49.31 vs. 49.11 | 0.41%↑ |
| Disturbed | 49.33 vs. 48.96 | 0.76%↑ | |
| BPD3PG vs. PD3PG | Undisturbed | 49.31 vs. 48.94 | 0.76%↑ |
| Disturbed | 49.33 vs. 48.44 | 1.84%↑ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, J.; Ye, L.; Zheng, J.; Jin, J. Bayesian Deep Reinforcement Learning for Operational Optimization of a Fluid Catalytic Cracking Unit. Processes 2025, 13, 1352. https://doi.org/10.3390/pr13051352
Qin J, Ye L, Zheng J, Jin J. Bayesian Deep Reinforcement Learning for Operational Optimization of a Fluid Catalytic Cracking Unit. Processes. 2025; 13(5):1352. https://doi.org/10.3390/pr13051352
Chicago/Turabian StyleQin, Jingsheng, Lingjian Ye, Jiaqing Zheng, and Jiangnan Jin. 2025. "Bayesian Deep Reinforcement Learning for Operational Optimization of a Fluid Catalytic Cracking Unit" Processes 13, no. 5: 1352. https://doi.org/10.3390/pr13051352
APA StyleQin, J., Ye, L., Zheng, J., & Jin, J. (2025). Bayesian Deep Reinforcement Learning for Operational Optimization of a Fluid Catalytic Cracking Unit. Processes, 13(5), 1352. https://doi.org/10.3390/pr13051352






