Techno-Economic Analysis for the Costs of Drying Chickpeas: An Example Showing the Trade-Off Between Capital and Operating Costs for Different Inlet Air Temperatures †
Abstract
1. Introduction
2. Materials and Methods
2.1. Capacity and Basis Calculations
2.2. Optimization and Trade-Offs
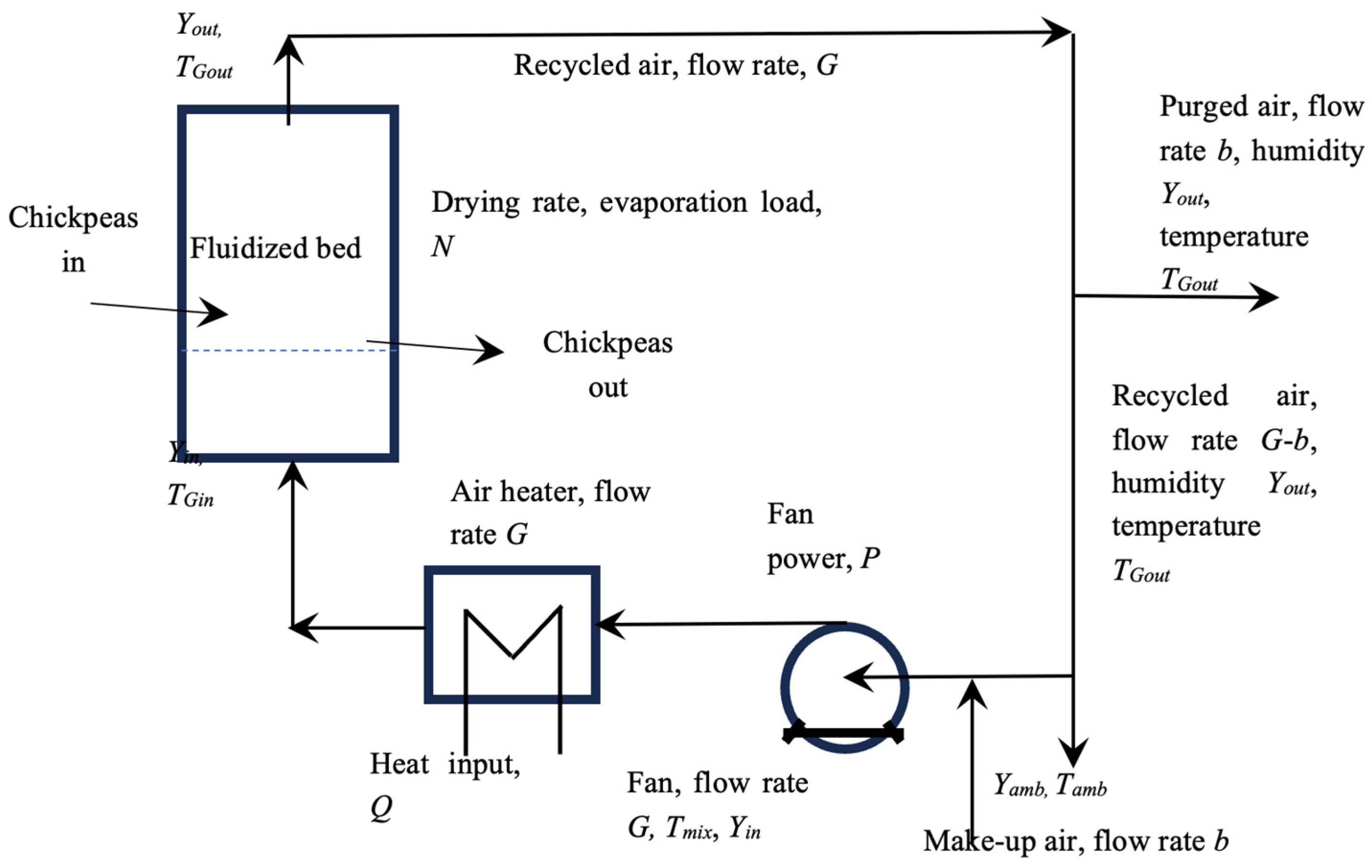
2.3. The Use of Air Recycling
2.4. Method of Techno-Economic Analysis
- Purchased Equipment Cost (PEC): The capital costs of each piece of the fluidized-bed dryers used in the processing were evaluated. These individual equipment costs formed the foundation for determining the overall Process Plant Cost.
- Process Plant Cost (PPC): The total cost of setting up the processing plant was estimated using the Lang factor, which scales the Purchased Equipment Cost (PEC) to reflect the full plant cost. According to Towler et al. [13], PPC is generally 3 to 4 times the PEC. This study uses a Lang factor of 4 to account for additional costs, including equipment installation, piping, electrical connections, and control systems.
- Capital Recovery Factor (CRF): The Capital Recovery Factor was applied to calculate the annualized capital expenditure. This factor accounts for the cost of recovering the initial capital investment over the equipment’s lifespan and incorporating both interest rates [14]. The CRF is a critical component for assessing the long-term financial sustainability and payback period of the processing facility.
2.5. Experimental Design
3. Results and Discussion
3.1. Open Loop
3.1.1. Drying Rate, Drying Flux, and Fluidized Bed Sizing Calculations
3.1.2. Capital Costs
3.1.3. Capital Costs Over Time: The Time Value of Money
3.1.4. Operating Costs
3.1.5. Raw Material Considerations
3.2. Closed-Loop Air Recycling
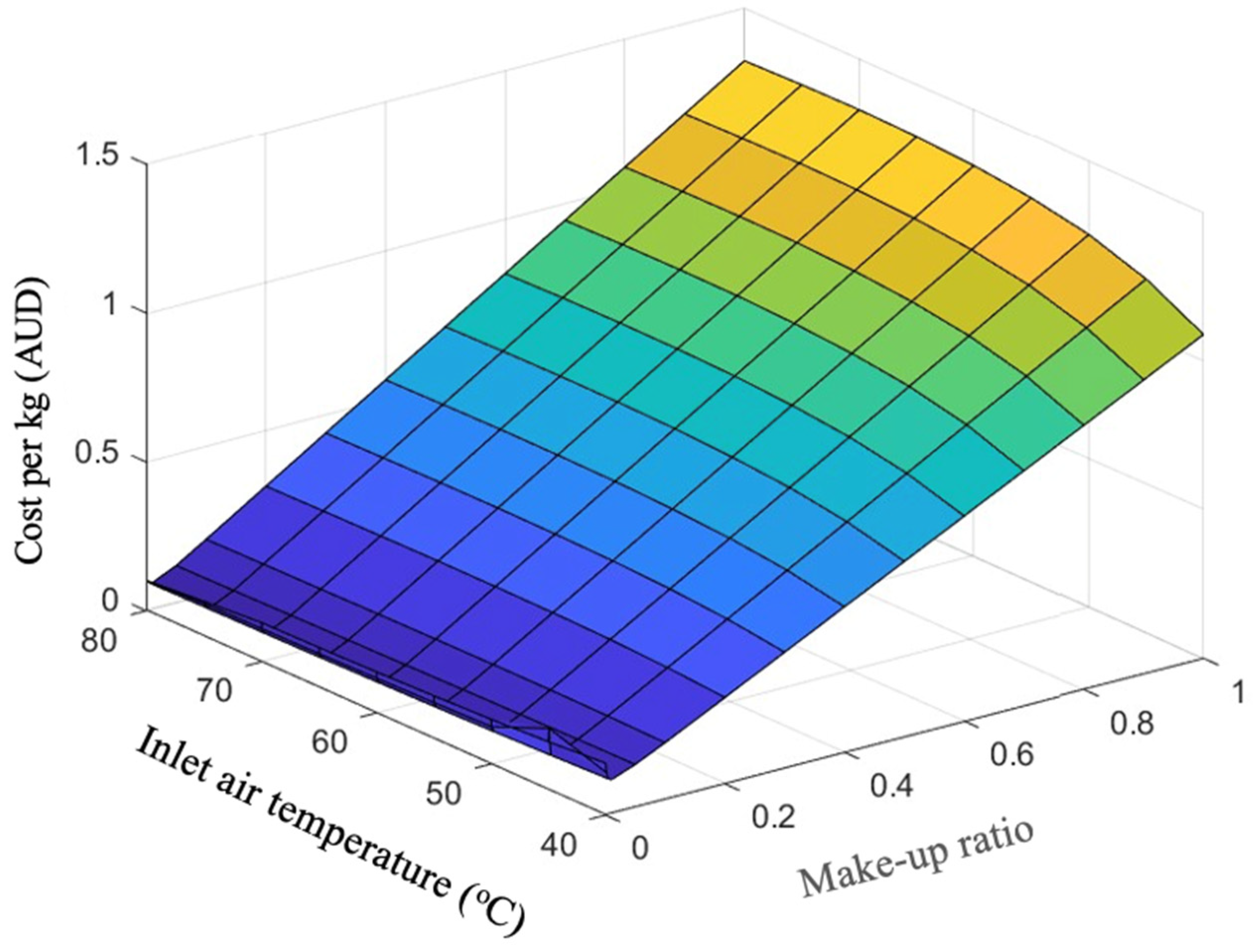
3.2.1. Capital Cost and Operating Cost
- Specify the inlet air temperature to the fluidized-bed dryer (TGin) and the make-up ratio (r).
- Guess the dryer cross-sectional area (A), the outlet gas humidity (Yout), and the outlet air temperature (TGout).
- Start the iteration.
- Calculate the gas flow rate (G) from Equation (9).
- Calculate the purge flow rate (b) from Equation (21).
- Calculate the inlet air humidity (Yin) from Equation (22).
- Calculate the mixed air temperature (Tmix) from Equation (23).
- Calculate the outlet air humidity (Yout) from Equation (12).
- Calculate the outlet air temperature (TGout) from Equation (13).
- Calculate the wet-bulb temperature (Twb) using the procedure outlined in Hecht et al. [22].
- Recalculate the dryer cross-sectional area (A) from Equation (5).
- Repeat the calculations from step 3.
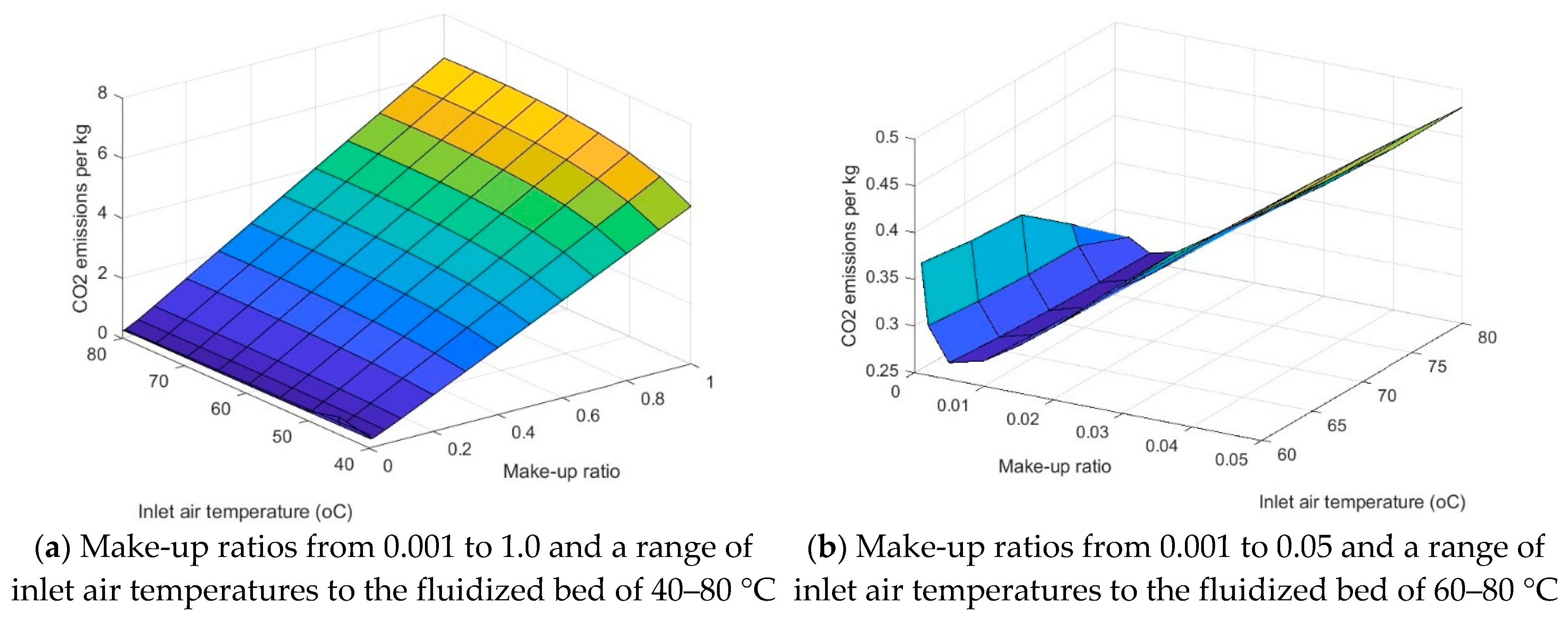
3.2.2. Carbon Emissions
3.2.3. Product Quality and Environmental Considerations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| T | Temperature | °C |
| Y | Humidity | kg kg−1 |
| A | Area | m2 |
| CRF | Capital recovery cost | AUD/USD |
| i | Interest rate | % |
| n | The number of repayments | year |
| G | Air mass flow rate | kg s−1 |
| ρ | Density | kg m3 |
| H | Latent heat | kJ kg−1 |
| CPY | Specific heat capacity of air | J kg−1 K−1 |
| Δp | Pressure drops | Pa |
| P | Power | W |
| Q | Heat | W |
| r | Make-up ratio | |
| Subscripts | ||
| G | Gas | |
| wb | Wet bulb | |
| vw | Vaporization for water | |
References
- AEGIC, Australian Export Grains Innovation Centre (2017). Australian Pulses: Quality, Versatility, Nutrition. Available online: https://www.aegic.org.au (accessed on 16 September 2023).
- Cheng, S.; Langrish, T.A.G. Fluidised bed drying of chickpeas: Developing a new drying schedule to reduce protein denaturation and remove trypsin inhibitors. J. Food Eng. 2023, 351, 111515. [Google Scholar] [CrossRef]
- Olabode, H.A.; Standing, C.N.; Chapman, P.A. Total energy to produce food servings as a function of processing and marketing modes. J. Food Sci. 1977, 42, 768–774. [Google Scholar] [CrossRef]
- Rao, M.A. Energy consumption for refrigerated, canned and frozen snap beans and corn. J. Food Process Eng. 1980, 3, 61–76. [Google Scholar] [CrossRef]
- Cheng, W.-C.; Langrish, T.A.G. Technico-economic analysis: A case study for orange juice liquids and spray-dried powders. In Chemeca 2018; Morison, K., Ed.; IChemE: Queenstown, New Zealand, 2018; ISBN 9781911446682. [Google Scholar]
- Nwakuba, N.; Okafor, V.; Okorafor, O. Techno-economic analysis of a hybrid solar-electric dryer. Energy Sources Part A Recover. Util. Environ. Eff. 2020, 46, 10289–10313. [Google Scholar] [CrossRef]
- Philip, N.; Duraipandi, S.; Sreekumar, A. Techno-economic analysis of greenhouse solar dryer for drying agricultural produce. Renew. Energy 2020, 199, 613–627. [Google Scholar] [CrossRef]
- Haque, N.; Somerville, M. Techno-economic and environmental evaluation of biomass dryer. Procedia Eng. 2013, 56, 650–655. [Google Scholar] [CrossRef]
- Shofinita, D.; Langrish, T.A.G. Spray drying of orange peel extracts: Yield, total phenolic content, and economic evaluation. J. Food Eng. 2014, 139, 31–42. [Google Scholar] [CrossRef]
- Langrish, T.; Cheng, S. Technico-Economic Analysis for the Costs of Drying Chickpeas: An Example Showing the Trade-off between Capital and Operating Costs for Different Inlet Air Temperatures. In Proceedings of the IDS 2024—23rd International Drying Symposium, Wuxi, China, 24 November 2024. [Google Scholar]
- Selina Wamucii (2024), Australia Chickpeas Prices. Available online: https://www.selinawamucii.com/insights/prices/australia/chickpeas/ (accessed on 3 January 2024).
- Grains Research & Development Corporation, Grownotes, Section 7, 2018, Chickpea, Harvest. Available online: https://grdc.com.au/__data/assets/pdf_file/0031/369418/GrowNote-Chickpea-North-12-Harvest.pdf (accessed on 29 March 2025).
- Towler, G.P.; Sinnott, R.K. Chemical Engineering Design: Principles, Practice and Economics of Plant and Process Design, 3rd ed.; Butterworth-Heinemann: Oxford, 2022; Chapter 7; ISBN 978-0-12-821179-3. [Google Scholar]
- Brennan, D. Process Industry Economics—Principles, Concepts and Applications, 2nd ed.; Elsevier: San Diego, CA, USA, 2020; ISBN 9780128194669. EISBN 9780128195604. [Google Scholar]
- Turton, R.A.; Shaeiwitz, J.; Bhattacharya, D.; Whiting, W.B. Analysis, Synthesis, and Design of Chemical Processes, 5th ed.; Prentice-Hall: Hoboken, NJ, USA, 2018; ISBN 978-0134177403. [Google Scholar]
- Keey, R.B.; Danckwerts, P.V. Drying: Principles and Practice; Pergamon: Oxford, UK, 2013; Chapter 1; pp. 1–18. [Google Scholar]
- Strumiłło, C.; Jones, P.L.; Żyłła, R. Energy Aspects in Drying. In Handbook of Industrial Drying, 4th ed.; Mujumdar, A.S., Ed.; ebook published; CRC Press: Boca Raton, FL, USA, 2014; Chapter 54; pp. 1077–1100. ISBN 9780429169762. [Google Scholar] [CrossRef]
- Pakowski, Z.; Mujumdar, A.S. Basic process calculations in drying. In Handbook of Industrial Drying; CRC Press: Boca Raton, FL, USA, 2020; pp. 10–13, 71–111. [Google Scholar]
- Venkateshan, S.P. Heat Transfer; Springer Nature: Berlin/Heidelberg, Germany, 2021; Chapter 2; pp. 17–57. [Google Scholar]
- Australian Energy Regulator, Whole Gas and Electricity Prices, Q3, 2023, Industry Charts, Monitoring Performance and Analysing Trends. Available online: https://www.aer.gov.au/industry/wholesale/charts (accessed on 29 December 2024).
- Davis, W.V.; Weber, C.; Wechsler, S.; Lucier, G.; Wakefield, H.; Vaiknoras, K. Vegetables and Pulses Outlook, December 2023. In Economic Research Service, Situation and Outlook Report; USDA, United States Department of Agriculture: Washington, DC, USA, 2023. [Google Scholar]
- Hecht, J.P.; Beimesch, W.E.; Dyvelkov, K.N.; Kemp, I.C.; Langrish, T.A.G.; Smith, F.L.; Stamper, J.A. Psychrometry. In Perry’s Chemical Engineers’ Handbook, 9th ed.; Green, M.Z., Southard, D.W., Eds.; McGraw-Hill Education: New York, NY, USA, 2019; Chapter 12.1; Available online: https://www.accessengineeringlibrary.com/content/book/9780071834087/toc-chapter/chapter12/section/section2 (accessed on 29 December 2024).
- Malik, D.P.; Kundu, K.K.; Singh, D.; Singh, K. Production and processing of chickpea in Haryana state-An economic analysis. Haryana J. Agron. 2009, 25, 48–53. [Google Scholar]
- Australian Bureau of Statistics, Products Price Indexes, Australia, Dec, 2024. Available online: https://www.abs.gov.au/statistics/economy/price-indexes-and-inflation/producer-price-indexes-australia/latest-release (accessed on 29 March 2025).
- DCCEEW, Department of Climate Change, Energy, the Environment, and Water, Australian National Greenhouse Accounts Factors, Australian Government, February 2023. Available online: https://www.dcceew.gov.au/sites/default/files/documents/national-greenhouse-accounts-factors-2022.pdf (accessed on 12 February 2024).
- Maharaj, P.; Freidrich, E. Environmental life cycle, carbon footprint and comparative economic assessment of rainwater harvesting systems in schools—A South African case study. Water SA 2014, 50, 80–91. [Google Scholar] [CrossRef]
- Hasan, M.; Langrish, T.A.G. Development of a sustainable methodology for life-cycle performance evaluation of solar dryers. Sol. Energy 2016, 135, 1–13. [Google Scholar] [CrossRef]

| Inlet Air Drying Temperature | Wet-Bulb Temperature for an Inlet Air Humidity of 0.0077 kg kg−1 | Drying Flux (Evaporative Flux) | Full-Scale Fluidized Bed Cross-Sectional Area |
|---|---|---|---|
| (°C) | (°C) | (kg m−2 bed area h−1) | (m2) |
| 40 | 21.04 | 1.97 | 8.06 |
| 60 | 26.50 | 3.48 | 4.56 |
| 80 | 31.06 | 5.09 | 3.12 |
| Inlet Air Drying Temperature | Basic Capital Cost (Based on Tray Dryer) (PEC) | Process Plant Cost After Using Lang Factor, Allowing for Stainless Steel (PPC) | Process Plant Cost in Australian Dollars (PPC) | Annual Capital Recovery Costs |
|---|---|---|---|---|
| (°C) | (USD) | (USD) | (AUD) | (AUD/year) |
| 40 | 20,800 | 108,160 | 162,240 | 26,445 |
| 60 | 17,000 | 88,400 | 132,600 | 21,614 |
| 80 | 11,700 | 60,840 | 91,260 | 14,875 |
| Inlet Air Drying Temperature | G, Airflow Rate for Fluidization | ΔY, Change in Air Humidity | ΔTG, Change in Air Temperature | Yout, Outlet Air Humidity | TGout, Outlet Air Temperature |
|---|---|---|---|---|---|
| (°C) | (kg s−1) | (×10−3 kg kg−1) | (°C) | (kg kg−1) | (°C) |
| 40 | 86.4 | 0.0510 | 0.112 | 0.010051 | 39.9 |
| 60 | 46.0 | 0.0959 | 0.211 | 0.010096 | 59.8 |
| 80 | 29.7 | 0.1490 | 0.327 | 0.010149 | 79.7 |
| Inlet Air Drying Temperature | Q, Thermal Energy Required to Heat the Air | P, Pumping Power Required to Fluidize the Bed | QL, Heat Losses |
|---|---|---|---|
| (°C) | (kW) | (kW) | (kW) |
| 40 | 1296 | 7.7 | 6.0 |
| 60 | 1632 | 4.3 | 8.0 |
| 80 | 1192 | 3.0 | 8.6 |
| Inlet Air Drying Temperature | Annual Gas Heating Costs | Annual Electricity (Fan) Costs | Utilities Cost per Unit Mass of Chickpeas | Total Operating Costs per Unit Mass of Chickpeas | Total Capital and Operating Costs per Unit Mass |
|---|---|---|---|---|---|
| (°C) | (AUD/year) | (AUD/year) | (AUD/kg) | (AUD/kg) | (AUD/kg) |
| 40 | 407,900 | 4410 | 0.86 | 1.03 | 1.09 |
| 60 | 505,700 | 2500 | 1.06 | 1.27 | 1.32 |
| 80 | 513,300 | 1710 | 1.07 | 1.29 | 1.32 |
| Open Loop, No Recycling | Closed Loop, Recycling Ratio 99% | |
|---|---|---|
| Inlet air temperature (°C) | 40 | 80 |
| Area of fluidized bed (m2) | 8.06 | 4.41 |
| Annualized capital costs (AUD per year−1) | 26,500 | 19,300 |
| Annual gas heating costs (AUD per year−1) | 407,900 | 17,000 |
| Gas flow rate (kg s−1) | 86.4 | 42.0 |
| Annual electricity (fan) costs (AUD per year−1) | 4410 | 2240 |
| Total processing cost per unit mass (AUD per kg−1) | 1.09 | 0.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Langrish, T.A.G.; Cheng, S. Techno-Economic Analysis for the Costs of Drying Chickpeas: An Example Showing the Trade-Off Between Capital and Operating Costs for Different Inlet Air Temperatures. Processes 2025, 13, 1178. https://doi.org/10.3390/pr13041178
Langrish TAG, Cheng S. Techno-Economic Analysis for the Costs of Drying Chickpeas: An Example Showing the Trade-Off Between Capital and Operating Costs for Different Inlet Air Temperatures. Processes. 2025; 13(4):1178. https://doi.org/10.3390/pr13041178
Chicago/Turabian StyleLangrish, Timothy A. G., and Shu Cheng. 2025. "Techno-Economic Analysis for the Costs of Drying Chickpeas: An Example Showing the Trade-Off Between Capital and Operating Costs for Different Inlet Air Temperatures" Processes 13, no. 4: 1178. https://doi.org/10.3390/pr13041178
APA StyleLangrish, T. A. G., & Cheng, S. (2025). Techno-Economic Analysis for the Costs of Drying Chickpeas: An Example Showing the Trade-Off Between Capital and Operating Costs for Different Inlet Air Temperatures. Processes, 13(4), 1178. https://doi.org/10.3390/pr13041178







