A Novel Ultra Local Based-Fuzzy PIDF Controller for Frequency Regulation of a Hybrid Microgrid System with High Renewable Energy Penetration and Storage Devices
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Literature Review
1.2.1. LFC with Conventional Control
1.2.2. LFC with Advanced Control
1.3. Contributions and Paper Organization
- A new combination of parallel ultra-local control (ULC) with classical PIDF and intelligent Fuzzy PIDF controllers has been proposed to solve the LFC problem.
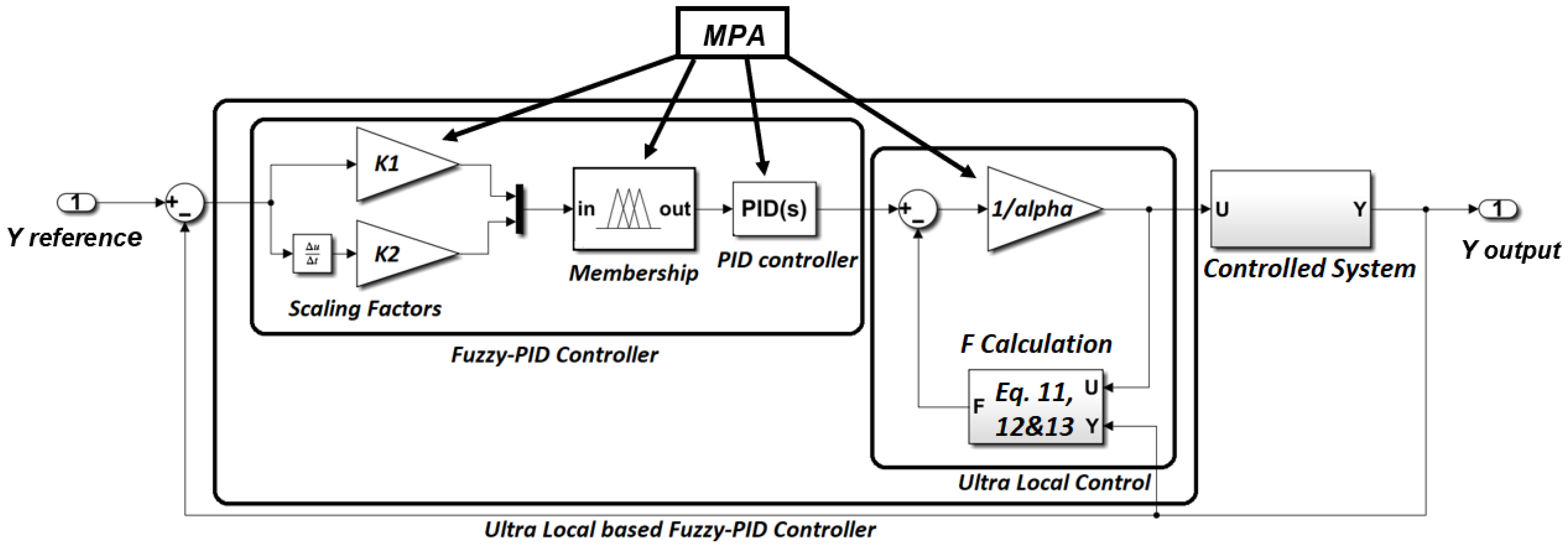
- The gains of the PIDF controller, the primary parameter of the ULC, as well as the input scaling factors and gains of the fuzzy PIDF controller are optimized using the MPA, a recent optimizer.
- Improving the proposed controller’s effectiveness by utilizing MPA to optimize the fuzzy controller’s membership function bounds.
- Evaluating the suggested controller’s resilience and efficacy in a hybrid microgrid under various scenarios, including the use of renewable energy sources and storage technologies.
2. System Structure
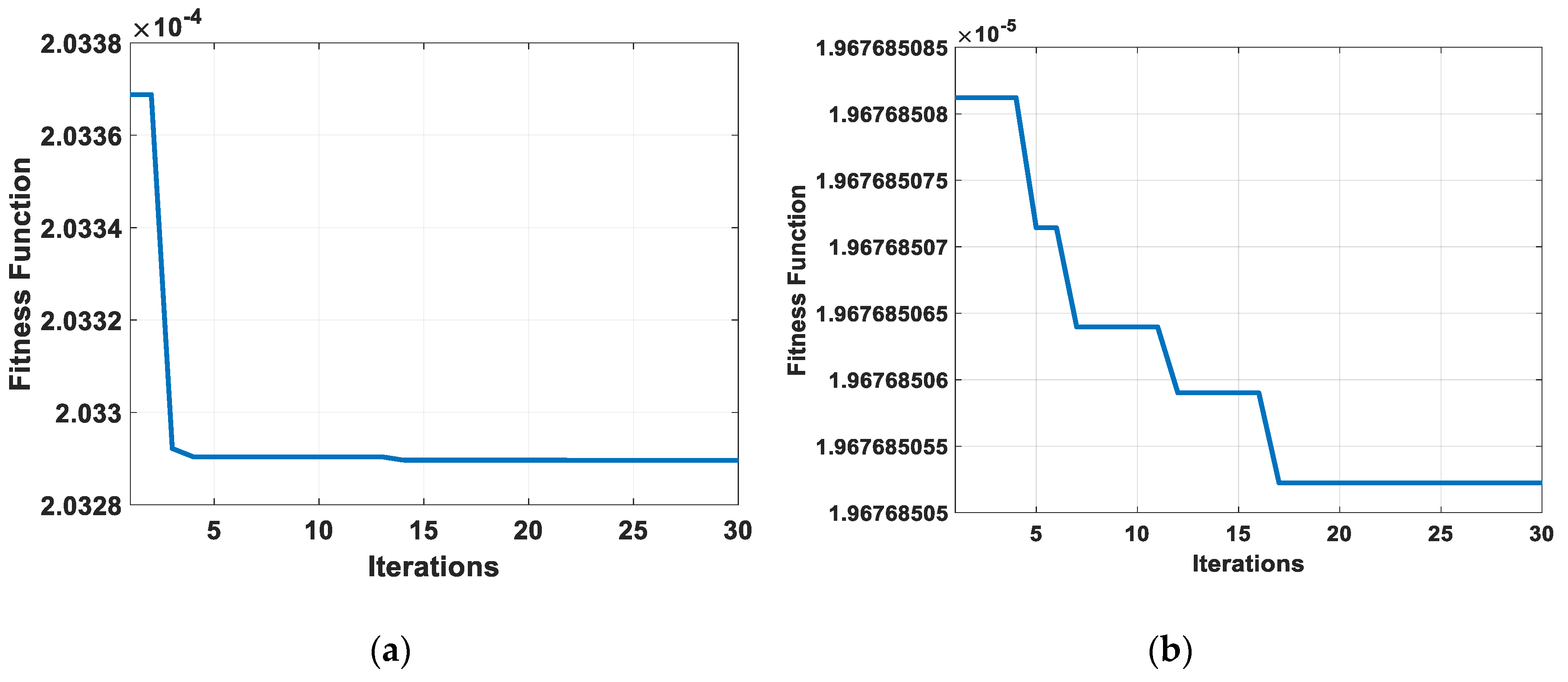
3. MPA Optimization Algorithm
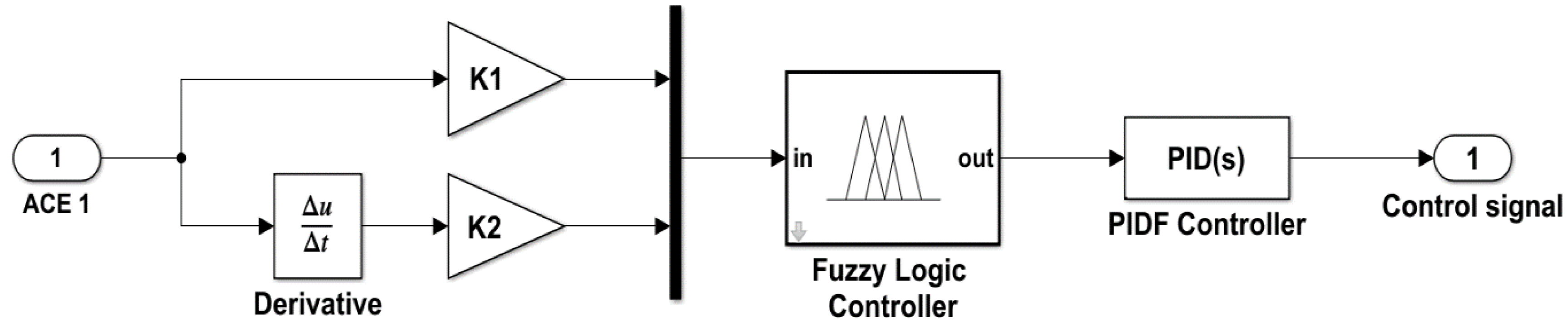
4. Formulation of the Problem and the Proposed Controller Structure
- (1)
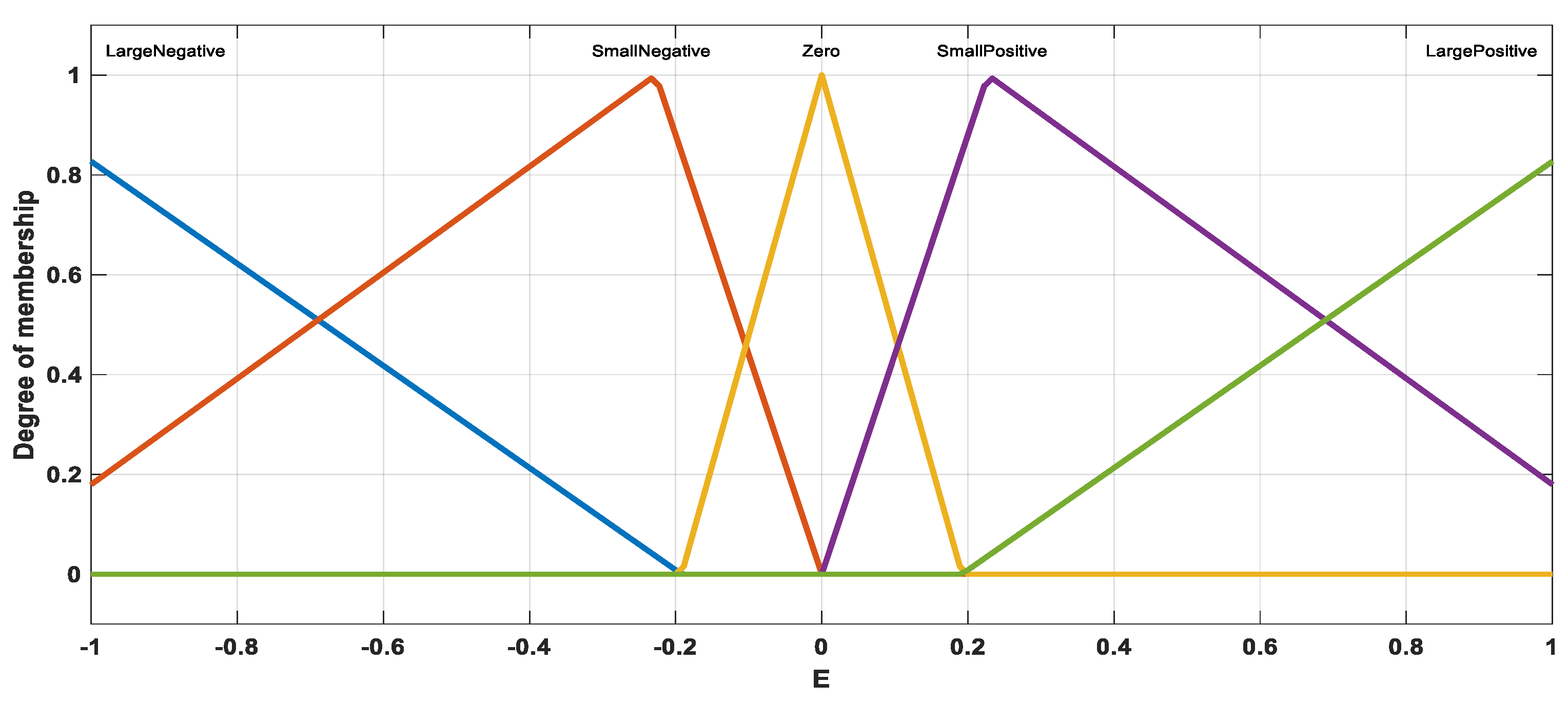
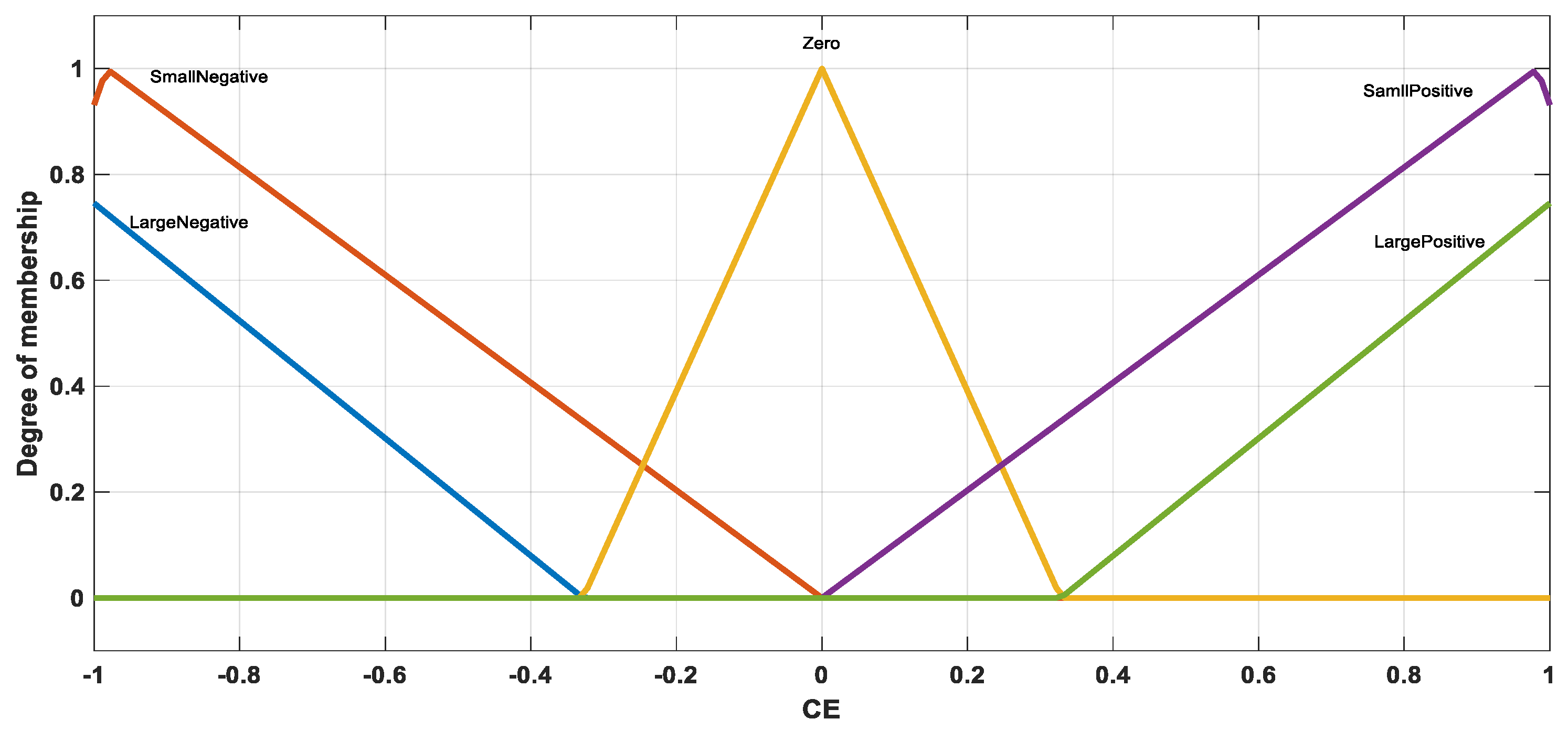
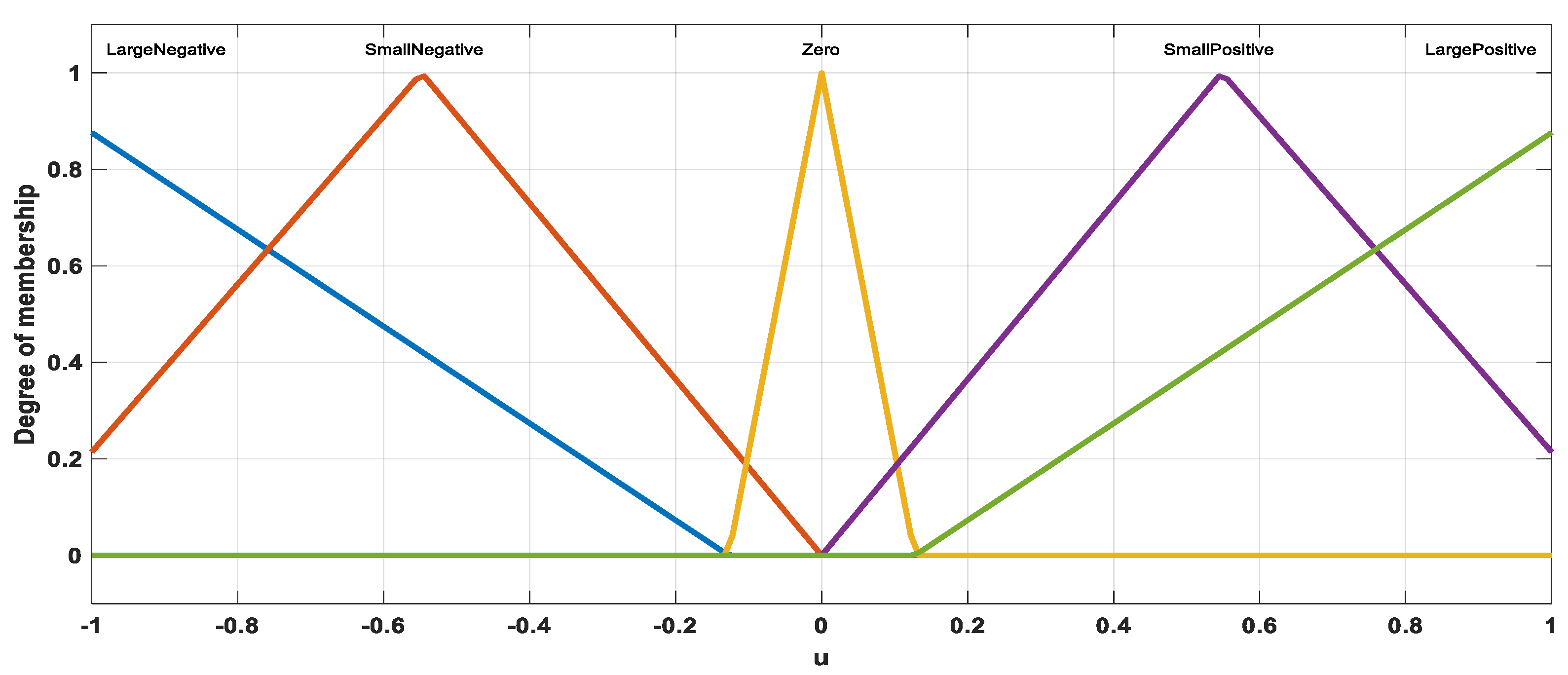
- Fuzzification: In this stage, the FLC transforms the error (E) and change of error (CE) variables into five language variables (LP, LN, Z, SP, SN).
- (2)
- Rule base formation: The FLC uses Mamdani fuzzy inference (FIS) to build fuzzy rules based on the linguistic variables obtained through the fuzzification process, as illustrated in Table 2. The experience of the creator determines the FLC’s rule foundation. To get the best possible reaction, each system has its own set of rules.
- (3)
5. Stability Analysis
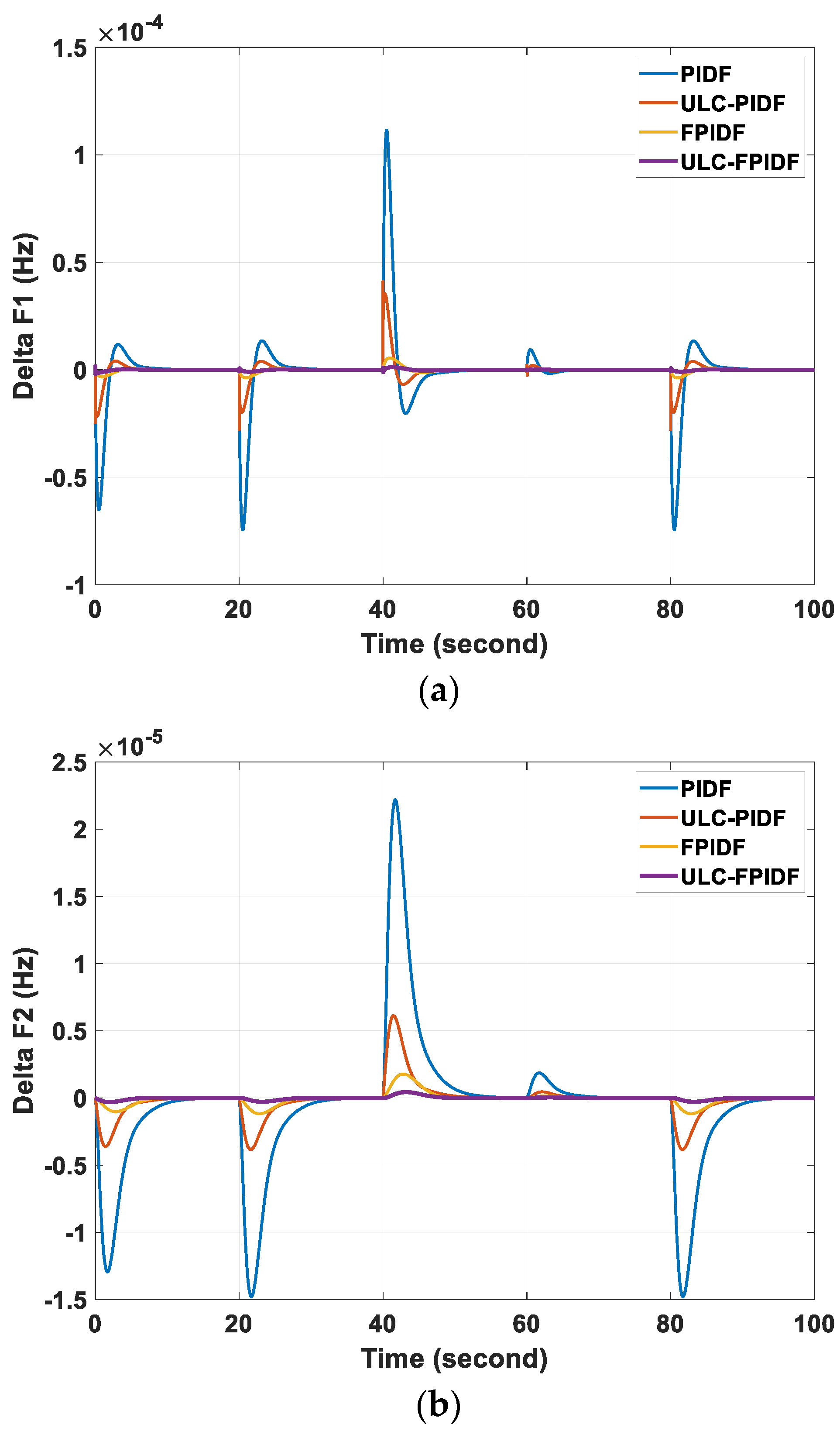
6. Results and Discussion
- Different small and large step load perturbations (SLP).
- Microgrid parameters variations.
- A continuous random load variation.
- Integration of different RES fluctuations.
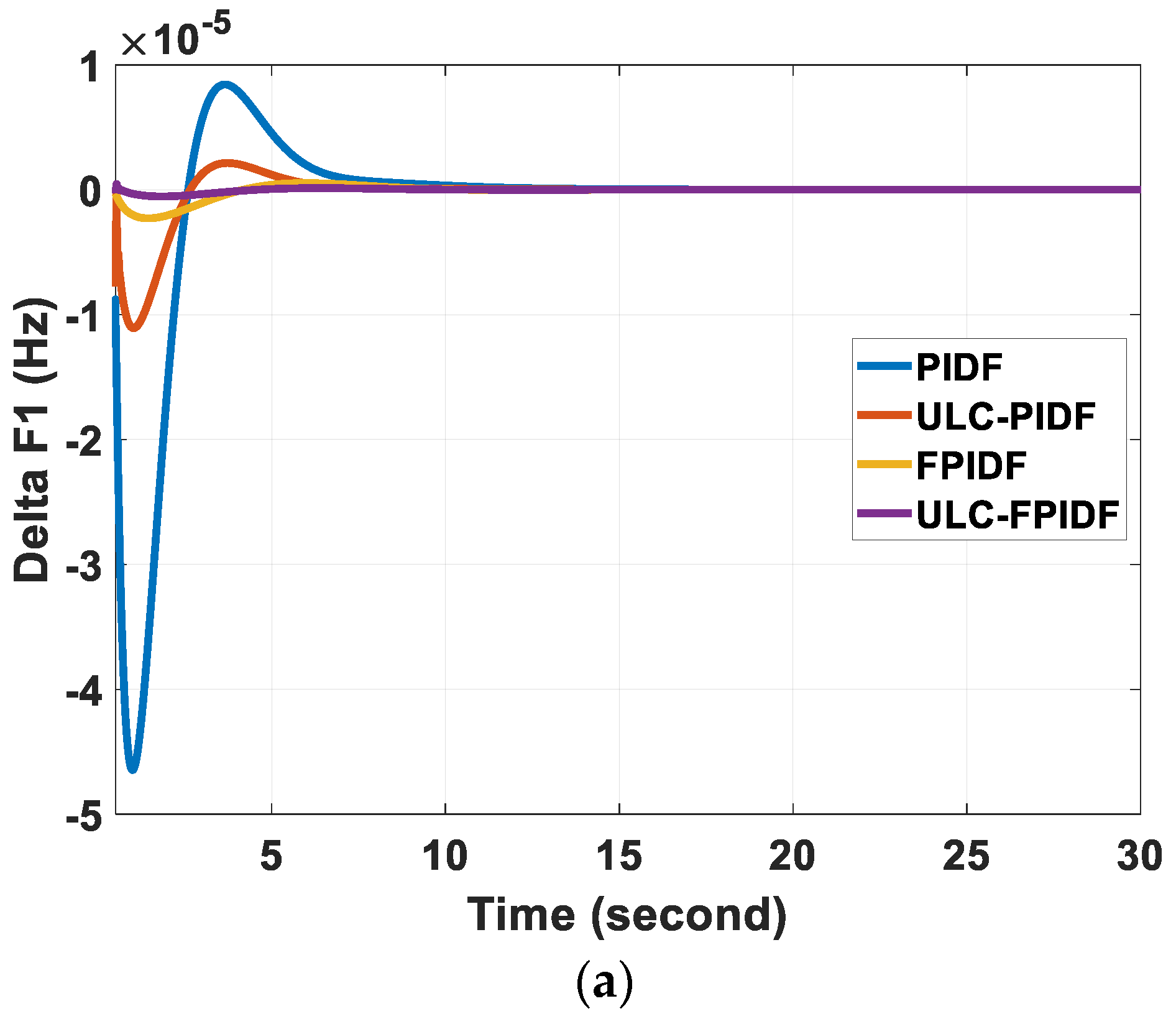
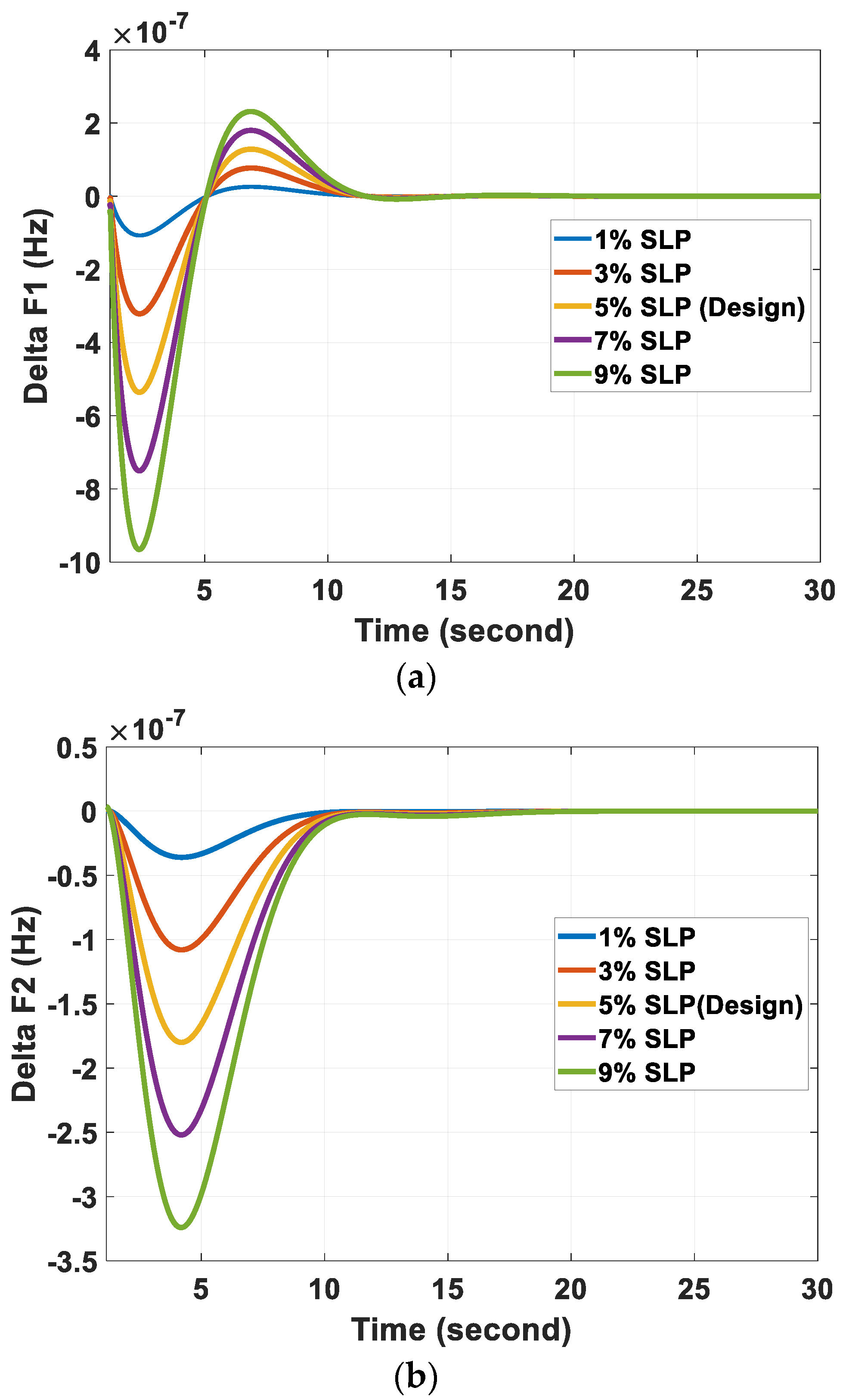
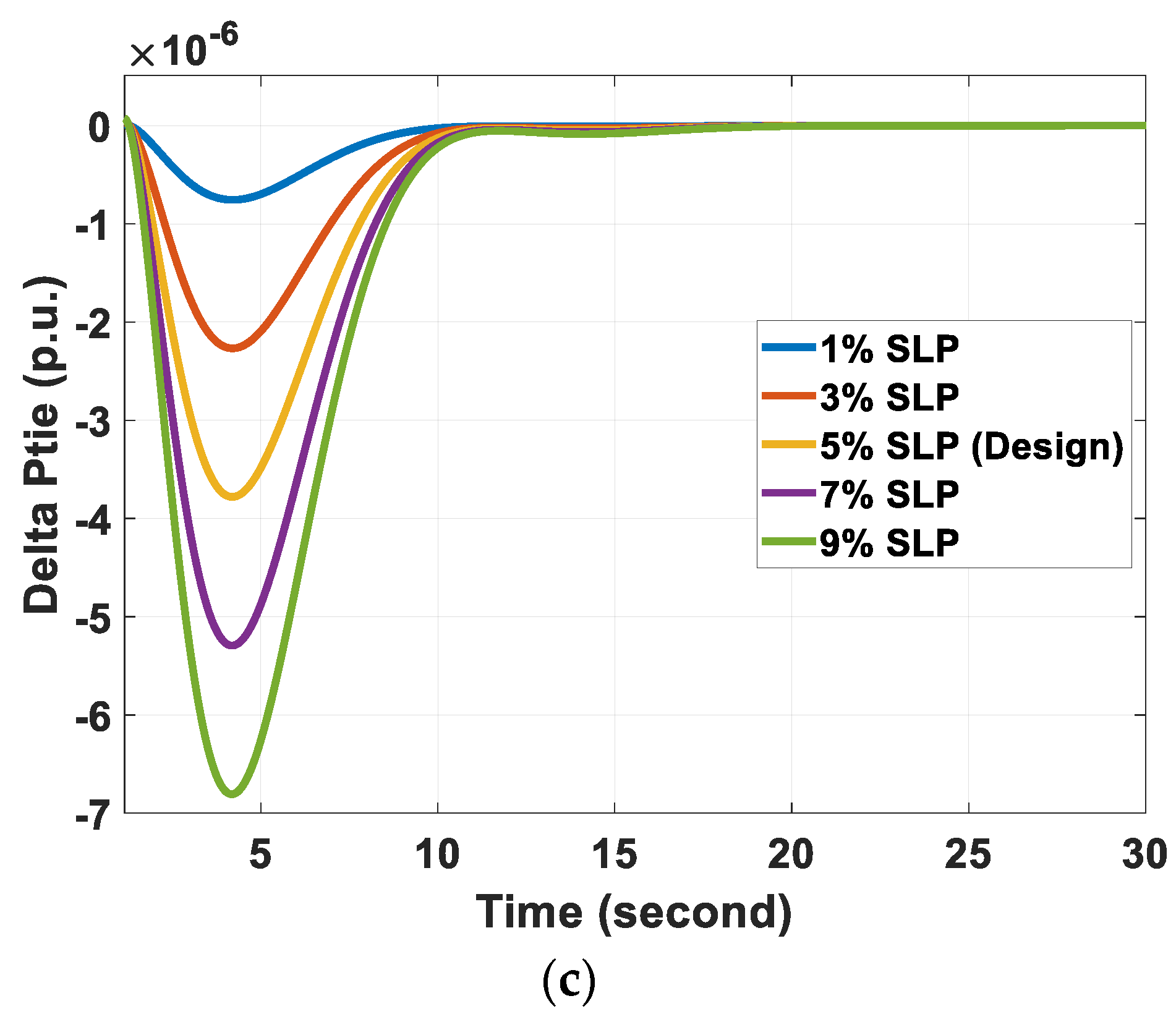
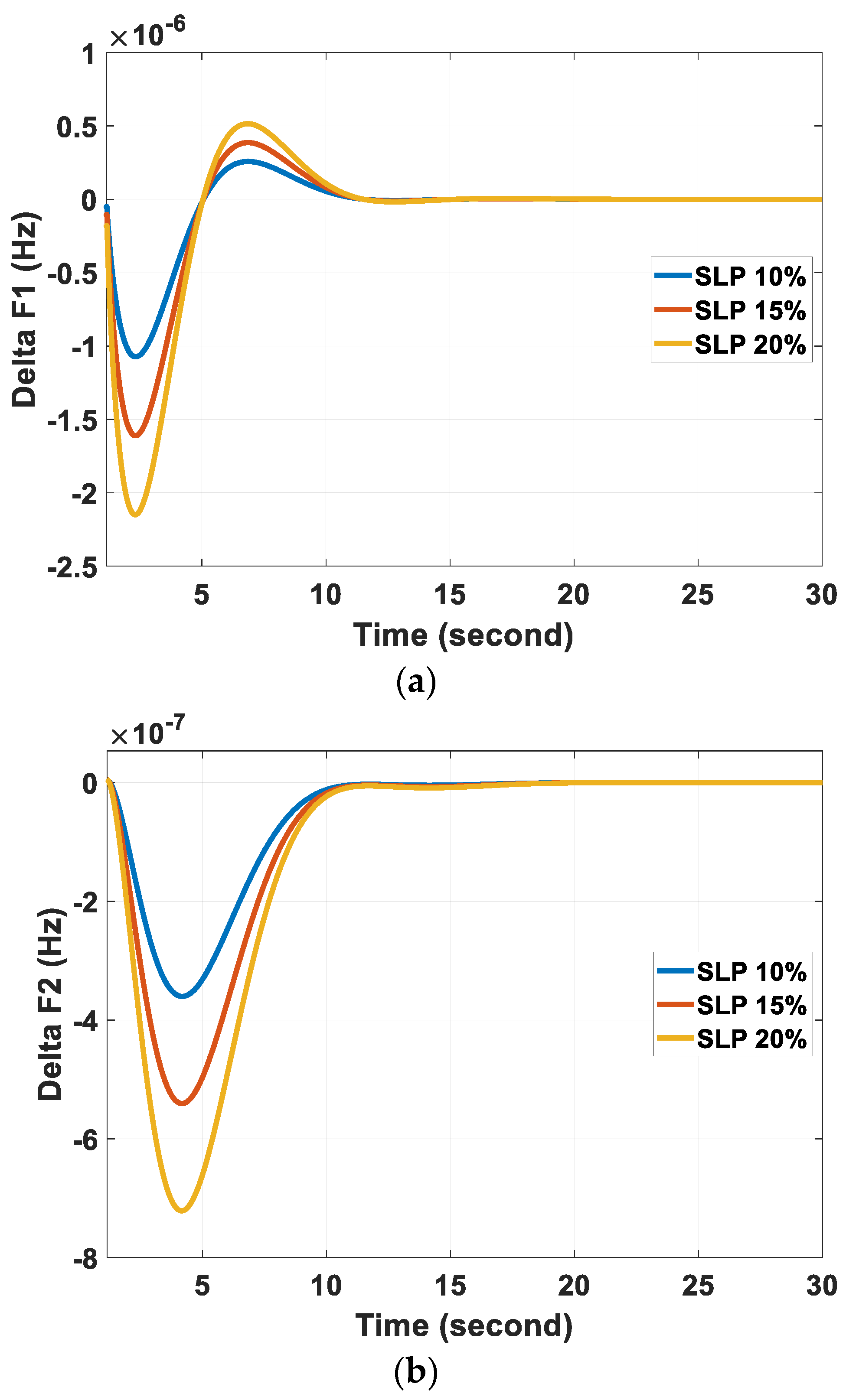
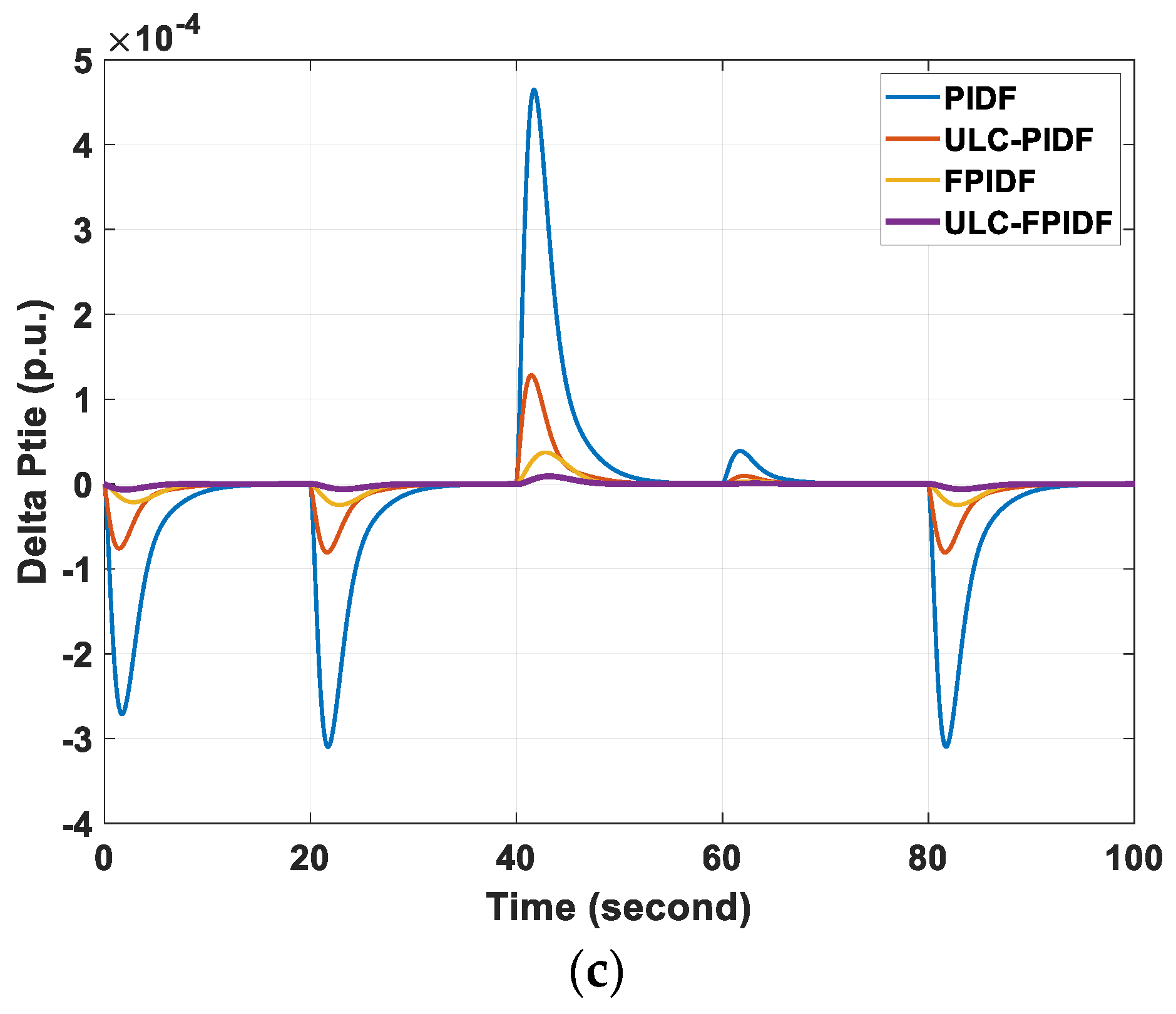
6.1. Scenario (I): Effect of Step Load Perturbation
6.2. Scenario (II): Sensitivity Analysis of System Parameters Change
6.3. Scenario (III): Effect of Random Load Variation
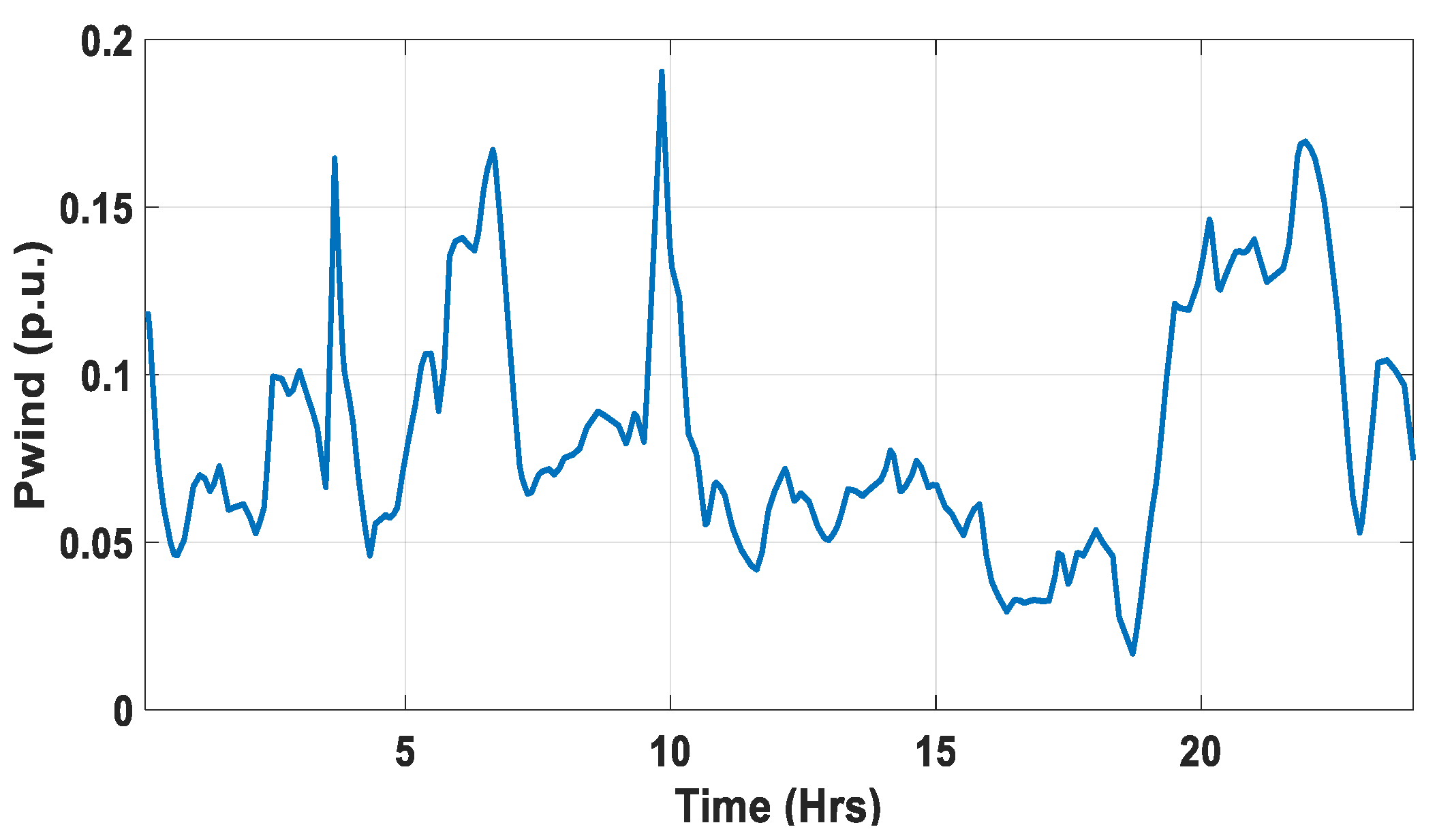
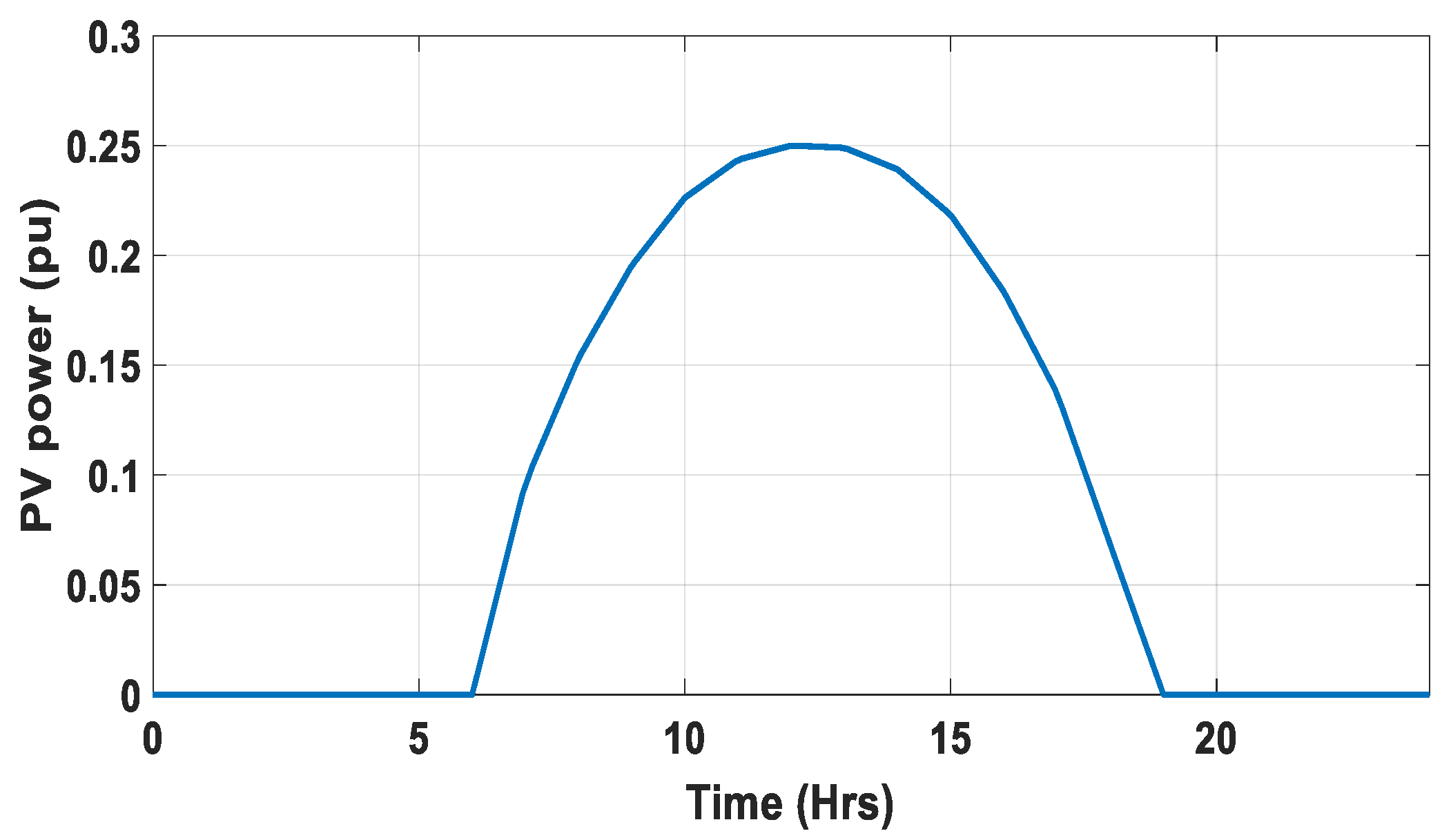
6.4. Scenario (IV): RES Fluctuation Effect
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- AboRas, K.M.; Ragab, M.; Shouran, M.; Alghamdi, S.; Kotb, H. Voltage and Frequency Regulation in Smart Grids via a Unique Fuzzy PIDD2 Controller Optimized by Gradient-Based Optimization Algorithm. Energy Rep. 2023, 9, 1201–1235. [Google Scholar] [CrossRef]
- Ali, M.; Kotb, H.; Kareem AboRas, M.; Nabil Abbasy, H. Frequency Regulation of Hybrid Multi-Area Power System Using Wild Horse Optimizer Based New Combined Fuzzy Fractional-Order PI and TID Controllers. Alex. Eng. J. 2022, 61, 12187–12210. [Google Scholar] [CrossRef]
- Ali, M.; Kotb, H.; Aboras, K.M.; Abbasy, N.H. Design of Cascaded PI-Fractional Order PID Controller for Improving the Frequency Response of Hybrid Microgrid System Using Gorilla Troops Optimizer. IEEE Access 2021, 9, 150715–150732. [Google Scholar] [CrossRef]
- Hasanien, H.M. Whale Optimisation Algorithm for Automatic Generation Control of Interconnected Modern Power Systems Including Renewable Energy Sources. IET Gener. Transm. Distrib. 2018, 12, 607–614. [Google Scholar] [CrossRef]
- Raja, S.K.; Badathala, V.P.; Ss, K. LFC Problem by Using Improved Genetic Algorithm Tuning PID Controller. Int. J. Pure Appl. Math. 2018, 120, 7899–7908. [Google Scholar]
- Rao, R.N.; Reddy, P.R.K. PSO Based Tuning of PID Controller for a Load Frequency Control in Two Area Power System. Int. J. Eng. Res. Appl. (IJERA) 2015, 1, 1499–1505. [Google Scholar]
- Saleh, B. Design of PID Controller with Grid Connected Hybrid Renewable Energy System Using Optimization Algorithms. J. Electr. Eng. Technol. 2021, 1–15. [Google Scholar] [CrossRef]
- Sobhy, M.A.; Abdelaziz, A.Y.; Hasanien, H.M.; Ezzat, M. Marine Predators Algorithm for Load Frequency Control of Modern Interconnected Power Systems Including Renewable Energy Sources and Energy Storage Units. Ain Shams Eng. J. 2021, 12, 3843–3857. [Google Scholar] [CrossRef]
- El-Fergany, A.A.; El-Hameed, M.A. Efficient Frequency Controllers for Autonomous Two-Area Hybrid Microgrid System Using Social-Spider Optimiser. IET Gener. Transm. Distrib. 2017, 11, 637–648. [Google Scholar] [CrossRef]
- Mehta, P.; Bhatt, P.; Pandya, V. Optimized Coordinated Control of Frequency and Voltage for Distributed Generating System Using Cuckoo Search Algorithm. Ain Shams Eng. J. 2018, 9, 1855–1864. [Google Scholar] [CrossRef]
- Sharma, J.; Hote, Y.V.; Prasad, R. PID Controller Design for Interval Load Frequency Control System with Communication Time Delay. Control. Eng. Pract. 2019, 89, 154–168. [Google Scholar] [CrossRef]
- Saha, D.; Saikia, L.C. Automatic Generation Control of an Interconnected CCGT-Thermal System Using Stochastic Fractal Search Optimized Classical Controllers. Int. Trans. Electr. Energy Syst. 2018, 28, e2533. [Google Scholar] [CrossRef]
- Barik, A.K.; Das, D.C. Integrated Resource Planning in Sustainable Energy-Based Distributed Microgrids. Sustain. Energy Technol. Assessments 2021, 48, 101622. [Google Scholar] [CrossRef]
- Khamies, M.; Magdy, G.; Hussein, M.E.; Banakhr, F.A.; Kamel, S. An Efficient Control Strategy for Enhancing Frequency Stability of Multi-Area Power System Considering High Wind Energy Penetration. IEEE Access 2020, 8, 140062–140078. [Google Scholar] [CrossRef]
- Sahu, R.K.; Gorripotu, T.S.; Panda, S. Automatic Generation Control of Multi-Area Power Systems with Diverse Energy Sources Using Teaching Learning Based Optimization Algorithm. Eng. Sci. Technol. Int. J. 2016, 19, 113–134. [Google Scholar] [CrossRef]
- Patel, N.C.; Debnath, M.K.; Bagarty, D.P.; Das, P. GWO Tuned Multi Degree of Freedom PID Controller for Load Frequency Control. Int. J. Eng. Technol. 2018, 7, 548–552. [Google Scholar] [CrossRef]
- Mudi, J.; Shiva, C.K.; Mukherjee, V. Multi-Verse Optimization Algorithm for LFC of Power System with Imposed Non-Linearities Using Three-Degree-of-Freedom PID Controller. Iran. J. Sci. Technol. 2019, 43, 837–856. [Google Scholar]
- Gheisarnejad, M. An Effective Hybrid Harmony Search and Cuckoo Optimization Algorithm Based Fuzzy PID Controller for Load Frequency Control. Appl. Soft Comput. 2018, 65, 121–138. [Google Scholar] [CrossRef]
- Bayati, N.; Dadkhah, A.; Vahidi, B.; Sadeghi, S.H.H. Fopid Design for Load-Frequency Control Using Genetic Algorithm. Sci. Int. 2015, 27, 3089–3094. [Google Scholar]
- Pan, I.; Das, S. Fractional Order AGC for Distributed Energy Resources Using Robust Optimization. IEEE Trans. Smart Grid 2016, 7, 2175–2186. [Google Scholar] [CrossRef]
- Tabak, A. Fractional Order Frequency Proportional-Integral-Derivative Control of Microgrid Consisting of Renewa-ble Energy Sources Based on Multi-Objective Grasshopper Optimization Algorithm. Trans. Inst. Meas. Control. 2022, 44, 378–392. [Google Scholar] [CrossRef]
- Pan, I.; Das, S. Frequency Domain Design of Fractional Order PID Controller for AVR System Using Chaotic Mul-ti-Objective Optimization. Int. J. Electr. Power Energy Syst. 2013, 51, 106–118. [Google Scholar] [CrossRef]
- Datta, A.; Koley, I.; Panda, G.K.; Atoche, A.C.; Castillo, J.V. Dynamic Power-Frequency Control in a Hybrid Wind-PV Plant Interlinked with AC Power System. J. Electr. Eng. Technol. 2021, 16, 1469–1479. [Google Scholar] [CrossRef]
- Taher, S.A.; Hajiakbari Fini, M.; Falahati Aliabadi, S. Fractional Order PID Controller Design for LFC in Electric Power Systems Using Imperialist Competitive Algorithm. Ain Shams Eng. J. 2014, 5, 121–135. [Google Scholar] [CrossRef]
- Fayek, H.H.; Kotsampopoulos, P. Central Tunicate Swarm NFOPID-Based Load Frequency Control of the Egyptian Power System Considering New Uncontrolled Wind and Photovoltaic Farms. Energies 2021, 14, 3604. [Google Scholar] [CrossRef]
- Ahmed, E.M.; Mohamed, E.A.; Elmelegi, A.; Aly, M.; Elbaksawi, O. Optimum Modified Fractional Order Controller for Future Electric Vehicles and Renewable Energy-Based Interconnected Power Systems. IEEE Access 2021, 9, 29993–30010. [Google Scholar] [CrossRef]
- Kumar Sahu, R.; Panda, S.; Biswal, A.; Chandra Sekhar, G.T. Design and Analysis of Tilt Integral Derivative Con-troller with Filter for Load Frequency Control of Multi-Area Interconnected Power Systems. ISA Trans. 2016, 61, 251–264. [Google Scholar] [CrossRef]
- Topno, P.N.; Chanana, S. Load Frequency Control of a Two-Area Multi-Source Power System Using a Tilt Integral Derivative Controller. J. Vib. Control. 2018, 24, 110–125. [Google Scholar] [CrossRef]
- Chintu, J.M.R.; Sahu, R.K.; Panda, S. Design and Analysis of Two Degree of Freedom Tilt Integral Derivative Con-troller with Filter for Frequency Control and Real Time Validation. J. Electr. Eng. 2020, 71, 388–396. [Google Scholar] [CrossRef]
- Shouran, M.; Anayi, F.; Packianather, M.; Habil, M. Load Frequency Control Based on the Bees Algorithm for the Great Britain Power System. Designs 2021, 5, 50. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, S.; Zhao, Q. Distributed Economic MPC for LFC of Multi-Area Power System with Wind Power Plants in Power Market Environment. Int. J. Electr. Power Energy Syst. 2021, 126, 106548. [Google Scholar] [CrossRef]
- Singh, A.; Sharma, V.; Dahiya, P.; Sharma, R.N. Model Predictive Based Load Frequency Control of Interconnected Power Systems. Recent Adv. Electr. Electron. Eng. (Former. Recent Pat. Electr. Electron. Eng.) 2018, 11, 322–333. [Google Scholar] [CrossRef]
- Ali, H.H.; Kassem, A.M.; Al-Dhaifallah, M.; Fathy, A. Multi-Verse Optimizer for Model Predictive Load Frequency Control of Hybrid Multi-Interconnected Plants Comprising Renewable Energy. IEEE Access 2020, 8, 114623–114642. [Google Scholar] [CrossRef]
- Ismail, M.M.; Bendary, A.F. Load Frequency Control for Multi Area Smart Grid Based on Advanced Control Techniques. Alex. Eng. J. 2018, 57, 4021–4032. [Google Scholar] [CrossRef]
- Fathy, A.; Kassem, A.M. Antlion Optimizer-ANFIS Load Frequency Control for Multi-Interconnected Plants Comprising Photovoltaic and Wind Turbine. ISA Trans. 2019, 87, 282–296. [Google Scholar] [CrossRef] [PubMed]
- Prakash, S.; Sinha, S.K. Automatic Load Frequency Control of Six Areas’ Hybrid Multi-Generation Power Systems Using Neuro-Fuzzy Intelligent Controller. IETE J. Res. 2018, 64, 471–481. [Google Scholar] [CrossRef]
- Aryanpour, H.; Shayeghi, H.; Nooshyar, M.; Esmaeili, M. Design of New Controller for Load Frequency Control of Isolated Microgrid Considering System Uncertainties. Int. J. Power Energy Convers. 2018, 9, 285. [Google Scholar] [CrossRef]
- Selvaraju, R.K.; Somaskandan, G. ACS Algorithm Tuned ANFIS-Based Controller for LFC in Deregulated Environment. J. Appl. Res. Technol. 2017, 15, 152–166. [Google Scholar] [CrossRef]
- Patowary, M.; Panda, G.; Naidu, B.R.; Deka, B.C. ANN-based Adaptive Current Controller for On-grid DG System to Meet Frequency Deviation and Transient Load Challenges with Hardware Implementation. IET Renew. Power Gener. 2018, 12, 61–71. [Google Scholar] [CrossRef]
- Shouran, M.; Anayi, F.; Packianather, M. The Bees Algorithm Tuned Sliding Mode Control for Load Frequency Control in Two-Area Power System. Energies 2021, 14, 5701. [Google Scholar] [CrossRef]
- Dombi, J.; Hussain, A. A New Approach to Fuzzy Control Using the Distending Function. J. Process Control. 2020, 86, 16–29. [Google Scholar] [CrossRef]
- Valdez, F.; Castillo, O.; Peraza, C. Fuzzy Logic in Dynamic Parameter Adaptation of Harmony Search Optimization for Benchmark Functions and Fuzzy Controllers. Int. J. Fuzzy Syst. 2020, 22, 1198–1211. [Google Scholar] [CrossRef]
- Yakout, A.H.; Kotb, H.; Hasanien, H.M.; AboRas, K.M. Optimal Fuzzy PIDF Load Frequency Controller for Hybrid Microgrid System Using Marine Predator Algorithm. IEEE Access 2021, 9, 54220–54232. [Google Scholar] [CrossRef]
- Rajesh, K.; Dash, S. Load Frequency Control of Autonomous Power System Using Adaptive Fuzzy Based PID Controller Op-Timized on Improved Sine Cosine Algorithm. J. Ambient. Intell. Humaniz. Comput. 2019, 10, 2361–2373. [Google Scholar] [CrossRef]
- Mishra, D.; Sahu, P.C.; Prusty, R.C.; Panda, S. Fuzzy Adaptive Fractional Order-PID Controller for Frequency Control of an Islanded Microgrid under Stochastic Wind/Solar Uncertainties. Int. J. Ambient. Energy 2021, 1–17. [Google Scholar] [CrossRef]
- Osinski, C.; Leandro, G.V.; da Costa Oliveira, G.H. A New Hybrid Load Frequency Control Strategy Combining Fuzzy Sets and Differential Evolution. J. Control Autom. Electr. Syst. 2021, 32, 1627–1638. [Google Scholar] [CrossRef]
- Ahmadi, S.; Talami, S.H.; Sahnesaraie, M.A.; Dini, F.; Tahernejadjozam, B.; Ashgevari, Y. FUZZY Aided PID Controller Is Optimized by GA Algorithm for Load Frequency Control of Multi-Source Power Systems. In Proceedings of the 2020 IEEE 18th World Symposium on Applied Machine Intelligence and Informatics (SAMI), Herlany, Slovakia, 23–25 January 2020. [Google Scholar]
- Fathy, A.; Kassem, A.M.; Abdelaziz, A.Y. Optimal Design of Fuzzy PID Controller for Deregulated LFC of Mul-ti-Area Power System via Mine Blast Algorithm. Neural Comput. Appl. 2020, 32, 4531–4551. [Google Scholar] [CrossRef]
- Yakout, A.H.; Attia, M.A.; Kotb, H. Marine Predator Algorithm Based Cascaded PIDA Load Frequency Controller for Electric Power Systems with Wave Energy Conversion Systems. Alex. Eng. J. 2021, 60, 4213–4222. [Google Scholar] [CrossRef]
- Thabet, H.; Ayadi, M.; Rotella, F. Experimental Comparison of New Adaptive PI Controllers Based on the Ultra-Local Model Parameter Identification. Int. J. Control Autom. Syst. 2016, 14, 1520–1527. [Google Scholar] [CrossRef]
- Thabet, H.; Ayadi, M.; Rotella, F. Design of Adaptive PID Controllers Based on Adaptive Smith Predictor for Ultra-Local Model Control. Int. J. Autom. Control 2017, 11, 222. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Liu, J.; Rodriguez, J.; Garcia, C. Model-Free Predictive Current Control of Power Converters Based on Ultra-Local Model. In Proceedings of the 2020 IEEE International Conference on Industrial Technology (ICIT), Buenos Aires, Argentina, 26–28 February 2020. [Google Scholar]
- Faraji, B.; Gheisarnejad, M.; Rouhollahi, K.; Esfahani, Z.; Khooban, M.H. Machine Learning Approach Based on Ultra-Local Model Control for Treating Cancer Pain. IEEE Sens. J. 2021, 21, 8245–8252. [Google Scholar] [CrossRef]
- Ding, F.; Zhang, X.; Xu, L. The Innovation Algorithms for Multivariable State-space Models. Int. J. Adapt. Control Signal Process. 2019, 33, 1601–1618. [Google Scholar] [CrossRef]
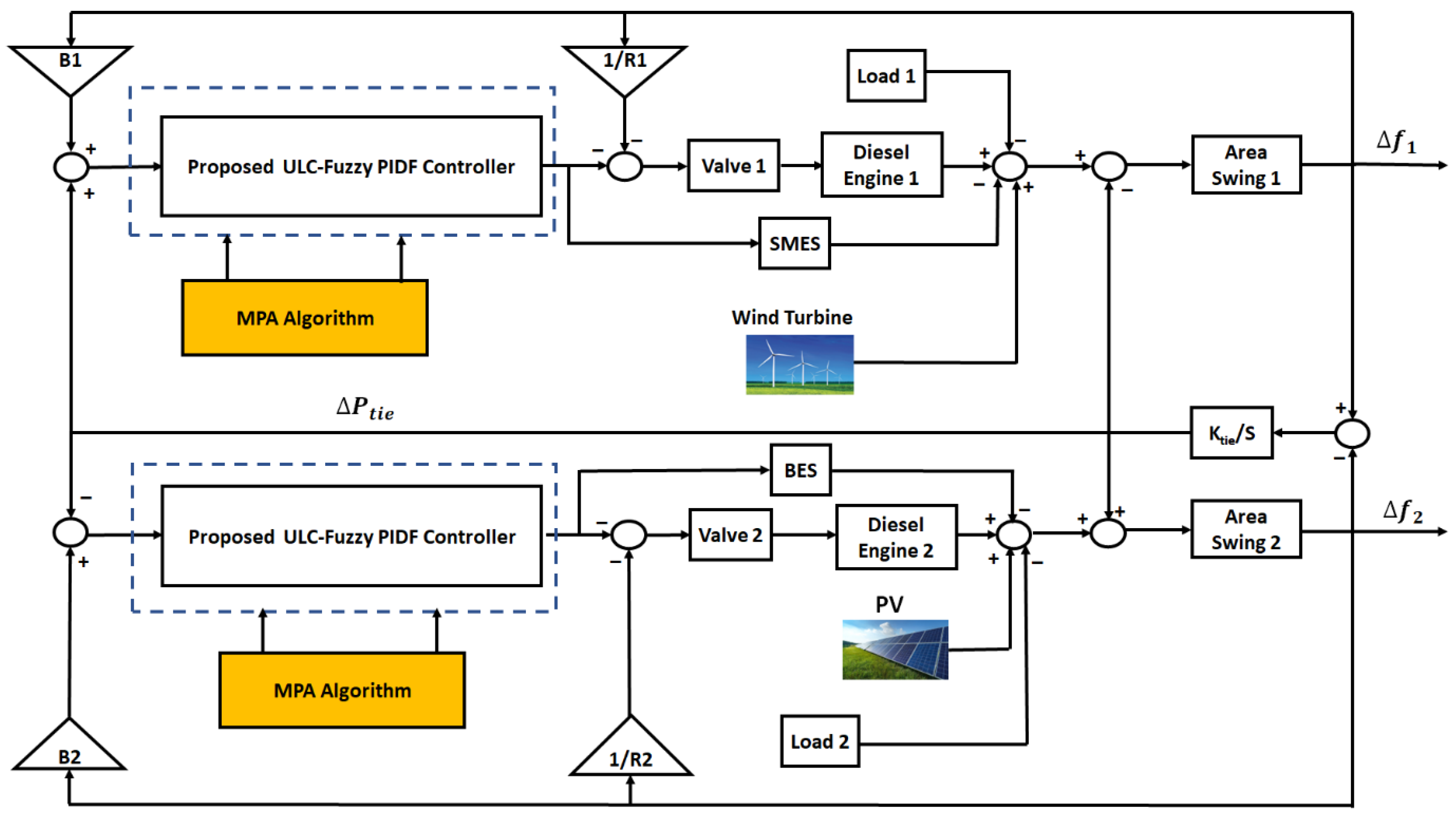






| Systems | Transfer Function | Parameters |
|---|---|---|
| Diesel generator | ||
| Valve actuator | ||
| Wind turbine | ||
| SMES | ||
| PV | ||
| BES | ||
| Area swing | ||
| Synchronizing coefficient | ||
| Speed droops | R1, R2 | R1 = R2 = 0.05 |
| Frequency bias coefficients | B1, B2 | B1 = B2 = 21 |
| E | CE | ||||
|---|---|---|---|---|---|
| LN | SN | Z | SP | LP | |
| LP | Z | SP | SP | LP | LP |
| SP | SN | Z | SP | SP | LP |
| Z | SN | SN | Z | SP | SP |
| SN | LN | SN | SN | Z | SP |
| LN | LN | LN | SN | SN | Z |
| Controller | Optimal FF | Area 1 | Area 2 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| kp1 | ki1 | kd1 | N1 | k1 | k2 | α | kp2 | ki2 | kd2 | N2 | k3 | k4 | α | ||
| PIDF [43] | 0.81 | 17.87 | 18.11 | 10.17 | 198 | -- | -- | -- | 19.98 | 19.98 | 11.61 | 199 | -- | -- | -- |
| ULC-PIDF | 0.20 | 17.87 | 18.11 | 10.17 | 198 | -- | -- | 5.84 | 19.98 | 19.98 | 11.61 | 199 | -- | -- | 5.84 |
| fuzzy PIDF [43] | 0.07 | 8.61 | 5.48 | 9.66 | 123 | 1.95 | 0.61 | -- | 5.71 | 7.11 | 8.24 | 195 | 1.54 | 1.64 | -- |
| ULC-fuzzy PIDF | 0.02 | 8.61 | 5.48 | 9.66 | 123 | 1.95 | 0.61 | 29.97 | 5.71 | 7.11 | 8.24 | 195 | 1.54 | 1.64 | 29.97 |
| ΔF1 (Hz) | ΔF2 (Hz) | ΔPtie (p.u.) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Controller | MUS | MOS | Ts (s) | MUS | MOS (Hz) | Ts (s) | MUS | MOS (p.u.) | Ts (s) |
| PIDF [43] | −4.66 | 0.84 | 18 | −9.28 | 0 | 18 | −1.94 | 0 | 18 |
| ULC-PIDF | −1.126 | 0.227 | 12 | −2.33 | 0 | −0.489 | 0 | 12 | |
| fuzzy PIDF [43] | −0.228 | 0.053 | 10 | −0.73 | 0 | 10 | −0.154 | 0 | 10 |
| ULC-fuzzy PIDF | −0.054 | 0.013 | 7 | −0.18 | 0 | 7 | −0.038 | 0 | 7 |
| SLP% | ΔF1 (Hz) | ΔF2 (Hz) | ΔPtie (p.u.) | |||
|---|---|---|---|---|---|---|
| MUS | MOS | MUS | MOS (Hz) | MUS | MOS (p.u.) | |
| 1 | −0.11 | 0.03 | −0.36 | 0 | −0.08 | 0 |
| 3 | −0.32 | 0.08 | −1.08 | 0 | −0.23 | 0 |
| 5 (Design value) | −0.54 | 0.13 | −1.80 | 0 | −0.38 | 0 |
| 7 | −0.75 | 0.18 | −2.52 | 0 | −0.53 | 0 |
| 9 | −0.97 | 0.23 | −3.24 | 0 | −0.68 | 0 |
| 10 | −1.073 | 0.26 | −3.60 | 0 | −0.76 | 0 |
| 15 | −1.61 | 0.39 | −5.40 | 0 | −1.14 | 0 |
| 20 | −2.15 | 0.51 | −7.21 | 0 | −1.52 | 0 |
| System Parameter | Percentage of Change | ΔF1 (Hz) | ΔF2 (Hz) | ΔPtie (p.u.) | |||
|---|---|---|---|---|---|---|---|
| MUS | MOS | MUS | MOS | MUS | MOS | ||
| Td1 | −25% | −0.527 | 0.1269 | −1.791 | 0 | −0.3761 | 0 |
| +25% | −0.5507 | 0.1303 | −1.815 | 0 | −0.3812 | 0 | |
| KSMES | −25% | −0.6088 | 0.1461 | −2.051 | 0 | −0.4308 | 0 |
| +25% | −0.478 | 0.1144 | −1.603 | 0 | −0.3366 | 0 | |
| B1 | −25% | −0.6818 | 0.1783 | −2.215 | 0 | −0.4652 | 0 |
| +25% | −0.4419 | 0.0974 | −1.516 | 0 | −0.3183 | 0 | |
| B2 | −25% | −0.5385 | 0.11 | −2.216 | 0 | −0.3490 | 0 |
| +25% | −0.5346 | 0.1408 | −1.516 | 0 | −0.3979 | 0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yakout, A.H.; AboRas, K.M.; Kotb, H.; Alharbi, M.; Shouran, M.; Abdul Samad, B. A Novel Ultra Local Based-Fuzzy PIDF Controller for Frequency Regulation of a Hybrid Microgrid System with High Renewable Energy Penetration and Storage Devices. Processes 2023, 11, 1093. https://doi.org/10.3390/pr11041093
Yakout AH, AboRas KM, Kotb H, Alharbi M, Shouran M, Abdul Samad B. A Novel Ultra Local Based-Fuzzy PIDF Controller for Frequency Regulation of a Hybrid Microgrid System with High Renewable Energy Penetration and Storage Devices. Processes. 2023; 11(4):1093. https://doi.org/10.3390/pr11041093
Chicago/Turabian StyleYakout, Ahmed H., Kareem M. AboRas, Hossam Kotb, Mohammed Alharbi, Mokhtar Shouran, and Bdereddin Abdul Samad. 2023. "A Novel Ultra Local Based-Fuzzy PIDF Controller for Frequency Regulation of a Hybrid Microgrid System with High Renewable Energy Penetration and Storage Devices" Processes 11, no. 4: 1093. https://doi.org/10.3390/pr11041093
APA StyleYakout, A. H., AboRas, K. M., Kotb, H., Alharbi, M., Shouran, M., & Abdul Samad, B. (2023). A Novel Ultra Local Based-Fuzzy PIDF Controller for Frequency Regulation of a Hybrid Microgrid System with High Renewable Energy Penetration and Storage Devices. Processes, 11(4), 1093. https://doi.org/10.3390/pr11041093










