Large Eddy Simulation of Conjugate Heat Transfer in a Ribbed Channel: Reynolds Number Effect
Abstract
:1. Introduction
2. Numerical Methods and Code Validation
2.1. Numerical Methods
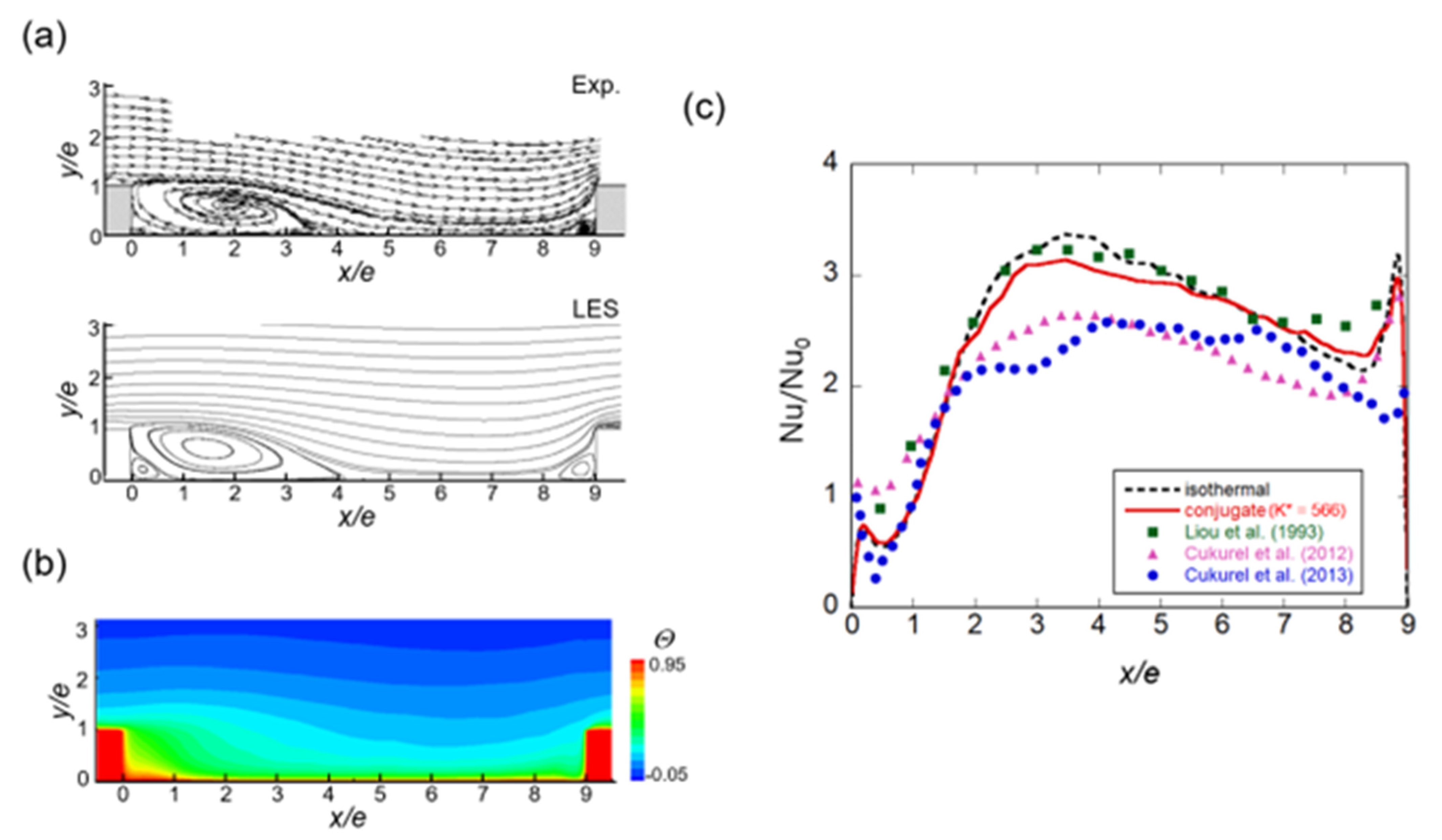
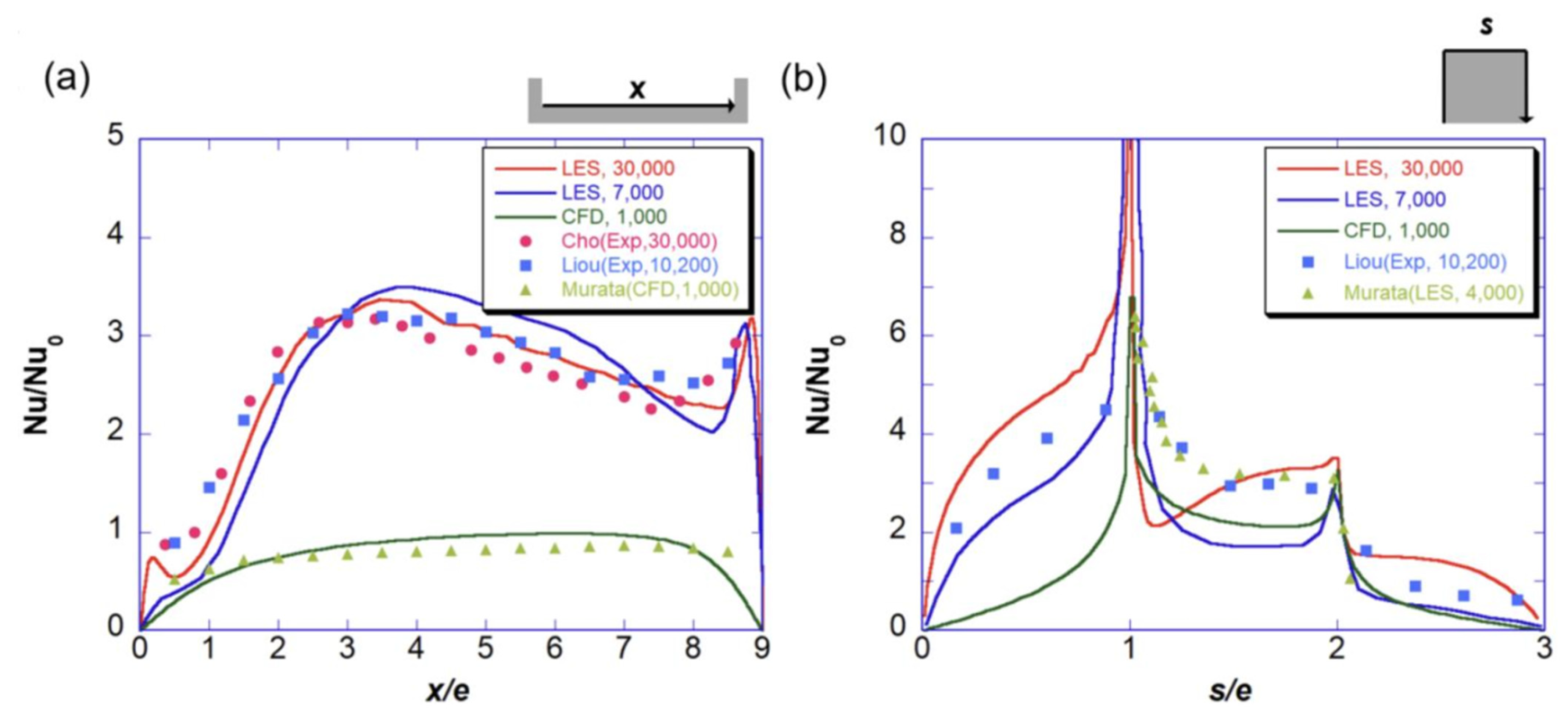
2.2. Code Validation
3. Results and Discussion
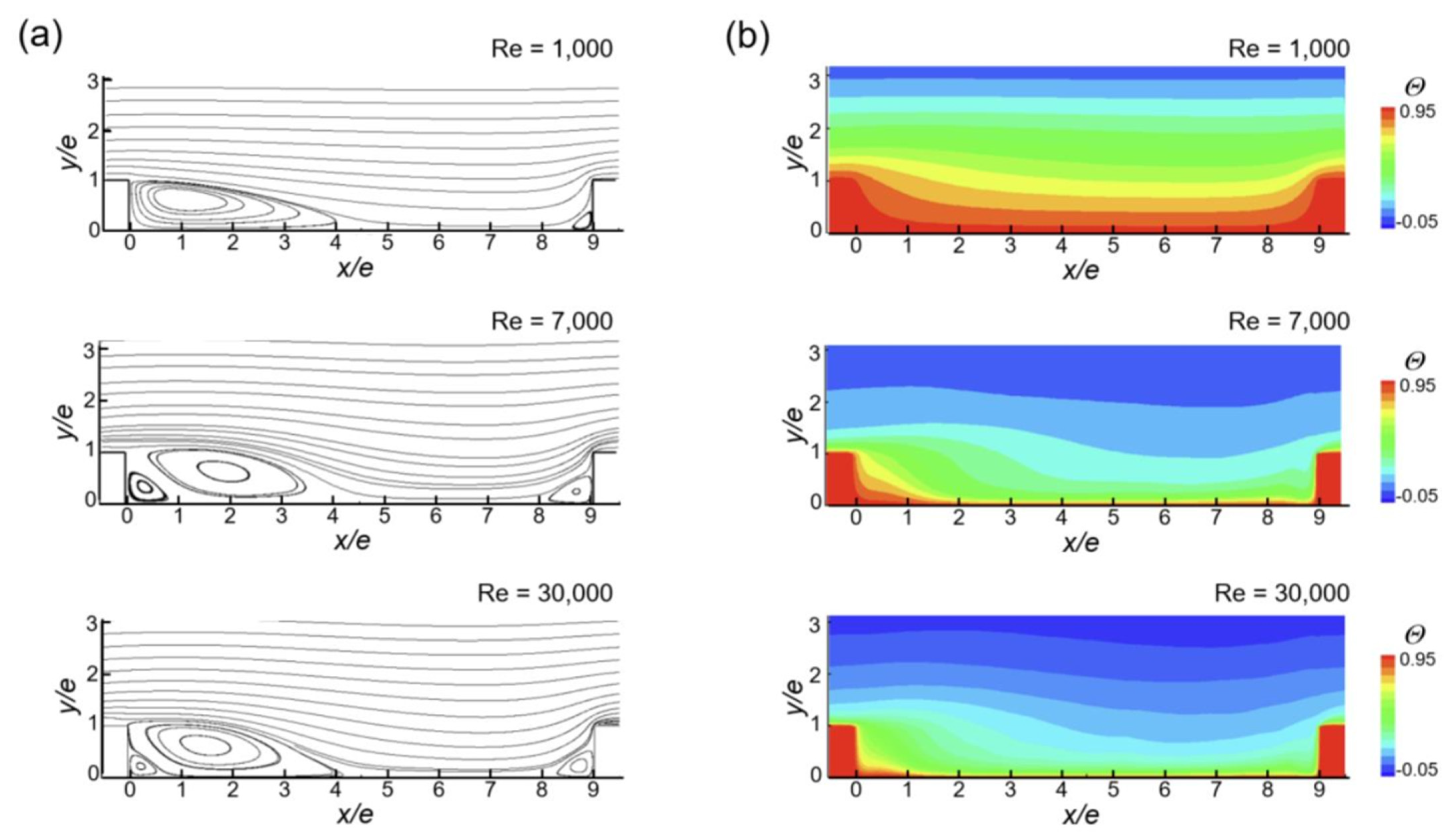
3.1. Effect of Reynolds Number on the Isothermal Ribbed Channel
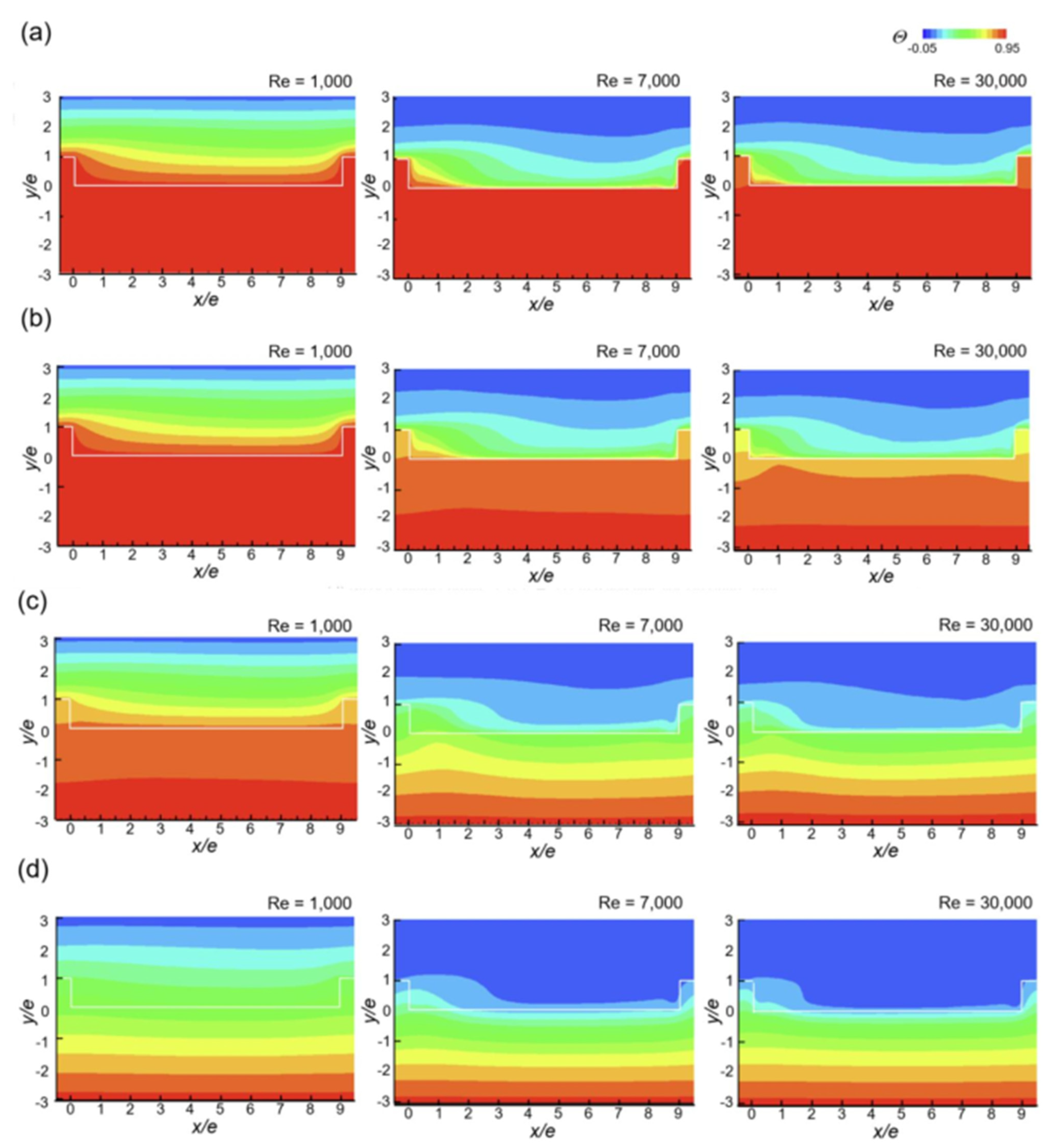
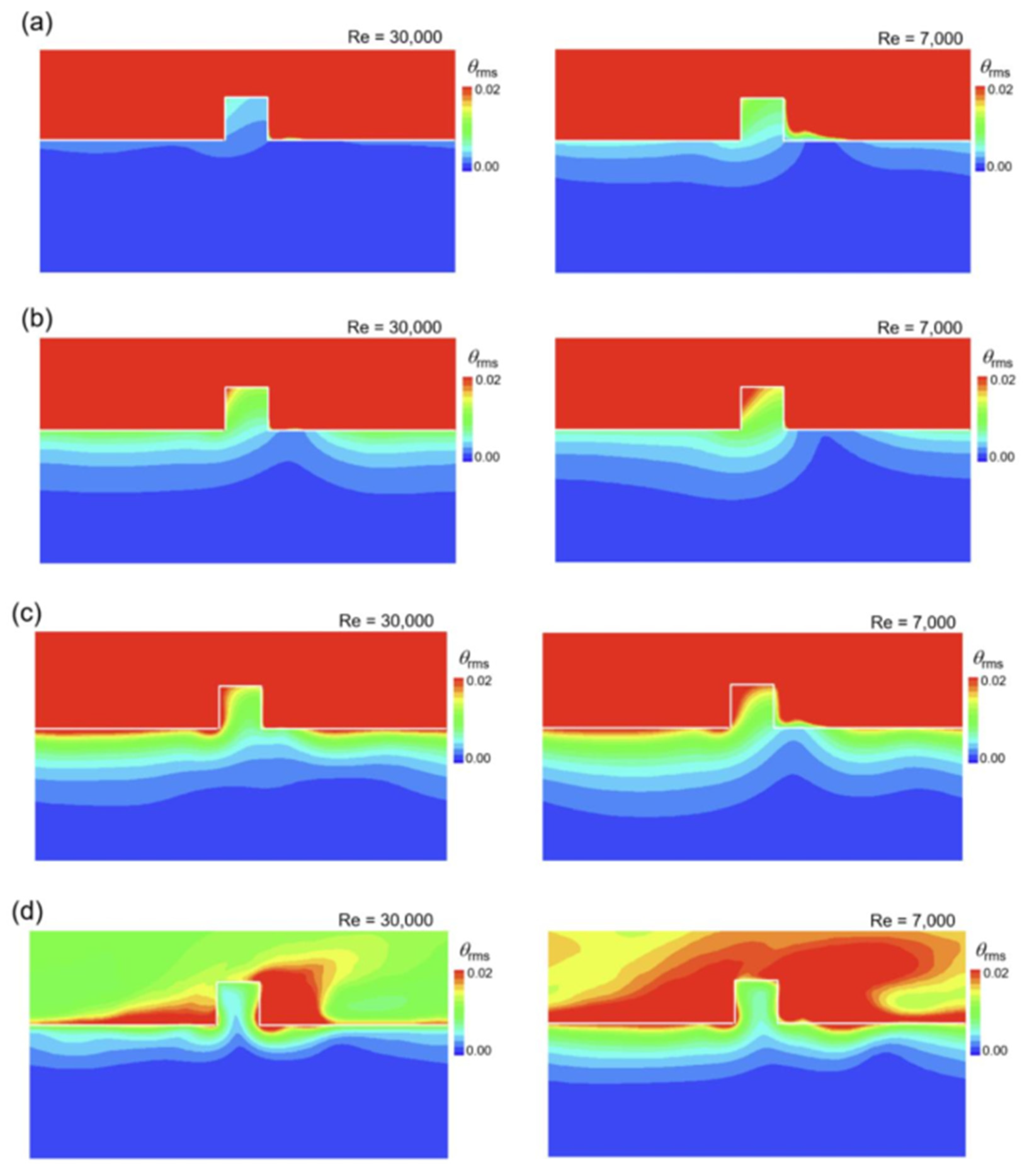
3.2. Time-Averaged Thermal Fields in the Conducting Ribbed Channel
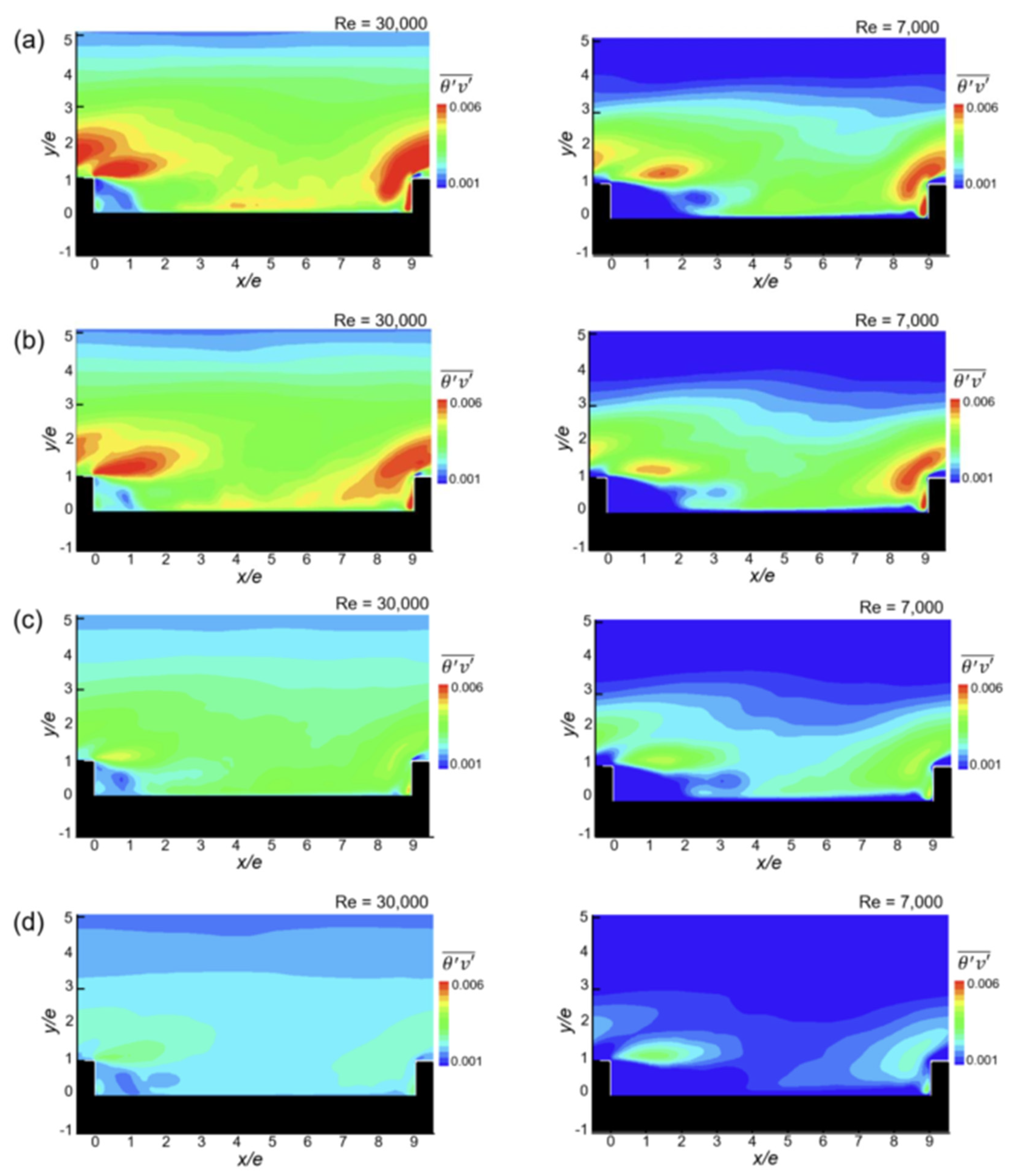
3.3. Turbulent Heat Transfer Statistics
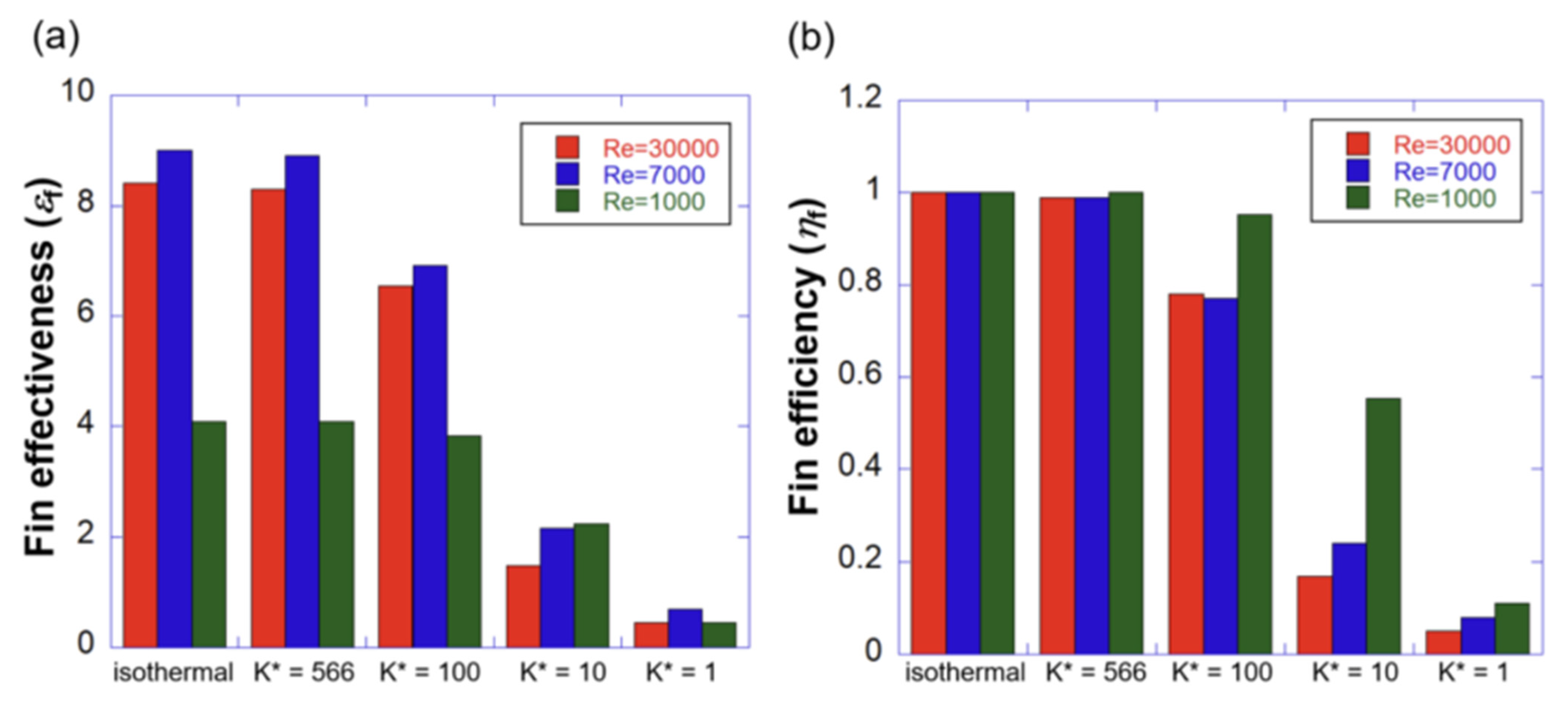
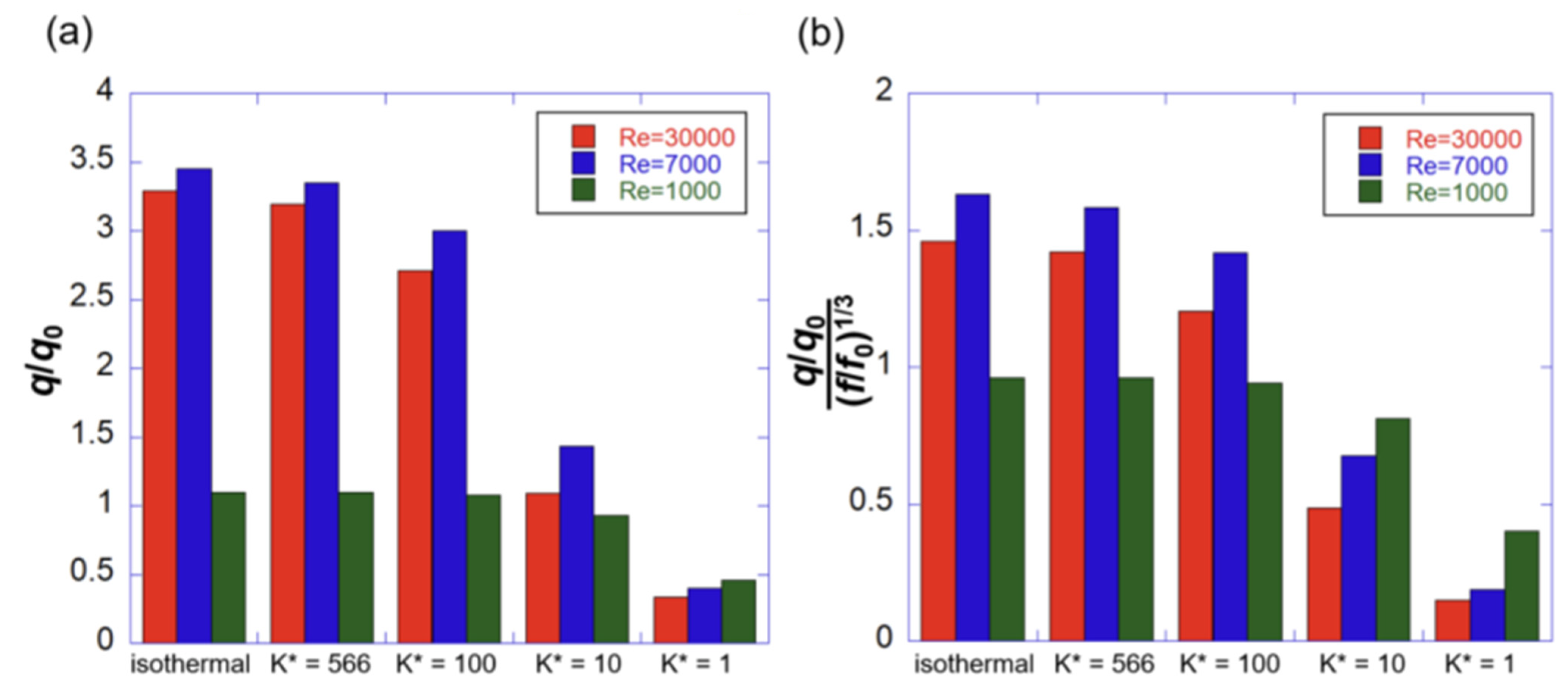
3.4. Thermal Performance
4. Conclusions
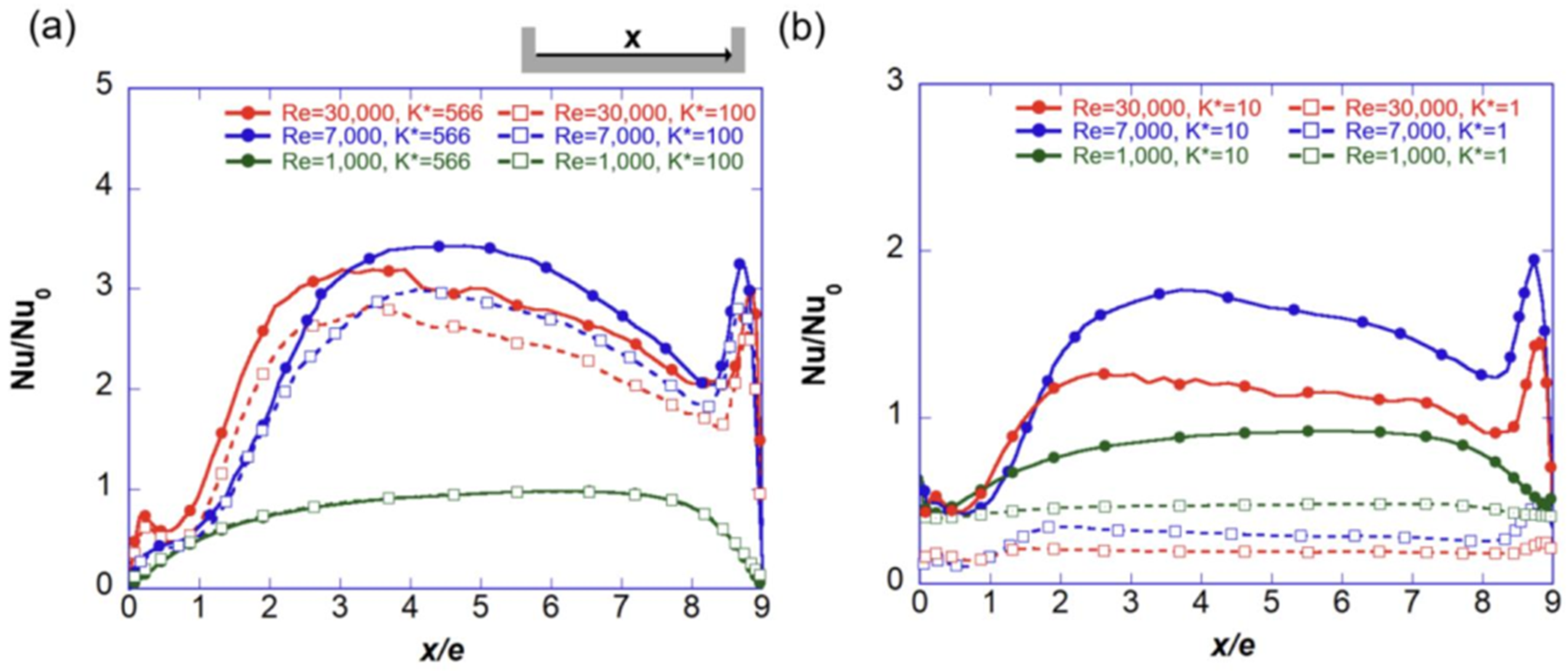
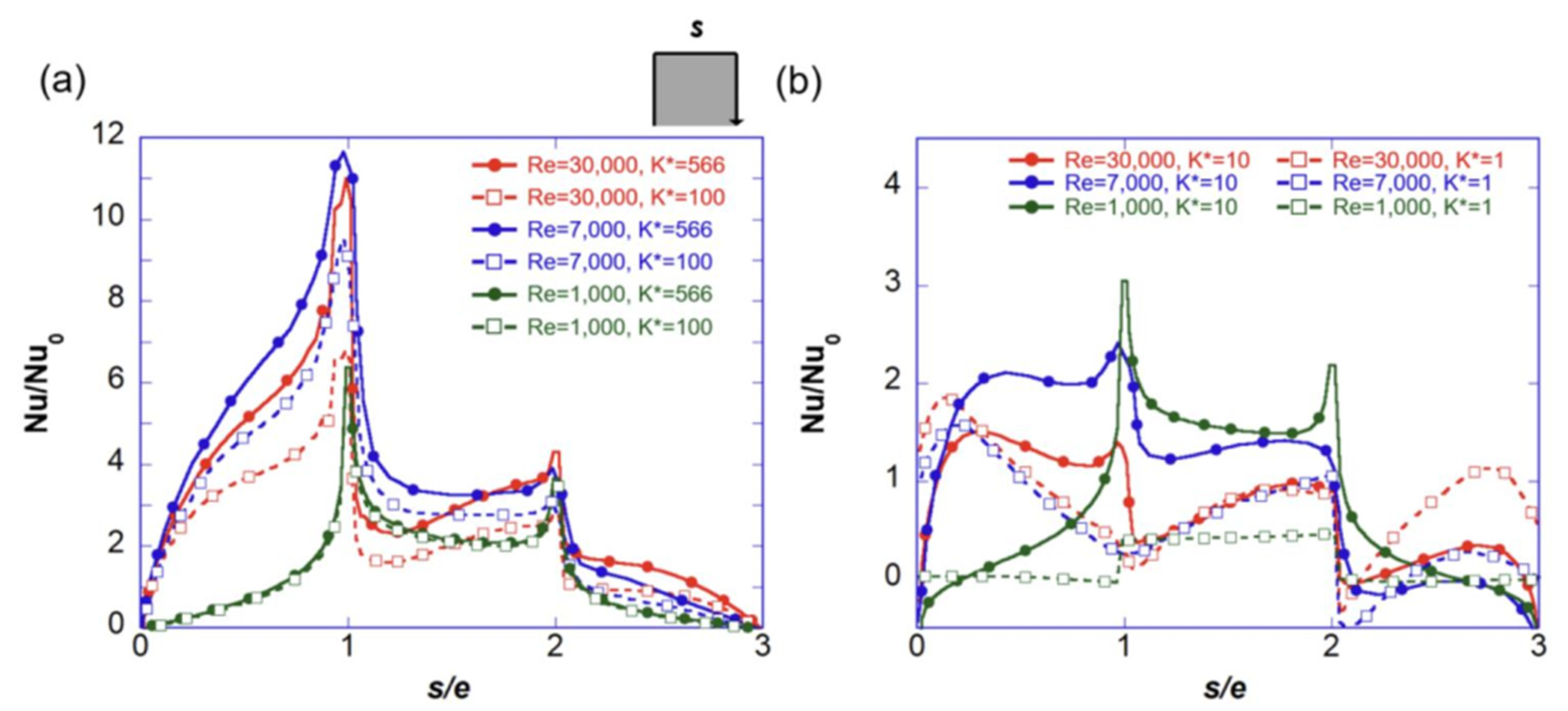
- In pure convection, when the Reynolds number is lowered from 30,000 to 7000, the heat transfer increases by 5% on the channel wall, but decreases by 20% on the rib.
- When the thermal conductivity ratio is more than 10, the Reynolds number effect is stronger in the rib than in the wall. When Re = 7000, the heat transfer coefficient ratio in the rib is larger than that when Re = 30,000.
- Compared with the turbulent flow, the effect of conduction in the laminar flow is observed at a low thermal conductivity ratio, and the effect of heat transfer promotion is not large in the typical ribbed channel geometry of the gas turbines.
- In the turbulent flow, when K* = 100 or more, the heat transfer promotion effect of the ribbed channel can be expected even at a low Reynolds number. If K* = 10 or less, then the heat transfer promotion performance of the rib becomes worse than that in the laminar flow, and thus, the effect of the rib cannot be expected under these conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Ac:b | cross-sectional area at the base |
| Arib | rib surface area |
| Bi | Biot number (=hd/ks) |
| C* | heat capacity ratio (=(ρ cp)f/(ρ cp)s) |
| d | thickness of the channel wall |
| f | frication factor |
| fi | momentum forcing |
| k | thermal conductivity |
| K* | thermal conductivity ratio (=ks/kf) |
| ms | mass source/sink |
| Nu | Nusselt number (=hDh/kf) |
| q” | heat flux |
| q | heat transfer rate |
| qf | heat transfer rate through a fin |
| Re | bulk Reynolds number (=UbDh/ν) |
| t | time |
| T | temperature |
| Tb | bulk temperature |
| Tw | wall temperature |
| Ub | bulk velocity |
| Greek symbols | |
| εf | fin effectiveness |
| ηf | fin efficiency |
| ν | kinematic viscosity |
| θ | dimensionless temperature (=(T − Tb)/(Tw − Tb)) |
| Θ | time-averaged dimensionless temperature |
| ω | index function between the solid and the fluid |
| Subscripts | |
| f | fluid or fin |
| rms | root-mean-square value |
| s | solid |
| 0 | fully developed value in a smooth pipe |
References
- Han, J.C. Fundamental Gas Turbine Heat Transfer. ASME J. Therm. Sci. Eng. Appl. 2013, 5, 021007. [Google Scholar] [CrossRef]
- Ligrani, P. Heat Transfer Augmentation Technologies for Internal Cooling of Turbine Components of Gas Turbine Engines. Int. J. Rotating Mach. 2013, 2013, 275653. [Google Scholar] [CrossRef]
- Ekkad, S.V.; Han, J.C. Detailed Heat Transfer Distributions in Two-pass Square Channels with Rib Turbulators. Int. J. Heat Mass Transf. 1997, 40, 2525–2537. [Google Scholar] [CrossRef]
- Xie, G.; Li, S.; Zhang, W.; Sunden, B. Computational Fluid Dynamics Modeling Flow Field and Side-Wall Heat Transfer in Rectangular Rib-Roughened Passages. ASME J. Energy Resour. Tech. 2013, 135, 042001. [Google Scholar] [CrossRef]
- Sharma, S.K.; Kalamkar, V.R. Computational Fluid Dynamics Approach in Thermo-hydraulic Analysis of Flow in Ducts with Rib Roughened Walls—A Review. Renew. Sustain. Energy Rev. 2016, 35, 756–788. [Google Scholar] [CrossRef]
- Acharya, S.; Dutta, S.; Myrum, T.A.; Baker, R.S. Periodically Developed Flow and Heat Transfer in a Ribbed Duct. Int. J. Heat Mass Transf. 1993, 36, 2069–2082. [Google Scholar] [CrossRef]
- Ooi, A.; Iaccarino, G.; Durbin, P.A.; Behnia, M. Reynolds Averaged Simulation of Flow and Heat Transfer in Ribbed Ducts. Int. J. Heat Fluid Flow 2002, 23, 750–757. [Google Scholar] [CrossRef]
- Murata, A.; Mochizuki, S. Comparison between Laminar and Turbulent Heat Transfer in a Stationary Square Duct with Transverse or Angled Rib Turbulators. Int. J. Heat Mass Transf. 2001, 44, 1127–1141. [Google Scholar] [CrossRef]
- Ahn, J.; Choi, H.; Lee, J.S. Large Eddy Simulation of Flow and Heat Transfer in a Channel Roughened by Square or Semicircle Ribs. ASME J. Turbomach. 2005, 127, 263–269. [Google Scholar] [CrossRef]
- Sewall, E.A.; Tafti, D.K.; Graham, A.B.; Thole, K.A. Experimental Validation of Large Eddy Simulations of Flow and Heat Transfer in a Stationary Ribbed Duct. Int. J. Heat Fluid Flow 2006, 23, 750–757. [Google Scholar] [CrossRef]
- Ahn, J.; Lee, J.S. Large Eddy Simulation of Flow and Heat Transfer in a Channel with a Detached Rib Array. Int. J. Heat Mass Transf. 2010, 53, 445–452. [Google Scholar] [CrossRef]
- Cho, H.H.; Wu, S.J.; Kwon, H.J. Local Heat/Mass Transfer Measurements in a Rectangular Duct with Discrete Ribs. ASME J. Turbomach. 2000, 122, 579–586. [Google Scholar] [CrossRef]
- Iaccarino, G.; Ooi, A.; Durbin, P.A.; Behnia, M. Conjugate Heat Transfer Predictions in Two-dimensional Ribbed Passages. Int. J. Heat Fluid Flow 2002, 23, 340–345. [Google Scholar] [CrossRef]
- Cukurel, B.; Arts, T.; Selcan, C. Conjugate Heat Transfer Characterization in Cooling Channels. J. Therm. Sci. 2012, 21, 286–294. [Google Scholar] [CrossRef]
- Cukurel, B.; Arts, T. Local Heat Transfer Dependency on Thermal Boundary Condition in Ribbed Cooling Channel Geometries. ASME J. Heat Transf. 2013, 135, 101001. [Google Scholar] [CrossRef]
- Halila, E.E.; Lenahan, D.T.; Thomas, T.T. High Pressure Turbine Test Hardware Detailed Design Report; NASA CR-167955; NASA: Washington, DC, USA, 1982; pp. 18–68. [Google Scholar]
- Scholl, S.; Verstraete, T.; Duchaine, F.; Gicquel, L. Influence of the Thermal Boundary Conditions on the Heat Transfer of a Rib-Roughened Cooling Channel Using LES. J. Power Energy 2015, 229, 498–507. [Google Scholar] [CrossRef]
- Scholl, S.; Verstraete, T.; Duchaine, F.; Gicquel, L. Conjugate Heat Transfer of a Rib-Roughened Internal Turbine Blade Cooling Channel Using Large Eddy Simulation. Int. J. Heat Fluid Flow 2016, 61, 650–664. [Google Scholar] [CrossRef]
- Song, J.C.; Ahn, J.; Lee, J.S. An Immersed-Boundary Method for Conjugate Heat Transfer Analysis. J. Mech. Sci. Technol. 2017, 31, 2287–2294. [Google Scholar] [CrossRef]
- Oh, T.K.; Tafti, D.K.; Nagendra, K. Fully Coupled Large Eddy Simulation-Conjugate Heat Transfer Analysis of a Ribbed Cooling Passage Using the Immersed Boundary Method. ASME J. Turbomach. 2021, 143, 041012. [Google Scholar] [CrossRef]
- Ahn, J.; Song, J.C.; Lee, J.S. Fully Coupled Large Eddy Simulation of Conjugate Heat Transfer in a Ribbed Channel with a 0.1 Blockage Ratio. Energies 2021, 14, 2096. [Google Scholar] [CrossRef]
- Ju, Y.; Feng, Y.; Zhang, C. Conjugate Heat Transfer Simulation and Entropy Generation Analysis of Gas Turbine Blades. ASME J. Eng. Gas Turbine Power 2021, 143, 081012. [Google Scholar] [CrossRef]
- Yusefi, A.; Nejat, A.; Sabour, H. Ribbed Channel Heat Transfer Enhancement of an Internally Cooled Turbine Vane Using Cooling Conjugate Heat Transfer Simulation. Therm. Sci. Eng. Prog. 2020, 19, 100641. [Google Scholar] [CrossRef]
- Neuberger, H.; Hernandez, F.; Ruck, S.; Arbeiter, F.; Bonk, S.; Rieth, M.; Stratil, L.; Muller, O.; Volker, K.-U. Advances in Additive Manufacturing of Fusion Materials. Fusion Eng. Des. 2021, 167, 112309. [Google Scholar] [CrossRef]
- Xi, L.; Gao, J.; Zhao, Z.; Li, Y. Numerical Analysis and Optimization on Flow and Heat Transfer Performance of a Steam-cooled Ribbed Channel. Case Stud. Therm. Eng. 2021, 28, 101442. [Google Scholar] [CrossRef]
- Ahn, J.; Song, J.C.; Lee, J.S. Dependence of Conjugate Heat Transfer in Ribbed Channel on Thermal Conductivity of Channel Wall: An LES Study. Energies 2021, 14, 5698. [Google Scholar] [CrossRef]
- Kasagi, N.; Hasegawa, Y.; Fukagata, K.; Iwamoto, K. Control of Turbulent Transport: Less Friction and More Heat Transfer. ASME J. Heat Transfer 2012, 134, 031009. [Google Scholar] [CrossRef]
- Blakey-Milner, B.; Gradl, P.; Snedden, G.; Brooks, M.; Pitot, J.; Lopez, E.; Leary, M.; Berto, F.; du Plessis, A. Metal Additive Manufacturing in Aerospace: A Review. Mater. Des. 2021, 209, 110008. [Google Scholar] [CrossRef]
- Chandra, P.R.; Alexander, C.R.; Han, J.C. Heat Transfer and Friction Behaviors in Rectangular Channels with Varying Number of Ribbed Walls. Int. J. Heat Mass Transf. 2003, 46, 481–495. [Google Scholar] [CrossRef]
- Cardwell, N.D.; Vlachos, P.P.; Thole, K.A. Developing and Fully Developed Turbulent Flow in Ribbed Channels. Exp. Fluids. 2011, 50, 1357–1371. [Google Scholar] [CrossRef]
- Mayo, I.; Arts, T.; E-Habib, A.; Parres, B. Two-Dimensional Heat Transfer Distribution of a Rotating Ribbed Channel at Different Reynolds Numbers. ASME J. Turbomach. 2015, 137, 031002. [Google Scholar] [CrossRef]
- Sewall, E.A.; Tafti, D.K. Large Eddy Simulation of Flow and Heat Transfer in the Developing Flow Region of a Rotating Gas Turbine Blade Internal Cooling Duct with Coriolis and Buoyancy Forces. ASME J. Turbomach. 2008, 130, 011005. [Google Scholar] [CrossRef]
- Tafti, D.K. Evaluating the Role of Subgrid Stress Modeling in a Ribbed Duct for the Internal Cooling of Turbine Blades. Int. J. Heat Fluid Flow 2005, 26, 92–104. [Google Scholar] [CrossRef]
- Choi, H.; Moin, P. Effects of the Computational Time Step on Numerical Solutions on Turbulent Flow. J. Comp. Phys. 1994, 113, 1–4. [Google Scholar] [CrossRef]
- Kim, J.; Kim, D.; Choi, H. An Immersed Boundary Finite Volume Method for Simulations of Flow in Complex Geometries. J. Comp. Phys. 2001, 171, 132–150. [Google Scholar] [CrossRef]
- Kim, J.; Choi, H. An Immersed Boundary Finite Volume Method for Simulation of Heat Transfer in Complex Geometries. KSME Int. J. 2004, 18, 1026–1035. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, P.; Moin, P.; Cabot, W.H. A Dynamic Sub-grid Scale Eddy Viscosity Model. Phys. Fluids 1991, A3, 1760–1765. [Google Scholar] [CrossRef]
- Lilly, D.K. A Proposed Modification of the Germano Sub-grid Scale Closure Model. Phys. Fluids 1992, A4, 633–635. [Google Scholar] [CrossRef]
- Kong, H.; Choi, H.; Lee, J.S. Dissimilarity Between the Velocity and Temperature Fields in a Perturbed Turbulent Thermal Boundary Layer. Phys. Fluids 2001, 13, 1466–1479. [Google Scholar] [CrossRef]
- Liou, T.M.; Hwang, J.J. Effect of Ridge Shapes on Turbulent Heat Transfer and Friction in a Rectangular Channel. Int. J. Heat Mass Transf. 1993, 36, 931–940. [Google Scholar] [CrossRef]
- Casarsa, L.; Arts, T. Experimental Investigation of the Aerothermal Performance of a High Blockage Rib-Roughened Cooling Channel. ASME J. Turbomach. 2005, 127, 580–588. [Google Scholar] [CrossRef]
- Incropera, F.P.; Dewitt, D.P.; Bergman, T.L.; Lavine, A.S. Principles of Heat and Mass Transfer, Global ed.; Wiley: Hoboken, NJ, USA, 2017; pp. 153–158. [Google Scholar]
- Cheloii, N.A.; Akbari, O.A.; Toghraie, D. Computational Fluid Dynamics and Laminar Heat Transfer of Water/Cu Nanofluid in Ribbed Microchannel with a Two-Phase Approach. Int. J. Num. Method Heat Fluid Flow 2019, 29, 1563–1589. [Google Scholar] [CrossRef]
- Esmaili, Q.; Ranjbar, A.A.; Porkhial, S. Experimental Analysis of Heat Transfer in Ribbed Microchannel. Int. J. Therm. Sci. 2018, 130, 140–147. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahn, J.; Song, J.C.; Lee, J.S. Large Eddy Simulation of Conjugate Heat Transfer in a Ribbed Channel: Reynolds Number Effect. Processes 2022, 10, 1928. https://doi.org/10.3390/pr10101928
Ahn J, Song JC, Lee JS. Large Eddy Simulation of Conjugate Heat Transfer in a Ribbed Channel: Reynolds Number Effect. Processes. 2022; 10(10):1928. https://doi.org/10.3390/pr10101928
Chicago/Turabian StyleAhn, Joon, Jeong Chul Song, and Joon Sik Lee. 2022. "Large Eddy Simulation of Conjugate Heat Transfer in a Ribbed Channel: Reynolds Number Effect" Processes 10, no. 10: 1928. https://doi.org/10.3390/pr10101928
APA StyleAhn, J., Song, J. C., & Lee, J. S. (2022). Large Eddy Simulation of Conjugate Heat Transfer in a Ribbed Channel: Reynolds Number Effect. Processes, 10(10), 1928. https://doi.org/10.3390/pr10101928







