1. Introduction
In this paper, we consider an investment–consumption problem. The decision maker manages the investment and consumption with a long-term perspective. General financial information for each investment class is observable. By analyzing the available financial information, the decision maker dynamically allocates the proportion of each investment class to maximize the utilities of consumptions in the long term. The objective under consideration can be traced back to the framework of Merton’s two-asset consumption and investment problem.
Since the financial crisis incurred by the credit risk and the subsequent liquidity risk shocked the banking and insurance system led to a global recession during 2007–2009, regulators and practitioners have paid more attention to risk measurement and management, and numerous techniques have been put forward in the finance and insurance literature. Solvency II, which gradually replaced the Solvency I regime and came into effect on 1 January 2016, is a fundamental review of the capital adequacy regime for the European insurance industry. Value at Risk (VaR) has been widely adopted to quantify and control risk exposure because it is convenient to use. Specifically, it is the maximum expected loss over a finite horizon period at a given confidence level. There are quite a few scholars who have utilized the idea of VaR in the pursuit of deriving optimal risk management strategies (see
Yiu 2004;
Yiu et al. 2010;
Chen et al. 2010;
Zhang et al. 2016).
Recent research raises a concern that decision makers generally fail to process all of the information in a rational manner as a result of finite information-processing capability. Under the information-processing constraint, the decision maker can only make decisions through “processed” or “observed” states, which is called “rational inattention”.
Sim (
2003,
2006) introduced the concept of “rational inattention” and claimed that the process of decision-making is subject to the information-processing constraint.
Huang and Liu (
2007) investigated the optimal portfolio selection strategies under rational inattention constraints.
Maćkowiak and Wiederholt (
2015) studied the business cycles within the rational inattention framework and developed a dynamic stochastic general equilibrium model. In addition, it costs to observe the signals and filter the necessary variables. It is natural that the decision maker pays to have a better estimation.
Andrei and Hasler (
2017) studied the investment and consumption strategies under the rational inattention constraint that an observation cost should be paid to observe key economic factors. See
Brennan and Xia (
2002),
Abel et al. (
2013),
Steiner et al. (
2017), and
Kacperczyk et al. (
2016) for more work on rational inattention.
Similar to
Andrei and Hasler (
2017), we also investigate the optimization problem with the information-processing cost. To be specific, in our model, one of the parameters that affect the return of the asset is not observable, thus formulating a partially observable problem. The decision maker can only implement the observable signal to estimate the observable factor. By using the Kalman filter
Liptser and Shiryaev (
2001), an optimization problem of five state variables and three control variables is formulated. However, our control problem is subject to the Value-at-Risk constraint. The decision maker in our framework controls the consumption, investment, and observation strength to maximize the utilities of consumptions under a given Value-at-Risk requirement.
Our work is also different from
Andrei and Hasler (
2017) in terms of methodology and research focus. For the research objective,
Andrei and Hasler (
2017) examined the relationships between attention, risk investment, and related state variables dynamically, whereas our work is dedicated to using an innovative method to achieve the optimal strategies. As for the methodology,
Andrei and Hasler (
2017) derived the Hamilton–Jacobi–Bellman (HJB) equation for its dynamic system and use the Chebyshev collocation method to approximate the solution of the HJB equation with a sum of certain “basis functions” (in their work, the sum of production of Chebyshev polynomials). Finding the coefficients of Chebyshev polynomials requires solving a system of linear equations. However, the dimension of the derived system of linear equations would increase significantly in our framework with the Value-at-Risk restriction. This limitation motivates us to come up with an alternative method to solve our problem of interest.
Note that the approach applied by
Andrei and Hasler (
2017) represents one typical way to solve a stochastic control problem, and the method falls into the category of dynamic programming. With dynamic programming, one is able to establish connections between the optimal control problem and a second-order partial differential equation called the HJB equation. If HJB is solvable, then the maximizer or minimizer of the Hamiltonian will be the corresponding optimal feedback control. A more detailed discussion of this field of work can be seen in
Yong and Zhou (
1999) and references therein. It is very likely that there is no explicit solution to the HJB equation because of the complex nature of a lot of dynamic systems. Thus, the search for effective numerical methods attracts the attention of many scholars accordingly. One common approach follows the track of a numerical method of solving partial differential equations (PDEs; see
Andrei and Hasler (
2017), for example). Most of the time, it requires good analytical properties such as differentiability and continuity for the dynamic system so that the PDE approach is feasible. The Markov-chain approximation method lies on the other side of the spectrum. It also tackles stochastic control problems but does not require particular analytical properties of the system. This method was proposed by Kushner (see
Kushner and Dupuis 2001). The basic idea is to approximate the original control problem with a simpler control process (a Markov chain in a finite state space) and the associated cost function for which the desired computation can be carried out. The state space is a “discretization” of the original state space of the control problem. Under certain conditions, one can prove that the sequence of optimal cost functions for the sequence of approximating chains converges to that for the underlying original process as the approximation parameter goes to zero. A potential problem with the Markov-chain approximation method is that one has to handle the solution of optimization in each iteration step, and this could be time-consuming for high-dimension systems. To deviate from the two popular methods mentioned above, we advocate for the use of Genetic Algorithms to solve stochastic control problems to overcome these issues.
A genetic algorithm (GA) is a metaheuristic inspired by the process of natural selection. Essentially, natural selection acts as a type of optimization process that is based on conceptually simple operations of competition, reproduction, and mutation. Genetic algorithms use these bio-inspired operators (selection, crossover, and mutation) to generate high-quality solutions to optimization problems
Mitchell (
1996). John Holland introduced genetic algorithms in 1960 on the basis of the concept of Darwin’s theory of evolution; afterward, his student Goldberg extended the GA in 1989
Sadeghi et al. (
2014). A fundamental difference between GAs and a lot of traditional optimization algorithms (e.g., gradient descent) is that GAs work with a population of potential solutions of the given problem. The traditional optimization algorithms start with one candidate solution and move it toward the optimum by updating this one estimate. GAs simultaneously consider multiple candidate solutions to the problem of maximizing/minimizing and iterate by moving this population of candidate solutions toward a global optimum. Because of the high dimensionality of parameters and the dynamic constraints in our dynamic system, we developed a Genetic Algorithm to study the optimal strategies.
Note that in recent years, a lot of machine learning methods (both supervised and unsupervised), such as logistic regression, neural networks, support vector machines,
k-nearest neighbors, and so on, have been widely used in the field of risk management. These machine learning models are closely related to the problem of optimization since they can be formulated as maximization/minimization of some profit/loss functions. In practical problems, these profit/loss functions tend to be high-dimensional, multi-peak/valley, or may have noise terms, and sometimes they are even discontinuous in some regions. For these situations, a genetic algorithm is a powerful tool for obtaining global optimal solutions. Genetic algorithms have been utilized as optimization methods since the 1980s and 1990s in the field of machine learning (
Goldberg and Holland 1988). In many studies, genetic algorithms and machine learning models (such as support vector machines, neural networks) have been used in combination to obtain optimal parameters. On the other hand, machine learning techniques have also been used to improve the performance of genetic and evolutionary algorithms (
Zhang et al. 2011).
The contributions of our work are as follows. First, we look at the investment–consumption optimization problem of information cost with the VaR restriction.Second, instead of applying the classical numerical algorithms in which differentiability or continuity assumption is required, we make use of the GA to carry out our analysis. It is very flexible and can handle many types of optimization problems, even if analytical properties such as continuity or differentiability break down. What is more, a lot of numerical algorithms, such as the Markov-chain approximation method, are local optimal algorithms. The GA is a global optimal algorithm instead, and we are thus able to achieve global optimal strategies. Last but not least, the GA is easy to implement and very efficiently handled high-dimensional data.
The rest of the paper is organized as follows. The formulation of the dynamics of wealth inflation, observation processes, and objective functions are presented in
Section 2. Numerical examples are provided in
Section 3 to illustrate the implementation of the genetic algorithm. Finally, additional remarks are provided in
Section 4.
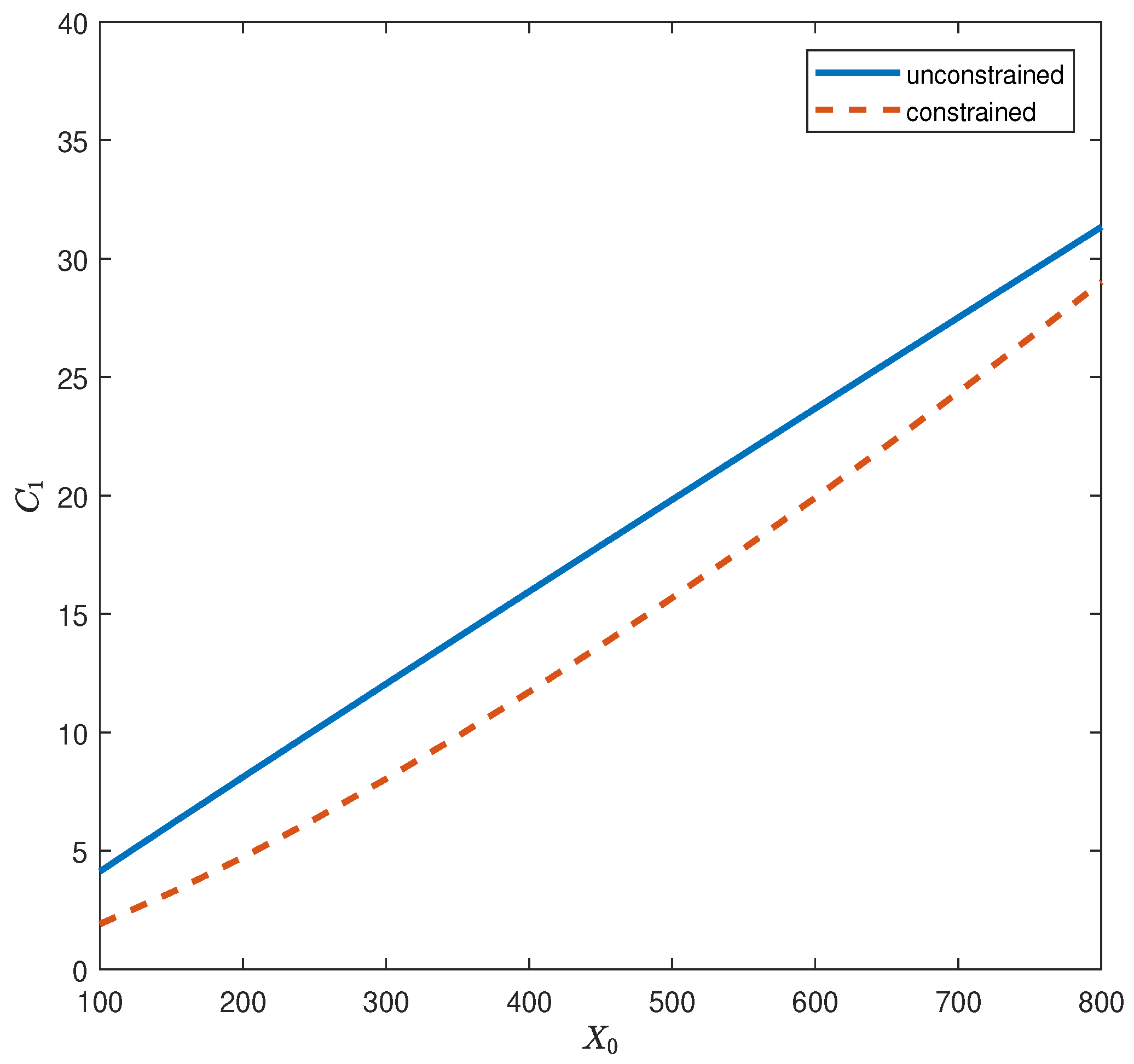
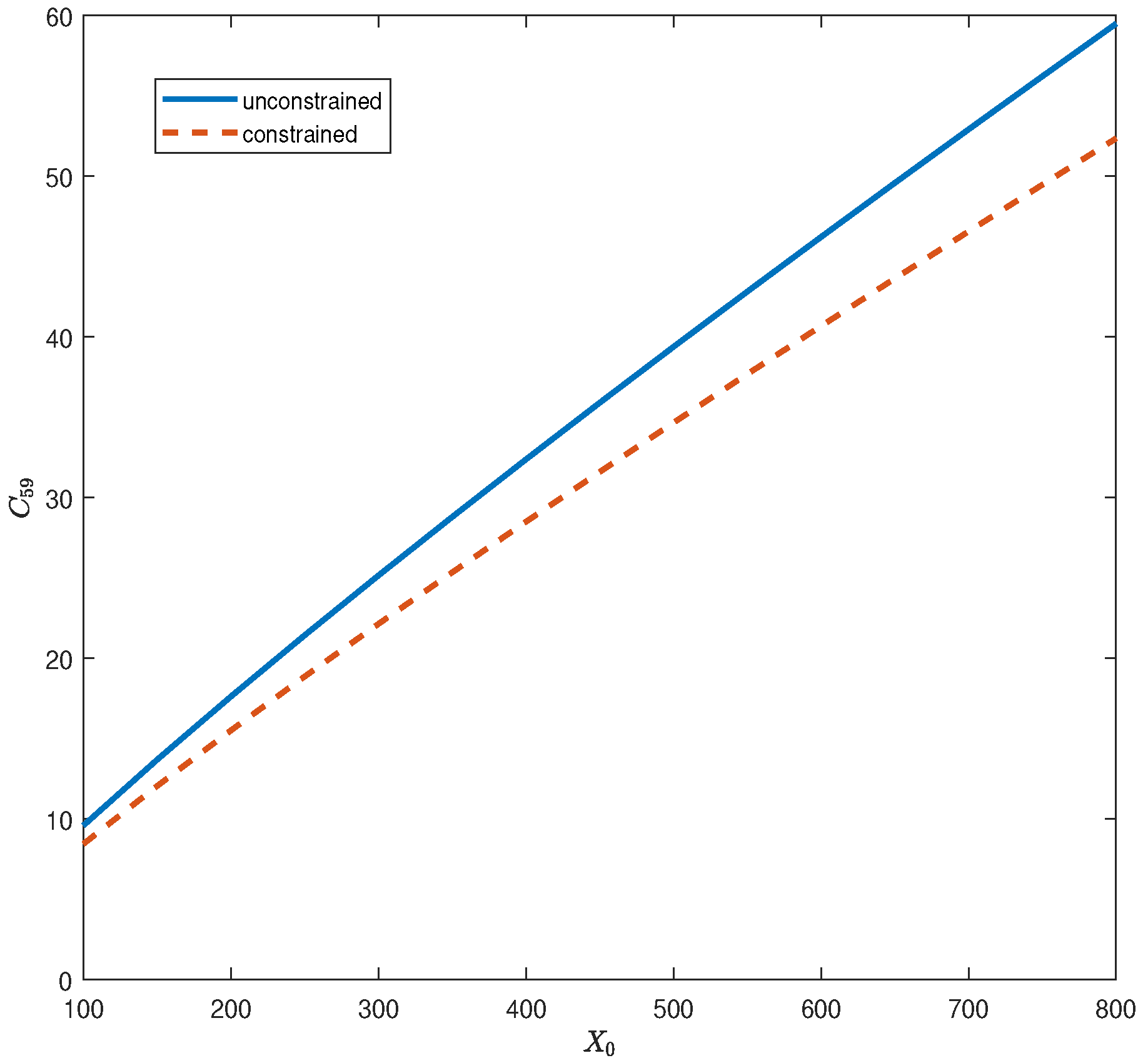
2. Formulation
Let
be a complete probability space, where
is a complete and right-continuous filtration generated by a 4-dimensional standard Brownian motion
.
is the filtration containing the information about the financial market and the investor’s observation at time
t, and
is a probability measure on
We consider an asset price process motivated by a fully stochastic volatility model,
where
is the expected average rate of return.
is an observable state variable that represents useful market information, such as the earnings-to-price ratio or a change in trading volumes to predict the future return rate;
is the impact coefficient of the state variable
and is an unobservable factor;
represents the stochastic volatility. Specifically, the observable variable
is assumed to follow a diffusion process
For the volatility
, we adopt the stochastic volatility below:
The unobservable factor
, which can be considered to be certain economic variables that cannot be completely observed, is assumed to follow
Note that for variables , , and above, we use , , and to denote the long-term average of variables and use , , and to refer to mean-reversion parameters. These parameters show the rates at which the variables , , and revert to their long-term means in these three mean-reverting processes.
Instead of observing
completely, we only have access to the observation of it with noise according to the following dynamics:
where
is a Brownian motion that denotes the observation noises and is independent of
. Note that
is a control variable, which determines the precision of our observations and is used to describe the capacity of observing and processing signals. The more frequently we observe the signals, the more precise information we have on the observation. Similarly, a smaller value of
implies less return predictability.
Note that
is the information set up to time
t and contains the realized return of the asset, innovations of predictive variable, changes in the volatilities of stock return, and observed signals. The estimated predictive coefficient is denoted by
, and its posterior variance is
. Using the standard filtering results from
Liptser and Shiryaev (
2001), we are able to get the dynamics of the estimated predictive coefficient
(filter) and the posterior variance
(uncertainty) as below:
So far, all state variables have become observable. We thus obtain a new dynamic system with observed variables satisfying the following dynamics:
where
, and
are independent Brownian motions under the investor’s observation filtration.
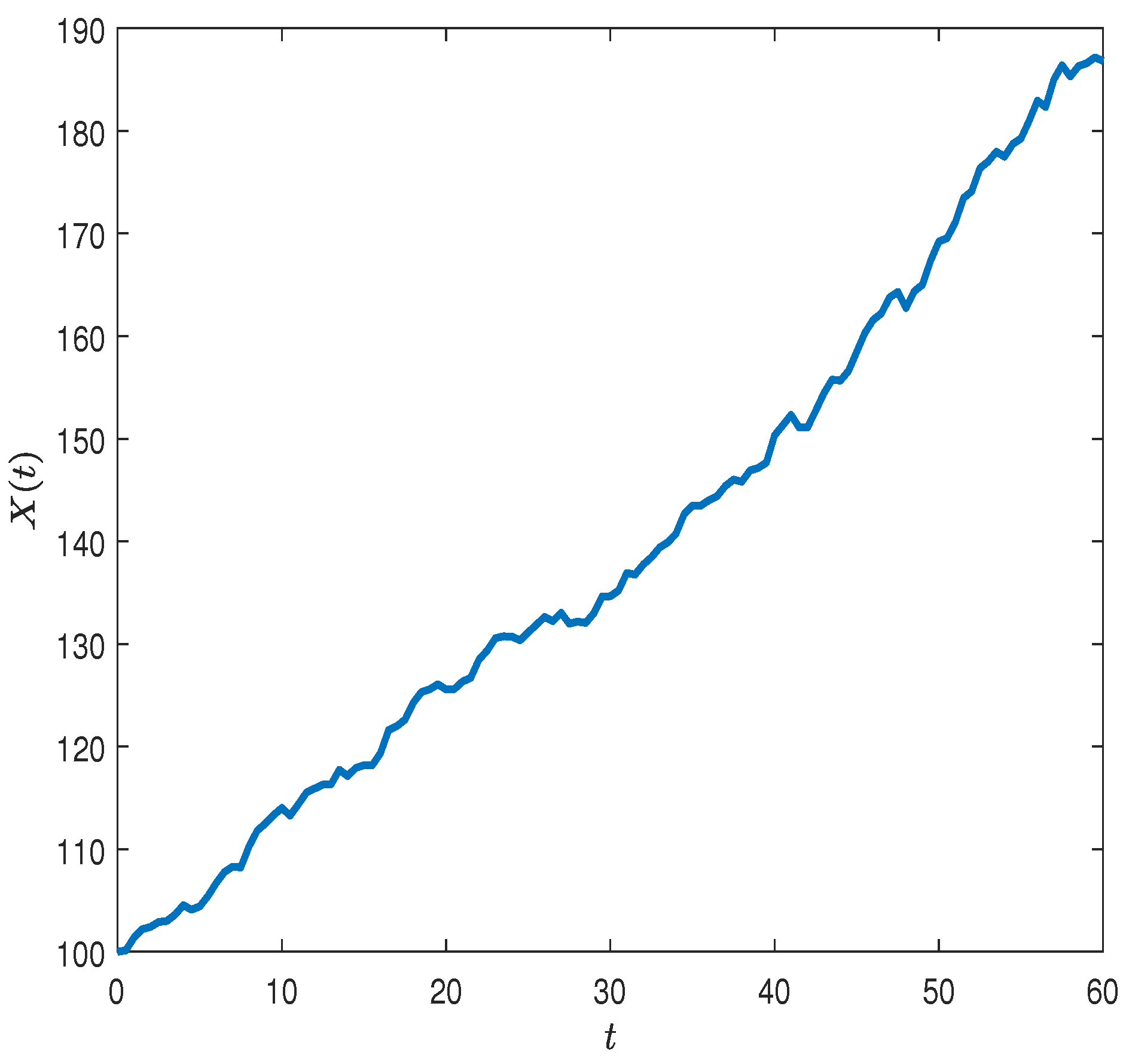
Combining risky assets with a risk-free asset, we can represent the wealth process as:
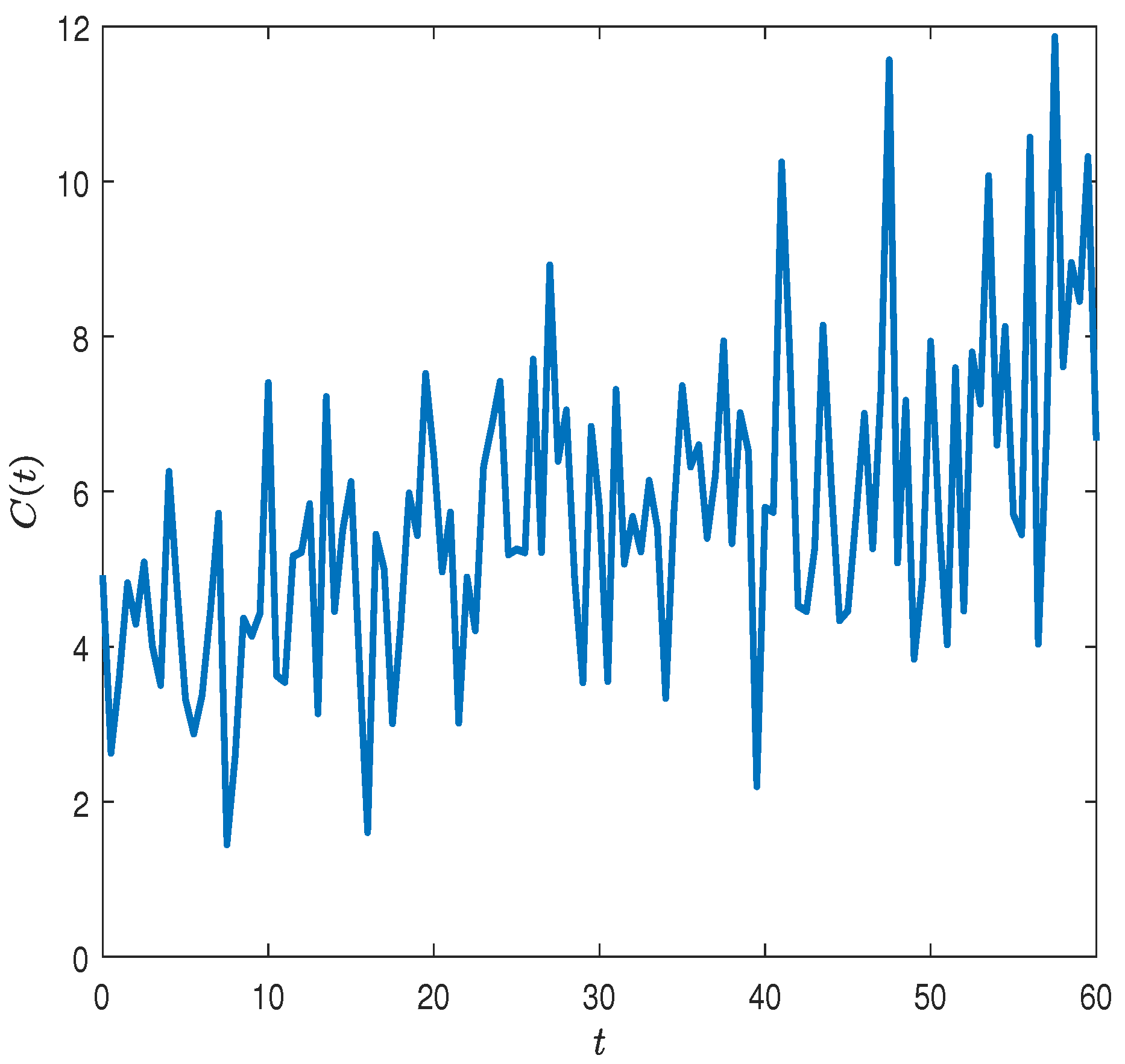
where
is the consumption by a representative investor, consumed at time
t;
is the risky investment share;
r is used to denote the risk-free rate of return; and
is the information cost.
Now, we proceed with the introduction of the VaR restriction. Note that with the phenomenal prosperity of financial markets, risk management has recently gained increasing attention from practitioners. Value at Risk has been the standard benchmark for measuring financial risks among banks, insurance companies, and other financial institutions. VaR is regarded as the maximum expected loss over a given time period at a given confidence level and is used to set up capital requirements. VaR constraints have been adopted by many studies on optimization problems to make the model more reasonable. Consistent with
Chen et al. (
2010), we define the dynamic VaR as follows.
For a small enough
, the loss percentage in interval
is defined by
The above definition tells us that relative loss is defined as the difference between the value yielded at time if we deposit the surplus in a bank account at time t and the surplus at time obtained by implementing reinsurance and investment strategies. can be interpreted as the value of time for one unit of currency after time period
For a given probability level
and a given time horizon
the VaR at time
denoted by
is defined by
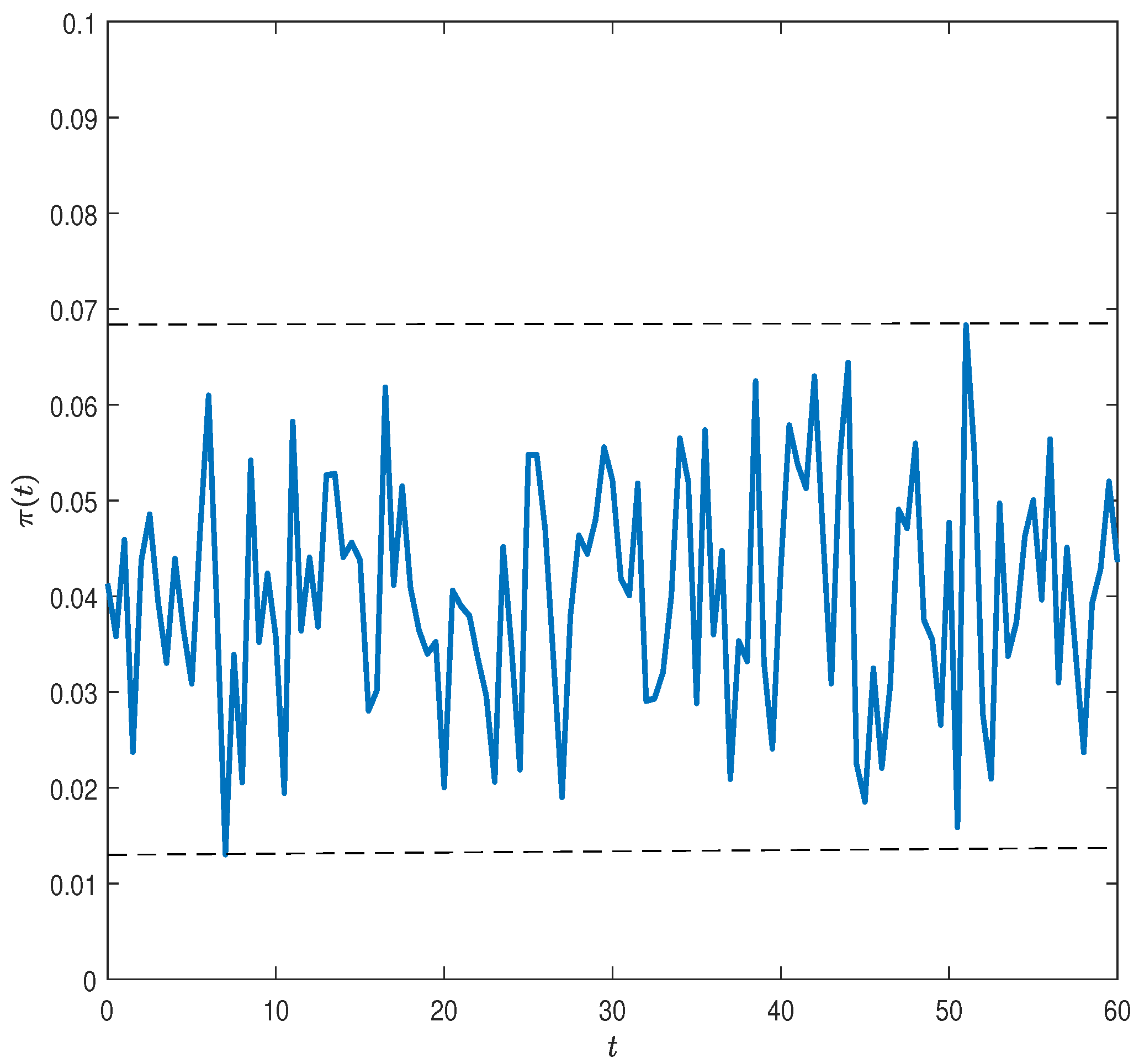
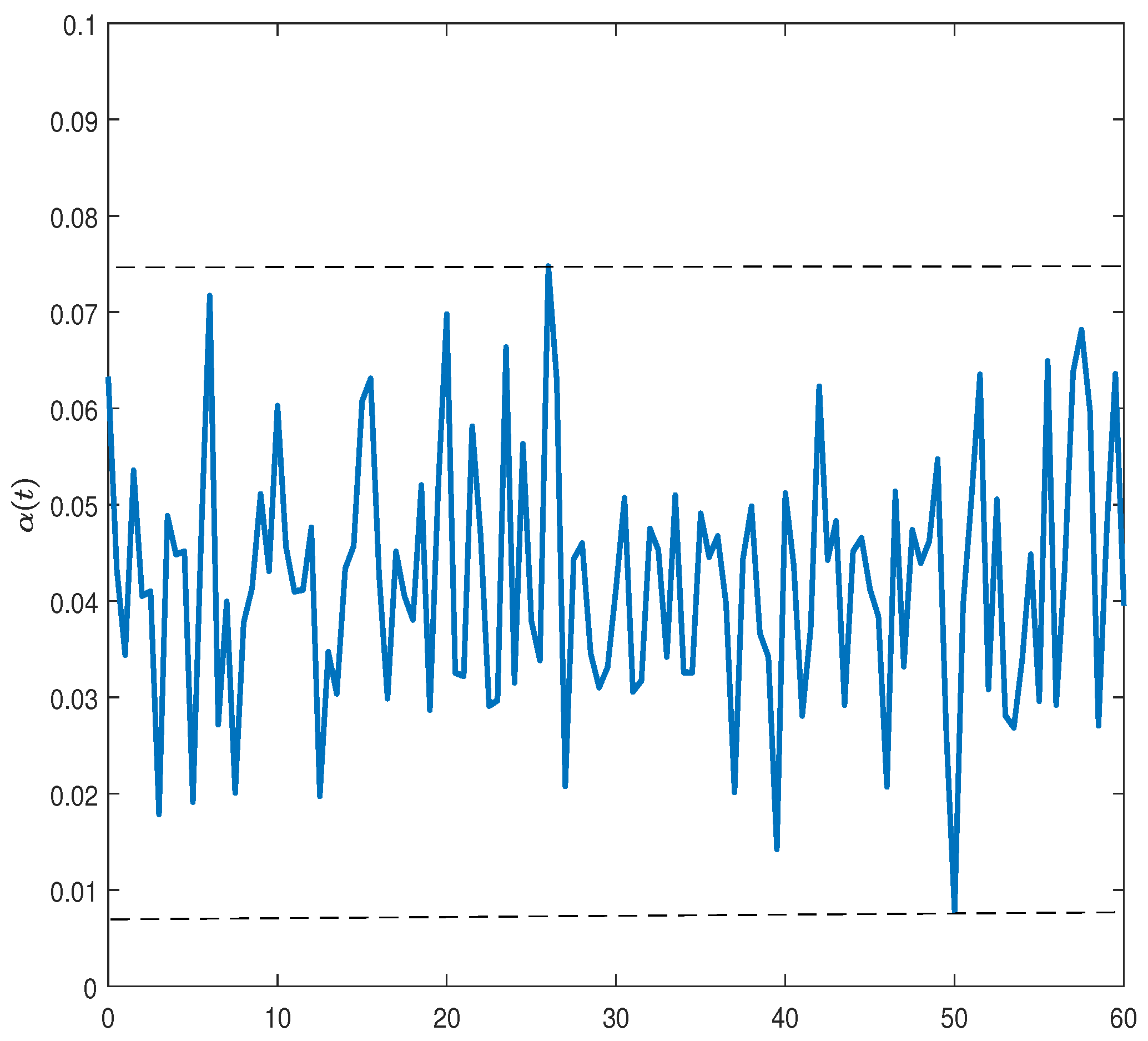
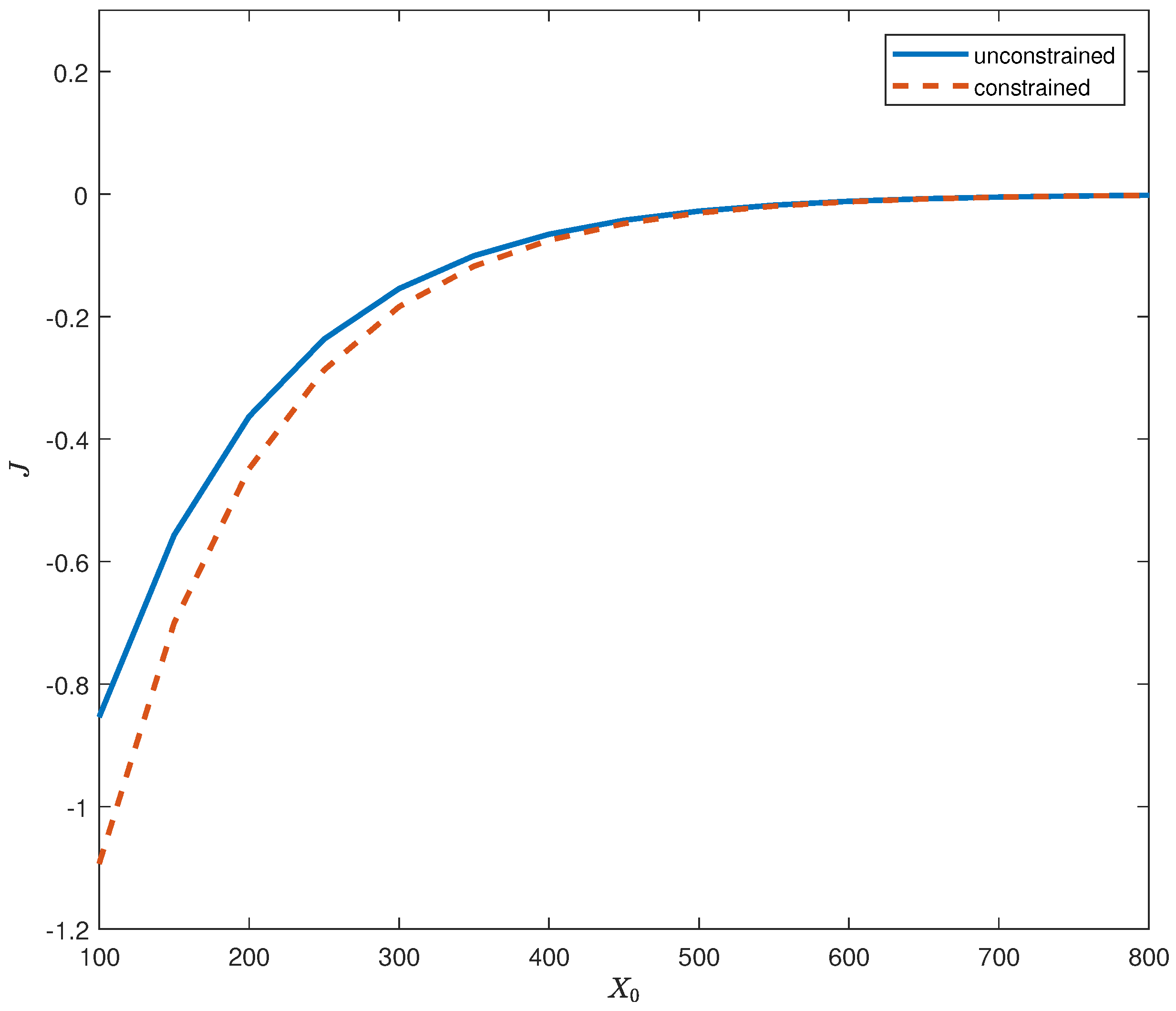
To proceed, let the control variable
be
as a triplet of control variables. Let
be the discount factor. Our objective is to choose consumption
, attention to news
, and the risky investment share
so as to maximize an individual’s expected utility of consumption over a given time horizon from
t to
T conditional on that individual’s information set at time
t:
subject to a constant level
of an upper boundary of VaR at all times.
Our interest in this work is the application of a genetic algorithm to solve the optimal investment and consumption strategies in a two-asset model. Compared with some other numerical algorithms, GA is a global optimization method. Moreover, it does not require the differentiability or even continuity of drift and diffusion of the dynamic process. What is more, it is very robust to a change in parameters and easy to implement (
Liu and Zhao 1998).
Originating from Darwinian evolution theory, a genetic algorithm can be viewed as an “intelligent” algorithm in which a probabilistic search is applied. In the process of evolution, natural populations evolve according to the principles of natural selection and “survival of the fittest”. Individuals who can more successfully fit in with their surroundings will have better chances to survive and multiply, while those who do not adapt to their environment will be eliminated. This implies that genes from highly fit individuals will spread to an increasing number of individuals in each successive generation. Combinations of good characteristics from highly adapted ancestors may produce even more fit offspring. In this way, species evolve to become progressively better adapted to their environments.
A GA simulates these processes by taking an initial population of individuals and applying genetic operators to each reproduction. In optimization terms, each individual in the population is encoded into a string or chromosome or some float number, which represents a possible solution to a given problem. The fitness of an individual is evaluated with respect to a given objective function. Highly fit individuals or solutions are given opportunities to reproduce by exchanging some of their genetic information with other highly fit individuals by a crossover procedure. This produces new “offspring” solutions (i.e., children), which share some characteristics taken from both parents. Mutation is often applied after crossover by altering some genes or perturbing float numbers. The offspring can either replace the whole population or replace less-fit individuals. This evaluation-selection-reproduction cycle is repeated until a satisfactory solution is found. The basic steps of a simple GA are shown below and in the next section, and we define the detailed steps of the GA after a specific example is introduced.
Generate an initial population and evaluate the fitness of the individuals in the population;
Select parents from the population;
Crossover (mate) parents to produce children and evaluate the fitness of the children;
Replace some or all of the population by the children until a satisfactory solution is found.