An Optimal Derivative Free Family of Chebyshev–Halley’s Method for Multiple Zeros
Abstract
1. Introduction
2. Construction of Higher-Order Scheme
Error for the General form of the Scheme (4)
3. Some Special Cases of Proposed Scheme
- Consider , then we have following new method denoted as
- Consider , then the new method denoted as is obtained as follows:
- Consider , then we have following new method denoted asSimilarly, many more methods can be created by adopting the following weight functions.
- .
- .
4. Numerical Illustration
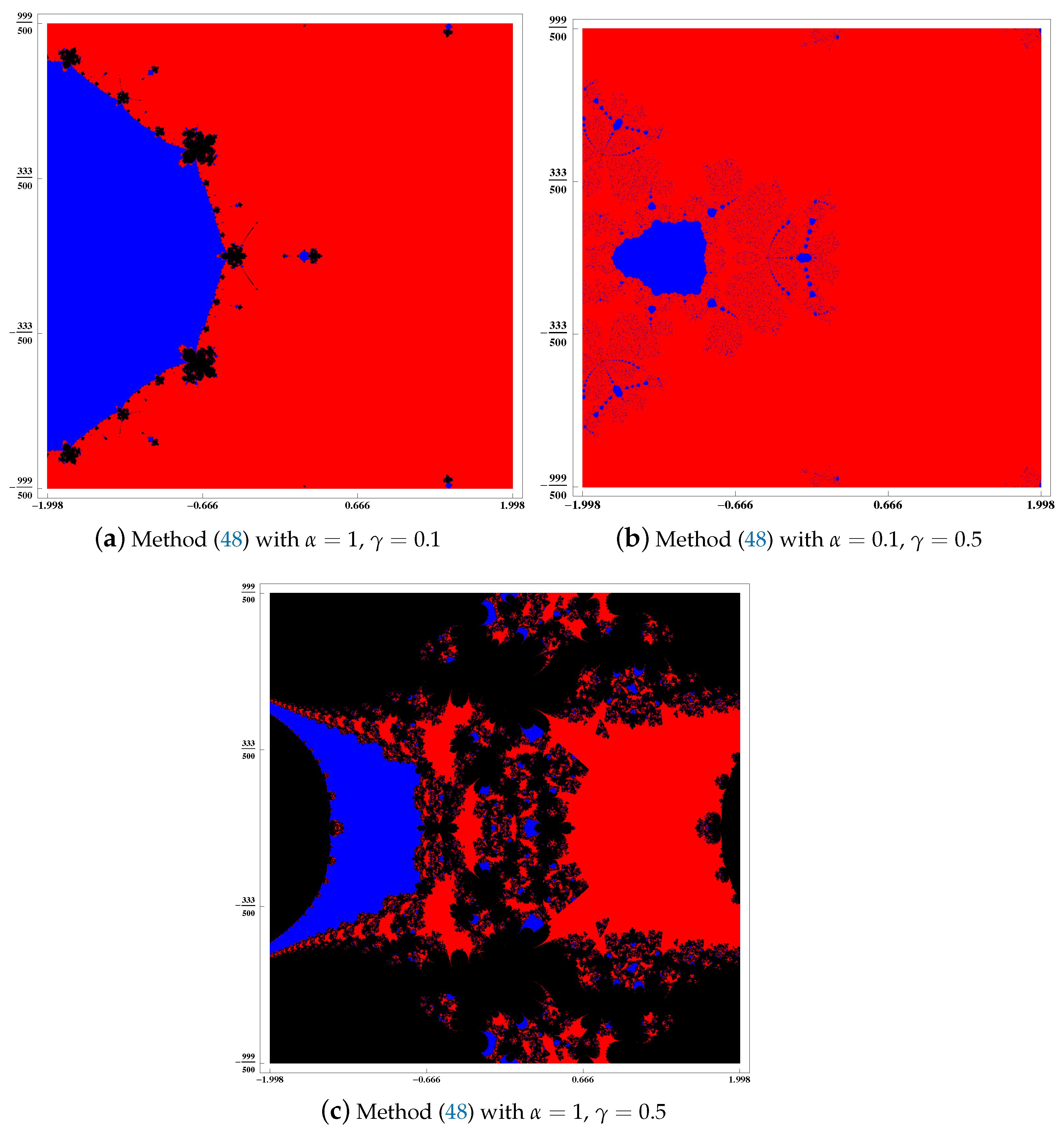
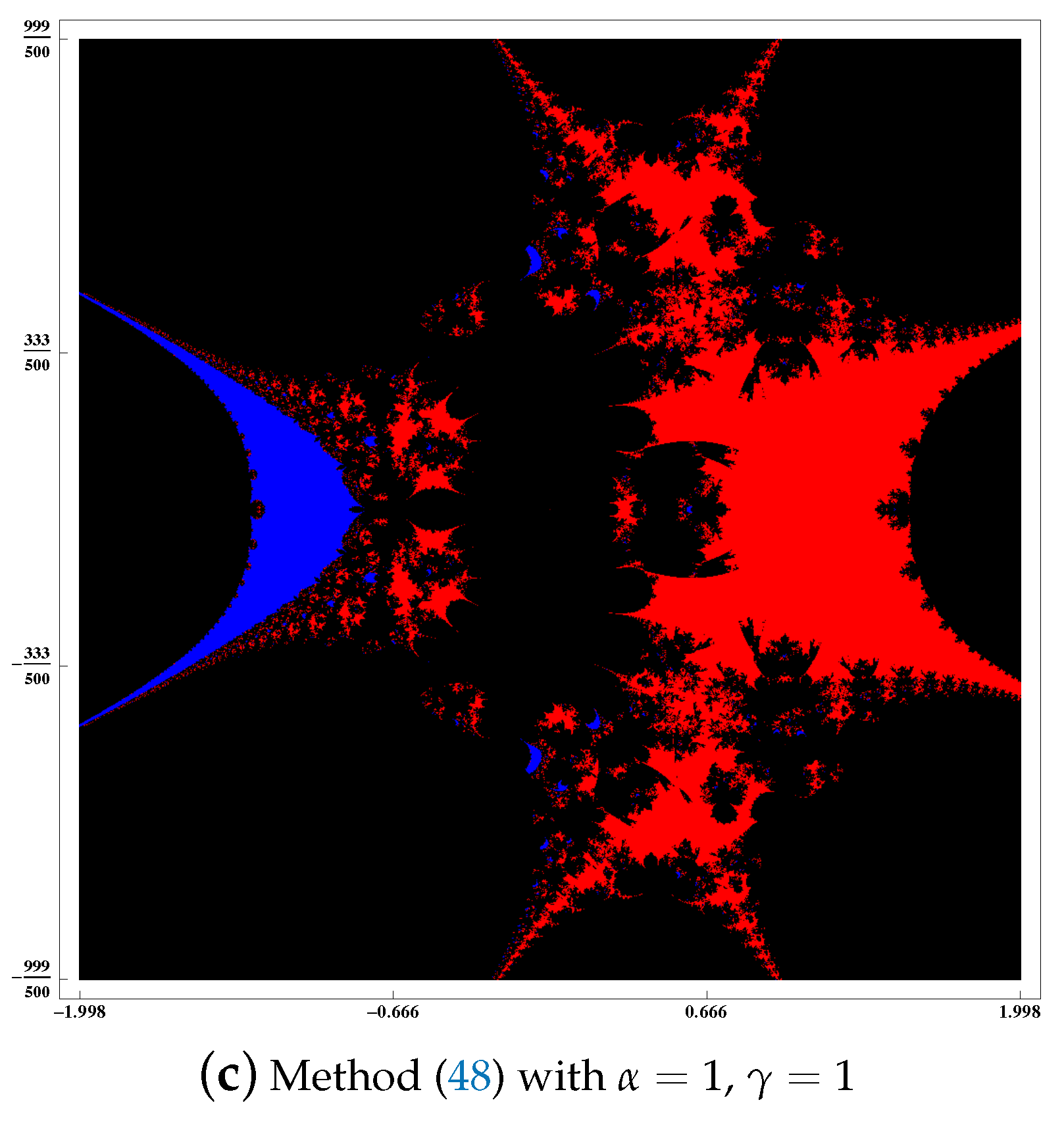
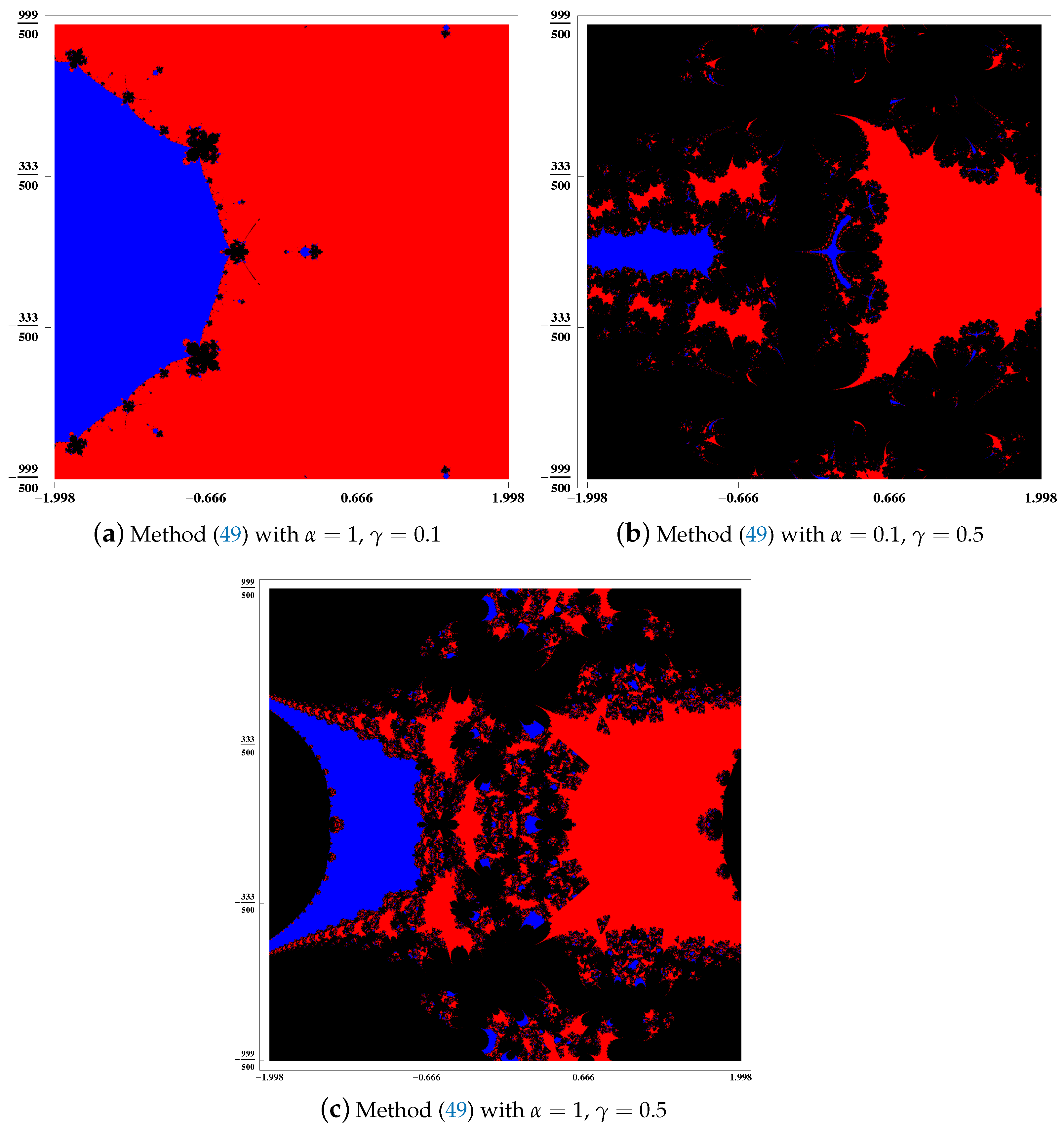
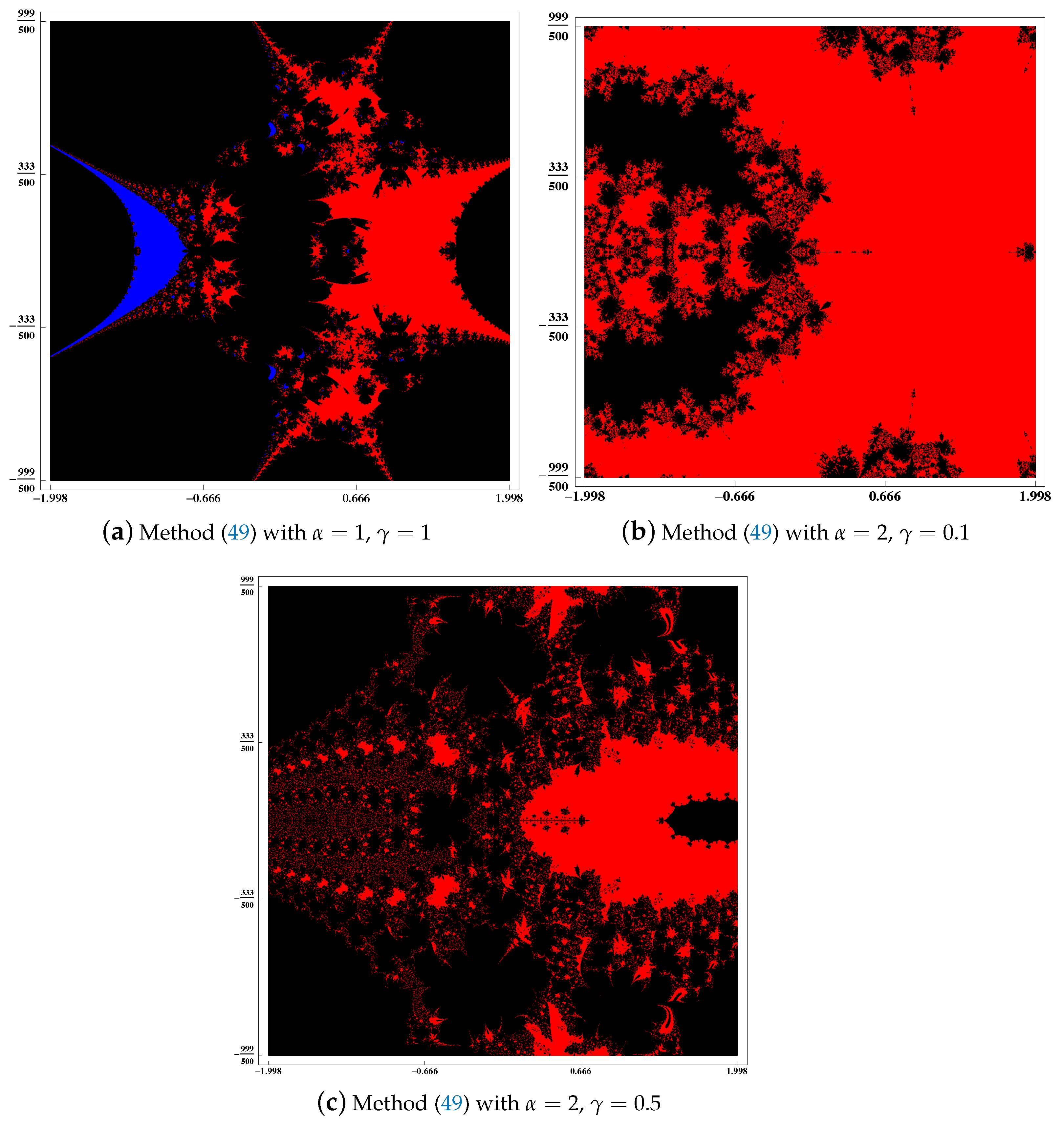
5. Dynamical Planes of (48) and (49)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, S.; Liao, X.; Cheng, L. A new fourth-order iterative method for finding multiple roots of nonlinear equations. Appl. Math. Comput. 2009, 215, 1288–1292. [Google Scholar]
- Sharma, J.R.; Sharma, R. Modified Jarratt method for computing multiple roots. Appl. Math. Comput. 2010, 217, 878–881. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, X.; Song, Y. Constructing higher-order methods for obtaining the multiple roots of nonlinear equations. J. Comput. Appl. Math. 2011, 235, 4199–4206. [Google Scholar] [CrossRef]
- Neta, B.; Chun, C.; Scott, M. On the development of iterative methods for multiple roots. Appl. Math. Comput. 2013, 224, 358–361. [Google Scholar] [CrossRef]
- Behl, R.; Cordero, A.; Motsa, S.S.; Torregrosa, J.R. On developing fourth-order optimal families of methods for multiple roots and their dynamics. Appl. Math. Comput. 2015, 265, 520–532. [Google Scholar] [CrossRef]
- Behl, R.; Cordero, A.; Motsa, S.S.; Torregrosa, J.R.; Kanwar, V. An optimal fourth-order family of methods for multiple roots and its dynamics. Numer. Algorithms 2016, 71, 775–796. [Google Scholar] [CrossRef]
- Geum, Y.H.; Kim, Y.I.; Neta, B. Constructing a family of optimal eighth-order modified Newton-type multiple-zero finders along with the dynamics behind their purely imaginary extraneous fixed points. J. Comput. Appl. Math. 2018, 333, 131–156. [Google Scholar] [CrossRef]
- Kansal, M.; Behl, R.; Mahnashi, M.A.A.; Mallawi, F. Modified Optimal Class of Newton-Like Fourth-Order Methods for Multiple Roots. Symmetry 2019, 11, 526. [Google Scholar] [CrossRef]
- Regmi, S. Optimized Iterative Methods with Applications in Diverse Disciplines; Nova Science Publisher: New York, NY, USA, 2021. [Google Scholar]
- Ostrowski, A.M. Solutions of Equations and System of Equations; Academic Press: New York, NY, USA, 1964. [Google Scholar]
- Traub, J.F. Iterative Methods for the Solution of Equations; Prentice-Hall Series in Automatic Computation: Englewood Cliffs, NJ, USA, 1964. [Google Scholar]
- Petković, M.S.; Neta, B.; Petković, L.D.; Džunić, J. Multipoint Methods for Solving Nonlinear Equations; Academic Press: New York, NY, USA, 2012. [Google Scholar]
- Hernádez, M.A.; Salanova, M.A. A family of chebyshev type methods in banach spaces. Int. J. Comput. Methods 1996, 61, 145–154. [Google Scholar] [CrossRef]
- Hueso, J.L.; Martínez, E.; Teruel, C. Determination of multiple roots of nonlinear equations and applications. Math. Chem. 2015, 53, 880–892. [Google Scholar] [CrossRef]
- Kumar, D.; Sharma, J.R.; Argyros, I.K. Optimal one-point iterative function free from derivatives for multiple roots. Mathematics 2020, 8, 709. [Google Scholar] [CrossRef]
- Sharma, J.R.; Kumar, S.; Jäntschi, L. On Derivative Free Multiple-Root Finders with Optimal Fourth Order Convergence. Mathematics 2020, 8, 1091. [Google Scholar] [CrossRef]
- Sharma, J.R.; Kumar, S.; Jäntschi, L. On a class of optimal fourth order multiple root solvers without using derivatives. Symmetry 2019, 11, 1452. [Google Scholar] [CrossRef]
- Sharma, J.R.; Kumar, S.; Argyros, I.K. Development of optimal eighth order derivative-free methods for multiple roots of nonlinear equations. Symmetry 2019, 11, 766. [Google Scholar] [CrossRef]
- Kung, H.T.; Traub, J.F. Optimal order of one-point and multipoint iteration. J. Assoc. Comput. Mach. 1974, 21, 643–651. [Google Scholar] [CrossRef]
- Ahlfors, I.V. Complex Analysis; McGraw-Hill Book, Inc.: New York, NY, USA, 1979. [Google Scholar]
- Soleymani, F.; Babajee, D.K.R.; Lotfi, T. On a numerical technique for finding multiple zeros and its dynamics. J. Egypt. Math. Soc. 2013, 21, 346–353. [Google Scholar] [CrossRef]
- Zafar, F.; Cordero, A.; Torregrosa, J.R. Stability analysis of a family of optimal fourth-order methods for multiple roots. Numer. AlgoriTheorem. 2018, 81, 947–981. [Google Scholar] [CrossRef]
- Behl, R.; Zafar, F.; Alshormani, A.S.; Junjua, M.U.D.; Yasmin, N. An optimal eighth-order scheme for multiple zeros of unvariate functions. Int. J. Comput. Methods 2019, 16, 1–16. [Google Scholar] [CrossRef]
- Bradie, B. A Friendly Introduction to Numerical Analysis; Pearson Education Inc.: New Delhi, India, 2006. [Google Scholar]
- Lotfi, T.; Magreñán, Á.A.; Mahdiani, K.; Javier Rainer, J. A variant of Steffensen-King’s type family with accelerated sixth-order convergence and high efficiency index: Dynamic study and approach. Appl. Math. Comput. 2015, 252, 347–353. [Google Scholar] [CrossRef]
- Gutiérrez, J.M.; Magreñán, Á.A.; Varona, J.L. The “gauss-Seidelization” of iterative methods for solving nonlinear equations in the complex plane. Appl. Math. Comput. 2011, 218, 2467–2479. [Google Scholar] [CrossRef]
- Amat, S.; Busquier, S.; Bermúdez, C.; Magreñán, Á.A. On the election of the damped parameter of a two-step relaxed Newton-type method. Nonlinear Dyn. 2016, 84, 9–18. [Google Scholar] [CrossRef]
- Magreñán, Á.A.; Gutiérrez, J.M. Real dynamics for damped Newton’s method applied to cubic polynomials. J. Comput. Appl. Math. 2015, 275, 527–538. [Google Scholar] [CrossRef]
- Cordero, A.; Feng, L.; Magreñán, Á.A.; Torregrosa, J.R. A new fourth-order family for solving nonlinear problems and its dynamics. J. Math. Chem. 2015, 53, 893–910. [Google Scholar] [CrossRef]
- Magreñán, Á.A. Different anomalies in a Jarratt family of iterative root-finding methods. Appl. Math. Comput. 2014, 233, 29–38. [Google Scholar]

| 4.9(−5) | 5.7(−21) | 1.1(−84) | 2.1(−1359) | ||
| 6.3(−6) | 2.7(−25) | 9.3(−103) | 3.4(−1651) | ||
| 9.6(−3) | 9.5(−5) | 3.9(−17) | 8.1(−135) | ||
| 1.1(−3) | 1.7(−14) | 1.1(−57) | 2.3(−922) | ||
| 6.4(−6) | 2.7(−25) | 9.4(−103) | 3.9(−1651) | ||
| 5.6(−6) | 1.3(−25) | 4.4(−104) | 9.3(−1673) | ||
| 5.3(−6) | 9.7(−26) | 1.1(−104) | 2.0(−1682) | ||
| 5.3(−6) | 9.7(−26) | 1.1(−104) | 1.8(−1682) | ||
| 4.9(−6) | 6.8(−26) | 2.5(−105) | 4.7(−1693) | ||
| 5.1(−6) | 8.1(−26) | 5.3(−105) | 1.1(−1687) | ||
| 5.2(−6) | 8.9(−26) | 7.7(−105) | 4.8(−1685) | ||
| 4.9(−6) | 6.8(−26) | 2.5(−105) | 4.7(−1693) | ||
| 5.4(−6) | 1.1(−25) | 2.2(−104) | 1.7(−1677) | ||
| 5.3(−6) | 9.7(−26) | 1.1(−104) | 1.8(−1682) | ||
| 6 | 5 | 5 | 5 | |
| 6 | 4 | 5 | 5 | |
| 6 | 6 | 6 | 7 | |
| 6 | 5 | 7 | 5 | |
| 6 | 4 | 5 | 5 | |
| 6 | 4 | 5 | 5 | |
| 6 | 4 | 5 | 5 | |
| 6 | 4 | 5 | 5 | |
| 6 | 4 | 5 | 5 | |
| 6 | 4 | 5 | 5 | |
| 6 | 4 | 5 | 5 | |
| 6 | 4 | 5 | 6 | |
| 6 | 4 | 5 | 5 | |
| 6 | 4 | 5 | 5 | |
| 6 | 4 | 5 | 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behl, R.; Bhalla, S.; Magreñán, Á.A.; Moysi, A. An Optimal Derivative Free Family of Chebyshev–Halley’s Method for Multiple Zeros. Mathematics 2021, 9, 546. https://doi.org/10.3390/math9050546
Behl R, Bhalla S, Magreñán ÁA, Moysi A. An Optimal Derivative Free Family of Chebyshev–Halley’s Method for Multiple Zeros. Mathematics. 2021; 9(5):546. https://doi.org/10.3390/math9050546
Chicago/Turabian StyleBehl, Ramandeep, Sonia Bhalla, Ángel Alberto Magreñán, and Alejandro Moysi. 2021. "An Optimal Derivative Free Family of Chebyshev–Halley’s Method for Multiple Zeros" Mathematics 9, no. 5: 546. https://doi.org/10.3390/math9050546
APA StyleBehl, R., Bhalla, S., Magreñán, Á. A., & Moysi, A. (2021). An Optimal Derivative Free Family of Chebyshev–Halley’s Method for Multiple Zeros. Mathematics, 9(5), 546. https://doi.org/10.3390/math9050546







