Abstract
Optimal fourth-order multiple-root finders with parameter were conjugated via the Möbius map applied to a simple polynomial function. The long-term dynamics of these conjugated maps in the -parameter plane was analyzed to discover some properties of periodic, bounded and chaotic orbits. The -parameters for periodic orbits in the parameter plane are painted in different colors depending on their periods, and the bounded or chaotic ones are colored black to illustrate -dependent connected components. When a red fixed component in the parameter plane branches into a q-periodic component, we encounter geometric bifurcation phenomena whose characteristics determine the desired boundary equation and bifurcation point. Computational results along with illustrated components support the bifurcation phenomena underlying this paper.
Keywords:
parameter plane; Möbius map; bifurcation point; circle; cardioid; fourth-order; multiple-root MSC:
65H05; 65H99; 41A25; 65B99; 37F10; 37G35
1. Introduction
The governing equations of natural phenomena are usually represented as nonlinear equations in the form of , when solving the relevant algebraic or differential equations obtained through the scientific observations, experiments, experiences as well as mathematical modeling. Since the exact solutions of such nonlinear governing equations are rarely feasible, it is considered best to rely on numerical solution techniques such as multi-point iterative methods [1,2,3,4], splitting methods [5,6], semi-explicit methods [7,8] as well as analytical-numerical methods [9]. Among such techniques, the most widely used multi-point iterative method under general circumstances is Newton’s method which converges quadratically to a simple root and linearly to a multiple root. In order to more accurately solve the nonlinear governing equations, many researchers have been developing new iteration methods with high convergence orders, including Newton’s method as a particular case. Motivation for writing this paper is to analyze the convergence behavior of these iterative numerical methods from the viewpoint of the limit behavior under the iteration dynamics with illustrative computational results.
Although the limit behavior of the aforementioned numerical solution techniques draws great attention to the readers, our study will focus on the limit behavior of a family of Newton-like iterative methods with a simple structure of a weight function possessing a -control parameter. The convergence behavior of these iterative numerical methods equipped with -control parameters can be analyzed from a viewpoint of iteration dynamics. Let us begin with a family of nonlinear governing equations with parameter as represented by the following nonlinear recurrence relation:
where is called the iteration function or fixed point operator [10]. If iteration index n is regarded as an indicator of time, then the nonlinear recurrence relation (1) would represent itself the relevant discrete dynamical system. Consequently, pursuing the convergence of the root of the nonlinear recurrence relation (1) is initiated by dealing with its limit behavior under the action of the nonlinear discrete dynamical system (1). The governing equation to be dealt with in this paper is a family of optimal [11] two-point Newton-like fourth-order multiple–root finders with parameter studied in Reference [3]:
where is analytic [12] in a neighborhood of with fixed and t is taken on the principal analytic branch of the m-th root. In the current study, we will employ a specific form of with a controllable parameter as follows:
The advantage of choosing such a rational function is to allow the conjugated to contain the low-order polynomial factor with exact -dependent roots, that is, the exact fixed points of from fixed-point relation (6) under the Möbius conjugacy to be introduced in Section 4. If a different type of , say, a polynomial were chosen, then the higher order of would hinder us from locating the exact fixed points.
In Reference [13], as a part of long-term dynamics for the conjugated map of (2), a study was conducted on bifurcation [14,15] phenomena occurring on the boundary curve of the yellow fixed component related to -free strange fixed point . The number of the component was turned out to be only one. Moreover, the equation of the boundary curve turned out to be a circle as one of the known geometric shapes. This simple circle allowed us to analyze the global bifurcations occurring on it without difficulties.
The aim of this paper is to study of the fixed points under the Möbius conjugacy map and to investigate in depth the boundary curves and other geometric properties of the hyperbolic components [16] in the -parameter plane (to be defined in Section 4). The current study will cover a challenging task not handled in the previous study in Reference [13]. We will extensively investigate the bifurcation phenomena of the red fixed component (whose notation and analysis will be described in Section 3 and Section 4) related to the strange fixed point , which is -dependent, that is, not -free as in the case of the previous study for the yellow fixed component. In particular, it is our curiosity and concern to find out whether the number of is more than one, and whether the equation of the boundary curve represents a known geometric figure. From the perspective of plane geometric curves, our main interest lies in the computational, theoretical and visual exploration of bifurcation phenomena occurring on the boundary curve of .
A theoretical formulation of the boundary equation of developed here will serve as a basis for describing bifurcation phenomena occurring in another discrete dynamical system. For example, it is helpful to establish the boundary equations of hyperbolic components with small periods in the Mandelbrot set [17] for a better analysis of bifurcation phenomena occurring there.
The remainder of this paper further describes the important points for the analysis of bifurcation phenomena. Described in Section 2 are preliminary results on the long-term behavior of a dynamical system and local bifurcations. In Section 3, we describe various properties of the fixed and critical points under the Möbius conjugacy map. Section 4 investigates a long-term dynamical behavior and the symmetry of the parameter plane. The location of the bifurcation points is extensively explored based upon the existence of a common osculating point between the fixed component (maximal connected set) [12] and q-periodic component. Section 5 describes the boundary curves of the fixed components along with their geometric properties. Finally in Section 6, we summarize overall studies and state the possible future work on the long-term dynamics of period-2 components.
2. Preliminary Results
Although iteration function in (1) is in general meromorphic, it suffices to treat the dynamics of rational functions only, in view of Lemma of 2.1 of Reference [13]. Indeed, we apply to obtain the conjugation of rational , namely, in the form of a rational function to be shown in (4) via the first-order rational Möbius conjugacy map , with [18].
The following definition of conjugacy and other assertions are useful for continuing discussion of the relevant dynamics.
Definition 1.
Letandrepresent two dynamical systems. The dynamical systemis said to be conjugate tovia h if there exists an isomorphismsuch that. Such h is called a conjugacy [19].
According to Theorem of 2.1 in Reference [13], we find:
Theorem 1.
Letand be conjugate to each other via the diffeomorphic conjugacy h. In addition, let ξ be a fixed point of. Then the following hold:
- (a)
- The fixed point property remains invariant under a topological conjugacy h, that is,
- (b)
- The Poincaré characteristic multiplier [15] of ξ by, denoted by, is invariant under a diffeomorphic conjugacy h, that is,
Remark 1.
Ifandare conjugate to each other via the topological conjugacy h, then we findand = . If and are further invertible, then we also find and . Hence, the topological conjugacy h gives an isomorphism between two orbits of and .
Letting in (2) yields for all . Then the orbit behavior of exhibits a behavior similar to that of the iterative function . According to Theorem 1, the invariant properties of the fixed point and the Poincaré characteristic multiplier after the conjugacy transformation address that and have the advantage that their orbit dynamics is invariant. Such an advantage may give the favorable geometric characteristics induced by the orbit behavior of .
Lemma 1.
Suppose thatis meromorphic and has a fixed pointwith. Then ψ has a unique fixed point ξ such that sequenceconverges to ξ for any given.
Proof.
(i) For , the proof is done by Lemma 1 of Reference [20]. (ii) For , it is possible to make under some restrictions on the form of , which can be justified based on the following description. By definition from Section 3.1 of Reference [21], is said to be analytic at ∞ if is analytic at 0 with . Due to Lemma 2.1 of Reference [13], we can express as a rational function with for . We further define a function and find by direct computation or from Section 2.6 of Reference [19]. Hence if restriction is made, then ∞ becomes an attracting fixed point of . □
If we select as a critical point of satisfying , then Lemma 1 with yields the following corollary.
Corollary 1.
Letand ξ be an attracting q-periodic point of ψ in Lemma 1. Then every critical orbit of ψ tends to ξ.
Corollary 1 will theoretically support the formation of hyperbolic components serving as important parts of the structure of the parameter space to be introduced later in Section 4.
We now define a function for a given parameter . Let and respectively denote a fixed point and a critical point of . Then, in view of Lemma 1, would influence the long-term orbit behavior of as the parameter varies across the boundary of region . The unit circle characterizes the stability and is better designated as the stability unit circle S for further analysis.
An abrupt change of such a long-term orbit behavior of often arises at , where the value of crosses the boundary of S. This kind of abrupt change in its dynamical behavior is said to be a bifurcation. Consulting the notions of such bifurcations in Reference [22], the following three types of bifurcation may occur:
- (1)
- If , then the bifurcation is of (cyclic) fold(saddle-node).
- (2)
- If , then the bifurcation is of flip(period-doubling).
- (3)
- If , then the bifurcation is of Neimark-Sacker(secondary Hopf),
with .
Such a control parameter in the parameter plane is called a bifurcation point whose location will be treated in Section 4.2.
3. Fixed and Critical Points under a Linear Fractional Möbius Conjugacy Map
The conjugated map of (2) under a linear fractional Möbius conjugacy map applied to a polynomial will be investigated regarding the relevant properties underlying its fixed and critical points for . We will explore its long-term dynamical behavior [10,18,23,24,25,26,27] behind the parameter plane via a linear fractional conjugacy map which is given by the Möbius conjugacy map , with . Let . Then the resulting represents:
where . Be aware that conjugacy makes free from parameters . In addition, we directly compute the derivative of from (4):
where .
The -dependent fixed points of are given by the roots of
where .
Consulting Sections 3.1 and 3.2 of Reference [20], we state following proposition for properties of and :
Proposition 1.
- (a)
- Ifis a fixed point of, then so is.
- (b)
- Ifis a critical point of, then so is.
- (c)
- Relationholds for anyand any.
- (d)
- Relationholds for anyand any fixed pointof.
According to Theorem 1-(a), the fixed points 0 and ∞ of with and respectively correspond to the fixed points a and b of , that is, the roots of polynomial . They are super-attractive, free of and also imply the critical points of in view of (5).
Nevertheless, because their orbits approach themselves, the dynamical impact is expected to be small. Fixed points excluding such fixed points are termed as strange fixed points [28] which are not the roots of . Notice that is a -free strange fixed point whose dynamics was explored in Reference [13]. The roots of in (6) are indeed -dependent strange fixed points. Simple computations directly prove the following lemma.
Lemma 2.
andhold for anyand any.
We seek -dependent strange fixed points by solving for a fixed . According to Proposition 1-(a), can be written in the form: , that is, where are the roots satisfying
Hence, we are able to express all the desired -dependent strange fixed points of as and with the notation for . Figure 4 of Reference [13] illustrates the stability surfaces of -dependent strange fixed points .
The super-attractors of can be found by solving for z and . Eliminating z in yields a 4-degree polynomial
from which we find for the desired super-attractors. Note that the cubic factor in (8) with positive discriminant value of has three distinct real roots.
On the other hand, eliminating in yields an 8-degree polynomial
which induces 8 supper-attractors denoted by 4 pairs of for with and . Lemma 2 leads us to only 4 pairs of super-attractors as follows:
The critical points of are given by the roots of . A quick glance of (5) reveals that is a -free critical point. Evidently and are critical points that respectively correspond to the roots a and b of the polynomial . The critical points excluding the both roots a and b are termed as free critical points [28]. Since the orbit behavior of -dependent critical point of draws our attention, we will treat free critical points that are -dependent.
4. Long-Term Orbit Behavior with Bifurcation Phenomena in the Parameter Plane
4.1. Parameter Plane and Long-Term Orbit Behavior
One way to efficiently handle the long-term orbit dynamics of the iterative map in (4) is to visually illustrate its dynamical orbit behavior in the -parameter plane whose definition will be made in this section. The long-term critical orbit under the action of will induce attracting periodic, finitely bounded or chaotic orbits for each given selected in the -parameter plane. It is certainly interesting to paint the point for which the long-term orbit approaches an attracting periodic orbit, with different color depending on its period.
Corollary 2 and Remark 2 well state the orbit behavior between two critical points z and of .
Corollary 2.
Letbe given. Ifis a q-periodic point of, then so is.
Proof.
Lemma 2 directly shows that and for a fixed point z of with a fixed . Hence there exists a topological conjugacy such that for a fixed point z. Hence, Remark 1 yields a relation . Clearly, gives , completing the proof. □
Remark 2.
If the orbit ofapproaches a q-periodic pointof, then the orbit ofalso approaches a q-periodic point, by virtue of Corollary 2.
In light of Remark 2, it suffices to consider only one branch of the critical points for its typical orbit behavior. We define the parameter plane(space) for iterative map as follows:
From now on, let denote the critical point for convenience. Consider the limit behavior of an orbit of approaching a number in the long run. If , then it draws very little attention to the limit behavior since . On the contrary, if is finite, then it will create a diversity of the limit behavior as varies. More importantly, if is finite as well as bounded, then Bolzano-Weierstass Theorem guarantees the existence of a subsequence of the orbit of converging to the fixed point . In other words, we can find a q-periodic point for some in such a way that
by expressing for any with and ; if , then it suggests that a non-periodic bounded orbit could exist. As a result, the q-periodic orbit of forms a q-cycle:
Taking the discussion in Section 3 into consideration, we find the possible fixed points . We now define a function for any given . As a consequence, establishes a bivariate rational function of z and on . Since the rational function has a finite number of zeros , that is, the fixed points of for any given , we can find a for any periodic-point being approached by the long-term critical orbit of .
To debate the stability of the q-periodic point , we first consider the case for . Due to the fact that and , we find that 0 and ∞ are the fixed points as well as super-attractors in view of Proposition 1-(d). In this case, regions of corresponding -values are respectively colored in cyan and magenta in the parameter space in Figure 1. For the fixed point , we have and for in the yellow region of in Figure 1. For the -dependent fixed points , we find and for .
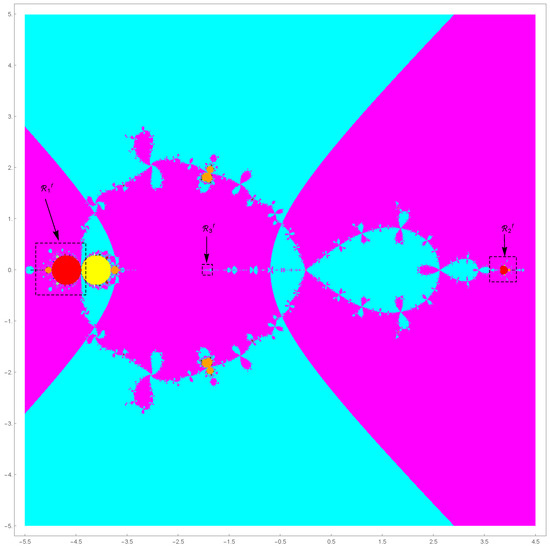
Figure 1.
Parameter space with three red fixed components .
Let us zoom in on the three regions indicated by the dotted rectangles in Figure 1 so that the red fixed components denoted by , , and arranged in order of their area size are clearly visible as magnified in Figure 2.
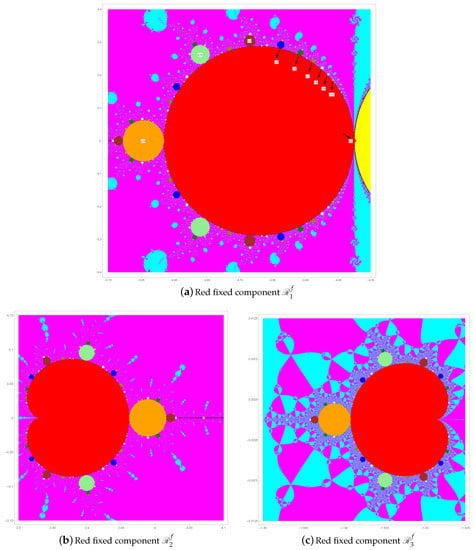
Figure 2.
Three Red fixed components .
The three attracting regions (hyperbolic components) related to the fixed points are extensively investigated in Section 5.1. The boundaries of will be comprised of six piecewise analytic branches associated with and for . We next consider the case for . Observe that the attracting fixed point maintains its stability for in the red region . As crosses the finite boundary of , that is, the fixed point loses its stability, but other attracting q-periodic points with
begin to emerge along the boundaries of . Hyperbolic components of -values for these q-periodic points are painted according to the color chart in Figure 5 of Reference [13]. Some of q-periodic components in are indicated by arrow numbers. If is chosen in such a q-periodic component, then the orbit of critical point attracts to a q-periodic point of . To generate the -parameter plane , Mathematica software has been used with 16-digits of precision for real and complex numbers. The desired convergence criterion for a q-periodic orbit was after maximum 3000 iterations.
It is evident that proper components of can be found to select best members of a family (2) locating the desired roots or with acceptable numerical stability, provided -parameters belong to such components.
According to Lemma 3.5 in Reference [29] and Theorem 5.2 in Reference [13], the parameter space is symmetric about its horizontal axis.
4.2. Bifurcation Points along a Red Fixed Component
Suppose that a point on a piecewise analytic curve in the complex plane satisfies relation:
An exemplary curve consisting of such points is sketched in Figure 3 along with attracting q-periodic satellite [17] components denoted by and identified by numbers . Observe that represents a tangential vector at a parametric location . We extensively pursue the case when traces a boundary curve of a typical red fixed component as varies. For convenience of notation, we let denote the finite boundary of , and write for simple treatment of derivatives.
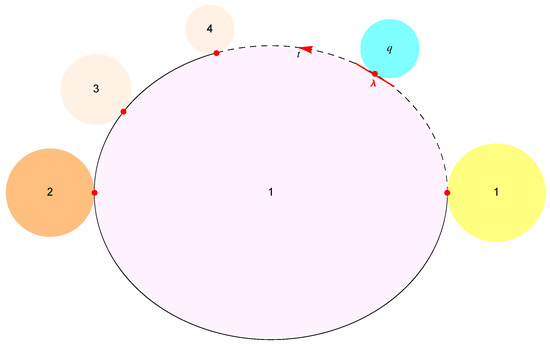
Figure 3.
Bifurcation geometry along the boundary of a typical fixed component.
Let be an osculating point where the -dependent critical orbit of approaches an attracting (hyperbolic) q-periodic point . We find that the q-periodic point is dependent upon parameter t, since the boundary depends on . Hence, we express with .
Given , the q-periodic point satisfies the following set of two equations at the common boundary point as shown in Figure 3.
Solving for from the fixed point relation via (4), we are able to obtain:
where is a rational function in z in view of (4) and differentiable at points except at a finite number of poles. This will trace a curve in the complex plane as parameter t varies. Hence, by the chain rules, we find the desired derivative at the fixed point :
from which we have in view of the fact that . Accordingly, Equation (14) reduces to:
Since represents a tangent line at a location t, Equation (16) states the common tangent line of and . The discussion thus far leads us to the notion of –bifurcation point below.
Definition 2.
Letbe given. Ifand, withandfor, then λ is called the–bifurcation point ofor–root point of.
By solving for , we are able to find the -bifurcation point in terms of ℓ and q, provided that a set of coprime values of are given. If then must occur and gives , which is the fold(saddle-node) bifurcation point in the sense of local bifurcations discussed in Section 2. At this kind of fold bifurcation point, another fixed component different from might arise or the same fixed component as itself merge together due to the connectedness of the component. In the latter case, such a fold bifurcation point might be a cusp-like point where itself becomes a primitive component. If , then becomes the flip (period-doubling) bifurcation point. If and , then becomes the Neimark-Sacker (secondary Hopf) bifurcation point.
We now conveniently denote the closed boundary curves of by for . Table 1, Table 2 and Table 3 list typical values of for on , and , respectively and some of them on as well as three of them on each are indicated by arrow lines in Figure 2 and Figure 4. The -bifurcation point is the one where the red fixed component is budded from itself or from other fixed component; its location is found to be for , for and for . It turns out that and are respectively regarded as primitive components, while is a satellite component budded from a yellow fixed component.

Table 1.
Typical along at , with for .

Table 2.
Typical along at , with for and for .

Table 3.
Typical along at , with for and for .
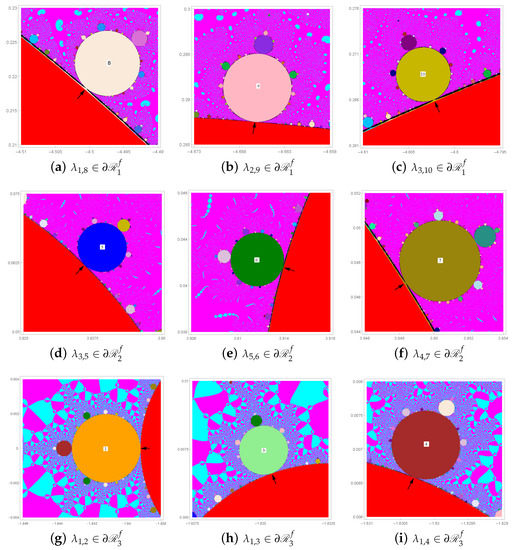
Figure 4.
Typical bifurcation points of q-periodic components occurring on .
Moreover, coprime pairs of give us the number of bifurcation points as the length of the Farey [30] sequence of order n. Theorem 4 in Reference [31] directly gives :
with as Euler’s totient function.
5. Constructing Boundary Equations of Red Fixed Components
5.1. Establishing Parametric Equations of
We establish a boundary equation for such an attracting red fixed component associated with a typical -dependent fixed point given by a root of . During the course of development, we will show the existence of three red fixed components , each boundary of which consists of two analytic branches forming a piecewise smooth closed curve. Details of such a boundary curve along with the location of bifurcation points will be discussed in the next section.
Consulting (5) and (6), we find that the fixed point satisfies a set of equations with as follows:
where are the two roots being dependent on from (7); moreover, for preferable algebraic treatments, expressions and are written as and in order. We reconstruct the second equation of (19) with a real parameter :
To make notations short, let us write , and compute from (7) in terms of c:
which defines a branch curve of . It is our interest to express in terms of the parameter t. By use of the symbolic Mathematica commands PolynomialQuotient and PolynomialRemainder described in Section 3.3.4 of Reference [32], we find:
where and are 9- and 6-degree polynomials in order; and with .
Due to the fact that , relation (20) directly yields:
where for can be expressed in terms of from (7). Since is not explicitly dependent on fixed points themselves but only on coefficient c, the stabilities of all four fixed points found from remain equal to one another. This kind of favorable dependence on c clearly reduces the possible lengthy algebraic work required for each fixed point.
Evidently, three roots of can be found for each in terms of from the cubic equation of (23):
with .
Further refined computations readily offer:
where reveals the complex conjugate of . We say the points t at which a complex function is not analytic on are called singular points or singularities of . Preferably, the continuity relations hold at the singular points and :
where and imply the respective limits from the above of a and the below of b.
In view of (21) and (24), we can express three -values at and . Denoting for leads us to the parametric expression for each as follows:
The result of Equation (27) suggests that the number of the red fixed components is three and enables us to construct the three boundaries of parametrically as varies. Indeed, and have also singular points at and .
Since in (21) is a function of c which is piecewise analytic with such singularities, we shall have same properties given by (25) and (26) with letter replaced by . In light of this observation along with the symmetry of , we characterize the three closed boundary curves of as for , with
Any of is generally comprised of piecewise analytic arcs with singularities at and . The functions are plotted for in Figure 5. Let be a closed plane curve traced by for , which represents the boundary of j-th red fixed component . The symmetry of clearly reflects the symmetry of with respect to the horizontal axis. The blue arcs correspond to ones with .
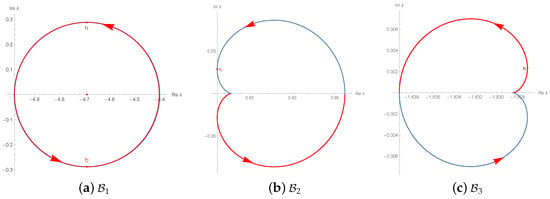
Figure 5.
Boundary curves of the three red fixed components .
5.2. Geometric Features of Boundaries
In this section, various typical geometric features, including curvatures, perimeters and bounding areas of the closed boundary curves , will be treated from a perspective of Euclidean planar curves. Let and respectively denote the real and imaginary part of . By elaborate computing with approximately 10 digits of accuracy, we obtain the arc lengths of :
as well as the bounding area enclosed by :
.
, with .
, with .
The curvatures of calculated when , and the average curvatures are shown in Table 4. In addition, the bounding areas and perimeters are listed together with them in Table 4. The following lemma immediately follows from the geometric properties listed in Table 4.

Table 4.
Some Geometric characteristics of Plane Curves and , and .
Lemma 3.
The shapes of boundary curveshave the following characterizations.
(i) is not a circle. (ii) Neither nor is a cardioid.
Remark 3.
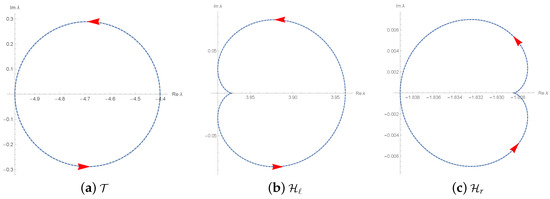
Consider a circleosculating at the topmost pointof, with, and. Letbe the distance from the centerofto a pointat a location t. Then by elaborate computations, we havefor alland findis completely inscribed in.
Let us define two cardioidsand, where. In view of geometric properties in Table 4,andrespectively resembleandwith exactly the same diametral chords. The curves of,andare evidently shown in Figure 6.

Figure 6.
Plane curves and closely resembling the boundaries of red-fixed components .
6. Conclusions
In the previous study in Reference [13], the only yellow fixed component related to -free strange fixed point had a circle as its boundary curve, which described branching phenomena without difficulties. On the other hand, in the present study, the formation of the red fixed component is more complicated because the strange fixed point (given by the roots of degree-4 polynomial in (6)) depends on , and thus the analysis of the desired bifurcation phenomena requires a higher level of tools. One such tool is to introduce a suitable parameter, say, t, to represent a curve on the complex plane. The expression , given at the beginning of Section 4.2, will be very helpful in describing the branching phenomena occurring in the -parameter plane . In particular, it has enabled us to draw some geometric properties of observed in .
Through the Möbius-conjugacy map applied to , we have studied the long-term orbit behavior of a -family of fourth-order multiple-root finders in . We have theoretically formulated the boundary equation of the red fixed hyperbolic component , by representing a point with parameter . The boundaries of have not turned out to be known geometric figures. In fact, they have proven to be neither circles nor cardioids. The number of is 3 higher than that of the yellow fixed component studied in Reference [13]. Equating the derivative of a q-periodic point to that of a -dependent fixed point at the common osculating point between and q-periodic components have induced the relation , which has enabled us to successfully locate the bifurcation points directly from with ℓ and q defined in Definition 2. With selected in the magenta or cyan region of , iterative scheme in (2) stably converges to the desired root. However, members of the family with selected in other regions would exhibit unfavorable numerical behavior.
According to Proposition 1-a, is composed of factors of the form for . Therefore, if the order of the governing equation (for instance, (7)) for the coefficients is not greater than 4, that is, the order of is not greater than 8, then it is possible to find the exact -dependent strange fixed point . Otherwise, the bifurcation phenomena will be resolved neither theoretically nor computationally. As our future study, we will challenge to investigate the bifurcation phenomena of the period-2 orange components shown in Figure 2 and locate the desired global bifurcation points by a theoretical formulation of the desired boundary equation, provided the order of is hopefully not greater than 8.
Author Contributions
Formal analysis, Y.I.K.; Investigation, Y.H.G. All authors have read and agreed to the published version of the manuscript.
Funding
The first author (Y.H. Geum) was partially supported by the National Research Foundation of Korea funded by the Ministry of Education under the research grant NRF-2018R1D1A1B07047715.
Acknowledgments
We authors would like to express our sincere gratitude to anonymous reviewers for providing valuable corrections and suggestions as well as correct vocabulary and English grammar.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Behl, R.; Cordero, A.; Motsa, S.; Torregrosa, J. On developing fourth-order optimal families of methods for multiple roots and their dynamics. Appl. Math. Comput. 2015, 265, 520–532. [Google Scholar] [CrossRef]
- Behl, R.; Cordero, A.; Motsa, S.; Torregrosa, J.; Kanwar, V. An optimal fourth-order family of methods for multiple roots and its dynamics. Numer. Algorithms 2016, 11, 775–796. [Google Scholar] [CrossRef]
- Geum, Y.H.; Kim, Y.I. A two-parameter family of fourth-order iterative methods with optimal convergence for multiple zeros. J. Appl. Math. 2013, 369067, 1–7. [Google Scholar]
- Neta, B.; Scott, M.; Chun, C. Basin attractors for various methods for multiple roots. Appl. Math. Comput. 2012, 218, 5043–5066. [Google Scholar] [CrossRef]
- Geiser, J. A multiple iterative splitting method for higher order differential equations. J. Math. Anal. Appl. 2015, 424, 1447–1470. [Google Scholar] [CrossRef]
- Hosseini, R.; Tatari, M. Some splitting methods for hyperbolic PDEs. Appl. Numer. Math. 2019, 146, 361–378. [Google Scholar] [CrossRef]
- Gao, J.; Liang, H.; Ma, S. Strong convergence of the semi-implicit Euler method for nonlinear stochastic Volterra integral equations with constant delay. Appl. Math. Comput. 2019, 348, 385–398. [Google Scholar] [CrossRef]
- González-Pinto, S.; Hernández-Abreu, D. Semi-implicit methods for differential systems with semi-stable equilibria. Appl. Numer. Math. 2006, 56, 210–221. [Google Scholar] [CrossRef]
- L-Jawary, M.A.A.; Azeez, M.M.; Radhi, G.H. Analytical and Numerical Solutions for the Nonlinear Burgers and Advection–Diffusion Equations by Using a Semi-Analytical Iterative Method. Comput. Math. Appl. 2018, 76, 155–171. [Google Scholar] [CrossRef]
- Campos, B.; Cordero, A.; Torregrosa, J.R.; Vindel, P. Orbits of period two in the family of a multipoint variant of Chebyshev-Halley family. Numer. Algorithms 2016, 73, 141–156. [Google Scholar] [CrossRef]
- Kung, H.T.; Traub, J.F. Optimal order of one-point and multipoint iteration. J. Assoc. Comput. Mach. 1974, 21, 643–651. [Google Scholar] [CrossRef]
- Ahlfors, L.V. Complex Analysis; McGraw-Hill Book, Inc.: New York, NY, USA, 1979. [Google Scholar]
- Geum, Y.H.; Kim, Y.I. Long-term orbit dynamics viewed through the yellow main component in the parameter space of a family of optimal fourth-order multiple-root finders. Discret. Contin. Dyn. Syst. Ser. B 2020, 22. [Google Scholar] [CrossRef]
- Hale, J.; Koçak, H. Dynamics and Bifurcations; Springer: New York, NY, USA, 1991. [Google Scholar]
- Thompson, J.M.T.; Stewart, H.B. Nonlinear Dynamics and Chaos; John Wieley & Sons Ltd.: New York, NY, USA, 1986. [Google Scholar]
- Carleson, L.; Gamelin, T.W. Complex Dynamics; Springer: New York, NY, USA, 1993. [Google Scholar]
- Peitgen, H.; Richter, P. The Beauty of Fractals; Springer: New York, NY, USA, 1986. [Google Scholar]
- Blanchard, P. The dynamics of Newton’s method. In Proceedings of Symposia in Applied Mathematics; American Mathematical Society: Providence, RI, USA, 1994; Volume 49, pp. 139–154. [Google Scholar]
- Beardon, A.F. Iteration of Rational Functions; Springer: New York, NY, USA, 1991. [Google Scholar]
- Lee, M.-Y.; Kim, Y.I. Bifurcations along the Boundary Curves of Red Fixed Components in the Parameter Space for Uniparametric, Jarratt-Type Simple-Root Finders. Mathematics 2020, 8, 51. [Google Scholar] [CrossRef]
- Devaney, R.L. An Introduction to Chaotic Dynamical Systems; Addison-Wesley Publishing Company, Inc.: New York, NY, USA, 1987. [Google Scholar]
- Nayfeh, A.H.; Balachandran, B. Applied Nonlinear Dynamics: Analytical, Computational, and Experimental Methods; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Argyros, I.K.; Magreñán, Á.A. On the convergence of an optimal fourth-order family of methods and its dynamics. Appl. Math. Comput. 2015, 252, 336–346. [Google Scholar] [CrossRef]
- Behl, R.; Cordero, A.; Motsa, S.; Torregrosa, J. Multiplicity anomalies of an optimal fourth-order class of iterative methods for solving nonlinear equations. Nonlinear Dyn. 2018, 91, 98–112. [Google Scholar] [CrossRef]
- Chun, C.; Neta, B.; Kim, S. On Jarratt’s family of optimal fourth-order iterative methods and their dynamics. Fractals 2014, 22, 1450013. [Google Scholar] [CrossRef]
- García-Olívo, M.; Gutíerrez, J.M.; Magreñán, Á.A. A complex dynamical approach of Chebyshev’s method. SeMA J. 2015, 71, 57–68. [Google Scholar] [CrossRef]
- Magreñán, Á.A. Different anomalies in a Jarratt family of iterative root-finding methods. Appl. Math. Comput. 2014, 233, 29–38. [Google Scholar]
- Chicharro, F.; Cordero, A.; Torregrosa, J.R. Drawing Dynamical and Parameters Planes of Iterative Families and Methods. Sci. World J. 2013, 2013, 1–11. [Google Scholar] [CrossRef]
- Geum, Y.H.; Kim, Y.I.; Magreñán, Á.A. A study of dynamics via Mobius conjugacy map on a family of sixth-order modified Newton-like multiple-zero finders with bivariate polynomial weight functions. J. Comput. Appl. Math. 2018, 344, 608–623. [Google Scholar] [CrossRef]
- Ainsworth, J.; Dawson, M.; Pianta, J.; Warwick, J. The Farey Sequence. 2012. Available online: http://www.maths.ed.ac.uk/~aar/fareyproject.pdf (accessed on 24 January 2020).
- Geum, Y.H.; Kim, Y.I. On Locating and Counting Satellite Components Born along the Stability Circle in the Parameter Space for a Family of Jarratt-Like Iterative Methods. Mathematics 2019, 7, 839. [Google Scholar] [CrossRef]
- Wolfram, S. The Mathematica Book, 5th ed.; Wolfram Media: Champaign, IL, USA, 2003. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).