An Oscillator without Linear Terms: Infinite Equilibria, Chaos, Realization, and Application
Abstract
:1. Introduction
- We introduce an oscillator without linear terms.
- There are infinite equilibria in the oscillator.
- The oscillator displays the boosting feature, which is useful for generating a signal with flexible amplitudes.
- Physical realization of the oscillator is reported.
- Special features of the oscillator are suitable for secure applications.
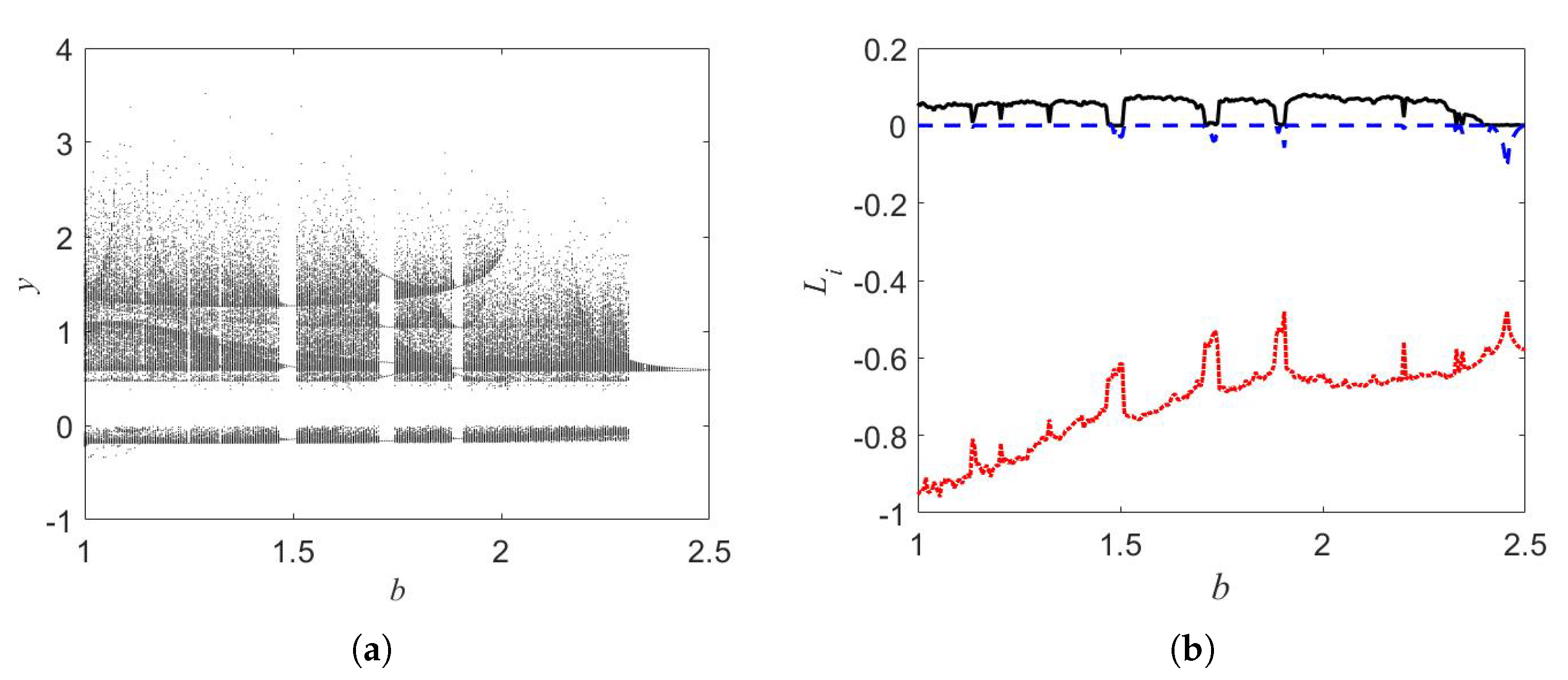
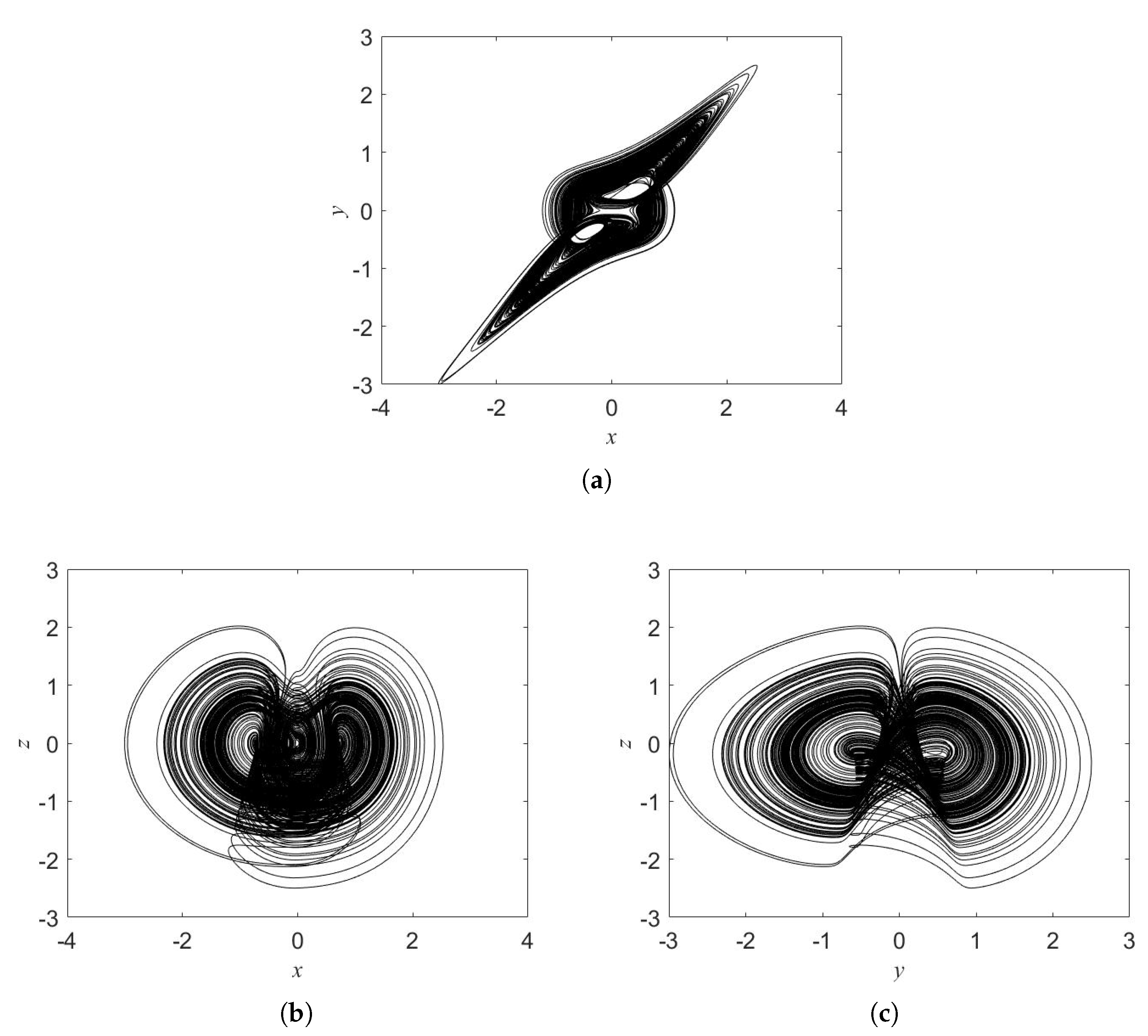
2. Oscillator and Oscillator’s Dynamics
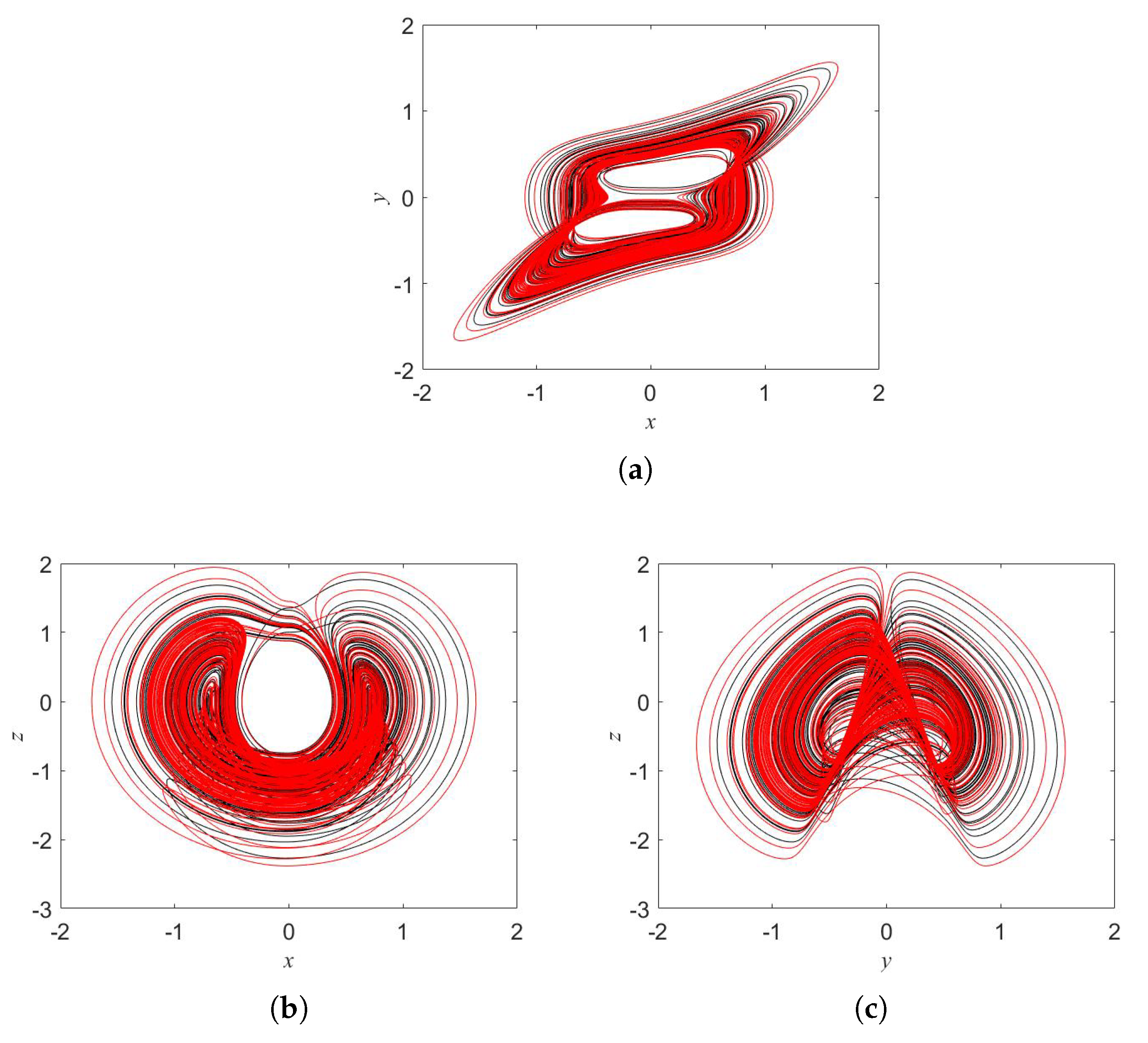
3. Oscillator Implementation
4. Random Number Generator (RNG) Using the Oscillator
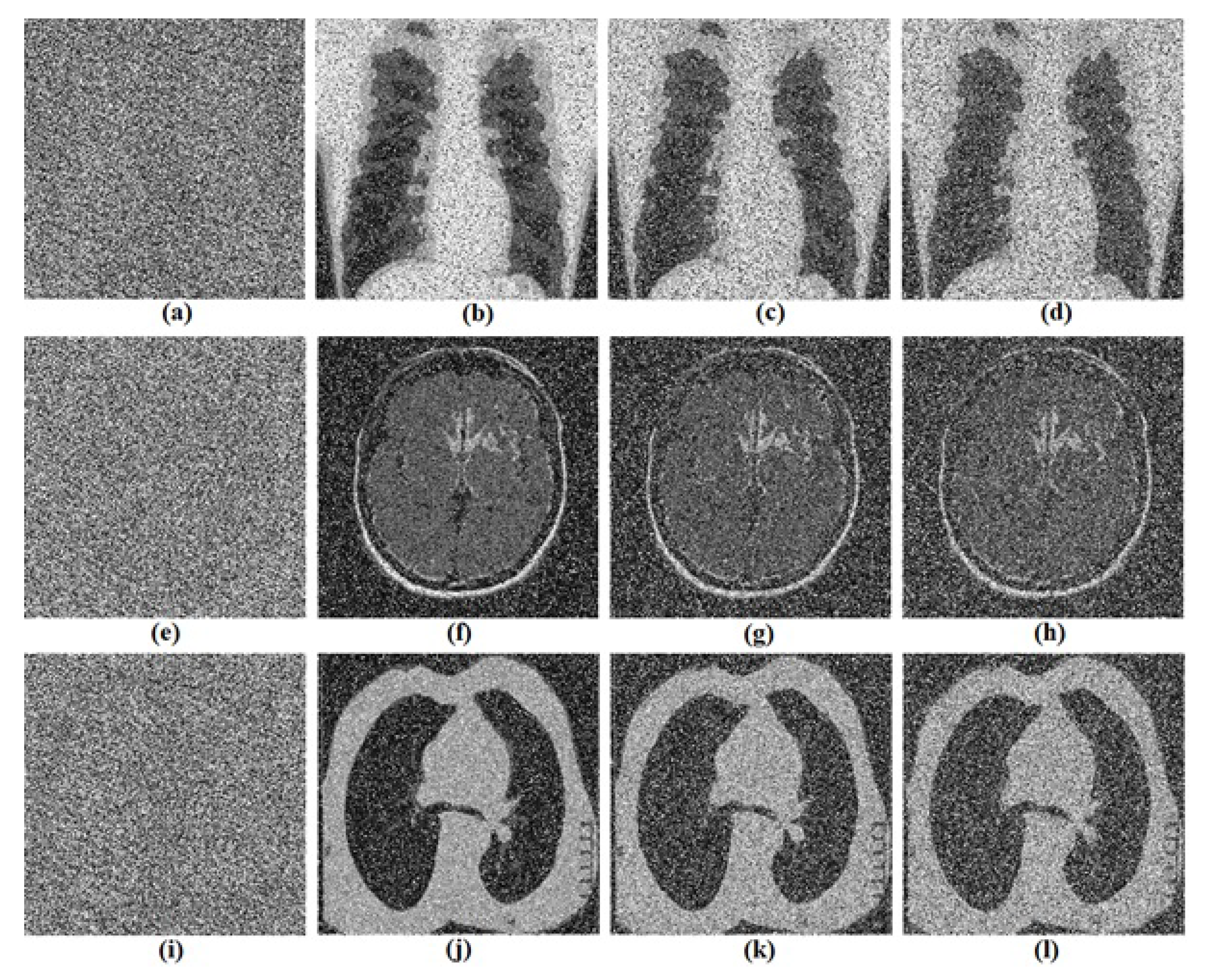
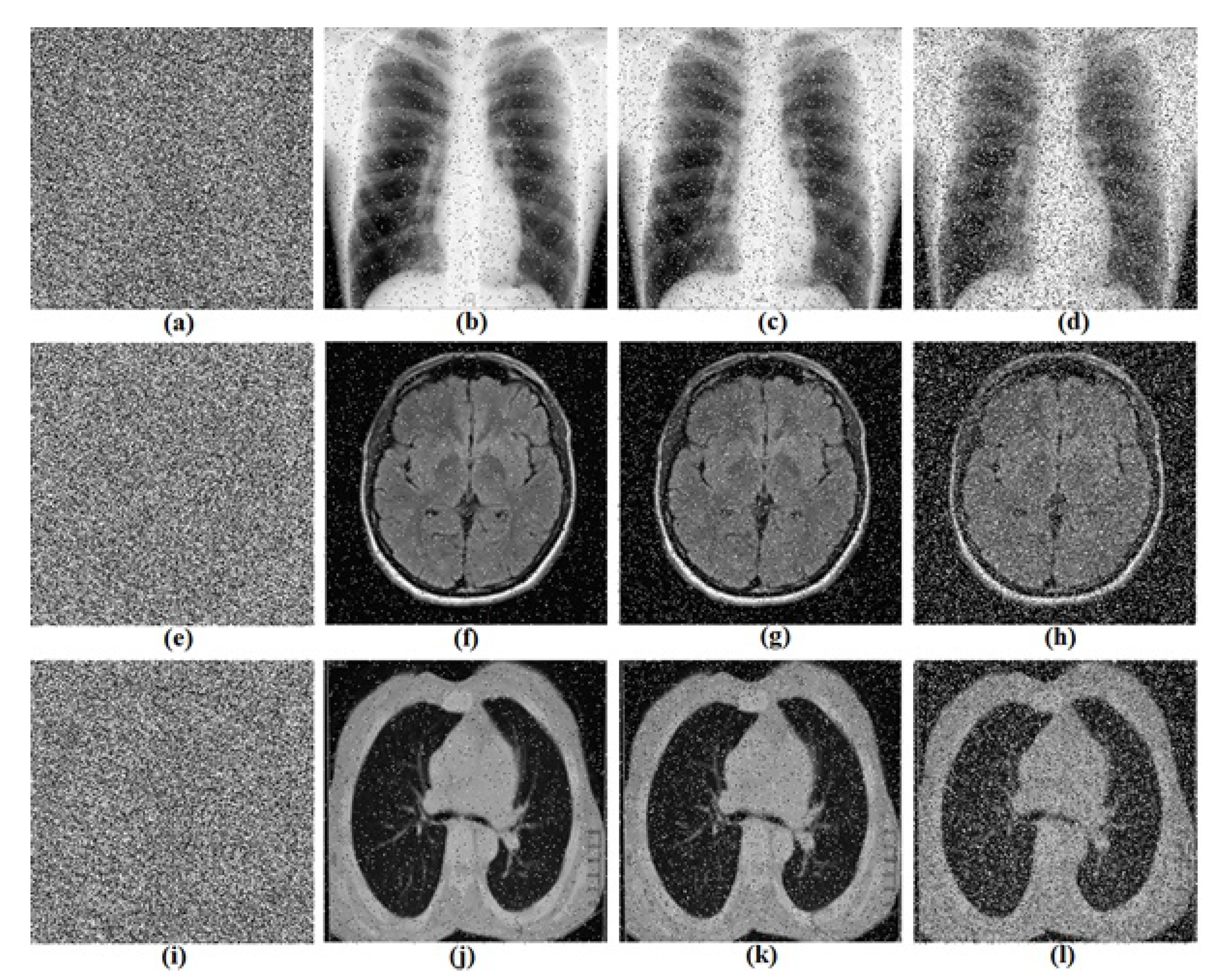
5. Biomedical Images Encryption Based on RNG Obtained from the Oscillator
5.1. Proposed Biomedical Images Encryption Algorithm
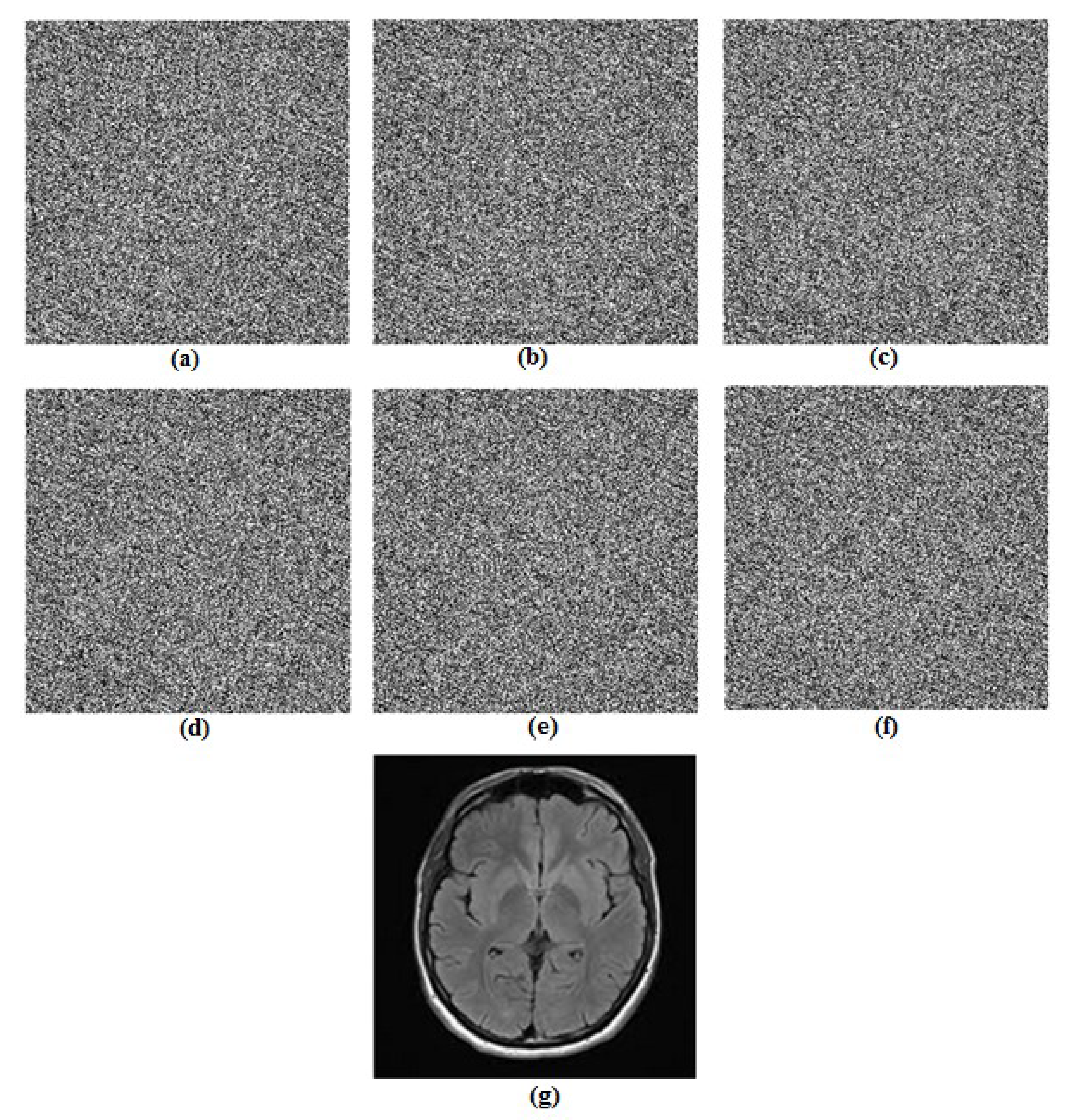
5.2. Computational Results
5.3. Security and Performance Analysis
5.3.1. Key Space Analysis
5.3.2. Key Sensitivity Analysis
5.3.3. Information Entropy
5.3.4. Noise Attacks
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ikeda, K.; Daido, H.; Akimoto, O. Optical turbulence: Chaotic behavior of transmitted light from a ring cavity. Phys. Rev. Lett. 1980, 45, 709–712. [Google Scholar] [CrossRef]
- Ikeda, K.; Matsumoto, K. High–dimensional chaotic behaviour in system with time–delayed feedback. Physics D 1987, 29, 223–235. [Google Scholar] [CrossRef]
- Shilnikov, L.P.; Shilnikov, A.L.; Turaev, D.V.; Chua, L.O. Methods of Qualitative Theory in Nonlinear Dynamics; World Scientific: Singapore, 1998. [Google Scholar]
- Ando, B.; Graziani, S. Stochastic Resonance: Theory and Applications; Kluwer: Norwel, MA, USA, 2000. [Google Scholar]
- Sanjuan, M.A.F.; Grebogi, C. Recent Progress in Controlling Chaos; World Scientific: Singapore, 2010. [Google Scholar]
- Rössler, O.E. An equation for continuous chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic non–periodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Nunez-Perez, J.C.; Adeyemi, V.A.; Sandoval-Ibarra, Y.; Perez-Pinal, F.J.; Tlelo-Cuautle, E. FPGA realization of spherical chaotic system with application in image transmission. Math. Probl. Eng. 2021, 2021, 5532106. [Google Scholar] [CrossRef]
- Natiq, H.; Ariffin, M.R.K.; Asbullah, M.A.; Mahad, Z.; Najah, M. Enhancing chaos complexity of a plasma model through power input with desirable random features. Entropy 2021, 23, 48. [Google Scholar] [CrossRef]
- Li, F.; Tai, C.; Bao, H.; Luo, J.; Bao, B. Hyperchaos, quasi-period and coexisting behaviors in second-order-memristor-based jerk circuit. Eur. Phys. J. Spec. Top. 2020, 229, 1045–1058. [Google Scholar] [CrossRef]
- Moysis, L.; Tutueva, A.; Volos, C.; Butusov, D.; Munoz-Pacheco, J.M.; Nistazakis, H. A two-parameter modified logistic map and its application to random bit generation. Symmetry 2020, 12, 829. [Google Scholar] [CrossRef]
- Pang, W.; Wu, Z.; Xiao, Y.; Jiang, C. Chaos control and synchronization of a complex Rikitake dynamo model. Entropy 2020, 22, 671. [Google Scholar] [CrossRef]
- Rajagopal, K.; Bayani, A.; Jafari, S.; Karthikeyan, A.; Hussain, I. Chaotic dynamics of a fractional order glucose-insulin regulatory system. Front. Inf. Technol. Electron. Eng. 2020, 21, 1108–1118. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Perseus Books: Boston, MA, USA, 1994. [Google Scholar]
- Chen, G.R. Controlling Chaos and Bifurcations in Engineering Systems; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Buscarino, A.; Fortuna, L.; Frasca, M.; Muscato, G. Chaos does help motion control. Int. J. Bifurc. Chaos 2007, 17, 3577–3581. [Google Scholar] [CrossRef]
- Abd-El-Atty, B.; Iliyasu, A.M.; Alaskar, H.; El-Latif, A.; Ahmed, A. A robust quasi-quantum walks-based steganography protocol for secure transmission of images on cloud-based e-healthcare platforms. Sensors 2020, 20, 3108. [Google Scholar] [CrossRef]
- El-Latif, A.A.A.; Abd-El-Atty, B.; Belazi, A.; Iliyasu, A.M. Efficient chaos-based substitution-box and its application to image encryption. Electronics 2021, 10, 1392. [Google Scholar] [CrossRef]
- Varan, M.; Akgul, A.; Kurugollu, F.; Sansli, A.; Smith, K. A Novel Security Methodology for Smart Grids: A Case Study of Microcomputer-Based Encryption for PMU Devices. Complexity 2021, 2021, 2798534. [Google Scholar] [CrossRef]
- Tutueva, A.V.; Karimov, T.I.; Moysis, L.; Nepomuceno, E.G.; Volos, C.; Butusov, D.N. Improving chaos-based pseudo-random generators in finite-precision arithmetic. Nonlinear Dyn. 2021, 105, 727–737. [Google Scholar] [CrossRef]
- Fataf, N.A.A.; Rahim, M.F.A.; He, S.; Banerje, S. A Communication Scheme based on Fractional Order Chaotic Laser for Internet of Things. Internet Things 2021, 15, 100425. [Google Scholar] [CrossRef]
- Kalayci, O.; Pehlivan, I.; Akgul, A.; Coskun, S.; Kurt, E. A New Chaotic Mixer Design Based on the Delta Robot and Its Experimental Studies. Math. Probl. Eng. 2021, 2021, 6615856. [Google Scholar] [CrossRef]
- la Fraga, L.G.D.; Mancillas-Lopez, C.; Tlelo-Cuautle, E. Designing an authenticated Hash function with a 2D chaotic map. Nonlinear Dyn. 2021, 104, 4569–4580. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, Z.; Sun, K.; Shaobo He, H.W.; Xu, Q.; Chen, M. Chaotic flows with special equilibria. Eur. Phys. J. Spec. Top. 2020, 229, 905–919. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C. Simple chaotic flows with a line equilibrium. Chaos Solitons Fractals 2013, 57, 79–84. [Google Scholar] [CrossRef]
- Pham, V.T.; Jafari, S.; Volos, C.; Kapitaniak, T. A gallery of chaotic systems with an infinite number of equilibrium points. Chaos Solitons Fractals 2016, 93, 58–63. [Google Scholar] [CrossRef]
- Li, Q.; Zeng, H.; Li, J. Hyperchaos in a 4D memristive circuit with infinitely many stable equilibria. Nonlinear Dyns. 2015, 79, 2295–2308. [Google Scholar] [CrossRef]
- Pham, V.T.; Jafari, S.; Kapitaniak, T. Constructing a chaotic system with an infinite number of equilibrium points. Int. J. Bifurc. Chaos 2016, 26, 1650225. [Google Scholar] [CrossRef]
- Sambas, A.; Vaidyanathan, S.; Bonny, T.; Zhang, S.; Hidayat, Y.; Gundara, G.; Mamat, M. Mathematical Model and FPGA Realization of a Multi-Stable Chaotic Dynamical System with a Closed Butterfly-Like Curve of Equilibrium Points. Appl. Sci. 2021, 11, 788. [Google Scholar] [CrossRef]
- Sambas, A.; Vaidyanathan, S.; Tlelo-Cuautle, E.; Zhang, S.; Guillen-Fernandez, O.; Hidayat, Y.; Gundarat, G. A novel chaotic system with two circles of equilibrium points: Multistability, electronic circuit and FPGA realization. Electronics 2019, 8, 1211. [Google Scholar] [CrossRef] [Green Version]
- Bao, B.; Zou, X.; Liu, Z.; Hu, F. Generalized memory element and chaotic memory system. Int. J. Bifurc. Chaos 2013, 23, 1350135. [Google Scholar] [CrossRef]
- Bao, H.; Wang, N.; Bao, B.; Chen, M.; Jin, P.; Wang, G. Initial condition-dependent dynamics and transient period in memristor-based hypogenetic jerk system with four line equilibria. Commun. Nonlinear Sci. Numer. Simul. 2018, 57, 264–275. [Google Scholar] [CrossRef]
- Karakaya, B.; Gulten, A.; Frasca, M. A true random bit generator based on a memristive chaotic circuit: Analysis, design and FPGA implementation. Chaos Solitons Fractals 2019, 119, 143–149. [Google Scholar] [CrossRef]
- Tuncer, S.A.; Kaya, T. True random number generation from bioelectrical and physical signals. Comput. Math. Methods Med. 2018, 2018, 3579275. [Google Scholar]
- Tuncer, T. The implementation of chaos-based PUF designs in field programmable gate array. Nonlinear Dyn. 2016, 86, 975–986. [Google Scholar] [CrossRef]
- Kaya, T. A true random number generator based on a Chua and RO-PUF: Design, implementation and statistical analysis. Analog Integr. Circuits Signal Process. 2020, 102, 415–426. [Google Scholar] [CrossRef]
- Seyedzadeh, S.M.; Mirzakuchaki, S. A fast color image encryption algorithm based on coupled two-dimensional piecewise chaotic map. Signal Process. 2012, 92, 1202–1215. [Google Scholar] [CrossRef]
- Tsafack, N.; Kengne, J.; Abd-El-Atty, B.; Iliyasu, A.; Hirota, K.; El-Latif, A. Design and implementation of a simple dynamical 4-D chaotic circuit with applications in image encryption. Inf. Sci. 2020, 515, 191–217. [Google Scholar] [CrossRef]







| Test-Name | p-Value | Result | ||
|---|---|---|---|---|
| X | Y | Z | ||
| Frequency | 0.01736 | 0.50790 | 0.49918 | Passed |
| Block-frequency | 0.18189 | 0.14409 | 0.18861 | Passed |
| Runs | 0.96599 | 0.15381 | 0.21472 | Passed |
| Longest runs of ones | 0.06335 | 0.65267 | 0.74264 | Passed |
| Rank | 0.49885 | 0.49928 | 0.44669 | Passed |
| DFT | 0.79219 | 0.30442 | 0.02589 | Passed |
| No overlapping templates | 0.05985 | 0.07790 | 0.00453 | Passed |
| Overlapping templates | 0.28548 | 0.37728 | 0.79657 | Passed |
| Universal | 0.07618 | 0.99902 | 0.35890 | Passed |
| Linear complexity | 0.79980 | 0.22241 | 0.94489 | Passed |
| Serial test 1 | 0.08187 | 0.68489 | 0.22395 | Passed |
| Serial test 2 | 0.03409 | 0.70814 | 0.11562 | Passed |
| Approximate entropy | 0.43162 | 0.72734 | 0.61123 | Passed |
| Cumulative sums (forward) | 0.02610 | 0.82875 | 0.45276 | Passed |
| Cumulative sums (reverse) | 0.01303 | 0.55867 | 0.49918 | Passed |
| Random excursions x = − 1 | 0.53667 | 0.68853 | 0.46270 | Passed |
| Random excursions variant x = − 1 | 0.83784 | 0.44510 | 0.53585 | Passed |
| Entropy | Greyscale Images | ||
|---|---|---|---|
| Chest | Brain | Lung | |
| Original image | 7.6578 | 5.8389 | 6.8364 |
| Encrypted version | 7.9965 | 7.9952 | 7.9955 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almatroud, O.A.; Tamba, V.K.; Grassi, G.; Pham, V.-T. An Oscillator without Linear Terms: Infinite Equilibria, Chaos, Realization, and Application. Mathematics 2021, 9, 3315. https://doi.org/10.3390/math9243315
Almatroud OA, Tamba VK, Grassi G, Pham V-T. An Oscillator without Linear Terms: Infinite Equilibria, Chaos, Realization, and Application. Mathematics. 2021; 9(24):3315. https://doi.org/10.3390/math9243315
Chicago/Turabian StyleAlmatroud, Othman Abdullah, Victor Kamdoum Tamba, Giuseppe Grassi, and Viet-Thanh Pham. 2021. "An Oscillator without Linear Terms: Infinite Equilibria, Chaos, Realization, and Application" Mathematics 9, no. 24: 3315. https://doi.org/10.3390/math9243315
APA StyleAlmatroud, O. A., Tamba, V. K., Grassi, G., & Pham, V.-T. (2021). An Oscillator without Linear Terms: Infinite Equilibria, Chaos, Realization, and Application. Mathematics, 9(24), 3315. https://doi.org/10.3390/math9243315





