Dynamical Behavior of a New Chaotic System with One Stable Equilibrium
Abstract
:1. Introduction
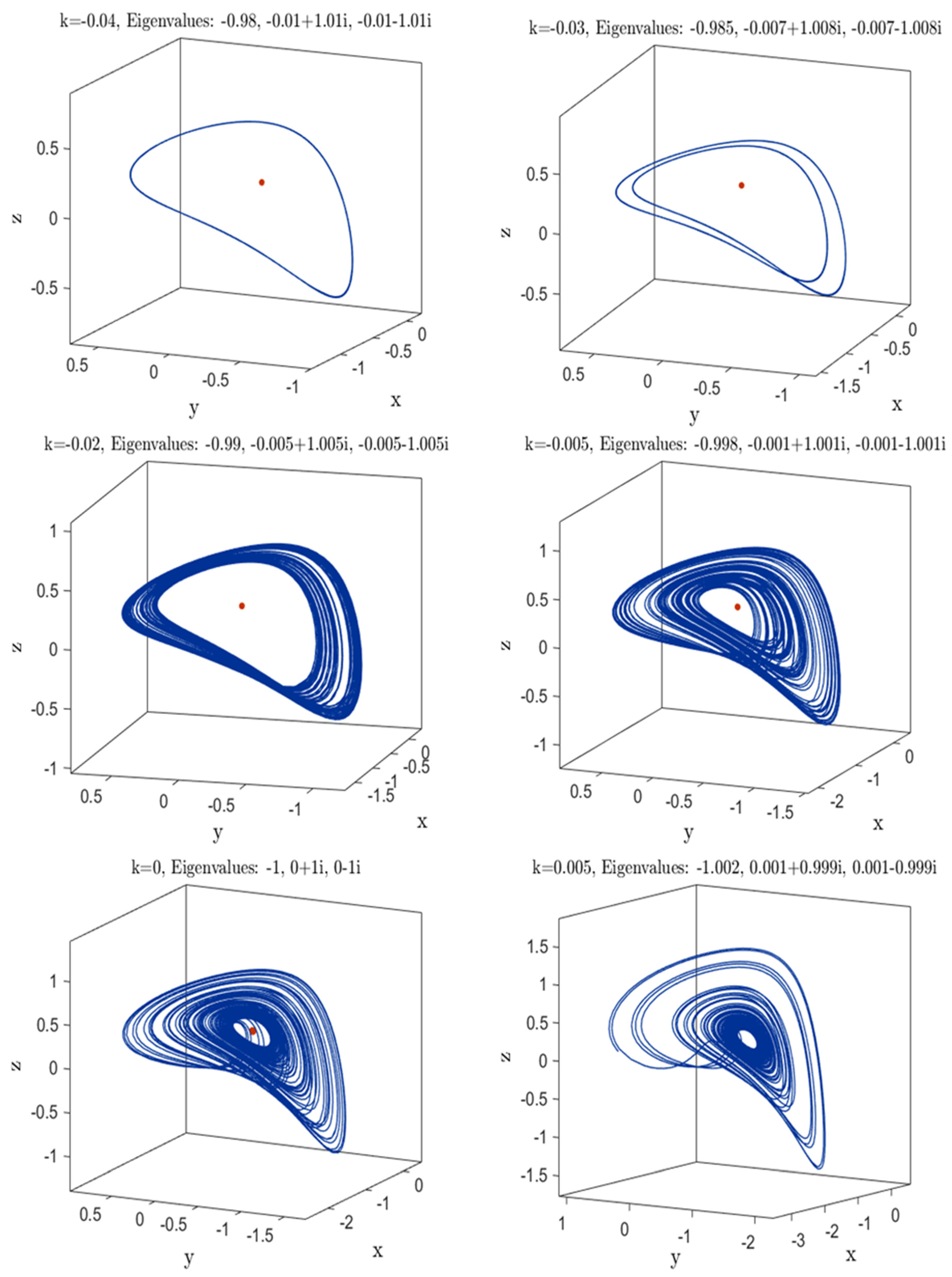
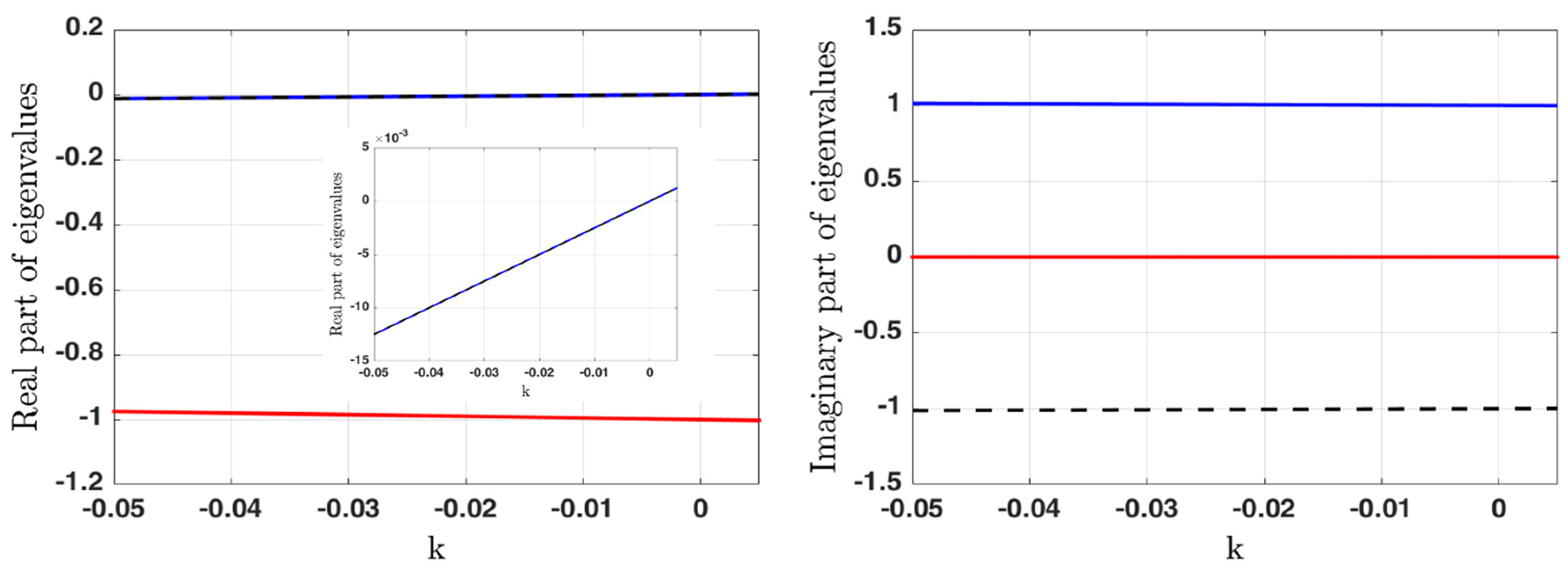
2. Proposed Systems Dynamics
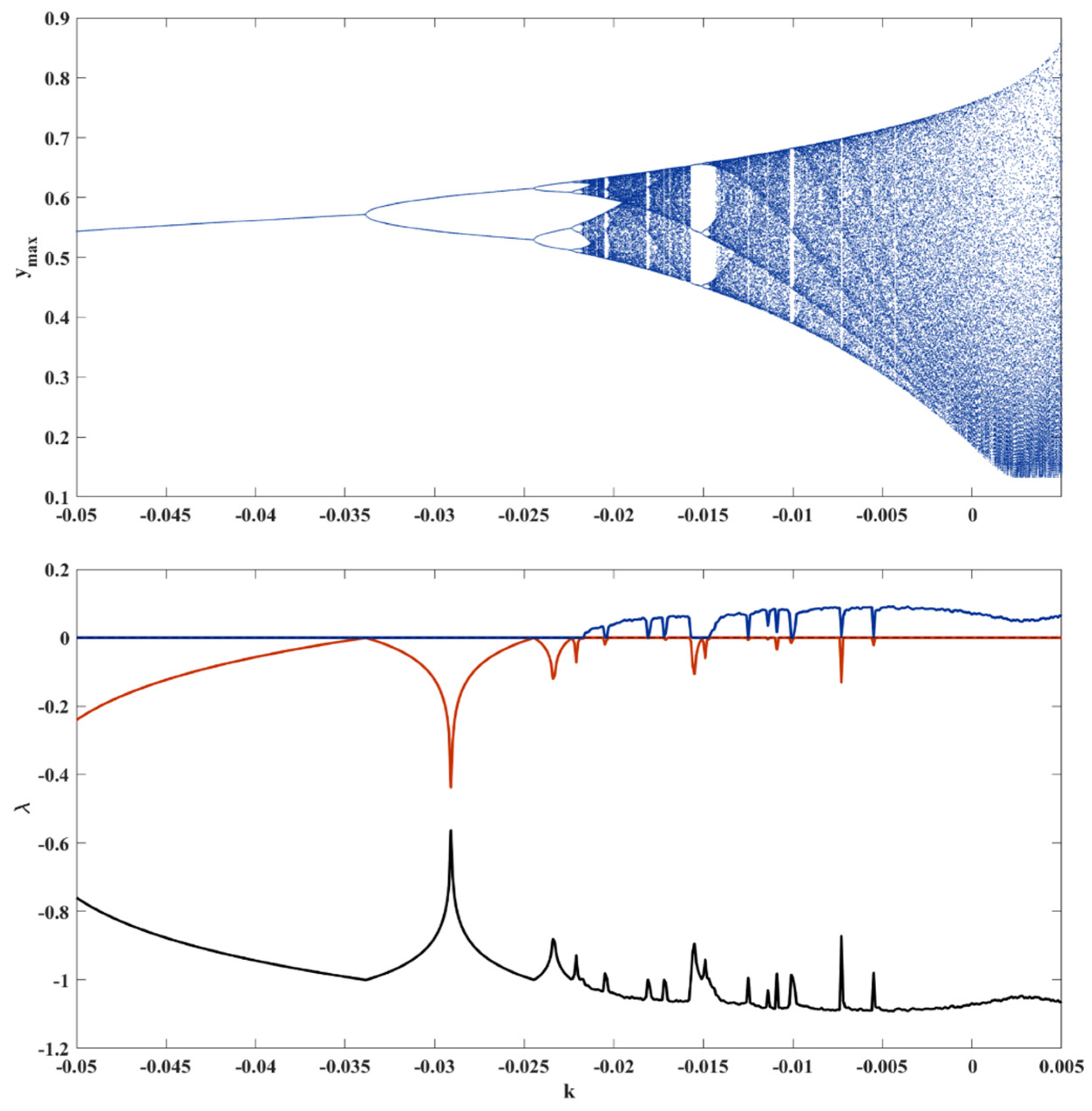
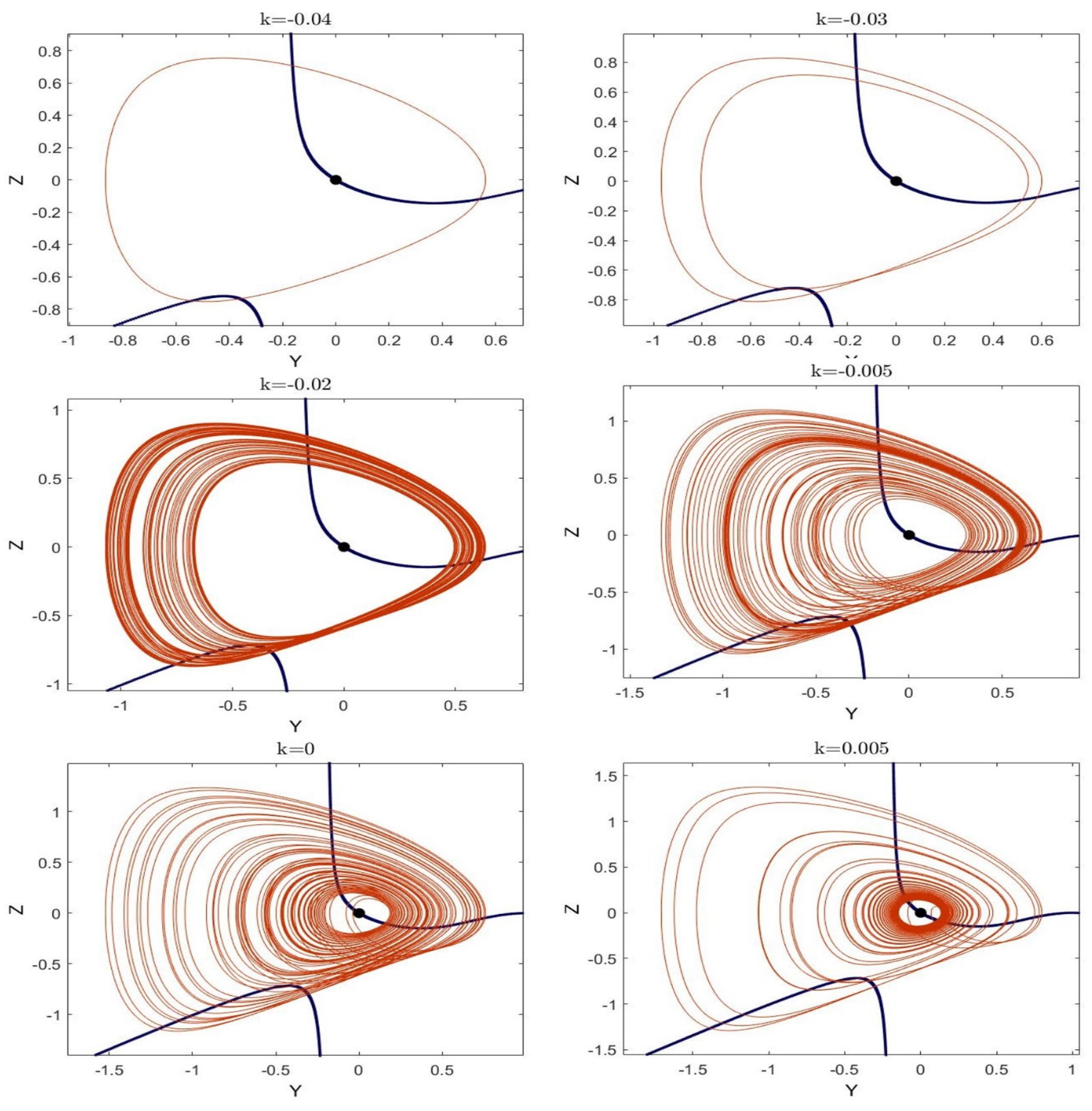
3. Bifurcation Diagram and Lyapunov Exponents
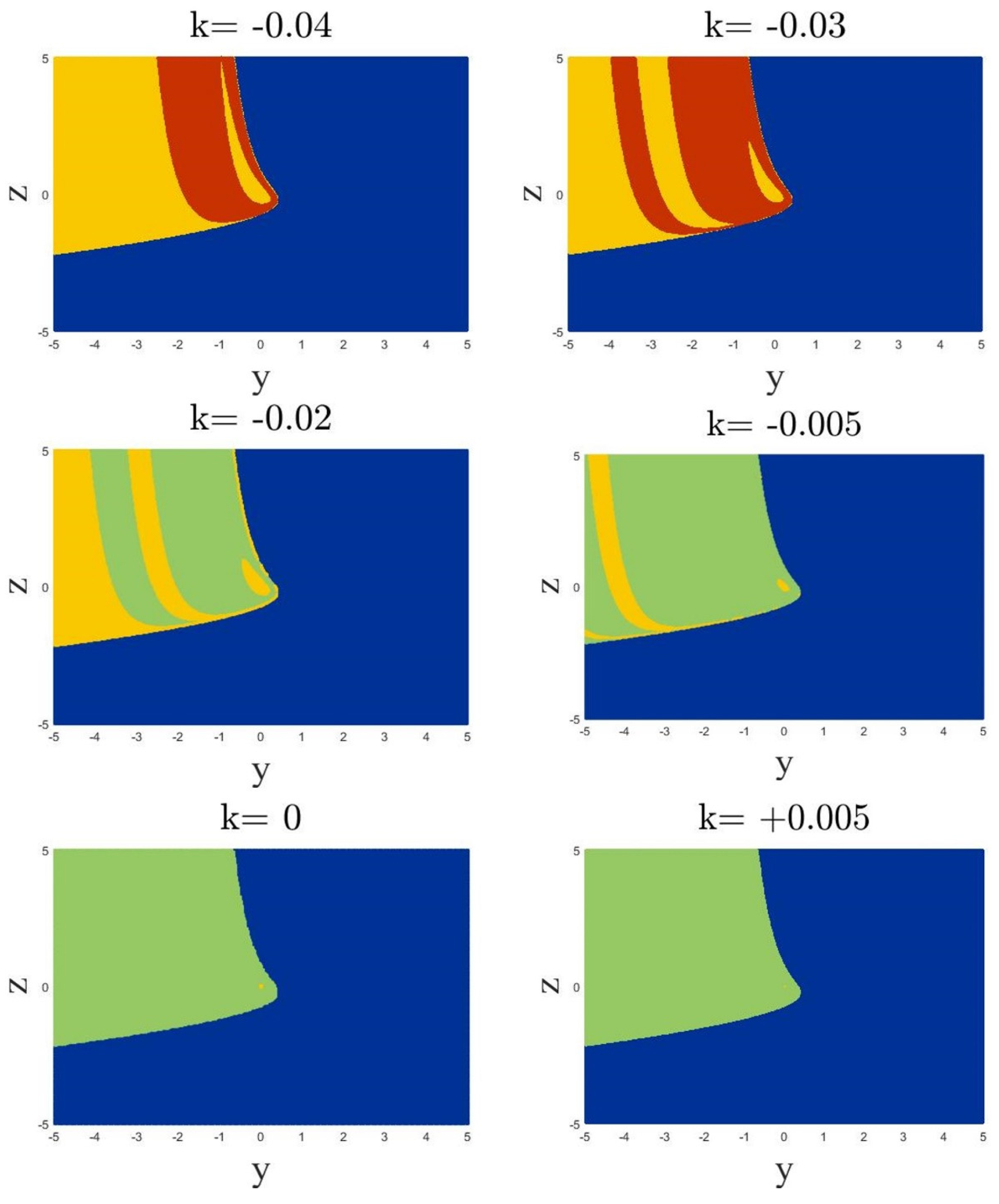
4. Basins of Attractions
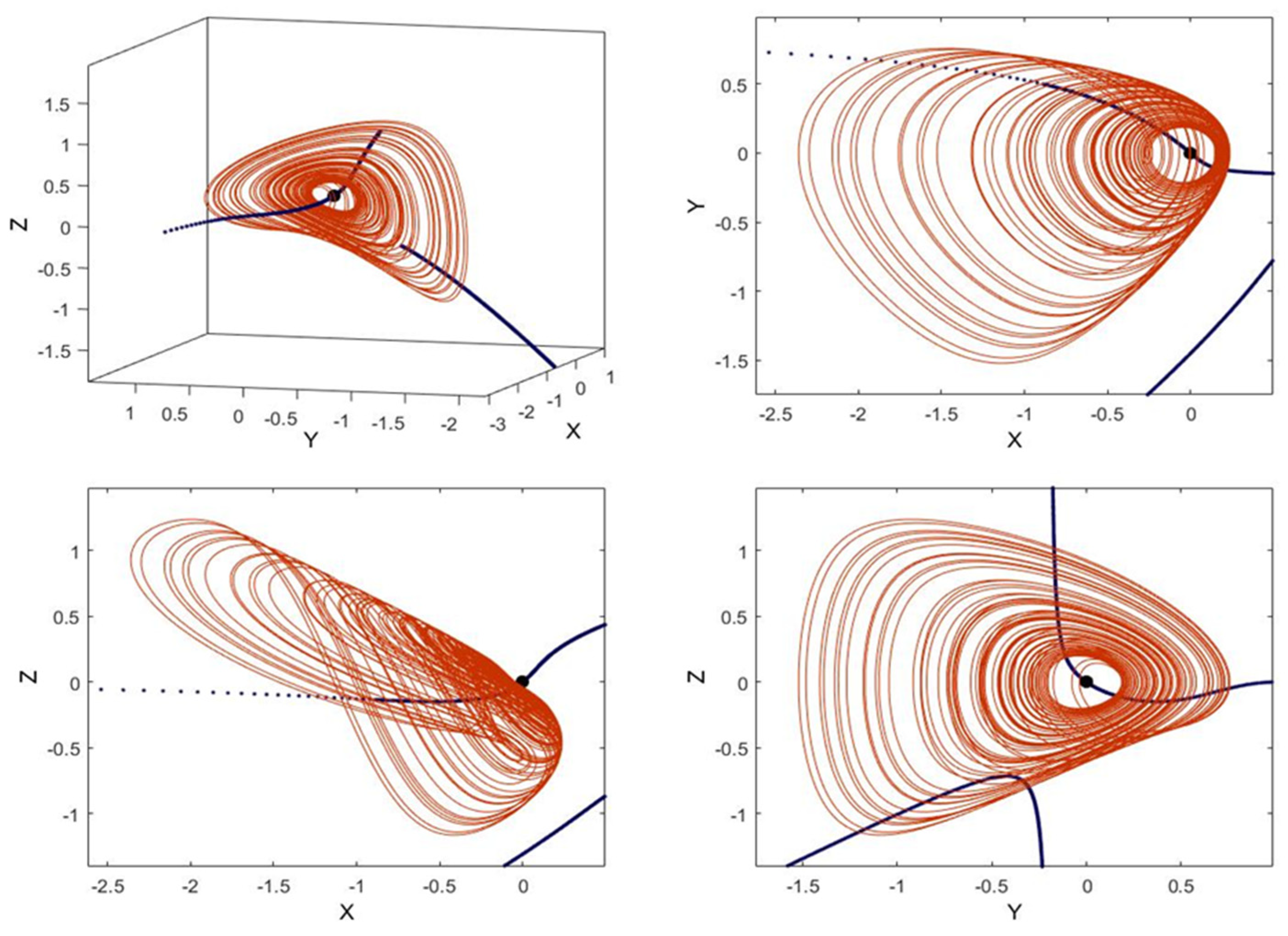
5. Connecting Curves
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sprott, J.C. Do we need more chaos examples? Chaos Theory Appl. 2020, 2, 49–51. [Google Scholar]
- Ma, C.; Mou, J.; Xiong, L.; Banerjee, S.; Liu, T.; Han, X. Dynamical analysis of a new chaotic system: Asymmetric multistability, offset boosting control and circuit realization. Nonlinear Dyn. 2021, 103, 2867–2880. [Google Scholar] [CrossRef]
- Wang, X.; Chen, G. A chaotic system with only one stable equilibrium. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1264–1272. [Google Scholar] [CrossRef] [Green Version]
- Sprott, J.C. Some simple chaotic flows. Phys. Rev. E 1994, 50, R647. [Google Scholar] [CrossRef]
- Rajagopal, K.; Duraisamy, P.; Tadesse, G.; Volos, C.; Nazarimehr, F.; Hussain, I. A fractional-order ship power system: Chaos and its dynamical properties. Int. J. Nonlinear Sci. Numer. Simul. 2021. [Google Scholar] [CrossRef]
- Rajagopal, K.; Shekofteh, Y.; Nazarimehr, F.; Li, C.; Jafari, S. A new chaotic multi-stable hyperjerk system with various types of attractors. Indian J. Phys. 2021, 1–7. [Google Scholar] [CrossRef]
- Pham, V.-T.; Jafari, S.; Kapitaniak, T.; Volos, C.; Kingni, S.T. Generating a Chaotic System with One Stable Equilibrium. Int. J. Bifurc. Chaos 2017, 27, 1750053. [Google Scholar] [CrossRef]
- Molaie, M.; Jafari, S.; Sprott, J.C.; Golpayegani, S.M.R.H. Simple chaotic flows with one stable equilibrium. Int. J. Bifurc. Chaos 2013, 23, 1350188. [Google Scholar] [CrossRef]
- Wei, Z.; Yang, Q. Dynamical analysis of the generalized Sprott C system with only two stable equilibria. Nonlinear Dyn. 2012, 68, 543–554. [Google Scholar] [CrossRef]
- Wang, X.; Akgul, A.; Cicek, S.; Pham, V.; Hoang, D.V. A chaotic system with two stable equilibrium points: Dynamics, circuit realization and communication application. Int. J. Bifurc. Chaos 2017, 27, 1750130. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; de la Fraga, L.G.; Pham, V.; Volos, C.; Jafari, S.; de Jesus Quintas-Valles, A. Dynamics, FPGA realization and application of a chaotic system with an infinite number of equilibrium points. Nonlinear Dyn. 2017, 89, 1129–1139. [Google Scholar] [CrossRef]
- Pham, V.-T.; Jafari, S.; Kapitaniak, T. Constructing a Chaotic System with an Infinite Number of Equilibrium Points. Int. J. Bifurc. Chaos 2016, 26, 1650225. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, X.; Zeng, Z. A simple no-equilibrium chaotic system with only one signum function for generating multidirectional variable hidden attractors and its hardware implementation. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 053129. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, S.N.; Ghosh, D. Hidden attractors: A new chaotic system without equilibria. Eur. Phys. J. Spec. Top. 2020, 229, 1299–1308. [Google Scholar] [CrossRef]
- Lu, H.; Rajagopal, K.; Nazarimehr, F.; Jafari, S. A New Multi-Scroll Megastable Oscillator Based on the Sign Function. Int. J. Bifurc. Chaos 2021, 31, 2150140. [Google Scholar] [CrossRef]
- Veeman, D.; Natiq, H.; Al-Saidi, N.M.G.; Rajagopal, K.; Jafari, S.; Hussain, I. A New Megastable Chaotic Oscillator with Blinking Oscillation terms. Complexity 2021, 2021, 5518633. [Google Scholar] [CrossRef]
- Li, X.; Mou, J.; Xiong, L.; Wang, Z.; Xu, J. Fractional-order double-ring erbium-doped fiber laser chaotic system and its application on image encryption. Opt. Laser Technol. 2021, 140, 107074. [Google Scholar] [CrossRef]
- Karthikeyan, A.; ÇİÇEK, S.; Rajagopal, K.; Duraisamy, P.; Srinivasan, A. New hyperchaotic system with single nonlinearity, its electronic circuit and encryption design based on current conveyor. Turk. J. Electr. Eng. Comput. Sci. 2021, 29, 1692–1705. [Google Scholar] [CrossRef]
- Cang, S.; Kang, Z.; Wang, Z. Pseudo-random number generator based on a generalized conservative Sprott-A system. Nonlinear Dyn. 2021, 1–18. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, G.; Kuznetsov, N.V.; Baoe, H. Hidden attractors and multistability in a modified Chua’s circuit. Commun. Nonlinear Sci. Numer. Simul. 2021, 92, 105494. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, C.; Yang, L. Four-wing hidden attractors with one stable equilibrium point. Int. J. Bifurc. Chaos 2020, 30, 2050086. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.; Nazarimehr, F. Recent new examples of hidden attractors. Eur. Phys. J. Spec. Top. 2015, 224, 1469–1476. [Google Scholar] [CrossRef]
- Dudkowski, D.; Jafari, S.; Kapitaniak, T.; Kuznetsov, N.V.; Leonov, G.A.; Prasad, A. Hidden attractors in dynamical systems. Phys. Rep. 2016, 637, 1–50. [Google Scholar] [CrossRef]
- Leonov, G.; Kuznetsov, N.; Vagaitsev, V. Localization of hidden Chua’s attractors. Phys. Lett. A 2011, 375, 2230–2233. [Google Scholar] [CrossRef]
- Kuznetsov, N.V. Hidden attractors in fundamental problems and engineering models: A short survey. In AETA 2015: Recent Advances in Electrical Engineering and Related Sciences; Springer: Berlin/Heidelberg, Germany, 2016; pp. 13–25. [Google Scholar]
- Dudkowski, D.; Prasad, A.; Kapitaniak, T. Perpetual Points: New Tool for Localization of Coexisting Attractors in Dynamical Systems. Int. J. Bifurc. Chaos 2017, 27, 1750063. [Google Scholar] [CrossRef] [Green Version]
- Nazarimehr, F.; Saedi, B.; Jafari, S.; Sprott, J.C. Are perpetual points sufficient for locating hidden attractors? Int. J. Bifurc. Chaos 2017, 27, 1750037. [Google Scholar] [CrossRef]
- Roth, M.; Peikert, R. A higher-order method for finding vortex core lines. In Proceedings of the Visualization’98 (Cat. No. 98CB36276), Research Triangle Park, NC, USA, 18–23 October 1998. [Google Scholar]
- Gilmore, R.; Ginoux, J.M.; Jones, T.; Letellier, C.; Freitas, U.S. Connecting curves for dynamical systems. J. Phys. A Math. Theor. 2010, 43, 255101. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
M.D., V.; Karthikeyan, A.; Zivcak, J.; Krejcar, O.; Namazi, H. Dynamical Behavior of a New Chaotic System with One Stable Equilibrium. Mathematics 2021, 9, 3217. https://doi.org/10.3390/math9243217
M.D. V, Karthikeyan A, Zivcak J, Krejcar O, Namazi H. Dynamical Behavior of a New Chaotic System with One Stable Equilibrium. Mathematics. 2021; 9(24):3217. https://doi.org/10.3390/math9243217
Chicago/Turabian StyleM.D., Vijayakumar, Anitha Karthikeyan, Jozef Zivcak, Ondrej Krejcar, and Hamidreza Namazi. 2021. "Dynamical Behavior of a New Chaotic System with One Stable Equilibrium" Mathematics 9, no. 24: 3217. https://doi.org/10.3390/math9243217
APA StyleM.D., V., Karthikeyan, A., Zivcak, J., Krejcar, O., & Namazi, H. (2021). Dynamical Behavior of a New Chaotic System with One Stable Equilibrium. Mathematics, 9(24), 3217. https://doi.org/10.3390/math9243217







