Impact of Strong Wind and Optimal Estimation of Flux Difference Integral in a Lattice Hydrodynamic Model
Abstract
:1. Introduction
2. Methods: The Modified Model
3. Discussion
3.1. Linear Stability Analysis
3.2. Nonlinear Analysis
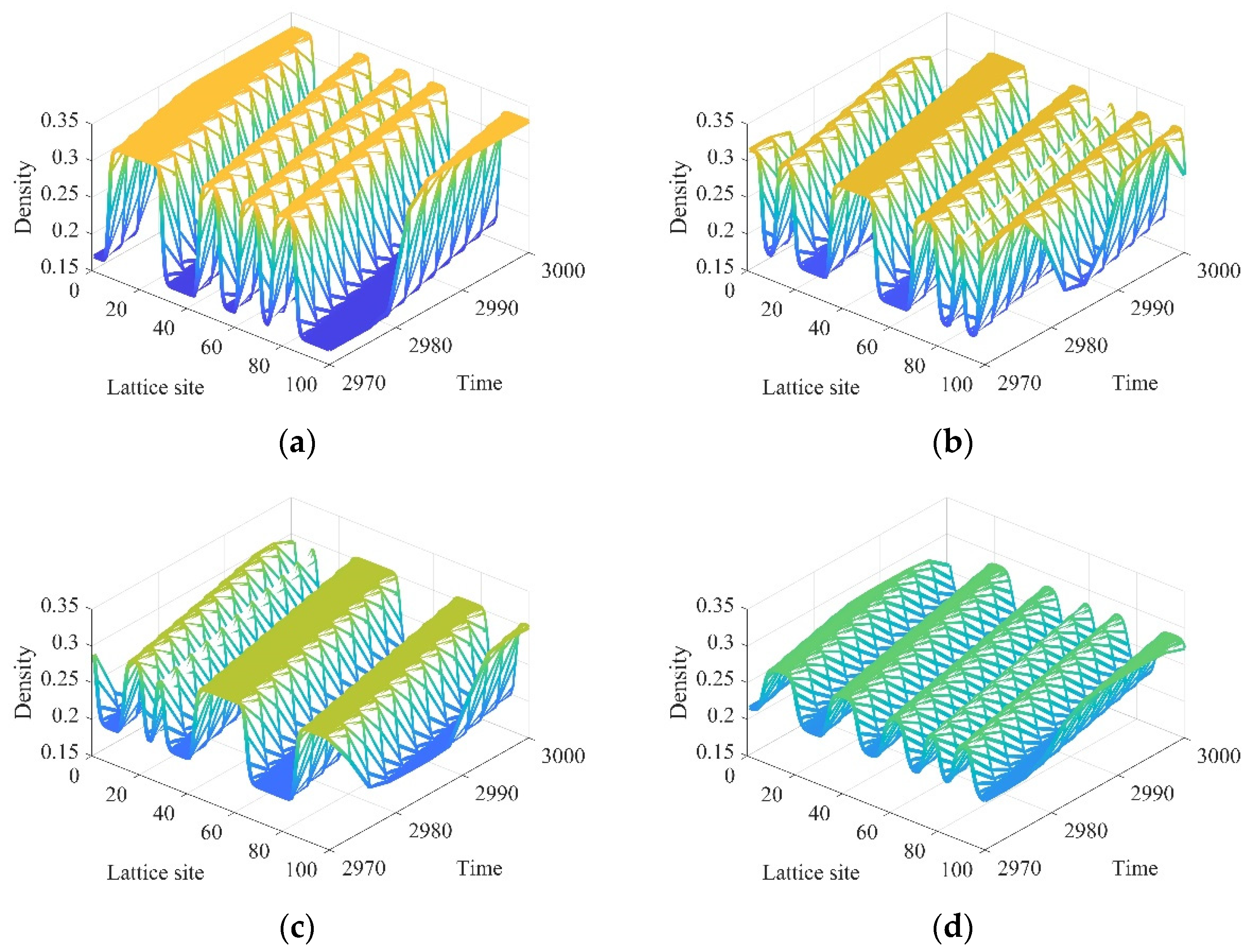
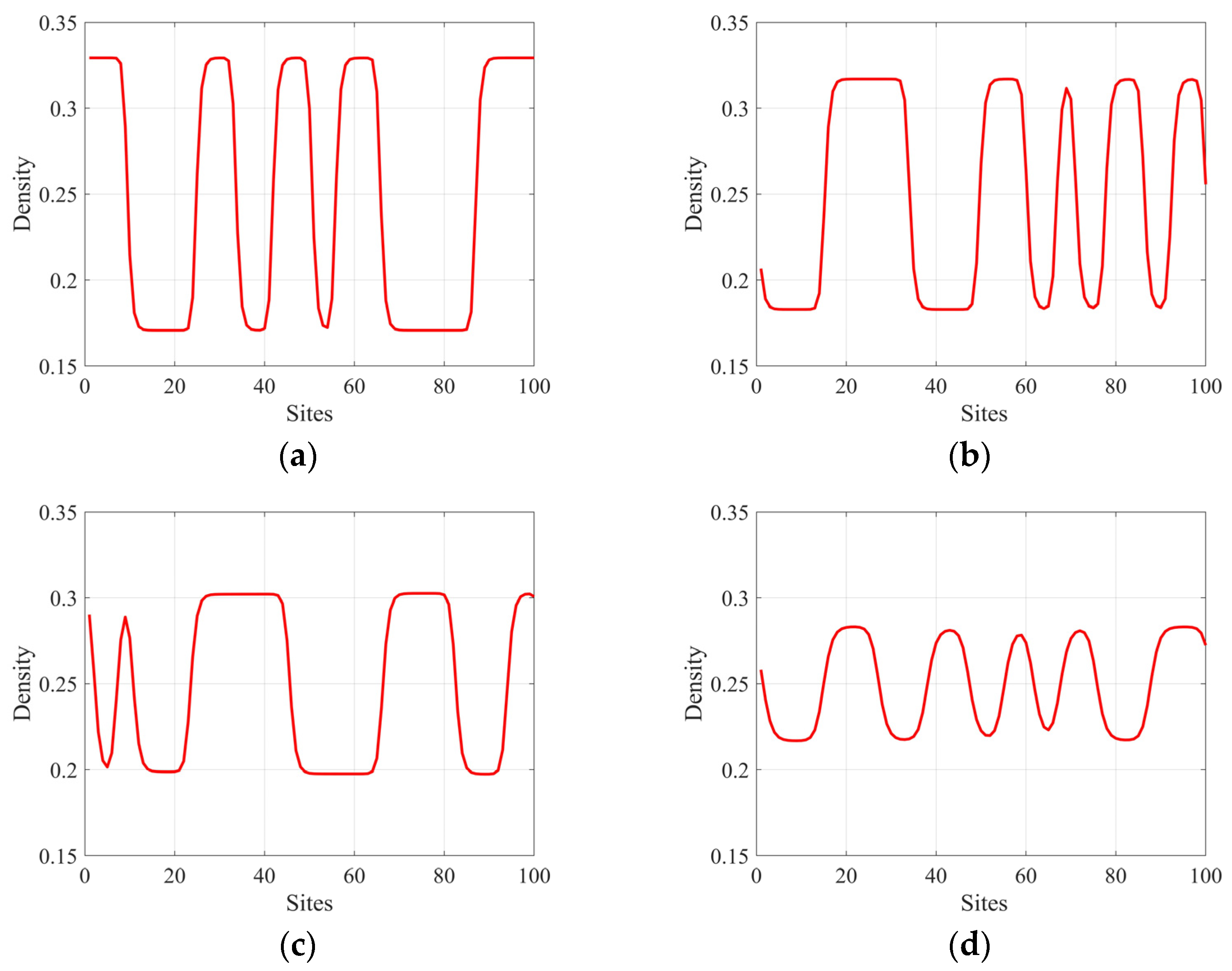
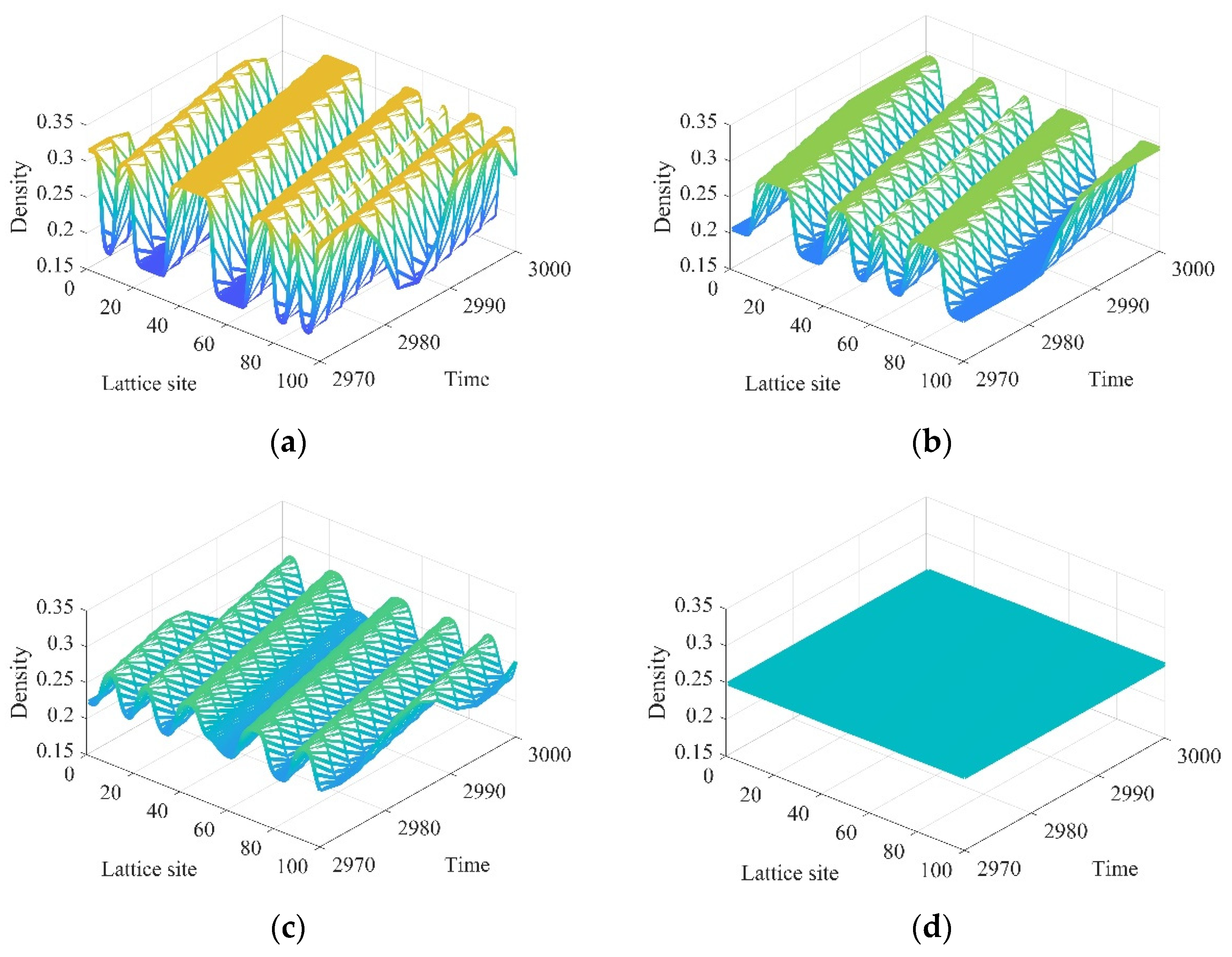
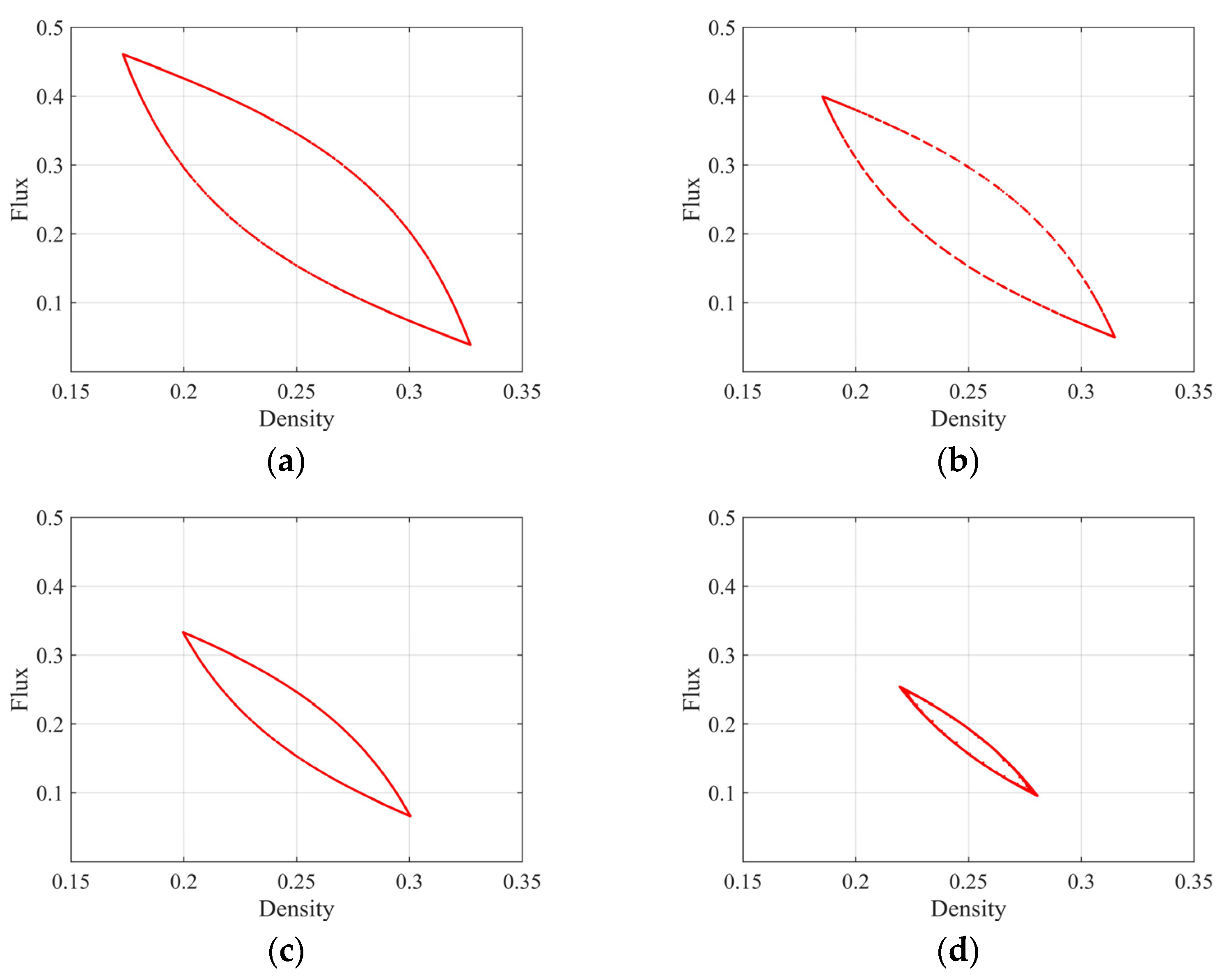
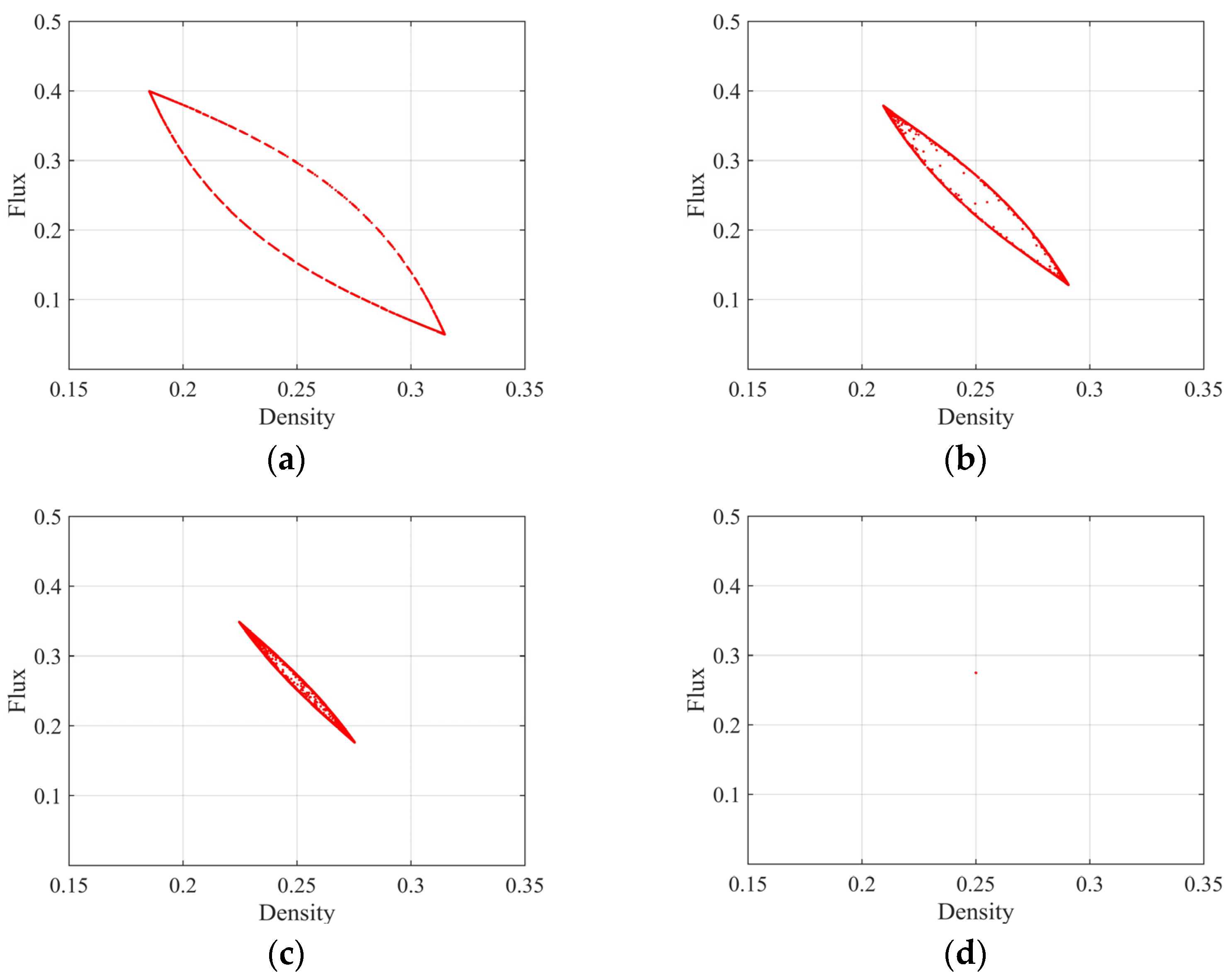
4. Results of Numerical Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, C.; Wei, H.; He, R. Distribution path robust optimization of electric vehicle with multiple distribution centers. PLoS ONE 2018, 13, e0193789. [Google Scholar]
- Ma, C.; Wei, H.; Pan, F. Road screening and distribution route multi-objective robust optimization for hazardous materials based on neural network and genetic algorithm. PLoS ONE 2018, 13, e0198931. [Google Scholar]
- Ma, C.; He, R.; Zhang, W. Path optimization of taxi carpooling. PLoS ONE 2018, 13, e0203221. [Google Scholar]
- Ma, C.; Wei, H.; Wang, A. Developing a coordinated signal control system for urban ring road under the vehicle-infrastructure connected environment. IEEE Access 2018, 6, 52471–52478. [Google Scholar] [CrossRef]
- Tang, T.; Luo, X.; Zhang, J.; Chen, L. Modeling electric bicycle’s lane-changing and retrograde behaviors. Phys. A 2018, 490, 1377–1386. [Google Scholar] [CrossRef]
- Tang, T.; Zhang, J.; Liu, K. A speed guidance model accounting for the driver’s bounded rationality at a signalized intersection. Phys. A 2017, 473, 45–52. [Google Scholar] [CrossRef]
- Wu, X.; Zhao, X.; Song, H. Effects of the prevision relative velocity on traffic dynamics in the ACC strategy. Phys. A 2019, 515, 192–198. [Google Scholar] [CrossRef]
- Tang, T.; Shi, W.; Huang, H. A route-based traffic flow model accounting for interruption factors. Phys. A 2019, 514, 767–785. [Google Scholar] [CrossRef]
- Guo, Y.; Xue, Y.; Shi, Y. Mean-field velocity difference model considering the average effect of multi-vehicle interaction. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 553–564. [Google Scholar] [CrossRef]
- Zhu, W.; Jun, D.; Zhang, L. A compound compensation method for car-following model. Commun. Nonlinear Sci. Numer. Simul. 2016, 39, 427–441. [Google Scholar] [CrossRef]
- Bando, M.; Hasebe, K.; Nakayama, A. Dynamical model of traffic congestion and numerical simulation. Phys. Rev. E 1995, 51, 1035–1042. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Zhang, L. Analysis of car-following model with cascade compensation strategy. Phys. A 2016, 449, 265–274. [Google Scholar] [CrossRef]
- Zhu, W.; Zhang, H. Analysis of mixed traffic flow with human-driving and autonomous cars based on car-following model. Phys. A 2018, 496, 274–285. [Google Scholar] [CrossRef]
- Wang, J.; Sun, F.; Ge, H. Effect of the driver’s desire for smooth driving on the car-following model. Phys. A 2018, 512, 96–108. [Google Scholar] [CrossRef]
- Zhu, W.; Zhang, L. A new car-following model for autonomous vehicles flow with mean expected velocity field. Phys. A 2018, 492, 2154–2165. [Google Scholar]
- Sun, Y.; Ge, H.; Cheng, R. An extended car-following model under V2V communication environment and its delayed-feedback control. Phys. A 2018, 508, 349–358. [Google Scholar] [CrossRef]
- Sun, Y.; Ge, H.; Cheng, R. An extended car-following model considering drivers memory and average speed of preceding vehicles with control strategy. Phys. A 2019, 521, 752–761. [Google Scholar] [CrossRef]
- Wang, T.; Cheng, R.; Ge, H. An extended two-lane lattice hydrodynamic model for traffic flow on curved road with passing. Phys. A 2019, 533, 121915. [Google Scholar] [CrossRef]
- Ou, H.; Tang, T. An extended two-lane car-following model accounting for inter-vehicle communication. Phys. A 2018, 495, 260–268. [Google Scholar] [CrossRef]
- Xin, Q.; Yang, N.; Fu, R. Impacts analysis of car following models considering variable vehicular gap policies. Phys. A 2018, 501, 338–355. [Google Scholar] [CrossRef]
- Tang, T.; Rui, Y.; Zhang, J.; Shang, H. A cellular automation model accounting for bicycle’s group behavior. Phys. A 2018, 492, 1782–1797. [Google Scholar] [CrossRef]
- Xue, Y.; Dong, L.; Dai, S. An improved one-dimensional cellular automaton model of traffic flow and the effect of deceleration probability. Acta Phys. Sin. 2001, 50, 445–449. [Google Scholar] [CrossRef]
- Gao, K.; Jiang, R.; Hu, S.; Wang, B.; Wu, Q. Cellular-automaton model with velocity adaptation in the framework of Kerner’s three-phase traffic theory. Phys. Rev. E 2007, 76, 026105. [Google Scholar] [CrossRef] [PubMed]
- Cheng, R.; Ge, H.; Wang, J. The nonlinear analysis for a new continuum model considering anticipation and traffic jerk effect. Appl. Math. Comput. 2018, 332, 493–505. [Google Scholar]
- Cheng, R.; Ge, H.; Wang, J. KdV-Burgers equation in a new continuum model based on full velocity difference model considering anticipation effect. Phys. A 2017, 481, 52–59. [Google Scholar] [CrossRef]
- Cheng, R.; Ge, H.; Wang, J. An extended continuum model accounting for the driver’s timid and aggressive attributions. Phys. Lett. A 2017, 381, 1302–1312. [Google Scholar] [CrossRef]
- Zhai, Q.; Ge, H.; Cheng, R. An extended continuum model considering optimal velocity change with memory and numerical tests. Phys. A 2018, 490, 774–785. [Google Scholar]
- Cheng, R.; Wang, Y. An extended lattice hydrodynamic model considering the delayed feedback control on a curved road. Phys. A 2019, 513, 510–517. [Google Scholar] [CrossRef]
- Kaur, R.; Sharma, S. Modeling and simulation of driver’s anticipation effect in a two lane system on curved road with slope. Phys. A 2018, 499, 110–120. [Google Scholar] [CrossRef]
- Jiang, C.; Cheng, R.; Ge, H. Mean-field flow difference model with consideration of on-ramp and off-ramp. Phys. A 2019, 513, 465–476. [Google Scholar] [CrossRef]
- Jiang, C.; Cheng, R.; Ge, H. An improved lattice hydrodynamic model considering the “backward looking” effect and the traffic interruption probability. Nonlinear Dyn. 2017, 91, 777–784. [Google Scholar] [CrossRef]
- Kaur, R.; Sharma, S. Analyses of a heterogeneous lattice hydrodynamic model with low and high-sensitivity vehicles. Phys. Lett. A 2018, 382, 1449–1455. [Google Scholar] [CrossRef]
- Peng, G.; Kuang, H.; Qing, L. A new lattice model of traffic flow considering driver’s anticipation effect of the traffic interruption. Phys. A 2018, 507, 374–380. [Google Scholar] [CrossRef]
- Wang, Q.; Ge, H. An improved lattice hydrodynamic model accounting for the effect of “backward looking” and flow integral. Phys. A 2019, 513, 438–446. [Google Scholar] [CrossRef]
- Redhu, P.; Gupta, A. Delayed-feedback control in a lattice hydrodynamic model. Commun. Nonlinear Sci. Numer. Simul. 2015, 27, 263–270. [Google Scholar] [CrossRef]
- Qin, S.; Ge, H.; Cheng, R. A new lattice hydrodynamic model based on control method considering the flux change rate and delay feedback signal. Phys. Lett. A 2018, 382, 482–488. [Google Scholar] [CrossRef]
- Chang, Y.; He, Z.; Cheng, R. An extended lattice hydrodynamic model considering the driver’s sensory memory and delayed-feedback control. Phys. A 2019, 514, 522–532. [Google Scholar] [CrossRef]
- Peng, G.; Zhao, H.; Liu, X. The impact of self-stabilization on traffic stability considering the current lattice’s historic flux for two-lane freeway. Phys. A 2019, 515, 31–37. [Google Scholar] [CrossRef]
- Nagatani, T. Modified KdV equation for jamming transition in the continuum models of traffic. Phys. A 1998, 261, 599–607. [Google Scholar] [CrossRef]
- Tian, J.; Yuan, Z.; Jia, B.; Li, M.; Jiang, G. The stabilization effect of the density difference in the modified lattice hydrodynamic model of traffic flow. Phys. A 2012, 391, 4476–4482. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, G.; Li, W.; Gu, T.; Zhou, D. Lattice hydrodynamic modeling of traffic flow with consideration of historical current integration effect. Phys. A 2018, 503, 1204–1211. [Google Scholar] [CrossRef]
- Sharma, S. Modeling and analyses of drivers characteristics in a traffic system with passing. Nonlinear Dyn. 2016, 86, 2093–2104. [Google Scholar] [CrossRef]
- Wang, J.; Sun, F.; Ge, H. An improved lattice hydrodynamic model considering the driver’s desire of driving smoothly. Phys. A 2019, 515, 119–129. [Google Scholar] [CrossRef]
- Kwon, S.; Kim, D.; Lee, S. Deisgn criteria of wind barriers for traffic. part 1: Wind barrier performance. Wind Struct. 2011, 14, 55–70. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Shi, Z.; Ai, W. An improved car-following model accounting for impact of strong wind. Math. Probl. Eng. 2017, 2017, 4936490. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Li, C.; Tang, X.; Tian, C. Effect of optimal estimation of flux difference information on the lattice traffic flow model. Phys. A 2016, 463, 394–399. [Google Scholar] [CrossRef]
- Peng, G.; Yang, S.; Xia, D.; Li, X. A novel lattice hydrodynamic model considering the optimal estimation of flux difference effect on two-lane highway. Phys. A 2018, 506, 929–937. [Google Scholar] [CrossRef]
- Ge, H.; Cui, Y.; Zhu, K.; Cheng, R. The control method for the lattice hydrodynamic model. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 903–908. [Google Scholar] [CrossRef]
- Zhu, C.; Zhong, S.; Li, G.; Ma, S. New control strategy for the lattice hydrodynamic model of traffic flow. Phys. A 2017, 468, 445–453. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Wang, Y. Impact of Strong Wind and Optimal Estimation of Flux Difference Integral in a Lattice Hydrodynamic Model. Mathematics 2021, 9, 2897. https://doi.org/10.3390/math9222897
Liu H, Wang Y. Impact of Strong Wind and Optimal Estimation of Flux Difference Integral in a Lattice Hydrodynamic Model. Mathematics. 2021; 9(22):2897. https://doi.org/10.3390/math9222897
Chicago/Turabian StyleLiu, Huimin, and Yuhong Wang. 2021. "Impact of Strong Wind and Optimal Estimation of Flux Difference Integral in a Lattice Hydrodynamic Model" Mathematics 9, no. 22: 2897. https://doi.org/10.3390/math9222897
APA StyleLiu, H., & Wang, Y. (2021). Impact of Strong Wind and Optimal Estimation of Flux Difference Integral in a Lattice Hydrodynamic Model. Mathematics, 9(22), 2897. https://doi.org/10.3390/math9222897






