Geary’s c and Spectral Graph Theory

Abstract

Spatial autocorrelation, of which Geary’s c has traditionally been a popular measure, is fundamental to spatial science. This paper provides a new perspective on Geary’s c. We discuss this using concepts from spectral graph theory/linear algebraic graph theory. More precisely, we provide three types of representations for it: (a) graph Laplacian representation, (b) graph Fourier transform representation, and (c) Pearson’s correlation coefficient representation. Subsequently, we illustrate that the spatial autocorrelation measured by Geary’s c is positive (resp. negative) if spatially smoother (resp. less smooth) graph Laplacian eigenvectors are dominant. Finally, based on our analysis, we provide a recommendation for applied studies.

1. Introduction

Spatial autocorrelation is fundamental to spatial science (Getis [1]). This is because it describes the similarity between signals on adjacent vertices. Strong positive (resp. negative) spatial autocorrelation occurs when most signals on adjacent vertices take similar (resp. dissimilar) values. If such clear tendencies do not exist, spatial autocorrelation is weak. Geary’s [2] c, which is a spatial generalization of the von Neumann [3] ratio, has traditionally been a popular measure of spatial autocorrelation. There exists

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{positive}\mathrm{spatial}\mathrm{autocorrelation}\hfill & \mathrm{if}c<1,\hfill \\ \mathrm{no}\mathrm{spatial}\mathrm{autocorrelation}\hfill & \mathrm{if}c=1,\hfill \\ \mathrm{negative}\mathrm{spatial}\mathrm{autocorrelation}\hfill & \mathrm{if}c>1.\hfill \end{array}\right.\end{array}$$

See, e.g., de Jong et al. [4] (Equation (6)). Herein, we provide a new perspective on Geary’s c. We discuss this using concepts from spectral graph theory/linear algebraic graph theory and, based on our analysis, provide a recommendation for applied studies.

To present our contributions more precisely, let us clarify the graph considered herein. Let $G=(V,E)$, where $V=\{v_1,\dots ,v_n\}$, denote an undirected graph without loops and multiple edges. We assume that n (the number of vertices) and m (the number of edges) are such that $2\le n<\infty$ and $m\ge 1$, respectively. Then, m satisfies $1\le m\le \frac{n(n-1)}{2}\left(=\left(\genfrac{}{}{0pt}{}{n}{2}\right)\right)<\infty$. For $i,j=1,\dots ,n$, let

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{w}_{ij}>0\hfill & \mathrm{if}\{v_i,v_j\}\in E,\hfill \\ w_{ij}=0\hfill & \mathrm{if}\{v_i,v_j\}\notin E,\hfill \end{array}\right.\end{array}$$

(1)

and $\mathit{W}=[w_{ij}]\in {\mathbb{R}}^{n\times n}$. Then, for $i,j=1,\dots ,n$, $w_{ij}\ge 0$, $w_{ij}=w_{ji}$, $w_{ij}=0$ if $i=j$, and ${\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{ij}>0$. Accordingly, $\mathit{W}$ is a non-negative, symmetric, hollow, and nonzero matrix.

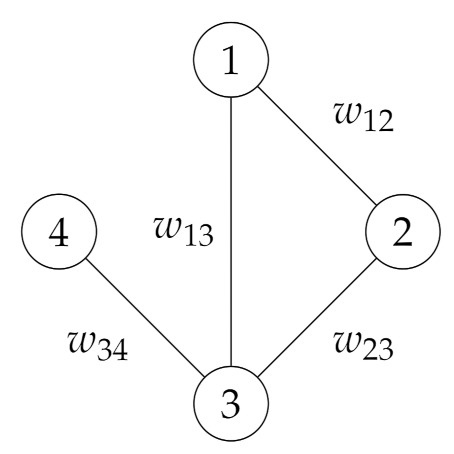
Example 1.

As an example of $G=(V,E)$, consider the graph $G_{†}=(V_{†},E_{†})$ such that $V_{†}=\{1,2,3,4\}$ and $E_{†}=\{\{1,2\},\{1,3\},\{2,3\},\{3,4\}\}$. See Figure 1, which depicts $G_{†}=(V_{†},E_{†})$. In this case, given that $\{1,4\}$ and $\{2,4\}$ do not belong to E, the corresponding $\mathit{W}$, denoted by ${\mathit{W}}_{†}$, is

$$\begin{array}{c}\hfill {\mathit{W}}_{†}=\left[\begin{array}{cccc}0& w_{12}& w_{13}& 0\\ w_{12}& 0& w_{23}& 0\\ w_{13}& w_{23}& 0& w_{34}\\ 0& 0& w_{34}& 0\end{array}\right]\in {\mathbb{R}}^{4\times 4},\end{array}$$

(2)

which is a non-negative, symmetric, hollow, and nonzero matrix.

Let $y_i$ denote the observation (signal) on the vertex i for $i=1,\dots ,n$ such that ${\sum }_{i=1}^n{(y_i-\overline{y})}^2>0$, where $\overline{y}=\frac{1}{n}{\sum }_{i=1}^n{y}_i$. Following Cliff and Ord [5,6,7,8], Geary’s c is defined as

$$\begin{array}{c}\hfill c=\frac{n-1}{2\Omega }\frac{{\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{ij}{(y_i-y_j)}^2}{{\sum }_{i=1}^n{(y_i-\overline{y})}^2},\end{array}$$

(3)

where $\Omega$ denotes the sum of all $w_{ij}$ for $i,j=1,\dots ,n$, i.e., $\Omega ={\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{ij}$, which is positive by assumption. Note that, as stated, Geary’s c is a spatial generalization of the von Neumann [3] ratio:

$$\begin{array}{c}\hfill \eta =\frac{n}{n-1}\frac{{\sum }_{i=2}^n{(y_i-y_{i-1})}^2}{{\sum }_{i=1}^n{(y_i-\overline{y})}^2}.\end{array}$$

(4)

We briefly describe this in the Appendix A.14.

Let $\mathit{D}=\mathsf{diag}(d_1,\dots ,d_n)$, where $d_i={\sum }_{j=1}^n{w}_{ij}$ for $i=1,\dots ,n$, and

$$\begin{array}{c}\hfill \mathit{L}=\mathit{D}-\mathit{W},\end{array}$$

(5)

which is referred to as graph Laplacian. By assumption, $\mathit{L}\in {\mathbb{R}}^{n\times n}$ is a symmetric matrix.

Example 2.

As an example of $\mathit{L}$, we show ${\mathit{L}}_{†}$, which denotes the graph Laplacian of $G_{†}=(V_{†},E_{†})$. That is,

$$\begin{array}{c}\hfill {\mathit{L}}_{†}=\left[\begin{array}{cccc}{w}_{12}+w_{13}& -w_{12}& -w_{13}& 0\\ -w_{12}& w_{12}+w_{23}& -w_{23}& 0\\ -w_{13}& -w_{23}& w_{13}+w_{23}+w_{34}& -w_{34}\\ 0& 0& -w_{34}& w_{34}\end{array}\right]\in {\mathbb{R}}^{4\times 4},\end{array}$$

which is a symmetric matrix.

As $\mathit{L}$ is a real symmetric matrix, it can be decomposed as

$$\begin{array}{c}\hfill \mathit{L}=\mathit{U}\Lambda {\mathit{U}}^{\top },\end{array}$$

(6)

where $\mathit{U}=[{\mathit{u}}_1,\dots ,{\mathit{u}}_n]\in {\mathbb{R}}^{n\times n}$ is an orthogonal matrix and $\Lambda =\mathsf{diag}({\lambda }_1,\dots ,{\lambda }_n)$ such that ${\lambda }_1\le \cdots \le {\lambda }_n$. Concerning the eigenvalues of $\mathit{L}$, we assume ${\lambda }_2<{\lambda }_n$.

Remark 1.

We note that by assuming ${\lambda }_2<{\lambda }_n$ we exclude the case such that ${\lambda }_2=\cdots ={\lambda }_n$. Then, it follows that

$$\begin{array}{c}\hfill (n-1){\lambda }_2<\sum _{i=2}^n{\lambda }_i<(n-1){\lambda }_n.\end{array}$$

(7)

We exclude it because in this case Geary’s c equals one for any $\mathit{y}$. For more details, see the Appendix A.1.

In spectral graph theory/linear algebraic graph theory, the following linear transformation:

$$\begin{array}{c}\hfill {\mathit{U}}^{\top }\mathit{y}={\left[{\mathit{u}}_1^{\top }\mathit{y},\dots ,{\mathit{u}}_n^{\top }\mathit{y}\right]}^{\top },\end{array}$$

(8)

where $\mathit{y}={[y_1,\dots ,y_n]}^{\top }$, is referred to as graph Fourier transform of $\mathit{y}$. In addition, ${\lambda }_i$ and ${\mathit{u}}_i$ for $i=1,\dots ,n$ are referred to as graph Laplacian eigenvalues and graph Laplacian eigenvectors, respectively (see Hammond et al. [9] and Shuman et al. [10]). Let

$$\begin{array}{c}\hfill \mathit{\alpha }={[{\alpha }_1,\dots ,{\alpha }_n]}^{\top }={\left[{\mathit{u}}_1^{\top }\mathit{y},\dots ,{\mathit{u}}_n^{\top }\mathit{y}\right]}^{\top }={\mathit{U}}^{\top }\mathit{y}.\end{array}$$

(9)

Then, given $\mathit{y}=\mathit{U}{\mathit{U}}^{\top }\mathit{y}=\mathit{U}\mathit{\alpha }$, $\mathit{y}$ can be represented as a linear combination of graph Laplacian eigenvectors, ${\mathit{u}}_1,\dots ,{\mathit{u}}_n$, as follows:

$$\begin{array}{c}\hfill \mathit{y}={\alpha }_1{\mathit{u}}_1+\cdots +{\alpha }_n{\mathit{u}}_n.\end{array}$$

(10)

Moreover, we have

$$\begin{array}{c}\hfill \sum _{i=1}^n{(y_i-\overline{y})}^2={\alpha }_2^2+\cdots +{\alpha }_n^2,\end{array}$$

(11)

which represents Parseval’s identity in the graph Fourier transform, see, e.g., Shuman et al. [11]. (Proof of (11) is provided in the Appendix A.2).

Remark 2.

(i) Harvey [12] (Equation (2.13)) represents Parseval’s identity in the Fourier representation of time series, which can be regarded as a special case of (11). See also Anderson [13] (Section 4.2.2). $\mathit{M}$ in Anderson [13] (Equations (14) and (21)) corresponds to $\mathit{U}$ in (6) for the case in which $\mathit{L}$ equals $A_0$ in Strang [14] (p. 136). (ii) The discrete cosine transform developed by Ahmed et al. [15] is an example of graph Fourier transform. For more details, see Appendix A.14.

Let $\mathit{z}\in {\mathbb{R}}^n$ denote the vector of the standard scores of $\mathit{y}$:

$$\begin{array}{c}\hfill \mathit{z}={[z_1,\dots ,z_n]}^{\top }={\left[\frac{y_1-\overline{y}}{s},\dots ,\frac{y_n-\overline{y}}{s}\right]}^{\top },\end{array}$$

(12)

where s denotes the sample standard deviation of $\mathit{y}$, i.e., the positive square root of $s^2=\frac{1}{n-1}{\sum }_{i=1}^n{(y_i-\overline{y})}^2$, and denote the graph Fourier transform of $\mathit{z}$ by $\mathit{\beta }$:

$$\begin{array}{c}\hfill \mathit{\beta }={[{\beta }_1,\dots ,{\beta }_n]}^{\top }={[{\mathit{u}}_1^{\top }\mathit{z},\cdots ,{\mathit{u}}_n^{\top }\mathit{z}]}^{\top }={\mathit{U}}^{\top }\mathit{z}.\end{array}$$

(13)

Now, we are ready to state our contributions. As stated, this paper reconsiders Geary’s c using concepts from spectral graph theory. Our contributions herein are twofold.

• We present three types of representations for it. As the first type of representation, we give two matrix form representations that use graph Laplacian $\mathit{L}$. As the second type of representation, we express it using ${\alpha }_2^2,\dots ,{\alpha }_n^2$ and ${\beta }_2^2,\dots ,{\beta }_n^2$. Recall that they are the graph Fourier transform of $\mathit{y}$ and $\mathit{z}$, respectively. As the third type of representation, we show its expression using squared Pearson’s correlation coefficients between ${\mathit{u}}_i$ and $\mathit{y}$ for $i=2,\dots ,n$.
• We illustrate that the spatial autocorrelation measured by Geary’s c is positive (resp. negative) if spatially smoother (resp. less smooth) graph Laplacian eigenvectors are dominant. Here, we note that ${\mathit{u}}_i$ is spatially smoother than ${\mathit{u}}_{i+1}$ for $i=1,\dots ,n-1$.

The organization of the paper is as follows. Section 2 fixes some notations and presents key preliminary results for $\mathit{L}$ in (5). Section 3 and Section 4 present the contributions stated above in order. Section 5 concludes the paper. In Section 5, we provide a recommendation for applied studies.

2. Preliminaries

2.1. Some Notations

Let $\mathit{\iota }={[1,\dots ,1]}^{\top }\in {\mathbb{R}}^n$, ${\mathit{I}}_n$ be the identity matrix of order n, ${\mathit{e}}_i$ denote the ith column of ${\mathit{I}}_n$ for $i=1,\dots ,n$, i.e., ${\mathit{I}}_n=[{\mathit{e}}_1,\dots ,{\mathit{e}}_n]$, and ${\mathit{Q}}_{\iota }={\mathit{I}}_n-\mathit{\iota }{({\mathit{\iota }}^{\top }\mathit{\iota })}^{-1}{\mathit{\iota }}^{\top }$. Note that ${\mathit{Q}}_{\iota }$ is the orthogonal projection matrix to the orthogonal complement of the space spanned by $\mathit{\iota }$. For a vector $\mathit{\gamma }={[{\gamma }_1,\dots ,{\gamma }_n]}^{\top }$, ${\parallel \mathit{\gamma }\parallel }^2={\mathit{\gamma }}^{\top }\mathit{\gamma }={\gamma }_1^2+\cdots +{\gamma }_n^2$. Let ${\mathit{\alpha }}_2={[{\alpha }_2,\dots ,{\alpha }_n]}^{\top }$, ${\Lambda }_2=\mathsf{diag}({\lambda }_2,\dots ,{\lambda }_n)$, and ${\mathit{U}}_2=[{\mathit{u}}_2,\dots ,{\mathit{u}}_n]$. For a vector $\mathit{\upsilon }\in {\mathbb{R}}^n$, denote Pearson’s correlation coefficient between ${\mathit{u}}_i$ and $\mathit{\upsilon }$ by $\rho ({\mathit{u}}_i,\mathit{\upsilon })$:

$$\begin{array}{c}\hfill \rho ({\mathit{u}}_i,\mathit{\upsilon })=\frac{{\mathit{u}}_i^{\top }{\mathit{Q}}_{\iota }\mathit{\upsilon }}{\sqrt{{\mathit{u}}_i^{\top }{\mathit{Q}}_{\iota }{\mathit{u}}_i}\sqrt{{\mathit{\upsilon }}^{\top }{\mathit{Q}}_{\iota }\mathit{\upsilon }}},i=2,\dots ,n.\end{array}$$

2.2. Key Preliminary Results for L

In this section, we provide key preliminary results for $\mathit{L}$ in (5).

First, given that $\mathit{W}$ is a symmetric matrix, $\mathit{L}$ satisfies

$$\begin{array}{c}\hfill {\mathit{y}}^{\top }\mathit{L}\mathit{y}=\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{w}_{ij}{(y_i-y_j)}^2.\end{array}$$

(14)

(Proof of (14) is provided in the Appendix A.3). Given that $w_{ij}\ge 0$ for $i,j=1,\dots ,n$, (14) leads to ${\mathit{y}}^{\top }\mathit{L}\mathit{y}\ge 0$, from which we have ${\lambda }_i\ge 0$ for $i=1,\dots ,n$. (See also (18) and (19)).

In addition, it follows that

$$\begin{array}{c}\hfill \mathit{L}\mathit{\iota }=\mathit{D}\mathit{\iota }-\mathit{W}\mathit{\iota }={[d_1,\dots ,d_n]}^{\top }-{[d_1,\dots ,d_n]}^{\top }=\mathbf{0},\end{array}$$

(15)

which implies that $\left(0,\frac{1}{\sqrt{n}}\mathit{\iota }\right)$ is an eigenpair of $\mathit{L}$. Combining these results, we obtain ${\lambda }_1=0$, ${\mathit{u}}_1=\frac{1}{\sqrt{n}}\mathit{\iota }$, and

$$\begin{array}{c}\hfill {\mathit{Q}}_{\iota }{\mathit{u}}_i={\mathit{u}}_i-\mathit{\iota }{({\mathit{\iota }}^{\top }\mathit{\iota })}^{-1}{\mathit{\iota }}^{\top }{\mathit{u}}_i={\mathit{u}}_i,i=2,\dots ,n.\end{array}$$

(16)

We note that (16) is natural because ${\mathit{u}}_2,\dots ,{\mathit{u}}_n$ belong to the orthogonal complement of the space spanned by $\mathit{\iota }$.

Moreover, given that $\mathit{L}$ is a symmetric matrix such that $\mathit{L}\mathit{\iota }=\mathbf{0}$, it follows that ${(\mathit{L}\mathit{\iota })}^{\top }={\mathit{\iota }}^{\top }{\mathit{L}}^{\top }={\mathit{\iota }}^{\top }\mathit{L}=\mathbf{0}$, which leads to

$$\begin{array}{c}\hfill {\mathit{Q}}_{\iota }\mathit{L}{\mathit{Q}}_{\iota }=\mathit{L}.\end{array}$$

(17)

Finally, we have the following result.

Lemma 1.

Let ${\mathit{b}}_{ij}=\sqrt{w_{ij}}({\mathit{e}}_i-{\mathit{e}}_j)\in {\mathbb{R}}^n$ for $i,j=1,\dots ,n$ and $\mathit{B}$ be an $n\times \frac{n(n-1)}{2}$ matrix such that $\mathit{B}=[{\mathit{B}}_1,\dots ,{\mathit{B}}_{n-1}]$, where ${\mathit{B}}_k=[{\mathit{b}}_{k(k+1)},\dots ,{\mathit{b}}_{kn}]\in {\mathbb{R}}^{n\times (n-k)}$ for $k=1,\dots ,n-1$. (Observe that ${\sum }_{k=1}^{n-1}(n-k)=n(n-1)-\frac{n(n-1)}{2}=\frac{n(n-1)}{2}\left(=\left(\genfrac{}{}{0pt}{}{n}{2}\right)\right)$). Then, it follows that

$$\begin{array}{c}{\mathit{f}}^{\top }\mathit{L}\mathit{f}={\parallel {\mathit{B}}^{\top }\mathit{f}\parallel }^2,\end{array}$$

(18)

$$\begin{array}{c}\parallel {\mathit{B}}^{\top }{\mathit{u}}_i{\parallel }^2={\lambda }_i,i=1,\dots ,n,\end{array}$$

(19)

where $\mathit{f}$ denotes an n-dimensional column vector.

Proof. 

See the Appendix A.4. □

Example 3

(Example of $\mathit{B}$). Denote $\mathit{B}$ corresponding to $G_{†}=(V_{†},E_{†})$ by ${\mathit{B}}_{†}$. Given $n=4$, ${\mathit{B}}_{†}$ is a $4\times \frac{4·3}{2}$ matrix such that

$$\begin{array}{cc}\hfill {\mathit{B}}_{†}& =[{\mathit{B}}_1,{\mathit{B}}_2,{\mathit{B}}_3]=[\underset{{\mathit{B}}_1}{\underbrace{{\mathit{b}}_{12},{\mathit{b}}_{13},{\mathit{b}}_{14}}},\underset{{\mathit{B}}_2}{\underbrace{{\mathit{b}}_{23},{\mathit{b}}_{24}}},\underset{{\mathit{B}}_3}{\underbrace{{\mathit{b}}_{34}}}]\hfill \\ \hfill & =[\sqrt{w_{12}}({\mathit{e}}_1-{\mathit{e}}_2),\sqrt{w_{13}}({\mathit{e}}_1-{\mathit{e}}_3),\mathbf{0},\sqrt{w_{23}}({\mathit{e}}_2-{\mathit{e}}_3),\mathbf{0},\sqrt{w_{34}}({\mathit{e}}_3-{\mathit{e}}_4)]\hfill \\ \hfill & =\left[\begin{array}{cccccc}\sqrt{w_{12}}& \sqrt{w_{13}}& 0& 0& 0& 0\\ -\sqrt{w_{12}}& 0& 0& \sqrt{w_{23}}& 0& 0\\ 0& -\sqrt{w_{13}}& 0& -\sqrt{w_{23}}& 0& \sqrt{w_{34}}\\ 0& 0& 0& 0& 0& -\sqrt{w_{34}}\end{array}\right],\hfill \end{array}$$

(20)

and thus we have

$$\begin{array}{c}\hfill {\mathit{B}}_{†}^{\top }{\mathit{u}}_i=\left[\begin{array}{c}\sqrt{w_{12}}({\mathit{e}}_1^{\top }-{\mathit{e}}_2^{\top }){\mathit{u}}_i\\ \sqrt{w_{13}}({\mathit{e}}_1^{\top }-{\mathit{e}}_3^{\top }){\mathit{u}}_i\\ 0\\ \sqrt{w_{23}}({\mathit{e}}_2^{\top }-{\mathit{e}}_3^{\top }){\mathit{u}}_i\\ 0\\ \sqrt{w_{34}}({\mathit{e}}_3^{\top }-{\mathit{e}}_4^{\top }){\mathit{u}}_i\end{array}\right]=\left[\begin{array}{c}\sqrt{w_{12}}(u_{i,1}-u_{i,2})\\ \sqrt{w_{13}}(u_{i,1}-u_{i,3})\\ 0\\ \sqrt{w_{23}}(u_{i,2}-u_{i,3})\\ 0\\ \sqrt{w_{34}}(u_{i,3}-u_{i,4})\end{array}\right],\end{array}$$

(21)

where ${\mathit{u}}_i={[u_{i,1},\dots ,u_{i,n}]}^{\top }$ for $i=1,\dots ,n$, and

$$\begin{array}{ccc}\parallel {\mathit{B}}_{†}^{\top }{\mathit{u}}_i{\parallel }^2& =& w_{12}{(u_{i,1}-u_{i,2})}^2+w_{13}{(u_{i,1}-u_{i,3})}^2\hfill \\ & & +w_{23}{(u_{i,2}-u_{i,3})}^2+w_{34}{(u_{i,3}-u_{i,4})}^2.\end{array}$$

Given $0={\lambda }_1\le \cdots \le {\lambda }_n$ and ${\lambda }_2<{\lambda }_n$, from Lemma 1, we immediately have the following inequalities:

$$\begin{array}{c}0=\parallel {\mathit{B}}^{\top }{\mathit{u}}_1{\parallel }^2\le \cdots \le {\parallel {\mathit{B}}^{\top }{\mathit{u}}_n\parallel }^2,\end{array}$$

(22)

$$\begin{array}{c}\parallel {\mathit{B}}^{\top }{\mathit{u}}_2{\parallel }^2<{\parallel {\mathit{B}}^{\top }{\mathit{u}}_n\parallel }^2.\end{array}$$

(23)

As illustrated in (21), ${\mathit{B}}^{\top }$ defined in Lemma 1 may be regarded as a spatial differencing matrix. Thus, (22) implies that the ith graph Laplacian eigenvector, ${\mathit{u}}_i$, is spatially smoother than the $(i+1)$th graph Laplacian eigenvector, ${\mathit{u}}_{i+1}$, for $i=1,\dots ,n-1$.

Remark 3.

(i) ${\mathit{f}}^{\top }\mathit{L}\mathit{f}$ in (18) is referred to as graph Laplacian quadratic form of $\mathit{f}$. In machine learning and statistics, use of graph Laplacian regularized filtering is becoming popular, see, e.g., Shuman et al. [10], Dong et al. [16], and Ricaud et al. [17]. (ii) As illustrated in (20), if $\{v_i,v_j\}\notin E$, then $w_{ij}=0$, from which the corresponding column of $\mathit{B}$ is $\mathbf{0}$.

We note that $\left(\frac{n(n-1)}{2}-m\right)$ columns of $\mathit{B}$ are equal to $\mathbf{0}$. By removing such columns from $\mathit{B}$, we can obtain an incidence matrix of $G=(V,E)$, which has n rows and m columns, see Bapat [18] and Gallier [19]. Accordingly, the following matrix is an incidence matrix of $G_{†}=(V_{†},E_{†})$:

$$\begin{array}{c}\hfill \left[\begin{array}{cccc}\sqrt{w_{12}}& \sqrt{w_{13}}& 0& 0\\ -\sqrt{w_{12}}& 0& \sqrt{w_{23}}& 0\\ 0& -\sqrt{w_{13}}& -\sqrt{w_{23}}& \sqrt{w_{34}}\\ 0& 0& 0& -\sqrt{w_{34}}\end{array}\right]\in {\mathbb{R}}^{|V_{†}|\times |E_{†}|}.\end{array}$$

3. Three Types of Representations for Geary’s $\mathit{c}$

In this section, we present three types of representations for Geary’s c: In Section 3.1, we show that it can be represented using $\mathit{L}$. In Section 3.2, we show that it can be expressed using ${\alpha }_2^2,\dots ,{\alpha }_n^2$ and ${\beta }_2^2,\dots ,{\beta }_n^2$. In Section 3.3, we show that it can be expressed using ${\rho }^2({\mathit{u}}_i,\mathit{y})$ for $i=2,\dots ,n$. Subsequently, in Section 3.4, we clarify the relationship between ${\alpha }_i^2$, ${\beta }_i^2$, and ${\rho }^2({\mathit{u}}_i,\mathit{y})$ for $i=2,\dots ,n$.

3.1. Graph Laplacian Representation

Geary’s c in (3) can be expressed in matrix notation as follows.

Proposition 1.

(i) Geary’s c can be represented using $\mathit{L}$ as

$$\begin{array}{c}\hfill c=\frac{n-1}{\Omega }\frac{{\mathit{y}}^{\top }\mathit{L}\mathit{y}}{{\mathit{y}}^{\top }{\mathit{Q}}_{\iota }\mathit{y}}.\end{array}$$

(24)

(ii) Geary’s c can also be represented using $\mathit{L}$ very succinctly as

$$\begin{array}{c}\hfill c=\frac{1}{\Omega }{\mathit{z}}^{\top }\mathit{L}\mathit{z}.\end{array}$$

(25)

Proof. 

See the Appendix A.5. □

Remark 4.

(i) (24) corresponds to de Jong et al. [4] (Equation (22)). The matrix $\mathit{B}$ in de Jong et al. [4] is $2\mathit{L}$ in our notation. It is notable that de Jong et al. [4] derived this. (ii) (24) also corresponds to Lebichot and Saerens [20] (Equation (7)). Here, we point out that 2 in the equation should be removed.

3.2. Graph Fourier Transform Representation

From (11), we have

$$\begin{array}{c}\hfill {\mathit{y}}^{\top }{\mathit{Q}}_{\iota }\mathit{y}=\sum _{i=1}^n{(y_i-\overline{y})}^2=\sum _{i=2}^n{\alpha }_i^2.\end{array}$$

(26)

In addition, given ${\lambda }_1=0$, we have

$$\begin{array}{c}\hfill {\mathit{y}}^{\top }\mathit{L}\mathit{y}={\mathit{y}}^{\top }\mathit{U}\Lambda {\mathit{U}}^{\top }\mathit{y}={\mathit{\alpha }}^{\top }\Lambda \mathit{\alpha }=\sum _{i=2}^n{\lambda }_i{\alpha }_i^2.\end{array}$$

(27)

Substituting (26) and (27) into (24), it follows that

$$\begin{array}{c}\hfill c=\frac{n-1}{\Omega }\frac{{\mathit{y}}^{\top }\mathit{L}\mathit{y}}{{\mathit{y}}^{\top }{\mathit{Q}}_{\iota }\mathit{y}}=\frac{n-1}{\Omega }\frac{{\sum }_{i=2}^n{\lambda }_i{\alpha }_i^2}{{\sum }_{i=2}^n{\alpha }_i^2}.\end{array}$$

(28)

Likewise, Geary’s c can also be represented as

$$\begin{array}{c}\hfill c=\frac{1}{\Omega }{\mathit{z}}^{\top }\mathit{L}\mathit{z}=\frac{1}{\Omega }{\mathit{z}}^{\top }\mathit{U}\Lambda {\mathit{U}}^{\top }\mathit{z}=\frac{1}{\Omega }\sum _{i=1}^n{\lambda }_i{({\mathit{u}}_i^{\top }\mathit{z})}^2=\frac{1}{\Omega }\sum _{i=2}^n{\lambda }_i{\beta }_i^2.\end{array}$$

(29)

Recall that ${\alpha }_2,\dots ,{\alpha }_n$ in (28) (resp. ${\beta }_2,\dots ,{\beta }_n$ in (29)) are graph Fourier transform of $\mathit{y}$ (resp. $\mathit{z}$).

We summarize the properties obtained above in the following proposition.

Proposition 2.

(i) Let ${\theta }_i=\frac{{\lambda }_i}{\Omega }$ and ${\nu }_i=\frac{1}{n-1}$ for $i=2,\dots ,n$. Then, Geary’s c can be expressed using ${\alpha }_2^2,\dots ,{\alpha }_n^2$ as

$$\begin{array}{c}\hfill c=\frac{n-1}{\Omega }\frac{{\sum }_{i=2}^n{\lambda }_i{\alpha }_i^2}{{\sum }_{i=2}^n{\alpha }_i^2}=\frac{{\sum }_{i=2}^n{\theta }_i{\alpha }_i^2}{{\sum }_{i=2}^n{\nu }_i{\alpha }_i^2},\end{array}$$

(30)

where both ${\sum }_{i=2}^n{\theta }_i{\alpha }_i^2$ and ${\sum }_{i=2}^n{\nu }_i{\alpha }_i^2$ are weighted averages of ${\alpha }_2^2,\dots ,{\alpha }_n^2$. In addition, ${\alpha }_2^2,\dots ,{\alpha }_n^2$ satisfy

$$\begin{array}{c}\hfill \sum _{i=2}^n{\alpha }_i^2=\sum _{i=1}^n{(y_i-\overline{y})}^2.\end{array}$$

(31)

(ii) Let ${\theta }_i=\frac{{\lambda }_i}{\Omega }$ for $i=2,\dots ,n$. Then, Geary’s c can be expressed using ${\beta }_2^2,\dots ,{\beta }_n^2$ as

$$\begin{array}{c}\hfill c=\frac{1}{\Omega }\sum _{i=2}^n{\lambda }_i{\beta }_i^2=\sum _{i=2}^n{\theta }_i{\beta }_i^2\end{array}$$

(32)

and it is a weighted average of ${\beta }_2^2,\dots ,{\beta }_n^2$, which are non-negative. In addition, ${\beta }_2^2,\dots ,{\beta }_n^2$ satisfy

$$\begin{array}{c}\hfill \sum _{i=2}^n{\beta }_i^2=n-1.\end{array}$$

(33)

Proof. 

See the Appendix A.6. □

Remark 5.

(i) Given $0\le {\lambda }_2\le \cdots \le {\lambda }_n$, we have

$$\begin{array}{c}\hfill 0\le {\lambda }_2=\frac{{\sum }_{i=2}^n{\lambda }_2{\alpha }_i^2}{{\sum }_{i=2}^n{\alpha }_i^2}\le \frac{{\sum }_{i=2}^n{\lambda }_i{\alpha }_i^2}{{\sum }_{i=2}^n{\alpha }_i^2}\le \frac{{\sum }_{i=2}^n{\lambda }_n{\alpha }_i^2}{{\sum }_{i=2}^n{\alpha }_i^2}={\lambda }_n.\end{array}$$

(34)

Given (30), multiplying (34) by $\frac{n-1}{\Omega }>0$ yields

$$\begin{array}{c}\hfill 0\le \frac{(n-1){\lambda }_2}{\Omega }\le c\le \frac{(n-1){\lambda }_n}{\Omega }.\end{array}$$

(35)

We note that the bounds of Geary’s c given by (35) were derived by de Jong et al. [4]. In addition, given that ${\lambda }_2<{\lambda }_n$ by assumption, it follows that

$$\begin{array}{c}\hfill \frac{(n-1){\lambda }_2}{\Omega }<\frac{(n-1){\lambda }_n}{\Omega }.\end{array}$$

(36)

(ii) Let ${\theta }_1=\frac{{\lambda }_1}{\Omega }$. Then, given ${\theta }_1=0$, (32) can be rewritten as

$$\begin{array}{c}\hfill c=\frac{1}{\Omega }\sum _{i=1}^n{\lambda }_i{\beta }_i^2=\sum _{i=1}^n{\theta }_i{\beta }_i^2.\end{array}$$

(37)

Thus, c is also a weighted average of ${\beta }_1^2,\dots ,{\beta }_n^2$.

From Proposition 2, we have the following results.

Corollary 1.

It follows that

$$\begin{array}{c}\hfill c=\left\{\begin{array}{cc}\frac{(n-1){\lambda }_2}{\Omega }<1\hfill & \mathrm{if}{\alpha }_2^2={\sum }_{i=1}^n{(y_i-\overline{y})}^2\mathrm{and}{\alpha }_3^2=\cdots ={\alpha }_n^2=0,\hfill \\ \frac{{\sum }_{i=2}^n{\lambda }_i}{\Omega }=1\hfill & \mathrm{if}{\alpha }_2^2=\cdots ={\alpha }_n^2=s^2,\hfill \\ \frac{(n-1){\lambda }_n}{\Omega }>1\hfill & \mathrm{if}{\alpha }_2^2=\cdots ={\alpha }_{n-1}^2=0\mathrm{and}{\alpha }_n^2={\sum }_{i=1}^n{(y_i-\overline{y})}^2,\hfill \end{array}\right.\end{array}$$

and

$$\begin{array}{c}\hfill c=\left\{\begin{array}{cc}\frac{(n-1){\lambda }_2}{\Omega }<1\hfill & \mathrm{if}{\beta }_2^2=n-1\mathrm{and}{\beta }_3^2=\cdots ={\beta }_n^2=0,\hfill \\ \frac{{\sum }_{i=2}^n{\lambda }_i}{\Omega }=1\hfill & \mathrm{if}{\beta }_2^2=\cdots ={\beta }_n^2=1,\hfill \\ \frac{(n-1){\lambda }_n}{\Omega }>1\hfill & \mathrm{if}{\beta }_2^2=\cdots ={\beta }_{n-1}^2=0\mathrm{and}{\beta }_n^2=n-1.\hfill \end{array}\right.\end{array}$$

Proof. 

See the Appendix A.7. □

Corollary 1 implies that plotting $({\alpha }_2^2,\dots ,{\alpha }_n^2)$ or $({\beta }_2^2,\dots ,{\beta }_n^2)$ is valuable for detecting spatial autocorrelation in $\mathit{y}$.

3.3. Pearson’s Correlation Coefficient Representation

In this section, we express Geary’s c using Pearson’s correlation coefficient.

Denote Geary’s c for the case in which $\mathit{y}$ equals ${\mathit{u}}_i$ by ${\kappa }_i$:

$$\begin{array}{c}\hfill {\kappa }_i=\frac{n-1}{\Omega }\frac{{\mathit{u}}_i^{\top }\mathit{L}{\mathit{u}}_i}{{\mathit{u}}_i^{\top }{\mathit{Q}}_{\iota }{\mathit{u}}_i}.\end{array}$$

(38)

Then, we have the following results.

Lemma 2.

${\kappa }_i$ can be expressed using ${\lambda }_i$ as follows:

$$\begin{array}{c}\hfill {\kappa }_i=\frac{(n-1){\lambda }_i}{\Omega },i=2,\dots ,n,\end{array}$$

(39)

which thus satisfy ${\kappa }_2\le \cdots \le {\kappa }_n$ and ${\kappa }_2<{\kappa }_n$.

Proof. 

See the Appendix A.8. □

Remark 6.

Given (35) and (39), ${\kappa }_2$ (resp. ${\kappa }_n$) is the lower (resp. upper) bound of Geary’s c.

In addition, we have the following result.

Lemma 3.

$\rho ({\mathit{u}}_i,\mathit{y})$ equals $\rho ({\mathit{u}}_i,\mathit{z})$ for $i=2,\dots ,n$.

Proof. 

See the Appendix A.9. □

Then, given Lemmata 2 and 3, we have the following representation of Geary’s c.

Proposition 3.

For $\mathit{\upsilon }=\mathit{y},\mathit{z}$, Geary’s c can be expressed using Pearson’s correlation coefficients as

$$\begin{array}{c}\hfill c=\sum _{i=2}^n{\kappa }_i·{\rho }^2({\mathit{u}}_i,\mathit{\upsilon }).\end{array}$$

(40)

In addition, such correlation coefficients satisfy ${\sum }_{i=2}^n{\rho }^2({\mathit{u}}_i,\mathit{\upsilon })=1$.

Proof. 

See the Appendix A.10. □

Remark 7.

Dray [21] represented Moran’s I using Pearson’s correlation coefficient. $c={\sum }_{i=2}^n{\kappa }_i·{\rho }^2({\mathit{u}}_i,\mathit{z})$ in Proposition 3 corresponds to Dray [21] (Equation (6)).

From Proposition 3, we have the following results.

Corollary 2.

For $\mathit{\upsilon }=\mathit{y},\mathit{z}$, it follows that

$$\begin{array}{c}\hfill c=\left\{\begin{array}{cc}\frac{(n-1){\lambda }_2}{\Omega }<1\hfill & \mathrm{if}{\rho }^2({\mathit{u}}_2,\mathit{\upsilon })=1\mathit{and}{\rho }^2({\mathit{u}}_3,\mathit{\upsilon })=\cdots ={\rho }^2({\mathit{u}}_n,\mathit{\upsilon })=0,\hfill \\ \frac{{\sum }_{i=2}^n{\lambda }_i}{\Omega }=1\hfill & \mathrm{if}{\rho }^2({\mathit{u}}_2,\mathit{\upsilon })=\cdots ={\rho }^2({\mathit{u}}_n,\mathit{\upsilon })=\frac{1}{n-1},\hfill \\ \frac{(n-1){\lambda }_n}{\Omega }>1\hfill & \mathrm{if}{\rho }^2({\mathit{u}}_2,\mathit{\upsilon })=\cdots ={\rho }^2({\mathit{u}}_{n-1},\mathit{\upsilon })=0\mathit{and}{\rho }^2({\mathit{u}}_n,\mathit{\upsilon })=1.\hfill \end{array}\right.\end{array}$$

Corollary 2 implies that plotting $({\rho }^2({\mathit{u}}_2,\mathit{y}),\dots ,{\rho }^2({\mathit{u}}_n,\mathit{y}))$ is also valuable for detecting spatial autocorrelation in $\mathit{y}$.

3.4. Some Remarks

Here, we clarify the relationship between ${\alpha }_i^2$, ${\beta }_i^2$, and ${\rho }^2({\mathit{u}}_i,\mathit{y})$ for $i=2,\dots ,n$. They are related as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\alpha }_i^2=\sum _{i=1}^n{(y_i-\overline{y})}^2·{\rho }^2({\mathit{u}}_i,\mathit{y})=s^2(n-1)·{\rho }^2({\mathit{u}}_i,\mathit{y}),\hfill \\ {\beta }_i^2=(n-1)·{\rho }^2({\mathit{u}}_i,\mathit{y}),\hfill \\ {\alpha }_i^2=s^2{\beta }_i^2,\hfill \end{array}\right.\end{array}$$

(41)

for $i=2,\dots ,n$. Therefore, ${\alpha }_i^2$, ${\beta }_i^2$, and ${\rho }^2({\mathit{u}}_i,\mathit{y})$ provide essentially the same information. Nevertheless, among them, we prefer ${\rho }^2({\mathit{u}}_i,\mathit{y})$ to ${\alpha }_i^2$ and ${\beta }_i^2$. This is because it satisfies

$$\begin{array}{c}0\le {\rho }^2({\mathit{u}}_i,\mathit{y})\le 1,i=2,\dots ,n,\end{array}$$

(42)

$$\begin{array}{c}\sum _{i=2}^n{\rho }^2({\mathit{u}}_i,\mathit{y})=1,\end{array}$$

(43)

and thus its distribution appears similar to probability distribution.

We note that (16) is obtainable by dividing (11) by ${\sum }_{i=1}^n{(y_i-\overline{y})}^2$, and therefore it is equivalent to Parseval’s identity in the graph Fourier transform in (11). Likewise, (33) is also equivalent to it. This is because (33) is obtainable by dividing (11) by $s^2$.

4. An Illustration of When Geary’s $\mathit{c}$ Becomes Greater or Lesser Than One

In this section, we illustrate that Geary’s c becomes greater (resp. lesser) than one if spatially smoother (resp. less smooth) graph Laplacian eigenvectors are dominant. In other words, we show that the spatial autocorrelation measured by Geary’s c is positive (resp. negative) if spatially smoother (resp. less smooth) graph Laplacian eigenvectors are dominant. Recall that, from (22), ${\mathit{u}}_i$ is spatially smoother than ${\mathit{u}}_{i+1}$ for $i=1,\dots ,n-1$.

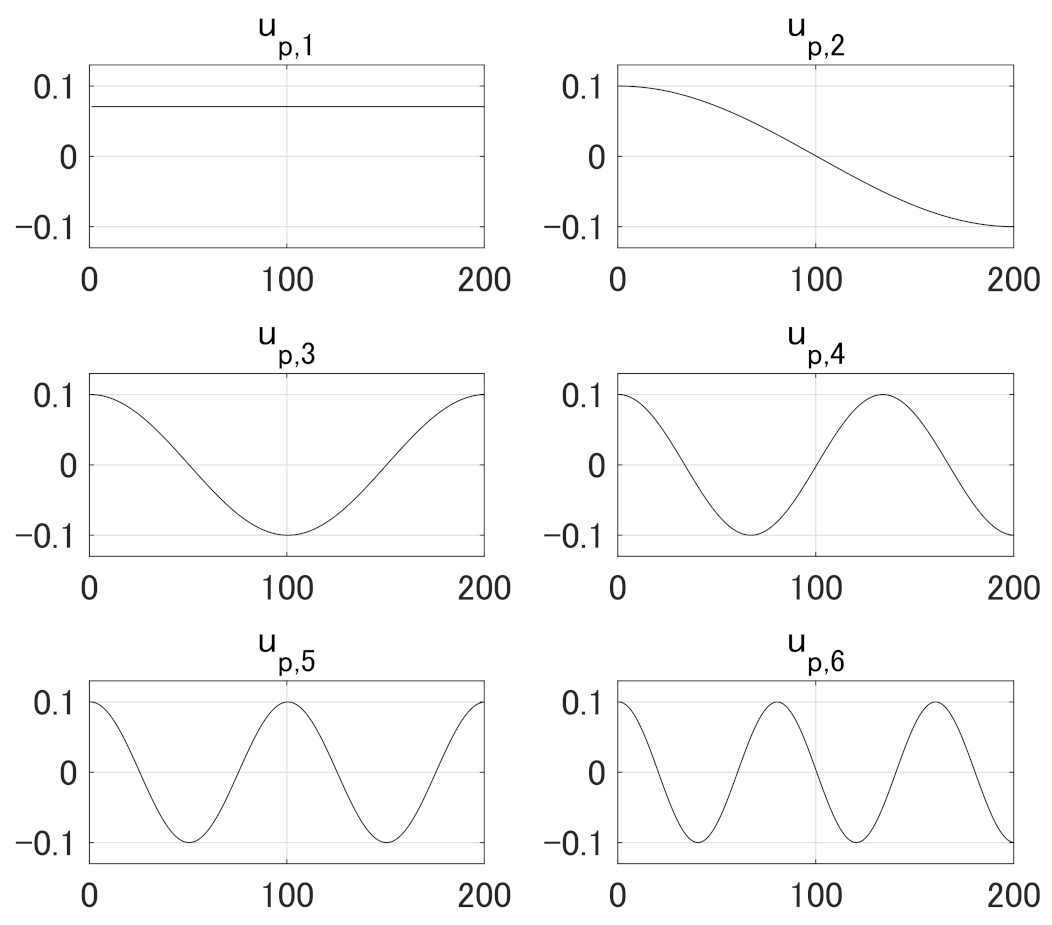
For this purpose, let

$$\begin{array}{c}\hfill {\zeta }_i=\frac{exp(-ai)}{\sqrt{{\sum }_{l=2}^{n}exp(-2al)}},i=2,\dots ,n,\end{array}$$

(44)

where a in (44) is a real number. Then, it immediately follows that

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\zeta }_2>\cdots >{\zeta }_n>0\hfill & \mathrm{if}a>0,\hfill \\ {\zeta }_2=\cdots ={\zeta }_n=\frac{1}{\sqrt{n-1}}>0\hfill & \mathrm{if}a=0,\hfill \\ 0<{\zeta }_2<\cdots <{\zeta }_n\hfill & \mathrm{if}a<0,\hfill \end{array}\right.\end{array}$$

(45)

and

$$\begin{array}{c}\hfill \sum _{i=2}^n{\zeta }_i^2=1.\end{array}$$

(46)

Other than these, concerning ${\zeta }_2,\dots ,{\zeta }_n$, we have the following results.

Lemma 4.

It follows that

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\zeta }_2\to 1\mathit{and}{\zeta }_i\to 0\mathit{for}i=3,\dots ,n\mathit{as}a\to \infty ,\hfill \\ {\zeta }_i\to 0\mathit{for}i=2,\dots ,n-1\mathit{and}{\zeta }_n\to 1\mathit{as}a\to -\infty .\hfill \end{array}\right.\end{array}$$

Proof. 

See the Appendix A.11. □

Figure 2 illustrates the results in Lemma 4. It plots ${\zeta }_2,\dots ,{\zeta }_n$ for $n=20$ and $a=3,1.5,0.5,0,-0.5,-1.5,-3$.

Let

$$\begin{array}{c}\hfill {\mathit{y}}_{*}\left(={[y_{*,1},\dots ,y_{*,n}]}^{\top }\right)=\mathit{U}\mathit{\zeta }={\zeta }_1{\mathit{u}}_1+\cdots +{\zeta }_n{\mathit{u}}_n,\end{array}$$

(47)

where $\mathit{\zeta }={[{\zeta }_1,\dots ,{\zeta }_n]}^{\top }$. Here, ${\zeta }_1$ is a real number, and ${\zeta }_i$ for $i=2,\dots ,n$ are defined in (44). Recall that $\{{\mathit{u}}_1,\dots ,{\mathit{u}}_n\}$ is a basis of n-dimensional Euclidean space, and any vector in the space can be represented uniquely as a linear combination of ${\mathit{u}}_1,\dots ,{\mathit{u}}_n$. In addition, we note that if ${\zeta }_i={\mathit{u}}_i^{\top }\mathit{y}(={\alpha }_i)$ for $i=1,\dots ,n$, then ${\mathit{y}}_{*}=\mathit{y}$. See (10).

Given the results presented above on ${\zeta }_2,\dots ,{\zeta }_n$ and the definition of ${\mathit{y}}_{*}$, we have the following results.

Proposition 4.

(i) c $\parallel {\mathit{B}}^{\top }{\mathit{y}}_{*}{\parallel }^2={\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{ij}{(y_{*,i}-y_{*,j})}^2$ can be represented as

$$\begin{array}{ccc}\parallel {\mathit{B}}^{\top }{\mathit{y}}_{*}{\parallel }^2& =& {\zeta }_2^2{\lambda }_2+\cdots +{\zeta }_n^2{\lambda }_n\end{array}$$

(48)

$$\begin{array}{ccc}& =& {\zeta }_2^2\parallel {\mathit{B}}^{\top }{\mathit{u}}_2{\parallel }^2+\cdots +{\zeta }_n^2{\parallel {\mathit{B}}^{\top }{\mathit{u}}_n\parallel }^2.\end{array}$$

(49)

(ii) $\parallel {\mathit{B}}^{\top }{\mathit{y}}_{*}{\parallel }^2$ satisfies the following inequalities:

$$\begin{array}{c}\hfill 0\le {\lambda }_2<{\parallel {\mathit{B}}^{\top }{\mathit{y}}_{*}\parallel }^2<{\lambda }_n.\end{array}$$

(50)

(iii) $\parallel {\mathit{B}}^{\top }{\mathit{y}}_{*}{\parallel }^2$ depends on a in (44) as

$$\begin{array}{c}\hfill \parallel {\mathit{B}}^{\top }{\mathit{y}}_{*}{\parallel }^2\left\{\begin{array}{cc}\to {\lambda }_2={\parallel {\mathit{B}}^{\top }{\mathit{u}}_2\parallel }^2\hfill & \mathrm{as}a\to \infty ,\hfill \\ =\frac{1}{n-1}\sum _{i=2}^n{\lambda }_i=\frac{1}{n-1}\sum _{i=2}^n{\parallel {\mathit{B}}^{\top }{\mathit{u}}_i\parallel }^2\hfill & \mathrm{if}a=0,\hfill \\ \to {\lambda }_n={\parallel {\mathit{B}}^{\top }{\mathit{u}}_n\parallel }^2\hfill & \mathrm{as}a\to -\infty .\hfill \end{array}\right.\end{array}$$

(51)

Proof. 

See the Appendix A.12. □

(i)

Recall that ${\lambda }_2$ (resp. ${\lambda }_n$) denotes the minimum (resp. maximum) of the graph Laplacian eigenvalues, ${\lambda }_2,\dots ,{\lambda }_n$, and $\frac{1}{n-1}{\sum }_{i=2}^n{\lambda }_i$ is the average of them. In addition, from (7), it follows that

$$\begin{array}{c}\hfill 0\le {\lambda }_2<\frac{1}{n-1}\sum _{i=2}^n{\lambda }_i<{\lambda }_n.\end{array}$$

(ii)

Lemma 4 and Proposition 4 imply that

(a)

as a increases from 0 to ∞, spatially smoother graph Laplacian eigenvectors become more dominant, and accordingly ${\mathit{y}}_{*}$ becomes spatially smoother;

(b)

as a decreases from 0 to $-\infty$, spatially less smooth graph Laplacian eigenvectors become more dominant, and accordingly ${\mathit{y}}_{*}$ becomes less spatially smoother; and

(c)

if a equals 0, then all graph Laplacian eigenvectors contribute to ${\mathit{y}}_{*}$ equally.

Let

$$\begin{array}{c}\hfill c_{*}=\frac{n-1}{2\Omega }\frac{{\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{ij}{(y_{*,i}-y_{*,j})}^2}{{\sum }_{i=1}^n{(y_{*,i}-{\overline{y}}_{*})}^2}=\frac{n-1}{\Omega }\frac{{\mathit{y}}_{*}^{\top }\mathit{L}{\mathit{y}}_{*}}{{\mathit{y}}_{*}^{\top }{\mathit{Q}}_{\iota }{\mathit{y}}_{*}},\end{array}$$

(52)

where ${\overline{y}}_{*}=\frac{1}{n}{\sum }_{i=1}^n{y}_{*,i}$. Note that $c_{*}$ represents Geary’s c for ${\mathit{y}}_{*}$ defined in (47).

Then, we have the following results.

Proposition 5.

(i) $c_{*}$ in (52) can be represented as follows:

$$\begin{array}{cc}\hfill c_{*}& =\frac{n-1}{2\Omega }\sum _{i=1}^n\sum _{j=1}^n{w}_{ij}{(y_{*,i}-y_{*,j})}^2\end{array}$$

(53)

$$\begin{array}{cc}& =\frac{n-1}{\Omega }({\zeta }_2^2{\lambda }_2+\cdots +{\zeta }_n^2{\lambda }_n)\end{array}$$

(54)

$$\begin{array}{cc}& =\frac{n-1}{\Omega }({\zeta }_2^2\parallel {\mathit{B}}^{\top }{\mathit{u}}_2{\parallel }^2+\cdots +{\zeta }_n^2\parallel {\mathit{B}}^{\top }{\mathit{u}}_n{\parallel }^2).\end{array}$$

(55)

(ii) $c_{*}$ satisfies the following inequalities:

$$\begin{array}{c}\hfill 0\le \frac{(n-1){\lambda }_2}{\Omega }<c_{*}<\frac{(n-1){\lambda }_n}{\Omega }.\end{array}$$

(56)

(iii) $c_{*}$ depends on a in (44) as

$$\begin{array}{c}\hfill c_{*}\left\{\begin{array}{cc}\to \frac{(n-1){\lambda }_2}{\Omega }=\frac{n-1}{\Omega }{\parallel {\mathit{B}}^{\top }{\mathit{u}}_2\parallel }^2<1\hfill & \mathrm{as}a\to \infty ,\hfill \\ =\frac{{\sum }_{i=2}^n{\lambda }_i}{\Omega }=\frac{n-1}{\Omega }\frac{1}{n-1}\sum _{i=2}^n{\parallel {\mathit{B}}^{\top }{\mathit{u}}_i\parallel }^2=1\hfill & \mathrm{if}a=0,\hfill \\ \to \frac{(n-1){\lambda }_n}{\Omega }=\frac{n-1}{\Omega }{\parallel {\mathit{B}}^{\top }{\mathit{u}}_n\parallel }^2>1\hfill & \mathrm{as}a\to -\infty .\hfill \end{array}\right.\end{array}$$

(57)

Proof. 

See the Appendix A.13. □

Remark 8.

(i) From (54), it follows that ${\zeta }_1$ does not affect $c_{*}$. (ii) Given that ${\zeta }_i^2>0$ for $i=2,\dots ,n$ and ${\sum }_{i=2}^n{\zeta }_i^2=1$, ${\zeta }_2^2{\lambda }_2+\cdots +{\zeta }_n^2{\lambda }_n$ in (47) is a weighted average of the graph Laplacian eigenvalues, ${\lambda }_2,\dots ,{\lambda }_n$.

By combining Lemma 4 and Proposition 5, it follows that (i) as a increases from 0 to ∞, spatially smoother graph Laplacian eigenvectors become more dominant, and accordingly the corresponding Geary’s c tends to $\frac{(n-1){\lambda }_2}{\Omega }(={\kappa }_2)$, which is its lower bound; (ii) as a decreases from 0 to $-\infty$, spatially less smooth graph Laplacian eigenvectors become more dominant, and accordingly the corresponding Geary’s c tends to $\frac{(n-1){\lambda }_n}{\Omega }(={\kappa }_n)$, which is its upper bound; and (iii) if a equals 0, then all graph Laplacian eigenvectors contribute to ${\mathit{y}}_{*}$ equally, and the corresponding Geary’s c equals 1.

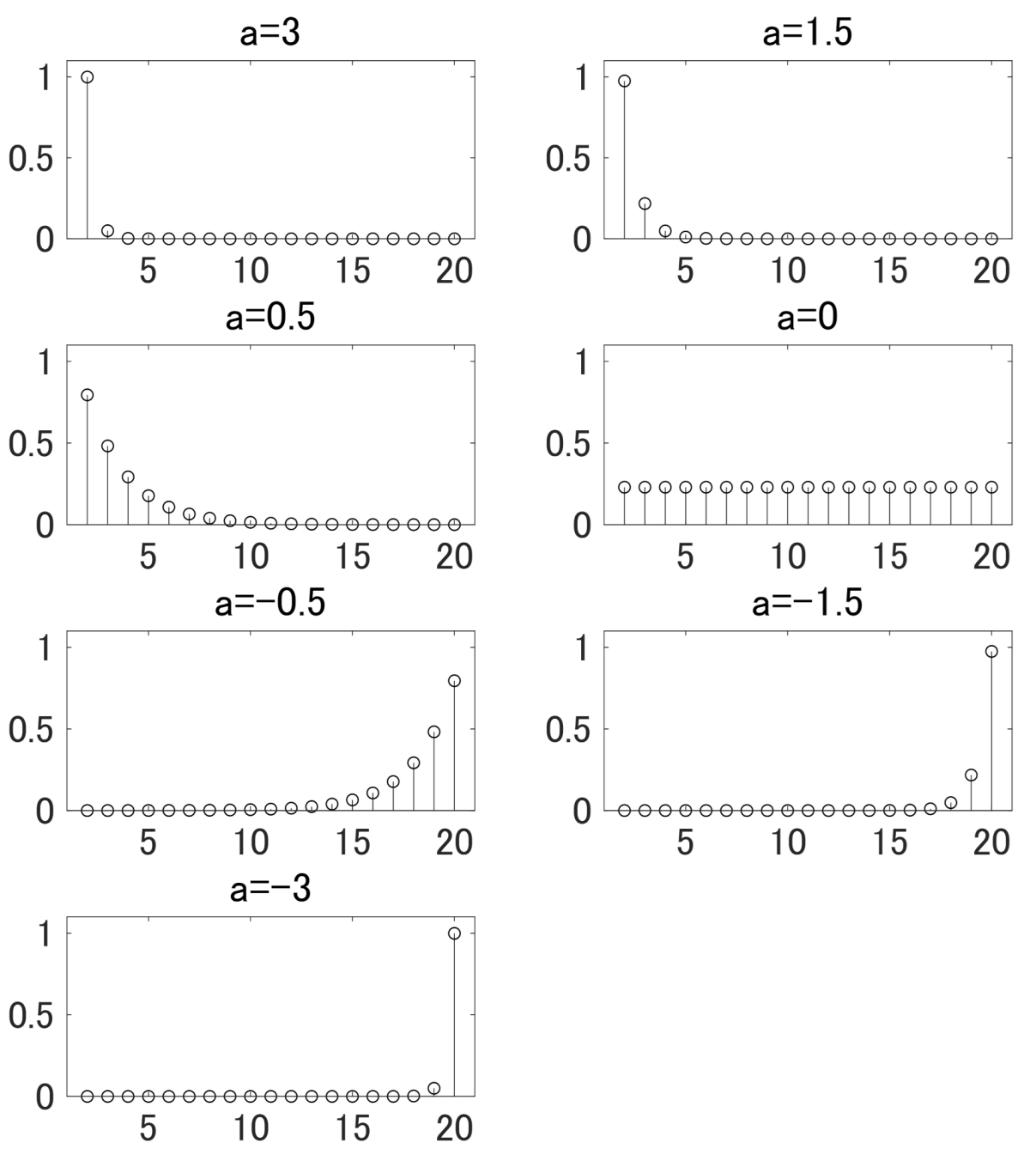
Let us illustrate Propositions 4 and 5 by specifying $\mathit{W}$. We consider three $\mathit{W}$’s. The first one is ${\mathit{W}}_{†}$ in (2) with $w_{12}=1$, $w_{13}=0.5$, $w_{23}=1$, and $w_{34}=1$. As stated, ${\mathit{W}}_{†}$ is a non-negative, symmetric, hollow, and nonzero matrix. The second one is

$$\begin{array}{c}\hfill {\mathit{W}}_p=\left[\begin{array}{ccccc}\hfill 0& \hfill 1& \hfill 0& \hfill \cdots & \hfill 0\\ \hfill 1& \hfill 0& \hfill 1& \hfill \ddots & \hfill ⋮\\ \hfill 0& \hfill \ddots & \hfill \ddots & \hfill \ddots & \hfill 0\\ \hfill ⋮& \hfill \ddots & \hfill 1& \hfill 0& \hfill 1\\ \hfill 0& \hfill \cdots & \hfill 0& \hfill 1& \hfill 0\end{array}\right]\in {\mathbb{R}}^{n\times n},\end{array}$$

(58)

where $n=20$. This matrix is the adjacency matrix of a path graph $G_p=(V_p,E_p)$ such that $V_p=\{1,\dots ,n\}$ and $E_p=\{\{1,2\},\dots ,\{n-1,n\}\}$. See Figure A1, which depicts $G_p=(V_p,E_p)$ where $n=6$. Observe that it is a non-negative, symmetric, hollow, and nonzero matrix. Some remarks on ${\mathit{W}}_p$ are provided in the Appendix A.14. The third one is ${\mathit{W}}_q$ shown in heatmap style in Figure A2. As shown in the figure, ${\mathit{W}}_q$ is also a nonnegative, symmetric, hollow, and nonzero matrix.

Table 1. Spatial smoothness and Geary’s c.

		${\mathit{W}}_{†}$			${\mathit{W}}_{\mathit{p}}$			${\mathit{W}}_{\mathit{q}}$
$\mathit{a}$		$\parallel {\mathit{B}}^{\top }{\mathit{y}}_{*}{\parallel }^2$	${\mathit{c}}_{*}$		$\parallel {\mathit{B}}^{\top }{\mathit{y}}_{*}{\parallel }^{\mathbf{2}}$	${\mathit{c}}_{*}$		$\parallel {\mathit{B}}^{\top }{\mathit{y}}_{*}{\parallel }^{\mathbf{2}}$	${\mathit{c}}_{*}$
LB		$0.8754$	$0.3752$		$0.0246$	$0.0123$		$1.7174$	$0.2334$
$3.0$		$0.8796$	$0.3770$		$0.0248$	$0.0124$		$1.7237$	$0.2343$
$2.5$		$0.8869$	$0.3801$		$0.0251$	$0.0126$		$1.7346$	$0.2357$
$2.0$		$0.9068$	$0.3886$		$0.0260$	$0.0130$		$1.7642$	$0.2398$
$1.5$		$0.9621$	$0.4123$		$0.0286$	$0.0143$		$1.8463$	$0.2509$
$1.0$		$1.1171$	$0.4787$		$0.0372$	$0.0186$		$2.0809$	$0.2828$
$0.5$		$1.5318$	$0.6565$		$0.0824$	$0.0412$		$2.8242$	$0.3838$
$0.0$		$2.3333$	$1.0000$		$2.0000$	$1.0000$		$7.3579$	$1.0000$
$-0.5$		$3.0711$	$1.3162$		$3.9176$	$1.9588$		$9.8861$	$1.3436$
$-1.0$		$3.3941$	$1.4546$		$3.9628$	$1.9814$		$9.9926$	$1.3581$
$-1.5$		$3.4988$	$1.4995$		$3.9714$	$1.9857$		$10.0142$	$1.3610$
$-2.0$		$3.5329$	$1.5141$		$3.9740$	$1.9870$		$10.0203$	$1.3618$
$-2.5$		$3.5447$	$1.5192$		$3.9749$	$1.9874$		$10.0222$	$1.3621$
$-3.0$		$3.5490$	$1.5210$		$3.9752$	$1.9876$		$10.0229$	$1.3622$
UB		$3.5514$	$1.5220$		$3.9754$	$1.9877$		$10.0233$	$1.3623$

Note: LB and UB, respectively, represent lower bound and upper bound of $\parallel {\mathit{B}}^{\top }{\mathit{y}}_{*}{\parallel }^2$ (resp. $c_{*}$) given by (50) (resp. (56)).

tabulates the results. LB and UB, respectively, represent lower bound and upper bound of $\parallel {\mathit{B}}^{\top }{\mathit{y}}_{*}{\parallel }^2$ (resp. $c_{*}$) given by (50) (resp. (56)). From the table, we can confirm that these results clearly illustrate Propositions 4 and 5. That is to say, for all $\mathit{W}$’s, we can observe that as a increases from 0 to 3 (resp. decreases from 0 to $-3$), ${\mathit{y}}_{*}$ becomes spatially smoother (resp. less smoother), and Geary’s c tends to $\frac{(n-1){\lambda }_2}{\Omega }$ (resp. $\frac{(n-1){\lambda }_n}{\Omega }$).

Remark 9.

(i) If $\mathit{W}={\mathit{W}}_{†}$, then $\frac{n-1}{\Omega }$ equals $\frac{3}{7}$. Thus, if $\mathit{W}={\mathit{W}}_{†}$, then it follows that $c_{*}=\frac{3}{7}{\parallel {\mathit{B}}^{\top }{\mathit{y}}_{*}\parallel }^2$. (ii) If $\mathit{W}={\mathit{W}}_p$, then $\frac{n-1}{\Omega }$ equals $\frac{1}{2}$. Thus, if $\mathit{W}={\mathit{W}}_p$, then it follows that $c_{*}=\frac{1}{2}{\parallel {\mathit{B}}^{\top }{\mathit{y}}_{*}\parallel }^2$. (iii) If $\mathit{W}={\mathit{W}}_q$, then $\frac{n-1}{\Omega }$ equals $\frac{19}{139.8}$. Thus, if $\mathit{W}={\mathit{W}}_q$, then it follows that $c_{*}=\frac{19}{139.8}{\parallel {\mathit{B}}^{\top }{\mathit{y}}_{*}\parallel }^2$.

5. Concluding Remarks

Herein, we have provided a new perspective on Geary’s c. We reconsidered it using concepts from spectral graph theory/linear algebraic graph theory.

First, we demonstrated three types of representations for it. The first is expressions based on graph Laplacian (Proposition 1), the second is expressions based on graph Fourier transform (Proposition 2), and the third is an expression based on Pearson’s correlation coefficient (Proposition 3).

Second, we illustrated that the spatial autocorrelation measured by Geary’s c is positive (resp. negative) if spatially smoother (resp. less smooth) graph Laplacian eigenvectors are dominant (Propositions 4 and 5 and Table 1).

In closing, based on our analysis, we provide a recommendation for applied studies: For detecting spatial autocorrelation, in addition to calculating Geary’s c, plotting ${\rho }^2({\mathit{u}}_i,\mathit{y})$, which is the squared Pearson’s correlation coefficient between ${\mathit{u}}_i$ and $\mathit{y}$, for $i=2,\dots ,n$ is valuable (see Section 3.4 for a related discussion). This is because

it provides more detailed information on spatial autocorrelation measured by Geary’s c. Its usefulness is similar to frequency domain analysis of univariate time series.